1 Introduction

Slope instabilities are among the frequent geo-environmental hazard that occurs mostly in mountainous and hilly regions of the world. Thus, more attention has been paid for many years to consider and solve the slope instability problems [1]. The slope of road constructed across the mountainous regions faces slope instability mainly during construction and modification of the road [2]. Many geotechnical engineers and engineering geologists have conducted several studies on slope stability analyses. Nevertheless, slope instability problems repeatedly occur due to human and natural disturbance to the delicate nature of the soil and rock slope [3]. Thus, slope design and stability analyses should be given deliberate attention by the design engineers above all during the slope cut and modification.

Most of the time, the possible occurrence of rock slope failure is high due to the combined effect of rock discontinuity, slope geometry, and factors which saturate the slope [4, 5]. Added, the geometry of the slope, failure plane orientation, surface, and groundwater conditions are the main internal governing factors while human activities, seismicity, and rainfall are the external governing factors [6, 7]. Rock slope instability occurs mostly in the form of planar, wedge, and toppling modes of failure [4, 8, 9]. With respect to the hard rock, the failure commonly occurs along the discontinuity planes [1, 4, 10]. Similarly, unevenly oriented discontinuities in a rock mass can cause slope instability along with the road cut [11]. The rock-cut failure is deeply associated with extreme rainfall and the occurrence of major tectonic faults or small-scale discontinuities [5]. Likewise, external factors like intense rainfall and seismic activity most commonly trigger slope failure and landslide in the mountainous region [5, 7, 12, 13]. The seismic response of the P wave can cause the differential agreement to occur at the surface slope while the S wave can bring horizontal deformation of the slope. In the same way, the deformation of the surface slope for the most part between high and low water levels was influenced by rapid water drawdown [14]. In addition, this seismic response between the slipping mass and slip bed of the rock is the main triggering factor of landslide [15].

Rock slope stability analyses can be undertaken through a two-step process [16]. The first step is evaluating kinematic analyses to determine the mode of rock slope failure followed by determining factor of safety most commonly through limit equilibrium methods (LEM). The kinematic method deals with the failure mode of the rock slope without reference to the forces that cause them to move [1, 8, 16], whereas the limit equilibrium method (LEM) determines the stability of the slope by evaluating the factor of safety which is the ratio of resisting force to driving force along failure plane [13, 17]. The cohesion and friction angle are the main component of resisting force along the failure plane [4, 7], and they can be determined either by the law of basic friction angle [18], empirical methods [19], and back analysis [20]. However, this study uses the Rocscience software to determine cohesion and friction angle along the failure plane and then execute the factor of safety through limit equilibrium methods.

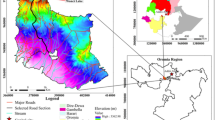
Besides, maintenance and serviceability of the road network in Ethiopia were regularly affected by slope instability [21]. Most of the north, south, and western regions of the Ethiopian plateau face a record of slope instability both in superficial materials and bedrocks due to the cutting of hills and roadsides [22]. As a result, landslide hazards and slope instability have been causing loss of lives, failures on engineering structures, damage to agricultural lands, and the natural environment [23]. Moreover, active slopes and landslide generated problems are found almost in all parts and especially in the highland part of Ethiopia. Consequently, over 100 km asphalt road was damaged, about 300 lives were claimed and demolished more than 200 dwelling houses, and 500 ha of land in the past decade [22]. The present study area was also found in the western part of Ethiopian highland where slope instability was one of the critical problems (Fig. 1). Thus, different slope instability problems like rock slope failure in the form of planar, wedge, and rockfall were encountered along the road section and then caused damage on the road and natural environment mainly during the rainy season. Hence, it is essential to assess and evaluates slope instability problems along these road sections. Though the impact of deformation on the stability of the identified critical slope was not taken into an account, the study aimed to determine the stability of rock slope along selected road sections through kinematic analyses that identify the mode of the rock slope failure and then followed by limit equilibrium method (LEM) that evaluates the factor of safety under different anticipated conditions. Both kinematic and limit equilibrium methods were executed using different Rocscience software packages. The quality of the rock which composes the identified critical slope sections was determined using a basic rock mass rating system [19].

Fig. 1
figure 1

Location of the study area. a Geological map of the study area. Source: Solomon and Mulgeta (2000) unpublished research work. b Location of critical rock slope section along the road

Full size image

2 Literature review

Different types of techniques were applied to analyze the stability of the slope and they were broadly classified as conventional analytic and numerical methods [7]. Among that, limit equilibrium methods are one of the oldest and simplest conventional analytic methods used to hastily determine the stability of the slope in terms of factor of safety [24]. As stated in [17], comparative results among different methods for analyses of uncomplicated slope stability problems give a similar result. Hence, limit equilibrium methods are the most preferable method to evaluate slope with uniform geometry and homogeneous geologic materials [7]. Moreover, input parameters used to analyze the stability of the slope in limit equilibrium methods can be easily obtained than the parameters used in numerical methods of analysis [17]. Even though it is a time-consuming, the numerical method is a suitable over-limit equilibrium method to analyze instability problems of the slope with complex geometry by considering stress and strain impact on the slope [17]. Because the slope geometry of the study area is not as much as complex, this study used the limit equilibrium method to analyze the stability of the identified critical slope sections. Among the input parameters used in the limit equilibrium methods, determining shear strength parameters along the failure plane is intricate to some extent [20]. Moreover, where there are no available core data, shear strength parameters along failure plane or joint surface can be determined through empirical law of basic friction angle [25] which is stated in (Eq. 9). In addition, [20] determine friction angle along failure plane from tan inverse (tan-1) of (Eq. 9) and that of cohesion using back analysis. And, back analysis can determine shear strength parameters of the sheared block by defining one unknown value and then calculating the second value based on the factor of safety one [26]. This study also determines shear strength parameters (both cohesion and friction angle) along the failure plane using (Eq. 9) which is built-in Rocdata software [27]. The rest input parameters such as slope geometry, conditions, and orientations of the joint set, and the slope can be determined in the field [28] and this paper also evaluates them based on the procedure outlined in [29]. Subsequently, the factor of safety (FS) for the planar mode of failure (Eq. 1) is the ratios of all forces which resist sliding to the total force which intends to induce sliding [2, 4].

$$Fs = \frac{{c*A [ \left( {W\left( {cos\psi p{-}\alpha *sin\psi p} \right) - U - V*sin\psi p} \right]tan\phi }}{{W\left( {sin\psi p + \alpha *cos\psi p} \right) + V*{\text{ cos}}\psi p}}$$
(1)

where \(c\) is the cohesion and \(\phi\) the friction along the failure plane, ψp is the failure plane dip, A is the base area of a wedge, \(U\) is the water forces acting on the failure plane, \(V\) the water pressure applied to tension crack, W is the weight of rock wedges that rest on failure plane, \(\alpha\) is the earthquake horizontal acceleration. According to [4, 10], water forces (\(W\)) which act at the mid-height of a failure plane and water pressure (\(V\)) applied to tension crack can be determined using (Eq. 2) and (Eq. 3), respectively.

$$U = \frac{\gamma w * Zw * A}{2}$$
(2)
$$V = \frac{\gamma w * Zw2* \cos \sec \psi p}{2}$$
(3)

where Zw is the slope height, γw unit weight of the water.

The factor of safety of wedge mode of failure was commonly determined by equation (Eq. 4) stated in [2, 4, 30]. The equation (Eq. 4) was also developed and built in the Swedge software. Thus, this study evaluated the factor of safety for wedge mode of failure using the Swedge software.

$$Fs = \frac{3}{\gamma * H}(cA*X + cB *) + (A - \frac{{{\gamma w}}}{2\gamma }*{\text{ X }})\tan \phi A + (B - \frac{{{\gamma w}}}{2\gamma }*{\text{ Y)tan}}\phi {\text{B}}$$
(4)

where \(cA\) and \(cB\) are the cohesive strength of plane \(A\) and \(B\), ϕA and ϕB are the friction angle of plane \(A\) and \(B\), \(\gamma\) the unit weight of the rock, γW the unit weight of the water, \(H\) is the total weight of the wedge, \(X\), \(Y\), \(A\) and \(B\) are dimensionless factors which depend on the geometry of the wedge.

If a particular slope is unstable (factor of safety less than one), it is necessary to stabilize the slope either by drainage or installation of remedial measures like rock bolts [4]. The equation (Eq. 5) stated in [4, 10, 31] can estimate the factor of safety due to the installed rock bolt.

$$Fs = \frac{{ c*A + \left[ { W \left( { cos\psi p - \alpha *sin\psi p } \right){-} U {-} V * sin\psi p + T * sin\theta } \right]tan\phi }}{{W \left( { sin\psi p + \alpha * cos\psi p } \right) + V * \cos \psi p {-} T * cos\theta }}$$
(5)

where \(\theta\) is an angle (deg) of rock bolt inclined to failure plane, \(T\) is rock bolt capacity in ton and the rest parameters were defined in equation (Eq. 4).

Furthermore, Eqs. 1–5 stated above were developed in Rocscience [31, 32]. Thus, this paper employs Rocscience software packages like Rocplane and Swedge to instantly and effortlessly evaluate the factor of safety through the limit equilibrium method and design suitable and possible remedial measures.

3 Description of the study area

3.1 Location and climate conditions

The study area occurs in Oromia regional state, western Ethiopia, Fig. 1a. It falls between 9° 37′ 56"N to 9° 49′ 31" N latitudes and 37° 17′ 50" E to 37° 28′ 44" E longitudes. The altitude ranges from 2432 to 600 m above mean sea level. The sugar produced at the Fincha sugar factory is transported to a different part of the country using this road (Fig. 1b). However, the road is subject to a different mode of failure that causes several forms of damages on the road. This road failure later causes many traffic incidences. Rainfall of the study area exhibits seasonal variation with minimum and maximum mean monthly rainfall of 16 and 322 mm, respectively. The highest rainfall that occurs during the summer season brought several rock slope failures. From field manifestations, slope instability in the study area occurs for the most part in the months of heavy rainfall (July to September). Furthermore, the lowest rainfall recorded during the winter season causes fewer slope failures.

3.2 Geology of the area

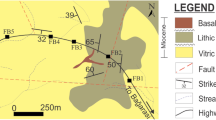
In Ethiopia geological history records millions of years with the major geological units such as Precambrian, Paleozoic sedimentary rock, Mesozoic sedimentary rock, Cenozoic rocks which include tertiary to quaternary volcanic and quaternary sediments [33]. According to Solomon and Mulgeta (2000) unpublished research work, Precambrian Proterozoic rock, Paleozoic sandstone, Mesozoic sandstone, and Cenozoic tertiary lower volcanic rocks occur in the study area, Fig. 1a. The road passes through three different rock units such as weakly foliated metagranite with strong strength, Paleozoic sandstone with medium strength, and that overlaid the metagranite, weak strength Mesozoic sandstone, and residual soil (Fig. 1b). The Mesozoic sandstone is found in the uppermost of the area which forms cliffs. It exhibits a gray to red color and at someplace it is found intercalated with gray mudstone. It is also highly fractured rock where several closely to widely spaced, small to non-persistent, open to filled, steeply to gently dipping joint sets were found over the exposed rock slope face.

The road was subjected to slope instability mainly in the Mesozoic sandstone unit. Geological structures like lineaments with an orientation of NNE, NNW, and N-S were found in the region. The minimum magnitude of the earthquake that can cause rock fall is approximately 4-5 M [5]. The horizontal seismic acceleration is one of the forces which add to the driving force along the failure plane and that can destabilize the planar mode of the rock the slope failures [7]. Thus, from the seismic risk map of Ethiopia [34], the study area falls within the seismic zone having a 7MM intensity scale and 0.08 g horizontal seismic acceleration. Hence, the dynamic loading condition of the study area was considered for stability analysis.

4 Methodology

A detailed field survey, data processing, and stability analysis methods were employed to fulfill the main objective of the study.

4.1 Detailed field survey

The geological structures, types of lithologies, in situ strength of the rocks, and groundwater conditions of the slopes were measured and estimated during a detailed field survey. Based on the field manifestation such as; removal of slope toe, development of tension cracks, bulging of slope face, and adversely oriented discontinuity that favor rock slope failures and stains of the spring over the slope face, critical slope failure was identified and located. Most of the time, the general rule that applies to rock slope design and stability analysis is collecting data about the geology, rock strength, and groundwater conditions [4, 9]. Thus, by using the standard outlined in [29] discontinuity characteristics of the rocks were evaluated.

Furthermore, dip and dip direction of the joint set and slope, joint set infill, aperture, persistence, roughness, and spacing between successive joints were measured. Saturation and groundwater conditions of selected critical slope sections were visually evaluated. Shear strength of the discontinuities and rock mass and to a lesser extent compressive strength of intact rocks are the essential rock strength parameter used in rock slope design and stability analyses [9]. Under this study, uniaxial compressive strength (UCS) of fresh and weathered rock was determined in situ using a portable instrument called Schmidt hammer by using the standard suggested by [29]. Afterward, the empirical relation developed according to [35] was used to execute the uniaxial compressive strength of the rock using equation (Eq. 6).

$$log10{\text{ }}\left( {\sigma _{C} } \right){\text{ }} = {\text{ }}0.00088*\gamma *R + 1.01$$
(6)

where σC is the uniaxial compressive strength (UCS) in Mpa; \(\gamma\) and \(R\) are the dry rock densities in kN/m3 and average Schmidt hammer rebound value, respectively.

The joint roughness coefficient (JRC) was also estimated in the field as follows. According to [36], different methods can evaluate the JRC. Among that, the visual comparison of the discontinuity surface roughness with the joint roughness profile standard developed by [35] was the most commonly used and promptly estimated JRC. However, it is the subjective method. The appearance of the discontinuity surface is compared visually with the profile developed by [35]. Later, the JRC value corresponding to the profile which most closely matches that of the discontinuity surface is chosen [18, 29, 35, 37].

4.2 Laboratory test

One of the parameters used to classify the quality of rock mass is intact rock strength that can be determined either from point load strength test or uniaxial compressive strength of the rock. In this study, the point load strength test according to [38] was conducted on the irregular rock sample taken at each selected critical rock slope section using (Eq. 7). Uniaxial compressive strength is preferable to classify intact rock with low strength [19]. As a result, the study converted the average value of the corrected point load strength to the uniaxial compressive strength of the rock using the empirical equation (Eq. 8) suggested by [39].

$$Is_{(50)} = \frac{F * P}{{De2}}$$
(7)
$$UCS{\text{ }} = {\text{ }}24*Is (50)$$
(8)

where \(P\) is the failure load in N, \(De2\) the equivalent core diameter in rmm2,\(F\) the size correction factor, Is (50) the corrected point load strength MPa.

4.3 Determining shear strength parameters along failure plane

Shear strength parameters like cohesion and friction angle are the main factors that define resisting force acting normal to the failure plane [7, 18]. The parameters, in turn, depend on the conditions of discontinuities such as joint set roughness, continuity, aperture, and filling [7, 18]. According to [18], shear strength along failure plane or natural joints can be evaluated using empirical law of basic friction angle first proposed by [25] nonlinear equation (Eq. 9).

$$\tau = \sigma_{n} *tan\left[ {JRC * log10 \left( {\frac{JCS}{{\sigma n}}} \right) + \, \phi_{b} } \right]$$
(9)

where \(\tau\) is peak shear strength (kPa), σn is effective normal stress (kPa), \(JRC\) is joint roughness coefficient, \(JCS\) is joint wall compressive strength (kPa) and ϕb is basic friction angle (degree). The joint roughness coefficient was estimated as described in Sect. (4.1). Likewise, the joint wall compressive strength was evaluated as follows. The joint wall compressive strength (JCS) of the un-weathered joint is equivalent to the unconfined compressive strength (σc) of intact rock [18, 37]. The appropriate value of uniaxial compressive strength (σc) can also be determined from the Schmidt rebound value (R) applied on an un-weathered rock surface with unit weight (γ) (Eq. 6) will represent the joint wall compressive strength of the rock (JCS) [40]. However, for nearly weathered joint surface or in the absence of Schmidt hammer reading, the JCS will become a fraction of the uniaxial compressive strength of the intact rock approximately (1/4σc) [29, 37].

Moreover, the basic friction angle (ϕb) is the angle with flat, planar, and an un-weathered rock surface and for most of the rock, its value ranges from 21º to 40º [8]. For variably weathered joints, the basic friction angle can be correlated with the residual friction angle \(( \phi\)r) as stated by [35] (Eq. 10).

$$\phi_{r} = \left[ {(\phi_{b} - {2}0) \, + { 2}0{\raise0.7ex\hbox{$r$} \!\mathord{\left/ {\vphantom {r R}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$R$}}} \right]$$
(10)

where \(r\) and \(R\) are the Schmidt rebound value on the weathered and un-weathered rock surface, respectively. In this study, cohesion and friction angle along a failure plane was determined according to equation (Eq. 9) built-in Rocdata software [27] and the following approach was adopted to obtain the equivalent (best fit) linear Mohr–Coulomb strength criterion or parameters (cohesion and friction angle) using Rocdata software which uses nonlinear failure criteria. The input parameter used to determine the cohesion and friction angle using Rocdata software are; joint roughness coefficient [35], joint wall compressive strength, basic friction angle [25], unit weight of the rock, and slope height. Rocdata software [27] comes with built-in tables and convenient charts of typical strength parameter values of various rock and soil types which are compiled from credible sources. Thus, the basic friction angle was taken from the built-in table from the Rocdata software. The joint roughness coefficient (JRC) was qualitatively and visually evaluated on the field by comparing it with [35] standard profile while joint wall compressive strength and slope height were determined in the field. Similarly, the unit weight of the rock was determined in the laboratory. Later on, all the input parameters stated above were imported into Rocdata software [27] and then cohesion and friction angle along the failure plane can be calculated as an output in the form of decimal number and graph (Fig. 2). The [18] is a nonlinear form and an empirical relationship widely used to model the shear strength of rock discontinuities using Rocdata software [27]. Thus, this paper carries out cohesion and friction angle along failure plane or discontinuities using Rocdata software which employs [18] nonlinear failure criteria based on the procedure stated above.

Fig. 2
figure 2

Analyses of shear strength parameter along a failure plane using Rocdata software.

Full size image

4.4 Stability analyses methods

4.4.1 Rock mass quality

The rock mass rating is a method used to determine the quality and performance of rock based on intact rock strength, rock quality designation index, and structural parameters [5]. In the present study, the quality of the rock mass which composes the critical slope section was determined according to [19] the basic rock mass classification system. Some of the five basic rock mass rating parameters used under this study were spacing of discontinuities, rock quality designation index according to [41], the condition of the discontinuity (infill material, persistence, aperture, roughness, and weathering conditions), and the saturation conditions of the slope and all of them were estimated on the field. However, the strength of intact rock was determined from a point load test which was later converted to the corresponding uniaxial compressive strength (UCS) using (Eq. 8).

4.4.2 Kinematic analysis

The kinematic analysis evaluates the stability of a rock slope by determining the type of rock slope mode of failure [4, 8,9,10]. Failure of rock slopes mostly takes place along structural discontinuities or weakness planes such as joints and faults. To verify the type of rock slope mode of failure identified in the field, the kinematic analysis was done using dips software [42] from the input parameters shown in Table 2. Some of the input parameters used in the analysis are joint set and slope orientations which were measured on the field, and friction cone determined using Rocdata software. To undergo the analysis, pole data stereographic projection was performed based on the procedure outlined in [4, 9].

4.4.3 Limit equilibrium method

Limit equilibrium methods (LEM) is one of the oldest methods used to analyze the stability of the slope. As well, there are various alternative limit equilibrium methods (LEMs) which differ in the assumption of defining the shape of failure surface (circular, planar, wedge) and equilibrium equation that can be satisfied (either moment or force equilibrium) [9, 17]. However, all of them determine the stability of the slope in terms of the factor of safety which is the ratio of resisting force to driving force [4, 13, 16]. In this study, different modes of rock slope failures identified by the kinematic method were further analyzed by the Limit equilibrium method (LEM) particularly, which satisfies force equilibrium. To undergo LEM analysis the Rocscience software packages like Rocplane [31] and Swedge [32] were used. Both of the software performs rock slope stability analysis based on the procedure stated by [4, 10, 30]. Slope geometries, orientations of discontinuities, slope height, and unit weight of the rock were the input parameter used in the stability analysis of the slope in the study area.

5 Results and discussion

During the extensive fieldwork, four critical rock slope failures namely slope sections D1S2, D1S3, D1S4, and D4S1 were identified based on field manifestations like the occurrence of scarp faces, crack observed on the ground, and unfavorable orientations of major rock discontinuities. The saturation conditions of the slope are one of the factors which determine the stability of the slope by inducing water pressure in the slope and reducing the shear strength along the failure plane. Thus, it was also visually estimated mainly during the dry season where the saturation condition of the slope can be most probably identified. Hence, the slope section D1S2 was found to be damp which instigates failure of the slope while the others were dry and are nearly resistant to failure. Besides, perennial and intermittent springs (Fig. 1b) which emanated at different parts of the slope through the rocks discontinuity were identified and it revealed that shallow groundwater table acts as slope destabilizing factors in addition to rainfall which triggers stability of the slope mainly during the summer season.

From a detailed field investigation, the dip of slope and persistent discontinuities that influence the stability of the slope was measured at critical slope sections and were found to be nearly steep which set off the slope failures (Table 6). Besides, conditions of discontinuities determined on the field illustrated that joint roughness varies from smooth to rough where some of them were filled with soft materials. Similarly, based on variation in color, texture, and hardness, the types of rocks that occur in the study area were; cliff-forming sandstone which has medium-coarse grained, sugary color, and medium strength that overlay deformed granite (Fig. 1b). Furthermore, in situ measurement of Schmidt hammer rebound value on weathered and un-weathered representative rocks surface was recorded, and later the average value was converted to the uniaxial compressive strength of rock using equation (Eq. 8). Thus, the lowest and highest strength of the rock as determined from Schmidt hammer (L-type) ranges from 20.13 to 96.05 MPa for slope sections D4S1 and D1S2, respectively (Table 1).

Table 1 Schmidt hammer rebound value and corresponding UCS (MPa).
Full size table

The uniaxial compressive strength of the rock determined on the field using the Schmidt hammer was classified according to [29]. Based on this, it was concluded that the rock at slope sections D1S4 and D4S1 have weak and medium strength, respectively, while the rest have strong strength. The corrected point load strength test result on a different irregular representative rock taken from each critical rock slope section (Table 2) revealed that the point load strength index of the rock rages from 0.39 to 2.23 MPa with the corresponding uniaxial compressive strength which ranges from 8.67 to 51.3 MPa. Based on the [29], the rock at slope sections D1S2 and D1S4 have weak strength while rocks at D1S3 have medium strength, and the rocks at D4S1 have strong strength.

Table 2 Point load test result and its corresponding uniaxial compressive strength.
Full size table

In rock which had medium to high strength, failure of the rock slope was mostly controlled by structural discontinuities while those with low strength along with unfavorably oriented rock discontinuities most probably causes failure of the rock slopes in the form of raveling and rock falls [17]. Similarly, the rock strength test results in this study also verify that some of the rock taken from critical slope sections like slope section D1S3 (Tables 1 and 2) have good to high strength and the respective rock slope modes of failure identified in the slope sections were controlled mostly by persistent (lengthy) structural discontinuities. The rocks at the rest slope sections have weak to medium strength. Hence, failures of the rock slopes were influenced by non-persistent structural discontinuities.

Shear strength parameters along the discontinuity plane are one of the parameters which control shear strength along failure planes. In this study, the shear strength parameters along the failure plane (joint set) were evaluated by Rocdata software (Table 3) and (Fig. 2). As an input parameter, for nearly weathered joints residual friction angle (ϕr) was determined from (Eq. 10) built-in Rock data software and it ranges from 21.5º to 21.6º (Table 3). Similarly, for un-weathered joints, the basic friction angle (ϕb) of sandstone was adopted from the standard table built-in Rocdata software and it ranges from 32.5º to 33º. However, the unit weight of the rock (γ) was determined in the laboratory according to [43, 44] and with a value of 21.46 (kPa) (Table 3). Finally, the cohesion and friction angle determined by Rocdata software for each failure plane became 15–36 (kPa) and 31.96–43.49 (deg), respectively (Table 3).

Table 3 Shear strength parameters along the discontinuity plane at each critical slope section as determined by Rocdata software.
Full size table

At the slope section, D1S4 and D4S1 conditions of the joint surface were nearly un-weathered so that joint wall compressive strength was equated to the uniaxial compressive strength of intact rock, determined in the field using the Schmidt hammer and ranging from 23-26 MPa (Table.3). However, at slope sections D1S2 and D1S3, the joint surface was weathered to some degree such that; the joint wall compressive strength corresponds to 25% of the uniaxial compressive strength of the intact rock ranges from 23-24 MPa. Furthermore, the joint roughness coefficient (JRC) was qualitatively and visually evaluated on-field by comparing it with [35] standard profile. Qualitatively it became planar, undulating planar, and slightly rough with respective roughness coefficients 5, 7, and 11, respectively, as determined from the joint roughness coefficient (JRC) standard profile built-in Rocdata software (Table 3). From the analyzed result, the cohesion along the failure plane (joint set) ranges from 0.015 to 0.036 MPa while the friction angle ranges from 31.96º to 43.49º (Table 3).

The quality of the rock which composes the critical rock slope sections in the study area was determined according to the [19] basic rock mass rating system. The five basic rock mass rating parameters such as the point load strength index and uniaxial compressive strength, the rock quality designation index, the spacing of discontinuities, condition of discontinuity, and groundwater conditions were evaluated as shown in (Table 4). According to [29], most of the determined spacing of the discontinuities ranges from 0.5 to 3.8 m which is classified as moderately spacing to wide spacing. Later, the rating value given for each parameter was added to classify the rock according to [19]. Based on the total rating value, rock at the critical slope section of D1S3 and D1S4 and D4S1 were classified as good rock while rock at slope section D1S2 was classified as a fair rock (Table 5).

Table 4 Input parameters used to classify rock at identified critical slope section.
Full size table
Table 5 Rock mass classification of critical rock slope section
Full size table

Based on the field manifestations, four critical rock slope failures, namely two planar and two wedge modes of failures, were identified. To verify the type of rock slope mode of failures identified on the field manifestations, the kinematic analysis was done using dips software [42] from the input parameter in (Table 6). According to the analysis result, the wedge mode of failure occurred due to the two joints set that intersect in the critical zone of wedge mode of failure (highlighted in red). Based on this, the wedge mode of failure encountered at critical rock slope sections D1S2 and D1S3. That means, at the slope section, D1S2, Fig. 3a, wedge failure occurred due to the intersections of joint set J2 and J4 in which the wedge can probably slide toward 088º. Similarly, at slope section, D1S3, Fig. 3b, wedge failure was encountered due to the intersection of set J1 and J2 within the critical zone for wedge mode of failure in which the probable wedge failure occurred toward 111º.

Table 6 Input parameters for kinematic analysis.
Full size table
Fig. 3
figure 3

Stereographic projection using dips software which show different critical rock slope mode of failure. a Wedge mode of failure at slope section D1S2 b Wedge mode of faiure at slope section D1S3. c Planar mode of failure at slope section D1S4. d Planar mode of failure at slope section D4S1

Full size image

Furthermore, the rock slope sections D1S4 and D4S1 were subjected to the planar mode of failure, Fig. 3c and Fig. 3d, respectively. From the analysis results, the planar mode of failure was identified by determining the pole of the joint set which fails within a critical zone of the planar mode of failure (highlighted in red). Based on this, at slope section D1S4, the pole of joint set J2 (PJ2) and J4 (PJ4) were plotted within a critical zone of planar failure (highlighted in red) showing that planar mode of failure occurred due to joint set J2 and J4, Fig. 3c. Similarly, at slope section D4S1; the pole of joint set J1 (PJ1) plotted within a critical zone of a planar mode of failure, Fig. 3d. This revealed that at slope section D4S1 planar mode of failure occurred due to joint set J1. Finally, further stability analyses in terms of safety factors for the identified wedge and planar mode of failure were conducted using the Limit equilibrium method (LEM).

From the kinematic analysis result in Fig. 3, the possible wedge mode of failure was identified from the two joint sets which intersect in the critical zone of wedge mode of failure (highlighted in red). Likewise, planar rock slope failure was evaluated by determining the pole of the joint set which falls within the critical zone of the planar mode of failure (highlighted in red). Based on this, the wedge mode of failure occurred at slope section D1S2 (Fig. 3a) due to the intersections of joint set J2 and J4 in the critical zone of wedge failure where the wedge can probably slide toward 088º. Similarly, at slope section D1S3 (Fig. 3b), wedge failure was encountered due to the intersection of set J1 and J2 within the critical zone for wedge mode of failure where probable wedge failure occurred toward 111º. Similarly, slope section D1S4 (Fig. 3c), the pole of joint set J2 (PJ2) and joint set J4 (PJ4), and at slope section D4S1 (Fig. 3d) pole of joint set J1 (PJ1) were plotted within the critical zone of planar failure. Thus, a possible planar mode of failure can be occurred due to joint set J2 and J4 for slope section D1S4 (Fig. 3c) and due to joint set J1 at slope section D4S1 (Fig. 3d). To further determine the stability of the slope, the analysis was performed by determining the factor of safety using Rocplane and Swedge software for planar and wedge mode of failure, respectively. Both of the software packages determine the stability of the slope based on the concept of the limit equilibrium method (LEM) of analysis by considering the failing rock plane as a unit mass.

The input parameters used to determine the safety factor of rock slope failures were; slope geometry, discontinuity orientation, shear strength parameters along the discontinuity plane which were evaluated by Rocdata software, Fig. 2. The slope height at each slope of the section (Fig. 4 to Fig. 6) was determined using meter tape mainly by dropping the meter tape from the top of the slope.

Fig. 4
figure 4

Field photograph indicating the slope conditions and 2D geometry of planar mode of failure done by Rocplane software. a Persistent joint set which forms planar mode of failure in slope section D1S4. b 2D geometry of planar mode of failure due to joint set (J2)in slope section D1S4. c 2D geometry of planar mode of failure due to joint set (J4) in slope section D1S4.

Full size image

Safety factors for planar rock slope failure were conducted by the Limit equilibrium method (LEM) from the input parameter indicated in Table 7. The critical slope section D1S4, occur in the upper sandstone that formed a cliff and there was a persistent joint set that oriented over the exposed slope face, Fig. 4a. The 2D geometry of the slope plotted using Rocplane software showed that the upper end of both joint sets intersects with the upper slope dip and daylight onto the slope face. Moreover, it revealed that different types of force applied to the failure plane, slope height, slope, and failure plane dip, Fig. 4b, c. The peak water pressure and horizontal seismic force with magnitude 10.656t/m2 and 1760.76t, respectively, were applied to the failing plane (joint set J2 highlighted in red) that in turn increases the magnitude of driving force, Fig. 4b. Similarly, under the same conditions, the peak water pressure and horizontal seismic force with magnitude 10.395t/m2 and 1513.74t, respectively, were applied to the failing plane identified as joint set J4, Fig. 4c. The factor of safety becomes smaller as the slope and failure plane angle increase. Thus, steepness of the slope and failure plane angle at both slope section (D1S4 and D4S1) and saturation condition of the slope for the most part favor instability of the slope as causative and triggering factors, respectively.

Table 7 Input parameters to determine the factor of safety for critical slopes with the planar mode of failure.
Full size table

What’s more, at slope section D4S1 the upper end of the joint set J1 terminated in a tension crack which dipped at 72º, Fig. 5a. The 2D geometry was plotted by using Rocplane software, particularly when the slope was assumed to be 100% saturated and horizontal seismic acceleration was expected to occur. Equation (Eq. 2) and (Eq. 3) were developed and built-in Rocplane software. Consequently, the peak water pressure at the mid-height of the slope and water pressure in the tension crack with the magnitude of 6.38t/m2 and 8.50t/m2, respectively, were applied to the failing plane, Fig. 5b. Similarly, the force with a magnitude of 324.28t was also applied to the failure plane by horizontal seismic.

Fig. 5
figure 5

a Field photographs which illustrate orientations of discontinuities at slope section D4S1. b 2D geometry of planar mode of failure done by Rocplane software.

Full size image

For slope section D1S4, Fig. 5, the analyzed safety factors using Rocplane from input parameters (shown in Table 7) indicated that the safety factor was less than one under all anticipated conditions (Table 8). These portray that the slope was unstable under all stated conditions especially during rainy seasons. Nevertheless, for slope section D4S1 the analyzed safety factor was approximately equal to one under dynamic dry and dynamic saturated conditions and greater than one under static dry and static saturation conditions. According to [4], the factor of safety equal to one indicates that the slope is on point of failure while the factor of safety greater than unity discloses a stable slope. Hence, slope section D4S1 is on verge of failure during dynamic dry and dynamic saturation conditions and stable during static dry and static saturation conditions.

Table 8 Factor of safety calculated under different anticipated conditions for planar mode of rock slope failure using Rocplane.
Full size table

The kinematic analysis result illustrated that the wedge mode of rock slope failure occurs at slope sections, D1S2 and D1S3 (Fig. 3a) and (Fig. 3b), respectively. Hence, stability analyses in terms of factor of safety were also undertaken using Swedge software under different anticipated conditions from the input parameters like slope geometry and discontinuity orientations, Table 9. The critical slope sections D1S2 and D1S3 were also found at steeply dipping and cliff-forming sandstone where the road enters into the escarpment from flat and high altitude topography. Similarly, the 3D geometry of the slope sections D1S2 (Fig. 6a) and D1S3 (Fig. 6d) were drawn by Swedge to show both the mode of wedge failure (highlighted in red) and plane along which the wedge slide. Based on the kinematic analyses (Fig. 3a), joint set (J2), and joint set (J4) were identified as the two joints which cause wedge mode of rock slope failure in slope section D1S2. Similarly, joint set J1 and J2 were the two joint set which causes wedge mode of failure at slope section D1S3 (Fig. 3b). Hence, the factor of safety was calculated alone for both slope sections using Swedge depicts that the factor of safety was less than one under all anticipated conditions, Table 10. This signifies that the slopes were unstable under all the specified conditions probably due to the combined effect of adversely oriented slope, discontinuities, and rainfall which saturate the slope.

Table 9 Input parameters used for determination of the safety factor for critical rock slopes having wedge mode of failure.
Full size table
Fig. 6
figure 6

a 3D geometry of wedge failure formed due to intersection of joint set J2 and J4 and done by Swedge software (at slope section D1S2). b Closely spaced joint sets which intersect and form wedge mode of failure (at slopes section D1S2). c 3D geometry of wedge failure in wireframe done by Swedge software (at slope section D1S2). d 3D geometry of wedge failure due to intersection of joint set J1 and J2 and done by Swedge software (at slope section D4S1). e Highly persistent joint sets which intersect and form wedge failure (at slope section D4S1).

Full size image
Table 10 Factor of safety calculated under different anticipated conditions for wedge rock slope failure using Swedge software.
Full size table

6 Possible remedial measures

The detailed stability analysis of the critical slope sections D1S4, D1S2, and D1S3 was identified as an unstable slope under all anticipated adverse conditions. Thus, suitable and possible remedial measures were needed for those unstable slope sections so that they remain stable even under the worst anticipated conditions. This study used Rocplane and Swedge software to design and provide the possible and suitable remedial measures for planar and wedge mode of failure, respectively. The Rocscience software packages can only design and provide remedial measures like rock bolts, shotcrete, and estimate the safe factor of safety based on the equation and techniques outlined in [4]. Hence, rock bolts oriented at 18º and bolt capacity 1000t each were installed to the critical slope section D1S4 which was subjected to the planar mode of failure (Fig. 7a and b). As a result, the factor of safety was increased to 1.56 and 1.46 for failure due to joint set J2 (Fig. 7a) and J4 (Fig. 7a), respectively. In the same way, for critical slope section subjected to wedge mode of failure slope sections D1S2 (Fig. 8a) and D1S3 (Fig. 8b) shotcrete with shear strength 2500t, rock bolts each with plunge direction 21º and bolt capacity 1500t was designed and installed so that their respective factor of safety was increased to 1.27 and 1.22, respectively. According to [4], a safety factor equal to 1.2 is recommended for road slope design. Consequently, after rock bolts were installed for all slope sections D1S2, D1S4, and D1S3 factor of safety became greater than 1.2 indicating a safe and stable slope.

Fig. 7
figure 7

Designed and installed rock bolts for slope section D1S4. a Planar failure due to joint set J2. b Planar failure due to joint set J4.c, d Increased factor of safety along failure plane joint set J2 and J4, respectively.

Full size image
Fig. 8
figure 8

Designed and installed rock bolts. a Slope section D1S2 and its Factor of Safety (FS) after installed rock bolt. b Slope section D1S3 and its Factor of Safety (FS) after installed rock bolt

Full size image

7 Conclusions

In this study, potentially unstable rock slopes that caused frequent and significant damage on the road and natural environments were identified based on the field manifestations. Hence, the slope stability analyses along selected road sections were performed using a detailed field survey, the basic rock mass rating, kinematic and limit equilibrium methods (LEM) of analyses. Based on the field manifestation, two planar and two wedge modes of failure were identified in the study area. Moreover, conditions of discontinuities, slope geometry, failure plane orientations, and in situ test on intact rock strength were conducted during the field survey. Subsequently, the data collected on the field were used as an input parameter to execute the kinematic and limit equilibrium methods of analysis. The Rocscience software package was also used to evaluate cohesion and friction angle along a failure plane and then to carry out kinematic and limit equilibrium methods of analyses. According to the basic rock mass rating (RMR), rocks at slope sections D1S3, D1S4, and D4S1 have good quality while those exposed at slope section D1S2 have a fair rock quality. The kinematic analyses depict that slope sections D1S2 and D1S3 were subjected to the wedge mode of rock slope failure while the planar mode of failures was encountered at slope sections D1S4 and D4S1. This result indicated that there is a strong agreement between the kinematic analysis result and the types of failure manifested in the field.

Furthermore, for the slope sections D1S2, D1S3, and D1S4 the calculated factor of safety using the Limit equilibrium method (LEM) was less than one under all anticipated conditions except at slope section D4S1. Hence, it was concluded that slope sections D1S2, D1S3, and D1S4 were unstable mainly during dynamic saturation conditions while the slope section D4S1 became nearly stable under all anticipated conditions. The analyses result revealed that factors that saturate the slope like a rainfall of the study area, groundwater manifested as spring along the slope section and horizontal seismic acceleration of the area were the triggering factors that make the slope unstable. Similarly, unfavorably oriented persistent joint sets and slopes were identified as the causative factor that makes the slope unstable. Rock bolts and shotcrete were designed by Rocscience software to stabilize un-stable slope sections.