The evolution of the urinary bladder as a storage organ: scent trails and selective pressure of the first land animals in a computational simulation

Abstract

The function of waste control in all living organisms is one of the vital importance. Almost universally, terrestrial tetrapods have a urinary bladder with a storage function. It is well documented that many marine and aerial species do not have an organ of such a function, or have one with very depressed storage functionality. Bladder morphology indicates it has evolved from a thin-walled structure used for osmoregulatory purposes, as it is currently used in many marine animals. It is hypothesised that the storage function of the urinary bladder allows for an evolutionary selective advantage in reducing the likelihood of successful predation. Random walks simulating predator and prey movements with simplified scent trails were utilised to represent various stages of the hunt: Detection and pursuit. A final evolutionary model is proposed in order to display the advantages over inter-generational time scales and illustrates how a bladder may evolve from an osmoregulatory organ to one of the storage. Data sets were generated for each case and analysed indicating the viability of such advantages. From the highly consistent results, three distinct characteristics of having a storage function in the urinary bladder are suggested: reduced scent trail detection rate; increased prey–predator separation (upon scent trail detection); and a reduced probability of successful capture upon scent detection by the predator. Furthered by the evolutionary model indicating such characteristics are conserved and augmented over many generations, it is concluded that prey–predator interactions provide a large selective pressure in the evolution of the urinary bladder and its storage function.

1 Introduction

The urinary bladder in mammals and other terrestrial animals is a muscular distensible organ that holds urine under low pressure and can be emptied under voluntary control. How can this organ evolve from a thin-walled structure in fish that is involved with electrolyte and water exchange? Teleost fish have a confluence of their ureters that forms a thin-walled urinary bladder. In salt water, fish lose most (90%) of their nitrogenous waste via their gills [1]. In fresh water, there is a demand for more urinary excretion of nitrogenous waste. Under brackish water conditions, fish that survive have even less ability to exchange ammonia across their gills, and excretion via the kidneys and urinary tract becomes a greater importance.

Teleost fish have a pronephros and mesonephros, but no metanephros. The electrolyte reabsorption and secretion and water reabsorption are limited compared to animals that have a metanephros and loop of Henle. The lower urinary tract and bladder in fresh water fish is a thin-walled organ that is involved in electrolyte exchange, not a storage organ. For example, rainbow trout bladders are capable of water and sodium reabsorption [2]. Mudskippers (amphibious gobioids, e.g. Periophthalminae of the family Oxudercinae) are a living example of amphibious fish that can spend several days out of water. They may represent an example of co-evolution that might be similar to the first amphibious animals to attempt to live on land, but are not living fossils [3] . They also might represent a morphological model for the ancestors of the first tetrapods. The mudskipper is even capable of producing urea when air-breathing [4].

Urinary bladders are found in many different animals and, it has been suggested, may have evolved twice [5].

There is an evolutionary argument for the development of a storage function in the urinary bladder that has been suggested by several authors [5] . If an animal crawled onto land and left a continuous scent trail, then this could be easily followed by a predator. By storing urine and discretely passing it in an intermittent fashion, the scent trail would be harder to follow, and the animal (prey) has a selective survival advantage.

Agent-based modelling is a way of describing emergent phenomena based on individual components of a complex system. An early example of this is Thomas Schelling’s ‘Dynamic Models of Segregation’ [6]. These techniques have then been used in areas such as population dynamics, for example ‘Aphid Population Dynamics of Agricultural Landscapes: An Agent-Based Simulation Model’ [7]. More recently, agent-based modelling has been used to describe the emergence of the evolution of grammar by Luc Steels [8].

In this study, agent-based modelling was used in order to test the hypothesis that there is a selective advantage to the evolution of a bladder with urinary storage capacity in prey. By considering continuous and discontinuous scent trails of individual prey and predators (the agents) in random walks on a two-dimensional grid, hunts were simulated in two phases: detection and pursuit. That is, the scent marker is left by the prey first on every location it visits—continuous then with a defined separation between the prey leaving a scent marker—discontinuous. The first simulation (Sect. 2.1.1 ‘Detection of Prey’) was a simple model where the prey and predator each had a random walk and if the predators walk intercepted the preys walk, then the prey was detected. The duration of prey survival was taken to be the number of steps that the agent had taken before being detected. In the second simulation (Sect. 2.1.2 ‘Pursuit of Prey’), a Monté Carlo simulation [9] was run to model the pursuit phase of the hunt. This was achieved by using the diffusion equation in order to model scent propagation and therefore define the pungency of a scent marker, and combining this with the distance between the predator and prey a probability was worked out that the prey would be caught. Then, if a random number is generated that is greater than this probability, the prey has been caught. This was used to give simulation 1 as an approximate minimum bound for the selective advantage of having a urinary bladder with storage capacity, simplifying the methodology of the third simulation (2.1.3 ‘Evolution’). Using the detection of the prey, as in simulation 1, as a metric for the hunt, simulation 3 had 100 prey in each generation. Each prey was assigned a probability of leaving a scent marker on each step. The top ten longest surviving prey were then used to infer the probability of leaving a scent marker for the next generation, with the top survivor and bottom survivors probabilities randomly mutated either up or down.

Simulation 1 demonstrated a huge survival advantage in a discontinuous scent trail (Sect. 3.1). Simulation 2 displayed that having a discontinuous scent trail greatly magnified this advantage during the pursuit phase (Sect. 3.2). This resulted in the use of simulation 1 as a minimum bound of the survival of the prey agents in simulation 3. In simulation 3, survival of the fittest prey related strongly to inheritance of the probability of leaving a discontinuous scent trail (bladder storage capacity). Over a thousand generations, the random mutation of only two of the prey was coupled with the selective pressure of predation, was enough to give the emergence of storage capacity in the urinary bladder (Sect. 3.3). This is discussed further in Sect. 3, before concluding in Sect. 4 that there is a huge in-silico selective advantage that in this agent-based model, there is a huge selective advantage to the evolution of urinary bladder storage capacity.

2 Methodology

All simulations were ran on Python 3.6.5 through Spyder 3.3.6 on a Dell Inspiron 13 7000 with an Intel 8th Gen. Core i5 processor.

2.1 The model

To test this hypothesis, predator and prey movements are simulated with random walks over an $n\times n$ lattice of the form in Fig. 1. Each step is given by the addition of S, such that

$$\begin{aligned} S \in \{ (-1,-1),(-1,0),(0,-1),(0,0),(1,0),(0,1),(1,1) \}, \end{aligned}$$

(1)

to the previous lattice position (x, y). For visual clarity, this can be represented by the matrix

$$\begin{aligned} M:= \begin{pmatrix} M_{11} & \quad M_{12} & \quad M_{13} \\ M_{21} & \quad M_{22} & \quad M_{23} \\ M_{31} & \quad M_{32} & \quad M_{33} \end{pmatrix} = \begin{pmatrix} \nwarrow & \uparrow & \nearrow \\ \leftarrow & \odot & \rightarrow \\ \swarrow & \downarrow & \searrow \end{pmatrix}, \end{aligned}$$

(2)

where each arrow denotes a unit step in that direction, and the $\odot$ denotes the step, $S = (0,0)$. That is, S is a two-dimensional Moore neighbourhood.

Fig. 1

Lattice layout for flat torus used to model plane of prey and predator movements. Each square denotes a single lattice point, as referred above

Each step is generated from the set,

$$\begin{aligned} m := \{ -1,0,1\}, \end{aligned}$$

(3)

by generating a random number from $\{ 1,2,3\}$ for an index to call an element of this set. This is done for both the x and y dimensions individually and then added to the previous location.

The lattice is modelled as a flat torus, and hence, for each new step it follows the algorithm

$$\begin{aligned}&(x_{i+1} \, \text {mod} \, (n+1),y_{i+1} \, \text {mod} \, (n+1)) \\&\quad =(x_i,y_i) + M_{jk}, \end{aligned}$$

(4)

where j, k are randomly generated.

The following three simulations were produced using this model.

2.1.1 Simulation 1—detection of prey

Starting positions were randomly generated on the lattice for the predator and the prey. N is defined as the number of steps taken before leaving a scent marker. When there is no bladder storage function, the scent trail is continuous, with a scent marker being left on every step by the prey, $N=1$. The prey will then ‘mark’ a location on the lattice for the $i{\mathrm{th}}$ step if and only if

$$\begin{aligned} i \, \text {mod} \, (N) = 0. \end{aligned}$$

(5)

The mark is referred to as a scent marker or scent mark. The number of steps from initial ‘spawn’ until the predator intercepts a scent marker of the prey are counted, this is the metric used to quantify the length of survival of the prey. This was done for lattices with $n=\in \{ 10,20,30,\ldots ,100\}$ with intervals of 10 in order to display the dependence of the step number on lattice size and for $N \in \{1,2,3,\ldots ,50 \}$ with integer intervals. For each case, the simulation was run $10^4$ times.

2.1.2 Simulation 2—pursuit of prey

In order to fully model the hunt, there are two processes: detection of the preys’ scent trail and following the scent trail to the prey (the pursuit).

Simulation 1 is run (as described above); then, giving a probability to a successful or failed continual pursuit by the predator of the prey, this section of the hunt is referred to as the pursuit. In this case, the predator has caught the prey only when arriving at the preys’ location. To allow this, the prey increases speed once a scent mark has been found, by the ratio

$$\begin{aligned} k := \frac{v_{\text {predator}}}{v_{\text {prey}}} \end{aligned}$$

(6)

where $k>1$ and constant.¹

For the case with $N=1$, the probability of capture is proposed to be,

$$\begin{aligned} P_c = \frac{1}{2}. \end{aligned}$$

(7)

This is chosen because the predator can either follow the scent trail in the correct direction to the prey upon detection, or go the wrong way along the scent trail. Assuming each direction has an equal probability, and as the scent trail is continuous, any other direction of the predator upon scent detection is assumed to not occur.

For $N>1$ (a discontinuous scent trail), scent propagation is now considered to allow the predator to pursue the prey. Observe that scent will propagate from each scent marker radially. Letting the scent have density $\rho$, from the diffusion equation (assuming propagation of scent is homogeneous and is at thermal equilibrium, that is, the scent has the same pressure and density as the surrounding atmosphere, and the density of the system is invariant),

$$\begin{aligned} S_c \propto \frac{1}{x}, \end{aligned}$$

(8)

where $S_c$ is the scent propagation and x is the radial distance from the scent marker (see "Appendix 2" for derivation). See Fig. 2 for a visual representation of scent propagation. To reduce complexity in the counting, and prevent a recursive algorithm, it is assumed that given the predator finding a scent marker, the next closest scent is a distance of $x = N$ from the previous scent marker left by the prey.

Fig. 2

Visual display of scent propagation from scent markers left by the prey. The bolder the colour, the stronger the scent

From this, the number of steps from the prey to the predator is found using

$$\begin{aligned} \zeta = \zeta _{t} - \zeta _{c} \end{aligned}$$

(9)

where $\zeta$ is the number of steps between predator and prey, $\zeta _{t}$ is the total number of steps so far, and $\zeta _{c}$ is the number of steps on the scent trail, at the predators arrival on the scent marker.

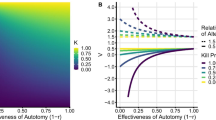
In the model, each further step of the predator is assumed to take the same amount of time and the predator is assumed to then follow an approximate path that nearly follows that of the prey; being that the random walk of the predator and prey is unbiased, and they are positioned on a flat torus; the expectation value of the distance from their respective starting positions is zero, and hence, the average value of the spatial separation of the predator and prey must be less then the size of the edge of the lattice. To smooth out the random walk of the prey for the predator to follow the number of steps separating the predator and prey is divided by a constant² such that $\zeta \mapsto \zeta ' = \frac{\zeta }{K}$. As such, the number of extra steps required by the predator to reach the position of the prey after $\zeta '$ steps is given by

$$\begin{aligned} \frac{\zeta '}{k}. \end{aligned}$$

(10)

Once the predator has reached this location, the prey has walked an extra $\frac{\zeta '}{k}$ steps, which will then take the predator an extra $\frac{1}{k}\frac{\zeta '}{k} = \frac{\zeta '}{k^2}$ steps.

Proposition 1

The total number of extra steps required for capture of the prey is given by

$$\begin{aligned} \zeta ' \frac{k}{k-1}. \end{aligned}$$

(11)

Proof

Assume, the $a\mathrm{th},a+1\mathrm{th}$ iteration of the predators pursuit results in

$$\begin{aligned} \frac{\zeta '}{k^a}, \frac{\zeta '}{k^{a+1}} \end{aligned}$$

(12)

extra steps, respectively.

At any point, the extra steps required get to the new preys new location are given by the distance between the predator and prey over the predator speed, k. As such, the $a+1\mathrm{th}$ iteration results in a step number of

$$\begin{aligned} \frac{1}{k}\frac{\zeta '}{k^a} = \frac{\zeta '}{k^{a+1}}. \end{aligned}$$

(13)

Hence, summing for all $a\in \mathbb {N}$, by the induction hypothesis the total number of steps required is the geometric series

$$\begin{aligned} \zeta ' \sum _{a=0}^{\infty }\frac{1}{k^a}, \end{aligned}$$

(14)

, and hence, the total number of extra steps required is

$$\begin{aligned} \zeta ' \frac{1}{1-\left( \frac{1}{k}\right) } = \zeta '\frac{k}{k-1}, \end{aligned}$$

(15)

as required in (11). $\square$

Therefore, from (7), (8), and (11), probability of capture once the predator is at a scent marker is given by

$$\begin{aligned} P_c = {\left\{ \begin{array}{ll} \frac{1}{2} \,\, \text {for} \,\, N = 1 \\ \frac{1}{2}\left( \frac{1}{N}\right) ^{\frac{\zeta ' k}{k-1}} \,\, \text {for} \,\, N>1,k>1. \end{array}\right. } \end{aligned}$$

(16)

Using a Monté Carlo algorithm [9] , a pseudorandom number, p, is generated such that $p\in [0,1]$. If $p<P_c$, then a successful hunt is observed. As with simulation 1, this was repeated $10^4$ times.

2.1.3 Simulation 3—evolution

Here, a simplified simulation of evolution is proposed. The algorithm is not dissimilar to the machine learning algorithms first described by John McCarthy [10]. As with the first simulation, the number of steps taken by the prey before the predator intersects a scent mark was the metric to quantify the length of survival by the prey.

100 prey are each initially set to have the number of steps between ‘voiding’/leaving scent as 0, by giving the probability of leaving a scent marker on every step, $p_\mathrm{sc}$, as 100%. This is achieved by equating an upper bound, A, and lower bound, B, as 100%, for the scent marking probability interval, $P_\mathrm{sc}$, such that

$$\begin{aligned} P_\mathrm{sc} := [A,B], \end{aligned}$$

(17)

and

$$\begin{aligned} p_\mathrm{sc} \in P_\mathrm{sc}. \end{aligned}$$

(18)

For each new generation, A and B are generated by taking the range, R, of $p_{ \mathrm sc}$ of the top ten longest surviving prey. Denoting the largest $p_{ \mathrm sc}$ of top 10 by $p_{\mathrm{sc}_t}$, and lowest $p_{ \mathrm sc}$ of the top 10 $p_{\mathrm{sc}_b}$. The upper bound and lower bound then become

$$\begin{aligned} \begin{aligned} A_\mathrm{new}&= p_{\mathrm{sc}_b} \pm \psi _A \\ B_\mathrm{new}&= p_{\mathrm{sc}_t} \pm \psi _B \end{aligned} \end{aligned}$$

(19)

where $\psi _A,\psi _B$ are generated by taking a random $r\in R$, such that

$$\begin{aligned} \begin{aligned} \psi _A&= {\left\{ \begin{array}{ll} c \,\,\,\,\, \text {if} \,\, r=0 \\ r \,\,\, \,\,\text {if} \,\, r\ne 0, \end{array}\right. } \\ \psi _B&= {\left\{ \begin{array}{ll} c \,\,\,\,\, \text {if} \,\, r=0 \\ r \,\,\,\,\, \text {if} \,\, r\ne 0, \end{array}\right. } \end{aligned} \end{aligned}$$

(20)

where c is an arbitrary constant defined by a pseudorandom number generator bounded above by 0.01. To prevent values of A, B being negative or more than 100%, the maximum and minimum values of A, B are capped at 0% and 100%.

The progeny is then generated to have a probability of leaving a scent marker on each step with new A, B for some randomly generated

$$\begin{aligned} p_\mathrm{sc} \in P_\mathrm{sc}. \end{aligned}$$

(21)

The following algorithm is followed to allow each animal in the $i\mathrm{th}$ generation to have a random,

$$\begin{aligned} p_{\mathrm{sc}_i} \in P_{\mathrm{sc}_i} = [ p_{\mathrm{sc}_{b_{i-1}}}\pm \psi _{A_i}, p_{\mathrm{sc}_{t_{i-1}}}\pm \psi _{B_i}]. \end{aligned}$$

(22)

In summary, the algorithm follows: Step 1, prey is modelled as with simulation 1, each with a continuous scent trail (no bladder); step 2, the next generation of prey is produced, with probability of scent marking from top ten surviving prey of the previous generation, but the probability of scent marking may be altered to a random extent; step 3, prey is modelled as with simulation 1 (again); step 4, top ten longest surviving preys’ probability of scent marking is recorded and then back to the second step. This is completely repeated over 1000 generations 200 times, each time taking the mean value of $p_\mathrm{sc}$. The selective advantage of urinary storage might be seen by the storage capacity measured in ‘storage-steps’ before a deposit of urine is made, in the $i\mathrm{th}$ generation.

3 Results and discussion

For each simulation, the $n\times n$ lattice was of the form as shown in Fig. 1. Each square denotes a lattice point. Figure 3 illustrates the random walks of the predator and prey.

Fig. 3

Example of random walk for $n=100,N=1$ simulation. Black represents the predators walk, the grey is the prey

3.1 Simulation 1—detection of prey

From the $10^4$ repetitions for each lattice size, data were generated and plotted using the method of least squares. For $n=50$, the results are displayed in Fig. 4. All other results are in "Appendix 1". For all lattice sizes, the mean step number is summarised in Fig. 5a, b.

Fig. 4

a Results plotted for simulation 1 for $n=50$ with fit found via method of least squares, following Eq. (26), with the corresponding constants found in Table 1. All other figures for lattice size $\{ 10,20,\ldots ,100\}\setminus \{50 \}$ are in Fig. 7. b–c Visualizations of all fitted plots from all lattice sizes. b shows all the fitted plots on the same axis as the plots for all lattice sizes, while c displays the surface found by plotting the fitted plots against the lattice size

Table 1 Constants, $\chi ',\phi$, found via method of least squares for (26) and each n simulated

Fig. 5

a Display of the mean step number required for successful hunt or exceeding the survival limit for both the detection and pursuit phases (blue), and the steps separating the prey and predator upon detection of the preys’ scent markers (orange). b Proportion of successfully completed hunts by the prey before exceeding the maximum hunt duration (the survival limit) of 10000 steps (orange), composite with the number of failed hunts via exceeding the survival limit (blue). It is noted that for low discrete separation, there are a proportion of hunts that exceed the step limit; the proportion here is too small to observe. c Mean number of interceptions of scent markers by the predator required before exceeding the survival limit or successful hunt. Note the reduction in the number of scent interceptions correlates with an overall reduction in scent interceptions by the predator. d Overall mean probability of successful capture given a scent interception by the predator, error bars are present, but too small to make out clearly

The greater the number of scent marks left by the prey, the more likely the predator will intercept one. However, given the possibility of the prey leaving a scent marker where one has been left already, only the steps left by the prey for each location on the lattice are counted once. Because the number of steps by the predator will equal the number of steps by the prey, it is assumed that there is a linear relationship between the uniquely located scent markers and the number of steps by the predator. Conversely, the greater the number of unmarked locations on the lattice, the less likely a successful hunt will be observed. As the area of the lattice increases, the greater this area will be for a given step number during the simulation. As such, it is assumed there is an inverse relationship between the area of the lattice and successful detection by the predator. Each iteration gives both the prey and predator a step, so the area is divided by 2. Using the same argument, the separation between the scent markers is assumed to be inversely related to the probability of capture.

Therefore, it is suggested that for a given step number, the probability of successful detection is

$$\begin{aligned} p_c \propto \frac{\chi }{\left( \frac{a}{2}\right) N} \end{aligned}$$

(23)

where $\chi$ is the number of uniquely located scent markers left by the prey, a is the area of the lattice, and N is the scent separation. Summing over $\chi$, a and N in order to find the probability density function of $P_c(\chi ,a,N)$. Approximating by the integral

$$\begin{aligned} P_c \approx \int \frac{\chi }{\left( \frac{a}{2}\right) N} \, \text {d}\chi \, \text {d}a \, \text {d}N \end{aligned}$$

(24)

solving,

$$\begin{aligned} P_c = \frac{\chi ^2}{2}\ln \left( \frac{a}{2}\right) \ln (N) + C. \end{aligned}$$

(25)

Subbing in $n^2=a$, and letting the coefficient of proportionality be denoted $\chi '$,

$$\begin{aligned} P_c = \chi ' \ln \left( N+\frac{n}{2}\right) + \phi \end{aligned}$$

(26)

where $\phi$ denotes the constants associated with the function (see "Appendix 3" for more).

Data were fitted by the method of least squares. See Table 1 for the constants found for $\chi ',\phi$.

For each function of the form (26), with constants defined by Table 1, has n as a constant. As such, the equation

$$\begin{aligned} P_c = f(n)f(\chi ',N,\phi ), \end{aligned}$$

(27)

where $f(n),f(\chi ',N,\phi )$ are considered orthogonal functions. This is visualised in Fig. 4 as the red line, demonstrating an extremely good fit between (26) and the data generated.

3.2 Simulation 2—pursuit of prey

From simulation 1, the lattice size can be considered as an orthogonal function to the mean step number, as such only one lattice size was used for simulation 2. In order to reduce computational time but also reduce effects from a smaller lattice, a $50\times 50$ lattice was chosen. $10^4$ repetitions were performed as described in Sect. 1.

From the results illustrated in Fig. 5a, the number of steps required for successful detection and pursuit of the prey increases progressively. Initially, as the discrete scent marker separation increases there is positive curvature to the mean step number and the step separation. The complete hunt gets progressively longer, particularly after $N=5$ ($\approx$800 steps) to $N=10$ ($\approx 2800$ steps), when the effect accelerates. This is because at $N\ge 10$, the proportion of unsuccessful (beyond the survival limit) hunts progressively increases (blue, Fig. 5b). This progressive increase is also observed in Fig. 5c for the same discrete scent separation, and reason. Figure 5c displays the mean number of times a predator is likely to intercept a scent marker, before a successful hunt is observed, this begins to reduce, because the proportion of terminated hunts begins to dominate, and therefore, the number of interception of scent markers before termination decreases. Figure 5d summarises the overall probability of capture upon scent detection. For $N=1$, probability of capture is $\frac{1}{2}$, as described in Sect. 1. For $N=5$ the probability of successful capture is $\approx 0.2$, and for $N=20$ is approximately 0.1.

3.3 Simulation 3—evolution

Similarly, to with simulation 2, a single lattice size was chosen. As the same metric for simulation 1 was used, it was assumed the lattice size effects will be minimal, with a $10\times 10$ lattice chosen in order to maximise the number of possible repeats.

Figure 6 shows a mean of 200 generations to get a discrete scent separation of $N=2$ ($\frac{1}{2}$ chance of scent marker being left per step). Another $\approx 100$ generations are needed for a discrete scent separation of $N-=3$ (1 / 3 probability of a scent marker being left), to get to a discrete scent separation of $N=4$, and another approximately 50 generations are needed. As such, once the spontaneous emergence of a bladder is observed, the storage function of the bladder rapidly increases.

Fig. 6

200 repeats of simulation 3—the evolution stage, done over 1000 generations for 100 prey in each. Each different path denotes a different repeat of the simulation. a denotes probability of leaving a scent marker, with probability of scent marking of 100% denoting no discrete scent separation, 50% denotes 1 discrete separation, etc. b Natural logarithm of the probability of scent marking, normalised to unity. Logarithm used to illustrate convergence to the evolution of the bladder, and the rate of change of N

Figure 6a shows the spontaneous formation of an organ with bladder capacity very quickly emerges. In order to display that this is converged to, rather than immediately appears, Fig. 6b displays the logarithm of this value. Each distinct path can be considered a different evolution of the bladder, with the wide range of paths taken by each distinct evolutionary route being a display of convergent evolution.

3.4 Discussion

This is the first simulated model attempting to show the survival advantages of having a urinary bladder acting as a storage organ, with a discontinuous (urine) scent trail. Furthermore, in a simulation of natural selection a bladder and its storage capacity (increasing number of steps between scent trail) developed. This was from a combination of selective pressures of a predator detecting a scent trail, an ability for the best survivors to be selected, and for their bladder capacity to be reproduced in their descendants, with a small element of random mutation. This recapitulates natural selection and shows the benefit of a bladder as a storage organ.

From simulation 1, the lattice size is considered, geometrically, as an orthogonal function to the mean step number, as in Fig. 4c. This allows the use of a single-sized lattice for simulations 2 and 3. Combining the results of simulations 1 and 2, there are three main advantages of having a bladder and one with increased capacity: lower scent detection rate; increased distance to capture prey upon scent detection; and reduced probability of correct path choice upon scent detection. Simulation 2 displays that extra advantages arise in the pursuit phase of hunt, more than simulation 1 illustrates (of an order $\approx 100$). Therefore, only using the metric of simulation 1 for simulation 3 gives an approximate (but very probable) lower bound for displaying the evolutionary advantages of having a bladder.

In Fig. 5a from simulation 2, it is observed that the value of the step number separating the prey and predator upon detection begins to decrease. This is because it was assumed that each scent marker is placed exactly at the distance of the relevant discrete scent separation, as such the index for $\zeta _c$ (only scent markers were recorded for the purposes of the simulation) was multiplied by the respective value of N. This, of course, is a massive simplification (and increase) of the actual values that would have been observed in the simulations. As such, the mean step separation upon detection reduces at high N.

The idea of using an individual agent to describe the actions of one object in a system, and the resultant emergent effects, had its first known use in the Von Neumann Machine—a self-replicating machine used to describe cellular automata [11]. The next notable use was in John Conway’s ‘Game of Life’, in which simple rules allowed the emergence of both unpredictable and highly complex emergent phenomena [12]. This generated significant interest in using the method to simulate complex systems, and early examples include quantifying the prisoners dilemma [13], with the first known biological use in Craig Reynolds’ modelling of flocks of large groups of birds [14]. In evolutionary biology, this has been used frequently, for example ‘The Evolution of Bacteriocin Production in Bacterial Biofilms’ [15] where biological observations were recreated in-silico and in the evolution of the parasitic Chaga’s disease [16] which used a three-dimensional Moore neighbourhood in a similar fashion to the two-dimensional one used here. This is build up of emergent behaviour from actions of the individual agent and therefore allows a simple model to describe large-scale properties of a system. This gives an intuitive way to then define the two phases of the hunt that are considered here, as well as the long-term effects of predator–prey relations in reinforcing certain biological attributes—the evolution of the storage function of the urinary bladder, for example.

Monté Carlo algorithms are widely used in computational statistical physics. Their simple nature coupled with their ability to model emergent systems lends themselves to methods in computational biology. In De Vladen and Barton’s 2011 review of statistical methods in evolutionary biology and ecology [17], examples of applying such methods in biological systems follow a similar methodology to that presented in the second simulation used in this study. In Szymura and Barton’s 1986 work [18] on the clines of fire-bellied toads, small parameter space changes are made, effectively forming a random walk in a six-parameter space, further bounded by a Monté Carlo step, allowing prediction of these clines. This is similar to the probability step used in the second simulation. While more rigour is laid out in Beaumont’s 2010 work on approximate Bayesian computation in evolution and ecology [19], it is possible to see how this work falls into a subset of the more general arguments made in Beaumont’s article and therefore greater insight into the analysis of the data produced by this study.

Olfactory hunters follow scent clues such as urine [20]. This correlates with the detection of the urine scent trail left by the prey in this study. Predator strategies can be categorised by ambush hunting (predator waits for prey) or pursuit strategies which consist of three stages: The stalk, attack, and subdue as described by Elliot et al in the African Lion [21]. Our study considers a pursuit predator, with no separation of the stalk, attack, and subdue with the whole process described as the pursuit.

If there is a selective pressure and advantage of having a urinary bladder for a land animal, what happens if this animal becomes airborne, develops flight? It would be predicted that animals which did this would no longer need a large bladder, and that the weight penalty of this would lead them to ‘lose’ this. Flying would by its nature lead to the scent trail deposited being unable to be followed by a land-borne predator. It is interesting to note that birds do not have a urinary bladder but a cloaca. Furthermore, a flightless bird might be expected to have a selective advantage in regaining a bladder function, and indeed, this is exactly what the ostrich has done [22] . Bladder capacity in bats is not widely described in the literature, but vampire bats start producing urine within in minutes of starting feeding to shed weight for flight [23]. Similarly, what happens to bladder storage function when tetrapods become aquatic once more and no longer have a selective advantage by avoiding leaving a scent trail? Bladder capacity in cetaceans has indeed been described by John Hunter as an order of magnitude smaller than land mammals [24].

However, this is clearly a simplified model with a number of limitations. In all three simulations, a discrete space is used to model the prey and predator movements, confining the possible set of random walks, and this could be improved upon by allowing a continuous space such as a subspace of $\mathbb {R}^2$.  Similarly in all simulations a flat torus is used in order to not constrain prey and predator path directions with boundary conditions. This may have unconsidered effects on the results. The results of simulation 2 also rely on a few non-ideal approximations, specifically relating to the pursuit phase of the chase and scent propagation. With perfectly homogeneous scent propagation assumed, weather and topographical effects on the pursuit phase are not considered, and it was assumed such effects would increase difficulty for the predator and prey in equal measure, although it would be interesting to see how such effects alter the results, especially given the importance of geography on evolution of tetrapods [25, 26]. Finally, in all simulations, no other senses (e.g. sight and hearing) are modelled by the predator and no evasive action, using any other senses, was made by the prey; it is not theorised as to the effects this would have on the data collected, as it is. It does, however, recapitulate a possible evolutionary process that has led to the urinary bladder acting as a storage organ for tetrapod land animals. Similarly, the negative impact of simply increasing progressively bladder capacity (and sustaining a weight penalty as a result) has not been addressed in this simplified model.

Simulation 3 is a highly simplified model. It shows, from a simple mathematical simulation, related to risk of detection, pursuit, and capture of prey by a predator, a selective advantage of having a bladder and a bladder capacity resulting in a discrete and interrupted scent trail is present. A combination of selective pressures, hereditary transmission over generations, and a small degree of variability from random mutation result in the natural selection of ‘bladder capacity’. It should also be noted that no evolutionary mechanism was modelled for the predator, unlike the prey. In the natural world, there would be an arms race between the predator and prey, likely to result in counter adaptations for the predator, for changes in the prey. This arms race has been described as a ‘red queen race’ [27,28,29].

4 Conclusion

This is the first study to use a simulation to model the development of the urinary bladder as a storage organ. This study indicates there are a number of distinct selective advantages to urine storage. Furthermore, when a multi-generational model is run with a combination of inheritance and a small degree of random variation, increasing bladder storage capacity in prey is indeed naturally selected. It is therefore concluded the selective pressure of predation is important to the emergence of the storage function of urinary bladders in terrestrial animals.

Appendices

Appendix 1: More results from simulation 1

See Fig. 7a–j.

Fig. 7

Results plotted for simulation 1, for all n used in simulation, with fit found via method of least squares, following Eq. (26), with the corresponding constants found in Table 1. This shows the mean steps required for detection as the discrete separation increases go up

Appendix 2: Propagation of scent

The system is assumed to be homogeneous, at thermal equilibrium, and the scent is assumed to be spherically symmetric (and as with real life, three-space is considered for scent propagation). As such the diffusion equation simplifies to

$$\begin{aligned} \nabla ^2\rho (x) = 0 \end{aligned}$$

(28)

hence

$$\begin{aligned} \begin{aligned} \frac{1}{x^2}\partial _x\left( x^2\partial _x\rho \right)&= 0, \\ \Rightarrow \partial _x\left( x^2\partial _x\rho \right)&= 0, \end{aligned} \end{aligned}$$

(29)

integrating, $x^2\partial _x \rho =$const. and

$$\begin{aligned} \begin{aligned} \rho&\propto \int \frac{1}{x^2} dx, \\&\Rightarrow \rho \propto \frac{1}{x}, \end{aligned} \end{aligned}$$

(30)

as required in (8).

Appendix 3: Fit for data in simulation 1—detection of prey

From (25),

$$\begin{aligned} \begin{aligned} P_c&= \frac{\chi ^2}{2}\ln \left( \frac{a}{2}\right) \ln N + C \\&= \frac{\chi ^2}{2}\ln \left( \frac{n^2}{2}\right) \ln N + C \\&= \chi ^2\ln \left( \frac{n}{2} + N\right) + C \\&= \chi '\ln \left( \frac{n}{2} + N\right) + \phi , \end{aligned} \end{aligned}$$

(31)

where $\phi = C$ and $\chi ' = \chi ^2$.