1 Introduction

Lately, researchers have been immersed on the study of flows on non-Newtonian fluids such as the chemically reactive and hydromagnetic fluids, conductive couple stress under the impact of thermal radiation because of its applicability in modern technology and industries. As explained in [1], such fluids are important in the exploration of crude oil from petroleum products, solidification of liquid crystals, cooling of metallic plates in bath to mention few. Furthermore to this, Eegunjobi and Makinde [1] in the analysis done on the hydromagnetic flow of couple stress fluid with radiative heat in a channel filled with a porous medium whereby it significantly interpreted the various factors affecting fluid matters, thermal energy transfer and rate of entropy generation of the flow regime.

Nonetheless, Adesanya and Makinde [2] investigated the natural irreversibility in thin flow of a viscous incompressible couple stress fluid down an inclined heated plate with adiabatic free surface flow where the aftermath of increasing values of couple stress parameter are observed to curtail the flow motion and temperature distributions. In addition to this, the couple stress fluid theory generalises the classical viscous Newtonian fluids which allow the maintenance of couple stresses and body couples in the fluid medium as explained in [3]. Likewise, many hydromagnetic reactive flow are often supplemented with heat transfer in many technological applications where different kinds of fluids are used as grease and oil. As a consequence of these, Adesanya et al. [4] delved into the rate of entropy generation in a reactive couple stress fluid flow through a passage saturated with porous materials. Also, Hassan et al. [5] investigated the effect of temperature-dependent fluid density on a reactive couple stress fluid flowing steadily in a vertical channel saturated with porous materials. Other studies carried out lately that shows the usefulness of couple stress fluid can be found in [5,6,7,8,9,10].

However, the significant impact of magnetic influence on any fluid flow can not be neglected. For example, Sheikholeslami et al. [11,12,13,14,15,16] devoted all their studies on the influence of variable magnetic field strength both on external and internal impact on fluid flow passing through porous cavity and on its solidification. In addition to that, Sheikholeslami and Zeeshan [17] analysed the flow and heat transfer in water based nanofluid due to magnetic field in a porous enclosure with constant heat flux and a rise in heat transfer augmentation is observed with increase of inclination angle and magnetic field strength parameter. Other related studies that showed the significant influence of magnetic field on flow regime can be found in literature such as [18, 19].

At the same time, the impact of thermal radiation on fluid flow cannot be overlooked owing to the substantive role it plays in space engineering as in [15, 20,21,22]. Most importantly, Mukhopadhyay [23] highlighted that thermal radiation impacts can play a vital role in monitoring heat transfer in polymer processing industries where the feature of the end product depends on the heat controlling factors determine the end product. The impact of thermal radiation on fluid motion and energy transfer problems are extensively mentioned in [24,25,26,27,28] but Mukhopadhyay and Layek [29] stated that very limited aspect on the impact of thermal radiation is studied. Also, the influence of thermal radiation and electric field on nanofluid hydrothermal treatment is presented in [22] together with [15] where the impact of external magnetic source is considered.

However, it is known that temperature may critically change the substantial properties of fluid and this becomes quite difficult to predict the safe and unsafe situations. In order to predict the flow behavior with the influence of thermal radiation, this research objectively examines the impact of thermal radiation on a reactive hydromagnetic heat generating couple stress fluid flowing steadily through a porous medium. The dimensionless expressions for fluid velocity and heat transfer are achieved using modified Adomian decomposition method (mADM). This method is very productive in such a way that it does not require any of linearisation, discretization and the use of guess value or perturbation technique as discussed in [20]. Moreso, the literature is rich on the mADM and investigation are readily available in [30,31,32,33] including the convergence with size-able iteration in [34, 35]. The comparison of the accuracy and its convergence were prepared in tables with respect to exact solution of fluid motion and discussed quantitatively the other thermophysical parameters present in the flow system.

2 Mathematical formulation

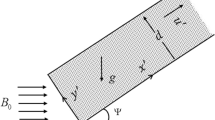
Consider a reactive MHD fluid of unidirectional flow of a combustible couple stress fluid through a porous channel with isothermal walls situated at \(y=0\) and \(y=h\) with the effect of heat source and thermal radiative flux as shown in Fig. 1. The flow is activated by a regular pressure gradient in the direction of the fluid flow under the influence of attractive magnetic field strength \(B_0\). Neglecting the consumption of the reactant, the internal heat generated is assumed to be a linear relation of temperature and the thermal radiation, following [4, 20], the equations governing the fluid motion and heat transfer are given in non-dimensionless form as:

Fig. 1
figure 1

The physical geometry of the flow regime

Full size image
$$\begin{aligned} 0&= -\frac{{\mathrm {d}}P}{{\mathrm {d}}x}+\mu \frac{{\mathrm {d}}^2{\overline{u}}}{{\mathrm {d}}{\overline{y}}^2}-\frac{\mu }{K}{\overline{u}}- \eta \frac{{\mathrm {d}}^4{\overline{u}}}{{\mathrm {d}}{\overline{y}}^4} - \frac{\sigma B_0^2}{\rho }{\overline{u}} \end{aligned}$$
(1)
$$\begin{aligned} 0&= k\frac{{\mathrm {d}}^2{\overline{T}}}{{\mathrm {d}}{\overline{y}}^2}+ Q C_0 A\mathrm {e}^{-\frac{E}{R {\overline{T}}}}+ \mu \left( \frac{{\mathrm {d}}{\overline{u}}}{{\mathrm {d}}{\overline{y}}}\right) ^2+\frac{\mu }{K}{\overline{u}}^2 + \frac{\sigma B_0^2}{\rho }{\overline{u}}^2 \nonumber \\&\quad + \eta \left( \frac{{\mathrm {d}}^2{\overline{u}}}{{\mathrm {d}}{\overline{y}}^2}\right) ^2 + Q_0\left( {\overline{T}}-T_0 \right) - \frac{{\mathrm {d}} q_r}{{\mathrm {d}}{\overline{y}}} \end{aligned}$$
(2)

subject to the following boundary conditions

$$\begin{aligned} {\overline{u}}(0)={\overline{u}}''(0)= {\overline{u}}''(h)= {\overline{u}}(h)=0\quad {\text{and}} \quad {\overline{T}}(0)={\overline{T}}(h)=T_0 \end{aligned}$$
(3)

Notably, the seventh and the last terms in Eq. (2) are respectively the heat source within the flow system as stated in [36,37,38] and the compelling aspect of the radiative energy transfer as discussed extensively in [20, 23, 39].

Meanwhile, the Rosseland approximation for thermal radiation is given as:

$$\begin{aligned} q_r=-\frac{4\sigma ^*}{3k^*}\frac{{\mathrm {d}} {\overline{T}}^4}{{\mathrm {d}} {\overline{y}}} \end{aligned}$$
(4)

where \(\sigma ^*\) represents the Stefan–Boltzmann constant and \(k^*\) stands for the mean absorption coefficient. A familiar inference with the difference in the temperature for the flow regime is such that \(T^4\) is expanded in Taylor series about the free-stream temperature, \(T_\infty \) and by disregarding the higher forms as accomplished in [20, 40] yield:

$$\begin{aligned} T^4\equiv 4 T_\infty ^3 T - 3 T_\infty ^4 \end{aligned}$$
(5)

and with that, the last term in (2) becomes:

$$\begin{aligned} \frac{{\mathrm {d}}q_r}{{\mathrm {d}}{\overline{y}}}=-\frac{16 \sigma ^* T_\infty ^3}{3 k^*}\frac{{\mathrm {d}}^2 {\overline{T}}}{{\mathrm {d}}{\overline{y}}^2} \end{aligned}$$
(6)

Additionally, the illustration representing the rate of entropy generation of the fluid regime due to heat transfer with appreciable radiative heat flux and the local entropy for viscous dissipation, effect of porosity, couple stress and magnetic field strength as discussed in [20] together with [41, 42] where entropy generation of nanofluid with numerical approach is hereby given as:

$$\begin{aligned} E_G&=\frac{k}{T_0^2}\left( \frac{{\mathrm {d}}{\overline{T}}}{{\mathrm {d}}{\overline{y}}}\right) ^2 \left[ 1+\frac{16 \sigma ^* T^3_\infty }{k k^*}\right] +\frac{1}{T_0}\left[ \mu \left( \frac{{\mathrm {d}}{\overline{u}}}{{\mathrm {d}}{\overline{y}}}\right) ^2+\frac{\mu }{K}{\overline{u}}^2\nonumber \right. \\&\quad \left. +\, \eta \left( \frac{{\mathrm {d}}^2{\overline{u}}}{{\mathrm {d}}{\overline{y}}^2}\right) ^2+\frac{\sigma B_0^2}{\rho }{\overline{u}}^2\right] \end{aligned}$$
(7)

In Eqs. (1–7), p stands for pressure, \({\overline{u}}\) represents dimensional axial velocity, \({\overline{T}}\) represents dimensional fluid temperature and K is the porous medium permeability constant, \(\mu \) stands for viscosity of the fluid, \(\eta \) represents the couple stress coefficient, \(\sigma \) is the electrical conductivity, \(\rho \) denotes fluid density evaluated at the mean temperature and h is the channel width. Also, k stands for thermal conductivity of the fluid, \(T_0\) represents the wall temperature, Q is the heat of the reaction term, \(C_0\) is the reactant species initial concentration, (x, y) respectively represent the distance measured in the axial and normal direction, A is the rate of reaction, E is the activation energy, U stands for fluid characteristic velocity, R is the universal gas constant and \(E_G\) is the dimensional entropy generation rate.

Introducing the following dimensionless parameters and variables in Eqs. (1–7):

$$\begin{aligned} y&=\frac{{\overline{y}}}{h},\quad u=\frac{{\overline{u}}}{UM},\quad \theta =\frac{E \left( {\overline{T}}-T_0\right) }{R T_0^2}, \quad \nonumber \\ M&=-\frac{h^2}{\mu U}\frac{{\mathrm {d}}p}{{\mathrm {d}}x},\quad \epsilon = \frac{R T_0}{E},\nonumber \\ \lambda&= \frac{QEAC_0h^2}{RT_0^2 k} \mathrm {e}^{-\frac{E}{RT_0}},\quad H^2=\frac{\sigma B_0^2 h^2}{\rho }, \quad \nonumber \\ \gamma&=\frac{h}{l},\quad l=\sqrt{\frac{\eta }{\mu }},\quad \beta = \sqrt{\frac{1}{Da}},\quad Da = \frac{K}{h^2},\quad \nonumber \\ \delta&= \frac{U^2\mu M^2 \mathrm {e}^{\frac{E}{RT_0}}}{QAC_0h^2},\quad \omega =\frac{Q_0RT_0^2}{QAEC_0 k}\mathrm {e}^{\frac{E}{RT_0}},\quad \nonumber \\ \alpha&= \frac{16 \sigma ^* T^3_\infty }{3kk^*}\quad \text{and}\quad N_s = \frac{h^2 E^2 E_G}{k R^2T_0^2} \end{aligned}$$
(8)

using the parameters and variables mentioned in Eq. (8) into (1)–(7), thereby obtaining the following boundary valued problems as:

$$\begin{aligned}&1+\frac{\mathrm{d}^{2}u}{{\mathrm{d}}y^{2}}-\frac{1}{\gamma }\frac{\mathrm{d}^{4}u}{{\mathrm {d}}y^4} -\left( \beta ^{2} +H^{2} \right) u = 0 \end{aligned}$$
(9)
$$\begin{aligned}&\left( 1+ \alpha \right) \frac{\mathrm{d}^{2}\theta }{{\mathrm{d}}y^{2}}+\lambda \left( \mathrm{e}^{\frac{\theta }{1+\epsilon \theta }}+\delta \left[ \left( \frac{{\mathrm{d}}u}{{\mathrm {d}}y}\right)^{2}+\frac{1}{\gamma }\left( \frac{\mathrm{d}^{2}u}{{\mathrm{d}}y^{2}}\right)^{2}\nonumber \right. \right. \\&\left. \left. \quad + \left( \beta ^{2} +H^{2} \right) u^{2}\right] +\omega \theta \right) =0 \end{aligned}$$
(10)

subject to the boundary conditions

$$\begin{aligned} u(0)= u''(0)= u''(1)= u(1)= 0 \quad \text{and}\quad \theta (0)= \theta (1)= 0 \end{aligned}$$
(11)

and the rate of entropy generation dimensionless form is:

$$\begin{aligned} N_s&=\left( 1+ \alpha \right) \left( \frac{{\mathrm {d}}\theta }{{\mathrm {d}}y}\right) ^2+\frac{\delta \lambda }{\epsilon }\left( \left( \frac{{\mathrm {d}}u}{{\mathrm {d}}y}\right) ^2 +\frac{1}{\gamma }\left( \frac{{\mathrm {d}}^2u}{{\mathrm {d}}y^2}\right) ^2\nonumber \right. \\&\quad \left. +\left( \beta ^2 +H^2\right) u^2\right) \end{aligned}$$
(12)

where u and \(\theta \) respectively stand for the motion and temperature of the fluid. Also, \(\alpha \), \(\gamma \), \(\lambda \), \(\epsilon \), \(\delta \), \(\beta \) and \(\omega \) are respectively parameters for conduction–radiation, the inverse of couple stress, Frank-Kamenetskii, activation energy, viscous heating, the porous medium permeability and heat source. Additionally, l is a relation representing the fluid molecular dimension, Da stands for Darcy number, H is the Hartman number for the magnetic strength and \(N_s\) represents the dimensionless entropy generation rate. Moreover, the solutions of Eqs. (9–11) exist naturally in a physical state, if and only if \(\gamma \ne 0\). Also, the present work is the same as [4] when \(\alpha \), H and \(\omega \) are all equal to zero.

3 Method of solution

In order to seek the solutions of the dimensionless equations (9) and (10) four and two times subject to boundary conditions (11) to obtain the followings:

$$\begin{aligned} u(y)&= b_0 y + \frac{a_0}{6} y^3 +\frac{\gamma }{24}y^4+\gamma \int _0^y\int _0^y\int _0^y\nonumber \\&\quad \int _0^y\left[ \frac{{\mathrm {d}}^2 u}{{\mathrm {d}}y^2}-\left( \beta ^2 +H^2 \right) u(y) \right] {\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y \end{aligned}$$
(13)
$$\begin{aligned} \theta (y)&=c_0 y - \frac{\lambda }{1+\alpha }\int _0^y\int _0^y\left[ \mathrm {e}^{\frac{\theta }{1+\epsilon \theta }}+\delta \left( \left( \frac{{\mathrm {d}}u}{{\mathrm {d}}y}\right) ^2\nonumber \right. \right. \\&\quad \left. \left. +\frac{1}{\gamma }\left( \frac{{\mathrm {d}}^2u}{{\mathrm {d}}y^2}\right) ^2+\left( \beta ^2+H^2\right) u^2\right) +\omega \theta \right] {\mathrm {d}}Y\;{\mathrm {d}}Y \end{aligned}$$
(14)

where \(a_0 = u'''(0)\), \(b_0 = u'(0)\) and \(c_0 = \theta '(0)\) which are to be ascertained by making use of the other boundary conditions stated in (11).

However, to obtain the solution to the governing equations (13) and (14), we introduce an infinite series solutions in the pattern of

$$\begin{aligned} u(y)=\sum _{n=0}^\infty u_n (y)\quad \text{and} \quad \theta (y)=\sum _{n=0}^\infty \theta _n (y) \end{aligned}$$
(15)

The series in (15) is replaced in Eqs. (13) and (14), to obtain the following:

$$\begin{aligned} u(y)&= b_0 y + \frac{a_0}{6} y^3 +\frac{\gamma }{24}y^4+\gamma \int _0^y\int _0^y\int _0^y\nonumber \\&\quad \int _0^y\left[ \frac{{\mathrm {d}}^2 \left( \sum _{n=0}^\infty u_n (y)\right) }{{\mathrm {d}}y^2}\right] {\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\nonumber \\&\quad -\gamma \left( \beta ^2 +H^2 \right) \int _0^y\int _0^y\int _0^y\nonumber \\&\quad \int _0^y\left( \sum _{n=0}^\infty u_n (y)\right) {\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y \end{aligned}$$
(16)
$$\begin{aligned} \theta (y)&=c_0 y -\frac{\lambda }{1+\alpha }\int _0^y\int _0^y\left[ \mathrm {e}^{\frac{\left( \sum _{n=0}^\infty \theta _n (y)\right) }{1+\epsilon \left( \sum _{n=0}^\infty \theta _n (y)\right) }}\nonumber \right. \\&\quad \left. +\,\delta \left( \left( \frac{{\mathrm {d}} \left( \sum _{n=0}^\infty u_n (y)\right) }{{\mathrm {d}}y}\right) ^2 +\frac{1}{\gamma }\left( \frac{{\mathrm {d}}^2 \left( \sum _{n=0}^\infty u_n (y)\right) }{{\mathrm {d}}y^2}\right) ^2\right) \right] \;{\mathrm {d}}Y\;{\mathrm {d}}Y\nonumber \\&\quad -\frac{\lambda }{1+\alpha }\left[ \delta \left( \beta ^2+H^2\right) \left( \sum _{n=0}^\infty u_n (y)\right) ^2+\omega \left( \sum _{n=0}^\infty \theta _n (y)\right) \right] {\mathrm {d}}Y\;{\mathrm {d}}Y \end{aligned}$$
(17)

However, to make use of ADM, the non-linear terms in (16) and (17) are thereby represented as:

$$\begin{aligned} \sum _{n=0}^\infty A_n(y)&=\frac{{\mathrm {d}}^2 \left( \sum _{n=0}^\infty u_n (y)\right) }{{\mathrm {d}}y^2}, \qquad \nonumber \\ \sum _{n=0}^\infty B_n(y)&=\mathrm {e}^{\frac{\left( \sum _{n=0}^\infty \theta _n (y)\right) }{1+\epsilon \left( \sum _{n=0}^\infty \theta _n (y)\right) }},\qquad \nonumber \\ \sum _{n=0}^\infty C_n(y)&=\left( \frac{{\mathrm {d}}\left( \sum _{n=0}^\infty u_n (y)\right) }{{\mathrm {d}}y}\right) ^2,\nonumber \\ \sum _{n=0}^\infty D_n(y)=&\left( \frac{{\mathrm {d}}^2 \left( \sum _{n=0}^\infty u_n (y)\right) }{{\mathrm {d}}y^2}\right) ^2\quad \text{and}\quad \nonumber \\ \sum _{n=0}^\infty E_n(y)=&\left( \sum _{n=0}^\infty u_n (y)\right) ^2 \end{aligned}$$
(18)

where the respective components \(A_0, A_1, A_2,\ldots \), \(B_0, B_1, B_2,\ldots \), \(C_0, C_1, C_2,\ldots \), \(D_0, D_1, D_2, \ldots \) and \(E_0, E_1, E_2, \ldots \) are referred to as Adomian polynomials. As s result of that, Eq. (18) is expanded to obtain the following:

$$\begin{aligned}&A_0 = u_0''(y),\; A_1 = u_1''(y),\; A_2 = u_2''(y),\;...\nonumber \\&B_0= \mathrm {e}^{\frac{\theta _0(y)}{\epsilon \theta _0(y)+1}},\; B_1=\frac{\theta _1(y) \mathrm {e}^{\frac{\theta _0(y)}{\epsilon \theta _0(y)+1}}}{\left( \epsilon \theta _0(y)+1\right) ^2},\nonumber \\&B_2= \frac{\mathrm {e}^{\frac{\theta _0(y)}{\epsilon \theta _0(y)+1}} \left( \theta _1(y){}^2 \left( -2 \epsilon ^2 \theta _0(y)-2 \epsilon +1\right) +2 \theta _2(y) \left( \epsilon \theta _0(y)+1\right) {}^2\right) }{2 \left( \epsilon \theta _0(y)+1\right) {}^4},\;...\nonumber \\&C_0= u_0'(y){}^2,\; C_1= 2 u_0'(y) u_1'(y),\; C_2=u_1'(y){}^2+2 u_0'(y) u_2'(y),\;... \nonumber \\&D_0= u_0''(y)^2,\; D_1= 2 u_0''(y) u_1''(y),\; D_2= u_1''(y)^2+2 u_0''(y) u_2''(y),\;...\nonumber \\&E_0=u_0(y)^2,\; E_1=2u_0(y)u_1(y),\; E_2=u_1(y)^2+2u_0(y)u_2(y),\;... \end{aligned}$$
(19)

With (18), the momentum and energy equations respectively reduce to:

$$\begin{aligned} u(y)&= b_0 y + \frac{a_0}{6} y^3 +\frac{\gamma }{24}y^4+\gamma \int _0^y\int _0^y\int _0^y\nonumber \\&\quad \int _0^y\left( \sum _{n=0}^\infty A_n(y)\right) {\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\nonumber \\&\quad -\gamma \left( \beta ^2 +H^2 \right) \int _0^y\int _0^y\int _0^y\int _0^y\left( \sum _{n=0}^\infty u_n (y)\right) {\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y \end{aligned}$$
(20)
$$\begin{aligned} \theta (y)&=c_0 y -\frac{\lambda }{1+\alpha }\int _0^y\int _0^y\left[ \sum _{n=0}^\infty B_n (y) +\delta \left( \sum _{n=0}^\infty C_n(y)\nonumber \right. \right. \\&\quad \left. \left. +\frac{1}{\gamma } \sum _{n=0}^\infty D_n(y)\right) \right] \;{\mathrm {d}}Y\;{\mathrm {d}}Y\nonumber \\&\quad -\frac{\lambda }{1+\alpha }\left[ \delta \left( \beta ^2+H^2\right) \left( \sum _{n=0}^\infty E_n (y)\right) +\omega \left( \sum _{n=0}^\infty \theta _n (y)\right) \right] {\mathrm {d}}Y\;{\mathrm {d}}Y \end{aligned}$$
(21)

Therefore, following iterative relation with the zeroth component as demonstrated in [32, 34, 43, 44] are obtained as follows:

$$\begin{aligned}&u_0(y)= b_0 y + \frac{a_0}{6} y^3 +\frac{\gamma }{24}y^4 \end{aligned}$$
(22)
$$\begin{aligned}&u_1(y)=\gamma \int _0^y\int _0^y\int _0^y\int _0^y\left( A_0(y)\right) {\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\nonumber \\&\qquad \quad -\gamma \left( \beta ^2 +H^2 \right) \int _0^y\int _0^y\int _0^y\int _0^y\left( u_0 (y)\right) {\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y \end{aligned}$$
(23)
$$\begin{aligned}&u_{n+1}(y)=\gamma \int _0^y\int _0^y\int _0^y\int _0^y\left( A_n(y)\right) {\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y \nonumber \\&\qquad \qquad -\gamma \left( \beta ^2 +H^2 \right) \int _0^y\int _0^y\int _0^y\int _0^y\left( u_n (y)\right) {\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y\;{\mathrm {d}}Y,\\ & \qquad\qquad\qquad n\;\ge \;1 \end{aligned}$$
(24)

and

$$\begin{aligned} \theta _0(y)&=0 \end{aligned}$$
(25)
$$\begin{aligned} \theta _1(y)&=c_0 y -\frac{\lambda }{1+\alpha }\int _0^y\int _0^y\left[ B_0(y) +\delta \left( C_0(y) +\frac{1}{\gamma } D_0(y) \nonumber \right. \right. \\&\quad \left. \left. +\left( \beta ^2+H^2\right) E_0 (y)\right) +\omega \; \theta _0 (y) \right] \;{\mathrm {d}}Y\;{\mathrm {d}}Y \end{aligned}$$
(26)
$$\begin{aligned} \theta _{n+1}(y)&=-\frac{\lambda }{1+\alpha }\int _0^y\int _0^y\left[ B_n(y) +\delta \left( C_n(y) \nonumber \right. \right. \\&\quad \left. \left. +\frac{1}{\gamma } D_n(y) +\left( \beta ^2+H^2\right) E_n (y)\right) +\omega \; \theta _n (y) \right] {\mathrm {d}}Y\;{\mathrm {d}}Y\;n\;\ge \;1 \end{aligned}$$
(27)

Therefore, Eqs. (22)–(27) are thereby programmed in a software package to secure the approximate series solutions used and discussed in the next section as

$$\begin{aligned} u(y)=\sum _{n=0}^k u_n (y)\quad \hbox {and} \quad \theta (y)=\sum _{n=0}^k \theta (y) \end{aligned}$$
(28)

However, to resolve the rate of entropy production rate within the fluid particles channel which are continuous due to transfer of heat and motion of the fluid. For easy computation, we split-up \(N_s\) in (12) as follows:

$$\begin{aligned} N_1&= \left( 1+ \alpha \right) \left( \frac{{\mathrm {d}}\theta }{{\mathrm {d}}y}\right) ^2 \quad \hbox {and} \quad N_2=\frac{\delta \lambda }{\epsilon }\left( \left( \frac{{\mathrm {d}}u}{{\mathrm {d}}y}\right) ^2\nonumber \right. \\&\quad \left. +\frac{1}{\gamma }\left( \frac{{\mathrm {d}}^2u}{{\mathrm {d}}y^2}\right) ^2+\left( \beta ^2 +H^2\right) u^2\right) \end{aligned}$$
(29)

where \(N_1\) indicates the irreversibility due to heat transfer with considerable radiative flux and \(N_2\) is the restricted entropy generation due to the outcome of viscous dissipation, couple stress, porous permeability and magnetic strength of the flow regime system.

In addition to that, the irreversibility distribution is defined as (\(\phi \)) and is given as:

$$\begin{aligned} \phi =\frac{N_2}{N_1} \end{aligned}$$
(30)

which shows that the heat transfer dominates when \(0\; \le \phi < \;1\) and fluid friction dominates when \(\phi \;>\;1\). This is used to determine the contribution of heat transfer in many engineering designs. As an alternative to the irreversibility distribution parameter, the Bejan number (Be) is defined as

$$\begin{aligned} Be=\frac{N_1}{N_s}=\frac{1}{1+\phi }, \quad \hbox {where} \quad 0\le Be\le 1 \end{aligned}$$
(31)

4 Results and discussion

In this section, we discuss the physical impact of important parameters on the fluid velocity, temperature and rate of entropy generation using tables and graphs. The impact of thermal radiation on a reactive hydromagnetic heat generating couple stress fluid flow through a porous channel is explained. In other words, our present result shall be coequal to [4] when the conduction–radiation parameter (\(\alpha \)), magnetic strength parameter called Hartman number (H) and internal heat source parameter (\(\omega \)) are all zero. Other effects of thermophysical parameters present in the fluid flow system that are not mentioned here were discussed in [4].

Table 1 Rapid convergence of the series solution for \(a_0\), \(b_0\) and \(c_0\)
Full size table
Table 2 Comparison of analytic result of velocity profile obtained using mADM
Full size table

The Table 1 indicates the rapid convergence of the series solution for the constants mentioned in Eqs. (20) and (21) with fewer iterations due to the mADM used to obtain the series solutions. Also, Table 2 showed the comparison of the series solution from mADM for velocity profile together with the exact solution. As observed, the absolute error of an average order of \(10^{-12}\) shows the efficiency and accuracy of mADM as alternative method to obtain approximate solutions to differential equations with either linear or non-linear terms or both.

The velocity distributions of fluid system with variation in inverse couple stress parameter (\(\gamma \)) and magnetic strength parameter (H) are respectively illustrated in Figs. 2 and 3. It is clearly seen that, the fluid velocity rises with an increment in (\(\gamma \)) in Fig. 2 while the reverse is noticed in Fig. 3 as H increases which is due to the retarding effect of magnetic strength in nature.

Fig. 2
figure 2

Effects of \(\gamma \) on u(y)

Full size image
Fig. 3
figure 3

Effects of H on u(y)

Full size image
Fig. 4
figure 4

Effects of \(\gamma \) on \(\theta (y)\)

Full size image
Fig. 5
figure 5

Effects of H on \(\theta (y)\)

Full size image
Fig. 6
figure 6

Effects of \(\omega \) on \(\theta (y)\)

Full size image
Fig. 7
figure 7

Effects of \(\alpha \) on \(\theta (y)\)

Full size image

The temperature distributions of the fluid regime are shown in Figs. 4, 5, 6 and 7 with respect to inverse couple stress parameter (\(\gamma \)) in Fig. 4, magnetic strength parameter (H) in Fig. 5, heat source parameter (\(\omega \)) in Fig. 6 and conduction–radiation parameter (\(\alpha \)) in Fig. 7. Clearly, it is observed that the fluid temperature of the fluid rises with rising values of (\(\gamma \)) in Fig. 4 and H in Fig. 5. The fluid property is due to the occurrence of Joules heating in heat equation thereby enhancing the increment in fluid temperature. Meanwhile, the converse is noticed in Figs. 6 and 7 where the increasing values of \(\omega \) in Fig. 6 and \(\alpha \) in Fig. 7 bring about a reduction in fluid temperature due to the thickness of fluid caused by inverse couple stress parameter and under the influence of thermal radiation.

The analysis of entropy generation in flow regime are displayed in Figs. 8, 9 and 10. In Fig. 8, the maximum rate of entropy generation occurs at the centreline of the flow channel and reduces with rising values of the magnetic strength parameter (H) while the maximum entropy generation rate occurs at the centreline of the flow channel as well but rises with increasing value of inverse couple stress parameter (\(\gamma \)) in Fig. 9. Interestingly, the entropy generation rate occurs at the walls of the plate channel and hereby slows down with the rising values of conduction–radiation parameter (\(\alpha \)). This shows that the impact of thermal radiation only affects the rate of disturbance at both upper and lower plates of the channel.

Fig. 8
figure 8

Effects of H on \(N_s\)

Full size image
Fig. 9
figure 9

Effects of \(\gamma \) on \(N_s\)

Full size image
Fig. 10
figure 10

Effects of \(\alpha \) on \(N_s\)

Full size image
Fig. 11
figure 11

Effects of H on Be

Full size image

The Bejan number of fluid flow systems are displayed in Figs. 11, 12 and 13. The irreversibility distribution ratio occurs at the centreline of the flow regime. In Fig. 11, an increment is noticed in Bejan number with rising values of Hartman number (H). Meanwhile, the Bejan number reduces with increasing values of conduction–radiation parameter (\(\alpha \)) in Fig. 12 and inverse couple stress parameter (\(\gamma \)) in Fig. 13.

Fig. 12
figure 12

Effects of \(\alpha \) on Be

Full size image
Fig. 13
figure 13

Effects of \(\gamma \) on Be

Full size image

5 Conclusion

In the present work carried out, the impact of thermal radiation on a reactive hydromagnetic couple stress fluid through a saturated channel filled with porous materials under the control of internal heat generation is investigated. The equations which govern momentum and energy are obtained using infinite series solutions in the form of mADM. The expressive impact of thermal radiation is broadly shown on the motion with the retarding effect of magnetic strength, reduction in fluid temperature due to thickness of fluid caused by inverse couple stress parameter, the rate of disturbance at both upper and lower plates and Bejan number of the fluid; which is a great insight to its application in industries and engineering fields which cannot be underestimated.