1 Introduction

Nowadays, Fast Fourier transform (FFT) is the significant approach in fast computing Discrete Fourier Transform (DFT) of the signals depending on its time complexity O(N log N), where N denotes the signal length. Recently, FFT is widely used all over the world for communications and signal processing [1,2,3]. However, it’s still a big challenge to how FFT can be outperformed and receives attention. Sparsity is the main feature of the signals to speed up FFT in the literature. Signal with N length is known as exactly K-sparse, where K non-zero frequencies with K < N. Secondly, the signal is generally K-sparse if all frequencies are non-zero [4, 5]. But we were only concerned about keeping the first K-largest (essential) frequencies in term of magnitudes and ignored the remainder, instead of estimating all frequencies [6].

Previously, H. Hassanieh et al. proposed the sparse Fast Fourier Transform (sFFT) [7,8,9]. The main idea of sFFT was to sample fewer frequencies (proportional to K) since most of the frequencies are zero or insignificant. In [9], BigBand was designed for the typical case of spectrum usage, where the occupied frequencies were randomly distributed with sparsity \(K = O(\sqrt N )\) whereas sFFT proved to be a worst-case distribution of occupied frequencies (sparsity), \(K = O(N)\). BigBand was designed under fewer constraints than sFFT so that it can be utilized more effectively compared to sFFT. Importantly, BigBand works with off-the-shelf low-speed analog to digital converters [9].

The impression behind sFFT is to sample less frequency (shortened as freq. hereafter) grids (proportional to K) instead of Keeping all freq. grids since most freq. grids are zero or insignificant. FFT based on such a downsampling strategy which will only cost O(K log K). Nevertheless, as the locations and values of the K non-zero freq. grids are unknown, downsampled freq. grids frequently lead to data loss and cannot achieve perfect reconstruction. Deal with this difficulty, sFFT utilizes the strategies of filtering and permutation, which can increase the probability of capturing useful information from downsampled freq. grids. sFFT [10] is state of the art, but there are some limitations, which is followed.1) Filtering and permutation operated on x and its related to N. The implementation of sFFT for generally k-sparse signals is very complicated, and it involves so many parameters that are difficult to set.

Recently, Ghazi et al. in MIT proposed another sFFT version [6] that costs O(KlogK) operations for exactly K-sparse signals. The basic idea is similar, first downsample original signals before recovering K non-zero freq. grids from the downsampled signals via error correction techniques, where [6] uses Reed-Solomon code, which is equivalent to the Moment-preserving problem considered in [7]. The key difference is that Ghazi et al.’s method recovers all K non-zero freq. grids once.

Hsieh et al. [10] proposed a new concept about sFFT by downsampling in the time domain (sFFT-DT)for the exactly K-sparse signals, assuming that distribution of the non-zero frequency grid is uniform. Their focus was to downsample the original input signal at the beginning; and then, directly conducts operations on downsampled signals, where the length of downsampled signals was kept proportional to \(O(K)\). Downsampling probably leads to “aliasing,” which means that different frequency grids of the original signal map into the same grid of the downsampled signal. In [10,11,12], the aliasing problem is reformulated as a moment-preserving problem (MPP) [13,14,15] and solved via existing approaches.

We proposed a new fast DFT method for generally sparse signals. The proposed method consists of three steps. First is downsampling of the original signal \({\mathbf{x}}\). Second is the calculation of the discrete Fourier Transform (DFT) of downsampled signals by using FFT, and third is the use of DFTs to determine and measure the K non-zero (significant) freq. grids \({\mathbf{X}}\). Downsampling will lead to “aliasing,” where different frequencies become indistinguishable in terms of their positions and values. According to, possible positions of nonzero freq. grid can be obtained from the solution of MPP. Based on the possible positions, several over-determined systems can be constructed, and the accurate positions and values of the aliasing terms can be determined by solving these systems. For generally sparse signals, the proposed method has a better recovery performance than the sFFT-DT method [10], and its complexity is reduced compared with the SFFT-DT method [10].

2 Methodology of proposed method

The proposed method consists of three steps. (1) Downsample the original signal in the time domain. (2) Calculate the discrete Fourier transform (DFT) of the downsampled signal by FFT. (3) Using the DFT of the downsampled signal to locate and estimate k-nonzero freq. girds of X. Steps 1 and 2 are simple and straightforward; thus, the proposed method focuses on step 3.

Suppose \({\mathbf{x}}_{d}\) is the downsampled signal taken from an original signal \({\mathbf{x}}\) of length N, where \(x_{d} [k] = x[dk],k \in \left[ {0,{N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d} - 1} \right]\) an integer \(d \ge 1\) is known as a downsampling factor. The length of the downsampled signal \({\mathbf{x}}_{d}\) is \({N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d}\). Let \({\mathbf{X}}_{d}\) be DFT of \({\mathbf{x}}_{d}\), where

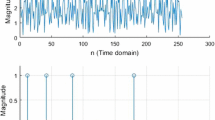
$$X_{d} [k] = \frac{1}{d}\left( {X[k] + X[k + {N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d}] + \cdots + X\left[ {k + {{(d - 1)N} \mathord{\left/ {\vphantom {{(d - 1)N} d}} \right. \kern-0pt} d}} \right]} \right).$$
(1)

From Eq. 1 it can be observed that each frequency grid \({\mathbf{x}}_{d}\) is the sum of d terms \({\mathbf{X}}\). When more than two terms on the right side of Eq. 1 are non-zero, “aliasing “occurs (Fig. 1).

Fig. 1
figure 1

Aliasing and its iterative solver

Full size image

For the solution of the aliasing problem, the shift property of DFT plays an important role [10]. Let \(x_{d,l} [k] = x[dk + l]\), where l represents the shift factor. Each freq. grid of \({\mathbf{X}}_{d,l}\), which is the DFT of \({\mathbf{x}}_{d,l}\), can be described as

$$X_{d,l} [k] = \frac{1}{d}\left( {X[k]e^{{{{i2\pi kl} \mathord{\left/ {\vphantom {{i2\pi kl} N}} \right. \kern-0pt} N}}} {\kern 1pt} + {\kern 1pt} X[k + \frac{N}{d}]e^{{i2\pi (k + \frac{N}{d}){l \mathord{\left/ {\vphantom {l N}} \right. \kern-0pt} N}}} {\kern 1pt} + \cdots + {\kern 1pt} X[k{\kern 1pt} + (d - 1)\frac{N}{d}]e^{{i2\pi (k + (d - 1)\frac{N}{d}){l \mathord{\left/ {\vphantom {l N}} \right. \kern-0pt} N}}} } \right).$$
(2)

\(X_{d,l} [k]\)’s can be obtained for different l’s. On the right side of Eq. 2, there usually exists d number of terms, and each term contains two unknown variables. For example, \(X[k]e^{{{{i2\pi kl} \mathord{\left/ {\vphantom {{i2\pi kl} N}} \right. \kern-0pt} N}}}\) composed of two variables \(X[k]\) and \(e^{{{{i2\pi kl} \mathord{\left/ {\vphantom {{i2\pi kl} N}} \right. \kern-0pt} N}}}\). Let a represent the number of non-zero terms on the right side of Eq. 2 and its ranges \(1 \le a \le d\). So, 2a equations are required to solve these 2a variables, and l lies within the range \(\left[ {0,2a - 1} \right].\)

Under the situation that no aliasing occurs (\(a = 1\)) we have \(X_{d,0} [k] = {{X[s_{1} ]} \mathord{\left/ {\vphantom {{X[s_{1} ]} d}} \right. \kern-0pt} d}\) and \(X_{d,1} [k] = {{X[s_{1} ]e^{{i2\pi s_{1} /N}} } \mathord{\left/ {\vphantom {{X[s_{1} ]e^{{i2\pi s_{1} /N}} } d}} \right. \kern-0pt} d}\), where \(s_{1}\) denote the position of the non-zero freq. grid term. The unknown position \(s_{1}\) can be obtained from \({{\left| {X_{d,1} [k]} \right|} \mathord{\left/ {\vphantom {{\left| {X_{d,1} [k]} \right|} {\left| {X_{d,0} [k]} \right|}}} \right. \kern-0pt} {\left| {X_{d,0} [k]} \right|}}\), and the value \(X[s_{1} ]\) at the position \(s_{1}\) can be estimated by \(X[s_{1} ] = dX_{d,0} [k].\)

When aliasing occurs, we shall consider Eq. 2 in another aspect. Let the product of known values \(d\) and \(X_{d,l} [k]\) be denoted by \(m_{l}\), i.e. \(m_{l} = dX_{d,l} [k]\). Let \(p_{j}\) and \(z_{j}^{l}\) describe the unknown \(X[s_{j} ]\) and \(e^{{{{i2\pi s_{j} l} \mathord{\left/ {\vphantom {{i2\pi s_{j} l} N}} \right. \kern-0pt} N}}}\), respectively, with \(1 \le j \le a\) and \(s_{j} \in S_{k}\), where \(S_{k} = \left\{ {k,k + \frac{N}{d}, \cdots ,k + \frac{(d - 1)N}{d}} \right\}\). Then (2) can be written as

$$m_{l} = p_{1} z_{1}^{l} + p_{2} z_{2}^{l} + \cdots + p_{a} z_{a}^{l} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le l \le 2a - 1$$
(3)

It is noticeable that \(m_{l}\) it is the “l”th moment with \(m_{l} = \sum\nolimits_{j = 1}^{a} {p_{j} z_{j}^{l} }\). The problem of solving \(p_{j}\)’s and zj’s with given different moments (\(m_{l}\)’s) is known as the MPP. Additionally, MPP is also equivalent to the error locator polynomial problem [13] reported by Ghazi et al.’s sFFT, which is a commonly used procedure in Reed-Solomon decoding [12]. Based on orthogonal polynomials [14], the solution of MPP is provided [15], and complete analytical solution for \(a \le 4\) was derived by Tsai et al. [15]. For example, the complete analytical solution \(a = 2\) is

$$\begin{aligned} & c_{d} = \left| {\begin{array}{*{20}c} {m_{0} } & {m_{1} } \\ {m_{1} } & {m_{2} } \\ \end{array} } \right|,c_{0} = \frac{1}{{c_{d} }}\left| {\begin{array}{*{20}c} { - m_{2} } & {m_{1} } \\ { - m_{3} } & {m_{2} } \\ \end{array} } \right|,c_{1} = \frac{1}{{c_{d} }}\left| {\begin{array}{*{20}c} {m_{0} } & { - m_{2} } \\ {m_{1} } & {m_{3} } \\ \end{array} } \right|, \\ & z_{0} = \frac{1}{2}\left[ { - c_{1} - (c_{1}^{2} - 4c_{0} )^{1/2} } \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z_{1} = \frac{1}{2}\left[ { - c_{1} + (c_{1}^{2} - 4c_{0} )^{1/2} } \right], \\ & p_{d} = z_{1} - z_{0} ,p_{0} = \frac{1}{{p_{d} }}\left| {\begin{array}{*{20}c} {m_{0} } & {m_{1} } \\ {m_{1} } & {z_{1} } \\ \end{array} } \right|,p_{1} = m_{0} - p_{0} . \\ \end{aligned}$$
(4)

Then the unknown positions \(s_{j}\)’s and values \(X[s_{j} ]\) of the aliasing non-zero terms on the right side of Eq. 2 can be determined from \(p_{j}\) and \(z_{j}^{l}\) with \(j = 1,2.\)

3 Proposed method

In this article, we propose a new method to fast compute DFT of generally K sparse signals. The schematic illustration of our proposed method \(a = 2\) is demonstrated in Fig. 2, and this method is feasible for \(a \le 4\) the analytic solutions of MPP.

Fig. 2
figure 2

Schematic illustration of the proposed method

Full size image

For \(a = 2\), we use three time shifts to get four downsampled signals \({\mathbf{x}}_{d,l}\) with \(0 \le l \le 3\).The DFT \({\mathbf{X}}_{d,l}\) of the downsampled signals can be expressed as

$$X_{d,l} [k] = \frac{1}{d}\left( {X[s_{1} ]e^{{{{i2\pi s_{1} l} \mathord{\left/ {\vphantom {{i2\pi s_{1} l} N}} \right. \kern-0pt} N}}} + X[s_{2} ]e^{{{{i2\pi s_{2} l} \mathord{\left/ {\vphantom {{i2\pi s_{2} l} N}} \right. \kern-0pt} N}}} } \right),\quad 0 \le l \le 3$$
(5)

where \(s_{1}\) and \(s_{2}\) denote positions of the two aliasing terms, and \(X[s_{1} ],X[s_{2} ]\) denote their values.

According to the above section, we can estimate the values of \((s_{1} ,s_{2} )\) based on the solution of MPP. If the signal-to-noise ratio (SNR) of the original signal x is sufficiently large, the solution of MPP can approach to the real value of \((s_{1} ,s_{2} )\). However, when the original signal is with low SNR, the estimated positions \((\hat{s}_{1} ,\hat{s}_{2} )\) based on the MPP method might no longer belong to the set \(S_{k}\). Let \(s^{\prime}_{1}\) and \(s^{\prime}_{2}\) denote the values in \(S_{k}\) that nearest to \(\hat{s}_{1}\) and \(\hat{s}_{2}\) respectively. Then we can consider that the real positions \((s_{1} ,s_{2} )\) satisfy.

$$\begin{aligned} s_{1} \in \left[ {s^{\prime}_{1} - {N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d},s^{\prime}_{1} ,s^{\prime}_{1} + {N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d}} \right], \hfill \\ s_{2} \in \left[ {s^{\prime}_{2} - {N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d},s^{\prime}_{2} ,s^{\prime}_{2} + {N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d}} \right]. \hfill \\ \end{aligned}$$
(6)

For simplicity, define \(\varGamma_{1} = \left[ {s^{\prime}_{1} - {N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d},s^{\prime}_{1} ,s^{\prime}_{1} + {N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d}} \right]\) and \(\varGamma_{2} = \left[ {s^{\prime}_{2} - {N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d},s^{\prime}_{2} ,s^{\prime}_{2} + {N \mathord{\left/ {\vphantom {N d}} \right. \kern-0pt} d}} \right]\). Then we can get nine possible \((s_{1} ,s_{2} )\) pairs, by choosing one value from \(\varGamma_{1}\) and choose the other one from \(\varGamma_{2}\). In order to determine the accurate positions \((s_{1} ,s_{2} )\), we use the possible pairs to construct over-determined systems. Then the accurate positions and values of the aliasing terms can be recovered by solving these systems [8].

For each possible pair of \((s_{1} ,s_{2} )\), Eq. 5 becomes an over-determined linear system of equations, in which there exist four equations and two unknowns \(X[s_{1} ],X[s_{2} ]\). Let \({\mathbf{z}} = \left[ {X[s_{1} ],X[s_{2} ]} \right]^{\text{T}}\) and \({\mathbf{y}} = \left[ {X_{d,0} [k],X_{d,1} [k],X_{d,2} [k],X_{d,3} [k]} \right]^{\text{T}}\). Then Eq. 5 can be written into matrix form as \({\mathbf{y}} = {\mathbf{Az}}\), where

$${\mathbf{A}} = \frac{1}{d}\left[ {\begin{array}{*{20}c} 1 & 1 \\ {e^{{i2\pi s_{1} /N}} } & {e^{{i2\pi s_{2} /N}} } \\ {e^{{i4\pi s_{1} /N}} } & {e^{{i4\pi s_{2} /N}} } \\ {e^{{i6\pi s_{1} /N}} } & {e^{{i6\pi s_{2} /N}} } \\ \end{array} } \right]$$
(7)

As the matrix A is with full column rank, the unknown z can be solved by \({\hat{\mathbf{z}}} = {\mathbf{A}}^{\dag } {\mathbf{y}}\), where \({\mathbf{A}}^{\dag } = ({\mathbf{A}}^{\text{H}} {\mathbf{A}})^{ - 1} {\mathbf{A}}^{\text{H}}\) is the Moore–Penrose pseudo-inverse of A.

The recovery error can be defined as \(e = \left\| {{\mathbf{y}} - {\mathbf{A\hat{z}}}} \right\|_{2}\). After solving the over-determined system for each possible pair, the accurate positions \((s_{1} ,s_{2} )\), as well as the corresponding values \(X[s_{1} ],X[s_{2} ]\), can be determined by finding the minimum recovery error.

In the BigBand method proposed by H. Hassanieh et al. [9], there are \({{d(d - 1)} \mathord{\left/ {\vphantom {{d(d - 1)} 2}} \right. \kern-0pt} 2}\) possible \((s_{1} ,s_{2} )\) pairs, which means that \({{d(d - 1)} \mathord{\left/ {\vphantom {{d(d - 1)} 2}} \right. \kern-0pt} 2}\) over-determined systems need to be solved. Meanwhile, with the assistance of the solution to MPP, only nine possible pairs need to be considered in our method. As normally \(d > > 5\), our method requires less digital computation compared to the BigBand method and sFFT-DT.

4 MMP error analysis problem

When we are dealing with generally k sparse signal, the solved roots no longer belong to the set \(S_{k}\) of real roots, as mentioned above. Which correspond to candidate correct positions. However, if SNR is large (> 20 dB), then the observation shows the z’s can approach real roots. Figure 3 shows the real roots (in red) and solves roots (in blue) in complex coordinates under different SNR values. The real roots must locate with in the unit circle with radius = 1, sine they belong to Sk, and each element of Sk satisfies \(\left| {e^{{i2\pi \left( {k + \frac{N}{2}}\right)l/N}} } \right| = 1.\)

Fig. 3
figure 3

The bias between solved roots/estimated locations (blue circle) and real roots/candidate locations (red circle) in the polar plane under SNR = 25

Full size image

Nevertheless, the solved roots could deviate from the real roots and cannot be located within the unit circles. In order to close the gap between the candidate positions and estimated positions, the proposed method uses the minimum mean square method.

5 Proposed algorithm flow chart

See Fig. 4.

Fig. 4
figure 4

Flow chart of the proposed algorithm

Full size image

6 Result and discussion

During simulations in the following work, the signal \({\mathbf{x}}\), in time domain was generated as followed. Firstly, generate a frequency-domain signal \({\mathbf{X}}_{0}\), which consists of K non-zero entries and N − K zeros where N = 1024, Then \({\mathbf{x}}\) is obtained by adding the inverse FFT of \({\mathbf{X}}_{0}\) with white Gaussian noise.

Simulations are conducted to compare the proposed method with SFFT-DT and BigBand in terms of recovery performance and computational time. For all three methods, the downsampling factor d = 16 is fixed, and we suppose that the maximum number of non-zero aliasing terms is \(a_{m} = 2\). Define successful rate as the fraction of occupied frequencies, which are successfully recovered. For different sparsity K, the successful rate of the proposed method versus SNR has been measured and reported in Fig. 5. Experimental results show that the recovery performance improves gradually with the decrease of K, as larger K causes more aliasing situations. Figure 6 shows the results of reconstruction accuracy versus SNR for the three methods mentioned before with K = 25. It is observed that our proposed method algorithm has a better recovery performance with the other two methods. In the BigBand method proposed by H.Hassanieh et al. [9], there are d(d − 1)/2 possible pairs, \((s_{1} ,s_{2} )\) which mean that d(d-1)/2 over-determined systems need to be solved. Meanwhile, with the assistance of the solution to MPP, only nine possible pairs are needed to be considered in our method. As normally d ≫ 5, our method requires less digital computation compared to BigBand as shown in Fig. 7].

Fig. 5
figure 5

Recovery performance on different SNRs

Full size image
Fig. 6
figure 6

Recovery performance comparisons

Full size image
Fig. 7
figure 7

Comparisons of false-alarm probability among the proposed method, BigBand, sFFT-DT

Full size image

The false-alarm probability is defined as the fraction of empty frequencies, incorrectly reported as occupied. Figure 7 shows that the proposed method has lower false-alarm rate compared with the other two methods under different SNRs. The false-alarm probability of proposed method stays below 0.04 with \({\text{SNR}} \ge 25\,{\text{dB}}\) (Fig. 8).

Fig. 8
figure 8

Computational time on different signal sparsity

Full size image

7 Conclusion

For generally sparse signals, this paper presents a new fast computing DFT method. This method is based on downsampling and combines MPP with the BigBand method. All operations of solving MPP are linear with analytical solutions involved. The BigBand method is utilized to modify the error of the solution to MPP, caused by the interference of insignificant freq. grids. Theoretical complexity analysis and simulation results demonstrate that the proposed method is hardware-friendly and has a better performance as compared to other reported algorithms.