1 Introduction

In the application of radar detection for the moving target, an effective approach for the improvement of the output signal-to-noise ratio (SNR) is prolonging the coherent integration time. However, the complex motion of the target will induce severe range migration and Doppler frequency migration after conducting range compression, which greatly degrade the detection ability of radar [1, 2].

The linear range migration, i.e., range walk, is caused by the uniform motion of the target during a long integration period. In order to remove range walk, some algorithms have been proposed which aim at accumulating the energy along the linear trajectory, such as Radon transform (RT) [3,4,5], Hough transform (HT) [6,7,8,9], Radon Fourier transform (RFT) [10,11,12] and improved axis rotation MTD (IAR-MTD) [13]. The above methods need to conduct the parameter searching process which has a high computational burden. In [14], keystone transform (KT) is proposed to rescale the slow time axis and eliminate the coupling between range frequency and slow time. As a linear correction algorithm, KT has a good anti-noise performance and does not require search. In [15], range frequency polynomial-phase transform (RFPPT) is proposed to correct range walk via reducing the order of slow time variable, which has a lower computational complexity than KT.

The target’s high-order motions will induce the nonlinear range migration, i.e., range curvature. Meanwhile, Doppler frequency migration will occur and cause the target’s energy to spread over multiple Doppler frequency cells. In order to accumulate the target’s energy in both range and Doppler dimensions, some brute-force searching algorithms have been proposed with a heavy computational load, e.g., the generalized Radon Fourier transform (GRFT) [16] and polynomial Radon-polynomial Fourier transform (PRPFT) [17]. In addition, the high-order KT algorithms without search have been adopted, e.g., the second-order keystone transform (SOKT) [18] and the third-order keystone transform (TOKT) [19]. However, there will be a residual trajectory existing after conducting KT when the maneuvering target has a complex motion, thus some extra operations are needed to compensate the residual range migration. In [20], the parameter separation (PS)–acceleration search (AS) approach is proposed for target focusing, it only needs to search for the target’s acceleration after isolating it from other motion parameters.

Improved from PS–AS, a novel maneuvering target detection algorithm is proposed in this paper. The main contributions of this work are presented as follows:

  1. 1.

    Through theoretical analysis, it is demonstrated that the proposed method has no need to search for the target’s motion parameters, thus a lower computational cost can be obtained compared with the traditional methods based on brute-force search.

  2. 2.

    The non-uniform sparse Fourier transform (NUSFT) has been proposed, which is the combination of non-uniform fast Fourier transform (NUFFT) [21,22,23,24] and sparse Fourier transform (SFT) [25].

  3. 3.

    The multiple targets detection ability of the proposed method has been analyzed.

  4. 4.

    The good detection performance of the proposed method has been validated via the results of some simulation experiments.

The outline of this paper is organized as follows. Section 2 gives the signal model of radar maneuvering target detection. Section 3 introduces the proposed method for mono- and multi- targets detection. Section 4 gives the computational complexity analysis. Section 5 shows the results of some simulation experiments. Finally, the conclusion is drawn in Sect. 6.

2 Signal model

Suppose that a radar transmits LFM pulses, where the number of coherent integrated pulses is \(M\), the pulse repetition interval is \(T_{r}\). The transmitted signal has the following form:

$$s_{t} (t_{m} ,t) = {\text{rect}}\left( {\frac{t}{{T_{p} }}} \right)\exp (j\pi \mu t^{2} )\exp (j2\pi f_{c} t_{m} )$$
(1)

In (1), \(t\) is the fast time, \(t_{m} = mT_{r}\) is the slow time, where \(m = - \frac{M - 1}{2}, \ldots , - 1,0,1, \ldots ,\frac{M - 1}{2}\), \(M\) is assumed to be an odd integer. \(T_{p}\), \(f_{c}\), \(\mu\) and \({\text{rect}}\left( \cdot \right)\) represent the pulse duration, carrier frequency, chirp rate and rectangle window, respectively.

The instantaneous slant range between radar and the maneuvering target can be represented as

$$R\left( {t_{m} } \right) = R_{0} + c_{1} t_{m} + c_{2} t_{m}^{2} + c_{3} t_{m}^{3}$$
(2)

where \(R_{0}\), \(c_{1}\), \(c_{2}\) and \(c_{3}\) denote the initial slant range, radial velocity, acceleration and jerk of the target, respectively.

The received baseband signal is expressed as

$$s_{r} (t_{m} ,t) = A_{1} {\text{rect}}\left[ {\frac{{t - 2R(t_{m} )/c}}{{T_{p} }}} \right]\exp \left[ {j\pi \mu \left( {t - \frac{{2R(t_{m} )}}{c}} \right)^{2} } \right]\exp \left[ { - j\frac{4\pi }{\lambda }R\left( {t_{m} } \right)} \right]$$
(3)

where \(A_{1}\) denotes the signal amplitude, \(\lambda = \frac{c}{{f_{c} }}\) is the wavelength of the transmitted signal, \(c\) denotes the light speed.

After performing pulse compression, the signal in the range frequency domain can be expressed as

$$S_{c} (t_{m} ,f) = A_{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left[ { - j\frac{4\pi }{c}\left( {f + f_{c} } \right)\left( {R_{0} + c_{1} t_{m} + c_{2} t_{m}^{2} + c_{3} t_{m}^{3} } \right)} \right]$$
(4)

where \(A_{2}\) denotes the signal amplitude, \(f\) is the range frequency variable, \(B = \mu T_{p}\) is the bandwidth of the transmitted signal.

After performing the range inverse fast Fourier transform (IFFT), the compressed signal in the range time domain is obtained as

$$\begin{aligned} s_{c} (t_{m} ,t) & = A_{3} {\text{sinc}}\left\{ {B\left[ {t - \frac{2}{c}\left( {R_{0} + c_{1} t_{m} + c_{2} t_{m}^{2} + c_{3} t_{m}^{3} } \right)} \right]} \right\} \\ & \quad \times \exp \left[ { - j\frac{4\pi }{\lambda }\left( {R_{0} + c_{1} t_{m} + c_{2} t_{m}^{2} + c_{3} t_{m}^{3} } \right)} \right] \\ \end{aligned}$$
(5)

where \(A_{3}\) denotes the signal amplitude after performing range IFFT. From (5), one can see that \(c_{1}\) will cause range walk and Doppler center shift, while \(c_{2}\) and \(c_{3}\) will cause range curvature and Doppler frequency migration. During a long integration time, both range migration and Doppler frequency migration will deteriorate the target detection performance. In the next section, we will propose an efficient algorithm to overcome the above problems and accumulate the target’s energy coherently.

3 Coherent integration via PS–SOKT–NUSFT

3.1 Mono-target detection

3.1.1 Range migration correction

According to the aforementioned signal model, it can be seen that the slow time axis is symmetric around \(t_{m} = 0\), then the reversed slow time variable \(\overleftarrow {{t_{m} }}\) can be expressed as below

$$\overleftarrow {{t_{m} }} = - mT_{r} \, \left( {m = - \frac{M - 1}{2}, \ldots , - 1,0,1, \ldots ,\frac{M - 1}{2}} \right)$$
(6)

Inserting (6) into (4), we obtain the slow time reversed form of the range compressed signal, i.e.,

$$S_{c} (\overleftarrow {{t_{m} }} ,f) = A_{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left[ { - j\frac{4\pi }{c}\left( {f + f_{c} } \right)\left( {R_{0} + c_{1} \overleftarrow {{t_{m} }} + c_{2} \overleftarrow {{t_{m} }}^{2} + c_{3} \overleftarrow {{t_{m} }}^{3} } \right)} \right]$$
(7)

Then, the PS operation is defined as [20]

$$\begin{aligned} S_{1} (t_{m} ,f) & = S_{c} (t_{m} ,f)S_{c} (\overleftarrow {{t_{m} }} ,f) \\ & = A_{2}^{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left[ { - j\frac{8\pi }{c}\left( {f + f_{c} } \right)R_{0} } \right] \\ & \quad \times \exp \left\{ { - j\frac{4\pi }{c}\left( {f + f_{c} } \right)\left[ {c_{1} \left( {m - m} \right)T_{r} } \right]} \right\} \\ & \quad \times \exp \left\{ { - j\frac{4\pi }{c}\left( {f + f_{c} } \right)\left[ {c_{2} \left( {m^{2} + m^{2} } \right)T_{r}^{2} } \right]} \right\} \\ & \quad \times \exp \left\{ { - j\frac{4\pi }{c}\left( {f + f_{c} } \right)\left[ {c_{3} \left( {m^{3} - m^{3} } \right)T_{r}^{3} } \right]} \right\} \\ & = A_{2}^{2} {\text{rect}}\left( {\frac{f}{B}} \right)\exp \left[ { - j\frac{8\pi }{c}\left( {f + f_{c} } \right)\left( {R_{0} + c_{2} t_{m}^{2} } \right)} \right] \\ \end{aligned}$$
(8)

The expression of (8) in the range time domain is written as below

$$s_{1} \left( {t_{m} ,t} \right) = A_{4} {\text{sinc}}\left\{ {B\left[ {t - \frac{4}{c}\left( {R_{0} + c_{2} t_{m}^{2} } \right)} \right]} \right\}\exp \left[ { - j\frac{8\pi }{\lambda }\left( {R_{0} + c_{2} t_{m}^{2} } \right)} \right]$$
(9)

where \(A_{4}\) denotes the signal amplitude.

In (9), it can be seen that the effect of target’s velocity and jerk has been removed, whereas there is still a trajectory existing, i.e.,

$$R'\left( {t_{m} } \right) = 2\left( {R_{0} + c_{2} t_{m}^{2} } \right)$$
(10)

In order to correct the residual range curvature, SOKT is conducted to remove the coupling between \(f\) and \(t_{m}^{2}\), i.e.,

$$t_{m} = \left( {\frac{{f_{c} }}{{f + f_{c} }}} \right)^{1/2} t_{n}$$
(11)

where \(t_{n}\) represents the scaled slow time after performing SOKT.

Inserting (11) into (8) and performing range IFFT, we obtain

$$s_{2} (t_{n} ,t) = A_{5} {\text{sinc}}\left[ {B\left( {t - \frac{{4R_{0} }}{c}} \right)} \right]\exp \left( { - j\frac{8\pi }{\lambda }c_{2} t_{n}^{2} } \right)$$
(12)

where \(A_{5}\) denotes the signal amplitude after performing range IFFT.

From (12), one can see that no range migration remains after conducting SOKT, thus the target’s energy is located in one fixed range cell. However, there is still Doppler frequency migration to be corrected in the slow time dimension.

3.1.2 Coherent integration via NUSFT

In (12), the extracted signal at \(t = \frac{{4R_{0} }}{c}\) is modeled as a LFM signal with zero centroid frequency, thus a direct fast Fourier transform (FFT) performed along the slow time axis is invalid because the sampling points are non-uniform. In order to realize coherent integration, we perform FT with respect to \(t_{n}^{2}\) as below

$$\begin{aligned} S_{3} (f_{n} ,t) & = \int {s_{2} (t_{n} ,t)} \exp \left( { - j2\pi f_{n} t_{n}^{2} } \right)dt_{n}^{2} \\ & = A_{6} {\text{sinc}}\left[ {B\left( {t - \frac{{4R_{0} }}{c}} \right)} \right]\text{sinc}\left( {f_{n} + \frac{{4c_{2} }}{\lambda }} \right) \\ \end{aligned}$$
(13)

where \(f_{n}\) represents the frequency variable with respect to \(t_{n}\), \(A_{6}\) denotes the signal amplitude after conducting FT.

It can be seen that in (13) that the signal’s energy is accumulated as a solo peak and the target can be detected. In realistic applications, performing non-uniform discrete Fourier transform (NUDFT) to realize FT needs a large number of complex multiplications which are computationally expensive. For the sake of improving efficiency, the existing NUFFT algorithm can be adopted to fulfill FT of the non-uniformly sampled signal, which has the same computational complexity as FFT [21,22,23,24]. Thus, the slow time FT conducted in (13) can be implemented via NUFFT which is faster than DFT. Here, noticing that the frequency domain output is sparse since \(M \gg 1\), thus the integration process can be further accelerated via replacing the FFT in NUFFT by a faster spectrum analysis tool, i.e., SFT [25]. Below, the procedures of the the proposed NUSFT algorithm are given.

Suppose that the input data \(s_{n}\) is sampled at non-uniform points \(x_{n}\) with the length of \(M\) which is equal to the length of output signal. Set the oversampling factor and interpolation length as \(p\) and \(L\), respectively. Select Kaiser-Bessel window as below [24]

$$\phi \left( x \right) = \sqrt {\frac{2}{\pi }} \frac{{\sinh \left( {\alpha \sqrt {L^{2} - x^{2} } } \right)}}{{\sqrt {L^{2} - x^{2} } }}$$
(14)
$$\phi \left( \xi \right) = \left\{ {\begin{array}{*{20}l} {I_{0} \left( {L\sqrt {\alpha^{2} - \xi^{2} } } \right),} \hfill & {\left| \xi \right| \le \alpha } \hfill \\ {0,} \hfill & {\left| \xi \right| > \alpha } \hfill \\ \end{array} } \right.$$
(15)

where \(\alpha = \pi \left( {2 - \frac{1}{p}} \right) - 0.01\) is the width of the window function.

Conduct the following steps:

  1. 1.

    Calculate the Fourier coefficients:

$$u_{{\mu_{n} + l}} = \sum\limits_{n = 1}^{M} {\sum\limits_{l = - L}^{L} {\frac{1}{{\sqrt {2\pi } }}\phi \left( {px_{n} - \mu_{n} - l} \right)s_{n} } }$$
(16)

where \(\mu_{n}\) is a vector which is the nearest integer to \(px_{n}\).

  1. 2.

    Compute the SFT of \(u_{j}\):

$$U_{j} = {\text{SFT}}\left( {u_{j} } \right)$$
(17)

where \(j = - \frac{pM}{2}, - \frac{pM}{2} + 1, \ldots ,\frac{pM}{2} - 1\).

  1. 3.

    Scale the values to obtain the NUSFT output:

$$S_{n} = \frac{{U_{n} }}{{\phi_{n} }}$$
(18)

where \(\, n = - \frac{M}{2}, - \frac{M}{2} + 1, \ldots ,\frac{M}{2} - 1\).

It should be noted that in (17), SFT is conducted to replace the \(pM\)-points FFT which is performed in NUFFT. Set the sparsity parameter in NUSFT as 1 and under the condition that \(p \ll M\), the computational complexities of NUSFT, NUFFT and NUDFT are, respectively, \(O\left( {\sqrt {N\log_{2} N} \log_{2} N} \right)\), \(O\left( {N\log_{2} N} \right)\), and \(O\left( {N^{2} } \right)\), thus it is evident that NUSFT can realize energy integration with the lowest computational cost.

3.2 Multi-targets detection

In the aforementioned analysis, the effectiveness of the proposed method for mono-target detection has been demonstrated. Nevertheless, there might be more than one target for radar to detect in practical situations, thus it is necessary to discuss the ability of PS–SOKT–NUSFT to suppress cross terms. Note that the number of targets is \(K\), then the compressed signal in the range frequency domain can be expressed as

$$\begin{aligned} S_{c} (t_{m} ,f) & = \sum\limits_{i = 1}^{K} {A_{2,i} {\text{rect}}\left( {\frac{f}{B}} \right)} \\ & \quad \times \exp \left[ { - j\frac{4\pi }{c}\left( {f + f_{c} } \right)\left( {R_{0,i} + c_{1,i} t_{m} + c_{2,i} t_{m}^{2} + c_{3,i} t_{m}^{3} } \right)} \right] \\ \end{aligned}$$
(19)

where \(R_{0,i}\), \(c_{1,i}\), \(c_{2,i}\) and \(c_{3,i}\) represent, respectively, the initial slant range, radial velocity, acceleration and jerk of the ith target. After performing PS and SOKT on \(S_{c} (t_{m} ,f)\), we obtain the compressed signal in the range time domain, i.e.,

$$\begin{aligned} s_{2} (t_{n} ,t) & = s_{2,self} (t_{n} ,t) + s_{2,cross} (t_{n} ,t) \\ & = \sum\limits_{i = 1}^{K} {A_{5,i} {\text{sinc}}\left[ {B\left( {t - \frac{{4R_{0,i} }}{c}} \right)} \right]\exp \left( { - j\frac{8\pi }{\lambda }c_{2,i} t_{n}^{2} } \right)} \\ & \quad + \sum\limits_{i = 1}^{K} {\sum\limits_{j = 1,j \ne i}^{K} {A_{5,ij} {\text{sinc}}\left[ {B\left( {t - \tau_{ij} } \right)} \right]} } \\ & \quad \times \exp \left[ { - j\frac{4\pi }{\lambda }\left( {\nabla R_{0,ij} + \Delta c_{1,ij} t_{n} + \nabla c_{2,ij} t_{n}^{2} + \Delta c_{3,ij} t_{n}^{3} } \right)} \right] \\ \end{aligned}$$
(20)

where

$$\tau_{ij} = \frac{{2\nabla R_{0,ij} + \Delta c_{1,ij} t_{n} - \Delta c_{3,ij} t_{n}^{3} }}{c}$$
(21)
$$\nabla R_{0,ij} = R_{0,i} + R_{0,j}$$
(22)
$$\Delta c_{1,ij} = c_{1,i} - c_{1,j}$$
(23)
$$\nabla c_{2,ij} = c_{2,i} + c_{2,j}$$
(24)
$$\Delta c_{3,ij} = c_{3,i} - c_{3,j}$$
(25)

From (20) to (25), it is obvious that after conducting PS and SOKT, the energy of each self term has been relocated in one range cell, whereas range migration still exists for cross terms. What’s more, the first- and third- order phase terms will affect the focusing performance of cross terms in the slow time domain. Therefore, the energy of cross terms will be suppressed while each self term will generate as a solo peak after conducting slow time NUSFT.

The detailed procedures of the proposed method are shown as below.

  1. 1.

    Perform pulse compression of the radar echo data and obtain the signal \(S_{c} (t_{m} ,f)\) in the range frequency domain.

  2. 2.

    Multiply \(S_{c} (t_{m} ,f)\) with its slow time reversed result \(S_{c} (\overleftarrow {{t_{m} }} ,f)\) to remove the effect of velocity and jerk.

  3. 3.

    Conduct SOKT and range IFFT to correct residual range curvature.

  4. 4.

    Carry out NUSFT along the slow time axis to fulfill coherent integration and detect the target.

The flowchart of the proposed algorithm is shown in Fig. 1.

Fig. 1
figure 1

Flowchart of the proposed method

Full size image

4 Computational complexity analysis

In this section, the computational complexity of the proposed method is analyzed. Denote that the number of range cells and integrated pulses are \(N\) and \(M\), respectively. The number of large frequency coefficients in NUSFT is set as 1. For the PS operation which needs a 2-D complex multiplication, the computational complexity is \(O\left( {NM} \right)\). Subsequently, the chirp-z transform (CZT) based SOKT and range IFFT are performed with the computational complexity of \(O\left[ {NM\left( {\log_{2} N + \log_{2} M} \right)} \right]\). Lastly, the slow time NUSFT is conducted with the computational complexity of \(O\left( {N\sqrt {M\log_{2} M} \log_{2} M} \right)\). As for the the energy accumulation process in the PS–AS algorithm [20], a 2-D matched filtering process is conducted in each search for acceleration, which has the computational complexity of \(O\left[ {N_{s2} NM\left( {1 + \log_{2} N + \log_{2} M} \right)} \right]\), where \(N_{s2}\) represents the searching times of acceleration. For comparison, Table 1 shows the computational complexities of PS–SOKT–NUSFT and PS–AS. Define the the computational complexity ratio as the complexity metric of PS–SOKT–NUSFT divided by that of PS–AS, Fig. 2 depicts the curve of computational complexity ratio against pulse number under the assumption that \(N = M = N_{s2}\). It is evident that with the increase of pulse number, PS–SOKT–NUSFT has a much lower computational complexity than PS–AS, due to its two advantages: (1) It has no need to search for the target’s motion parameters; (2) It applies NUSFT instead of NUDFT to speed up the coherent integration process.

Table 1 Computational complexities
Full size table
Fig. 2
figure 2

Computational complexity ratio

Full size image

5 Numerical experiments and performance analysis

In this section, several simulation experiments are conducted to validate effectiveness of the proposed method. Radar system parameters are listed in Table 2, complex white Gaussian noise is added to the radar echo signal with the input SNR set as − 3 dB.

Table 2 Radar system parameters
Full size table

5.1 Proposed method with mono-target detection

Consider a maneuvering target which has the motion parameters of \(c_{1} = 100{\text{ m/s}}\), \(c_{2} = 30{\text{ m/s}}^{2}\) and \(c_{3} = 15{\text{ m/s}}^{3}\), respectively. At \(t_{m} = 0\), the target is located at the \(200{\text{th}}\) range cell. Figure 3a shows the target’s trajectory after performing range compression, it can be seen that severe range migration occurs due to the long time complex motion of the target. Figure 3b gives the target’s trajectory after conducting the PS operation, it is observed that only the symmetric range curvature caused by acceleration exists. According to (2) and (10), it can be calculated that the migrated range cells before and after conducting PS operation are, respectively, \(183{\text{th}} \to 200{\text{th}} \to 230{\text{th}}\) and \(413{\text{th}} \to 400{\text{th}} \to 413{\text{th}}\).

Fig. 3
figure 3

Simulation results of a single maneuvering target. a Target’s trajectory after performing range compression. b Target’s trajectory after performing the PS operation. c Target’s trajectory after performing SOKT. d Focused result of slow time NUSFT

Full size image

Figure 3c shows the result after performing SOKT, it is evident that the range curvature has been corrected effectively. Finally, the target is well focused via carrying out the slow time NUSFT, as shown in Fig. 3d.

5.2 Proposed method with multi-targets detection

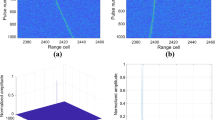
In this section, the radar is used to detect two maneuvering targets. The motion parameters of target 1 are the same as that in Sect. 5.1, the motion parameters of target 2 are \(c_{1} = 30{\text{ m/s}}\), \(c_{2} = - 15{\text{ m/s}}^{2}\) and \(c_{3} = - 5{\text{ m/s}}^{3}\), respectively. At \(t_{m} = 0\), target 2 is located at the \(220{\text{th}}\) range cell. The result of range compression is shown in Fig. 4a, where severe range migration occurs for both targets. Figure 4b gives the result after performing PS, it can be seen that two trajectories of cross terms exist in addition to that of self terms. Subsequently, SOKT is conducted and the result is shown in Fig. 4c, it is evident that the range curvature of self terms has been removed, while range migration still remains for cross terms. Lastly, slow time NUSFT is conducted to accumulate the energy of self terms and detect the targets, as shown in Fig. 4d. For comparison, Fig. 4e and f give the vertical views of the proposed method which is implemented by NUSFT and NUFFT, respectively. It can be seen that NUFFT outputs all the accumulated coefficients, whereas NUSFT only outputs the large frequency coefficients while setting the small coefficients (including the outputs of noise and cross terms) as 0.

Fig. 4
figure 4

Simulation results of two maneuvering targets. a Target’s trajectory after performing range compression. b Target’s trajectory after performing the PS operation. c Target’s trajectory after performing SOKT. d Focused result of slow time NUSFT. e Vertical view of slow time NUSFT. f Vertical view of slow time NUFFT

Full size image

5.3 Detection performance and runtime

In this section, the detection performance of PS–SOKT–NUSFT is compared with PS–AS and RFPPT. The number of searches in PS–AS is set as 1000. For each input SNR, 500 Monte Carlo experiments are conducted. Figure 5 shows the curves of detection probability against input SNR for the three methods. It can be seen that as a coherent integration method, PS–SOKT–NUSFT outperforms RFPPT which neglects the target’s high-order motion. However, PS–SOKT–NUSFT suffers a slight performance loss compared with PS–AS due to the effect of interpolation and subsampled FFT in NUSFT. Each coin has its two sides, according to the runtime comparison in Table 3, it is evident that PS–SOKT–NUSFT has a much higher efficiency than PS–AS.

Fig. 5
figure 5

Detection probability comparison

Full size image
Table 3 Runtime comparison
Full size table

6 Conclusion

This paper focuses on the topic of radar maneuvering target detection and proposes a fast algorithm to correct range migration and Doppler frequency migration. The proposed method includes three steps: PS, SOKT and slow time NUSFT, which can realize acceleration isolation, range curvature correction and coherent integration, respectively. As a non-searching method, PS–SOKT–NUSFT can avoid the 4-D brute-force search which is widely adopted in the traditional methods such as GRFT and PRPFT. The simulation experiments have validated the effectiveness of the proposed method in multiple targets detection. In addition, the runtime of PS–SOKT–NUSFT and PS–AS in the numerical experiment are, respectively, 106.23 s and 2168.67 s, which indicates that PS–SOKT–NUSFT has a higher efficiency due to its non-searching process and NUSFT operation. Since the target’s highest motion order considered in PS–SOKT–NUSFT is 3, the future work might concern the fast detection of the target with a higher order motion model. Besides, it might be of interest to research the algorithm under the clutter or interference background.