Effect of hall current on propagation of plane wave in transversely isotropic thermoelastic medium with two temperature and fractional order heat transfer

Abstract

This research is devoted to the study of plane wave propagation in homogeneous transversely isotropic magneto-thermoelastic rotating medium with combined effect of hall current and two temperature. The research is applied to fractional order theory with three-phase lag heat transfer. It is analysed that, for 2-D assumed model, three types of coupled longitudinal waves (quasi-longitudinal, quasi-transverse and quasi-thermal) are present. The wave characteristics like phase velocity, specific loss, attenuation coefficients, energy ratios, penetration depths and amplitude ratios of transmitted and reflected waves are computed numerically and illustrated graphically. The impact of hall current parameter by taking different values is represented graphically. Some particular cases are also derived from this research.

1 Introduction

The medium deformed due to thermal shock and application of the magnetic field, produces an induced magnetic and electric field in the media. These magnetic and electric field produce the voltage (known as Hall voltage) across conductor. The composite material such as a magneto-thermoelastic material gained considerable importance since last decade because these materials show the required coupling effect between magnetic and electric fields. Study of plane wave propagation in a thermoelastic solids gained considerable importance because of its applications in the area of inspecting materials, magnetometers, geophysics, nuclear fields and related topics. In last decade significant attention has been given in the area of plane wave propagation in thermoelastic and magneto-thermoelastic (MT) medium.

Borejko [1] deliberated the coefficients of transmission and reflection for 3D plane waves in elastic media. Sinha and Elsibai [2] discoursed the refraction and reflection of thermoelastic waves with two relaxation times at the boundary of two semi-infinite media. Ting [3] explored propagation of surface wave in an anisotropic rotating media. Othman and Song [4, 5] presented different hypotheses about magnetothermoelastic waves in homogeneous isotropic medium. Kumar and Chawla [6] discussed the plane wane propagation in anisotropic two and three phase lag (TPL) model. Deswal and Kalkal [7] discussed the problem in a surface suffering a time dependent thermal shock for thermo-viscoelastic interactions in a 3-D homogeneous isotropic media.

The reflection of plane periodic wave’s occurrence in thermoelastic micropolar homogeneous transversely isotropic (HTI) media had been studied by Kumar and Gupta [8] to find out the complex velocities of the four waves i.e. quasi-longitudinal displacement (qLD), quasi- transverse microrotational (qTM), quasi-transverse displacement (qTD) and quasi thermal (qT) waves. Abouelregal [9] had investigated the induced displacement, temperature, and stress fields in transversely isotropic boundless medium with cylindrical cavity with moving and harmonically heat source with dual phase lag (DPL) model. The effects of reflection and refraction are studied by Gupta [10] at the boundary of elastic and a thermoelastic diffusion media, for plane waves by expanding the Fick law with DPL diffusion model with delay times of both mass flow as well as potential gradient. Beside, Kumar et al. [11] depicted the effect of time, thermal and diffusion phase lags for an axisymmetric heat supply in a ring for DPL model for transfer of heat and diffusion by considering upper and lower surfaces of the ring as friction free.

Youssef [12, 13] proposed a two-temperature model for an elastic half-space with constant elastic parameters and with generalized thermoelasticity without energy dissipation. Sharma and Kaur [14] had investigated the transverse vibrations due to time varying patch loads in homogeneous thermoelastic thin beams. However, Kumar et al. [15] had explored of uncertainties due to thermomechanical sources (concentrated and distributed) using Laplace and Fourier transform technique in a homogeneous transversely isotropic thermoelastic (HTIT) rotating medium with magnetic effect, two temperature and by G–N in presence and absence of energy dissipation w.r.t. thermomechanical sources. Kumar et al. [16] investigated the Rayleigh waves in a MT rotating media in the presence of hall current and two temperature.

Othman et al. [17] proposed a model for generalized magneto-thermoelasticity in an isotropic elastic medium rotated with a uniform angular velocity and with two–temperature and initial stress under LS (Lord–Shulman), GL (Green–Lindsay) and CT (coupled theory) theories of generalized thermoelasticity. Kumar and Kansal [18] found reflected and refracted waves occurrence in MT diffusive half-space medium with voids. Maitya et al. [19] presented plane wave propagation in fibre-reinforced medium with GN –I and II type theories and rotation. Bayones and Abd-Alla [20] discussed 2D problem of thermoelasticity regarding thermoelastic wave propagation in a rotating medium with time-dependent heat source.

Alesemi [21] demonstrated the efficiency of the thermal relaxation time depending upon LS theory, Coriolis and Centrifugal Forces on plane wave’s reflection coefficients in an anisotropic MT rotating medium. Despite of this several researchers worked on different theory of thermoelasticity Marin [22,23,24,25], Marin and Baleanu [26], Ezzat et al. [27], Marin [28, 29] Ezzat et al. [30], Ezzat et al. [31], Marin and Stan [32], Marin and Nicaise [33], Ezzat and El-Bary [34], Othman and Marin [35], Chauthale et al. [36], Marin [37], Kumar et al. [38], Marin et al. [39], Lata and Kaur [40,41,42] and Lata and Kaur [43, 44]. Inspite of these, not much work has been carried out in study of the plane wave propagation with combined effect of hall current, fractional order TPL heat transfer and two temperature.

In this paper, we have attempted to study the plane wave propagation with combined effect of hall current, fractional order TPL heat transfer and two temperature in HTI magneto thermo elastic medium.

2 Basic equations

Following Kumar et al. [45], the simplified Maxwell’s equations for a slowly moving and conducting elastic solid are

$$curl \vec{h} = \vec{j} + \varepsilon_{0} \frac{{\partial \vec{E}}}{\partial t},$$

(1)

$$curl \vec{E} = - \mu_{0} \frac{{\partial \vec{h}}}{\partial t},$$

(2)

$$\vec{E} = - \mu_{0} \left( {\frac{{\partial \vec{u}}}{\partial t} + \vec{H}_{0} } \right),$$

(3)

$$div \vec{h} = 0.$$

(4)

Maxwell stress components [45] are given by

$$t_{ij} = \mu_{0} \left( {H_{i} h_{j} + H_{j} h_{i} - H_{k} h_{k} \delta_{ij} } \right).$$

(5)

The constitutive relations for a HTIT medium are given by

$$t_{ij} = C_{ijkl} e_{kl} - \beta_{ij} T.$$

(6)

Equation of motion as described by Schoenberg and Censor [46] for a HTI medium rotating uniformly with an angular velocity and Lorentz force

$$t_{ij,j} + F_{i} = \rho \left\{ {\ddot{u}_{i} + \left( {\Omega \times (\Omega \times {\text{u}}} \right)_{i} + (2\Omega \times \dot{u})_{i } } \right\},$$

(7)

where $F_{i} = \mu_{0} \left( {\vec{j} \times \vec{H}_{0} } \right)$ are the components of Lorentz force. The terms $\Omega \times \left( {\Omega \times {\text{u}}} \right)$ and $2\Omega \times \dot{u}$ are the centripetal acceleration and Coriolis acceleration due to the time-varying motion respectively.

The Eqs. (1)–(7) are appended by generalized Ohm’s law for finite conductivity and hall current effect [47]:

$$J = \frac{{\sigma_{0} }}{{1 + m^{2} }}\left( {E + \mu_{0} \left( {\dot{u} \times H - \frac{1}{{en_{e} }}J \times H_{0} } \right)} \right).$$

(8)

The heat conduction equation

$$K_{ij} \left( {1 + \frac{{\left( {\tau_{t} } \right)^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}} \right)\dot{\varphi }_{,ji} + K_{ij}^{*} \left( {1 + \frac{{\left( {\tau_{v} } \right)^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}} \right)\varphi_{,ji} = \left( {1 + \frac{{\left( {\tau_{q} } \right)^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }} + \frac{{\left( {\tau_{q} } \right)^{2\alpha } }}{2\alpha !}\frac{{\partial^{2\alpha } }}{{\partial t^{2\alpha } }}} \right)\left[ {\rho C_{E} \ddot{T} + \beta_{ij} T_{0} \ddot{e}_{ij}} \right],$$

(9)

where $\beta_{ij} = C_{ijkl} \alpha_{ij}$,

$$e_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right),\quad i,j = 1,2,3.$$

(10)

$$T = \varphi - a_{ij} \varphi_{,ij},$$

$\beta_{ij} = \beta_{i} \delta_{ij} , K_{ij} = K_{i} \delta_{ij} , K_{ij}^{*} = K_{i}^{*} \delta_{ij}$ i is not summed.

Here $C_{ijkl} \left( {C_{ijkl} = C_{klij} = C_{jikl} = C_{ijlk} } \right)$ are elastic parameters and having symmetry $(C_{ijkl} = C_{klij} = C_{jikl} = C_{ijlk} )$. The basis of these symmetries of C_ijkl is due to

• 1. The stress tensor is symmetric, which is only possible if $\left( {C_{ijkl} = C_{jikl} } \right)$

• 2. If a strain energy density exists for the material, the elastic stiffness tensor must satisfy $C_{ijkl} = C_{klij}$

• 3. From stress tensor and elastic stiffness tensor symmetries infer $\left( {C_{ijkl} = C_{ijlk} } \right)$ and $C_{ijkl} = C_{klij} = C_{jikl} = C_{ijlk}$

3 Formulation and solution of the problem

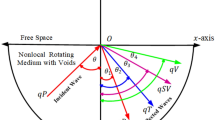
We consider a perfectly conducting HTI magnetothermoelastic rotating medium with an angular velocity $\Omega$ and two temperature and TPL fractional order model of generalized thermoelasticity initially at a uniform temperature T₀, with an initial magnetic field $\vec{H}_{0} = \left( {0, H_{0} , 0} \right)$ acting towards y axis. The rectangular Cartesian co-ordinate system $\left( {x, y, z} \right)$ having origin on the surface (z = 0) with z axis directing vertically downwards into the medium is used. For 2-D problem in xz—plane, we consider

$$\varvec{u} = \left( {u,0,w} \right).$$

In addition, we consider that

$$\varvec{E} = 0,\varvec{\Omega}= \left( {0,\Omega , 0} \right).$$

From the generalized Ohm’s law

$$J_{2} = 0 .$$

(11)

The J₁ and J₃ using (8) are given as

$$J_{1} = \frac{{\sigma_{0} \mu_{0} H_{0} }}{{1 + m^{2} }}\left( {m\frac{\partial u}{\partial t} - \frac{\partial w}{\partial t}} \right),$$

(12)

$$J_{3} = \frac{{\sigma_{0} \mu_{0} H_{0} }}{{1 + m^{2 } }}\left( {\frac{\partial u}{\partial t} + m\frac{\partial w}{\partial t}} \right).$$

(13)

Now using the transformation on Eqs. (7)–(9) following Slaughter [48] are as under:

$$\begin{aligned} & C_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + C_{13} \frac{{\partial^{2} w}}{\partial x\partial z} + C_{44 } \left( {\frac{{\partial^{2} u}}{{\partial z^{2} }} + \frac{{\partial^{2} w}}{\partial x\partial z}} \right) - \beta_{1 } \frac{\partial }{\partial x}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} \\ & \quad - \mu_{0} J_{3} H_{0} = \rho \left( {\frac{{\partial^{2} u}}{{\partial t^{2} }} - \Omega^{2} u + 2\Omega \frac{\partial w}{\partial t}} \right), \\ \end{aligned}$$

(14)

$$\begin{aligned} & \left( {C_{13} + C_{44 } } \right)\frac{{\partial^{2} u}}{\partial x\partial z} + C_{44} \frac{{\partial^{2} w}}{{\partial x^{2} }} + C_{33 } \frac{{\partial^{2} w}}{{\partial z^{2} }} - \beta_{3 } \frac{\partial }{\partial z}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} - \mu_{0} J_{1} H_{0} \\ & \quad = \rho \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} - \Omega^{2} w - 2\Omega \frac{\partial u}{\partial t}} \right), \\ \end{aligned}$$

(15)

$$\begin{aligned} & K_{1} \left( {1 + \frac{{\left( {\tau_{t} } \right)^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}} \right)\frac{{\partial^{2} \dot{\varphi }}}{{\partial x^{2} }} + K_{3} \left( {1 + \frac{{\left( {\tau_{t} } \right)^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}} \right)\frac{{\partial^{2} \dot{\varphi }}}{{\partial z^{2} }} + K_{1}^{*} \left( {1 + \frac{{\left( {\tau_{v} } \right)^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}} \right)\frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + K_{3}^{*} \left( {1 + \frac{{\left( {\tau_{v} } \right)^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}} \right)\frac{{\partial^{2} \varphi }}{{\partial z^{2} }} \\ & \quad = \left( {1 + \frac{{\left( {\tau_{q} } \right)^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }} + \frac{{\left( {\tau_{q} } \right)^{2\alpha } }}{2\alpha !}\frac{{\partial^{2\alpha } }}{{\partial t^{2\alpha } }}} \right)\left[ {\rho C_{E} \frac{{\partial^{2} }}{{\partial t^{2} }}\left[ {\varphi - a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} - a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right] + T_{0} \left\{ {\beta_{1} \frac{{\partial \ddot{u}}}{\partial x} + \beta_{1} \frac{{\partial \ddot{w}}}{\partial z}} \right\}} \right], \\ \end{aligned}$$

(16)

and

$$t_{xx} = C_{11} e_{xx} + C_{13} e_{xz} - \beta_{1 } T,$$

(17)

$$t_{zz} = C_{13} e_{xx} + C_{33} e_{zz} - \beta_{3 } T,$$

(18)

$$t_{xz} = 2C_{44} e_{xz} ,$$

(19)

where

$$\begin{aligned} T & = \varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right), \\ \beta_{1 } & = \left( {C_{11} + C_{12} } \right)\alpha_{1} + C_{13} \alpha_{3} , \\ \beta_{3 } & = 2C_{13} \alpha_{1} + C_{33} . \\ \end{aligned}$$

To facilitate the solution, below mentioned dimensionless quantities are used:

$$\begin{aligned} & x^{\prime } = \frac{x}{L},\quad z^{\prime } = \frac{z}{L},\quad u^{\prime } = \frac{{\rho c_{1}^{2} }}{{L\beta_{1} T_{0} }}u,\quad w^{\prime } = \frac{{\rho c_{1}^{2} }}{{L\beta_{1} T_{0} }}w,\quad t^{\prime } = \frac{{c_{1} }}{L}t,\quad \Omega^{\prime } = \frac{L}{{C_{1} }}\Omega , \\ & \varphi^{\prime } = \frac{\varphi }{{T_{0} }},\quad t_{xx}^{\prime} = \frac{{t_{xx} }}{{\beta_{1} T_{0} }},\quad t_{xz}^{\prime} = \frac{{t_{xz} }}{{\beta_{1} T_{0} }}, \quad t_{zz}^{\prime} = \frac{{t_{zz} }}{{\beta_{1} T_{0} }}, \quad \tau_{T}^{\prime} = \frac{{C_{1} }}{L}\tau_{T} , \quad \tau_{v}^{\prime} = \frac{{C_{1} }}{L}\tau_{v} , \quad \tau_{q}^{\prime} = \frac{{C_{1} }}{L}\tau_{q} . \\ \end{aligned}$$

(20)

Using (20) in Eqs. (14)–(16) and after suppressing the primes, yield

$$\begin{aligned} & \frac{{\partial^{2} u}}{{\partial x^{2} }} + \delta_{1} \frac{{\partial^{2} w}}{\partial x\partial z} + \delta_{2} \frac{{\partial^{2} u}}{{\partial z^{2} }} - \frac{\partial }{\partial x}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} \\ & \quad = \frac{M}{{1 + m^{2} }}\left[ {\frac{\partial u}{\partial t} + m\frac{\partial w}{\partial t}} \right] + \frac{{\partial^{2} u}}{{\partial t^{2} }} - \Omega^{2} u + 2\Omega \frac{\partial w}{\partial t}, \\ \end{aligned}$$

(21)

$$\begin{aligned} & \delta_{1} \frac{{\partial^{2} u}}{\partial x\partial z} + \delta_{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \delta_{3} \frac{{\partial^{2} w}}{{\partial z^{2} }} - \frac{{\beta_{3} }}{{\beta_{1} }}\frac{\partial }{\partial z}\left\{ {\varphi - \left( {a_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + a_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)} \right\} \\ & \quad = - \frac{M}{{1 + m^{2} }}\left[ {m\frac{\partial u}{\partial t} - \frac{\partial w}{\partial t}} \right] + \frac{{\partial^{2} w}}{{\partial t^{2} }} - \Omega^{2} w - 2\Omega \frac{\partial u}{\partial t}, \\ \end{aligned}$$

(22)

$$\begin{aligned} & \left( {1 + \frac{{C_{1} \left( {\tau_{t} } \right)^{\alpha } }}{\alpha !L}\frac{{\partial^{\alpha + 1} }}{{\partial t^{\alpha + 1} }}} \right)\left( {K_{1} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + K_{3} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right)_{1} + \left( {1 + \frac{{\left( {\tau_{v} } \right)^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}} \right)\left( {K_{1}^{*} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + K_{3}^{*} \frac{{\partial^{2} \varphi }}{{\partial z^{2} }}} \right) \\ & \quad = \left( {1 + \frac{{\left( {\tau_{q} } \right)^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }} + \frac{{\left( {\tau_{q} } \right)^{2\alpha } }}{2\alpha !}\frac{{\partial^{2\alpha } }}{{\partial t^{2\alpha } }}} \right)\left[ {\rho C_{E} \ddot{T} + \frac{{\beta_{1} }}{\rho }T_{0} \left\{ {\beta_{1} \frac{{\partial \ddot{u}}}{\partial x} + \beta_{1} \frac{{\partial \ddot{w}}}{\partial z}} \right\}} \right], \\ \end{aligned}$$

(23)

where

$$\delta_{1} = \frac{{c_{13} + c_{44} }}{{c_{11} }},\quad \delta_{2} = \frac{{c_{44} }}{{c_{11} }}, \quad \delta_{3} = \frac{{c_{33} }}{{c_{11} }}, \quad M = \left( {\frac{{L\sigma_{0} \mu_{0}^{2} H_{0}^{2} }}{{\rho C_{1} }}} \right)$$

4 Plane wave propagation

We pursue plane wave equations of the form

$$\left( {\begin{array}{*{20}c} u \\ w \\ \varphi \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} U \\ W \\ {\varphi^{*} } \\ \end{array} } \right)e^{{i\left( {\omega t - \xi (x sin\theta - z cos\theta } \right))}} ,$$

(24)

where $\sin \theta , \cos \theta$ denotes the projection of wave normal to the x–z plane.

Upon using Eq. (24) in Eqs. (21)–(23) we get

$$\begin{aligned} & U\left[ {\zeta_{1} \xi^{2} + \zeta_{2} } \right] + W\left[ {\zeta_{3} \xi^{2} + \zeta_{4} } \right] + \varphi^{*} \left[ {\zeta_{5} \xi + \zeta_{6} \xi^{3} } \right] = 0, \\ & U\left[ {\zeta_{7} \xi^{2} + \zeta_{8} } \right] + W\left[ {\zeta_{9} \xi^{2} + \zeta_{10} } \right] + \varphi^{*} \left[ {\zeta_{11} \xi + \zeta_{12} \xi^{3} } \right] = 0, \\ & \quad \zeta_{13} \xi U + \zeta_{14} \xi W + \varphi^{*} \left[ {\zeta_{15} \xi^{2} + \zeta_{16} } \right] = 0. \\ \end{aligned}$$

and by equating determinant of coefficients of U, W and $\varphi^{*}$ to zero we yields the characteristic equation as

$$A\xi^{6} + B\xi^{4} + C\xi^{2} + D = 0,$$

(25)

where

$$\begin{aligned} & A = \zeta_{13} \zeta_{3} \zeta_{12} - \zeta_{9} \zeta_{6} \zeta_{13} - \zeta_{14} \zeta_{1} \zeta_{12} + \zeta_{7} \zeta_{6} \zeta_{14} + \zeta_{9} \zeta_{1} \zeta_{15} - \zeta_{15} \zeta_{7} \zeta_{3} , \\ & B = \zeta_{3} \zeta_{13} \zeta_{11} + \zeta_{4} \zeta_{12} \zeta_{13} - \zeta_{9} \zeta_{5} \zeta_{13} - \zeta_{10} \zeta_{6} \zeta_{13} - \zeta_{14} \zeta_{1} \zeta_{11} - \zeta_{14} \zeta_{2} \zeta_{12} + \zeta_{14} \zeta_{7} \zeta_{5} \\ & \quad + \zeta_{6} \zeta_{8} \zeta_{14} + \zeta_{16} \zeta_{9} \zeta_{1} + \zeta_{15} \zeta_{9} \zeta_{2} + \zeta_{1} \zeta_{10} \zeta_{15} - \zeta_{16} \zeta_{3} \zeta_{7} - \zeta_{15} \zeta_{8} \zeta_{3} - \zeta_{15} \zeta_{4} \zeta_{7} , \\ & C = \zeta_{13} \zeta_{4} \zeta_{11} - \zeta_{5} \zeta_{10} \zeta_{13} + \zeta_{14} \zeta_{8} \zeta_{5} + \zeta_{16} \zeta_{9} \zeta_{2} + \zeta_{16} \zeta_{1} \zeta_{10} + \zeta_{10} \zeta_{{2\zeta_{15} }} - \zeta_{3} \zeta_{8} \zeta_{16} - \zeta_{7} \zeta_{4} \zeta_{16} - \zeta_{8} \zeta_{4} \zeta_{15} , \\ & D = \zeta_{2} \zeta_{10} \zeta_{16} - \zeta_{8} \zeta_{4} \zeta_{16} , \\ \end{aligned}$$

$$\begin{aligned} & \zeta_{1} = - \sin^{2} \theta - \delta_{2} \cos^{2} \theta , \\ & \zeta_{2} = \frac{ - M}{{1 + m^{2} }}i\omega + \omega^{2} + \Omega^{2} , \\ & \zeta_{3} = \delta_{1} \sin \theta \cos \theta , \\ & \zeta_{4} = \frac{ - Mm}{{1 + m^{2} }}i\omega - 2\omega \Omega i, \\ & \zeta_{5} = i\sin \theta , \\ & \zeta_{6} = ia_{1} \sin^{3} \theta + ia_{3} \sin \theta \cos^{2} \theta , \\ & \zeta_{7} = \zeta_{3} , \\ & \zeta_{8} = = \frac{Mm}{{1 + m^{2} }}i\omega + 2\omega \Omega i, \\ & \zeta_{9} = \delta_{2} \sin^{2} \theta - \delta_{3} \cos^{2} \theta , \\ & \zeta_{10} = \frac{ - Mm}{{1 + m^{2} }}i\omega + \omega^{2} + \Omega^{2} , \\ & \zeta_{11} = - i\frac{{\beta_{3} }}{{\beta_{1} }}\cos \theta , \\ & \zeta_{12} = i\frac{{\beta_{3} }}{{\beta_{1} }}\cos \theta \left( {a_{1} \sin^{2} \theta + a_{3} \cos^{2} \theta } \right), \\ & \zeta_{13} = - \frac{{\beta_{1}^{2} }}{\rho }T_{0} \omega^{2} i\sin \theta , \\ & \zeta_{14} = \frac{{\beta_{1} \beta_{3} T_{0} \omega^{2} i\cos \theta ,}}{\rho } \\ & \zeta_{15} = - \left[ {1 + \frac{{C_{1} }}{L}\frac{{\tau_{T}^{\alpha } }}{\alpha !}\left( {i\omega } \right)^{\alpha + 1} } \right]\left[ {K_{1} \sin^{2} \theta + K_{3} \cos^{2} \theta } \right] - \left[ {1 + \frac{{\tau_{v}^{\alpha } }}{\alpha !}\left( {i\omega } \right)^{\alpha } } \right]\left[ {K_{1}^{*} \sin^{2} \theta + K_{3}^{*} \cos^{2} \theta } \right] \\ & \quad + \left[ {1 + \frac{{\tau_{q}^{\alpha } }}{\alpha !}\left( {i\omega } \right)^{\alpha } + \frac{{\tau_{q}^{2\alpha } }}{2\alpha !}\left( {i\omega } \right)^{2\alpha } } \right]C_{1}^{2} \rho C_{E} \omega^{2} \left( {a_{1} \sin^{2} \theta + a_{3} \cos^{2} \theta } \right), \\ & \zeta_{16} = \left[ {1 + \frac{{\tau_{q}^{\alpha } }}{\alpha !}\left( {i\omega } \right)^{\alpha } + \frac{{\tau_{q}^{2\alpha } }}{2\alpha !}\left( {i\omega } \right)^{2\alpha } } \right]C_{1}^{2} \rho C_{E} \omega^{2} . \\ \end{aligned}$$

The roots of Eq. (25) give six roots of $\xi$ that is, $\pm \xi_{1}$, $\pm \xi_{2}$ and $\pm \xi_{3}$, and we are concerned to the roots with positive imaginary parts. Resultant to these roots, there exists three waves according to descending order of their velocities namely QL, QTS and QT. The phase velocities, attenuation coefficients, specific loss and penetration depth of these waves are obtained by the following expressions.

• 1. Phase velocity

The phase velocities are given by

$$V_{i} = \frac{\omega }{{Re\left( {\xi_{i} } \right)}},\quad {\text{i }} = 1, 2, 3$$

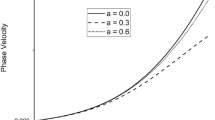
where $V_{1} , V_{2} , V_{3}$ are the velocities of QL, QTS and QT waves respectively (Fig. 1).

Fig. 1

Geometry of the problem

• 2. Attenuation coefficient

The attenuation coefficient is defined as

$$Q_{i} = Img\left( {\xi_{i} } \right),\quad {\text{i }} = 1, 2, 3.$$

where $Q_{1} , Q_{2} , Q_{3}$ are the attenuation coefficients of QL, QTS and QT waves respectively.

• 3. Specific loss

The specific loss is define as:

$$W_{i} = \left( {\frac{\Delta W}{W}} \right)i = 4\pi \left| {\frac{{Img\left( {\xi_{i} } \right)}}{{Re\left( {\xi_{i} } \right)}}} \right|,\quad {\text{i }} = 1, 2, 3.$$

where $W_{1} , W_{2} , W_{3}$ are specific loss of QL, QTS and QT waves respectively.

• 4. Penetration depth

The penetration depth of plane wave is given by

$$S_{i} = \frac{1}{{Img\left( {\xi_{i} } \right)}}, \quad {\text{i }} = 1, 2, 3.$$

where $S_{1} , S_{2} , S_{3}$ are penetration depth of QL, QTS and QT waves respectively.

5 Reflection and transmission at the boundary surfaces

We consider a HTI magneto-thermoelastic half-space occupying the region z ≥ 0. Incident QL, QTS and QT waves at the stress free and thermally insulated surface (z = 0) will generate reflected QL, QTS and QT waves in the half-space z > 0. The total displacements, conductive temperature are given by

$$\left( {u,w,\varphi } \right) = \mathop \sum \limits_{j = 1}^{6} (1,d_{j} ,l_{j} )A_{j} e^{{iM_{j} }} ,$$

(26)

where

$$\begin{aligned} & M_{j} = \omega t - \xi_{j} \left( {x\sin \theta_{j} - z\cos \theta_{j} } \right),\quad j = 1,2,3, \\ & M_{j} = \omega t - \xi_{j} \left( {x\sin \theta_{j} + z\cos \theta_{j} } \right),\quad j = 4,5,6. \\ \end{aligned}$$

Here subscripts j = 1, 2, 3 respectively denote the quantities corresponding to incident QL, QTS and QT-mode, whereas the subscripts j = 4, 5, 6 denote the corresponding reflected waves, $\xi_{j}$ are the roots obtained from Eq. (25).

$$\begin{aligned} & d_{j} = \frac{{\zeta_{2} \zeta_{16} + \left( {\zeta_{2} \zeta_{15j} - \zeta_{5j} \zeta_{13j} + \zeta_{16} \zeta_{1j} } \right)\xi_{j}^{2} + (\zeta_{1} j\zeta_{15j} - \zeta_{6j} \zeta_{13j} )\xi_{j}^{4} }}{{(\zeta_{9j} \zeta_{15j} - \zeta_{12j} )\xi_{j}^{4} + \left( {\zeta_{10} \zeta_{15j} + \zeta_{9j} \zeta_{16} - \zeta_{11j} \zeta_{14j} } \right)\xi_{j}^{2} - \zeta_{10} \zeta_{16} }},\quad {\text{j}} = 1,2,3. \\ & l_{j} = \frac{{\left( {\zeta_{2} \zeta_{10} - \zeta_{4} \zeta_{8} } \right) + \left( {\zeta_{10} \zeta_{1j} + \zeta_{2} \zeta_{9j} - \zeta_{4} \zeta_{7j} + \zeta_{8} \zeta_{3j} } \right)\xi_{j}^{2} + (\zeta_{1} j\zeta_{9j} - \zeta_{3j} \zeta_{7j} )\xi_{j}^{4} }}{{(\zeta_{9j} \zeta_{15j} - \zeta_{12j} )\xi_{j}^{4} + \left( {\zeta_{10} \zeta_{15j} + \zeta_{9j} \zeta_{16} - \zeta_{11j} \zeta_{14j} } \right)\xi_{j}^{2} - \zeta_{10} \zeta_{16} }},\quad {\text{j}} = 1,2,3. \\ & d_{j} = \frac{{\zeta_{2} \zeta_{16} + \left( {\zeta_{2} \zeta_{15j} - \zeta_{5j} \zeta_{13j} + \zeta_{16} \zeta_{1j} } \right)\xi_{j}^{2} + (\zeta_{1} j\zeta_{15j} - \zeta_{6j} \zeta_{13j} )\xi_{j}^{4} }}{{(\zeta_{9j} \zeta_{15j} - \zeta_{12j} )\xi_{j}^{4} + \left( {\zeta_{10} \zeta_{15j} + \zeta_{9j} \zeta_{16} - \zeta_{11j} \zeta_{14j} } \right)\xi_{j}^{2} - \zeta_{10} \zeta_{16} }},\quad {\text{j}} = 4,5,6. \\ & l_{j} = \frac{{\left( {\zeta_{2} \zeta_{10} - \zeta_{4} \zeta_{8} } \right) + \left( {\zeta_{10} \zeta_{1j} + \zeta_{2} \zeta_{9j} + \zeta_{4} \zeta_{7j} + \zeta_{8} \zeta_{3j} } \right)\xi_{j}^{2} + (\zeta_{1} j\zeta_{9j} - \zeta_{3j} \zeta_{7j} )\xi_{j}^{4} }}{{(\zeta_{9j} \zeta_{15j} - \zeta_{12j} )\xi_{j}^{4} + \left( {\zeta_{10} \zeta_{15j} + \zeta_{9j} \zeta_{16} - \zeta_{11j} \zeta_{14j} } \right)\xi_{j}^{2} - \zeta_{10} \zeta_{16} }},\quad {\text{j}} = 4,5,6. \\ \end{aligned}$$

6 Boundary conditions

The dimensionless boundary conditions at the free surface z = 0, are given by

$$t_{33} = 0,$$

(27)

$$t_{31} = 0,$$

(28)

$$\frac{\partial \varphi }{\partial z} = 0.$$

(29)

Using Eq. (26) into the Eqs. (27)–(29), we obtain

$$\begin{aligned} & \mathop \sum \limits_{j = 1}^{3} A_{j} e^{{i\left( {\omega t - \xi_{j} \left( {xsin\theta_{j} } \right)} \right)}} \left[ { - C_{13} i\xi_{j} sin\theta_{j} + C_{33} id_{j} \xi_{j} cos\theta_{j} - \beta_{3} l_{j} } \right] \\ & \quad - \mathop \sum \limits_{j = 4}^{6} A_{j} e^{{i\left( {\omega t - \xi_{j} \left( {xsin\theta_{j} } \right)} \right)}} \left[ {C_{13} i\xi_{j} sin\theta_{j} + C_{33} id_{j} \xi_{j} cos\theta_{j} + \beta_{3} l_{j} } \right] = 0, \\ \end{aligned}$$

(30)

$$\mathop \sum \limits_{j = 1}^{3} A_{j} e^{{i\left( {\omega t - \xi_{j} \left( {xsin\theta_{j} } \right)} \right)}} \left[ {\xi_{j} cos\theta_{j} - d_{j} \xi_{j} sin\theta_{j} } \right] - \mathop \sum \limits_{j = 4}^{6} A_{j} e^{{i\left( {\omega t - \xi_{j} \left( {xsin\theta_{j} } \right)} \right)}} \left[ {\xi_{j} cos\theta_{j} + d_{j} \xi_{j} sin\theta_{j} } \right] = 0,$$

(31)

$$\mathop \sum \limits_{j = 1}^{3} A_{j} e^{{i\left( {\omega t - \xi_{j} \left( {xsin\theta_{j} } \right)} \right)}} \left[ {il_{j} \xi_{j} cos\theta_{j} } \right] - \mathop \sum \limits_{j = 4}^{6} A_{j} e^{{i\left( {\omega t - \xi_{j} \left( {xsin\theta_{j} } \right)} \right)}} \left[ {il_{j} \xi_{j} cos\theta_{j} } \right] = 0.$$

(32)

The Eqs. (30)–(32) are satisfied for all values of x, therefore we have

$$M_{1} \left( {x,0} \right) = M_{2} \left( {x,0} \right) = M_{3} \left( {x,0} \right) = M_{4} \left( {x,0} \right) = M_{5} \left( {x,0} \right) = M_{6} \left( {x,0} \right).$$

(33)

From Eqs. (26) and (33), we obtain

$$\xi_{1} sin\theta_{1} = \xi_{2} sin\theta_{2} = \xi_{3} sin\theta_{3} = \xi_{4} sin\theta_{4} = \xi_{5} sin\theta_{5} = \xi_{6} sin\theta_{6} .$$

(34)

The Eqs. (30)–(32) and (34) yield

$$\mathop \sum \limits_{p = 1}^{3} X_{ip} A_{p} + \mathop \sum \limits_{j = 4}^{6} X_{ij} A_{j} = 0,\quad \left( {i = 1,2,3} \right),$$

(35)

where for p = 1,2,3 we have,

$$X_{1p} = \frac{{ - C_{13} }}{{\rho C_{1}^{2} }}i\xi_{p} sin\theta_{p} + \frac{{C_{33} }}{{\rho C_{1}^{2} }}id_{p} \xi_{p} cos\theta_{p} - \frac{{\beta_{3} }}{{\beta_{1} }}\left[ {1 - a_{1} \xi_{p}^{2} sin^{2} \theta_{p} - a_{3} \xi_{p}^{2} cos^{2} \theta_{p} } \right]l_{p} ,$$

(36)

$$X_{2p} = i\xi_{p} cos\theta_{p} - id_{p} \xi_{p} sin\theta_{p} ,$$

(37)

$$X_{3p} = il_{p} \xi_{p} cos\theta_{p} .$$

(38)

and for j = 4, 5, 6 we have

$$X_{1j} = \frac{{ - C_{13} }}{{\rho C_{1}^{2} }}i\xi_{p} sin\theta_{p} - \frac{{C_{33} }}{{\rho C_{1}^{2} }}id_{p} \xi_{p} cos\theta_{p} - \frac{{\beta_{3} }}{{\beta_{1} }}\left[ {1 - a_{1} \xi_{p}^{2} sin^{2} \theta_{p} - a_{3} \xi_{p}^{2} cos^{2} \theta_{p} } \right]l_{p} ,$$

(39)

$$X_{2j} = - i\xi_{j} cos\theta_{j} - id_{j} \xi_{j} sin\theta_{j} ,$$

(40)

$$X_{3j} = - il_{j} \xi_{j} cos\theta_{j} .$$

(41)

6.1 Incident QL-wave

In case of QL wave, the subscript p takes only one value, that is p = 1, which means $A_{2} = A_{3} = 0$. Dividing the set of Eqs. (35) throughout by A₁, by solving with Cramer’s rule we get three homogeneous equations as

$$A_{1i} = \frac{{A_{i + 3} }}{{A_{1} }} = \frac{{\Delta_{i}^{1} }}{\Delta },$$

(42)

6.2 Incident QTS-wave

In case of QTS wave, the subscript q takes only one value, that is q = 2, which means $A_{1} = A_{3} = 0$. Dividing the set of Eqs. (35) throughout by A₂,  by solving with Cramer’s rule we get three homogeneous equations as

$$A_{2i} = \frac{{A_{i + 3} }}{{A_{2} }} = \frac{{\Delta_{i}^{2} }}{\Delta }.$$

(43)

6.3 Incident QT-wave

In case of QT wave, the subscript q takes only one value, that is q = 3, which means $A_{2} = A_{1} = 0$. Dividing the set of Eq. (35) throughout by A₃, by solving with Cramer’s rule we get three homogeneous equations as

$$A_{3i} = \frac{{A_{i + 3} }}{{A_{3} }} = \frac{{\Delta_{i}^{3} }}{\Delta },$$

(44)

where Z_i (i = 1,2,3) are the amplitude ratios of the reflected QL, QTS, QT -waves to that of the incident QL-(QTS or QT) waves respectively.Here

$$\Delta = \left| {A_{{i\left( {i + 3} \right)}} } \right|_{3X3}$$

(45)

$$\Delta_{i}^{p} , \left( {i = 1,2,3} \right)$$

(46)

can be obtained by replacing, respectively, the 1st, 2nd and 3rd columns of ∆ by $\left[ { - X_{1p} , - X_{2p} , - X_{3p} } \right]^{{\prime }}$

The energy flux across the surface element is represented as

$$P^{*} = t_{lm} n_{m} \dot{u}_{l} ,$$

(47)

where n_m are the direction cosines of the unit normal and $\dot{u}_{l}$ are the components of the particle velocity.

The time average $P^{*}$, is the average energy transmission per unit surface area per unit time and is given at the interface z = 0 as

$$\left\langle {P^{*} } \right\rangle = \left\langle {Re\left( {t_{13} } \right) \cdot Re\left( {\dot{u}_{1} } \right) + Re\left( {t_{33} } \right) \cdot Re\left( {\dot{u}_{3} } \right)} \right\rangle .$$

(48)

For complex functions a and b, we take

$$\left\langle {Re\left( a \right)} \right\rangle \left\langle {Re\left( b \right)} \right\rangle = \frac{1}{2}Re\left( {a\bar{b}} \right).$$

(49)

The energy ratios E_i(i = 1,2,3) expressions for reflected QL, QT, QTH-wave are given as

• 1. QL- wave

  $$E_{1i} = \frac{{\left\langle {P_{i + 3}^{*} } \right\rangle }}{{\left\langle {P_{1}^{*} } \right\rangle }},\quad i = 1,2,3.$$

  (50)

• 2. QTS- wave

  $$E_{1i} = \frac{{\left\langle {P_{i + 3}^{*} } \right\rangle }}{{\left\langle {P_{1}^{*} } \right\rangle }},\quad i = 1,2,3.$$

  (51)

• 3. QT- wave

  $$E_{1i} = \frac{{\left\langle {P_{i + 3}^{*} } \right\rangle }}{{\left\langle {P_{1}^{*} } \right\rangle }},\quad i = 1,2,3.$$

  (52)

where $\left\langle {P_{i}^{*} } \right\rangle$ i = 1, 2, 3 are corresponding to incident QL, QTS, QT waves respectively and $\left\langle {P_{i + 3}^{*} } \right\rangle$ i = 1, 2, 3 are corresponding to reflected QL, QTS, QT waves respectively.

7 Particular cases

• 1. If α = 1 we obtain results for plane wave propagation in magneto-thermoelastic transversely isotropic solid with rotation, hall effect, with two temperature, and with and without energy dissipation and TPL effects.

• 2. If $\alpha = 1\; {\text{and}}\;\tau_{T} = 0, \tau_{v} = 0,\tau_{q} = 0$ and $K^{*} \ne 0$ we obtain results for plane wave propagation in magneto-thermoelastic transversely isotropic solid with rotation, hall effect, with two temperature and GN III theory (thermoelasticity with energy dissipation).

• 3. If $\alpha = 1 , \tau_{T} = 0, \tau_{v} = 0,\tau_{q} = 0$ and $K^{*} = 0$ we obtain results for plane wave propagation in magneto-thermoelastic transversely isotropic solid with rotation, hall effect, two temperature and GN II theory (generalized thermoelasticity without energy dissipation).

• 4. If $\alpha = 1$ and $K^{*}$ = 0 we obtain results for plane wave propagation in magneto-thermoelastic transversely isotropic solid with rotation, hall effect, with two temperature and GN II theory with TPL effect

• 5. If $\alpha = 1 , \tau_{T} = 0, \tau_{v} = 0 ,\tau_{q} = \tau_{0} > 0$ and $K^{*}$ = 0, and ignoring $\tau_{q}^{2}$ we obtain results for plane wave propagation in magneto-thermoelastic transversely isotropic solid with rotation, Hall Effect, with two temperature and Lord–Shulman model.

If $\alpha = 1,\tau_{T} = 0, \tau_{v} = 0,\tau_{q} = 0$ and if the medium is not permeated with the magnetic field i.e. μ₀ =  H₀ =  0 then we obtain results for plane wave propagation in transversely isotropic thermoelastic solid with rotation, and with two temperature

• 6. If $\alpha = 1, C_{11} = C_{33} = \lambda + 2\mu , C_{12} = C_{13} = \lambda ,C_{44} = \mu , \alpha_{1} = \alpha_{3} = \alpha^{\prime } , a_{1} = a_{3} = a, \beta_{1} = \beta_{3} = \beta , K_{1} = K_{3} = K, K_{1}^{*} = K_{3}^{*} = K^{*}$ we obtain expressions for magneto-thermoelastic isotropic materials with rotation, Hall Effect, two temperature and with and without energy dissipation with TPL effect.

• 7. If $\alpha = 1,a_{1} = a_{3} = 0$ we obtain results for magneto-thermoelastic transversely isotropic solid with rotation, Hall Effect, without two temperature, and with and without energy dissipation with TPL effects.

• 8. If $\alpha = 1,$ Ω = 0, then we obtain results for plane wave propagation in transversely isotropic magneto-thermoelastic solid with Hall Effect, with and without energy dissipation, with two temperature and with TPL.

8 Numerical results and discussion

To demonstrate the theoretical results and effect of rotation, relaxation time and two temperature, the physical data for cobalt material, which is transversely isotropic, is taken from Dhaliwal and Singh [49] is given as

$$\begin{aligned} & c_{11} = 3.07 \times 10^{11} \;{\text{Nm}}^{ - 2} ,\quad c_{33} = 3.581 \times 10^{11} \;{\text{Nm}}^{ - 2} , \quad c_{13} = 1.027 \times 10^{10} \;{\text{Nm}}^{ - 2} , \\ & c_{44} = 1.510 \times 10^{11} \;{\text{Nm}}^{ - 2} , \quad \beta_{1} = 7.04 \times 10^{6} \;{\text{Nm}}^{ - 2} \;{ \deg }^{ - 1} , \\ & \beta_{3} = 6.90 \times 10^{6} \;{\text{Nm}}^{ - 2} \;{ \deg }^{ - 1} ,\quad \rho = 8.836 \times 10^{3} \;{\text{Kg}}\;{\text{m}}^{ - 3} , \\ & C_{E} = 4.27 \times 10^{2} {\text{j}}\;{\text{Kg}}^{ - 1} \;{ \deg }^{ - 1} , \quad K_{1} = 0.690 \times 10^{2} \;{\text{Wm}}^{ - 1} \;{\text{K}}\;{ \deg }^{ - 1} ,\quad \\ & K_{3} = 0.690 \times 10^{2} \;{\text{W}}\;{\text{m}}^{ - 1} \;{\text{K}}^{ - 1} ,\quad K_{1}^{*} = 1.313 \times 10^{2} \;{\text{W}}\;{\text{s}}, \quad K_{3}^{*} = 1.54 \times 10^{2} \;{\text{W}}\;{\text{s}}, \\ & {\text{T}}_{0} = 298 {\text{K}},\;{\text{H}}_{0} = 1 {\text{J}}\;{\text{m}}^{ - 1} \;{\text{nb}}^{ - 1} ,\quad \varepsilon _{0} = 8.838 \times 10^{ - 12} {\text{Fm}}^{ - 1} ,\quad {\text{L}} = 1. \\ \end{aligned}$$

The values of fractional order parameter α and two Temperature a₁ and a₃ are taken as 0.5, 0.02, and 0.04 respectively. For the determination of the values of penetration depth, phase velocity, specific loss, attenuation coefficient, amplitude ratios and energy ratios reflected QL, QTS and QT waves w.r.t. incident QL, QTS, and QT waves respectively we have used package MATLAB 8.0.4 and drawn graphically to show the effect of hall current.

• 1. The line in black colour with square symbol represent $m = 0.0,$

• 2. The line in red colour with circle symbol represent $m = 0.3,$

• 3. The line in blue colour with triangle symbol represent $m = 0.6,$

8.1 Phase velocity

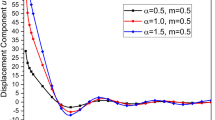
Figures 2, 3 and 4 indicate the change of phase velocities w.r.t. frequency ω respectively. The phase velocity $V_{1 }$ oscillates in the initial range of the frequency for different value of hall current and remain same in rest of the range. In almost all the frequency range and for all the values of m,  the phase velocity V₂, V₃ follows the same pattern.

Fig. 2

Variations of phase velocity v₁ with frequency ω

Fig. 3

Variations of phase velocity v₂ with frequency ω

Fig. 4

Variations of phase velocity v₃ with frequency ω

8.2 Attenuation coefficients

Figures 5, 6 and 7 shows that the values of attenuation w.r.t. frequency respectively. From the graphs it is clear that attenuation coefficient Q₁, Q₂ increases for the initial values of the frequencies and then after decreasing the follow the same pattern for all the values of hall current. The value of attenuation coefficient $Q_{3}$ increases in the initial range of frequency and have same pattern with different magnitude for different values of hall current.

Fig. 5

Variations of attenuation coefficient Q₁ with frequency ω

Fig. 6

Variations of attenuation coefficient Q₂ with frequency ω

Fig. 7

Variations of attenuation coefficient Q₃ with frequency ω

8.3 Specific loss

Figures 8, 9 and 10 exhibits the variations of Specific loss w.r.t. frequency. From the graphs it is clear that the value of specific loss W₁ shows the oscillatory pattern for the initial value of the frequency for all the cases and then shows the same magnitude for rest of the range. The value of specific loss W₂ shows rise in the initial value of frequency and then after decreasing it comes to steady state for rest of the frequency range in all the cases similar variations. While the value of specific loss W₃ gradually decreases with different magnitudes for all the cases of hall current.

Fig. 8

Variations of specific loss W₁ with frequency ω

Fig. 9

Variations of specific loss W₂ with frequency ω

Fig. 10

Variations of specific loss W₃ with frequency ω

8.4 Penetration depth

Figures 11, 12 and 13 shows the variations of penetration depth $S_{1,} S_{2} ,S_{3}$ w.r.t. frequency. Here, we notice a sharp decrease in $S_{2 } \;{\text{and}}\; S_{3}$ for all the cases in range $0.0 \le \omega \le 2$, and the variations approach the boundary surface by increasing slowly and smoothly in the rest.

Fig. 11

Variations of penetration depth S₁ with frequency ω

Fig. 12

Variations of penetration depth S₂ with frequency ω

Fig. 13

Variations of penetration depth S₃ with frequency ω

8.5 Energyratios

8.5.1 Incident QL wave

Figure 14 depicts the change of energy ratio E₁₁ w.r.t. angle of incidence θ. It shows that the values of E₁₁ decreases gradually with the change in angle of incidence corresponding to all the cases of hall current. Figure 15 shows the variations of energy ratio E₁₂ w.r.t. angle of incidence θ. Here the value increases and show same increasing pattern but difference in magnitude. Figure 16 depicts the changes of Energy ratio E₁₃ w.r.t. angle of incidence θ. It is noticed that the values decreases sharply in the initial range of angle and increase gradually throughout the range.

Fig. 14

Variations of energy ratio E₁₁ with angle of incidence θ

Fig. 15

Variations of energy ratio E₁₂ with angle of incidence θ

Fig. 16

Variations of energy ratio E₁₃ with angle of incidence θ

8.5.2 Incident QTS wave

Figure 17 depicts the change of Energy ratio E₂₁ w.r.t. angle of incidence θ. Here corresponding to all the cases, we notice similar decreasing trends with difference in magnitudes for the whole range and show significantly variation for m. Figure 18 depicts the Variations in E₂₂ w.r.t. angle of incidence θ. Here corresponding to all the cases, there is sharp increases in initial range and then shows steady state for rest of range of θ Fig. 18. Variations of E₂₃ w.r.t. angle of incidence θ are shown in Fig. 19. Here, we notice values decreases sharply in the initial range of angle and increase gradually throughout the range.

Fig. 17

Variations of energy ratio E₂₁with angle of incidence θ

Fig. 18

Variations of energy ratio E₂₂ with angle of incidence θ

Fig. 19

Variations of energy ratio E₂₃ with angle of incidence θ

8.5.3 Incident QT wave

Figures 20, 21 and 22 depict the Variations of Energy ratios E₃₁, E₃₂, E₃₃ w.r.t. angle of incidence θ. Hereafter sharp increase E₃₁ E₃₂ and E33, with increase in angle of incidence θfor all the cases of hall current.

Fig. 20

Variations of energy ratio E₃₁ with angle of incidence θ

Fig. 21

Variations of energy ratio E₃₂ with angle of incidence θ

Fig. 22

Variations of energy ratio E₃₃ with angle of incidence θ

8.6 Amplitude ratios

8.6.1 Incident QL wave

Figures 23, 24 and 25 shows variations of amplitude ratio A₁₁, A₁₂, A₁₃ w.r.t. angle of incidence θ. Here, we notice that, initially, there is linear increase in the values of A₁₁ for $m = 0.0,0.3$ while for $m = 0.6,$ it shows the curve form. The amplitude ratio A₁₂ and A₁₃ shows different pattern for every case of hall current with angle of incidence θ

Fig. 23

Variations of amplitude ratio A₁₁ with angle of incidence θ

Fig. 24

Variations of amplitude ratio A₁₂ with angle of incidence θ

Fig. 25

Variations of amplitude ratio A₁₃ with angle of incidence θ

8.6.2 Incident QTS wave

Figures 26, 27 and 28 depicts the variations of amplitude ratio A₂₁, A₂₂, A₂₃ w.r.t. angle of incidence θ. Here, we notice that a linear increase in amplitude ratios A₂₁ for all the cases of hall current while A₂₂ and A₂₃ shows opposite behaviour for all the cases of m.

Fig. 26

Variations of amplitude ratio A₂₁ with angle of incidence θ

Fig. 27

Variations of amplitude ratio A₂₂ with angle of incidence θ

Fig. 28

Variations of amplitude ratio A₂₃ with angle of incidence θ

8.6.3 Incident QT wave

Figures 29, 30 and 31 show the variations of amplitude ratios A₃₁, A₃₂, A₃₃ w.r.t. angle of incidence θ respectively.. Here, we notice that these variations shows effect of hall effect parameter α on the amplitude ratios A₃₁, A₃₂, A₃₃.

Fig. 29

Variations of amplitude ratio A₃₁ with angle of incidence θ

Fig. 30

Variations of amplitude ratio A₃₂ with angle of incidence θ

Fig. 31

Variations of amplitude ratio A₃₃ with angle of incidence θ

9 Conclusions

From the analysis of graphs we conclude

• 1. The frequency of waves formed in the material have significant effect on the phase velocity, attenuation coefficients, specific loss and penetration depth of various kinds of waves.

• 2. The magnitude of energy ratios is also effected by the angle of incidence. As angle of incidence increases, we notice less variation in the magnitudes of energy ratios.

• 3. Hall current and two temperature changes the magnitude of waves. With the increase in the hall current, the magnitude of waves are reduced.

• 4. The plane waves signals provides information about the inner earth structure and also useful in inspection of materials, magnetometers, geophysics, nuclear fields and related topics.