1 Introduction

Nowadays, technologies play a great role in human life, advancing the ways of living and working but engineers still have many issues to solve in various filed of technology. The vibration of mechanical structure remains one of the most studied problems due to the difficulty to completely avoid vibration in many applications.

Currently, a large number of algorithms and literature for curve fitting structural data is available; consequently, the determination of the optimal method has become difficult for each situation. Hence, the main objective of this paper is the comparison among several modal parameter extraction algorithms from response vibration measurements in order to highlight not only their pros and cons. Moreover, this article focuses on how these methods can be implemented in a simple way in order to find the natural frequencies and the damping ratios to make them easy to use in the dynamic environment. As these authors are aware, in the literature the detailed explanation on the steps used to implement these methods or the tricks necessary to achieve good results are not provided. This mostly happens when the least square complex exponential method, the eigensystem realization algorithm method and the rational fraction polynomial method are used. on the other hand, the peak amplitude and the circle fit methods are well clarified and achieved. Therefore, it was decided to use the latters to get initial estimation of the modal parameters. Furthermore, the implementation of these methods highly differs between authors. In this work, a simplified and efficient implementation on Matlab ® is illustrated, in order to extract modal parameters. The basic problem in experimental modal analysis is to extract the natural frequency and especially the damping ratio of dynamical structure. With this knowledge, a theoretical finite element models [1] can validate and gain a better comprehension of corresponding structure. A further widely used application of these modal parameters is to control the health of a structure. The modal analysis methods can be separated in two leading categories which are the time domain and the frequency domain methods [2]; the earliest method works in the frequency domain and is classified as an SDOF algorithm such as the peak amplitude method (PPM) [3] and the circle fit method (CFM) [4]. These methods give errors in results, particularly in the damping estimation, where the modes are close to each other and coupled. In addition, the SDOF algorithm should not be used when the data contains noise around the resonance [5]. When the MDOF algorithms operate in the time domain and frequency domain methods, data are managed by assorting the FRFs in the domain. The least square complex exponential method (LSCEM) is considered one of the fast time domain methods. [6, 7]. This method uses the FRFs as an input in spite the fact that it works in the time domain. The LSCEM uses the Least Square Method to find the modal parameters. The eigensystem realization algorithm method (ERAM) is another major MDOF time domain approach [8, 9]. This method uses the Singular Values Decomposition of the so-called Hankel Matrix which is usually a matrix with a high number of rows and columns; for such a reason this algorithm is computationally complex [10]. One more MDOF is the rational fraction polynomial method (RFPM) [11]; it works in the frequency domain and it uses the Least Square technique to minimize the error function. For more information concerning modal analysis techniques can be addressed in Ref [12, 13].

In the frequency domain method, the lower number of order is, the more accurate the results are. However, they have specific problems related to the fast Fourier transform (FFT) analysis [14, 15], such as the leakage [16]. Furthermore, the frequency domain methods determine the frequency response function, but this task usually requires the input excitation data to be detailed. In time domain, signals are monitored by the time domain methods using output responses only. Time domain methods are considered very useful for experimental tests due to this characteristic. Another useful property of time domain method is the ability to recognize two modes when they are very close one to each other. In general, the time domain work better than the frequency domain when the damping is low, and the frequency domain estimators work better for high damping, as demonstrated in [17, 18].

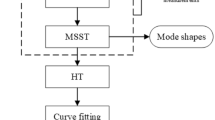
It has always been a difficult task to define the poles of a system, including the damping and the frequency, from the response vibration responses. In this work, the carcass, one of the gear box components, was separately considered for a better estimation of the FRFs [19]. The measurements were carried out after adding a constrained layer to the carcass of gear box to make the damping degree similar to the free–free condition. The structure was excited by a hammer with a periodic impulse. The residues or the zeros of the system Frequency Response Function (FRFs) can be equivalently determined using the periodic response. The original contribution of this study is related to the implementation of several methods in Maltab ® to extract their modal parameters in order to then compare their results, discuss the limits of each method and its suitable domain of employment. For the comparison, the following common methods of modal analysis were used: peak amplitude methods (PPM), circle fit method (CFM), least square complex exponential method (LSCEM), eigen system realization algorithm method (ERAM) and rational fraction polynomial method (RFPM). The process followed to determine the poles is shown in the flowchart of Fig. 1.

Fig. 1
figure 1

Analysis procedure’s flowchart

Full size image

2 Background and algorithms implementation

2.1 The peak picking method (PPM)

The PPM, sometimes referred as a peak-amplitude method or 3 dB method, is a single-input single output (SISO) and it is the simplest of the modal parameter estimation methods that works in the frequency domain [20, 21]. It consists of separating each single mode in order to determine their modal parameters. Thus, the natural frequency, damping factor and residues will be determined as follows, respectively:

$$\omega_{r} = { \hbox{max} }\left({FRF} \right)$$
(1)
$$\zeta_{r} \cong \frac{{ \omega_{a} - \omega_{b} }}{{2\omega_{r}}}$$
(2)
$$A_{pq}^{r} = 2\left| {\tilde{\alpha}} \right|_{pq} \omega_{r}^{2} \zeta$$
(3)

Note that \(\omega_{a}\) and \(\omega_{b}\) are the frequencies on the half-power points.

2.2 Circle fit method (CFM)

The CFM in the past was known as the Kennedy–Pancu method [4]; it is a single-input single output method and it works in the frequency domain. A detailed study has been established in Ref [22]. Similar to the PPM, it is designed to separate each single mode in the system. The concept of this method is to consider the FRF values in the vicinity of the resonance as a circle in the Nyquist plot. In fact, once the natural frequency and the damping factor were estimated, the diameter of circle is used to estimate the residues. According to the algorithm, the Circle-Fit method can be described by the following sequences:

  • Selection of points to be used.

  • Circle fitting based on these points and calculation of the fitting quality.

  • Estimation of damping ratios and natural frequencies

  • Calculation of multiple damping estimates and their mean and scatter.

  • Determination of the modal constant.

$$\omega_{r} = max\left({\Delta \theta} \right)$$
(4)
$$\zeta_{r} = \frac{{\omega_{i + 1}^{2} - \omega_{i}^{2}}}{{2\omega_{r} \left({\omega_{i + 1} \tan \left({\frac{{\theta_{i + 1}}}{2}} \right) + \omega_{i} \tan \left({\frac{{\theta_{i}}}{2}} \right)} \right)}}$$
(5)
$$A_{pq}^{r} = 2\left| {\tilde{\alpha}} \right|_{pq} \omega_{r}^{2} \zeta$$
(6)

The robustness of this method has been demonstrated by several studies as given in Ref. [13,14,15,16,17,18,19,20,21,22,23].

2.3 Least Square Complex Exponential Method (LSCEM)

The LSCEM was introduced in 1979 [7], it is a single-input multi-outpout method (SIMO) and it works in the time domain. This method starts using the FRF receptance of a general MDOF system with a general viscous damping. Then, the impulse response function will be obtained by an inverse Fourier trasformation as follows:

$$\alpha_{pq} \left({j\omega} \right) = \mathop \sum \limits_{r = 1}^{2N} \frac{{A_{pq}^{r}}}{{j\omega - \lambda_{r}}}\mathop{\longrightarrow}\limits^{{{\mathcal{F}} ^{- 1}}}h_{ij} \left(t \right) = \mathop \sum \limits_{r = 1}^{2N} A_{pq}^{r} e^{{\lambda_{r} t}}$$

For the \(l{\text{th}}\) sample.

$$\begin{aligned} h_{l} & = \mathop \sum \limits_{r = 1}^{2N} C_{r} V_{r}^{l} l = 0, 1 \ldots ,N - 1 \\ & \quad with\;\left\{ {\begin{array}{*{20}c} {C_{r} = A_{pq}^{r} } \\ {V_{r} = e^{{\lambda_{r} t}} } \\ \end{array} } \right. \\ \end{aligned}$$
(7)

Equation (7) extended to the full data set of \(l\) samples, gives:

$$\begin{aligned} \left[{\begin{array}{*{20}c} 1 & 1 & 1 & \ldots & 1 \\ {V_{1}} & {V_{2}} & {V_{3}} & \ldots & {V_{2N}} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {V_{1}^{l}} & {V_{2}^{l}} & {V_{3}^{l}} & \ldots & {V_{2N}} \\ \end{array}} \right]\left[{\begin{array}{*{20}c} {C_{1}} \\ {C_{2}} \\ \vdots \\ {C_{2N}} \\ \end{array}} \right] = \left[{\begin{array}{*{20}c} {h_{0}} \\ {h_{1}} \\ \vdots \\ {h_{2N}} \\ \end{array}} \right] \hfill \\ \hfill \\ \end{aligned}$$
(8)

Or, in compact form:

$$\left[V \right]\left[C \right] = \left[h \right]$$
(9)

\(\left[V \right]\;{\text{and}}\;\left[C \right]\) are unknowns.

This equation can be solved by using Prony’s Method [24], the roots \(\lambda_{r}\) for an underdamped system always occur in complex conjugate pairs. It always exists a polynomial in \(V_{r}\) of order \(l\) with real coefficients β, (called the Autoregressive coefficients) such as the following relation is verified:

$$\beta_{0} + \beta_{1} V + \beta_{2} V^{2} + \cdots + \beta_{l} V^{l} = 0$$
(10)

After some steps explained in detail in the Ref [8], the following equation will be obtained:

$$\left[{\begin{array}{*{20}c} {h_{0}} & {h_{1}} & {h_{2}} & \ldots & {h_{2N - 1}} \\ {h_{0}} & {h_{1}} & {h_{3}} & \ldots & {h_{2N}} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {h_{2N - 1}} & {h_{2N}} & {h_{2N + 1}} & \ldots & {h_{4N - 1}} \\ \end{array}} \right]\left[{\begin{array}{*{20}c} {\beta_{1}} \\ {\beta_{2}} \\ \vdots \\ {\beta_{2N - 1}} \\ \end{array}} \right] = - \left[{\begin{array}{*{20}c} {h_{2N}} \\ {h_{2N + 1}} \\ \vdots \\ {h_{4N - 1}} \\ \end{array}} \right]$$
(11)

From Eq. (11), coefficients β will be determined by using the single impulse response via a Least Square Method. Instead of using a single impulse response function (IRF), LSCEM estimates coefficients β by using several IRF’s, as follows.

$$\left[{\begin{array}{*{20}c} {h_{11}} \\ {h_{12}} \\ \vdots \\ {h_{p}} \\ \end{array}} \right]\left[\beta \right] = - \left[{\begin{array}{*{20}c} {\widetilde{{h_{11}}}} \\ {\widetilde{{h_{12}}}} \\ \vdots \\ {\widetilde{{h_{p}}}} \\ \end{array}} \right]$$
(12)

In compact form,

$$\left[H \right]\left[\beta \right] = \left[{\tilde{h}} \right]$$
(13)

Coefficient \(\beta\) will be obtained by using pseudoinverse technique. Now coefficients \(\beta_{0},\beta_{1}, \ldots \beta_{2N - 1}\),are known and Eq. (10) can be solved to yield the \(V_{r}\) roots. Then, poles \(\lambda_{r}\) can be calculated as.

$$\lambda_{r} = \frac{{ln\left({V_{r}} \right)}}{\Delta t}$$
(14)

The mode shapes of the system can be calculated immediately by substituting \(\left[V \right]\) in Eq. (9). The challenge of this method is to construct a good Hankel matrix \(\left[H \right]\) where the number of columns represents the number of order and the number of rows are arbitrary. In order to minimize the Least Square Error, some studies supposed to consider a high number of rows [21, 25]. In this study the number of rows will be determined by increasing the number of rows one at a time then the best number of rows will be found by observing the stabilization diagram [26]. If the stabilization diagram obtained was not clear enough, the range of time should be changed. A small diagram in Fig. 2 explains the procedure of the implementation in Matlab ®.

Fig. 2
figure 2

Steps of the LSCEM implemented in Matlab ®

Full size image

If it is not possible to obtain a clear stabilization diagram, the range of selected data must be changed and the same procedure mentioned above will be repeated. This method suffers when the damping is high as demonstrated in Ref [27].

2.4 Eigensystem realization algorithm method (ERAM)

The ERAM is a multi-input multi-output method (MIMO) and it works in the time domain [9]. It includes information not only from different output locations, but also from several input reference points on the structure. This method succeeded in dealing with the problem of missing one of the vibration modes from output responses, this occasionally happens following the application of a SIMO method. The Singular Values Decomposition (SVD) in this method can significantly reduce the effect of noise [7]. The ERAM is a very effective method for system identification by using Hankel matrix; further details about this method can be found in Ref [13, 28].

Let assume a state space dynamic system as follows:

$$x\left({t + 1} \right) = \varvec{A}x\left(t \right) + \varvec{B}u\left(t \right)$$
(15)
$$y\left(t \right) = \varvec{C}x\left(t \right) + \varvec{D}u\left(t \right)$$

Let consider an impulse force at t = 0, and the initial condition equal to zero:

$$\left\{ {\begin{array}{*{20}l} {u(0) = 1;} \hfill \\ {u(t) = 0,\quad t > 0} \hfill \\ {D = 0} \hfill \\ \end{array} } \right.$$

Hence, by iterating the system of Eq. (11) in time, the following parameters will be obtained.

$$\begin{aligned} x\left(0 \right) = 0; & \to y\left(0 \right) = 0; \\ x\left(1 \right) = Ax\left(0 \right) + Bu\left(0 \right) = B & \to y\left(1 \right) = CB; \\ x\left(2 \right) = AB; & \to y\left(2 \right) = CAB; \\ \end{aligned}$$

where \(y\left(0 \right), y\left(1 \right), y\left(2 \right) \ldots,y\left(t \right)\) are the so called Markov parameters.

By constructing the Hankel matrix \(H_{0}\) of the Markov parameters as:

$$\underbrace {{H_{0}}}_{{\left({p x q} \right)}} = \left[{\begin{array}{*{20}c} {y\left(0 \right)} & {y\left(1 \right)} & \ldots & {y\left(p \right)} \\ {y\left(1 \right)} & {y\left(2 \right)} & \ldots & {y\left({p + 1} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {y\left(q \right)} & {y\left({q + 1} \right)} & \ldots & {y\left({p + q - 1} \right)} \\ \end{array}} \right]$$
(16)

And by apply the SVD to the matrix \(H_{0}\)

$$\left[{\underbrace {H\left(0 \right)}_{pxq}} \right] = \underbrace {{\left[\varvec{U} \right]}}_{px2N}\underbrace {{\left[\varvec{\varSigma}\right]}}_{2Nx2N}\underbrace {{\left[\varvec{V} \right]^{T}}}_{2Nxq}$$
(17)

And by shifting the Hankel matrix as follows:

$$\underbrace {{H_{1}}}_{{\left({p x q} \right)}} = \left[{\begin{array}{*{20}c} {y\left(1 \right)} & {y\left(2 \right)} & \ldots & {y\left({p + 1} \right)} \\ {y\left(2 \right)} & {y\left(3 \right)} & \ldots & {y\left({p + 2} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {y\left({q + 1} \right)} & {y\left({q + 2} \right)} & \ldots & {y\left({p + q + 1} \right)} \\ \end{array}} \right]$$
(18)

After some manipulations [13], the identified discrete state-space \(\hat{A}, \hat{B} \;{\text{and}}\;\hat{C}\) can be written

$$\left[{\hat{A}} \right] = \left[{\varvec{\varSigma}_{2N}} \right]^{{- \frac{1}{2}}} \left[{\varvec{U}_{2N}} \right]^{T} \left[{H\left(1 \right)} \right]\left[{\varvec{V}_{2N}} \right]\left[{\varvec{\varSigma}_{2N}} \right]^{{- \frac{1}{2}}}$$
(19)
$$\left[{\hat{B}} \right] = \left[{\varvec{\varSigma}_{2N}} \right]^{1/2} \left[{\varvec{V}_{2N}} \right]^{T} \left[{E_{q}} \right]$$
(20)
$$\left[{\hat{C}} \right] = \left[{E_{p}} \right]^{T} \left[{\varvec{U}_{2N}} \right]\left[{\varvec{\varSigma}_{2N}} \right]^{{\frac{1}{2}}}$$
(21)

In modal analysis, the goal is to determine matrices \({\hat{\text{A}}}\) and \({\hat{\text{C}}}\), where the eigenvalues of \(\hat{A}\) consist of the complex conjugates poles of the system. From each pole the natural frequency and the damping ratio can be obtained. The mode shapes are related to matrix \(\hat{C}\). By using matrix \(\hat{A}\) and by solving the Eigen-problem, the mode shapes can be determined in terms of the physical coordinates of system:

$$\left[{\hat{A} } \right]\left[{\psi_{u}} \right] = \varLambda \left[{\psi_{u}} \right]$$
(22)

The transformation given by Eq. (11) must be used:

$$\underbrace {\psi}_{px1} = \left[\varvec{C} \right]\left[{\psi_{u}} \right]$$
(23)

\(\varLambda = \left\{{\varLambda_{1}, \varLambda_{2}, \ldots, \varLambda_{2N}} \right\}\) is the eigenvalues and \(\left[{\psi_{u}} \right]\) is the eigenvector. The poles will be determined by the following formulae:

$$\lambda_{r} = \frac{{ln\left({\varLambda_{r}} \right)}}{\Delta t}$$
(24)

The ERAM was implemented in Matlab ® by fixing a number of order N and generating the matrix \(\left[{\hat{A}} \right]\) by iteration. For each iteration, matrix \(\left[{\hat{A}} \right]\) was generated as a square matrix (1 × 1, 2 × 2,…,N × N). Then it was possible to extract the eigenvalues and the eigenvector. Furthermore, the poles were calculated by applying Eq. (24) and the physical mode shapes by using Eq. (20). Thus, the poles and the mode shapes were determined. The final step consists of plotting the stabilization diagram from which the stable poles are extracted. Figure 3 represents the main steps used to implement this method in Matlab ®.

Fig. 3
figure 3

Steps of the ERAM implemented in Matlab ®

Full size image

2.5 Rational fraction polynomial method (RFPM)

This method works in the Frequency Domain [11], and it is a single-input single-output method (SISO), based on a multi degrees of freedom approach. The Rational Polynomial Method (RFPM) is a special version of the general Curve-Fitting method, but it is based on the FRF which is expressed in the Rational fraction form [13]. Thus, the FRF requires an expression of the frequency response function as the ratio of two polynomials, with the roots of numerator permitting to determine the modal constant while the roots of the denominator yielding the poles (frequency, damping). Generally, the numerator and the denominator orders are independent one to each other. The denominator is considered as the characteristic polynomial of the system. By Curve-Fitting the FRF against the analytical form in Eq. (25), and then solving the roots of the numerator and the characteristic polynomials, the zeros and poles of the FRF can be determined.

$$\alpha \left({j\omega} \right) = \frac{{\mathop \sum \nolimits_{k = 0}^{2N - 1} a_{k} \left({j\omega} \right)^{k}}}{{\mathop \sum \nolimits_{k = 0}^{2N} b_{k} \left({j\omega} \right)^{k}}}$$
(25)

The curve fitting in the RFPM consists of determining the coefficients \(a_{k} \;({\text{with}}\;k = 0, \ldots 2N - 1)\) and \(b_{k} \;\left({{\text{with}}\;k = 0, \ldots 2N} \right)\), in such a way the error between the analytical formulae (25) and the FRF is minimized over a chosen range; more information is given in Ref [29].

The RFPM was implemented in Matlab ® by firstly selecting a small range of frequency and by “invfreqs” command the coefficients \(a_{k}\) and \(b_{k}\) were determined. Then, the poles and the residues were determined by using “residue” command. More information about “invfreqs” and “residue” command are included in Ref [30]. If it is not possible to obtain a clear stabilization diagram, the range of the frequency will be changed. Figure 4 describes the important steps that were used to implement the RFPM.

Fig. 4
figure 4

Steps of the RFPM implemented in Matlab ®

Full size image

This method requires more time with respect to other methods to achieve a good estimation for the frequency and damping ratio.

3 Measurement and analysis

Measurements were carried out on an aluminum carcass of gearbox with dimension of about 150 mm by 100 mm by 40 mm with carcass’s thickness of 5 mm. The carcass was supported by soft bungee cords fixed on a frame, in order to consider its dynamic behavior as a free–free condition. Figure 5 shows the set-up of the test measurement used in this study. As it can be seen, the periodic impulsive excitation is generated by using a hammer (PCB 068C04), while the response is measured by using PCB piezoelectric accelerometer (freq. range 1–10000 Hz). One accelerometer was positioned, and the system was excited by a hammer in 34 points. In particular, the response point was remained fixed during the tests, while the excitation changed from one measurement point to another in order to get the FRFs for all the considered points [31, 32]. The measured data were recorded using software LMS Test-Lab ® [33] and the post processing was performed in Matlab ® environment. The signals were acquired by using Nyquist frequency of 12,800 Hz and frequency resolution \(\Delta f = 1.5625\,{\text{Hz}}\) compromising with the type of carcass gear box and the kind of constraint condition. An exponential window for the force signals is used in order to decrease the leakage. The input autopower-spectra, output power-spectra and cross-power-spectra are estimated and reserved for each measurement location. In addition, the FRFs are determined by using \(H_{v}\) estimator [33]. The coherence function is controlled as an on-line check of data quality. The periodic response was calculated by using the synchronous averaging method as reported in [19] with the aim of obtaining a good estimation of the frequency response function.

Fig. 5
figure 5

Measurement set-up

Full size image

In detail, 34 periodic responses were selected to have a better estimation of the modal parameters, i.e. natural frequencies and damping ratios. The method used to make the EMA is the traditional procedure in which both excitation and response are measured together to obtain the accelerance. Figure 6 shows all the FRFs measured, in total 34 functions are plotted.

Fig. 6
figure 6

Amplitude of all the measured frequency response functions

Full size image

Five methods used for the estimation of modal parameters are shown in this work. At the beginning, the Peak Amplitude and Circle Fit were the simplest methods to be applied to calculate the first estimation as their implementation is easier with respect to the other methods. Once the results were obtained by these two methods, they were compared with the results of several methods that, according to literature, are considered more accurate; these methods are the LSCEM, ERAM, and RFPM.

A stabilization diagram was constructed for the last three methods to identify the physical modes from the computational modes. Normally, a tolerance, in percentage is given for the stability of each modal parameters.

4 Results and discussion

The natural frequencies and damping ratios were extracted for the first 5 modes by the methods described in Sect. 2, in the following manner. In the LSCEM, ERAM and RFPM, all modes fulfilling the stabilization criteria with tolerance 1% for the natural frequencies, 5% for the damping ratios and the MAC [34] values greater than 90%.

In the LSCEM the stable poles that have stability in frequency and damping in the stabilization diagram were plotted. The LSCEM stability diagram shows that the vectors are not engaged, because the non- physical poles appear with the increase of the number of orders. Consequently, it will be hard to reach a good estimation of the mode shapes. In the ERAM the stability of vector and the stable poles were schemed. In order to compare the mode shapes between the iteration, the Modal Assurance Criterion (MAC) was used to detect the stability of vectors. When the RFPM method is applied, the stability of the vector can be rarely found because as the number of orders increases the ill conditioning problem starts to appear. Therefore, its plot was eliminated in the stabilization diagram of the RFPM.

The results are summarized in Tables 1 and 2, where the average value of poles and the corresponding scatter are listed and schemed in the Figs. 10 and 11. The scatter was calculated as the normalized random error er (standard deviation divided by the average value) for LSCEM, ERAM and RFPM. It is important to mention here that the minimum number of pole estimates of each mode was 12.

Table 1 Estimated natural frequencies, and corresponding normalized random errors, er, for the 5 methods
Full size table
Table 2 Estimated damping ratios, and corresponding normalized random errors, er, for the 5 methods
Full size table

The estimation of the stable poles can be seen in Figs. 7, 8 and 9. Figures 7 and 8 show the stabilization diagrams extracted by LSCEM and ERAM, respectively, with a number of order 80. In both cases, the presence of 5 physical modes can be detected in the frequency range [0 4500] Hz. It can be noticed that the stable poles start to appear when the number of order surpasses 26 for the LSCEM (Fig. 7). In Fig. 9 all modes were isolated, and for each mode a stabilization diagram was established with a number of order 20. When the frequency bandwidth is narrowed around the Peaks, these modes immediately appear when the number of order exceed one, and their estimation becomes more accurate.

Fig. 7
figure 7

Stabilization diagram extracted by LSCE

Full size image
Fig. 8
figure 8

Stabilization diagram extracted by ERAM

Full size image
Fig. 9
figure 9

a Stabilization diagram close to the first mode; b second modes; c third mode; d fourth mode; e fifth mode

Full size image

It is evident from Table 1 that the natural frequencies of all modes determined by these methods were very similar and their errors er were very low; thus, the difference between the method results is insignificant. Regarding the damping factor, it can be noted in Table 2 that the results were very distant, and it is difficult to detect a good damping estimation. The comparison between the PPM and CFM and the other methods in Table 2 shows that their results were slightly different, while some similarity can be noticed on several modes. It can be deduced that although the PPM and CFM are generally considered simple and very basic as described in Sect. 2, they managed to give good results in comparison to the other methods. Therefore, these two methods can be very useful as a first estimation because they provide good results for the major part of the modes.

In this study, the error values \(er\) is an indicator of how good a method works. When the error is low, the stability of the poles is high in the stabilization diagram, hence the method can be considered reliable. In this context, a comparison was made between RFPM, ERAM and LSCEM in Figs. 10 and 11; it was clear that the RFP was the method that presented the lowest values of error which make it the best method among the three studied. The only issue here is that the error obtained by RFPM was the lowest on all the modes except the third mode, where it has a value (0.15%) greater than the error given by the LSCEM and almost equal to the one given by the ERAM. This error can be due to the noise present in the experimental FRF.

Fig. 10
figure 10

Scatter of frequency for each mode, determined by LSCEM, ERAM and RFPM

Full size image
Fig. 11
figure 11

Scatter of damping for each mode, determined by LSCEM, ERAM and RFPM

Full size image

5 Conclusions

This paper presents a comparison between several methods of experimental modal analysis for the detection of the frequency and damping ratio values. The results achieved during the study serve to understand the factors affecting the accuracy of the frequency and the damping in respect to the method in use. It can be observed that the natural frequency values obtained by all methods were very similar and the differences between the results were insignificant.

It was revealed that it is convenient to use the Peak Picking Method and Circle Fit Method as a first estimation; these methods succeeded in giving good estimation of the natural frequency and damping. They are also simple to use and fast to implement.

Regarding the other methods, if the stability of poles dispersed in the stabilization diagram was taken into consideration, the Rational Fraction Polynomial method did the best job in detecting the damping and frequency values. This method presented the least scatter on all modes except on the third, probably due to the noise present in the measured frequency response function. The results obtained by the LSCEM and the ERAM were reasonable for both frequency and damping. The scatter was found slightly greater in the ERAM than in the LSCEM.

In addition, it has been noted by following this procedure of implementation. The fast method to extract the natural frequencies and the damping ratios was the ERAM next come the LSCEM then the RFPM.