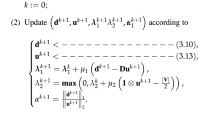1 Introduction

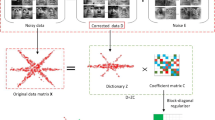
Graphical representations, which characterize the affinities among data points, have played an important role in machine learning, image processing [1,2,3,4], writer identification [5,6,7], visual tracking [8,9,10,11,12], and especially for clustering problems [13,14,15,16]. For graph-based clustering methods, the graph construction is guided under certain learned or pre-defined pairwise similarities [17, 18]. Most graph-based clustering methods focus on how to build a good affinity matrix, and regard the graph construction as a back-end operation [19,20,21]. In this paper, we aim to explore the great potential value of graph construction. By analyzing the prior knowledge of the number of clusters, it is proved that the spectral clustering method has better block structure preservation. We propose a graph refining strategy to iteratively optimize the affinity matrix of the graph, which can significantly improve the clustering result. Such a strategy is based on the block structure-preserving property of spectral clustering method: given an original affinity matrix \(\mathbf {A}\), a new affinity matrix \(\mathbf {B}\) can be obtained by doing spectral clustering on the Laplacian matrix of \(\mathbf {A}\). If \(\mathbf {A}\) is a block diagonal matrix, so is the new matrix \(\mathbf {B}\). Moreover, \(\mathbf {A}\) and \(\mathbf {B}\) have the same block structure. Based on this property, the original affinity matrix \(\mathbf {A}\) can be refined by forcing \(\mathbf {A}\) and the constructed affinity matrix \(\mathbf {B}\) to have the same block structure. Then, the refining strategy can be achieved in an iterative manner (Fig.1).

Fig. 1
figure 1

An illustration for the proposed graph refining strategy, where \(\mathbf {S},\mathbf {Z}\) and \(\mathbf {F}\) are the original affinity matrix, the intermediary affinity matrix and the final output affinity matrix, respectively. The step a is the initialization of \(\mathbf {Z}\). In step (b), we construct \(\mathbf {F}\) by minimizing the differences between \(\mathbf {F}\) and \(\mathbf {Z}\). Mutually, in step (c), \(\mathbf {F}\) conducts to build a new \(\mathbf {Z}\) by spectral clustering method and a certain pre-defined affinity measurement function. After certain number of alternations, we expect the graph of estimated \(\mathbf {F}\) and the graph of intermediary \(\mathbf {Z}\) will have the same cluster structure, which means there exists a permutation matrix \(\mathbf {P}\) such that \(\mathbf {P} \mathbf {F}\) and \(\mathbf {P} \mathbf {Z}\) are both diagonal block and have the same block structure

Full size image

In fact, the graph refining strategy can be formulated with a regularization framework [22,23,24]. The starting point of this framework is to find a multiple output affinity function: \(f: \mathscr {X} \rightarrow \mathbb {R}^N\), which can be used to measure the affinities between the input instance and the other N instances. The multiple output affinity function f can be chosen in a well-designed hypothesis space, called reproducing kernel Hilbert spaces of vector-valued functions (RKHSvv), which is in favor of doing kernel tricks on graph reconstruction. Given N instances \((\mathbf {x}_1, \mathbf {x}_2, \ldots , \mathbf {x}_N) \in \mathscr {X}\), an affinity matrix \(\mathbf {F}\) of these instances: \(\mathbf {F} = [f(\mathbf {x}_1), f(\mathbf {x}_2), \ldots , f(\mathbf {x}_N)]\) , can be obtained. And the affinity matrix \(\mathbf {F}\) can be obtained in a form of multiplication between a kernel matrix and an unknown coefficient matrix. Besides, a specific graph refining model can be also provided. The coefficient matrix in such a model can be solved column by column by a standard convex quadratic programming method [25]. We evaluate the proposed model on both synthetic and real data, and promising results are obtained. To summarize, the main contributions of the paper are as follows:

  • We provide a graph reconstruction strategy which can refine the original graph by giving the number of clusters. Such a strategy is based on the block structure-preserving properties of spectral clustering.

  • We formulate an iterative regularization framework to implement the graph refining strategy and design a new reproducing kernel Hilbert spaces of vector-valued functions as the hypothesis space for the regularization framework. To the best of our knowledge, this paper is the first one introducing RKHSvv to study the clustering problems.

  • We provide an effective graph refining model based on the iterative regularization framework.

The rest of the paper is organized as follows: We give a related work in Sect. 2. The model RKHSvv which we formulated to study the clustering problems is given in Sect. 3, the property of block structure preserving is derived in Sect. 3.1, and the framework formulation is provided in Sect. 3.2. We give the definition of RKHSvv and the corresponding representer theorem in Sect. 3.3. Using the representer theorem and a Euclidean distance loss function, we provide a specific graph refining model in Sect. 3.4. The optimization method is provided in Sect. 3.5, the experimental results are given in Sect. 4, and the conclusion is drawn in Sect. 5.

2 Related work

As an extensive review of graph clustering and regularization framework beyond the scope of this paper, we review the work related to our approach including graph-based clustering and the framework of regularization, the reproducing kernel theory will be a review as well.

Graph clustering is the combination of vertices of the graph, taking into account the edge structure of the graph; each cluster should have multiple edges, and the cluster is relatively small [19, 21]. Generally speaking, given a dataset, the goal of clustering is to divide the dataset into multiple categories, so that the elements assigned to a particular class are similar or connected in some pre-defined sense. However, not all graphs have the structure of natural clusters. If the structure of the graph is completely uniform, and the edges are distributed on the vertex set, the clustering of any algorithm is arbitrary [26].

Regularization has become the main theme of machine learning and statistics. It provides an intuitive and principle tool for learning from high-dimensional data. The consistency of the results of the practical algorithms and general theory of linear algebra has been studied in-depth by means of Euclidean norms or regularized Hilbertian specifications [27,28,29]. While based on the advantages of dealing with nonlinear problems, the kernels methods have been widely used in the literature [30,31,32].

Reproducing kernel theory has significant implementations in integral equations, differential equations, probability, and statistics [33]. In the recent times, this theory is applied for various model problems by many authors [34,35,36]. The simplest and most practical method of multitask learning is the regularized multitask learning, which solutions to related tasks are close to each other. Due to its general and simple formulation, regularized multitask learning has been applied to various types of learning problems, such as regression and classification [37]. And some works [38,39,40] generalized RKHS of scalar-valued functions to vector-valued cases to deal with the multiple task learning [41].

Our works can be regarded as an extension to such a generalization in clustering problem. Nie et al. [42] provided methods to reconstruct a graph from the original graph, which is related to ours in the aspect of the problem consideration. Compared with [42], our works in this paper can be considered as a more general formulation, which lets [42] be the special cases of ours.

3 The proposed approach

In this section, we will first introduce the block structure-preserving property and then propose the iterative regularization framework for graph refining based on the reproducing kernel Hilbert spaces for vector-valued, followed by the method and optimization, with which the block structure can enhance the model.

3.1 Block structure preserving

We have the following lemma about block diagonalization:

Lemma 1

[43] If \(\mathbf {A} \in \mathbb {R}^{N \times N}\), the spectrum of \(\mathbf {A}\) is \(\sigma (\mathbf {A}) = \{\mu _1,\mu _2, \dots , \mu _s\}\), there exist such a nonsingular matrix \(\mathbf {P}\) and a set of matrix \((\mathbf {A}_1, \mathbf {A}_2, \cdots , \mathbf {A}_s)\) that \(\mathbf {P}^{-1} \mathbf {A} \mathbf {P} = \hbox {diag } \begin{bmatrix} \mathbf {A}_1&0&...&0\\ 0&\mathbf {A}_2&...&0\\ ...&...&...&...\\ 0&0&...&\mathbf {A}_s \end{bmatrix}\) and the spectrum of \(\mathbf {A}_i\) is \(\sigma (\mathbf {A}_i) = \{\mu _i\}\). That means, \(\mathbf {P}^{-1} \mathbf {A} \mathbf {P} = \hbox {diag } \begin{bmatrix} \mu _1 \mathbf {v}_1 \mathbf {v}_1^T&0&...&0\\ 0&\mu _1 \mathbf {v}_2 \mathbf {v}_2^T&...&0\\ ...&...&...&...\\ 0&0&...&\mu _s \mathbf {v}_s \mathbf {v}_s^T \end{bmatrix}\), where \(\mu _i \mathbf {v}_i \mathbf {v}_i^T = \mathbf {A}_i\).

Given an affinity matrix \(\mathbf {A} \in \mathbb {R}^{N \times N}\), where N is the number of instances, the spectral clustering methods optimize the following problem by:

$$\begin{aligned} \mathbf {Y}^* = \min _{\mathbf {Y}, \mathbf {Y}^T \mathbf {Y} = \mathbf {I}} \,\,tr(\mathbf {Y}^T \mathbf {L}_{\mathbf {A}} \mathbf {Y}), \end{aligned}$$
(1)

where \(\mathbf {Y} \in \mathbb {R}^{N \times C}\), C is the number of clusters, and \(\mathbf {L}_{\mathbf {A}}\) is the Laplacian matrix of \(\mathbf {A}\). The optimal solution \(\mathbf {Y}^*\) can be obtained by finding the C eigenvectors of \(L_{\mathbf {A}}\) corresponding to the C smallest eigenvalues. Equation (1) can be regarded as a feature extraction procedure, which generates N new samples of C-dim features from original pairwise affinities \(\mathbf {A}\). Therefore, each row of \(\mathbf {Y}\) is a data point. Using these data points, we can construct a new affinity matrix by setting some pre-defined affinity measurement function. Suppose that we use the inner product as the measurement function and all of rows in \(\mathbf {Y}\) are normalized, we have an affinity matrix \(\mathbf {B}\), and \(\mathbf {B} = \mathbf {Y}^* \mathbf {Y}^{*T}\).

From Lemma 1, we can easily have the following theorem about \(\mathbf {B}\).

Theorem 1

If \(\mathbf {B} \in \mathbb {R}^{N \times N} = \mathbf {Y} \mathbf {Y}^T, \mathbf {Y} \in \mathbb {R}^{N \times C}, \mathbf {Y}^T\mathbf {Y} = \mathbf {I}\), there exist such a nonsingular matrix \(\mathbf {P}\) and a set of unit vectors \((\mathbf {v}_1, \mathbf {v}_2, \cdots , \mathbf {v}_C)\) that satisfy \(\mathbf {P}^{-1} \mathbf {B} \mathbf {P} = diag( \mathbf {v}_1 \mathbf {v}_1^T, \mathbf {v}_2 \mathbf {v}_2^T, \cdots , \mathbf {v}_C \mathbf {v}_C^T)\).

Proof

Since \(rank(\mathbf {B}) = rank(\mathbf {Y}^{} \mathbf {Y}^{T})=C\), we have \(\sigma (\mathbf {A}) = \{\mu _1,\mu _2, \dots , \mu _C\}\), where \(\mu _1 = \mu _2 = \cdots = \mu _C = 1\). From Theorem 1, there exist such a nonsingular matrix \(\mathbf {P}\) and a set of unit vectors \((\mathbf {v}_1, \mathbf {v}_2, \cdots , \mathbf {v}_C)\) that \(\mathbf {P}^{-1} \mathbf {B} \mathbf {P} = diag( \mathbf {v}_1 \mathbf {v}_1^T, \mathbf {v}_2 \mathbf {v}_2^T, \cdots , \mathbf {v}_C \mathbf {v}_C^T)\). \(\square\)

We also have the following theorem about \(\mathbf {B}\) when \(\mathbf {A}\) is diagonally block.

Theorem 2

Given a diagonal block affinity matrix \(\mathbf {A}\) with C blocks, its Laplacian matrix is denoted as \(\mathbf {L}_{\mathbf {A}}\). If \(\mathbf {Y}^*\) is the optimal solution of Eq. (1), where the Laplacian matrix is \(\mathbf {L}_{\mathbf {A}}\), the affinity matrix \(\mathbf {B} = \mathbf {Y}^* \mathbf {Y}^{*T}\) is also a diagonal block and the blocks structure is same as \(\mathbf {A}\) (see Fig. 2).

Proof

We unfold the expression in Eq. (1):

$$\begin{aligned} \mathbf {Y}^* =&\min _{\mathbf {Y}^T \mathbf {Y} = \mathbf {I}} \,\,\sum _{i,j=1}^{N}(\mathbf {A})_{ij}\Vert \mathbf {y}_i - \mathbf {y}_j\Vert _2^2\nonumber \\ =&\min _{\mathbf {Y}^T \mathbf {Y} = \mathbf {I}} \,\, \left( - \sum _{i,j=1}^{N}(\mathbf {A})_{ij} \langle \mathbf {y}_i, \mathbf {y}_j\rangle \right) \nonumber \\ =&\max _{\mathbf {Y}^T \mathbf {Y} = \mathbf {I}, \mathbf {B} = \mathbf {Y} \mathbf {Y}^{T}} \,\, \sum _{i,j=1}^{N}(\mathbf {A})_{ij} (\mathbf {B})_{ij}, \end{aligned}$$
(2)

where \((\cdot )_{ij}\) denotes the element in the i-th row and the j-th column. Intuitively, the construction of \(\mathbf {B}\) is guided by \(\mathbf {A}\). Maximizing \(\sum _{i,j=1}^{N}(\mathbf {A})_{ij} (\mathbf {B})_{ij}\) makes the data points in \(\mathbf {B}\) becomes similar to those of \(\mathbf {A}\). Meanwhile, from Theorem 1, we know \(\mathbf {B}\) is similar to a certain diagonal block matrix. Therefore, \(\mathbf {B}\) should have the same block structures as \(\mathbf {A}\). \(\square\)

Theorem 2 reveals that the spectral clustering has a property of Block Structure Preserving [44]: given an original affinity matrix \(\mathbf {A}\) which is diagonal block, the affinity matrix which constructed by doing spectral clustering on \(\mathbf {L}_{\mathbf {A}}\) is also diagonal block and has the same block structure as the original affinity matrix \(\mathbf {A}\) (shown in Fig. 2).

3.2 The iterative regularization framework for graph refining

Let \(\mathscr {X}\) denote the input space, in which each element represents a certain sample. Let \(\mathscr {S} \subset \mathbb {R}^{N}\) denote the affinity space, the element in \(\mathscr {S}\) indicates the affinities of N samples. Given a set of observations: \(\{(\mathbf {x}_i, \mathbf {s}_i ) | \mathbf {x}_i \in \mathscr {X}, \mathbf {s}_i \in \mathscr {S}, i = 1,2,\ldots , N\}\) , the number of clusters: C, and two loss function \(\mathscr {L}_1, \mathscr {L}_2 : \mathscr {S} \times \mathscr {S} \rightarrow \mathbb {R}\), the regularization framework can be formulated as:

$$\begin{aligned}&f^* = \min _{ f \in \mathscr {H}} \sum _{i = 1}^{N}\mathscr {L}_1(\mathbf {s}_i, f(\mathbf {x}_i)) + \lambda _1\sum _{i = 1}^{N}\mathscr {L}_2(\mathbf {z}_i, f(\mathbf {x}_i)) + \lambda _2\Vert f\Vert _{\mathscr {H}}^2\nonumber \\&s.t. \nonumber \\&\mathbf {Z} = \mathscr {G}(\mathbf {F}),\nonumber \\&\forall \mathbf {x}_i \in \mathscr {X}, f(\mathbf {x}_i) \ge \mathbf {0}, \langle f(\mathbf {x}_i), \mathbf {1} \rangle _{\mathscr {S}} = 1, \end{aligned}$$
(3)

where \(\mathscr {H}\) is a Hilbert space of vector-valued functions \(f: \mathscr {X} \rightarrow \mathscr {S}\), and \(\Vert \Vert _{\mathscr {H}}\) is the inner product induced norm of \(\mathscr {H}\). \(\mathbf {F} = [f(\mathbf {x}_1), f(\mathbf {x}_2), \dots , f(\mathbf {x}_N)]\) is the learned affinity matrix. \(\mathbf {Z} = [\mathbf {z}_1, \mathbf {z}_2, \dots , \mathbf {z}_N]\) is the intermediary affinity matrix. \(\mathscr {G}\) is an operation that generates a new affinity matrix by giving the original one. \(\lambda _1\) and \(\lambda _2\) are two hyper-parameters, which are used to balance the influences of corresponding terms. The first term is used to guarantee that the learned affinity matrix F is not changed too much compared with the original affinity matrix. The last term is the inner product induced norm \(\Vert f\Vert _{\mathscr {H}}\), which is used to stabilize f [29]. \(\mathbf {Z}\) is constructed by \(\mathbf {Y}\), where \(\mathbf {Y}\) is calculated by doing spectral clustering on \(\mathbf {L}_{\mathbf {F}}\). \(\mathbf {L}_{\mathbf {F}}\) is the Laplacian of \(\mathbf {F}\). Then, we find \(\mathbf {Z}\) by solving the following sub-problem:

$$\begin{aligned} (\mathbf {Z})_{ij} = g((\mathbf {Y}^{*T})_i, (\mathbf {Y}^{*T})_j), \mathbf {Y}^* = \min _{\mathbf {Y}, \mathbf {Y}^T \mathbf {Y} = \mathbf {I}} \,\,tr(\mathbf {Y}^T \mathbf {L}_{\mathbf {F}} \mathbf {Y}), \end{aligned}$$
(4)

where \((\mathbf {Z})_{ij}\) indicates the element of \(\mathbf {Z}\) in the i-th row and the j-th column, \((\mathbf {Y}^{*T})_i\) and \((\mathbf {Y}^{*T})_j\) indicate the i-th column and j-th column of \(\mathbf {Y}^{*T}\), respectively. \(g: \mathbb {R} \times \mathbb {R} \rightarrow \mathbb {R}_{+}\) is an affinity measurement function. If g is the inner product in \(\mathbb {R}^C\), \(\mathbf {Z} = \mathbf {Y}^{*}\mathbf {Y}^{*T}\).

The second term of objective function is to minimize the difference between \(\mathbf {Z}\) and \(\mathbf {F}\). If \(\mathbf {Z} = \mathbf {Y}^{*}\mathbf {Y}^{*T}\), from the analysis in Sect. 3.1, we know that the graph of \(\mathbf {Z}\) always has C clusters. The minimization in the second term actually preserves the information of C clusters structure for the graph of \(\mathbf {F}\). The rest two constraints about f are used to ensure that the learned function is nonnegative and normalized.

Note that, our regularization framework can be put into an iteratively optimization procedure, in which Eqs. (3) and (4) both are solved alternately. We give this optimization procedure in Algorithm 1 to preserve the information of C clusters structure for the graph of \(\mathbf {F}\).

figure a
Fig. 2
figure 2

An illustration for the property of Block Structure Preserving. a The clear diagonal block affinity matrix \(\mathbf {A}\); b The constructed affinity matrix \(\mathbf {B}\) where \(\mathbf {B} = \mathbf {Y} \mathbf {Y}^T\), \(\mathbf {Y}\) is obtained by do spectral clustering on \(\mathbf {L}_{\mathbf {A}}\)

Full size image

3.3 Hypothesis space of RKHSvv

In general cases, the regularization framework is considered as a setting of binary classification or regression, of which the hypothesis space is defined as a Hilbert space of scalar-valued function. By defining a reproducing kernel [45] in such a space, a reproducing kernel Hilbert space (RKHS) [33] is obtained. Although considering the hypothesis space as a general RKHS has gained numerous achievements in machine learning [34,35,36, 46], the function form of scalar-valued outputs is limited in some tasks which need vector-value outputs. To deal with the limitation, the generalization from the scalar-valued RKHS to vector-valued , called RKHSvv, has been introduced and applied in the literature [37, 38]. We use RKHSvv as the hypothesis space \(\mathscr {H}\) for Eq. (3). To define such RKHSvv in this work formally, we first define reproducing kernel in a Hilbert spaces for vector-valued function.

Definition 1

(Vector-valued reproducing Kernel) Let \((\mathscr {H}, \langle ,\rangle _{\mathscr {H}})\) be a Hilbert space of functions from a certain input space \(\mathscr {X}\) to \(\mathscr {S}\). A function \(k:\mathscr {X} \times \mathscr {X} \rightarrow \mathbb {R}\), is called a reproducing kernel for \(\mathscr {H}\) if, for all \(\mathbf {x} \in \mathscr {X}\), \(\mathbf {c} \in \mathscr {S}\) , and \(f \in \mathscr {H}\), we have that \(k(\mathbf {x}, \cdot )\mathbf {c} \in \mathscr {H}\) and the reproducing property holds: \(\langle f(\mathbf {x}),\mathbf {c}\rangle _{\mathscr {S}} = \langle f, k(\mathbf {x}, \cdot )\mathbf {c}\rangle _{\mathscr {H}}\).

We can also generalize the concept of positive definite :

Definition 2

(Vector-valued Positive-Definite Kernel) A kernel \(k: \mathscr {X} \times \mathscr {X} \rightarrow \mathbb {R}\) is positive definite (PD) in a vector-valued setting if

$$\begin{aligned} \sum _{i,j=1}^{N} \langle \mathbf {c}_i, \mathbf {c}_j \rangle _{\mathscr {S}}\, k(\mathbf {x}_i, \mathbf {x}_j) \ge 0, \end{aligned}$$

for any \(N \in \mathbb {N}\) and any choice of \(\mathbf {x}_1, \mathbf {x}_2, \cdots , \mathbf {x}_n\) from input space \(\mathscr {X}\), and \(\mathbf {c}_1, \mathbf {c}_2, \cdots , \mathbf {c}_n \in \mathscr {S}\).

It’s easy to verify that common scalar-valued PD kernels , e.g., linear kernel and RBF kernel, are also vector-valued PD.

Definition 3

(Reproducing Kernel Hilbert Spaces for vector-valued function (RKHSvv)) Let \((\mathscr {H}, \langle ,\rangle _{\mathscr {H}})\) be a Hilbert space of functions from certain input space \(\mathscr {X}\) to \(\mathscr {S}\), \(\mathscr {H}\) is a reproducing kernel Hilbert space if, for all \(\mathbf {x} \in \mathscr {X}\), there exist \(\mathbf {c} \in \mathscr {S}\) and \(\delta _x \in \mathbb {R}\) so that,

$$\begin{aligned} \langle f(\mathbf {x}), \mathbf {c} \rangle _{\mathscr {S}} \le \delta _x \int _{\mathscr {X}}\langle f(\mathbf {t}), \mathbf {c} \rangle _{\mathscr {S}} d \mathbf {t}, , \forall f \in \mathscr {H}. \end{aligned}$$

A function \(k(\mathbf {x}, \cdot )\mathbf {c}\) in a RKHSvv \(\mathscr {H}\) has the reproducing property:

Corollary 1

(Reproducing property of RKHSvv) A RKHSvv \(\mathscr {H}\) has the reproducing property that means, for all \(f \in \mathscr {H}\), there exists a function \(k(\mathbf {x},\cdot ) \mathbf {c} \in \mathscr {H}, \mathbf {x} \in \mathscr {X}, \mathbf {c} \in \mathscr {S}\) so that,

$$\begin{aligned} \langle f(\mathbf {x}), \mathbf {c} \rangle _{\mathscr {S}} = \langle k(\mathbf {x}, \cdot ) \mathbf {c}, f \rangle _{\mathscr {H}}. \end{aligned}$$

Proof

From the definition of RKHSvv, for all \(\mathbf {x} \in \mathscr {X}\) and \(f \in \mathscr {H}\), there exists a bounded linear functional \(\phi _{\mathbf {x}}[f] = <f(\mathbf {x}), \mathbf {c}>_{\mathscr {S}}\). Then, according to the Riesz representation theorem, there also exists such a function \(k(\mathbf {x}, \cdot ) \mathbf {c} \in \mathscr {H}\) that \(\phi _x[f] = \langle k(\mathbf {x}, \cdot ) \mathbf {c}, f \rangle _{\mathscr {H}}\). \(\square\)

Next, we clarify some differences between our definitions of RKHSvv and the previous works in multiple task learning [37,38,39,40, 47, 48]. In these works, the reproducing kernel is defined as a function in a form of \(\varGamma :\mathscr {X} \times \mathscr {X} \rightarrow \mathscr {S}^2\). According to the definition of \(\mathscr {S}\), the output is a M-by-M matrix. The reason for building such a formulation is that if \(\varGamma\) is separable, a structure matrix \(\mathbf {A} \in \mathscr {S}^2\) can be separated from \(\varGamma\): \(\mathbf {A} k(\mathbf {x}, \cdot ) = \varGamma (\mathbf {x}, \cdot )\), where \(k(\mathbf {x}, \cdot )\) is a scalar-valued kernel. \(\mathbf {A}\) is very useful for multiple tasks learning, since it encodes the structure information for tasks. However, in our affinity reconstruction problem, such information is not needed. Since the function itself in RKHSvv is used to describe the structure of input: affinities, we do not need to define a matrix-output reproducing kernel any more.

Similar to the scalar setting [35], we can easily obtain a representer theorem for RKHSvv.

Theorem 3

(Representer Theorem for RKHSvv) Given an input space \(\mathscr {X}\), affinity space \(\mathscr {S}\), a PD kernel (vector-value setting) \(k: \mathscr {X} \times \mathscr {X} \rightarrow \mathbb {R}\), a set of observations \((\mathbf {x}_1, \mathbf {s}_1), (\mathbf {x}_2, \mathbf {s}_2), \ldots , (\mathbf {x}_N, \mathbf {s}_N) \in \mathscr {X} \times \mathscr {S}\), and a clustering structure \(\mathbf {Y}\), the minimizer over the RKHSvv \(\mathscr {H}\) in Eq. (3) can be represented by the expression:

$$\begin{aligned} f(\mathbf {x})= \sum _{i = 1}^{N} k(\mathbf {x}_i, \mathbf {x}) \mathbf {c}_i, \end{aligned}$$

for some \((\mathbf {c}_1, \mathbf {c}_2, \ldots , \mathbf {c}_N) \in \mathscr {S}^N\).

By the representer theorem of RKHSvv, the graph refining iterative regularization framework can be rewritten in a reproducing kernel Hilbert space. The significance of the theorem is that it shows that a whole range of learning algorithms have solutions that can be expressed as expansions in terms of the training examples.

3.4 Block structure enhanced model

For an implementation of our proposed regularization framework, we provide a specific model by giving the definitions for the loss functions \(\mathscr {L}_1, \mathscr {L}_2\) and the affinity measurement function g.

We use the Euclidean distance as the loss function in Eq. (3). From Theorem 3, we have:

$$\begin{aligned} \mathbf {C}^* =&\min _{\mathbf {C}} \Vert \mathbf {S} - \mathbf {K} \mathbf {C}\Vert _F^2 + \lambda _1 \Vert \mathbf {Z} - \mathbf {K} \mathbf {C}\Vert _F^2 + \lambda _2 tr(\mathbf {C}^T \mathbf {K} \mathbf {C}) \nonumber \\&s.t. \nonumber \\&\forall i \in \{1, 2, \ldots , N\}, (\mathbf {K} \mathbf {C})_i \ge \mathbf {0}, \langle (\mathbf {K} \mathbf {C})_i, \mathbf {1} \rangle = 1, \end{aligned}$$
(5)

where \(\mathbf {S}, \mathbf {K} \in \mathbb {R}^{N \times N}\) are the original affinity matrix and a pre-defined vector-valued PD kernel matrix, \(\mathbf {C} = [\mathbf {c}_1, \mathbf {c}_2, \ldots , \mathbf {c}_N] \in \mathbb {R}^{N \times N}\) is the coefficient matrix of f, and \((\mathbf {K} \mathbf {C})_i\) indicates the i-th column of \(\mathbf {K} \mathbf {C}\).

We use Eq. (4) to generate \(\mathbf {Z}\), where we define \(g(\mathbf {y}_i^*,\mathbf {y}_j^*) = \langle \mathbf {y}_i^*, \mathbf {y}_j^* \rangle + (\mathbf {S})_{ij}\). Then, we have the following model:

$$\begin{aligned}&(\mathbf {Z})_{ij} = g(\mathbf {y}_i^*,\mathbf {y}_j^*) ,\nonumber \\&[\mathbf {y}_1^*, \dots , \mathbf {y}_N^*]^T = \mathbf {Y}^* = \min _{\mathbf {Y}, \mathbf {Y}^T \mathbf {Y} = \mathbf {I}} \,\,tr(\mathbf {Y}^T \mathbf {L}_{\mathbf {F}} \mathbf {Y}). \end{aligned}$$
(6)

The reason to set affinity measurement function g in such a formulation is based on an observation of block structure enhanced effect (see Fig. 3).

We call Eqs. (5) and (6) as the block structure enhanced (BSE) model for graph refining.

Fig. 3
figure 3

An illustration for the effect of Block Structure Enhanced. a The noisy diagonal block affinity matrix \(\mathbf {A}\); b The constructed affinity matrix \(\mathbf {B}\) where \(\mathbf {B} = \mathbf {Y} \mathbf {Y}^T\), \(\mathbf {Y}\) is obtained by do spectral clustering on \(\mathbf {L}_{\mathbf {A}}\); c The matrix of \(\mathbf {A} + \mathbf {B}\), it is distinct to see that the characteristic of diagonally block has been enhanced

Full size image

In Eq. (5), suppose the optimized function is \(f^*\) with a coefficient matrix \(\mathbf {C}^*\), the optimized affinity matrix \(\mathbf {F}^*\) among the input samples \((\mathbf {x}_1, \mathbf {x}_2, \cdots , \mathbf {x}_N)\) is:

$$\begin{aligned} \mathbf {F}^* = [f^*(\mathbf {x}_1), f^*(\mathbf {x}_2), \ldots , f^*(\mathbf {x}_N)] =\mathbf {K} \mathbf {C}^*. \end{aligned}$$
(7)

It turns out that finding the optimal multiple outputs affinity function is equivalent to construct a affinity matrix, which is in a form of \(\mathbf {K} \mathbf {C}^*\). This conclusion gives us a point of view to consider the construction of affinity matrix: given a pre-defined vector-valued PD kernel matrix \(\mathbf {K}\), such an affinity reconstruction problem can be converted into a problem of finding representation coefficient, where the dictionary is \(\mathbf {K}\) and the represented object is the optimal affinity matrix \(\mathbf {F}^*\).

3.5 Optimization for block structure enhanced model

The overall optimization procedure for the BSE model is same as Algorithm 1, where we alternately solve Eq. (5) and Eq. (6). It is simple to solve Eq. (6), since we only need to do spectral clustering on \(\mathbf {L}_{\mathbf {F}}\). To solve Eq. (5), we rewrite the expression in Eq. (5) as:

$$\begin{aligned} \sum _{i=1}^{N} \Vert \mathbf {s}_i - \mathbf {K} \mathbf {c}_i \Vert _2^2 + \lambda _1\Vert \mathbf {z}_i - \mathbf {K} \mathbf {c}_i \Vert _2^2 +\lambda _2 l(\mathbf {c}_i), \end{aligned}$$
(8)

where \(\mathbf {z}_i = (\mathbf {Z})_i\), \(\mathbf {s}_i\) is the i-th column of \(\mathbf {S}\) and,

$$\begin{aligned} l(\mathbf {c}_i) = \sum _{ j\ne i}^{N} \langle \mathbf {c}_i, \mathbf {c}_j k(\mathbf {x}_i, \mathbf {x}_j) \rangle + k(\mathbf {x}_i, \mathbf {x}_i)\langle \mathbf {c}_i, \mathbf {c}_i \rangle . \end{aligned}$$
(9)

Then, we have the derived optimization problem:

$$\begin{aligned} \mathbf {C}^* =&\min _{\mathbf {C} = [\mathbf {c}_1, \mathbf {c}_2, \ldots , \mathbf {c}_N]} \sum _{i=1}^{N} \mathbf {c}_i^T \mathbf {H} \mathbf {c}_i + \langle \mathbf {q}_i, \mathbf {c}_i \rangle , \nonumber \\&s.t. \nonumber \\&\forall i \in \{1, 2, \ldots , N\}, \mathbf {K} \mathbf {c}_i \ge 0, \langle \mathbf {b}, \mathbf {c}_i\rangle = 1, \end{aligned}$$
(10)

where

$$\begin{aligned} \mathbf {H}&= (1 + \lambda _1)\mathbf {K}^T \mathbf {K}+ \lambda _2\mathbf {I}, \nonumber \\ \mathbf {q}_i&= - 2\mathbf {s}_i - 2\lambda _1\mathbf {z}_i + \lambda _2 \sum _{ j\ne i}^{N} k(\mathbf {x}_i, \mathbf {x}_j) \mathbf {c}_j, \nonumber \\ \mathbf {b}&= \mathbf {K} \mathbf {1}. \end{aligned}$$
(11)

For Eq. (10), we can solve \(\mathbf {C}\) in a column-by-column way, in which every \(\mathbf {c}_i\) can be independently solved as a standard quadratic programming problem [25].

Connection with constrained Laplacian rank method In Eqs. (5) and (6), let \(\mathbf {K} = \mathbf {I}\), \(g(\mathbf {y}_i^*,\mathbf {y}_j^*) = -\Vert \mathbf {y}_i^* - \mathbf {y}_j^*\Vert _2^2\), and \(\lambda _2 = 0\), we have the following model:

$$\begin{aligned} \mathbf {C}^* =&\min _{\mathbf {C} = [\mathbf {c}_1, \mathbf {c}_2, \cdots , \mathbf {c}_N]} \Vert \mathbf {S} - \mathbf {C}\Vert _F^2 + 2\lambda _1\sum _{i,j=1}^{N}\mathbf {c}_{ij}\Vert \mathbf {y}_i^* - \mathbf {y}_j^*\Vert _2^2 + \lambda _1\sum _{i = 1}^{N}\mathbf {c}^T_i \mathbf {c}_i, \nonumber \\&s.t. \nonumber \\&\forall i \in \{1, 2, \cdots , N\}, \mathbf {c}_i \ge 0, \langle \mathbf {1}, \mathbf {c}_i\rangle = 1, \end{aligned}$$
(12)

That is, if we omit the differences between hyper-parameters, the above model is exactly the L2-constrained Laplacian rank (CLR) [42], as means CLR is one special case of our framework.

4 Experiments

In this section, we evaluate the performance of the BSE model on both synthetic and real data. In the case of regularization, a form of capacity control leads to choosing an optimal fixed parameter for a given dataset. The key point of our work is to define and bound the capacity of the regularization framework for block structure enhanced model. In the experiments, we use the fixed hyper-parameters: \(\lambda _1 = 0.1, \lambda _2 = 0.01\). We observe that in practice, our affinity matrix converges from random initialization in a few iterations, so the number of iterations is also fixed to \(T = 15\). In the experiment on synthetic data, we compare the results of BSE with that of CLR [42]. In the experiment on real data, we compare the results of BSE with that of CLR [42] and LSR [20].

4.1 Refining results on block diagonal synthetic data

This synthetic data is a \(100 \times 100\) matrix with four diagonally arranged \(25 \times 25\) block matrices. These block matrices represent four different clusters. The data inside the block matrices stand for the affinities of two corresponding points, while the data outside are noise. The data in each blocks are randomly set in the range from 0 to 1, and noise data are randomly set in the range from 0 and \(\gamma\). We find out that, when \(\gamma \le 0.8\), there are almost no differences between the BSE model and the compared models. Therefore, we set \(\gamma\) from 0.8 to 0.95 at an interval of 0.1 in the experiment. Since there is no data for us to define the kernel matrix, we set \(\mathbf {K} = \mathbf {I}\). We use the default hyper-parameters for CLR provided in its code. The experimental results are provided in Fig. 5a, where we can clearly see that our BSE model greatly outperforms CLR when \(\gamma \ge 0.9\). Figure 4 shows that the graph refining results when \(\gamma = 0.9\). It is surprising that the original affinity matrix is even hard for human to distinguish the block structure, our model still have a good performance. The main reason is the graph refining strategy has an ability to strengthen the intrinsic diagonal block of original affinity matrix. Such an ability has been enhanced by the BSE effect (Fig. 3).

Fig. 4
figure 4

An illustration for the graph refining results under \(\gamma = 0.9\). a The original affinity matrix; b The refining result of CLR [42]. c The refining result of ours

Full size image

4.2 Refining results on real data

Datasets We use two popular facial databases: Extended Yale Database B (YaleB) [49] and AR database [50]. For YaleB, we use the first 10 class data, each class contains 64 images. The images are resized into \(32 \times 32\). We also test a subset of AR which consists of 1400 clean faces distributed over 50 male subjects and 50 female subjects. All the AR images are downsized and normalized from \(165 \times 120\) to \(55 \times 40\). For computational efficiency, we also perform principal component analysis (PCA) to reduce the dimensionality of the YaleB and AR by reserving \(98\%\).

We use LSR [20] to generate the original affinity matrix with different hyper-parameters : \(\mathbf {S}_o = (\mathbf {X}^T \mathbf {X} + \tau \mathbf {I})^{-1} \mathbf {X}^T \mathbf {X}\) and \(\mathbf {S} = (\mathbf {S}_o + \mathbf {S}_o^T)/2\) , where \(\mathbf {S}\) is the generated original affinity matrix and \(\mathbf {X}\) is the data matrix. The hyper-parameters \(\tau\) is set in a range from 0.001 to 0.1 at an interval 0.001. We compare BSE (\(\mathbf {K} =\mathbf {I}\)), BSE (Gaussian kernel) with CLR and LSR. The experimental results of YaleB and AR are shown in Fig. 5b, c, respectively.

Fig. 5
figure 5

a Accuracy(ACC)-\(\gamma\) variation plot for the experiment of block diagonal synthetic data. b Accuracy(ACC)-\(\tau\) variation plot for the experimental results of YaleB dataset. c The experimental results of AR dataset

Full size image

In the experiments, we find out that both of the BSE with \(\mathbf {K} = \mathbf {I}\) and the BSE with Gaussian kernel are convergent after only 3 iterations averagely, and the maximum iteration is less than 6.

BSE with \(\mathbf {K} =\mathbf {I}\) and BSE (Gaussian kernel) both significantly outperform the original LSR and CLR. The only difference between BSE (\(\mathbf {K} = \mathbf {I}\)) and CLR is the affinity measurement function g:

$$\begin{aligned} (\text {BSE})\,\,\,g(\mathbf {y}_i^*,\mathbf {y}_j^*)&= \langle \mathbf {y}_i^*, \mathbf {y}_j^* \rangle + (\mathbf {S})_{ij}, \nonumber \\ (\text {CLR})\,\,\,g(\mathbf {y}_i^*,\mathbf {y}_j^*)&= -\Vert \mathbf {y}_i^* - \mathbf {y}_j^*\Vert _2^2. \end{aligned}$$
(13)

CLR only considers the affinities obtained by \(\mathbf {Y}^*\). However, such affinities could be heavily disturbed if \(\mathbf {L}_{\mathbf {F}}\) of last iteration is not good enough (Fig. 3b). In contrast, BSE has an ability to enhance the characteristic of diagonal block (Fig. 3c), which in favor of improving the clustering performance. BSE with Gaussian kernel is more stable compared with BSE (\(\mathbf {K} =\mathbf {I}\)), because the kernel matrix provides additional affinities information for the graph refining.

5 Conclusions

In this paper, we provide an iterative regularization framework to refine the graph by giving the number of clusters. We design a new reproducing kernel Hilbert spaces of vector-valued functions as the hypothesis space for this regularization framework. Moreover, we also provide a specific graph refining model which based on the observation of block structure enhanced the effect. The experiment results on synthetic and real data show the competitiveness of our method compared with CLR and LSR, which are used. The exhaustive analyses on the experiment results with different attributes present the capabilities of our method.