1 Introduction

Boring operation is one of the critical machining operations, and moreover handling chatter in internal turning operations is a difficult part of the manufacturing process. In boring operation, boring bar plays a vital role and it affects the surface roughness, tool wear and influences the cutting forces due to the boring bar vibrations or deflections. In boring operation, vibration is the main factor, which effects the surface roughness, tool wear and cutting forces [1]. Mourad et al. [2] indicated that identification of chatter in machining processes is critical part for enhancing the surface quality and eliminating the noise and cutting tool wear. It is important to choose appropriate boring bar in order to reduce or minimize the chatter in boring process Ihsan et al. [3] specified that the size of the boring bar and assessed based on L/D ratio (length diameter ratio) of boring bar. They performed experiments with different ratios and shown the best L/D ratio as 3, and the results indicated that there is less chatter in boring operation. In the present work has given preference to the L/D ratio as 3 to reduce the vibrations.

In metal cutting operations, one of the foremost important requirement of precision machining parts is surface quality. Surface finish is one of the important quality factors of many bored work pieces. Different aspects that is tool and work piece materials, machining forces, cutting tool materials and cutting conditions are influence the surface roughness [4]. In aircraft and aerospace industries to design the machine components toughness and strength are the requirements for fundamental design. AISI 4340 high strength low alloy steels are generally used in both the industries and also automobile industries for manufacturing machine components such as spindles, axle and main shafts, gears, power transmission gears and couplings. Suresh et al. [5] investigate the influence of cutting parameters and machining time on machinability characteristics using RSM on AISI 4340 high strength low alloy steel using coated carbide inserts and they reported that the combinations of low machining parameters and machining time to minimize the machining characteristics.

In metal cutting operations, direct measurement of online cutting forces, work piece vibration, cutter vibration signals are not easy and it is a complex setup. In present applications researchers used laser doppler vibrometers (LDV) [6, 7] to measure the vibrations on rotating work pieces and cutters. The usage of LDV is comfortable and non-contact type of measuring device, setting up of LDV is stress-free and it is used to measure the work piece vibration as well as cutter vibration in very less time, when compared with other vibration measuring devices like accelerometers [8]. The LDV measures the vibration in the form of acousto-optic emission (AOE) signals and a fast Fourier transformer (FFT) was used to generate features from AOE signals changed to frequency domain [6].

The machining of various hard materials the three major factors to be considered such as cutting forces, surface roughness and tool wear. Controlling the machining process, cutting forces is one of the significant characteristic and it influence the machining system stability. The cutting force depends on the complex arrangements of the machining parameters such as cutting speed, feed rate, depth of cut and geometrical parameters such as tool rake angle, inclination angle, side and end cutting edge angles, nose radius, cutting tool and work piece materials [9]. Lalwani et al. [10] studies and optimized the effect of machining process variables on cutting forces during hard turning operation. They observed that feed rate and depth of cut have the significant contributions on cutting and thrust forces and cutting speed not significantly influence the forces, and moreover depth of cut was the most influenced then feed and cutting velocity.

The manufacturing industries are monitored and focused continuously to enhance the effective ness and efficiency of their production goals. Development of statistical and mathematical models are important to optimal cutting conditions in order to achieve quality products with minimal production cost, time. Machining variables optimization and evolution of the statistical models are vital role in production process [1]. Hosseini et al. [11] made a review on optimization methods and techniques, they reported the use of optimization problems in the field of manufacturing and also they concluded that many of the authors are extensively used optimization of input processing variables. Munish et al. [12] investigated the influence the process parameters on machining characteristics such as cutting forces, tool wear, surface finish and cryogenic conditions (dry and wet) during the machining 0f AISI 4340. The GRA is executed to study the significant and optimum settings of process parameters and they reported that using GRA and ANOVA machining performance was enhanced. Mohammad et al. [13] adopted the support vector machine (SVM) approach to predict blast-induced ground vibration. They studied in two limestone quarries and therefore the observational data was employed to train the SVM. They compared the experimental data with predicted the values. They found that SVM is predicted the blast-induced ground vibration levels with coefficient error of 0.944 which means that predicted values are closed to experimental results. RSM, Taguchi methods are the statistical modelling methods are extensively used by researchers to prepare design of experiments and optimization. RSM is performing a vital role for optimization of process variables in studies of the machinability [14]. Mandal et al. [14] investigate the effect of cutting parameters on machining forces in finish hard turning of AISI 4340 steel using developed Zirconia Toughened Alumina (ZTA) insert prepared by powder metallurgy technique. They performed RSM to identify significant parameters on machining forces. They revealed that cutting speed and depth of cut have predominant effect on feed force whereas feed and depth of cut influencing the thrust force and all the cutting parameters are significant effect on cutting force. Neseli et al. [15] used the RSM technique for the effect of cutting tool geometry parameters on surface roughness. The indicated results shows that tool nose is the dominant factor to effect the surface finish.

According to author’s knowledge, very few literature is presented on machining with multi-layered cutting inserts as well as the effect of machining parameters on over all significant machining characteristics such as surface roughness, tool flank wear, cutting forces and work piece vibrations using statistic and predicted models. In this present study, boring experiments were conducted on AISI 4340 steels with multi-layered cutting tool inserts in dry cutting condition. Mathematical models such as GRA and prediction methods such as SVM and RSM are established in between process variables and machining process variables to optimize and prediction. Analysis of Variance (ANOVA) is also used to identify the influencing factors that affect the surface roughness, tool flank wear, cutting force, tangential force and work piece vibration and performed the overall performance to identify the optimal machining parameters.

2 Multi-objective optimization method

2.1 Grey relational analysis and data pre-processing

It has been identified that if the GRA alone was used for experimental investigations, a unique optimal solution was not obtained for all the performance characteristics. Grey relational analysis based on the grey system is a statistical technique to solve multi response optimization [16].

GRA converts the multi response optimization problem into the single response optimization. In general to evaluate the sequence characteristics GRA is used. GRG is the quantitative index in the GRA [17]. In the present study pre-processing raw data was used as the“smaller is better” for expected sequence data, to normalize the surface roughness, cutting tool flank wear, cutting force, tangential force and work piece vibration which were performed in the range between 0 and 1. The original sequence is normalized in Eq. (1) [17,18,19].

$$x_{p}^{*} (q) = \frac{{{\hbox{max}}\,x_{p}^{o} (q) - x_{p}^{o} (q)}}{{{\hbox{max}}\,x_{p}^{o} (q) - {\hbox{min}}\,x_{p}^{o} (q)}}.$$
(1)

where p = 1,…,m; q = 1,….,n. ‘m’ is the number of experimental data items and ‘n’ is the number of machining parameters. \(x_{p}^{*} (q)\) is the sequence after the data pre-processing, \(x_{p}^{o} (q)\) is the original sequence. \({\hbox{max}} x_{p}^{o} (q)\) is the largest value of \(x_{p}^{o} (q)\) and \({\hbox{min}} x_{p}^{o} (q)\) is the lowest value of \(x_{p}^{o} (q)\).

2.2 Calculation of grey relation coefficient (GRC) and grey relation grade (GRG)

To represent the correlation between the required response and the experimental data, the grey relation coefficient (GRC) is to be used and it is calculated from the normalized data by the following Eq. (2) [17,18,19].

$$\xi_{p} (k) = \frac{{\Delta_{\hbox{min} } + \zeta \Delta_{\hbox{max} } }}{{\Delta_{0p} (q) + \zeta \Delta_{\hbox{max} } }}$$
(2)

where \(\xi_{p} (k)\) is the GRC, the \(\Delta_{0p} (q)\) is the offset in the absolute values of the reference sequence \(x_{p}^{o} (q)\) and comparability sequence \(x_{p}^{*} (q)\). \(\Delta_{\hbox{min} }\) and \(\Delta_{\hbox{max} }\) are the minimum and maximum values of \(\Delta_{0p} (q)\). \(\zeta\) is the distinguishing coefficient. The value can be adjusted to the range between 0 and 1 [17].

After the grey relational coefficient (GRC) acquired the average values of the grey relational coefficients are considered as a grey relational grade (GRG). To calculate grey relation grade by using Eq. (3) to assess the multiple response into a single response [18].

$$\gamma = \frac{1}{n}\mathop \sum \limits_{q = 1}^{n} \xi_{p} (q) ,\gamma \in (0 - 1)$$
(3)

3 Support vector machine (SVM)

Support vector machine was initially proposed by Vapnik [19] to classify the regression concerns of appropriate generalization. In ANN approach, large quantity of samples or facts is essential to get expected responses or results. But using the SVM approach, much to a lesser extent variety of samples or records is sufficient to get the expected responses with much lesser errors [20]. They used the SVM methodology to predict processing time and electrode wear, they used with less number of experimental data. SVM is superior to conventional experimental risk minimization principle and the advantage of SVM is its structure risk minimization principle. The linear function is formulated in the high dimensional feature space, with the form following by Eq. (4) [20, 21].

$$y(x) = w^{t} \varphi (x) + b$$
(4)

where \(\varphi (x)\) is the high dimensional feature space, which is nonlinearly mapped from the input space x. The weight vector \(w\) and bias \(b\) are estimated by minimizing.

$$R(c) = C \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} L (d_{i} ,y_{i} ) + \frac{1}{2} \left\| {w^{2}} \right\|$$
(5)

where

$$L_{\varepsilon } (d,y) = \left\{ {\begin{array}{*{20}l} {\left| {d - y} \right| - \varepsilon ,} \hfill & {\left| {d - y(x)} \right| \ge \varepsilon } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. .$$
(6)

L (d, y) is called the \(\varepsilon\)-intensive loss function. This function indicates that errors below \(\varepsilon\) are not penalized. The term \(C\frac{1}{n}\sum\nolimits_{i = 1}^{n} {L (d_{i} ,y_{i} )}\) is the empirical error. \(\frac{1}{2}w^{2}\) measures the smoothness of the function. Both \(C\) and \(\varepsilon\) are prescribed parameters, \(\varepsilon\) is called the tube size of SVM, and \(C\) is the regularization constant determining the trade-off between the empirical error and the regularized term. The SVM methodology was also used in estimating the surface roughness in turning process [22]. In this study SVM used to train the GRG values from experimental data to predict the GRG values.

4 Response surface methodology (RSM)

RSM is enumerates the relationships between the controllable input process parameters and the obtained output response variables [15]. RSM was execute to identify the effect and influence of process parameter variables such as surface roughness, cutting tool flank wear, cutting force, tangential force and work piece vibrations and also used to predict the GRG values obtained from the experimental data. The RSM is one of the effective tool to identify the significant parameters and optimizing the responses by using mathematical and statistical procedures for modelling and analysis of experimental results [21]. Jeyakumar et al. [23] performed the experimental investigation and RSM methodology for modelling on the machinability of aluminium (Al6061) silicon carbide particulate (SiCp) metal matrix composite (MMC) during end milling operation. The prediction model RSM was used to determine the combined effect of machining parameters such as cutting speed, feed rate, depth of cut and nose radius on the cutting force, cutting tool wear and surface finish. Hessainia et al. [24] used response surface methodology (RSM) to optimize the cutting parameters based on surface roughness and tool vibrations in the hard turning of 42CrMo4 hardened steel by Al2O3/TiC mixed ceramic cutting tool under different cutting conditions. The results observed that the feed rate is the dominant factor affecting the surface roughness, whereas vibrations on radial and in main cutting force directions have a low effect on it. Bhardwaj et al. [25] also performed RSM methodology with centre composite rotatable design on AISI 1091 steel during the turning operation to observed influenced parameter on surface roughness. The agreement of the results revealed that the feed and depth of cut was found as significant parameter on surface roughness. In RSM the quantitative relationship between input and output variables is in the following Eq. (7) [26].

$$x = f(a_{1} ,a_{2} ,a_{3} , \ldots ,a_{n} ) \pm e_{\text{f}}$$
(7)

where \(x\) is the desired response and \(f\) is the function, dependent variable and \(a_{1} ,a_{2} ,a_{3} , \ldots ,a_{n}\) are independent variables and \(e_{\text{f}}\) is fitting error. In the present study, RSM was used according to central composite design (CCD) for the prediction of GRG values obtained from experimental data.

5 Experimental procedure

5.1 Work piece material, cutting tool and experimental method

In the present experiments AISI 4340 high strength low alloy steel of hardness 228 HV was chosen as a work piece material. The length, outer and inner diameters of the work piece are 100 mm, 90 mm and 40 mm, respectively. These steels are generally used in automobile industries for manufacturing machine components such as spindles, axle, main shafts, gears, power transmission gears and couplings. The chemical composition of AISI 4340 steel with all the percentages of elements is presented in Table 1. Multi-layered (TiCN, Al2O3, TiN) chemical vapour deposition (CVD)-coated tungsten carbide cutting tool inserts (DCMT11T304GP) were used in this experiment with the nose radii of 0.8 mm as shown in Fig. 1. Cutting tool geometry is shown in Table 2. Standard boring bar (S25RSDUCR 11) with insert attached to dynamometer is shown in Fig. 2. The experiments are planned in dry cutting condition using design of experiment with three levels of spindle speed (SS), feed rate (F) and depth of cut (DOC) as a control factors which consist of 27 runs of experiments and it is shown in Table 3. Experimental setup is prepared as shown in Fig. 3. Each and every experiment was stared with a fresh cutting edge and the machining was continued for the length of 100 mm. In order to minimize the influence of vibrations on the tool and work piece a recommended L/D ratio of 3 for boring operations [3] was used in the present experiments. Surface finish (Ra) of the machined surfaces at end of the each cut is measured along the feed direction using surftest SJ 301 over the sampling length of 0.8 mm. Cutting tool flank wear (VB) maximum was observed by using olympus metallurgical microscope. Cutting force (Fx) and Tangential force (Fz) were measured for each cut using by piezo-electric dynamometer (Make: Kistler, Model: 9272). The rotating work piece vibration signals are measured by using LDV for each trail cut in the machining process. According to the PloyTec 100 V Laser Doppler vibrometer manual optimum measuring distance from the rotating object is 3 m. In the present study LDV is placed 1.5 m distance from the rotating spindle. Vibration is measured in the feed direction. Vibration data is acquired during the 2nd cut in every test condition. Cutting tool rejection criteria or tool failure is made based on flank wear reaches 0.6 mm (ISO 3685:1993). Experimental measured variables data are listed in Table 3.

Table 1 Chemical composition of AISI 4340
Full size table
Fig. 1
figure 1

Tool inserts

Full size image
Table 2 Cutting parameters with their levels
Full size table
Fig. 2
figure 2

Boring bar with attached to dynamometer

Full size image
Table 3 Experimental results based on design of experiments and measured responses
Full size table
Fig. 3
figure 3

Experimental setup for boring operation and measurement of cutting forces and work piece vibrations with data acquisition (DAQ) systems

Full size image

6 Results and discussion

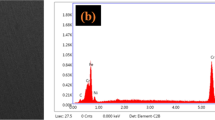
Experimental results of the output responses such as surface roughness (Ra), tool wear (VB), cutting force (Fx), tangential force (Fz) and work piece vibration (VA) are shown in Table 3. These responses are used to develop statistical and predictive methods to identify the significant parameters. The maximum flank wear was measured by using optical microscope. These images are used to prominent tool wear occurred during machining process. Crater wear and flank wear of the multi-layered cemented carbide inserts are presented in Fig. 4. Better magnification and study of the wear patterns scanning electronic microscopy (SEM) images were used, and nose wear and flank wear on the cutting tool insert are illustrated in Fig. 5. The time domain and frequency domain spectrographs of work piece vibrations were measured with LDV. The acousto-optic emission (AOE) signals acquired during machining and fast Fourier transform (FFT) analyser are used to process the AOE signals into different frequency domains, and it is presented in Fig. 6. The machining force signals were measured with piezo-electric dynamometer. The DynoWare software was used to analyse the machining forces signals as shown in Fig. 7. All the images are presented for the experimental test run of 360 rpm, 0.12 mm/rev of feed, 0.2 mm of DOC.

Fig. 4
figure 4

a Flank wear and b crater wear of multi-layered cutting tool insert

Full size image
Fig. 5
figure 5

Scanning electronic microscopy (SEM) images of (a) nose wear and (b) flank wears

Full size image
Fig. 6
figure 6

Work piece vibration signals in (a) time domain (b) frequency domain spectrographs

Full size image
Fig. 7
figure 7

Sample cutting force signal from dynamometer (make: kristler) using DynoWare software

Full size image

7 Grey relational analysis

7.1 Normalizing the experimental data

In the present study performance characteristics such as surface roughness, tool wear, cutting force, tangential force and work piece vibrations with lower or smaller value indicated better functioning. To execute data pre-processing in the grey relational analysis process, performance characteristics are taken as “lower is the better.” The GRA is used to study the relation between degree of the factor sequence and performance sequence, since the GRG represents the correlation degree of two data sequences. Firstly raw data is pre-processed which was called grey relational generation. The raw data is changed to dimensionless sequences in Eq. (1). The factors and performance sequences are set to be \(x_{p}^{*} (q)\). The normalized data sequences \(x_{p}^{*} (q)\) can be calculated by using Eq. (1) and values are listed in Table 4. It is shows the results of the pre-processes data. The normalized data range is between 0 and 1. The preeminent normalized experimental result should be equal to 1.

Table 4 GRA data pre-processing and normalizing experimental data, deviation sequence, GRC and GRG
Full size table

7.2 Calculation grey relational coefficient

After normalizing the experimental results, the normalized performance reference and comparability sequences are substituted into Eq. (2) and the deviation sequence \(\Delta_{0p} (q)\) was calculated. Then the calculation of grey relation coefficient for each experiment was done by using Eq. (2). In the present study, the distinguishing coefficient \(\zeta\) is aimed as 0.5 for calculating the grey relational coefficients [17] and the results of the deviation sequence are shown in Table 4. The grey relation coefficient values are presented in Table 4.

7.3 Calculation of grey relational grade

Finally to determine the grey relational grade (GRG), the mean value of the grey relational coefficients was acquired. To calculate each grey relational grade for experiment Eq. (3) was used in the same method. Grey relational grade was generally executed to assess the multiple responses as a single response [18]. The grey relational coefficients and grey relational grades are presented in Table 4. It is clearly identified the experimental number 10 has the highest GRG value. Therefore the experimental run number 10, i.e. 360 rpm spindle speed, 0.16 mm/rev feed rate and 0.2 mm depth of cut is indicated that the optimal cutting parameters setting for minimum surface roughness, flank wear, cutting force and tangential force and work piece vibration, simultaneously which is the best multi-performance characteristics among the 27 experiments. Grey Relational Grade (GRG) signifies the correlation between the comparability sequence and the reference sequence. Grater values of GRG represent that compare sequence incorporates a stronger correlation to the reference sequence [27].

8 Prediction of grey relational grade (GRG) values with SVM

In the Present study GRG values are established as an individual for SVM model. For SVM model a nonlinear kernel was taken because of the machining operation is nonlinear and also for the better concert [20]. Then dot function kernel was selected as kernel function for the model. In rapidminner 5.0 software SVM coefficients C and ε are optimized using optimization of SVM parameters. The optimized values of C and ε are 1000 and 0.001 for grey relational grade values and then for experimental data separate SVM model was trained. Predicted grey relational grade (GRG) values are presented in Table 5. It is identified that there is no significant deviations between predicted responses of GRG values as well as experimental GRG values. The obtained value of the root mean square error (RMS) was 0.056 which shows that means the SVM model method predicted the results are close or near to the experimental GRG results as illustrated in Fig. 8. Prediction models like ANN requires large number of sample data whereas SVM model needs less range of samples data for training. Amit kumar [28] also used RSM, ANN, SVR methods to develop the empirical relation methods to predict the surface finish, cutting tool wear and required power in turning operation. The results indicated that ANN and SVM models were higher than RSM model within the prediction of cutting parameters.

Table 5 Experimental and predicted responses of GRG
Full size table
Fig. 8
figure 8

Variation of GRG-experimental, GRG-predicted RSM and GRG-predicted SVM

Full size image

9 ANOVA results for grey relational grade (GRG) predicted values

In the present study, effect and significance of spindle speed, feed rate and depth of cut on GRG-predicted values were studied. Analysis of variance (ANOVA) was executed to determine the predicted responses of GRG statistically and also to find out significant machining parameters and significant interaction of machining parameters on the GRG-predicted values. The ANOVA was executed at the confidence level of 95%, and the machining parameters which are aiming P value less than 0.05 are recognized as significant [23]. ANOVA results for GRG-predicted values are presented in Table 6. According to the p values, it was identified that the feed rate and the interactions of the feed rate and depth of cut are to be significant parameters on GRG-predicted values. Regression or empirical equation for GRG-predicted values in terms of spindle speed, depth of cut and feed rate are shown in Eq. (8).

$$\begin{aligned} {\text{GRG}}\;{\text{predicted}} & = 2.246 - 0.00280\;{\text{SS}} - 5.62\;F - 2.018\;{\text{DOC}} \\ & \quad + \; 0.000003\;{\text{SS}}*{\text{SS}}\; + \;13.7\;F*F\; + \;2.079\;{\text{DOC}}*{\text{DOC}}\; + \;0.00171\;{\text{SS}}*F \\ & \quad - \;0.000022\;{\text{SS}}*{\text{DOC}} - 2.02\;F*{\text{DOC}} \\ \end{aligned}$$
(8)

with using the above regression equation, the RSM methodology had predicted the GRG-predicted values for all the experiments and are presented in Table 5. The RMS was executed using MINITAB 18 software. Before applying the two methods, the experimental data was divided into two parts such as 22 samples for training and 5 samples for the validation. The RSM and SVM models were trained with the 22 samples and tested with remaining 5 samples. Error between the experimental data and predicted results was found to be less than 5% for the two methods. It was observed that there is no significant deviations between the GRG-predicted responses of SVM and RSM. The GRG-predicted responses by both the methods SVM and RSM are precise and close to experimental values as illustrated in Fig. 8; however, SVM model exhibit better predicted responses. This is in good agreement with the previous literature [21, 28].

Table 6 ANOVA for GRG-predicted values
Full size table

10 Overall performance of machining parameters

A multi response optimization method was used to optimize machining parameters for maximizing the grey relational grade prediction value. This method works on the concept of desirability function. Hung-Chun Lin et al. [29] used a mathematical transformation methods to design the desirability function and the application of desirability function which is characterized by the gradient algorithm that indicates to the best optimal solution than other similar methods for optimizing of multi responses. The desirability function value is calculated using gradient algorithm between 0 and 1 [30]. Acceptance of optimization is decided with desirability function. There are two types of desirability functions such as individual desirability function for individual responses and a composite desirability function for over all responses [31]. If the desirability response value is to be 1 or near to 1 only then the response is adequate. If the desirability values are close to 0 then the response is not accepted. In this work machining variables were optimized for maximizing the GRG prediction value as illustrated in Fig. 9. Desirability value of experimental GRG prediction values was found as 0.9147. In this work, optimization and calculation of desirability function MINITAB 17 software was used. Optimum machining parameters were found with a spindle speed 360 rpm, with feed rate of 0.12 mm/rev and depth of cut 0.2 mm. The results revealed that, in the machining process, feed rate is one of the critical parameter among the process parameters. When the feed rate and depth of cut is increased, the cutting tool has to remove more material from the work piece and the removed material flows over the tool in the form of chip. This results in generation of heat and higher stresses, therefore tool damage takes place through thermal softening, cracks and diffusion. Due to this surface quality might be affected and also tool life decreases and this is a good agreement with other literatures [32]. Figure 5a, b shows the prominent tool wear for the spindle speed 360 rpm, with feed rate of 0.12 mm/rev and depth of cut 0.2 mm. Figures 6 and 7 show that in the machining process, when feed rate and depth of cut are increased, it is required to remove high amount of material. Obviously, high cutting forces and vibrations are induced in the cutting process, it might be because of the more contact area developed between the work piece and cutting tool. It is good agreement with previous experimental works [33].

Fig. 9
figure 9

Multi response optimization for GRG prediction values

Full size image

11 Conclusions

In this present work, the experiments were accomplished on AISI 4340 high strength low alloy steel using multi-layered coated carbide insert to assessment of the surface roughness, flank wear, cutting force, tangential force and work piece vibration. Multi-objective optimization methods and predictive techniques such as GRA, SVM and RSM were used and found to be effective techniques for perform analysis and prediction of responses. The Conclusions drawn based on this study can be summarized as follows:

  1. 1.

    Use of accelerometers, radioactive sensors and piezo-electric actuators is not possible to measure rotating objects vibrations. But the LDV’s are found to be capable to measure rotating objectives vibrations in less time with simple experimental arrangement.

  2. 2.

    From the average GRG, the greatest value of grey relational coefficient for the processing parameters was found. These values are suggested as controllable levels of processing parameters to maximize machining performance.

  3. 3.

    SVM and RSM methods were used for predicted GRG values. SVM method was found to be better than RSM model in the prediction of machining parameters. The Predicted GRG values obtained a minimal root mean square error of 0.039.

  4. 4.

    In the ANOVA for GRG prediction values, it was indicated that the feed rate and interaction of feed rate and depth of cut are found to be significant parameters.

  5. 5.

    A multi response optimization technique for overall performance was conducted to identify the machining parameter for minimum surface roughness, flank wear, cutting force, tangential force and vibration of the work piece. Optimum machining parameters were found as 360 rpm of spindle speed, 0.12 mm/rev of feed and 0.2 mm of depth of cut.