1 Introduction

Regarding the rapid popularity of polymers reinforced with carbon nanotubes (CNTs) in different industries like automotive, aerospace, packaging and wind turbines, calculating their mechanical properties and modeling their behavior have attracted the attention of many researchers. Studies have shown that increasing 1% carbon nanotube to a matrix increases its hardness o by 36% to 42% and its tensile strength by 25% [1]. Also, experimental studies and atomic modeling have indicated that carbon nanotubes have very high modulus and strength in the range of 300–1000 GPa which is obviously higher than that of carbon fibers [2]. Among other characteristics of these materials are high geometrical ratio and high hardness to weight and strength to weight ratios. By using carbon nanotubes in some matrices, special nanocomposites with above characteristics can be obtained and optimally utilized [3]. Recently, polymer bases have been more commonly used but other materials like ceramic and metal are also used. Carbon nanotubes are used for producing nanocomposite materials because of their homogeneous distribution characteristic. Improvement of composites’ mechanical characteristics depends on load transmission mechanism between matrix and fiber. If the cohesion between fiber and matrix is not strong enough for tolerating high loads, advantage of high tensile strength of carbon nanotubes becomes useless. Very high surface cohesion has been reported for some polymers. Andrews et al. produced multi-walled carbon nanotube composites by shear mixing method such that 15% increase in tensile modulus was obtained by adding 5% multi-walled carbon nanotube [4]. Calculation of mechanical, thermal and electrical characteristics of the material is an important issue in manufacturing processes and designing modern nanocomposites. Calculation methods can be categorized into two groups: molecular dynamics (MD) and continuum mechanics methods. Molecular dynamics method provides many modeling results for studying and understanding the behavior of carbon nanotubes individually or in group; although calculation strengthens and numerical algorithms of this method have rapidly developed, they are limited to very short time and length scales. So, molecular dynamics modeling is not efficient in the analysis of nanocomposites with long length and long time scale and continuum mechanics method is preferred for analyzing such problems. This method was successfully used for the mechanical modeling of carbon nanotubes which could exist in the form of beam, thin shell or solid cylinders [5,6,7]. Lia & Chen developed a solid 3D model for carbon nanotube reinforced composite which completely provided accuracy and compatibility between carbon nanotubes and matrix in the composite [8]. Some researchers have analyzed the mechanical properties of nanocomposites using representative volume element (RVE) and continuum mechanics methods [9,10,11,12]. Various factors affect the efficiency of these nanocomposites and the main factor determining the efficiency of nanotube reinforcement is the mechanism of load transfer from matrix to carbon nanotube. Thus, before understanding the mechanical behavior of nanocomposites at macro level, their corresponding physical efficiencies should be evaluated. To do so, a good simulation method with relevant details was applied. The interface adhesion between nanotube and its neighboring polymer is one of the important issues in load transfer and reinforcement phenomena. The atomic structure of carbon nanotubes is composed of SP2 hybridized carbon atoms which prevent strong covalent bonds with the surrounding polymer matrix. Although chemical functionalization can improve load transfer in the interphase by covalent bonds between carbon nanotube and polymer molecules, this method has the great drawback of making some defects in the nano structure of carbon nanotubes due to the formation of SP3 hybridized sites. Carbon nanotubes naturally interact with polymer chains of the matrix with weak van der Waals and electrostatic interactions.

Mechanical interlocking, which improves the adhesion between fiber and matrix in fibrous composites, was not used due to the smooth surface of carbon nanotubes. Various methods have been used to evaluate the interaction between nanotube and neighboring matrix including experimental methods, atomic modeling and continuum modeling. In this study, by systematic studies and considering the advantages and disadvantages of continuum methods, it was attempted to present the best solution to evaluate the behavior of interaction between nanotube and polymer matrix. The presented method should have high precision, be simple and could be done with minimum costs. More recently, several theoretical and experimental research works with CNTs as reinforcing fibers have been conducted to determine mechanical and electrical properties of nanotube-based composites [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].

This study aimed to evaluate the mechanical properties of single walled carbon nanotube reinforced composite using 3-D representative volume element (RVE). Then, RVE was created by finite element method and its elastic behavior was simulated. Also, the longitudinal elastic module of Polyethylene/ CNT nanocomposite was computed and compared with experimental results.

2 Problem statement and assumptions

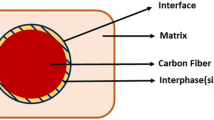
Various studies have been conducted on the effect of adding carbon nanotube on different matrices including polymer and various analytical and numerical methods have been developed to study the behavior of nanocomposites among which finite element method has received much attention. The main purpose of this study was to introduce a proper modeling technique to obtain the properties of nanocomposites and present the required formulas to extract the results from the finite element software. Also, the evaluation and extraction of interface properties of carbon nanotube were among other purposes of this study. The effect of adding carbon nanotube to four types of matrices with different elastic modules was examined by modeling. Then, the effect of the reinforcer added to polyethylene matrix was examined by elastic nanocomposite model. In this study, it was assumed that the nanotube and matrix within the representative volume element were both elastic continuum, homogenous and isotropic and their Young’s modulus and Poisson’s ratio were known. Also, to simulate the interface between nanotube and matrix, a separate section was created and its properties were extracted from the atomic simulations [13]. The results were compared and validated with experimental results [14].

3 Representative volume elements to achieve elastic module

The results of atomic simulations or molecular dynamics of carbon nanotubes are used mostly to perceive the mechanical and electronic behaviors. However, these simulations are restricted to very small lengths, short-time scales and based on calculation limitations (e.g. a cubic volume \(10 \times 10 \times 10\,\upmu{\text{m}}^{3}\) is composed of 1012 atoms) the atomic methods cannot analyze bigger longitudinal scales in nanocomposites. In engineering applications, nanocomposites being used with micro scale and even longitudinal macro scales, should be evaluated using a combination of molecular dynamic methods. Continuum mechanic methods are used in the analysis of cases where single walled carbon nanotubes act as beam, thin shell or cylindrical solid volume. Also, the researchers have shown that continuum methods are suitable to evaluate carbon nanotubes with 100 nm or higher lengths. The best methods to simulate carbon nanotube reinforced composites are multi-scale methods in which molecular dynamics and continuum methods are combined; these are also the best methods for nanoscopic physics presenting correct responses for big longitudinal scales. In this research, the interaction of carbon nanotube and matrix and the transfer capability of stress of nanotubes were investigated by 3-D elastic models. The researches have shown that these models had higher precision compared to beam or shell models. In continuum-based 3-D models, representative volume elements have been widely used. Nanotubes are dispersed in different sizes and forms in matrix to make the nanocomposite material. They can also be in the form of single-walled or multi-walled and from some nm to micrometer as well as being straight, wrapped, wavy or rope-shaped. The dispersion and orientation of nanotubes in matrix can be uniform, unidirectional or random. All the mentioned issues can make simulation of carbon nanotube reinforced composites more complex. Thus, the concept of unit cell or representative volume element of carbon nanotube reinforced composites at micro-scale were modified to be used at nano-scale, as was applied in the study. In representative volume element, a unit nanotube (or some nanotubes) with the surrounding matrix material are modeled as a unit cell. Different methods including finite element method, boundary element and mesh-free methods are used for numerical analysis of representative volume elements under different loading conditions. Representative volume elements, as shown in Fig. 1, can be circular, square and hexagonal. The cylindrical volume elements are used to model nanotubes with different diameters or when the nanotube is embedded in an ordinary carbon fiber. Also, for symmetrical and non-symmetrical loadings, 2-D symmetrical model for cylindrical volume elements can considerably reduce computer calculation volume. Volume elements with square or hexagonal sections are suitable when nanotubes are inside a matrix with square or hexagonal arrays. This study applied a cylindrical representative volume element to achieve longitudinal elastic module.

Fig. 1
figure 1

Three nanoscale representative volume elements

Full size image

4 The required calculation formulas to achieve longitudinal elastic modulus

It was assumed that both CNTs and matrix in a RVE were continua of linear elastic, isotropic and homogenous materials, with given young’s modulus and Poisson ratios. The volume element consisted of a carbon nanotube, as shown in Fig. 2. The geometry of a hollow cylinder model with length L, inner radius ri and outer radius R.

Fig. 2
figure 2

Cross-sectional view of a cylindrical RVE

Full size image

As the materials are isotropic, 3-D strain-stress relations are as follows:

$$\left\{ {\begin{array}{*{20}l} {\upvarepsilon_{\text{x}} } \hfill \\ {\upvarepsilon_{\text{y}} } \hfill \\ {\upvarepsilon_{\text{z}} } \hfill \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {\frac{1}{{{\text{E}}_{\text{x}} }}} \hfill &\quad { - \frac{{\upgamma_{\text{xy}} }}{{{\text{E}}_{\text{x}} }}} \hfill &\quad { - \frac{{\upgamma_{\text{zx}} }}{{{\text{E}}_{\text{z}} }}} \hfill \\ { - \frac{{\upgamma_{\text{xy}} }}{{{\text{E}}_{\text{x}} }}} \hfill &\quad { \frac{1}{{{\text{E}}_{\text{x}} }}} \hfill &\quad { - \frac{{\upgamma_{\text{zx}} }}{{{\text{E}}_{\text{z}} }}} \hfill \\ { - \frac{{\upgamma_{\text{zx}} }}{{{\text{E}}_{\text{z}} }}} \hfill &\quad { - \frac{{\upgamma_{\text{zx}} }}{{{\text{E}}_{\text{z}} }}} \hfill &\quad { \frac{1}{{{\text{E}}_{\text{z}} }}} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\upsigma_{\text{x}} } \hfill \\ {\upsigma_{\text{y}} } \hfill \\ {\upsigma_{\text{z}} } \hfill \\ \end{array} } \right\}$$
(1)

The above Equation was used for cylinderical coordinate (\({\text{r}},\,\uptheta,\,{\text{z}}\)). To find four above unknowns, \(\upgamma_{\text{zx}} ,\upgamma_{\text{yx}} ,{\text{E}}_{\text{x}} = {\text{E}}_{\text{y}} ,{\text{E}}_{\text{z}}\), we need four equations based on elasticity theory as obtained by different loading states.

It is worth mentioning that other unknown variables depend on four main parameters:

$${\text{E}}_{\text{x}} = {\text{E}}_{\text{y}} ,\quad\upgamma_{\text{yx}} =\upgamma_{\text{xy}} ,\quad\upgamma_{\text{zy}} =\upgamma_{\text{zx}} ,\quad\upgamma_{\text{yz}} =\upgamma_{\text{xz}} = \frac{{{\text{E}}_{\text{x}} }}{{{\text{E}}_{\text{z}} }}\upgamma_{\text{zx}}$$
(2)

In axial loading, stress and strain components in each point of lateral surface are:

$$\upsigma_{\text{x}} =\upsigma_{\text{y}} =\upsigma_{\text{r}} =\upsigma_{\uptheta} = 0,\quad\upvarepsilon_{\text{z}} = \frac{{\Delta {\text{L}}}}{\text{L}}$$
(3)
$$\Delta {\text{L}} > 0,\;\Delta {\text{R}}_{\text{a}} < 0 :\;{\text{where}}\quad\upvarepsilon_{\uptheta} = \frac{{\Delta {\text{R}}_{\text{a}} }}{\text{R}}$$

In above equation, \(\Delta {\text{R}}_{\text{a}}\) is radius displacement and \(\uptheta\;{\text{and}}\;{\text{r}}\) are radius and tangent components in cylindrical system.

Based on the third equation in Eq. (1), we can write:

$${\text{E}}_{\text{z}} = \frac{{\upsigma_{\text{z}} }}{{\upvarepsilon_{\text{z}} }} = \frac{\text{L}}{{\Delta {\text{L}}}}\upsigma_{\text{ave}}$$
(4)

\(\upsigma_{\text{ave}}\) is obtained from Eq. (5):

$$\upsigma_{\text{ave}} = \frac{1}{\text{A}}\int {\upsigma_{\text{z}} \left( {{\text{x}},{\text{y}},\frac{\text{L}}{2}} \right){\text{dxdy}}}$$
(5)

Where, A is the area of the end surface and \(\upsigma_{\text{ave}}\) is obtained from FEM results.

Also, based on Eq. (1) in cylindrical coordinate and above results, we can write:

$$\upvarepsilon_{\uptheta} = - \frac{{\upgamma_{\text{zx}} }}{{{\text{E}}_{\text{z}} }}\upsigma_{\text{z}} = -\upgamma_{\text{zx}} \frac{{\Delta {\text{L}}}}{\text{L}} = \frac{{\Delta {\text{R}}_{\text{a}} }}{\text{R}}$$

Thus,

$$\upgamma_{\text{zx}} = - \frac{{\left( {\frac{{\Delta {\text{R}}_{\text{a}} }}{\text{R}}} \right)}}{{\frac{{\Delta {\text{L}}}}{\text{L}}}}$$
(6)

As it was said, Eqs. (4) and (6) were applied to obtain longitudinal young’s modulus (E z) and Poisson ratio \(\upgamma_{\text{zx}} \left( { =\upgamma_{\text{zy}} } \right)\) and \(\Delta {\text{R}}_{\text{a}}\) and \(\upsigma_{\text{ave}}\) were achieved from FEM results under axial loading conditions. \({\text{E}}_{\text{x}}\) and \(\upgamma_{\text{xy}}\) coefficients were computed by extensive lateral load or torsional load.

5 The analytic results based on materials strength theory

Some simple analytical equations or rule of mixtures which were achieved based on materials strength theory were summarized to compute longitudinal elastic modulus (Ez). These equations could be used to compare and verify the results obtained from finite element with those obtained based on formulas of Sect. 4. It can be said that materials strength theory is not an exact method to compute the stress including the stress of interface in nanocomposites but the results obtained from the rule of mixture can be used under axial loading.

5.1 Carbon nanotube along representative volume element (Fig. 3a)

If carbon nanotube was relatively long (high geometry ratio), the model is created by a representative volume element and the volume ratio of carbon nanotube:

$${\text{V}}^{\text{t}} = \frac{{\uppi\left( {{\text{r}}_{0}^{2} - {\text{r}}_{\text{i}}^{2} } \right)}}{{\uppi\left( {{\text{R}}_{0}^{2} - {\text{r}}_{\text{i}}^{2} } \right)}} = \frac{{{\text{r}}_{0}^{2} - {\text{r}}_{\text{i}}^{2} }}{{{\text{R}}_{0}^{2} - {\text{r}}_{\text{i}}^{2} }}$$
(7)
Fig. 3
figure 3

Nanocomposite with long and short fiber under axial loading

Full size image

By materials strength theory, we assumed that matrix and carbon nanotube deformation were not related under the displacement of \(\Delta {\text{L}}\) (Fig. 3a).

By compatibility of strains and stress equilibrium equations, Eq. (8) was achieved to compute the longitudinal elastic modulus:

$${\text{E}}_{{\text{z}}} = {\text{E}}^{{\text{t}}} {\text{V}}^{{\text{t}}} + {\text{E}}^{{\text{m}}} (1 - {\text{V}}^{{\text{t}}} )$$
(8)

\(\varvec{E}^{\varvec{m}}\) and Et are elastic moduli of matrix and carbon nanotube respectively. Equation (8) is the rule of mixtures as applied to compute the effective Young’s modulus along the fiber for fiber-reinforced composites with good approximation for equality of Poisson coefficient of matrix and fiber and is consistent with the results of elastic equations.

5.2 Nanotube inside the representative volume element (Fig. 3b)

If a short carbon nanotube is inside the representative volume element, the volume element is divided into two parts. One part is associated to two ends with length Le and elastic modulus \({\mathbf{E}}^{{\mathbf{m}}}\), the other part is used for central part with length \({\mathbf{L}}_{{\mathbf{c}}}\) and young’s modulus \({\mathbf{E}}^{{\mathbf{c}}}\). In this case, two hemispherical caps at two ends of the nanotubes were not considered since the core part was similar to the previous state and Fig. 3a, its young’s modulus was obtained based on the following equation:

$${\text{E}}^{{\text{c}}} = {\text{E}}^{{\text{t}}} {\text{V}}^{{\text{t}}} + {\text{E}}^{{\text{m}}} (1 - {\text{V}}^{{\text{t}}} )$$
(9)

By Eq. (8) in which Vt was achieved from Eq. (7), elastic modulus for the central part was computed. From compatibility equation of strains and stress equilibrium equations, Eq. (10) was obtained to compute the elastic modulus of the two end parts:

$${\text{E}}_{\text{z}} = \left[ { \frac{1}{{{\text{E}}_{\text{m}} }}\left( {\frac{{{\text{L}}_{\text{e}} }}{\text{L}}} \right) + \frac{1}{{{\text{E}}_{\text{c}} }}\left( {\frac{{{\text{L}}_{\text{c}} }}{\text{L}}} \right)\left( {\frac{\text{A}}{{{\text{A}}_{\text{c}} }}} \right) } \right]^{ - 1}$$
(10)

Or simply:

$$\frac{1}{{{\text{E}}_{\text{z}} }} = \frac{1}{{{\text{E}}_{\text{m}} }}\left( {\frac{{{\text{L}}_{\text{e}} }}{\text{L}}} \right) + \frac{1}{{{\text{E}}_{\text{c}} }}\left( {\frac{{{\text{L}}_{\text{c}} }}{\text{L}}} \right)\left( {\frac{\text{A}}{{{\text{A}}_{\text{c}} }}} \right)$$
(11)

In Eqs. (8) and (9), we have: \({\text{A}}_{\text{c}} =\uppi\left( {{\text{R}}_{0}^{2} - {\text{r}}_{\text{i}}^{2} } \right)\;{\text{and}}\;{\text{A}} =\uppi{\text{R}}^{2}\). Equations (10) and (11) are extended Equations of the rules of mixture being used to calculate Young’s modulus of nanocomposites with short carbon nanotubes (Fig. 3b).

For example, if we consider a representative volume element with the following specifications:

$${\text{L}} = 100\,{\text{nm}},\;{\text{L}}_{\text{e}} = L_{c} = 50\,{\text{nm}}$$
(12a)
$${\text{R}} = 10\,{\text{nm}},\;r_{o} = 5\,{\text{nm}},\;r_{i} = 4.6\,{\text{nm}},\;E^{t} = 5E^{m}$$
(12b)
$$V^{t} = 0.04871,\;E^{c} = 1.1948{\text{E}}^{\text{m}} ,\;{\text{E}}_{\text{z}} = 0.9701{\text{E}}^{\text{m}}$$
(12c)

As shown, elastic modulus of the composite was lower in comparison to matrix modulus. This showed that if the stiffness of carbon nanotube was not high compared to the matrix, it could not compensate the shortage of the lost material of matrix in which carbon nanotube was used. Thus, with similar items, if we have Et = 10Em, the results are as follows:

$${\text{E}}_{\text{z}} = 1.0628{\text{E}}^{\text{m}}$$
(13)

Thus, composite modulus was increased by 6.28%. If the length of carbon nanotube was equal to the length of volume element (Fig. 3a) or Le = 0 and LC = L = 100 nm, then \(\varvec{E}_{\varvec{z}}\) = \({\mathbf{E}}^{{\mathbf{c}}}\)  = 1.4384Em. In other words, the effective Young’s modulus of composite was increased by 43.84%. More parametric studies by Eqs. (8) and (10) can be applied for rapid prediction of axial Young’s modulus of carbon nanotube reinforced nanocomposites with different materials and sizes. The mentioned equations can be easily and directly generalized to the elements with more than one carbon nanotube or with square and hexagonal area.

6 Numerical results

In this section, a 3-D modeling was performed for short and long carbon nanotube. Abaqus version 6.12-3 software and second order elements with good results in stress analyses were used in the analysis.

6.1 Long carbon nanotube fiber along the representative volume element

In this section, a representative volume element with a long nanotube was studied as shown in Fig. 3a. The sizes of fiber, matrix and interphase are shown in Table 1.

Table 1 Dimension and Properties of RVE
Full size table

The selected values for Young’s modulus show the matrices in the range of polymer to steel. One of the most important sections of modeling is the property being used for the cohesive zone and in this study, the results of atomic simulation [13] were used to determine interface properties. Figure 4 shows traction-displacement plot in the mentioned study.

Fig. 4
figure 4

Traction-displacement plot obtained from atomic simulation

Full size image

The slope of the initial section of the plot showed the stiffness on length unit for the interface.

$${\text{M}} = \frac{{\left( {0.1 - 0} \right)}}{{\left( {3 - 0} \right)}} = 0.03333\,{\text{GPa/A}}^{ \circ } ,\;{\text{L}}_{\text{CNT}} = 122\,{\text{A}}^{ \circ }$$
(14)

LCNT is the length of the element of the nanotube. As in the molecular dynamics analysis of Namilae, s. and Chandra [11], the length of nanotube was \(122\,{\text{A}}^{ \circ }\) and by the multiplication of this value by the slope, the stiffness of the interface was obtained as embedded direclty in ABAQUS software.

$${\text{E}}_{\text{int}} = {\text{m}} \times {\text{L}}_{\text{CNT}}$$
(15a)
$${\text{E}}_{\text{int}} = 0.03333 \times 122 = 4.06\,{\text{Gpa}}$$
(15b)

The properties of the interface of the initial section of the chart were extracted for displamcent \(5\,{\text{A}}^{ \circ }\). This selection was logical based on the maximum displacement of 0.5 nm as applied on all models of this project. Poisson ratio for the interface was 0.3 and its thickness was 0.4 nm. The applied load was the displacement applied to the free end of the volume element. By Eq. (6), the longitudinal elastic modulus of nanocomposite was obtained and compared with the results of the rules of mixture. The results of finite element method and rules of mixture are shown in Table 2. Due to simple geometry and loading, the results of finite element method were similar to those of the rule of mixtures. Generally, due to the nano-scale and complexities of the interface in carbon nanotube reinforced composite, the rules of materials strength did not present accurate results in the evaluation of the properties of these materials. The results showed that with carbon nanotube volume fraction of 5%, the elastic modulus of nanocomposte was is increased more than 9 times (for Et/Em = 200).

Table 2 Computed effective elastic modulus for long CNT
Full size table

6.2 short carbon nanotube inside the representative volume element

The model of short carbon nanotube inside the matrix was similar to that of Fig. 3b. All sizes were similar to the previous section except carbon nanotube length which was reduced to 50 nm. The mechanical properties of matrix, carbon nanotube and interface were considered to be similar to the previous section. The results of finite element method and rule of mixtures (Eq. 8) are shown in Table 3. We found Et/Em = 5. The elastic modulus of nanocomposite was reduced because of the low percent of carbon nanotube and its high strengths could not compensate the shortage of carbon nanotube material in this state. Thus, these results showed that reinforcement of short carbon nanotube fibers was not as effective as long fibers.

Table 3 Computed effective elastic modulus for short CNT
Full size table

6.3 Calculation of elastic modulus of polyethylene-carbon nanotube nanocomposites and its validation with experimental results

In this section, the reinforcement effect of carbon nanotube in polyethylene matrix with the dimensions shown in Table 4 and different weight fraction was examined.

Table 4 Dimension and Properties of RVE with polyethylene matrix
Full size table

In order to change the parameter of weight fraction, a symmetrical model as shown in Fig. 5 showed that by changing parameter x, different volume fraction and weight fractions were achieved and the effect of the addition of carbon nanotubes was studied.

Fig. 5
figure 5

Polyethylene/ CNT nanocomposite

Full size image

The volume of nanotube and representative volume element were calculated as:

$${\text{V}}_{\text{CNT}} =\uppi\left( {(5)^{2} - (4.6)^{2} } \right) \times \left( {150} \right)$$
(16)
$${\text{V}}_{\text{RVE}} =\uppi\left( {\left( {\frac{2x + 10}{2}} \right)} \right)^{2} \times \left( {2x + 150} \right)$$
(17)

Volume fraction was obtained by the following Equation:

$${\text{V}}_{\text{f}} = \frac{{{\text{V}}_{\text{CNT}} }}{{{\text{V}}_{\text{RVE}} }} \times 100$$
(18a)
$${\text{V}}_{\text{f}} = \frac{{{\text{V}}_{\text{CNT}} }}{{{\text{V}}_{\text{RVE}} }} = \frac{\text{wf}}{{{\text{wf}} + \left( {\frac{{\uprho{\text{f}}}}{{\uprho{\text{m}}}}} \right)\left( {1 - {\text{w}}_{\text{f}} } \right)}}$$
(18b)

where \(\uprho_{f}\) = 1.68 g/cm3 is the density of nanotube, \(\rho_{m}\) = 0.94 g/cm3 is the matrix density and \(\text{w}_{f}\) is weight fraction of fibers. For each volume fraction, we could obtain x simply by solving the cubic Eq. (19b):

$${\text{V}}_{\text{RVE}} = \frac{{{\text{V}}_{\text{CNT}} }}{\text{vf}} \times 100$$
(19b)
$$\uppi\left( {\frac{2x + 10}{2}} \right)^{2} \times \left( {2x + 150} \right) = \frac{{\uppi\left( {\left( {\frac{10}{2}} \right)^{2} - \left( {\frac{9.2}{2}} \right)^{2} } \right) \times 150}}{\text{vf}} \times 100$$
(19b)

The length and diameter of the representative volume element are obtained based on Fig. 5 and Eqs. 13 and 14 in terms of nm:

$${\text{D}}_{\text{RVE}} = 2x + 20$$
(20)
$${\text{L}}_{\text{RVE}} = 2x + 150$$
(21)

The volume fraction consistent with experimental results [14] was considered based on weights fractions 0.5, 1 and 1.5 by solving Eq. (19b) and the value of x was obtained and by having x value for each volume fraction, the dimensions of representative volume elements were obtained. The results are shown in Table 5.

Table 5 RVE’s dimension for various weight factors
Full size table

The elastic modulus of this modeling method is shown in Table 6 and is compared with the experimental results [11]:

Table 6 Computed effective elastic modulus for Polyethylene/CNT nanocomposite (MPa)
Full size table

Based on the modeling results, the increase of weight fraction of nanotubes was equal to the increase of elastic modulus of nanocomposites.

In this study, the effect of thickness and strength of interface zone on longitudinal elastic modulus of polyethylene/carbon nanotube nanocomposite was evaluated (Fig. 6).

Fig. 6
figure 6

Variation of elastic modulus with weight fraction of CNT

Full size image

As the thickness of carbon nanotube was equal to the thickness of graphene or 3.4 Angstrom meter (Am), it was assumed that carbon atoms were located in the middle circle of this thickness. Also, resin could not penetrate into the nanotube and the innermost resin layer was equal to external surface of nanotube. Thus, the minimum thickness of interphase was equal to 1.7Am. Depending on the quality of the bonding of nanotube to resin, this value was increased. Figure 7 shows the effect of interface thickness on longitudinal elastic modulus of polyethylene/carbon nanotube nanocomposite (1% weight). As shown, by the increase of the thickness of the interphase, the stiffness and the longitudinal Young’s modulus were increased. Indeed, by reduction of the thickness of the interphase, the effective forces between nanotube atoms and resin were weakened and by weak bonds, load transfer from resin to nanotube was not performed well.

Fig. 7
figure 7

The effect of interface thickness on the elastic modulus of polyethylene/carbon nanotube nanocomposite

Full size image

Two states of full transfer of stress from interphase and lack of transfer of stress between the matrix and fiber are boundary conditions of the load transfer from the interphase. In other words, if no load transfer was occurred, elastic modulus of nanocomposite was equal to the elastic modulus of matrix. The stiffness of the composite was increased with the increase of strength of interphase and increase of transferability of stress. In maximum load transfer or full transfer of load, elastic modulus of the interphase had the highest value. This is shown in Fig. 8 for different weight fraction. If the chemical bonds between the matrix and carbon nanotube were high, the elastic modulus of interphase was about 5Gpa and this was associated with the ideal state of load transfer from the matrix to the carbon nanotube. If the elasticity modulus of the interphase was about 5Mpa, the elastic modulus of the composite was close to the elastic modulus of the matrix.

Fig. 8
figure 8

The effect of interphase strength on elastic modulus of polyethylene/carbon nanotube nanocomposite

Full size image

7 Summary and conclusion

The experimental study of the mechanical behavior of carbon nanotube reinforced polyethylene requires considerable time and cost. Thus, various researchers have attempted to use theoretical methods and present a good model to study the mechanical behavior of nanocomposites. This study evaluated the modeling of representative volume element. The interface between carbon nanotube and matrix as the most important zone in the evaluation of stress transfer and other properties of nanocomposites was used as an interphase with low thickness and to determine its properties, the results of atomic modeling were used.

Based on the modeling results, the increase of weight fraction of nanotubes led to the increase of equal elastic modulus of nanocomposite. By increasing the volume ratio of carbon nanotube in the experiments, the dispersion of particles was much difficult and the empirical results of elastic modulus were lower than the results predicted by the finite element software.