1 Introduction

The presence of natural fractures controls groundwater flow because water can flow more quickly and much greater distances along these fractures than it could flow through matrix in subsurface fractured rocks. Fractures and fracture networks determine the permeability of many natural rocks [2]. For characterization of disorder and irregular media, fractal geometry and technique are believed to be effective tools [5, 7, 33, 38]. Studies illustrated that porous media can be described by fractal geometry theory (e.g., [12, 29]). Fractures have also been shown to demonstrate fractal characteristics [8, 28]. There have been many studies of flow characteristics in porous media using fractal geometry theory (e.g., [6, 21, 34, 37, 39]). There have also been many investigations of flow and conduction in fractal fracture network (e.g., [16, 17, 22, 35, 36]). Xu et al. [35] derived the expression for the equivalent permeability based on the fractal-like tree network model. Recently, Miao et al. [22] used fractal geometry theory and technique to study seepage characteristics and obtained the analytical expression for permeability of fracture networks. The model includes microstructure parameters of fractures and does not contain any empirical constant. Liu et al. [17] proposed the fractal scaling law for the fracture length in the flow direction and determined the average equivalent permeability in relation to the fractal dimension using numerical simulations. Miao et al. [23] derived an analytical model based on the fractal geometry theory and technique for porous media with the length distribution of fractures obeying the fractal scaling law in dual-porosity porous media where the porous matrix was assumed to consist of a bundle of tortuous capillaries whose size distribution follows the fractal scaling law. Li et al. [16] derived the permeability of fracture networks by assuming that each fracture cuts through the model domain from the left inlet boundary to the right outlet boundary when the aperture distribution follows the fractal scaling law. For more compressive summary of recent studies on the relationship between fractal characteristics and permeability, refer to several recent reviews (e.g., [18, 19, 32]).

Studies at various scales have shown that the distribution of length and displacement (aperture) often follows a power law [3, 15, 30]

$$a = \beta l^{n}$$
(1)

where a is the fracture aperture (displacement), l is the length of fracture, β is a proportionality coefficient related to the rock properties, and n is the scaling exponent.

However, it has been suggested that there are separate regions of behavior in the form of Eq. (1) that necessitate two separate equations [1, 10]

$$a = \left\{ {\begin{array}{*{20}c} {\beta_{1} l^{{n_{1} }} } & {l \le l_{b} } \\ {\beta_{2} l^{{n_{2} }} } & {l > l_{b} } \\ \end{array} } \right.$$
(2)

This illustrates that there is a scaling break at some length lb. If this relationship is plotted in a log–log plot, two straight lines don’t have the same slope, in which the slope change occurs at the critical length lb. The critical length and the slope vary with rock formations. The scaling is not consistent of a universal scaling law. At 90% confidence level, a distinct change in scaling from n ≈ 2 to n ≈ 1 at fracture length of about 10 times the mechanical grain size provided by the cooling joints [10].

The orientations of each fracture can be defined by two angles, the fracture azimuth and fracture dip. The orientations of fractures in the medium are not uniform, but usually with a preferred orientation. It has been shown that the averaged/mean angle, the fracture azimuth and fracture dip of all fractures are constant (e.g., [14]). In practical applications the mean dip of fractures between fracture orientations and fluid flow direction has been generally assumed and used [23]. However, the fracture orientation distribution in real-world networks is of a great interest and should be considered in more general context [24].

Therefore, the objective of this study is twofold. First we develop analytical solutions of effective permeability for a fractal fracture network where there is a scaling break to examine the significance of the scaling break on the effective permeability of a fractal fracture network. Then we derive expression to quantify reduction in the effective permeability of fracture network and investigate the effect of dispersion in individual fracture orientation from the mean orientation on the effective permeability. The fractal fracture domain is two-dimensional with variable trace length in the cutting plane. The fracture sides that cross the boundaries form the traces, which have lengths and apertures that follow a power law relationship with a scaling break. The flow through the fracture domain is due to a hydraulic gradient imposed perpendicularly to the domain boundaries. We develop analytical expressions for the corresponding component of the permeability tensor. The overall flow direction is assumed to take place in the one-dimensional direction of decreasing hydraulic head. Although the flow is not strictly one-dimensional due to the orientation dispersion of fractures, we conceptualize the flow as one-dimensional by taking the orientation dispersion into account through the idea of effective permeability. In other words, the effective permeability is fracture orientation dependent.

2 Methods

2.1 Effect of fractal scaling break on effective permeability

The fracture network is often statistically self-similar [3, 11, 31]. In this study, it is assumed that the area distribution of fractures in a fractal fracture network can be described by [20]

$$N\left( {S \ge s} \right) = \left( {\frac{{a_{max} l_{max} }}{al}} \right)^{{D_{f} /2}}$$
(3)

where N represents the total number of fractures with area greater than al, amaxlmax represents the maximum fracture area with amax and lmax being the maximum aperture and maximum trace length, respectively, and Df is the fractal dimension for fracture length, 0 < Df < 2 in the two dimension fracture network. For the facture network considered in the study, the total number of fractures, N, is distributed over the domain in which the total fracture area, A, can be expressed in Eq. (19) below.

It is further assumed that the fractured domain behaves like a porous medium where Darcy’s law applies. Then, the fractal dimension Df can be related to the porosity and minimum and maximum fracture lengths in the fractal fracture network as [22]

$$D_{f} = d_{E} + \frac{ln\phi }{{ln\left( {l_{max} /l_{min} } \right)}}$$
(4)

where lmax and lmin are the minimum and maximum lengths, respectively, and ϕ is the effective porosity of fractures in a rock. From Eq. (4), the porosity can be expressed in terms of the lengths and fractal dimension for a two-dimensional fractal fracture network (i.e., dE = 2) as follows

$$\phi = \left( {\frac{{l_{max} }}{{l_{min} }}} \right)^{{\left( {D_{f} - 2} \right)}} = \left( {\frac{{l_{min} }}{{l_{max} }}} \right)^{{\left( {2 - D_{f} } \right)}}$$
(5)

As discussed earlier, the scaling exponent expressed in Eq. (2) changes from a larger value of about 2 to a smaller value of about 1 [10]. In this study, the aperture of fracture is assumed to follow the scaling relationship with the trace length having a scaling break as expressed in Eq. (2). Based on numerous observations [10], the ratio of n1/n2 should be generally larger than 1. The influences of different values of n1 and n2 are examined in this study.

From Eq. (2), the relation between the aperture a and trace length l can be expressed as

$$log\left( a \right) = \left\{ {\begin{array}{*{20}c} {log\left( {\beta_{1} } \right) + n_{1} log\left( l \right)} & { l \le l_{b} } \\ {log\left( {\beta_{2} } \right) + n_{2} log\left( l \right)} & {l > l_{b} } \\ \end{array} } \right.$$
(6)

At l = lb, a (or log(a)) should have a same value, which leads to

$$log\left( {\beta_{2} } \right) = log\left( {\beta_{1} } \right) + \left( {n_{1} - n_{2} } \right)log\left( {l_{b} } \right)$$
(7)

It can then be obtained that

$$a = \left\{ {\begin{array}{*{20}c} {\beta_{1} l^{{n_{1} }} } & { l \le l_{b} } \\ {\beta_{1} l_{b}^{{\left( {n_{1} - n_{2} } \right)}} l^{{n_{2} }} } & { l > l_{b} } \\ \end{array} } \right.$$
(8)

If the scaling break occurs at a trace length between the minimum and maximum lengths in a fractal fracture network (i.e., lmax > lb > lmin) for the fractal network length, then the following expressions can be developed by substituting Eq. (8) into (3)

$$N\left( {L \ge l} \right) = \left\{ {\begin{array}{*{20}c} {\left[ {\frac{{\beta_{1} l_{b}^{{\left( {n_{1} - n_{2} } \right)}} l_{max}^{{n_{2} }} l_{max} }}{{\beta_{1} l^{{n_{1} }} l}}} \right]^{{D_{f} /2}} } & {l \le l_{b} } \\ {\left[ {\frac{{\beta_{1} l_{b}^{{\left( {n_{1} - n_{2} } \right)}} l_{max}^{{n_{2} }} l_{max} }}{{\beta_{1} l_{b}^{{\left( {n_{1} - n_{2} } \right)}} l^{{n_{2} }} l}}} \right]^{{D_{f} /2}} } & {l > l_{b} } \\ \end{array} } \right.$$
(9)

which can be further simplified as

$$N\left( {L \ge l} \right) = \left\{ {\begin{array}{*{20}c} {l_{b}^{{\frac{{\left( {n_{1} - n_{2} } \right)D_{f} }}{2}}} l_{max}^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} l^{{ - \frac{{\left( {n_{1} + 1} \right)D_{f} }}{2}}} } & {l \le l_{b} } \\ {l_{max}^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} l^{{ - \frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} } & {l > l_{b} } \\ \end{array} } \right.$$
(10)

Then the number of fractures that is in the range from l to l + dl can be determined as

$$- dN\left( l \right) = \left\{ {\begin{array}{*{20}c} {\left[ {\frac{{\left( {n_{1} + 1} \right)D_{f} }}{2}} \right]l_{b}^{{\frac{{\left( {n_{1} - n_{2} } \right)D_{f} }}{2}}} \cdot l_{max}^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} \cdot l^{{ - \frac{{\left( {n_{1} + 1} \right)D_{f} + 2}}{2}}} dl} & {l \le l_{b} } \\ {\left[ {\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}} \right]l_{max}^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} \cdot l^{{ - \frac{{\left( {n_{2} + 1} \right)D_{f} + 2}}{2}}} dl } & {l > l_{b} } \\ \end{array} } \right.$$
(11)

By definition the effective porosity can be expressed as

$$\phi = \frac{{A_{f} }}{A}$$
(12)

where A is the area that is represented by the effective permeability, and Af is the total area of all fractures, which can be related to the fractal characteristics from the following integration

$$A_{f} = - \mathop \int \limits_{{l_{min} }}^{{l_{max} }} a \cdot l \cdot dN\left( l \right) = - \mathop \int \limits_{{l_{min} }}^{{l_{b} }} a \cdot l \cdot dN\left( l \right) - \mathop \int \limits_{{l_{b} }}^{{l_{max} }} a \cdot l \cdot dN\left( l \right)$$
(13)

which means the integration has two portions depending on the location of scaling break, lb.

$$A_{f} = A_{f1} + A_{f2}$$
(14)

The fracture area related to the fracture length smaller than the scaling break lb is

$$\begin{aligned} A_{f1} & = - \mathop \int \limits_{{l_{min} }}^{{l_{b} }} a \cdot l \cdot dN\left( l \right) \\ & = \mathop \int \limits_{{l_{min} }}^{{l_{b} }} \beta_{1} l^{{n_{1} }} \cdot l \cdot \left[ {\frac{{\left( {n_{1} + 1} \right)D_{f} }}{2}} \right]l_{b}^{{\frac{{\left( {n_{1} - n_{2} } \right)D_{f} }}{2}}} \cdot l_{max}^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} \cdot l^{{ - \frac{{\left( {n_{1} + 1} \right)D_{f} + 2}}{2}}} dl \\ \end{aligned}$$
(15)

which leads to

$$A_{f1} = \beta_{1} \left( {\frac{{D_{f} }}{{2 - D_{f} }}} \right)l_{b}^{{\left( {n_{1} + 1} \right)}} \left( {\frac{{l_{max} }}{{l_{b} }}} \right)^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} \left[ {1 - \left( {\frac{{l_{min} }}{{l_{b} }}} \right)^{{\frac{{2n_{1} + 2 - \left( {n_{1} + 1} \right)D_{f} }}{2}}} } \right]$$
(16)

The fracture area related to the fracture length larger than the scaling break lb can be determined similarly

$$\begin{aligned} A_{f2} & = - \mathop \int \limits_{{l_{b} }}^{{l_{max} }} a \cdot l \cdot dN\left( l \right) \\ & = \mathop \int \limits_{{l_{b} }}^{{l_{max} }} \beta_{1} l_{b}^{{\left( {n_{1} - n_{2} } \right)}} l^{{n_{2} }} \cdot l \cdot \left[ {\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}} \right]l_{max}^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} \cdot l^{{ - \frac{{\left( {n_{2} + 1} \right)D_{f} + 2}}{2}}} dl \\ \end{aligned}$$
(17)

which leads to

$$A_{f2} = \beta_{1} \left( {\frac{{D_{f} }}{{2 - D_{f} }}} \right)l_{b}^{{\left( {n_{1} + 1} \right)}} \left( {\frac{{l_{max} }}{{l_{b} }}} \right)^{{\left( {n_{2} + 1} \right)}} \left[ {1 - \left( {\frac{{l_{b} }}{{l_{max} }}} \right)^{{\frac{{2n_{2} + 2 - \left( {n_{2} + 1} \right)D_{f} }}{2}}} } \right]$$
(18)

The total area of the fractal fracture network A is then related to the fracture area Af by the following relationship

$$A = \frac{{A_{f} }}{\phi } = \frac{{A_{f1} + A_{f2} }}{{\left( {\frac{{l_{min} }}{{l_{max} }}} \right)^{{\left( {2 - D_{f} } \right)}} }}$$
(19)

In each fracture with aperture a and trace length l, the flowrate q is related to the hydraulic gradient \(\nabla h\) by the following cubic law (e.g., [25]

$$q = \frac{{\rho ga^{3} l}}{12\mu } \cdot \nabla h$$
(20)

In this study, we assume that the rock matrix is assumed to be impermeable. Therefore, the total flowrate Q in the fracture network can be determined by the following integrations

$$Q = - \mathop \int \limits_{{l_{min} }}^{{l_{max} }} q\left( l \right)dN\left( l \right) = - \mathop \int \limits_{{l_{min} }}^{{l_{b} }} q\left( l \right)dN\left( l \right) - \mathop \int \limits_{{l_{b} }}^{{l_{max} }} q\left( l \right)dN\left( l \right)$$
(21)

which indicates the total flowrate is contributed from two portions

$$Q = Q_{1} + Q_{2}$$
(22)
$$\begin{aligned} Q_{1} & = - \mathop \int \limits_{{l_{min} }}^{{l_{b} }} q\left( l \right)dN\left( l \right) \\ & = \mathop \int \limits_{{l_{min} }}^{{l_{b} }} \frac{{\rho ga^{3} l}}{12\mu } \cdot \nabla h\left[ {\frac{{\left( {n_{1} + 1} \right)D_{f} }}{2}} \right]l_{b}^{{\frac{{\left( {n_{1} - n_{2} } \right)D_{f} }}{2}}} \cdot l_{max}^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} \cdot l^{{ - \frac{{\left( {n_{1} + 1} \right)D_{f} + 2}}{2}}} dl \\ \end{aligned}$$
(23)

which leads to

$$\begin{aligned} Q_{1} & = \frac{{\rho g\beta_{1}^{3} \nabla h}}{12\mu }\left[ {\frac{{\left( {n_{1} + 1} \right)D_{f} }}{{6n_{1} + 2 - \left( {n_{1} + 1} \right)D_{f} }}} \right]l_{b}^{{\left( {3n_{1} + 1} \right)}} \\ & \quad \cdot \left( {\frac{{l_{max} }}{{l_{b} }}} \right)^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} \left[ {1 - \left( {\frac{{l_{min} }}{{l_{b} }}} \right)^{{\frac{{6n_{1} + 2 - \left( {n_{1} + 1} \right)D_{f} }}{2}}} } \right] \\ \end{aligned}$$
(24)
$$\begin{aligned} Q_{2} & = - \mathop \int \limits_{{l_{b} }}^{{l_{max} }} q\left( l \right)dN\left( l \right) \\ & = \mathop \int \limits_{{l_{b} }}^{{l_{max} }} \frac{{\rho ga^{3} l}}{12\mu } \cdot \nabla h\left[ {\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}} \right]l_{max}^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} \cdot l^{{ - \frac{{\left( {n_{2} + 1} \right)D_{f} + 2}}{2}}} dl \\ \end{aligned}$$
(25)

which results in

$$\begin{aligned} Q_{2} & = \frac{{\rho g\beta_{1}^{3} }}{12\mu } \cdot \nabla h\left[ {\frac{{\left( {n_{2} + 1} \right)D_{f} }}{{6n_{2} + 2 - \left( {n_{2} + 1} \right)D_{f} }}} \right]l_{b}^{{\left( {3n_{1} + 1} \right)}} \left( {\frac{{l_{max} }}{{l_{b} }}} \right)^{{\left( {3n_{2} + 1} \right)}} \\ & \quad \left[ {1 - \left( {\frac{{l_{b} }}{{l_{max} }}} \right)^{{\frac{{6n_{2} + 2 - \left( {n_{2} + 1} \right)D_{f} }}{2}}} } \right] \\ \end{aligned}$$
(26)

In performing the integrations (15), (17), (23) and (25), it is assumed that the fractures do not intersect, which means they do not overlap.

In this study, it is assumed that the fractal fracture network behaves similarly to a porous medium with an effective permeability k. We also assume that each fracture cuts through the model domain from the inlet boundary to the outlet boundary [16]. Then Darcy’s law for groundwater flow can be written as

$$Q = \frac{k\rho gA}{\mu }\nabla h$$
(27)

where ρ is the water density, μ is the viscosity, and g is the gravitational acceleration. Equation (27) can be re-arranged to obtain the effective permeability of the fractal fracture network k

$$k = \frac{Q\mu }{A\rho g\nabla h}$$
(28)

Then similar to the flowrate, the effective permeability can also be expressed in two parts

$$k = \frac{{\mu \left( {Q_{1} + Q_{2} } \right)}}{A\rho g\nabla h} = k_{1} + k_{2}$$
(29)
$$\begin{aligned} k_{1} & = \frac{{\mu Q_{1} }}{A\rho g\nabla h} = \frac{\mu }{A\rho g\nabla h}\frac{{\rho g\beta_{1}^{3} \nabla h}}{12\mu }\left[ {\frac{{\left( {n_{1} + 1} \right)D_{f} }}{{6n_{1} + 2 - \left( {n_{1} + 1} \right)D_{f} }}} \right]l_{b}^{{\left( {3n_{1} + 1} \right)}} \\ & \quad \cdot \left( {\frac{{l_{max} }}{{l_{b} }}} \right)^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} \left[ {1 - \left( {\frac{{l_{min} }}{{l_{b} }}} \right)^{{\frac{{6n_{1} + 2 - \left( {n_{1} + 1} \right)D_{f} }}{2}}} } \right] \\ \end{aligned}$$
(30)

which can be further simplified as,

$$\begin{aligned} k_{1} & = \frac{{\beta_{1}^{3} }}{{12\left( {A_{f1} + A_{f2} } \right)}}\left[ {\frac{{\left( {n_{1} + 1} \right)D_{f} }}{{6n_{1} + 2 - \left( {n_{1} + 1} \right)D_{f} }}} \right]l_{b}^{{\left( {3n_{1} + 1} \right)}} \\ & \quad \cdot \left( {\frac{{l_{min} }}{{l_{max} }}} \right)^{{\left( {2 - D_{f} } \right)}} \left( {\frac{{l_{max} }}{{l_{b} }}} \right)^{{\frac{{\left( {n_{2} + 1} \right)D_{f} }}{2}}} \left[ {1 - \left( {\frac{{l_{min} }}{{l_{b} }}} \right)^{{\frac{{6n_{1} + 2 - \left( {n_{1} + 1} \right)D_{f} }}{2}}} } \right] \\ \end{aligned}$$
(31)
$$\begin{aligned} k_{2} & = \frac{{\mu Q_{2} }}{A\rho g\nabla h} = \frac{\mu }{A\rho g\nabla h}\frac{{\rho g\beta_{1}^{3} }}{12\mu } \\ & \quad \cdot \nabla h\left[ {\frac{{\left( {n_{2} + 1} \right)D_{f} }}{{6n_{2} + 2 - \left( {n_{2} + 1} \right)D_{f} }}} \right]l_{b}^{{\left( {3n_{1} + 1} \right)}} \left( {\frac{{l_{max} }}{{l_{b} }}} \right)^{{\left( {3n_{2} + 1} \right)}} \left[ {1 - \left( {\frac{{l_{b} }}{{l_{max} }}} \right)^{{\frac{{6n_{2} + 2 - \left( {n_{2} + 1} \right)D_{f} }}{2}}} } \right] \\ \end{aligned}$$
(32)

which can be further simplified as,

$$\begin{aligned} k_{2} & = \frac{{\beta_{1}^{3} }}{{12\left( {A_{f1} + A_{f2} } \right)}} \cdot \left[ {\frac{{\left( {n_{2} + 1} \right)D_{f} }}{{6n_{2} + 2 - \left( {n_{2} + 1} \right)D_{f} }}} \right]l_{b}^{{\left( {3n_{1} + 1} \right)}} \\ & \quad \cdot \left( {\frac{{l_{min} }}{{l_{max} }}} \right)^{{\left( {2 - D_{f} } \right)}} \left( {\frac{{l_{max} }}{{l_{b} }}} \right)^{{\left( {3n_{2} + 1} \right)}} \left[ {1 - \left( {\frac{{l_{b} }}{{l_{max} }}} \right)^{{\frac{{6n_{2} + 2 - \left( {n_{2} + 1} \right)D_{f} }}{2}}} } \right] \\ \end{aligned}$$
(33)

While Eqs. (21) through (26) indicate that the flowrate in the domain only depends on the total number of fractures, the resulting effective permeability in Eqs. (29) through (33) is directly related to the total fracture area. This is a direct result from the fact that the total area, density, and number of fractures are all related for the considered fracture domain in this study.

2.2 Fracture orientation effect on effective permeability

The distribution of orientation about a mean set orientation is typically modeled using a Fisher distribution. The Fisher distribution function gives the probability of finding a direction within an angular area centered at an angle θ from the true mean. The angular area is expressed in steradians with the total angular area of a sphere being 4π steradians. Orientations are distributed according to the probability density function [4, 9, 27]

$$f_{A} \left( \theta \right) = \frac{{t \cdot e^{{t \cdot { \cos }\theta }} }}{{2\pi \left( {e^{t} - e^{ - t} } \right)}}$$
(34)

where θ is the angle between the mean flow direction and the fracture orientation. The mean flow occurs in the direction of θ = 0, which is also the orientation of the Fisher’s pole. t is the precision parameter in Eq. (34). This is a symmetric distribution about the mean orientation, and as expected, the distribution has a maximum at the true mean (θ = 0).

If ζ is taken as the azimuthal angle about the true mean direction, the probability of a direction with an angular area dA, fA(θ), can be expressed as

$$f_{A} \left( \theta \right)dA = f_{A} \left( \theta \right)sin\left( \theta \right)d\theta d\upzeta$$
(35)

The sin(θ) term appears because the area of a band width dθ varies as sin(θ). The Fisher distribution is normalized so that \(\mathop \int \nolimits_{{\upzeta = 0}}^{2\pi } \mathop \int \nolimits_{\theta = 0}^{\pi } f_{A} \left( \theta \right)sin\left( \theta \right)d\theta d\upzeta = 1.\)

Then the probability of finding a direction in a band of width dθ between θ and θ + dθ, f(θ)dθ, is then given by

$$f\left( \theta \right)d\theta = \mathop \int \limits_{{\upzeta = 0}}^{2\pi } f_{A} \left( \theta \right)sin\left( \theta \right)d\theta d\upzeta = 2\pi f_{A} \left( \theta \right)sin\left( \theta \right)d\theta = \frac{{tsin\left( \theta \right)e^{{t \cdot { \cos }\theta }} }}{{\left( {e^{t} - e^{ - t} } \right)}}d\theta$$
(36)

Therefore, the probability density function of fracture deviation angle from the mean direction can be expressed as

$$f\left( \theta \right) = \frac{{t{ \sin }\theta e^{{t \cdot { \cos }\theta }} }}{{e^{t} - e^{ - t} }}$$
(37)

With the Fisher distribution, the angle from the true mean within which a given percentage of directions lie can be determined, which is related to t. The angle with which 50% of directions lie is \(\theta_{50} = 67.5{^\circ } /\sqrt t\). The critical angle that contains 95% of directions is given by \(\theta_{95} = 140{^\circ } /\sqrt t\).

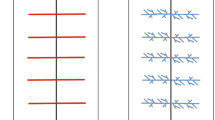
A large t predicts a distribution more strongly concentrated about the true mean [13]. Figure 1 shows the effect of precision parameter t on the orientation distribution. It can be seen that the orientation distribution is more clustered and moves toward zero with a larger t value. In the extreme case of infinite t, the orientation deviation angle is zero, which means that the all fractures would have the same orientation angle of zero in relation to the hydraulic gradient. Under this condition, the effective permeability would be the largest.

Fig. 1
figure 1

Fisher probability density function of fracture deviation angles from the mean angle

Full size image

If a fracture has the azimuth of zero and dip angles of θ, respectively, the actual flowrate in the fracture is reduced by a factor of cos2θ [23, 26]

$$q = \frac{{\rho ga^{3} l}}{12\mu } \cdot \nabla h \cdot { \cos }^{2} \theta$$
(38)

Since fracture area and total area are not affected by the angle as long as the aperture and length don’t change, a simple reduction factor (RF) can be defined to measure the overall effect of fracture orientation distribution (dispersion) on the effective permeability

$$RF = \frac{{k_{\theta } }}{k}$$
(39)

where kθ denotes the effective permeability when fractures are not parallel to the hydraulic gradient direction. The RF can be determined as

$$RF = \mathop \int \limits_{0}^{\pi } { \cos }^{2}\uptheta\,f\left( \theta \right)d\theta = \mathop \int \limits_{0}^{\pi } { \cos }^{2}\uptheta\frac{{t{ \sin }\theta e^{{t \cdot { \cos }\theta }} }}{{e^{t} - e^{ - t} }}d\theta$$
(40)

which can be integrated as

$$RF = 1 - 2\left[ {\frac{{t{ \cosh }\left( t \right) - { \sinh }\left( t \right)}}{{t^{2} { \sinh }\left( t \right)}}} \right]$$
(41)

Note that in the extreme case of orientation dispersion (t → 0), it can be shown that

$$\mathop {\lim }\limits_{t \to 0} \left[ {\frac{{t{ \cosh }\left( t \right) - { \sinh }\left( t \right)}}{{t^{2} { \sinh }\left( t \right)}}} \right] = \frac{1}{3}$$
(42)

which means

$$\mathop { \lim }\limits_{t \to 0} RF = 1 - 2\left( {\frac{1}{3}} \right) = \frac{1}{3}$$
(43)

In the other extreme case of no orientation dispersion (t → ∞), it can be shown that

$$\mathop {\lim }\limits_{t \to \infty } \left[ {\frac{{t{ \cosh }\left( t \right) - { \sinh }\left( t \right)}}{{t^{2} { \sinh }\left( t \right)}}} \right] = 0$$
(44)

which leads to

$$\mathop { \lim }\limits_{t \to \infty } RF = 1$$
(45)

Therefore, the reduction factor of effective permeability due to orientation variations of fractures varies in the range from 1/3 for the most extreme orientation dispersion to 1 for no orientation dispersion.

3 Results and discussion

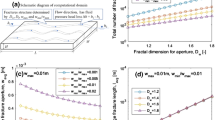
Figure 2 shows the influence of the scaling exponent before the break, n1, on the effective permeability of fractal fracture network. Since n2 is set to be 1, the change of n1 from 1 to 2 means that the scaling relationship changes from no break to a strong break. The influence from this break change can be explained by Eq. (8). When the scaling break occurs at the minimum length in the fractal fracture network, the bottom relationship in Eq. (8) (i.e., l > lb) applies for all fractures in the network. When lb is at the smallest length lmin, the aperture would always be reduced by a factor \(l_{b}^{{\left( {n_{1} - n_{2} } \right)}}\), which becomes smaller as n1 increases. This scaling relationship explains why the effective permeability of fractal fracture network decreases with increasing n1 while keeping n2 a constant. The flows in the fracture network are mainly dominated by the fractures with large aperture as is evident from Eq. (20), which are mostly those with l > vlb. Further analysis indicates that when lb/lmax is equal to 0.2 under otherwise same conditions in Fig. 2, the network effective permeability does not change with n1. Since lb = 0.2lmax = 1 m for this particular parameter combination, the value of n1 does not affect the effective permeability of fractal fracture network. When lb > 0.2lmax, the aperture increases with n1 for a given length fracture, and as a result the effective permeability also increases with n1 as seen from the results in Fig. 2.

Fig. 2
figure 2

The impact of scaling exponent n1 before the break on the effective permeability of a fractal fracture network. The other parameters are: Df = 1.5, β1 = 0.002, lmin/lmax = 0.001, lmax = 5.0 m, and n2 = 1.0

Full size image

The significance of the scaling exponent after the break n2 is shown in Fig. 3. The flow is mainly controlled by fractures with large fractures. When lb/lmax = lmin/lmax, the aperture for a given length fracture is totally controlled by the bottom formula in Eq. (8), which can be re-arranged as \(a = \beta_{1} l_{b}^{{n_{1} }} \left( {l/l_{b} } \right)^{{n_{2} }}\). Since l/lb is always larger than 1 when the scaling break occurs at the minimum length in the network, the aperture at any given length increases with n2. As a result, both the flowrate and effective permeability in the network also increase with the scaling exponent after the break n2. When lb/lmax = 1, since all the fracture apertures follow the top formula in the scaling relationship (Eq. 8), the n2 value is irrelevant. Therefore the effective permeability of fractal fracture network does not change with the scaling exponent after the break n2. In this case, the scaling relationship does not have a break for the entire range of lengths in the fractal fracture network. For any other lb/lmax between lmin/lmax and 1, the aperture increases especially for the long fractures as n2 increases. Therefore, the flow capacity under the same hydraulic gradient also increases, which explains why the effective permeability increases with the scaling exponent n2 after the scaling break. When lb/lmax becomes larger, the rate of increase of effective permeability with n2 becomes smaller, as seen from the results in Fig. 3. Eventually in the extreme case of lb/lmax = 1, the effective permeability does not change with n2.

Fig. 3
figure 3

The impact of scaling exponent n2 after the break on the effective permeability of a fractal fracture network. The other parameters are: Df = 1.5, β1 = 0.002, lmin/lmax = 0.001, lmax = 5.0 m, and n1 = 2.0

Full size image

In Fig. 4, the effective permeability of fractal fracture network is plotted in relation to the scaling break length ratio lb/lmax at a few selected values of the scaling exponent before the break n1. It can be seen that the effective permeability increases with the scaling break length ratio for all n1 values which are > 1. When the scaling exponent before the break n1 is larger, the increase of effective permeability is more significant. Since the scaling exponent after the break n2 is set to 1, the sharpest contrast of the break occurs when the scaling exponent before the break n1 is equal to 2 and the effect of the scaling break length ratio lb/lmax on the effective permeability is largest, which manifests as the most dramatic increase seen in Fig. 4.

Fig. 4
figure 4

The effective permeability of a fractal fracture network as a function of the scaling break length ratio lb/lmax at a few selected values of n1. The other parameters are: Df = 1.5, β1 = 0.002, lmin/lmax = 0.001, lmax = 5.0 m, and n2 = 1.0

Full size image

It is interesting to notice that all the effective permeability results converge to the same value at lb/lmax = 0.2, which means lb = 1 m. In this case the factor \(l_{b}^{{\left( {n_{1} - n_{2} } \right)}}\) is the same for all the n1 and n2 values, and as a result the effective permeability of fractal fracture network with different n1 values is the same. When lb/lmax is below 0.2, the effective permeability is larger for smaller n1, while for lb/lmax above 0.2, this trend is reversed.

The influence of the scaling break length ratio lb/lmax at a few selected values of the scaling exponent after the break n2 is shown in Fig. 5. In calculating the results shown in Fig. 5, the value of scaling exponent before the break n1 is set at 1.5. When n2 is also 1.5, which means there is not scaling break, the value of the scaling break length ratio lb/lmax is no longer relevant, which is reflected in the constant value of effective permeability with the changing value of lb/lmax shown in Fig. 5.

Fig. 5
figure 5

The effect of the scaling break length ratio lb/lmax on the effective permeability of a fractal fracture network at a few selected values of n2. The other parameters are: Df = 1.5, β1 = 0.002, lmin/lmax = 0.001, lmax = 5.0 m, and n1 = 1.5

Full size image

Overall, the effective permeability of fractal fracture network always increases with increasing lb/lmax. Since the scaling exponent n2 after the break is smaller than n1 before the break, an increasing lb/lmax means that the effect of smaller n2 in decreasing flow is reduced. The net result is that the effective permeability of fractal fracture network increases with increasing lb/lmax. Increasing n2 while keeping n1 at a fixed value at any value of lb/lmax means that the aperture of a fracture becomes larger. Therefore, the flow capacity becomes larger, which is reflected by the fact that the effective permeability of fractal fracture network also becomes larger, as demonstrated in Fig. 5.

The impact of fractal dimension Df on the effective permeability of fractal fracture network is plotted in Fig. 6, which shows that the effective permeability increases with Df. The increase in the effective permeability is mainly due to the increase of the fracture area with Df. For the extreme case when Df = dE, the porosity is 1 and the entire network is fractures. In other words, the interaction between the porosity and fracture area of the fracture network dictates the effective permeability.

Fig. 6
figure 6

The effect of the fractal dimension Df on the effective permeability of a fractal fracture network at a few selected values of lb/lmax. The other parameters are: β1 = 0.002, lmin/lmax = 0.001, lmax = 5.0 m, n1 = 1.5, and n2 = 1.0

Full size image

Figure 7 shows the effect of precision parameter t on the effective permeability reduction factor of fracture network. Since the precision parameter represents the overall extent of deviation of individual fracture angle from the mean, the net effect is always to reduce the effective permeability when any fracture orientation deviates from the mean, which is reflected by the fact that the reduction factor is always smaller than 1 shown in Fig. 7. We can see that the effect of aperture orientation is reflected in reducing the effective permeability. In each individual fracture, however, the flow is still in the direction parallel to the trace. When the precision parameter t is small, which means the orientation of factures is more disperse, the reduction of effective permeability is more significant. As it has been shown earlier, the reduction factor approaches 1/3 in the case of extreme orientation dispersion when the precision parameter t approaches 0, as shown in Fig. 7. At the other end when the precision parameter t is large, the reduction factor RF approaches 1, indicating no reduction in the effective permeability of fracture network. In other words, the reduction in the effective permeability of fracture network varies from 2/3 to 0 depending on the degree of orientation dispersion of fractures in the network.

Fig. 7
figure 7

The effect of the precision parameter t in the Fisher probability density function on the reduction factor of effective permeability of the fracture network

Full size image

The main objective of this study is to examine the effects of scaling break in the relationship between the aperture and trace length on the effective permeability by assuming that each fracture cuts through the model domain and that the trace length and aperture follow the fractal scaling law. Therefore, the solutions developed in this study are unable to calculate the effective permeability of fractured mass with variable fracture lengths in the general flow directions, which deserve further studies. The other main assumption is that the fractured domain behaves like a porous medium where Darcy’s law applies.

4 Conclusions

In this study, new analytical expressions were developed to compute the effective permeability of fractal fracture network in which there might be non-universal scaling between the fracture aperture and length. In addition, a new solution was also derived that includes the influence of fracture orientation dispersion on the effective permeability of fracture network. The main conclusions are summarized as follows:

  1. 1.

    Depending on where the scaling break occurs, the effective permeability of the fractal fracture network may either increase or decrease with the increasing scaling exponent before the break. When the scaling break occurs early, the effective permeability decreases with the scaling exponent before the break. However, if the scaling break occurs late, the effective permeability increases with the scaling exponent before the break.

  2. 2.

    The scaling exponent after the break also significantly affects the effective permeability of fractal fracture network. The effective permeability increases with the scaling exponent after the break. However, the extent of increase varies with the location of the scaling break. If the scaling break occurs early, the increase in the effective permeability is more significant.

  3. 3.

    The effective permeability of fractal fracture network varies with the location of scaling break. If the location of scaling break moves toward a longer length, the effective permeability of fractal fracture network increases.

  4. 4.

    The increase in the effective permeability with fractal dimension is mainly due to the increase of the fracture area with the fractal dimension.

  5. 5.

    The reduction in the effective permeability due to the individual fracture orientation variations becomes more significant if the fracture orientation becomes more disperse. The range of the reduction in the effective permeability varies from 0 to 2/3 depending on the degree of fracture orientation dispersion in the network.