Introduction

The dynamics of waveguide structures such as rods and beams can be described in terms of waves that travel along the structure: they are reflected from boundaries and reflected and transmitted at discontinuities. Beams can support both propagating waves and nearfield waves, whose amplitudes decay exponentially with distance. The nearfield waves can be pronounced in a region close to an excitation source or a discontinuity in the beam [1].

For linear structures, time harmonic incident waves produce time harmonic reflected and transmitted waves, but the situation is more complicated for nonlinear structures. This paper analyses the effects of both propagating and nearfield flexural waves in a Euler–Bernoulli beam incident on a nonlinear boundary. A wave approach is employed, and reflection coefficients for time harmonic incident waves are found when both nearfield and propagating waves are incident on the boundary. In contrast to the linear system, these reflection coefficients depend on the amplitudes of the incident waves.

For real structures, the vibration is often nonlinear, because of structural or material nonlinearity [16] or nonlinear boundaries, although the nonlinearity is often weak. However, linear approximations have been used for decades and are still relevant in many designs. Wave propagation and reflection in continuous structures with linear boundaries is relatively straightforward and has been studied extensively [2,3,4,5,6,7,8].

In [9, 10], wave propagation and reflection in structures with cracks and damage were studied. The transient dynamics of structures with localized nonlinearities was considered in [11,12,13,14,15], while the present paper concerns steady-state, harmonic wave behaviour. In particular, the focus of this work concerns the reflection of time harmonic waves from a nonlinear boundary. The axial vibration of a rod attached to a nonlinear boundary stiffness was studied for weak nonlinearity by considering only one incident wave and reflected waves of higher harmonics in [17]. It was shown that the nonlinear boundary stiffness affects the reflection coefficients significantly. As the number of harmonics retained in the analysis increases, the reflection coefficient for the fundamental (lowest) harmonic decreases, and there is a leakage of energy from the reflected wave of the fundamental frequency to the higher frequencies. In [17] the nonlinearity was assumed to be cubic, so that only odd harmonics were present in the equations. Subsequently, an analytical study was done in [18] using an averaging method to find an approximate solution for the reflection coefficients of higher harmonics when the linear force of the spring is comparable to the nonlinear force. In [17, 18], a wave approach was used to analyse the dynamic behaviour; however, there are other numerical and analytical methods to calculate wave reflections of joints [19,20,21] and boundaries of beams and rods, e.g., wave and finite element method (FEM). In [22], a wave FEM approach was applied to a composite structure with a nonlinear coupling between two waveguides to find the reflection and transmission coefficients. The equations were derived with 3 harmonics taken into account, and reflection coefficients were determined when only one propagating wave was incident on the boundary. The method was also used by Apalowo et al. [23] to detect damage in layered sandwich plates. The wave coefficients as functions of crack depth were measured and results were shown for different boundary conditions. Another method was introduced by Chouvion [24] for studying nonlinear vibration in continuous structures. The idea of this method is based on the ray-tracing method in which the structure is composed of an assembly of waveguide elements, including incident and reflected waves. The focus of this work was on the forced response of a rod and a specific kind of beam with nonlinear boundary stiffness and comparing the results with the finite element method. In a subsequent study by the author [25], the same method was applied to the nonlinear vibration of a beam with a nonlinear energy sink. The parameters for linear and nonlinear dynamic stiffness defined in [24, 25] were the same as the previous works [17, 18], i.e., the nonlinearity was assumed to be weak. Brennan et al. [26] used the same wave approach and parameters as in [17, 18] and studied the axial and flexural vibrations of a rod and a beam with a nonlinear boundary stiffness. Both softening and hardening behaviour were considered, and the nonlinearity was assumed to be weak. The reflection coefficients of the structures were studied for the case when there is only one incident propagating wave or one incident nearfield wave. It is known that in nonlinear vibration, time harmonic waves are reflected into waves at different frequencies. In [26], only reflected waves with the fundamental frequency were considered in the system. It was shown when the existence of time harmonic waves at only one frequency is considered, for a hardening stiffness boundary, similar to the linear case, the magnitude of the reflection coefficient for the propagating wave is always one, and nonlinearity only causes a change in the phase of the reflection coefficient.

In [27], the same models as in [26] were studied, and the natural frequencies of the rod and beam were calculated using the phase closure principle, again assuming time harmonic vibration at only one frequency. The focus was to show the effect of nonlinear boundary stiffness on the natural frequencies of the structure. It was shown that for negative stiffness, a dynamically unstable solution occurs. A more complex case for axial vibration was studied when waves of more than one frequency are incident on the boundary [28]. It was seen that multiple incident propagating waves can have a profound effect on the reflection coefficients. Furthermore, when the amplitudes of all the incident waves at the boundary are pure real, the reflection coefficient of the 1st harmonic can be greater than one. A general solution for axial and flexural elastic waves was developed in [29], including all incident and reflected propagating waves. First, results were shown for the case when there is only one incident propagating wave in the system and by retention of higher harmonic reflected waves. The case with essential nonlinearity, i.e., when there is no linear stiffness in the system, was considered and results were shown for the case of multiple incident propagating waves. For some specific values, it was seen that multiple solutions occur for the reflection coefficients. In this study, the effects of incident nearfield waves were not considered. The effect of nearfield waves in a monotonic chain was studied in [30] using a perturbation method. Abdi et al. [31] studied the effect of the nonlinear boundary stiffness on the reflection coefficients when there is only one incident propagating wave in the system, but the case with multiple incident propagating waves in the presence of nearfield waves was not studied. This paper can be considered as an extension of [28,29,30,31] to show the effects of multiple incident nearfield and propagating waves and results are compared to those when only propagating waves are incident on the boundary. The pronounced nearfield waves incident on a boundary can be due to a discontinuity or excitation close to the boundary. The nearfield waves can have a significant effect on the dynamic behaviour of the system and affect the wave reflection from the boundary.

The paper is organized as follows. In the next section, the governing equations are derived, and a wave approach is introduced including reflected and incident propagating and nearfield waves at many frequencies, and reflection coefficients are defined with respect to the amplitude of the 1st incident propagating wave. Real world examples in which effects of incident nearfield waves on the boundary can be relevant are also discussed. In the following section, the case when a point excitation is applied close to the boundary is considered as an example. In the next section, equations specifying the nonlinear boundary are introduced, and relations governing wave motion in the beam for the case of cubic nonlinearity are developed. In the following section, numerical results are shown for different cases by retaining different number of propagating and nearfield incident and reflected waves. Furthermore, numerical results for the net excited waves are shown and interpreted for the case when a point force is applied to the beam. Finally, the last section is the conclusion.

Equations of Motion

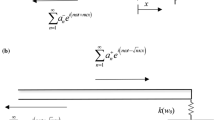
The vibrational behaviour of a semi-infinite Euler–Bernoulli beam lying along the x-axis is considered. The beam is attached to a spring with nonlinear boundary stiffness at x = 0 as shown in Fig. 1 and undergoes flexural vibrations with transverse displacement w(x,t). The governing equation of motion for flexural vibrations of the beam is [2]

$$EI\frac{{\partial^{4} w(x,t)}}{{\partial x^{4} }} + \rho S\frac{{\partial^{2} w(x,t)}}{{\partial t^{2} }} = 0,$$
(1)

where \(\rho\), S, E, I are the density, cross-sectional area, elastic modulus and second moment of area of the cross section.

Fig. 1
figure 1

Waves in a semi-infinite beam with incident and reflected propagating and nearfield waves at the boundary

Full size image

The nonlinear spring at x = 0 exerts a force on the beam. It is now assumed that an infinite number of propagating waves \(a_{n}^{ + }\) and nearfield waves \(a_{N,n}^{ + }\) are incident on the boundary at x = 0. The waves are time harmonic with frequencies \(n\omega\), where \(\omega\) is the frequency of the fundamental and the subscript n = 1,2,3,… indicates the harmonic number. The wavenumber \(\kappa_{n}\) of the nth harmonic at frequency \(n\omega\) is \(\sqrt n \kappa\), with \(\kappa = \sqrt \omega\sqrt[4]{(\rho S/EI)}\).

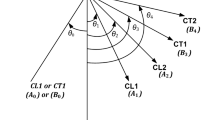
The incident nearfield waves can be produced by various reasons. First, there might be time harmonic point force and/or moment excitation at some point close to the boundary as shown in Fig. 2a. This generates time harmonic positive and negative-going propagating waves \(q^{ \pm }\) and nearfield waves \(q_{N}^{ \pm }\), the positive going waves being incident on the boundary and subsequently reflected. Second, there might be some discontinuity attached close to or at the boundary as shown in Fig. 2b. Waves incident on this discontinuity \(b_{n}^{ + }\) are reflected (\(b_{n}^{ - }\) and \(b_{N,n}^{ - }\)) and transmitted (\(c_{n}^{ + }\) and \(c_{N,n}^{ + }\)), with the result that the region between the discontinuity and the boundary carries a wavefield comprising propagating and nearfield waves of various frequencies, leading to the set of waves \(a_{n}^{ \pm }\) and \(a_{N,n}^{ \pm }\) being incident on the boundary. Note that if the excitation or the discontinuity are located at \(x = - x_{0}\) then the amplitudes of the nearfields decay by the factor \(\exp \left( { - \sqrt n \kappa x_{0} } \right)\) and are hence only significant if the excitation or discontinuity is close to the boundary.

Fig. 2
figure 2

Incident, reflected and transmitted waves produced by a a point force or moment applied to the beam close to a boundary b a discontinuity close to a boundary

Full size image

The waves incident on the boundary (Fig. 1) produce an infinite number of reflected waves \(a_{n}^{ - }\) and \(a_{N,n}^{ - }\) at the same frequencies. The flexural displacement of the beam shown in Fig. 1 can thus be written as a superposition of incident and reflected waves

$$w\left( {x,t} \right) = \sum\limits_{n = 1}^{\infty } {a_{n}^{ + } e^{{i\left( {n\omega t - \sqrt n \kappa x} \right)}} } + \sum\limits_{n = 1}^{\infty } {a_{N,n}^{ + } e^{in\omega t} e^{ - \sqrt n \kappa x} } + \sum\limits_{n = 1}^{\infty } {a_{n}^{ - } e^{{i\left( {n\omega t + \sqrt n \kappa x} \right)}} } + \sum\limits_{n = 1}^{\infty } {a_{N,n}^{ - } e^{in\omega t} } e^{\sqrt n \kappa x} + {\text{CC}},$$
(2)

where CC denotes the complex conjugate of the preceding terms. The wave amplitudes are complex and can be written as

$$a_{n}^{ + } = \left| {a_{n}^{ + } } \right|e^{{i\Phi_{n} }} ,\,\,a_{N,n}^{ + } = \left| {a_{N,n}^{ + } } \right|e^{{i\psi_{n} }} ,\,\,a_{n}^{ - } = \left| {a_{n}^{ - } } \right|e^{{i\phi_{n} }} ,\,\,a_{N,n}^{ - } = \left| {a_{N,n}^{ - } } \right|e^{{i\theta_{n} }} .$$
(3)

For simplicity and without loss of generality,\(\Phi_{1} = 0\) [29], so that \(a_{1}^{ + }\) is real. The wave amplitudes are now normalized with respect to \(a_{1}^{ + }\), giving the incident propagating wave amplitude ratios \(\alpha_{n}\), reflection coefficients of propagating waves rn, reflection coefficients of nearfield waves \(r_{N,n}\), and ratio of the incident propagating waves and incident nearfield waves \(\mu_{n}\) defined as

$$\alpha_{n} = {{a_{n}^{ + } } \mathord{\left/ {\vphantom {{a_{n}^{ + } } {a_{1}^{ + } }}} \right. \kern-0pt} {a_{1}^{ + } }},\,\,\mu_{n} = {{a_{N,n}^{ + } } \mathord{\left/ {\vphantom {{a_{N,n}^{ + } } {a_{1}^{ + } }}} \right. \kern-0pt} {a_{1}^{ + } }},\,{{r_{n} = \,a_{n}^{ - } } \mathord{\left/ {\vphantom {{r_{n} = \,a_{n}^{ - } } {a_{1}^{ + } }}} \right. \kern-0pt} {a_{1}^{ + } }},\,\,\,r_{N,n} = {{a_{N,n}^{ - } } \mathord{\left/ {\vphantom {{a_{N,n}^{ - } } {a_{1}^{ + } }}} \right. \kern-0pt} {a_{1}^{ + } }}.$$
(4)

Hence, Eq. (2) becomes

$$w\left( {x,t} \right) = a_{1}^{ + } \left( {\sum\limits_{n = 1}^{\infty } {\alpha_{n} e^{{i\left( {n\omega t - \sqrt n \kappa x} \right)}} } + \sum\limits_{n = 1}^{\infty } {\mu_{n} e^{in\omega t} e^{ - \sqrt n \kappa x} } + \sum\limits_{n = 1}^{\infty } {r_{n} e^{{i\left( {n\omega t + \sqrt n \kappa x} \right)}} } + \sum\limits_{n = 1}^{\infty } {r_{N,n} e^{in\omega t} } e^{\sqrt n \kappa x} + CC} \right).$$
(5)

Waves Due to Point Excitation Close to the Boundary

Here we consider the case when a point time harmonic force \(F_{0} \exp \left( {i\omega t} \right)\) and/or moment \(M_{0} \exp \left( {i\omega t} \right)\) are applied at a small distance x0 from the boundary. When only a force F0 is applied at the beam, the excited wave amplitudes are [3]

$$\left\{ \begin{gathered} q^{ + } \hfill \\ q_{N}^{ + } \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} q^{ - } \hfill \\ q_{N}^{ - } \hfill \\ \end{gathered} \right\} = \frac{{ - F_{0} }}{{4EI\kappa^{3} }}\left\{ \begin{gathered} i \hfill \\ 1 \hfill \\ \end{gathered} \right\},$$
(6)

while when only a moment M0 is applied to the beam, the excited wave amplitudes are [3]

$$\left\{ \begin{gathered} q^{ + } \hfill \\ q_{N}^{ + } \hfill \\ \end{gathered} \right\} = - \left\{ \begin{gathered} q^{ - } \hfill \\ q_{N}^{ - } \hfill \\ \end{gathered} \right\} = \frac{{M_{0} }}{{4EI\kappa^{2} }}\left\{ {\begin{array}{*{20}c} 1 \\ { - 1} \\ \end{array} } \right\}.$$
(7)

The positive-going waves travel to the boundary, so that the incident propagating wave is \(q^{ + } \exp \left( { - i\kappa x_{0} } \right)\), while the amplitude of the incident nearfield is \(q_{N}^{ + } \exp \left( { - \kappa x_{0} } \right)\). For the case of point force excitation, the ratio of the amplitudes of the incident nearfield and propagating wave is

$$\mu_{1} = e^{{ - \kappa x_{0} }} e^{{ + i\left( {\kappa x_{0} - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}} \right)}} .$$
(8)

Note that for the case considered, there are no other propagating waves incident on the force location. When a force is applied at the end of the beam (x0 = 0), \(\mu_{1} = - i\). Similarly, for the case when a moment is applied at the end of the beam (x0 = 0), \(\mu_{1} = - 1\). For the case when both force and moment are applied at the end of the beam [32] excited waves can be represented as a superposition of the waves excited by the force alone and the moment alone.

As can be seen in Fig. 2a, the resulting net upstream excited propagating wave at frequency \(\omega\) is the superposition of the wave reflected from the boundary and the upstream wave generated by the point excitation. Assuming \(q^{ + }\) is real, the net upstream wave at x0 is

$$q^{ - } + r\left( {q^{ + } e^{{ - i\kappa x_{0} }} } \right)e^{{ - i\kappa x_{0} }} .$$
(9)

In “Point excitation”, numerical examples are presented for the case when only a force is applied at the end of the beam (x0 = 0). For this case, from (6), \(q^{ - } = q^{ + }\) and the net upstream wave, (9) becomes \(q^{ - } \left( {1 + r} \right)\).

Nonlinear Stiffness at the Boundary

At the boundary (Fig. 1), the shear force in the beam equals the force on the boundary. The stiffness at the boundary k(w0) is now assumed to be a polynomial function of the displacement at x = 0 with constant coefficients km, so that [29]

$$V\left( {0,t} \right) = - EI\frac{{\partial^{3} w\left( {0,t} \right)}}{{\partial x^{3} }} = - \sum\limits_{m = 1}^{M} {k_{m} w_{0}^{m} \left( t \right);\,\,\,\,\,} w_{0} \left( t \right) = w\left( {0,t} \right).$$
(10)

The nonlinear boundary stiffness can be due to different sources of nonlinearity, including geometry, material etc. In this paper, we aim to get insights into the effects of nearfield waves incident on the boundary, so a spring with stiffness a cubic function of \(w\left( {0,t} \right)\) is considered for simplicity, so that

$$V\left( {0,t} \right) = - k_{1} w_{0} - k_{3} w_{0}^{3} .$$
(11)

The bending moment M at the end of the beam is zero and hence

$$M\left( {0,t} \right) = EI\frac{{\partial^{2} w\left( {0,t} \right)}}{{\partial x^{2} }} = 0.$$
(12)

By gathering terms in each frequency, Eq. (12) leads to the relation:

$$r_{N,\,n} = \alpha_{n} + r_{n} - \mu_{n} .$$
(13)

Substituting the transverse displacement (5) into the boundary condition (11) gives

$$\begin{gathered} EI\kappa^{3} \left[ {\left( {\sum\limits_{n = 1,3,5, \ldots }^{\infty } {n\sqrt n \left[ {\,\alpha_{n} \left( {1 + i} \right) + r_{n} \left( {1 - i} \right) - 2\mu_{n} } \right]\,} e^{in\omega t} } \right) + CC} \right] \hfill \\ - 2k_{1} \left[ {\left( {\sum\limits_{n = 1,3,5, \ldots }^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + CC} \right] - 8k_{3} a_{1}^{ + 2} \left[ {\left( {\sum\limits_{n = 1,3,5, \ldots }^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + CC} \right]^{3} = 0. \hfill \\ \end{gathered}$$
(14)

Dimensionless parameters

$$\Omega = {\omega \mathord{\left/ {\vphantom {\omega {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }},\,K = {{k_{1} } \mathord{\left/ {\vphantom {{k_{1} } {\omega_{0} Z}}} \right. \kern-0pt} {\omega_{0} Z}},\,A = {{k_{3} a_{1}^{ + 2} } \mathord{\left/ {\vphantom {{k_{3} a_{1}^{ + 2} } {\omega_{0} Z}}} \right. \kern-0pt} {\omega_{0} Z}}$$
(15)

are now defined, where \(\omega_{0}\) is a reference frequency and \(Z = \sqrt[4]{{EI\left( {\rho S} \right)^{3} }}\sqrt {\omega_{0} }\) [29]. When the cross section is rectangular with thickness h, at the reference frequency,\(\omega_{0}\), the wavenumber, \(\kappa_{0}\) is \({1 \mathord{\left/ {\vphantom {1 h}} \right. \kern-0pt} h}\)[31]. In Eq. (15), K and A denote the effects of the linear and nonlinear boundary stiffnesses and \(\Omega\) is the frequency ratio. The equation of motion thus becomes

$$\begin{gathered} \Omega^{3/2} \left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {n\sqrt n \left[ {\,\alpha_{n} \left( {1 + i} \right) + r_{n} \left( {1 - i} \right) - 2\mu_{n} } \right]\,} e^{in\omega t} } \right) + {\text{CC}}} \right] \hfill \\ - 2K\left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + {\text{CC}}} \right] - 8A\left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + {\text{CC}}} \right]^{3} = 0. \hfill \\ \end{gathered}$$
(16)

As can be seen, the reflection coefficient of the nth propagating harmonic, rn, depends on the dimensionless parameters (15) and incident wave coefficients \(\alpha_{n}\) and \(\mu_{n}\). The infinite sums are then truncated at some finite value N and solved numerically. The harmonic balance method is used to collect the coefficients of different harmonics. It is known that retaining higher harmonics will give a more accurate approximation for the numerical solution, but it has been shown that the qualitative behaviour is similar for N = 3,5,7,… [29]. Hence, the numerical results are shown below by taking into account only the first and third harmonics, N = 3.

Equation (16) can be written as

$$\begin{gathered} \left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {n\sqrt n \left[ {\,\alpha_{n} \left( {1 + i} \right) + r_{n} \left( {1 - i} \right) - 2\mu_{n} } \right]\,} e^{in\omega t} } \right) + {\text{CC}}} \right] \hfill \\ - 2\eta \left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + {\text{CC}}} \right] - 8\gamma \left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + {\text{CC}}} \right]^{3} = 0 \hfill \\ \end{gathered}$$
(17)

where \(\eta = {K \mathord{\left/ {\vphantom {K {\Omega^{3/2} }}} \right. \kern-0pt} {\Omega^{3/2} }}\) and \(\gamma = {A \mathord{\left/ {\vphantom {A {\Omega^{3/2} }}} \right. \kern-0pt} {\Omega^{3/2} }}\). For the case of essential nonlinearity, when K = 0, Eq. (17) becomes

$$\left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {n\sqrt n \left[ {\,\alpha_{n} \left( {1 + i} \right) + r_{n} \left( {1 - i} \right) - 2\mu_{n} } \right]\,} e^{in\omega t} } \right) + {\text{CC}}} \right] - 8\gamma \left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + {\text{CC}}} \right]^{3} = 0.$$
(18)

Numerical Examples

No Incident Nearfield Waves

For the case when there are only incident propagating waves and no incident nearfield waves (\(\mu_{n} = 0\)), truncating Eq. (18) at N = 3 results in

$$\begin{gathered} \left[ {\left( {1 + i} \right) + \left( {1 - i} \right)r_{1} } \right] + \hfill \\ - 24\gamma \left[ {\left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)^{2} + 2\left( {r_{1} + 1} \right)\left( {\alpha_{3} \overline{\alpha }_{3} + r_{3} \overline{r}_{3} + \alpha_{3} \overline{r}_{3} + \overline{\alpha }_{3} r_{3} } \right) + \left( {\alpha_{3} + r_{3} } \right)\left( {\overline{r}_{1} + 1} \right)^{2} } \right] = 0, \hfill \\ \end{gathered}$$
(19)
$$\begin{gathered} 3\sqrt 3 \,\left[ {\alpha_{3} \left( {1 + i} \right) + r_{3} \left( {1 - i} \right)} \right] + \hfill \\ - 8\gamma \left[ {\left( {r_{1} + 1} \right)^{3} + 3\left( {r_{3} + \alpha_{3} } \right)^{2} \left( {\overline{r}_{3} + \overline{\alpha }_{3} } \right) + 6\left( {r_{1} + 1} \right)\left( {\overline{r}_{1} + 1} \right)\left( {r_{3} + \alpha_{3} } \right)} \right] = 0. \hfill \\ \end{gathered}$$
(20)

This case was studied in detail in [29]. Some numerical results are shown in Fig. 3 for the case of essential nonlinearity and when retaining two propagating incident and reflected waves. As can be seen in Fig. 3, for \(\left| {\alpha_{3} } \right| = 1\) the minimum reflection coefficient for the 1st harmonic \(\left| {r_{1} } \right|_{\min } \simeq 0.44\) and occurs at \(\Phi_{3} = \pi\), while \(\left| {r_{1} } \right|_{\max } \simeq 2.4\) and occurs at \(\Phi_{3} = 0\). When r1 is maximum r3 is minimum due to the energy conservation. When \(\gamma \ll 1\) and \(\gamma \gg 1\), \(\left| {r_{1} } \right|\) and \(\left| {r_{3} } \right|\) asymptote to 1.

Fig. 3
figure 3

The magnitudes of the reflection coefficients of the 1st and 3rd harmonics \(\left| {\alpha_{3} } \right| = 1\) as functions of \(\gamma\); a |r1|, b |r3|. Dotted blue lines \(\Phi_{3} = 0\); red straight line \(\Phi_{3} = \pi\) (colour figure online)

Full size image

One Incident Propagating Wave and One Incident Nearfield Wave

The effect of nearfield waves is now considered. For the case when there are one propagating wave and one nearfield wave incident on the boundary \(\left( {\mu_{1} \ne 0,\mu_{n} = 0;\,\,(n > 1)} \right)\) with the reflected waves with frequencies \(\omega\) and \(3\omega\), Eq. (16) becomes

$$\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \left( {i - ir_{1} + 1 + r_{1} - 2\mu_{1} } \right) - 2K\left( {1 + r_{1} } \right) - 24A\left( {\left( {1 + r_{1} } \right)^{2} \left( {1 + \overline{r}_{1} } \right) + r_{3} \left( {1 + \overline{r}_{1} } \right)^{2} + 2r_{3} \overline{r}_{3} \left( {1 + r_{1} } \right)} \right) = 0,$$
(21)
$$3\sqrt 3 \Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} r_{3} \left( {1 - i} \right) - 2Kr_{3} - 8A\left( {\left( {1 + r_{1} } \right)^{3} + 3\overline{r}_{3} r_{3}^{2} + 6r_{3} \left( {1 + r_{1} } \right)\left( {1 + \overline{r}_{1} } \right)} \right) = 0.$$
(22)

when the system is linear

$$r_{1} = r_{{{\text{lin}}}} = \frac{{1 - \left( {1 - 2\eta } \right)i}}{{1 + \left( {1 - 2\eta } \right)i}} + \frac{{2\mu_{1} i}}{{1 + \left( {1 - 2\eta } \right)i}};\,\,\,\,\,\,\,\,\,\,\,r_{3} = 0.$$
(23)

When \(\eta \ll 1\), \(r_{1} \cong \frac{{2\mu_{1} - \left( {i + 1} \right)}}{1 - i},\) while when \(\eta \gg 1\), \(r_{1}\) asymptotes to − 1 as shown in Fig. 4 for two cases: when a force \(\left( {\psi_{1} = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}} \right)\) or a moment \(\left( {\psi_{1} = \pi } \right)\) is applied at the end of the beam. As illustrated, \(\left| {r_{1} } \right|_{\max } \simeq 3\) and occurs at \(\psi_{1} = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\), while \(\left| {r_{1} } \right|_{\min } \simeq 0.41\) and occurs at \(\psi_{1} = \pi\).

Fig. 4
figure 4

The magnitude of the reflection coefficients of the 1st as a function of \(\eta\) for various \(\psi_{1}\) with A = 0 and \(\left| {\mu_{1} } \right| = 1\)

Full size image

For the case of essential nonlinearity, Eqs. (21) and (22) become

$$i + 1 + r_{1} \left( {1 - i} \right) - 2\mu_{1} - 24\gamma \left( {\left( {1 + r_{1} } \right)^{2} \left( {1 + \overline{r}_{1} } \right) + r_{3} \left( {1 + \overline{r}_{1} } \right)^{2} + 2r_{3} \overline{r}_{3} \left( {1 + r_{1} } \right)} \right) = 0,$$
(24)
$$3\sqrt 3 r_{3} \left( {1 - i} \right) - 8\gamma \left( {\left( {1 + r_{1} } \right)^{3} + 3\overline{r}_{3} r_{3}^{2} + 6r_{3} \left( {1 + r_{1} } \right)\left( {1 + \overline{r}_{1} } \right)} \right) = 0.$$
(25)

It is shown that as \(\left| {\mu_{1} } \right|\) increases, |r1| increases [31]. Numerical results are shown in Fig. 5, for the same cases as in Fig. 4. As can be seen for \(\left| {\mu_{1} } \right| = 1\), \(\left| {r_{1} } \right|_{\max } \simeq 2.85\) and occurs at \(\psi_{1} = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\), while \(\left| {r_{1} } \right|_{\min } \simeq 0.17\) and occurs at \(\psi_{1} = \pi\). Due to the effects of nonlinearity \(\left| {r_{1} } \right|_{\min }\) and \(\left| {r_{1} } \right|_{\max }\) decrease and energy leaks from the 1st harmonic to the 3rd harmonic. Comparing \(\left| {r_{1} } \right|_{\max }\) and \(\left| {r_{1} } \right|_{\min }\) in Figs. 3 and 5 shows that the effect of nonlinearity is more pronounced for the case when there is a nearfield wave incident on the boundary than the case with only propagating waves are incident.

Fig. 5
figure 5

The magnitudes of the reflection coefficients of the 1st and 3rd harmonics with \(\left| {\mu_{1} } \right| = 1\) as functions of \(\gamma\); a |r1|, b |r3|. Dotted blue lines \(\psi_{1} = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\); red straight line \(\psi_{1} = \pi\) (colour figure online)

Full size image

Two Incident Propagating Waves and One Incident Nearfield Wave

It is shown that with multiple incident propagating waves the effect of nonlinearity is stronger than the case of one incident wave; furthermore, presence of the nearfield waves in the system pronounces the effects of nonlinearity. Now, the aim is to consider both effects in the numerical simulation, i.e., multiple incident propagating waves in the presence of incident nearfield waves. Hence, a more complex case is considered with three incident waves including two propagating waves and one nearfield wave. Using Eq. (18) for essential nonlinearity and with the reflected waves of the 1st and 3rd harmonics results in

$$\begin{gathered} \left[ {\left( {1 + i} \right) + \left( {1 - i} \right)r_{1} - 2\mu_{1} } \right] + \hfill \\ - 24\gamma \left[ {\left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)^{2} + 2\left( {r_{1} + 1} \right)\left( {\alpha_{3} \overline{\alpha }_{3} + r_{3} \overline{r}_{3} + \alpha_{3} \overline{r}_{3} + \overline{\alpha }_{3} r_{3} } \right) + \left( {\alpha_{3} + r_{3} } \right)\left( {\overline{r}_{1} + 1} \right)^{2} } \right] = 0, \hfill \\ \end{gathered}$$
(26)
$$\begin{gathered} 3\sqrt 3 \left[ {\alpha_{3} \left( {1 + i} \right) + r_{3} \left( {1 - i} \right)} \right] + \hfill \\ - 8\gamma \left[ {\left( {r_{1} + 1} \right)^{3} + 3\left( {r_{3} + \alpha_{3} } \right)^{2} \left( {\overline{r}_{3} + \overline{\alpha }_{3} } \right) + 6\left( {r_{1} + 1} \right)\left( {\overline{r}_{1} + 1} \right)\left( {r_{3} + \alpha_{3} } \right)} \right] = 0. \hfill \\ \end{gathered}$$
(27)

Now, the reflection coefficients depend on \(\left| {\alpha_{3} } \right|,\,\Phi_{3} ,\,\left| {\mu_{1} } \right|,\,\psi_{1}\) and \(\gamma\). In Fig. 6, results are shown for the case with \(\,\left| {\mu_{1} } \right| = 1\), \(\left| {\alpha_{3} } \right| = 1\), \(\psi_{1} = 0\), and different values of \(\Phi_{3}\), as functions of \(\gamma\). As can be seen, the phase difference between the propagating waves has a profound effect on the reflection coefficients. As illustrated for some values of \(\Phi_{3}\), \(\left| {r_{1} } \right|_{\max }\) can be larger than the previous case which shows that with three incident waves the effects of nonlinearity can be stronger. In contrast to the case when there is no nearfield in the system, \(\left| {r_{1} } \right|_{\max }\) occurs when both propagating waves are in anti-phase, i.e., at \(\Phi_{3} = \pi\). At this point \(\left| {r_{1} } \right|_{\max } \simeq 4\), while \(\left| {r_{3} } \right|_{\min } \simeq 0.74\).

Fig. 6
figure 6

The magnitudes of the reflection coefficients of the 1st and 3rd harmonics with \(\left| {\mu_{1} } \right| = 1\), \(\left| {\alpha_{3} } \right| = 1\), \(\psi_{1} = 0\) and different values of \(\Phi_{3}\) as functions of \(\gamma\); a |r1|, b |r3|

Full size image

In Fig. 7, results are shown with \(\left| {\mu_{1} } \right| = 1\), \(\left| {\alpha_{3} } \right| = 1\),\(\Phi_{3} = 0\) and different values of \(\psi_{1}\) as functions of \(\gamma\). It can be noted that as the phase difference between the incident nearfield wave and the 1st propagating incident wave decreases from 0 to \(- {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\), \(\left| {r_{1} } \right|_{\max }\) increases. Figure 8 shows the results for the phase differences \(\Phi_{3} = 0,\pi\) and \(\psi_{1} = {{0, - \pi } \mathord{\left/ {\vphantom {{0, - \pi } 2}} \right. \kern-0pt} 2},\,\pi\). In Fig. 8, when \(\psi_{1} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0pt} 2}\) and \(\Phi_{3} = 0\), maximum of \(\left| {r_{1} } \right|\) occurs; \(\left| {r_{1} } \right|_{\max } \simeq 4.42\), while when \(\psi_{1} = \pi\) and \(\Phi_{3} = \pi\), minimum of \(\left| {r_{1} } \right|\) occurs;\(\left| {r_{1} } \right|_{\min } \simeq 0.13\).

Fig. 7
figure 7

The magnitudes of the reflection coefficients of the 1st and 3rd harmonics with \(\left| {\mu_{1} } \right| = 1\), \(\left| {\alpha_{3} } \right| = 1\),\(\Phi_{3} = 0\) and different values of \(\psi_{1}\) as functions of \(\gamma\); a |r1|, b |r3|

Full size image
Fig. 8
figure 8

The magnitudes of the reflection coefficients of the 1st and 3rd harmonics with \(\left| {\mu_{1} } \right| = 1\), \(\left| {\alpha_{3} } \right| = 1\), and different values of \(\psi_{1}\) and \(\Phi_{3}\) as functions of \(\gamma\); a |r1|, b |r3|

Full size image

In Fig. 9, results are shown with \(\left| {\mu_{1} } \right| = 1\), \(\psi_{1} = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\),\(\Phi_{3} = 0\) and different values of \(\left| {\alpha_{3} } \right|\) as functions of \(\gamma\). As illustrated with increasing \(\left| {\alpha_{3} } \right|\), \(\left| {r_{1} } \right|_{\max }\) increases. When \(\left| {\alpha_{3} } \right| = 2\), \(\left| {r_{1} } \right|_{\max }\) is about 5.5 which is significantly greater than the case when only propagating waves are incident on the boundary.

Fig. 9
figure 9

The magnitudes of the reflection coefficients of the 1st and 3rd harmonics with,\(\left| {\mu_{1} } \right| = 1\), \(\psi_{1} = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\),\(\Phi_{3} = 0\) and different values of \(\left| {\alpha_{3} } \right|\) as functions of \(\gamma\); a |r1|, b |r3|

Full size image

Point Excitation

It is now assumed that there are only incident and reflected waves generated by a point excitation in the system as shown in Fig. 2b. When incident waves with only frequency \(\omega\) exist in the system, i.e., for the case with only one harmonic, the governing equation is

$$\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \left( {i - ir_{1} + 1 + r_{1} - 2\mu_{1} } \right) - 2K\left( {1 + r_{1} } \right) - 24A\left( {1 + r_{1} } \right)^{2} \left( {1 + \overline{r}_{1} } \right) = 0,$$
(28)

or

$$\left( {i - ir_{1} + 1 + r_{1} - 2\mu_{1} } \right) - 2\eta \left( {1 + r_{1} } \right) - 24\gamma \left( {1 + r_{1} } \right)^{2} \left( {1 + \overline{r}_{1} } \right) = 0,$$
(29)

If waves with frequencies \(3\omega\) are generated, then we have

$$i + 1 + r_{1} \left( {1 - i} \right) - 2\mu_{1} - 2\eta \left( {1 + r_{1} } \right) - 24\gamma \left( {\left( {1 + r_{1} } \right)^{2} \left( {1 + \overline{r}_{1} } \right) + r_{3} \left( {1 + \overline{r}_{1} } \right)^{2} + 2r_{3} \overline{r}_{3} \left( {1 + r_{1} } \right)} \right) = 0,$$
(30)
$$3\sqrt 3 r_{3} \left( {1 - i} \right) - 2\eta r_{3} - 8\gamma \left( {\left( {1 + r_{1} } \right)^{3} + 3\overline{r}_{3} r_{3}^{2} + 6r_{3} \left( {1 + r_{1} } \right)\left( {1 + \overline{r}_{1} } \right)} \right) = 0.$$
(31)

As mentioned in “Waves due to point excitation close to the boundary”, the net upstream excited wave when a force is applied at the end of the beam is \(q^{ - } \left( {1 + r_{1} } \right)\). In this section, numerical results for \(\left| {1 + r_{1} } \right|\) are shown for the linear and nonlinear cases. From Eq. (23) for the linear case

$$1 + r_{{{\text{lin}}}} = \frac{{2\left( {1 + \mu_{1} i} \right)}}{{1 + \left( {1 - 2\eta } \right)i}}.$$
(32)

For this case, when \(\psi_{1} = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\) or \(\mu_{1} = - i\), \(\left| {1 + r_{1} } \right|_{\max } = 4\) and occurs at \(\eta = 0.5\). When \(\eta \ll 1\), \(1 + r_{1} \cong \mu_{1} \left( {1 + i} \right) + 1 - i,\) while when \(\eta \gg 1\), \(\left| {1 + r_{1} } \right|\) asymptotes to 0. For the nonlinear case, results are shown in Fig. 10 for the case with essential nonlinearity, when only a force is applied at the end of the beam. It can be seen that at some value of \(\gamma\), the nonlinearity is stronger, i.e., \(\left| {1 + r_{1} } \right|\) has a maximum which is larger than the cases of \(\gamma \ll 1\)(free end) and \(\gamma \gg 1\)(fixed end). As illustrated when \(\mu_{1} = - i\) and only the 1st reflected wave is retained \(\left| {1 + r_{1} } \right|_{\max } = 4\), while when the 1st and 3rd harmonics are retained, \(\left| {1 + r_{1} } \right|_{\max } = 3.85\) and due to the nonlinearity energy leaks to the 3rd harmonic. In Fig. 11 results are shown for different values of \(\eta\) by retaining the 1st and 3rd harmonic reflected waves. As illustrated, as \(\eta\) decreases, the effects of nonlinearity become more pronounced and \(\left| {1 + r_{1} } \right|_{\max }\) decreases.

Fig. 10
figure 10

The magnitudes of \(\left( {1 + r_{1} } \right)\) for the case with essential nonlinearity,\(\eta = 0\) with, \(\mu_{1} = - i\) as a function of \(\gamma\) (by retaining the 1st and 3rd harmonics)

Full size image
Fig. 11
figure 11

The magnitudes of \(\left( {1 + r_{1} } \right)\) for the nonlinear case with,\(\mu_{1} = - i\), and different values of \(\eta\) as a function of \(\gamma\) (by retaining the 1st and 3rd harmonics)

Full size image

Conclusion

This paper was concerned the dynamic behaviour of a beam with a nonlinear boundary stiffness. A wave approach was used, including all propagating and nearfield incident and reflected waves. The aim was to study the effect of incident nearfield wave when multiple incident propagating waves are incident on the boundary. An infinite number of equations were derived, then truncated at some finite value. Results were shown for different cases and different number of incident propagating and nearfield waves. It was seen that the incident nearfield waves can have a profound effect on the reflection coefficient in flexural vibrations of the beam. The minimum and maximum reflection coefficient of the 1st harmonic can be significantly smaller or larger than the case when only propagating incident waves exist in the system. Furthermore, multiple incident waves pronounce the effects of nonlinearity. Results showed that the presence of the incident nearfield wave completely changes the reflection coefficient behaviour; for example, in the absence of incident nearfield waves, the minimum reflection coefficient of the 1st harmonic occurs when \(\Phi_{3} = \pi\), while in the presence of incident nearfield wave this can occur at \(\Phi_{3} = 0\). It should be noted that retaining higher harmonics has a little effect on this minimum and can be neglected. Furthermore, the effects of nonlinearity on the net propagating excited wave were shown for N = 1 and N = 3. For the case of essential nonlinearity and when only a force is applied at the end the beam, \(\left| {1 + r_{1} } \right|_{\max } = 4\) for N = 1, while this amount can be decreased to 3.85 for N = 3.