Reflection of waves in a waveguide from a boundary with nonlinear stiffness: application to axial and flexural vibrations

Abstract

The reflection of time-harmonic waves in a waveguide with a nonlinear boundary stiffness is considered with applications to rods and beams. Incident waves at frequencies that are multiples of a fundamental frequency give rise to reflected propagating and nearfield waves at the same frequencies. An infinite set of equations is developed for the reflection coefficients, which depend on the amplitudes and phases of the incident waves. Nonlinear boundary conditions are applied, and equations is truncated by using the harmonic balance method and solved numerically. The case of zero linear boundary stiffness, i.e. essential nonlinearity, is studied. First, the case where there is only one incident wave is considered. An approximate solution is found when retaining only two reflected waves. Numerical examples are presented, energy being seen to leak into the higher harmonics. The minimum magnitudes of the reflection coefficients of axial and flexural vibrational waves at the fundamental frequency and the maximum energy that can leak into the higher harmonics are determined. Accuracy and convergence when retaining different numbers of reflected harmonics are illustrated. The case of two incident waves is then considered. Multiple incident waves affect the leakage of energy to higher harmonics and can have a significant effect on the reflection coefficient for the fundamental harmonic. With some parameters, a much lower reflection coefficient is obtained for the wave at the fundamental frequency as compared to the case of one incident wave. It is seen that with two incident flexural waves, the reflection coefficients can be multi-valued for certain values of the system parameters. A numerical study is performed to show the region of multiple solutions.

1 Introduction

Exploiting nonlinearity to control vibrations in elastic structures such as rods and beams is of interest to academia and industry. This paper concerns the reflection of time-harmonic axial and flexural waves in a thin rod and an Euler–Bernoulli beam from a boundary with nonlinear stiffness. The nonlinearity typically scatters energy into higher frequencies; the energy then decays more rapidly.

Many previous papers have concerned the effects of a linear boundary condition on wave reflection in uniform and non-uniform continuous structures such as rods, plates, Euler–Bernoulli beams and Timoshenko beams (e.g. [1,2,3,4,5,6,7]). The wave propagation approach has also been widely used to study vibrations of nanorods [8] and nanobeams [9] with cracks. In these studies, the crack has been modelled as a linear spring element.

Some studies concerned initial value problems and free wave propagation and developed solutions based on the d’Alembert’s method [10,11,12,13,14]. This paper concerns steady-state, time-harmonic axial and flexural waves in a rod or a beam with a nonlinear boundary stiffness using a wave propagation approach. Nonlinear dynamic systems typically have more involved behaviour than their linear counterparts. The source of nonlinearity might be in the material properties of the system or due to large deformations (geometrical nonlinearities) or at boundaries. Many studies concern vibrations of elastic structures with material and geometrical nonlinearities using a wave approach, e.g. [15].

Different analytical and numerical approaches can be used to study nonlinear vibrations in rods and beams. Santo et al. [16] studied the vibrational behaviour of a rod with multiple springs with both linear and nonlinear stiffness using perturbation and polynomial methods.

Wave propagation approaches have also been used to model the dynamics. Nayfeh et al. [17] and Vakakis [18] studied the axial vibration of a rod with a Duffing-type nonlinear boundary stiffness through wave scattering. A wave incident on a boundary can be scattered into an infinite number of reflected waves with higher frequencies. It was shown that the physical behaviour of the system can be described by considering only the lower harmonics. In these studies, the nonlinearity was weak, and the strength of nonlinearity was defined in terms of the linear force of the boundary spring compared to the nonlinear force, so that the case of essential nonlinearity, i.e. when the linear spring force is zero, was not investigated. Although the power transferring from the first harmonic to higher harmonics was studied, the maximum energy that can leak into higher harmonics was not investigated. Furthermore, the results were shown for the case when only one wave is incident on the boundary. The purpose of this paper is to extend these works for the cases of a beam or a rod in a more general form, i.e. by including incident and reflected waves with higher harmonics and studying the case of essential nonlinearity. The higher harmonic incident waves might, for example, arise from the reflection of the negative-going waves from a boundary or discontinuity elsewhere on the waveguide.

Wave propagation in beams is more complex than in rods since nearfield waves also exist. Nearfield or evanescent waves have amplitudes that decay exponentially with distance and do not propagate energy along the waveguide [19]. Following the analysis presented in [17, 18], Brennan et al. [20] studied hardening and softening nonlinear boundaries for rods and beams. However, in this study, the effects of incident and reflected waves of higher harmonics were neglected: only a single incident and reflected wave was considered. It was shown that, for hardening boundary stiffness, when retaining only the first harmonic, the magnitude of the reflected wave is identical to that of the incident wave, but there is a phase change in the reflected wave. This conclusion also follows from the conservation of energy. However, with softening stiffness and when a nearfield wave is incident upon the boundary, the displacement at the end of the beam was seen to jump at certain frequencies, and the solution becomes multi-valued. No jump was found in the displacement at the end of the rod and beam with hardening boundary stiffness.

Tang et al. [21] followed the previous study [20] and calculated the natural frequencies of a rod and a beam by using a phase closure principle. It was shown that softening-type stiffness substantially affects the phases of the reflection coefficients with instabilities in a certain range of frequencies. In [21, 22], the nonlinearity was also weak, and the case of essential nonlinearity was not considered. The present paper can also be considered as an extension in the methodology and results of works [20, 21] by retaining incident and reflected waves with higher harmonics and investigating the case of essential nonlinearity.

Other wave approaches have also been used to study the vibration of nonlinear systems. In [22, 23] a wave finite element method was used to analyse composite structures with damage. The damage was modelled by a nonlinear coupling element, and only the first incident wave was considered; however, reflected waves with higher frequencies were retained. Chouvion [24] used a different wave approach and worked on nonlinear vibrations of beam-like structures. The principle behind this matrix-based approach was the ray-tracing method. In Chouvion’s approach, reflected and incident waves matrices were coupled and connected at discontinuities. The method was applied to a rod and a turbine blade (beam-like network) with damping. Essential nonlinear stiffness boundaries have a wide range of physical applications as they can absorb the system’s vibrational energy in a one-way and irreversible process. The nonlinear energy sink (NES) is a well-known application of such systems [25]. Chouvion [26] applied the same approach as in [24] to a beam with an NES in a subsequent study. The beam was connected to a linear torsional spring at each end, and the nonlinearity of the spring component of the NES was assumed to be cubic. The frequency response functions of the system were determined by the retention of waves with higher harmonics. However, the focus in [24] and [26] was on the time-harmonic forced response of the systems, rather than the calculation of the reflection coefficients, and the effects of the magnitude and phase of incident waves with higher harmonics on the reflection coefficients were not studied. Furthermore, the maximum leakage of energy from the first harmonic to the higher harmonics was not investigated.

In the present paper, the same wave approach as in [17, 18] and [20, 21] is used to study the nonlinear vibration of a semi-infinite, uniform, thin rod and an Euler–Bernoulli beam. Incident, reflected and reflected nearfield waves with multiple frequencies are considered. Under the assumption of cubic nonlinearity, a set of equations is developed for the reflection coefficients. The infinite set of equations is then truncated at an arbitrary number of harmonics and solved by using the harmonic balance method. The case of essential nonlinearity, for which the effects of nonlinearity are strongest, is investigated. For the case of one incident wave and essential nonlinearity, reflected waves with higher frequencies are retained to study energy transfer and the maximum energy that can leak from the first harmonic to higher harmonics.

It is also shown that multiple incident waves have significant effects on the reflection coefficients and can decrease or increase their magnitudes. Numerical examples are presented, and the conditions for which the reflection coefficient of the first harmonic is minimum are indicated. Furthermore, it is seen that, for flexural vibration, with two incident waves, at certain frequencies the response becomes multi-valued, and there are at least two solutions for the reflection coefficients. The region in which jumps occur in the magnitudes of the reflection coefficients is determined.

The paper is organized as follows: In Sect. 2, the governing equations are derived, and reflection coefficients are defined. The nondimensional parameters and strength of nonlinearity are defined regarding a reference frequency, and a set of equations is developed in terms of the reflection coefficients for the case of cubic nonlinearity. In Sect. 3, equations are truncated using the harmonic balance method for the case when there is only one incident wave and an arbitrary number of reflected waves. In Sect. 4, an analytical solution based on the method of expansion in a small parameter is found, and expressions are derived for the reflection coefficients when one incident and two reflected waves are retained. Section 5 presents the equations for the case of multiple incident and reflected waves. Numerical results are presented in Sect. 6, and finally, Sect. 7 is the conclusion. The focus is primarily on flexural waves, but results for the simpler case of axial waves are also presented.

2 Problem description and equations of motion

We consider the dynamic behaviour of a semi-infinite waveguide lying along the x-axis. The boundary at x = 0 is attached to a spring with nonlinear stiffness. Figure 1 shows two examples that will be considered in detail: Fig. 1a shows a thin rod (an example of a system that obeys the wave equation) undergoing axial vibrations with displacement u(x,t), while Fig. 1b shows an Euler–Bernoulli beam, which vibrates transversely in bending with displacement w(x,t). The boundary applies a nonlinear axial or transverse force on the waveguide (the beam is assumed to have zero moment at the end for simplicity), which depends only on the displacement at x = 0. It is assumed that the stiffness and the force can be written as a polynomial in the spring extension.

Fig. 1

Incident and reflected waves at a boundary with nonlinear stiffness: a axial vibrations of a rod and b flexural vibrations of a beam

We now assume that a group of time harmonic waves of amplitudes $a_{n}^{ + }$ at frequencies $n\omega$ (n integer) are incident upon the boundary at x = 0. The source of the incident waves might be either excitation or the reflection of the negative-going waves from a boundary or discontinuity at some point $x < 0$. The incident waves produce a group of reflected waves of amplitudes $a_{n}^{ - }$ and, for the beam, reflected nearfield waves of amplitudes $a_{N.n}^{ - }$ at the same frequencies. The response in the waveguide is assumed to be the superposition of the positive- and negative-going waves.

The case of flexural vibrations of an Euler–Bernoulli beam with a nonlinear boundary is now considered. The equations for the simpler and less interesting system of a thin rod in axial vibrations can be found using the same approach and are merely stated at the end of this section.

2.1 Flexural vibrations of an Euler–Bernoulli beam

The governing equation of motion for flexural vibrations of the beam is [1]:

$$ EI\frac{{\partial^{4} w(x,t)}}{{\partial x^{4} }} + \rho S\frac{{\partial^{2} w(x,t)}}{{\partial t^{2} }} = 0 $$

(1)

where $w\left( {x,t} \right)$ is the transverse displacement and $\rho$, S, E, I are the density, cross-sectional area, elastic modulus and second moment of area of the cross-section. For time-harmonic behaviour at frequency $\omega$ free waves of the form $\exp i\left( {\omega t \mp \kappa x} \right)$ can propagate in the positive and negative x-directions, respectively, together with nearfield or evanescent (non-propagating) waves of the form $\exp \left( {i\omega t \mp \kappa x} \right)$, whose amplitudes decay exponentially in the positive and negative x-directions. Here

$$ \kappa = \sqrt[4]{{\frac{{\rho S\omega^{2} }}{EI}}} $$

(2)

is the wavenumber, while the phase velocity $c_{p} = \sqrt[4]{{{{EI} \mathord{\left/ {\vphantom {{EI} {\rho S}}} \right. \kern-\nulldelimiterspace} {\rho S}}}}\sqrt \omega$ is a function of frequency, the flexural waves being dispersive. For the wave groups in Fig. 1b, the wavenumber of the n^th harmonic at frequency $n\omega$ is thus $\sqrt n \kappa$ for flexural waves.

The spring applies a force, which is assumed to be a polynomial function of the displacement at x = 0 with constant coefficients k_m so that the boundary conditions, assuming zero bending moment M, can be written as

$$ \begin{gathered} M\left( {0,t} \right) = EI\frac{{\partial ^{2} w\left( {0,t} \right)}}{{\partial x^{2} }} = 0, \hfill \\ V\left( {0,t} \right) = - EI\frac{{\partial ^{3} w\left( {0,t} \right)}}{{\partial x^{3} }} = - \sum\limits_{{m = 1}}^{M} {k_{m} w_{0}^{m} \left( t \right);\,\,\,\,\,} w_{0} \left( t \right) = w\left( {0,t} \right), \hfill \\ \end{gathered} $$

(3)

where V is the shear force.

The displacement of the beam is assumed to be the superposition of the positive- and negative-going waves shown in Fig. 1b and thus can be written as:

$$ w\left( {x,t} \right) = \sum\limits_{n = 1}^{\infty } {a_{n}^{ + } e^{{i\left( {n\omega t - \sqrt n \kappa x} \right)}} } + \sum\limits_{n = 1}^{\infty } {a_{n}^{ - } e^{{i\left( {n\omega t + \sqrt n \kappa x} \right)}} } + \sum\limits_{n = 1}^{\infty } {a_{N,n}^{ - } e^{in\omega t} } e^{\sqrt n \kappa x} + CC $$

(4)

where CC denotes the complex conjugate of the preceding terms. The ratios of the amplitude of the n^th incident wave, reflected propagating and reflected nearfield wave relative to that of the first incident wave are defined as:

$$ \alpha_{n} = {{a_{n}^{ + } } \mathord{\left/ {\vphantom {{a_{n}^{ + } } {a_{1}^{ + } }}} \right. \kern-\nulldelimiterspace} {a_{1}^{ + } }},\,\,\,{{r_{n} = \,a_{n}^{ - } } \mathord{\left/ {\vphantom {{r_{n} = \,a_{n}^{ - } } {a_{1}^{ + } }}} \right. \kern-\nulldelimiterspace} {a_{1}^{ + } }},\,\,\,r_{N,n} = {{a_{N,n}^{ - } } \mathord{\left/ {\vphantom {{a_{N,n}^{ - } } {a_{1}^{ + } }}} \right. \kern-\nulldelimiterspace} {a_{1}^{ + } }} $$

(5)

Note that the reflection coefficients $r_{n}$ and $r_{N,n}$ are functions of $a_{1}^{ + }$ and $\alpha_{n}$, in contrast to the linear case. Substituting (5) in (4), the flexural displacement of the beam in terms of $\alpha_{n}$,$r_{n}$ and $r_{N,n}$ becomes:

$$ w\left( {x,t} \right) = \left[ {a_{1}^{ + } \left( {\sum\limits_{n = 1}^{\infty } {\alpha_{n} e^{{i\left( {n\omega t - \sqrt n \kappa x} \right)}} } + \sum\limits_{n = 1}^{\infty } {r_{n} e^{{i\left( {n\omega t + \sqrt n \kappa x} \right)}} } + \sum\limits_{n = 1}^{\infty } {r_{N,n} e^{in\omega t} } e^{\sqrt n \kappa x} } \right) + CC} \right] $$

(6)

2.1.1 Effect of the phase of the fundamental incident wave

The wave amplitudes are complex and can be expressed in terms of magnitude and phase. The phases of the n^th incident, reflected and reflected nearfield waves are defined as $\Phi_{n} ,\,\,\phi_{n}$ and $\psi_{n}$, respectively. First, assume $a_{1}^{ + }$ is pure real, i.e. $\Phi_{1} = 0$. Hence, at x = 0, incident waves $a_{1}^{ + } \exp \left( {i\omega t} \right)$ and $\left| {a_{n}^{ + } } \right|\exp \,\left( {i\left( {n\omega t + \Phi_{n} } \right)} \right)$ give rise to reflected waves $\left| {a_{n}^{ - } } \right|\exp \left( {i\left( {n\omega t + \phi_{n} } \right)} \right)$ and reflected nearfield waves $\left| {a_{N,n}^{ - } } \right|\exp \left( {i\left( {n\omega t + \psi_{n} } \right)} \right)$. It follows that

$$ \,r_{n} \left( {\Phi_{1} = 0,\Phi_{n} } \right) = \left| {{{a_{n}^{ - } } \mathord{\left/ {\vphantom {{a_{n}^{ - } } {a_{1}^{ + } }}} \right. \kern-\nulldelimiterspace} {a_{1}^{ + } }}} \right|e^{{i\phi_{n} }} ,\,\,\,\,r_{N,n} \left( {\Phi_{1} = 0,\Phi_{n} } \right) = \left| {{{a_{N,n}^{ - } } \mathord{\left/ {\vphantom {{a_{N,n}^{ - } } {a_{1}^{ + } }}} \right. \kern-\nulldelimiterspace} {a_{1}^{ + } }}} \right|e^{{i\psi_{n} }} $$

(7)

Now suppose that $a_{1}^{ + }$ is complex, i.e. $\Phi_{1} \ne 0$, so that the first incident wave at x = 0 is $\left| {a_{1}^{ + } } \right|\exp \left( {i\left( {\omega t + \Phi_{1} } \right)} \right)$. Defining $t^{\prime} = t + {{\Phi_{1} } \mathord{\left/ {\vphantom {{\Phi_{1} } \omega }} \right. \kern-\nulldelimiterspace} \omega }$, the relations between the phases of the reflected waves are given by:

$$ r_{n} \left( {\Phi_{1} ,\Phi_{n} } \right) = r_{n} \left( {0,\Phi_{n}^{\prime } } \right)e^{{ - i\left( {n - 1} \right)\Phi_{1} }} ,\,\,\,\,\,\,r_{N,n} \left( {\Phi_{1} ,\Phi_{n} } \right) = r_{N,n} \left( {0,\Phi_{n}^{\prime } } \right)e^{{ - i\left( {n - 1} \right)\Phi_{1} }} $$

(8)

in which $\Phi_{n}^{\prime } = \Phi_{n} - n\Phi_{1}$. For simplicity, henceforth it is assumed that $\Phi_{1} = 0$ unless otherwise stated.

2.2 Cubic nonlinear stiffness

Generally, the reflection coefficients can be found by substituting Eq. (6) for the response into the boundary conditions (3), separating terms at each frequency and solving. Given that the nonlinear boundary spring stiffness can potentially include an infinite number of terms (i.e. $M = \infty$ in Eq. 3), this can be a formidable task. However, for simplicity, it is now assumed that the spring possesses cubic nonlinearity and that $k_{2} = 0$. Under this assumption, an incident wave at one frequency produces reflected waves with only odd multipliers of the fundamental frequency [17, 18]. Consequently, the second part of Eq. (3) becomes.

$$ V\left( {0,t} \right) = - k_{1} w_{0} - k_{3} w_{0}^{3} $$

(9)

The bending moment is zero and it follows that

$$ r_{N,\,n} = \alpha_{n} + r_{n} . $$

(10)

This is substituted into Eq. (6) to give

$$ w\left( {x,t} \right) = a_{1}^{ + } \left( {\sum\limits_{n = 1,3,5,..}^{\infty } {\alpha_{n} e^{{i\left( {n\omega t - \sqrt n \kappa x} \right)}} } + \sum\limits_{n = 1,3,5,..}^{\infty } {r_{n} e^{{i\left( {n\omega t + \sqrt n \kappa x} \right)}} } + \sum\limits_{n = 1,3,5,..}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } e^{\sqrt n \kappa x} } \right) + CC $$

(11)

Putting x = 0 in Eq. (11) results in

$$ w_{0} = 2\left[ {\left( {a_{1}^{ + } \sum\limits_{n = 1,3,5,..}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + CC} \right] $$

(12)

The shear force at x = 0 is given by:

$$ V\left( {0,t} \right) = - EI\kappa^{3} \left[ {\left( {a_{1}^{ + } \sum\limits_{n = 1,3,5,...}^{\infty } {n\sqrt n \left[ {\,\alpha_{n} \left( {1 + i} \right) + r_{n} \left( {1 - i} \right)} \right]\,} e^{in\omega t} } \right) + CC} \right]. $$

(13)

Substituting Eqs. (12 and 13) into Eq. (9) results in

$$ \begin{gathered} EI\kappa^{3} \left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {n\sqrt n \left[ {\alpha_{n} \left( {1 + i} \right) + r_{n} \left( {1 - i} \right)} \right]} e^{in\omega t} } \right) + CC} \right] \hfill \\ - 2k_{1} \left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + CC} \right] - 8k_{3} a_{1}^{ + 2} \left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + CC} \right]^{3} = 0. \hfill \\ \end{gathered} $$

(14)

To put the equations in a non-dimensional form, a reference frequency $\omega_{0} = \tfrac{1}{12}\sqrt {{{ES} \mathord{\left/ {\vphantom {{ES} {\rho I}}} \right. \kern-\nulldelimiterspace} {\rho I}}}$ is introduced. For a rectangular cross-section of width b and thickness h, then $\kappa h = 1$ at this frequency. For a beam with an arbitrary cross-section, $\sqrt {12} \kappa r_{g} = 1$ at this frequency, where $r_{g}$ is the radius of gyration of the cross-section. The characteristic impedance (the ratio of the shear force to transverse velocity for a propagating wave) of the beam at $\omega_{0}$ is $Z = \sqrt[4]{{EI\left( {\rho S} \right)^{3} }}\sqrt {\omega_{0} }$. The dimensionless parameters

$$ \Omega = \frac{\omega }{{\omega_{0} }};\,K = \frac{{k_{1} }}{{\omega_{0} Z}};\,A = \frac{{k_{3} a_{1}^{ + 2} }}{{\omega_{0} Z}}, $$

(15)

are introduced, where Ω represents the non-dimensional frequency ratio, K is the relative linear stiffness of the boundary spring ($k\left( {w_{0} } \right)$) to that of the beam at frequency $\omega_{0}$ and represents linear effects, while A is the ratio of the nonlinear force in the spring (due only to the first incident wave) and that of the beam at frequency $\omega_{0}$ and represents the nonlinear effects.

Equation (14) can now be rewritten in terms of the dimensionless parameters as

$$ \begin{gathered} \Omega^{3/2} \left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {n\sqrt n \left[ {\alpha_{n} \left( {1 + i} \right) + r_{n} \left( {1 - i} \right)} \right]} e^{in\omega t} } \right) + CC} \right] - \hfill \\ 2K\left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + CC} \right] - 8A\left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + CC} \right]^{3} = 0. \hfill \\ \end{gathered} $$

(16)

It can be seen that the reflection coefficients depend on the three dimensionless parameters together with the magnitudes and phases of $\alpha_{n}$. In this paper, weak nonlinearity is defined to be the case when the dimensionless nonlinear force is small compared to the linear forces of the spring and beam together, i.e. $A \ll \left( {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} + K} \right)$. This is in contrast to previous studies [17, 18] and [20, 21] where weak nonlinearity was defined to be the case when the relative forces of the linear and nonlinear boundary springs are small, i.e. $A \ll K$ or ${{k_{3} a_{1}^{ + 2} } \mathord{\left/ {\vphantom {{k_{3} a_{1}^{ + 2} } {k_{1} }}} \right. \kern-\nulldelimiterspace} {k_{1} }} < < 1$. Our definition allows us to study the case of essential nonlinearity (K = 0 or k₁ = 0) at which the nonlinearity can be stronger. However, it should be noted that K = 0 does not necessarily mean strong nonlinearity since the linear dynamic stiffness of the beam can be large compared to A, i.e. ${A \mathord{\left/ {\vphantom {A {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}$ may be small and the nonlinearity is weak.

2.3 Power and conservation of energy

The time average power in a time-harmonic propagating wave of amplitude $a^{ \pm }$ at frequency $\omega$ is $\frac{1}{2}\rho S\omega^{2} \,c_{g} \left| {a^{ \pm } } \right|^{2}$, in which $c_{g} = 2\sqrt[4]{{{{EI} \mathord{\left/ {\vphantom {{EI} {\rho S}}} \right. \kern-\nulldelimiterspace} {\rho S}}}}\sqrt \omega$ is the group velocity of flexural waves. Due to energy conservation at the boundary, the net power, i.e. the difference between the powers of the positive- and negative-going waves, must be zero, the nonlinearity causing energy to leak into higher harmonics. However, evanescent (nearfield) flexural waves carry no power. Hence, the net time average power ($\overline{\Pi }$) of the incident and reflected flexural waves is given by:

$$ \overline{\Pi } = \frac{1}{2}\rho S\omega^{2} c_{g} \sum\limits_{n = 1}^{\infty } {\left[ {n^{2} \sqrt n \,\left( {\,\left| {\alpha_{n} } \right|^{2} - \left| {r_{n} } \right|^{2} } \right)} \right] = 0} $$

(17)

When there is only one incident wave, Eq. (17) in terms of the reflection coefficients becomes:

$$ \sum\limits_{n = 1}^{N} {n^{2} \sqrt n \left| {r_{n} } \right|^{2} } = 1 $$

(18)

2.4 Axial waves in a thin rod

The analysis for the case of a rod in axial vibrations follows the same steps as above, although there are of course no nearfields. Only the main results are stated here.

Axial vibrations of a rod are governed by equation [1]

$$ ES\frac{{\partial^{2} u\left( {x,t} \right)}}{{\partial x^{2} }} - \rho S\frac{{\partial^{2} u\left( {x,t} \right)}}{{\partial t^{2} }} = 0;\,\,\,\,\,\,\,\,\,\,\,P\left( {x,t} \right) = ES\frac{{\partial u\left( {x,t} \right)}}{\partial x} $$

(19)

where u is the axial displacement and P is the axial force. The boundary condition at x = 0 for cubic stiffness is

$$\begin {aligned} P\left( {0,t} \right) = ES\frac{{\partial u\left( {0,t} \right)}}{\partial x} = - k_{1} u_{0} - k_{3} u_{0}^{3} ;\\& u_{0} \left( t \right) = u\left( {0,t} \right) \end {aligned}$$

(20)

For time-harmonic motion, the wave speed $c_{g}$, wavenumber $\kappa$ and characteristic impedance Z of the rod at frequency $\omega$ are [1]

$$ c_{g} = \sqrt {{E \mathord{\left/ {\vphantom {E \rho }} \right. \kern-\nulldelimiterspace} \rho }} ,\,\,\,\,\,\,\kappa = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-\nulldelimiterspace} c}_{g} ,\,\,\,\,\,\,Z = S\sqrt {E\rho } = \rho Sc_{g} . $$

(21)

Axial waves are non-dispersive so that the wavenumber of the n^th harmonic wave at frequency $n\omega$ is $n\kappa$. The displacement of the rod can be written as:

$$ u\left( {x,t} \right) = \sum\limits_{n = 1}^{\infty } {a_{n}^{ + } e^{{in\left( {\omega t - \kappa x} \right)}} } + \sum\limits_{n = 1}^{\infty } {a_{n}^{ - } e^{{in\left( {\omega t + \kappa x} \right)}} } + CC. $$

(22)

Substituting (5) into equation (22) gives

$$ u\left( {x,t} \right) = \left[ {a_{1}^{ + } \left( {\sum\limits_{n = 1}^{\infty } {\alpha_{n} e^{{in\left( {\omega t - \kappa x} \right)}} } + \sum\limits_{n = 1}^{\infty } {r_{n} e^{{in\left( {\omega t + \kappa x} \right)}} } } \right) + CC} \right]. $$

(23)

A reference frequency $\omega_{0} = \sqrt {{E \mathord{\left/ {\vphantom {E {\rho S}}} \right. \kern-\nulldelimiterspace} {\rho S}}}$ is now defined, at which $\kappa \sqrt S = 1$. The characteristic impedance Z is given by Eq. (21), and the dimensionless parameters of equation (15) are introduced. Putting x = 0 in Eq.(23), from Eq. (20) we get

$$ \begin{gathered} \left[ {i\Omega \left( {\sum\limits_{n = 1,3,5,...}^{\infty } {n\left( {\alpha_{n} - r_{n} } \right)e^{in\omega t} } } \right)} \right] + CC \hfill \\ - K\left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + CC} \right] - A\left[ {\left( {\sum\limits_{n = 1,3,5,...}^{\infty } {\left( {\alpha_{n} + r_{n} } \right)e^{in\omega t} } } \right) + CC} \right]^{3} = 0. \hfill \\ \end{gathered} $$

(24)

Weak nonlinearity is again defined to be the case when ${A \mathord{\left/ {\vphantom {A {(K + \Omega )}}} \right. \kern-\nulldelimiterspace} {(K + \Omega )}} \ll 1$. As can be seen, Eq. (24) is very similar to Eq. (16); hence, in Sects. 3, 4 and 5 equations for flexural waves are analysed in detail, and equivalent equations for axial waves are presented in Appendix B.

Note that the time average power of an axial wave at frequency $\omega$ and of amplitude $a^{ + }$ equals $\frac{1}{2}Z\omega^{2} \left| {a^{ + } } \right|^{2}$. Hence, the net time average power

$$ \overline{\Pi } = \frac{1}{2}Z\omega^{2} \left[ {\sum\limits_{n = 1}^{N} {n^{2} \left( {\left| {\alpha_{n} } \right|^{2} - \left| {r_{n} } \right|^{2} } \right)} } \right] = 0, $$

(25)

or, for the case of one incident wave in terms of reflection coefficients,

$$ \sum\limits_{n = 1}^{N} {n^{2} \left| {r_{n} } \right|^{2} } = 1. $$

(26)

3 The case of only one incident wave and higher harmonic reflected waves

Consider the case when there is only one incident wave, i.e. $\alpha_{n} = 0,(n > 1)$, so that Eq. (16) becomes

$$ \begin{gathered} \Omega^{3/2} \left[ {\left( {\left( {i - ir_{1} + 1 + r_{1} } \right)e^{i\omega t} + \sum\limits_{n = 3,5,...}^{\infty } {n\sqrt n r_{n} \left( {1 - i} \right)\,} e^{in\omega t} } \right) + CC} \right] - \hfill \\ 2K\left[ {e^{i\omega t} + \sum\limits_{n = 1,3,5,...}^{\infty } {r_{n} e^{in\omega t} } + CC} \right] - 8A\left[ {e^{i\omega t} + \sum\limits_{n = 1,3,5,...}^{\infty } {r_{n} e^{in\omega t} } + CC} \right]^{3} = 0. \hfill \\ \end{gathered} $$

(27)

3.1 Truncation and solution

The infinite set of equations (27) can be truncated at some finite value of n = N and solved through the harmonic balance method. The accuracy of the solution depends on the value chosen for N and is discussed in Sect. 6.2. The terms of $e^{in\omega t}$ are collected and the coefficients are equated to zero. For example, taking N = 9 and collecting the terms in $e^{i\omega t}$, the equation for the first harmonic is:

$$ \begin{gathered} \left[ {\Omega ^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} \left( {i - ir_{1} + 1 + r_{1} } \right) - 2K\left( {1 + r_{1} } \right)} \right] \hfill \\ + ( - 24A)\left\{ {\left( {\bar{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)^{2} } \right. \hfill \\ + r_{3} \left[ {\left( {\bar{r}_{1} + 1} \right)^{2} + 2\bar{r}_{3} \left( {r_{1} + 1} \right)} \right] \hfill \\ + r_{5} \left[ {2\bar{r}_{3} \left( {\bar{r}_{1} + 1} \right) + 2\bar{r}_{5} \left( {r_{1} + 1} \right)} \right] + r_{3} ^{2} \bar{r}_{5} \hfill \\ + r_{7} \left[ {\bar{r}_{3} ^{2} + 2\bar{r}_{5} \left( {\bar{r}_{1} + 1} \right) + 2\bar{r}_{7} \left( {r_{1} + 1} \right)} \right] + 2r_{3} r_{5} \bar{r}_{7} \hfill \\ \left. { + r_{9} \left[ {2\bar{r}_{3} \bar{r}_{5} + 2\bar{r}_{7} \left( {\bar{r}_{1} + 1} \right) + 2\bar{r}_{9} \left( {r_{1} + 1} \right)} \right] + 2r_{3} r_{7} \bar{r}_{9} + r_{5} ^{2} \bar{r}_{9} } \right\} = 0, \hfill \\ \end{gathered} $$

(28)

where the overbar represents the complex conjugate. Similarly, collecting and equating the coefficients of time-dependent terms at frequency $3\omega$ result in

$$ \begin{gathered} \left[ {3\sqrt 3 \Omega ^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} r_{3} \left( {1 - i} \right) - 2Kr_{3} } \right] \hfill \\ + ( - 8A)\left\{ {\left( {r_{1} + 1} \right)^{3} } \right. \hfill \\ + r_{3} \left[ {3\bar{r}_{3} r_{3} + 6\left( {\bar{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)} \right] \hfill \\ + r_{5} \left[ {3\left( {\bar{r}_{1} + 1} \right)^{2} + 6\left( {\bar{r}_{3} \left( {r_{1} + 1} \right) + r_{3} \bar{r}_{5} } \right)} \right] \hfill \\ + 6r_{7} \left[ {\bar{r}_{3} \left( {\bar{r}_{1} + 1} \right) + \bar{r}_{5} \left( {r_{1} + 1} \right) + r_{3} \bar{r}_{7} } \right] + 3\bar{r}_{7} r_{5} ^{2} \hfill \\ \left. { + 6r_{9} \left[ {\bar{r}_{5} \left( {\bar{r}_{1} + 1} \right) + \bar{r}_{7} \left( {r_{1} + 1} \right) + r_{3} \bar{r}_{9} } \right] + 3r_{9} \bar{r}_{3} ^{2} + 6r_{5} r_{7} \bar{r}_{9} } \right\} = 0. \hfill \\ \end{gathered} $$

(29)

In a similar way, by collecting terms of higher harmonics, equations for n = 5, 7 and 9 can be found as presented in Appendix A. The analysis for large values of N can become extremely cumbersome.

3.2 Case of one reflected wave (N = 1)

In previous studies [20, 21], it was shown that if all higher harmonics are neglected, i.e. truncating the system of equations at N = 1, the nonlinearity has no effect on the magnitude of the reflection coefficient $r_{1}$, only a change in its phase. Thus, the magnitude of the reflection coefficient is similar to that of the linear case, i.e. $\left| {r_{1} } \right| = 1$. Since there is no energy dissipation at the boundary, all the incident energy is necessarily reflected into the first harmonic. It should be noted that putting N = 1 in Eq. (16) results in the same equations as those developed in [20, 21].

4 A solution for the case of one incident wave and two reflected waves

In order to give insight into the underlying behaviour of the system, first the case when there is only one incident wave and only the first and third reflected harmonics are retained is discussed. Truncating Eq. (27) at N = 3 results in

$$ \begin{gathered} \Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} \left( {i - ir_{1} + 1 + r_{1} } \right) - 2K\left( {1 + r_{1} } \right) \hfill \\ - 24A\left[ {\left( {1 + r_{1} } \right)^{2} \left( {1 + \overline{r}_{1} } \right) + r_{3} \left( {1 + \overline{r}_{1} } \right)^{2} + 2r_{3} \overline{r}_{3} \left( {1 + r_{1} } \right)} \right] = 0, \hfill \\ \end{gathered} $$

(30)

$$ 3\sqrt 3 \Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} r_{3} \left( {1 - i} \right) - 2Kr_{3} - 8A\left[ {\left( {1 + r_{1} } \right)^{3} + } \right.\left. {3\overline{r}_{3} r_{3}^{2} + 6r_{3} \left( {1 + r_{1} } \right)\left( {1 + \overline{r}_{1} } \right)} \right] = 0. $$

(31)

This set of equations can be solved for various values of parameters. Special cases are when A or K is zero. When A = 0, then the system is linear with

$$ r_{1} = r_{lin} = \frac{{1 - \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i}}{{1 + \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i}} $$

(32)

In this case, the denominator is the complex conjugate of the numerator so that |r₁|= 1, and since energy is conserved, r₃ = 0. At low-frequency ratios $({{\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} } \mathord{\left/ {\vphantom {{\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} } K}} \right. \kern-\nulldelimiterspace} K} \ll 1)$, the behaviour of the beam is similar to one with a simply supported boundary and $r_{1} = r_{SS} = - 1$, while, at high frequencies (${{\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} } \mathord{\left/ {\vphantom {{\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} } K}} \right. \kern-\nulldelimiterspace} K} \gg 1$), the beam behaves the same as one with a free end and $r_{1} = r_{free} = - i$.

4.1 Essential nonlinearity

When the linear stiffness K = 0, the wave reflection is governed by essential nonlinearity. Note that even in this case the nonlinearity can be weak when $A < \Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}}$. A new parameter

$$ \gamma = \frac{A}{{\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }} $$

(33)

is now introduced. Equations (30 and 31) can thus be rewritten in terms of $\gamma$ as

$$ \left[ {i - ir_{1} + 1 + r_{1} } \right] - 24\gamma \left[ {\left( {1 + r_{1} } \right)^{2} \left( {1 + \overline{r}_{1} } \right) + r_{3} \left( {1 + \overline{r}_{1} } \right)^{2} + 2r_{3} \overline{r}_{3} \left( {1 + r_{1} } \right)} \right] = 0, $$

(34)

$$ \left[ {3\sqrt 3 r_{3} \left( {1 - i} \right)} \right] - 8\gamma \left[ {\left( {1 + r_{1} } \right)^{3} + } \right.\left. {3\overline{r}_{3} r_{3}^{2} + 6r_{3} \left( {1 + r_{1} } \right)\left( {1 + \overline{r}_{1} } \right)} \right] = 0. $$

(35)

It can be seen that the reflection coefficients depend only on $\gamma$. The case $\gamma \ll 1$ denotes weak nonlinearity and the beam behaviour effectively corresponds to that of a beam with a free end, i.e. $r_{1} = r_{free} = - i,r_{3} = 0$. On the other hand, if $\gamma \gg 1$ the beam behaves similar to a beam with a simply supported boundary and $r_{1} = r_{SS} = - 1,r_{3} = 0$. Hence, at some value of $\gamma$, |r₁| reaches a minimum and |r₃| reaches a maximum, which implies that the effects of nonlinearity are strongest.

4.2 Analytical solution using small parameter expansion for weak nonlinearity

The method of expansion in a small parameter is used to find an approximate solution to Eqs. ( (30 and 31). Assuming $\varepsilon$ to be a small parameter, $\varepsilon A$ denotes weak nonlinearity. Hence, Eqs. (30 and 31) become

$$ \begin{gathered} \Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} \left( {i - ir_{1} + 1 + r_{1} } \right) - 2K\left( {1 + r_{1} } \right) \hfill \\ - 24\varepsilon A\left[ {\left( {1 + r_{1} } \right)^{2} \left( {1 + \overline{r}_{1} } \right) + r_{3} \left( {1 + \overline{r}_{1} } \right)^{2} + 2r_{3} \overline{r}_{3} \left( {1 + r_{1} } \right)} \right] = 0, \hfill \\ \end{gathered} $$

(36)

$$ 3\sqrt 3 \Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} r_{3} \left( {1 - i} \right) - 2Kr_{3} - 8\varepsilon A\left[ {\left( {1 + r_{1} } \right)^{3} + } \right.\left. {3\overline{r}_{3} r_{3}^{2} + 6r_{3} \left( {1 + r_{1} } \right)\left( {1 + \overline{r}_{1} } \right)} \right] = 0. $$

(37)

The solution to Eqs. (36 and 37) in terms of the small parameter $\varepsilon$ is

$$ r_{1} = r_{01} + \varepsilon r_{11} + \varepsilon^{2} r_{21} + O(\varepsilon^{3} ), $$

(38)

$$ r_{3} = r_{03} + \varepsilon r_{13} + \varepsilon^{2} r_{23} + O(\varepsilon^{3} ). $$

(39)

Since the difference between the amplitudes of the first incident and reflected waves is at least of order $O(\varepsilon^{2} )$, we consider a second-order expansion. Substituting (38 and 39) in (36 and 37) and equating the coefficients of $\varepsilon^{n}$, the terms in the expansion of r₁ are:

$$ \begin{gathered} r_{01} = r_{lin} = \left( {\frac{{1 - \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i}}{{1 + \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i}}} \right);\,\,\,\,r_{11} = \left[ {\left( {\frac{{24\left( {{A \mathord{\left/ {\vphantom {A {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)i}}{{1 + \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i}}} \right)\left( {1 + r_{01} } \right)^{2} \left( {1 + \overline{r}_{01} } \right)} \right],\, \hfill \\ \hfill \\ r_{21} = \left[ {\left( {\frac{{24\left( {{A \mathord{\left/ {\vphantom {A {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)i}}{{1 + \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i}}} \right)\left( {\overline{r}_{11} \left( {r_{01} + 1} \right)^{2} + r_{13} \left( {\overline{r}_{01} + 1} \right)^{2} + 2r_{11} \left( {r_{01} + 1} \right)\left( {\overline{r}_{01} + 1} \right)} \right)} \right]. \hfill \\ \end{gathered} $$

(40)

Similarly, for r₃

$$ \begin{gathered} \,r_{03} = 0\,;\,\,\,\,r_{13} = \left[ {\left( {\frac{{8\left( {{A \mathord{\left/ {\vphantom {A {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)i}}{{3\sqrt 3 \, + \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i}}} \right)\left( {1 + r_{01} } \right)^{3} } \right], \hfill \\ \hfill \\ r_{23} = \left[ {\left( {\frac{{8\left( {{A \mathord{\left/ {\vphantom {A {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)i}}{{3\sqrt 3 \, + \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i}}} \right)\left( {3r_{11} \left( {r_{01} + 1} \right)^{2} + 6r_{13} \left( {r_{01} + 1} \right)\left( {\overline{r}_{01} + 1} \right)} \right)} \right]. \hfill \\ \end{gathered} $$

(41)

As can be seen from the coefficients of $\varepsilon^{0}$, $r_{03} = 0$ and $r_{01} = r_{lin}$ and the reflection coefficients depend on the linear parameters of the system (K and Ω). A appears in the expressions for the higher-order terms of the series, so that r₁₁ and r₂₁ are functions of $\beta_{1} = {{24\left( {{A \mathord{\left/ {\vphantom {A {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)i} \mathord{\left/ {\vphantom {{24\left( {{A \mathord{\left/ {\vphantom {A {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)i} {\left[ {1 + \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {1 + \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i} \right]}},$ while r₁₃ and r₂₃ are functions of $\beta_{3} = {{8\left( {{A \mathord{\left/ {\vphantom {A {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)i} \mathord{\left/ {\vphantom {{8\left( {{A \mathord{\left/ {\vphantom {A {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)i} {\left[ {3\sqrt 3 \, + \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {3\sqrt 3 \, + \left( {1 - \left( {{{2K} \mathord{\left/ {\vphantom {{2K} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right. \kern-\nulldelimiterspace} {\Omega^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} }}} \right)} \right)i} \right]}}$ with ${{\left| {\beta_{1} } \right|} \mathord{\left/ {\vphantom {{\left| {\beta_{1} } \right|} 3}} \right. \kern-\nulldelimiterspace} 3} \ge \left| {\beta_{3} } \right|$. It can be noted that r₀₁ is of order 1, $r_{11} = O\left( {\beta_{1} } \right),\,\,r_{21} = O\left( {\beta_{1}^{2} } \right)$ while $r_{03} = 0,\,\,r_{13} = O\left( {\beta_{3} } \right),\,\,r_{23} = O\left( {\beta_{1} \beta_{3} } \right)$. The perturbation method is accurate when the nonlinearity is weak, i.e. $\left| {\beta_{1} } \right|$ is small.

5 Case of two incident and reflected waves

It is now assumed that in Eq. (16) $\alpha_{3} \ne 0$, i.e. the second incident wave with frequency $3\omega$ is considered. Taking N = 3 in Eq. (16) and collecting the first and third harmonic terms result in:

$$ \begin{gathered} \Omega^{3/2} \left[ {\left( {1 + i} \right) + \left( {1 - i} \right)r_{1} } \right] - 2K\left[ {r_{1} + 1} \right] + \hfill \\ - 24A\left[ {\left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)^{2} + \left( {\alpha_{3} + r_{3} } \right)\left( {\overline{r}_{1} + 1} \right)^{2} }\, +2\left( {r_{1} + 1} \right)\left( {\alpha_{3} \overline{\alpha }_{3} + r_{3} \overline{r}_{3} + \alpha_{3} \overline{r}_{3} + \overline{\alpha }_{3} r_{3} } \right) \right] = 0, \hfill \\ \end{gathered} $$

(42)

$$ \begin{gathered} 3\sqrt 3 \,\Omega^{3/2} \left[ {\alpha_{3} \left( {1 + i} \right) + r_{3} \left( {1 - i} \right)} \right] - 2K\left[ {r_{3} + \alpha_{3} } \right] + \hfill \\ - 8A\left[ {\left( {r_{1} + 1} \right)^{3} + 3\left( {r_{3} + \alpha_{3} } \right)^{2} \left( {\overline{r}_{3} + \overline{\alpha }_{3} } \right) + 6\left( {r_{1} + 1} \right)\left( {\overline{r}_{1} + 1} \right)\left( {r_{3} + \alpha_{3} } \right)} \right] = 0. \hfill \\ \end{gathered} $$

(43)

For the case of essential nonlinearity, these equations can be written in terms of $\gamma$ as

$$ \begin{gathered} \left[ {\left( {1 + i} \right) + \left( {1 - i} \right)r_{1} } \right] \hfill \\ - 24\gamma \left[ {\left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)^{2} + \left( {\alpha_{3} + r_{3} } \right)\left( {\overline{r}_{1} + 1} \right)^{2} }\,+2\left( {r_{1} + 1} \right)\left( {\alpha_{3} \overline{\alpha }_{3} + r_{3} \overline{r}_{3} + \alpha_{3} \overline{r}_{3} + \overline{\alpha }_{3} r_{3} } \right) \right] = 0, \hfill \\ \end{gathered} $$

(44)

$$ \begin{gathered} 3\sqrt 3 \,\left[ {\alpha_{3} \left( {1 + i} \right) + r_{3} \left( {1 - i} \right)} \right] \hfill \\ - 8\gamma \left[ {\left( {r_{1} + 1} \right)^{3} + 3\left( {r_{3} + \alpha_{3} } \right)^{2} \left( {\overline{r}_{3} + \overline{\alpha }_{3} } \right)\; +\; 6\left( {r_{1} + 1} \right)\left( {\overline{r}_{1} + 1} \right)\left( {r_{3} + \alpha_{3} } \right)} \right] = 0. \hfill \\ \end{gathered} $$

(45)

6 Numerical examples

In this section, various numerical examples are presented. Sections 6.1, 6.2 and 6.3 present results for flexural vibrations, while Sect. 6.4 is dedicated to results for axial vibrations. First, the results from numerical and analytical solutions are shown for the case of essential nonlinearity and when there is only one incident wave and only two reflected waves (N = 3) are retained. Then, the effects of K and A on the magnitudes of r₁ and r₃ are studied. In Sect. 6.2, the accuracy and convergence of the solution are studied by retention of an increasing number of harmonics, and the maximum leakage of energy for the case of essential nonlinearity is determined. The effects of the second incident wave on the reflection coefficients are investigated in Sect. 6.3 with K = 0. Finally, results for axial vibrations are presented in Sect. 6.4.

6.1 Flexural waves: one incident wave and two reflected waves (N = 3)

6.1.1 Flexural waves: case of essential nonlinearity (K = 0)

Figure 2 shows the magnitudes and phases of the reflection coefficients for essential nonlinearity as a function of $\gamma = {A \mathord{\left/ {\vphantom {A {\Omega^{3/2} }}} \right. \kern-\nulldelimiterspace} {\Omega^{3/2} }}$, where A is a measure of nonlinearity and $\Omega^{3/2}$ represents the linear dynamic stiffness of the beam. Hence, $\gamma$ denotes the ratio of the nonlinear boundary force (due to $a_{1}^{ + }$ alone) to that of the linear internal force of the beam when K = 0. Equations (34 and 35)are solved numerically using the fsolve function in MATLAB and implementing the iterative Levenberg–Marquardt algorithm. The numerical results are in good agreement with the analytical solutions for weak nonlinearity, while, as $\gamma$ increases, the accuracy of the analytical method decreases, and additional terms of $\varepsilon^{3}$ and higher should be included to find a good approximation.

Fig. 2

Flexural waves: magnitudes and phases of the reflection coefficients as a function of $\gamma$ from numerical and analytical solutions for the case of essential nonlinearity, with only one incident wave and retaining only two reflected waves: a |r₁|, b $\phi_{1}$, c |r₃|, d $\phi_{3}$. Blue dotted line numerical solution; red dotted line small parameter expansion. (Color figure online)

The case $\gamma \ll 1$ denotes weak nonlinearity and the beam behaviour effectively corresponds to that of a beam with a free end, i.e. r₁ = -i. We are interested in investigating the effects of stronger nonlinearity on the reflection coefficients with increasing $\gamma$. It can be seen from the figures that, first, when nonlinearity increases |r₁| decreases. However, when A or $\gamma$ is very large, the beam behaves similar to a beam with a simply supported boundary, as expected, and r₁ = -1. Since energy is conserved, the magnitude of the reflection coefficient of the first harmonic for the case of one incident wave cannot be larger than one and energy leaks from the first harmonic to the third harmonic. Consequently, there is a minimum value of |r₁| when the effects of nonlinearity are strongest. The leakage of energy depends on the value of $\gamma$. With increasing $\gamma$, first |r₁| decreases while |r₃| increases. At $\gamma \simeq$ 0.073, the minimum magnitude of r₁ is about 0.8, and the maximum magnitude of r₃ is about 0.15. From this point, as $\gamma$ increases, the end of the beam will be effectively pinned and r₁ asymptotes to − 1. Figures 2c and d show the changes in the phases of reflection coefficients. When $\gamma < < 1$, the phases of the first and third harmonics are − 90°. As $\gamma$ increases, $\phi_{1} \,{\text{and}}\,\,\phi_{3}$ asymptote to 180° and 90°, respectively.

6.1.2 Flexural waves: general case (K ≠ 0 and A ≠ 0)

Figure 3 shows the magnitudes of the reflection coefficients of the first and third harmonics as a function of frequency ratio $\Omega$ for A = 0.01 and three different values of K. The minimum magnitude of the reflection coefficient of the first harmonic and the maximum magnitude of the reflection coefficient of the third harmonics are defined as |r₁|_min and |r₃|_max. As can be seen in Fig. 3, when K = 0, |r₁|_min is minimum and |r₃|_max is maximum. As K increases, |r₁|_min increases since the linear stiffness becomes more pronounced and decreases the effect of nonlinearity. From energy conservation $\left| {r_{1} } \right|_{min}^{2} + 9\sqrt 3 \left| {r_{3} } \right|_{max}^{2} = 1$, and hence, in Fig. 3, as |r₁|_min increases, |r₃|_max necessarily decreases.

Fig. 3

Flexural waves: single incident wave and retaining only two reflected waves: the effect of K on the magnitudes of the reflection coefficients of the first and third harmonics with A = 0.01, as a function of frequency: a |r₁|; b |r₃|. Red line K = 0; blue dotted line K = 0. 01; black dotted line.K = 0.1. (Color figure online)

In Fig. 4, the effect of the nonlinear stiffness on the magnitudes of the reflection coefficients is examined. Results are presented for K = 0.1 in Fig. 4a and b as a function of the frequency ratio $\Omega$. As can be noted from Fig. 4a, increasing A changes the frequency at which |r₁|_min and |r₃|_max occur. Furthermore, as A increases |r₁|_min decreases and asymptotes to about 0.8 and |r₃|_max increases and asymptotes to about 0.15.

Fig. 4

Flexural waves: single incident wave and retaining only two reflected waves: the effect of A on the magnitudes of the reflection coefficients of the first and third harmonics with K = 0.1, as a function of frequency: a |r₁|, b |r₃|. Red dotted line A = 0.0001; blue dotted line A = 0.001;.green dotted line A = 0.01; black line A = 0.1. (Color figure online)

Examining the results in Figs. 3 and 4 indicates that generally, as the nonlinear effects become more pronounced, i.e. the linear component (K) decreases or nonlinear component (A) increases, |r₁|_min and |r₃|_max asymptote to those values in the case of essential nonlinearity in Fig. 2. Results are shown only for the case of essential nonlinearity in the rest of the paper since this case is of primary interest and effect of nonlinearity is more pronounced.

6.2 Flexural waves: one incident wave, multiple reflected waves and convergence

In this section, the solutions to the system of equations truncated at a higher number of harmonics (N = 5, N = 7, and N = 9) are presented and compared to the results with N = 3 for the case of essential nonlinearity. Results show that the underlying behaviour of the system is the same as that seen when retaining only the first and third reflected waves and that the solutions converge as N increases.

The set of equations are truncated for various N, and the magnitudes and phases of the reflection coefficients are illustrated in Fig. 5 as a function of $\gamma$. The qualitative behaviour is the same as when N = 3. There is a significant difference between |r₁|_min and |r₃|_max for N = 3 and 5; however, these two parameters are almost identical for N = 5, 7 and 9. Comparing the magnitudes of r₁ to r₉ shows that, as the order of the odd harmonic increases, the magnitude of the reflection coefficient decreases, i.e. $\left| {r_{1} } \right| > \left| {r_{3} } \right| > \left| {r_{5} } \right| > \left| {r_{7} } \right| > \left| {r_{9} } \right|$. Retaining a higher number of harmonics has less effect on the phases of the reflected waves than on their magnitudes.

Fig. 5

Flexural waves: The magnitudes and phases of the reflection coefficients as a function of $\gamma$ with K = 0 retaining 3, 5, 7 and 9 harmonics in the response: a |r₁|, b $\phi_{1}$, c |r₃|, d $\phi_{3}$, e |r₅|, f $\phi_{5}$, g |r₇|, h $\phi_{7}$, i |r₉|, j $\phi_{9}$. Black dotted line N = 3; Blue line N = 5; Green dotted line N = 7; Red dotted line N = 9. (Color figure online)

To study the accuracy of the solution, the relative error $\left| {r_{n} } \right|_{{m_{N} }}$ of the maximum or minimum magnitudes of the n^th reflected wave retaining N harmonics is defined as the error with respect to $\left| {r_{n} } \right|_{{m_{9} }}$. Table 1 shows the errors together with |r_n|_m when N = 9. Truncating the equations at N = 9 results in very good accuracy for the reflection coefficients of lower harmonics (r₁ and r₃), good accuracy for r₅ and a reasonable accuracy for r₇.

Table 1 Flexural waves: reflection coefficients, reflected power and the percentage error of the minimum or maximum magnitude of the reflection coefficients with respect to the value when N = 9

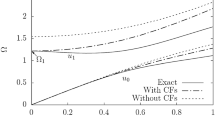
The parameter $\Pi_{n}$, which denotes the normalized power $n^{2} \sqrt n \left| {r_{n} } \right|^{2}$ of the n^th harmonic, is shown in Fig. 6 as a function of $\gamma$ with essential nonlinearity (K = 0). When the system is linear $\Pi_{1} = 1$, however, as illustrated in Fig. 6, with nonlinearity the power leaks from the first harmonic to the higher harmonics. Comparing the powers shows that $\Pi_{1} > \Pi_{3} > \Pi_{5} > \Pi_{7} > \Pi_{9}$. As expected, the incident energy is mostly reflected into the first and third harmonics and only about 5% reflected to the higher harmonics. Furthermore, there is substantial leakage of energy ($\simeq$ 33%) from the first harmonic to the third harmonic.

Fig. 6

Flexural waves: Essential nonlinearity (K = 0): power in each harmonic as a function of $\gamma$, N = 9; inset figure: power of the first harmonic. Red line $\Pi_{1}$; Green dotted line $\Pi_{3}$; blue dotted line $\Pi_{5}$; black line $\Pi_{7}$; pink dotted line $\Pi_{9}$. (Color figure online)

From the net power equation for flexural waves (Eq. (18)), the accuracy of the harmonic balance solution can be defined as the difference between the total power of the reflected waves and unity (the power of the incident wave). For example, for flexural waves with N = 9, the error is

$$ {\text{Error}} = 1 - \left| {r_{1} } \right|^{2} - 9\sqrt 3 \left| {r_{3} } \right|^{2} - 25\sqrt 5 \left| {r_{5} } \right|^{2} - 49\sqrt 7 \left| {r_{7} } \right|^{2} - 81\sqrt 9 \left| {r_{9} } \right|^{2} . $$

(46)

With small enough solver tolerances that used in MATLAB, this error is less than 10^–8.

6.3 Flexural waves: case of two incident and reflected waves

The results presented in this section concern the effect of multiple incident waves on the wave reflections at the end of the beam for the case of essential nonlinearity. The reflection coefficients now depend on $\gamma$ together with the magnitude and phase of $\alpha_{3}$. The source of the multiple incident waves might be either multi-harmonic excitation or the reflection of the negative-going waves with different frequencies and phases from a boundary or discontinuity at some point $x < 0$.

6.3.1 Flexural waves: the effect of $\Phi_{3}$ on the magnitudes of the reflection coefficients

Figures 7 and 8 show the effect of the phase difference $\Phi_{3}$ between the incident waves with $\left| {\alpha_{3} } \right| = 1$ as a function of $\gamma$. (Fig. 7 is a contour plot, while Fig. 8 is a 2D plot for the same parameters). It can be seen that the reflection coefficients depend strongly on the phase of the incident third harmonic. For example, when $\Phi_{3} = \pi$ and $\gamma \ll 1$, $\left| {r_{1} } \right| \simeq 1$, then, with increasing $\gamma$, |r₁| increases and reaches a local maximum and then decreases and reaches a minimum, again increases and reaches a local maximum and finally asymptotes to 1 (|r₁| has two maximums and one minimum). However, when $\Phi_{3} = 0$ and $\gamma \ll 1$, $\left| {r_{1} } \right| \simeq 1$, then as $\gamma$ increases the magnitude of r₁ decreases and reaches a minimum, then increases and reaches a maximum, again decreases and reaches a minimum and for $\gamma \gg 1$ asymptotes to 1 (|r₁| has one maximum and two minimums). As illustrated in Figs. 7a and 8a, the minimum value |r₁|_min occurs when $\Phi_{3} \simeq \pi$, while |r₁|_max occurs at $\Phi_{3} \simeq 0$. Since energy is conserved $\left| {r_{1} } \right|^{2} + 9\sqrt 3 \left| {r_{3} } \right|^{2} = 1 + 9\sqrt 3 \left| {\alpha_{3} } \right|^{2}$, and hence when $\left| {r_{1} } \right|$ is maximum $\left| {r_{3} } \right|$ is minimum as shown in Figs. 7b and 8b. Figures 7a and 8a show that, in contrast to the case of one incident wave, $\left| {r_{1} } \right|$ can be significantly larger than 1 if $\Phi_{3} \simeq 0$. Furthermore, with two incident waves, |r₁|_min can be smaller than when $\alpha_{3} = 0$. When $\Phi_{3} \simeq 0$, both incident waves are in phase when $t = {{n\pi } \mathord{\left/ {\vphantom {{n\pi } \omega }} \right. \kern-\nulldelimiterspace} \omega }$ and produce a larger displacement. On the other hand, when $\Phi_{3} \simeq \pi$ the incident waves are out of phase and produce a smaller displacement. As illustrated in Figs. 7b and 8b, although $\Phi_{3}$ has a significant effect on $\left| {r_{1} } \right|$, it does not substantially affect $\left| {r_{3} } \right|$ due to dominance of the direct reflection of the incident third harmonic.

Fig. 7

Flexural waves: Retaining two incident and two reflected waves: the magnitudes of the reflection coefficients of the first and third harmonics for the case of essential nonlinearity with $\left| {\alpha_{3} } \right| = 1$ as functions of $\gamma$ and $\Phi_{3}$: a |r₁|, b |r₃|

Fig. 8

Flexural waves: Retaining two incident and two reflected waves: the magnitudes of the reflection coefficients of the first and third harmonics for the case of essential nonlinearity with $\left| {\alpha_{3} } \right| = 1$ and various $\Phi_{3}$ as a function of $\gamma$: a |r₁|, b |r₃|

Figures 9 and 10 show the magnitudes of the reflection coefficients as functions of $\gamma$ and $\left| {\alpha_{3} } \right|$ for $\Phi_{3} = 0,\pi$. (Fig. 9 is a contour plot, while Fig. 10 is a 2D plot for the same parameters). The figures illustrate the effect of $\left| {\alpha_{3} } \right|$ on the magnitudes of the reflection coefficients and identify the value of $\left| {\alpha_{3} } \right|$ at which |r₁|_min is minimum (when $\Phi_{3} \simeq \pi$) and |r₁|_max is maximum (when $\Phi_{3} \simeq 0$). It can be seen from Fig. 9a or 10a that when both incident waves are pure real, |r₁| can be greater than 1 and reaches a maximum of about 2.5 at $\left| {\alpha_{3} } \right| \simeq 1.5$. Furthermore, in Fig. 9c or 10c, |r₁| reaches a minimum of about 0.4 at $\left| {\alpha_{3} } \right| \simeq 0.5$, which is significantly smaller than the case with one incident wave ($\left| {r_{1} } \right|_{min} \simeq 0.8$). Figures 9b or 10b and 9d or 10d show that the reflected third harmonic, $a_{3}^{ - }$, is dominated by the incident wave, $a_{3}^{ + }$.

Fig. 9

Flexural waves: Retaining two incident and two reflected waves: the magnitudes of the reflection coefficients of the first and third harmonics for the case of essential nonlinearity as functions of $\gamma$ and $\left| {\alpha_{3} } \right|$: a |r₁|, $\Phi_{3} = 0$, b |r₃|, $\Phi_{3} = 0$, c |r₁|, $\Phi_{3} = \pi$, d |r₃|, $\Phi_{3} = \pi$

Fig. 10

Flexural waves: Retaining two incident and two reflected waves: the magnitudes of the reflection coefficients of the first and third harmonics for the case of essential nonlinearity with various $\left| {\alpha_{3} } \right|$ as a function of $\gamma$: a |r₁|, $\Phi_{3} = 0$, b |r₃|, $\Phi_{3} = 0$, c |r₁|, $\Phi_{3} = \pi$, d |r₃|, $\Phi_{3} = \pi$

6.3.2 Flexural waves: multiple solutions

For some parameter values, there are multiple solutions for the reflection coefficients. This behaviour is not uncommon in nonlinear systems, e.g. the Duffing oscillator. These are accompanied by jumps in the values of |r| as $\gamma$ increases or decreases, i.e. by exciting the beam at certain frequencies there are two possible reflection coefficients for the beam.

When $\gamma \ll 1$, there are no jumps in the magnitudes of the reflection coefficients; however, as $\gamma$ increases, for some values of $\Phi_{3}$ and $\left| {\alpha_{3} } \right|$ the effects of nonlinearity are strong and the magnitudes of r₁ and r₃ are multivalued, undergoing a rapid change or jump as $\gamma$ changes. When both incident waves are pure real, there is no jump, as shown in Figs. 9a, b, 10a and b. In Figs. 7 and 8, multiple solutions occur when $0.0039 < \gamma < 0.0071$ and ${\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-\nulldelimiterspace} 3} \le \Phi_{3} \le {{5\pi } \mathord{\left/ {\vphantom {{5\pi } 6}} \right. \kern-\nulldelimiterspace} 6}$, while in Figs. 9c, d, 10c and d, there are two solutions for the reflection coefficients in the range $0.0126 < \gamma < 0.0215$ and $0.5 \le \left| {\alpha_{3} } \right| \le 0.8$. As demonstrated in Figs. 11 and 12, in these parameter ranges, the magnitudes of the reflection coefficients become multi-valued for some values of $\gamma$ and there are at least two possible solutions for |r₁| and |r₃|. Results for the reflection coefficients are shown for both increasing and decreasing $\gamma$. As can be seen in Figs. 11 and 12, due to energy conservation, when |r₁| jumps up from the lower branch to the upper branch, |r₃| jumps down.

Fig. 11

Flexural waves: Magnitudes of the reflection coefficients of the first and third harmonics with $\left| {\alpha_{3} } \right| = 1$ as a function of $\gamma$: a |r₁| b |r₃|, green dotted line Solution 1; red dotted line Solution 2. (Color figure online)

Fig. 12

Flexural waves: Magnitudes of the reflection coefficients of the first and third harmonics with $\Phi_{3} = \pi$ as a function of $\gamma$: a |r₁| b |r₃|, green dotted line Solution 1; red dotted line Solution 2. (Color figure online)

For example, in Fig. 12, when $\left| {\alpha_{3} } \right| = 0.6$, the magnitudes of r₁ and r₃ change substantially in the region $0.0175 < \gamma < 0.018$. The difference between the two solutions is largest at $\Phi_{3} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-\nulldelimiterspace} 3}$ in Fig. 11 and at $\left| {\alpha_{3} } \right| = 0.6$, in Fig. 12.

Note that to have an accurate solution, the tolerances should be small enough. The error of the numerical method for multiple combinations of initial conditions is less than 10^–8.

Numerical studies have been performed to determine the magnitude and phase of $\alpha_{3}$ for which there are multiple solutions. The parameter region in which the solution is multi-valued is shown in Fig. 13. When $40^{0} < \Phi_{3} < 193^{0}$ or $0.45 < \left| {\alpha_{3} } \right| < 1.27$, there is more than one solution for the magnitudes of the reflection coefficients for some values of $\gamma$.

Fig. 13

Flexural waves: the region in which the solution is multi-valued

6.4 Axial waves

In this section, various numerical examples are presented for axial waves with essential nonlinearity. First, results with only one incident wave and two reflected waves being retained (i.e. N = 3) are presented. Then, the convergence of the solution is illustrated. Finally, the case with two incident and reflected waves is considered.

6.4.1 Axial waves: the case of one incident wave and two reflected waves

The magnitude and phase of the reflection coefficients of the first and third harmonics are shown in Fig. 14 as a function of $\gamma = (A/\Omega )$ with K = 0. Numerical results are shown, together with the analytical solutions for weak nonlinearity presented in Appendix B. As for the case of flexural waves, results are in good agreement for small values of $\gamma$. However, as $\gamma$ increases, the nonlinear effects become more pronounced, and the analytical results become less accurate: more terms need to be included in the expansion to give better accuracy, but this becomes increasingly intractable, especially when more harmonics are retained.

Fig. 14

Axial waves: Retaining one incident wave and two reflected waves; the magnitudes and phases of the reflection coefficients as a function of $\gamma$ from numerical and analytical solutions for the case of essential nonlinearity: a |r₁| b $\phi_{1}$, c |r₃|, d $\phi_{3}$ blue dotted line numerical solution; red dotted line small parameter expansion. (Color figure online)

As illustrated in Fig. 14, the qualitative behaviour of the rod is similar to that of the beam. When $\gamma \ll 1$ the end of the rod is in effect free and $r_{1} = 1$. The magnitude of the reflection coefficient of the first harmonic has a minimum value of about 0.9193 at $\gamma \simeq 0.29$, while the magnitude of r₃ has a maximum value of 0.1311. At this point, the effects of the nonlinearity are strongest and the maximum leakage of energy from the first to the third harmonic occurs. As $\gamma$ increases further, r₁ increases while r₃ decreases. When $\gamma > > 1$, the end of the rod effectively becomes fixed and $r_{1} = - 1$. In Fig. 14c, it can be seen that the phase of the first harmonic increases from zero when $\gamma < < 1$ to 180° when $\gamma > > 1$ (i.e. from that of a rod with a free end to one with a fixed end), while $\phi_{3}$ is 90° when $\gamma = 0$ and asymptotes to 90° when $\gamma > > 1$.

6.4.2 Axial waves: higher harmonics for one incident wave

Table 2 shows the results of a convergence study similar to that in Sect. 6.2. The errors are shown together with the magnitude of the reflection coefficients and power in each harmonic with N = 9. When only the first and third harmonics are retained, |r₁|_min = 0.9193. When the fifth harmonic is retained |r₁|_min decreases to 0.9141; however, it does not change significantly when higher harmonics are retained. When the fifth harmonic is retained, |r₃|_max decreases noticeably from 0.1312 (when only the first and third harmonics are retained) to 0.1267. When the seventh harmonic is taken into account, |r₃|_max decreases slightly to 0.1264. Furthermore, retaining the ninth harmonic has little effect on the magnitude of r₃. As for the case of the beam, as higher harmonics are retained, the maximum magnitudes of the higher reflection coefficients decrease and $\left| {r_{3} } \right|_{max} > \left| {r_{5} } \right|_{max} > \left| {r_{7} } \right|_{max} > \left| {r_{9} } \right|_{max}$. The normalized power in the n^th reflected harmonic for axial waves, $n^{2} \left| {r_{n} } \right|^{2}$ is also shown in Table 2. As can be seen, $n^{2} \left| {r_{n} } \right|^{2}$ decreases rapidly with increasing n. Retaining N harmonics gives moderate accuracy for r_N, good accuracy for r_N-2 and very good accuracy for the reflection coefficients for lower harmonics.

Table 2 Axial waves: Reflection coefficients, reflected power and the percentage error of the minimum or maximum magnitude of the reflection coefficients with respect to the value when N = 9

6.4.3 Axial waves: case of two incident waves and two reflected waves

In Figs. 15, 16, 17 and 18, the magnitudes of the reflection coefficients are shown as a function of $\gamma$ for the case of essential nonlinearity when there are two incident and reflected axial waves. First, in Figs. 15 and 16, the dependence on $\Phi_{3}$ is shown with $\left| {\alpha_{3} } \right| = 1$, while Figs. 17 and 18 show the dependence on $\left| {\alpha_{3} } \right|$ for $\Phi_{3} = 0,\pi$. Similar to the case of flexural waves, $\left| {\alpha_{3} } \right|$ affects the reflection coefficients substantially, but the behaviour is a little different from those of flexural waves. This is due to the interaction of waves with different frequencies, which makes the vibration of the system more complex. When $\Phi_{3} \simeq \pi$, $\left| {r_{1} } \right|$ is minimum and hence $\left| {r_{3} } \right|$ is maximum. Furthermore, comparing Figs. 14 and 17 it is seen that the minimum magnitude of $r_{1}$ can be smaller than when there is just one incident wave. Additionally, the magnitude of $r_{1}$ can be larger than one. As can be seen in Figs. 15a or 16a, the maximum value of $\left| {r_{1} } \right|$ is about 1.4 and occurs when $\Phi_{3} \simeq 0$. In contrast to the first harmonic, as illustrated in Fig. 15b or 16b, $\Phi_{3}$ has little effect on $r_{3}$ due to the dominance of the third incident wave. When $\left| {\alpha_{3} } \right| \simeq 0.7$ and $\Phi_{3} = 0$, $\left| {r_{1} } \right|$ is maximum and $\left| {r_{3} } \right|$ is minimum; however, when $\left| {\alpha_{3} } \right| \simeq 0.4$ and $\Phi_{3} = \pi$, $\left| {r_{1} } \right|$ is minimum and $\left| {r_{3} } \right|$ is maximum. Examining Figs. 17 and 18, it can be noted that when $\left| {\alpha_{3} } \right| > 1$, $a_{3}^{ + }$ is dominant and, $\left| {r_{3} } \right| \simeq \left| {\alpha_{3} } \right|$.

Fig. 15

Axial waves: Retaining two incident and two reflected waves; the magnitudes of the reflection coefficients of the first and third harmonics for the case of essential nonlinearity with $\left| {\alpha_{3} } \right| = 1$ as functions of $\gamma$ and $\Phi_{3}$ a |r₁|, b |r₃|

Fig. 16

Axial waves: Retaining two incident and two reflected waves; the magnitudes of the reflection coefficients of the first and third harmonics for the case of essential nonlinearity with $\left| {\alpha_{3} } \right| = 1$ as functions of $\gamma$ and $\Phi_{3}$ a |r₁|, b |r₃|

Fig. 17

Axial waves: The magnitudes of the reflection coefficients of the first and third harmonics as functions of $\gamma$ and $\left| {\alpha_{3} } \right|$, retaining only the first and third harmonics: a |r₁|, $\Phi_{3} = 0$, b |r₃|, $\Phi_{3} = 0$, c |r₁|, $\Phi_{3} = \pi$, d |r₃|, $\Phi_{3} = \pi$

Fig. 18

Axial waves: The magnitudes of the reflection coefficients of the first and third harmonics for various values of $\left| {\alpha_{3} } \right|$ as a function of $\gamma$ and retaining only the first and third harmonics: a |r₁|, $\Phi_{3} = 0$, b |r₃|, $\Phi_{3} = 0$, c |r₁|, $\Phi_{3} = \pi$, d |r₃|, $\Phi_{3} = \pi$

7 Conclusion

This paper presented analytical and numerical studies of the reflection coefficients for time-harmonic waves in a waveguide from a boundary with nonlinear stiffness. A wave solution was applied to a semi-infinite, thin rod and a semi-infinite Euler–Bernoulli beam. Incident, reflected propagating and nearfield waves comprising a series of harmonics at integer multiples of the frequency of the first incident wave were included. For simplicity, the nonlinearity was assumed to be cubic, with only odd harmonics incident and reflected at the boundary. An infinite set of equations was derived, and solutions were developed using the harmonic balance method by truncating these and including a finite number of harmonics. The conclusions obtained are as follows.

• (1) Dimensionless parameters It was shown that the reflection coefficients depend on three dimensionless parameters: the frequency ratio, the linear stiffness and the nonlinear stiffness of the spring, together with the relative amplitudes of the incident waves $\alpha_{n}$.

• (2) Strong nonlinearity Weak nonlinearity was defined to be the case when ${A \mathord{\left/ {\vphantom {A {\left( {K + \Omega } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {K + \Omega } \right)}} \ll 1$ for axial waves and ${A \mathord{\left/ {\vphantom {A {\left( {K + \Omega^{3/2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {K + \Omega^{3/2} } \right)}} \ll 1$ for flexural waves. So that the case of essential nonlinearity was studied. For essential nonlinearity (K = 0), the reflection coefficients depend only on the nondimensional parameter $\gamma = {A \mathord{\left/ {\vphantom {A \Omega }} \right. \kern-\nulldelimiterspace} \Omega }$ and $\alpha_{n}$.

• (3) Minimum reflection with one incident wave For the case with one incident wave and when two reflected waves are retained (N = 3), the method of expansion in a small parameter was used to find analytical expressions for the reflection coefficients of the first and third harmonics. Results were compared with numerical solutions for essential nonlinearity. It was seen that the magnitude of the reflection coefficient of the first harmonic for axial and flexural waves has a minimum and energy leaks from the first harmonic to the third harmonic. Since energy is conserved, with increasing $\gamma$, the magnitude of the reflection coefficient of the first harmonic decreases and reaches a minimum, while the magnitude of r₃ increases and reaches a maximum. The minimum magnitude of r₁ was about 0.92 for axial waves and about 0.8 for flexural waves. For a single incident wave, the maximum energy that leaks from the first harmonic wave is about 16% of the incident energy for axial waves and 36% for flexural waves. The qualitative behaviour was similar for axial and flexural vibrations.

• (4) Linear and nonlinear effects The effects of K and A on |r₁|_min and |r₃|_max were studied. It was shown that as we increase nonlinearity or decrease linearity of the system, the minimum or maximum magnitudes of the reflection coefficients asymptote to those values for essential nonlinearity, i.e. for large values of A/K, $\left| {r_{1} } \right|_{min} \simeq 0.8$ for flexural waves and $\left| {r_{1} } \right|_{\min } \simeq 0.92$ for axial waves.

• (5) Higher harmonics and convergence For the case with one incident wave and truncating the system of equations at N = 5, 7 and 9, the reflection coefficients and powers in each harmonic were obtained and compared with the results for N = 3. The results showed that the qualitative behaviour of the system with a larger number of retained reflected waves is the same as that with N = 3 and that the solution was seen to converge for increasing N. Retaining the fifth harmonic gives very good accuracy for the first and third harmonics.

• (6) Multiple incident waves The case of two incident and two reflected waves was studied. The reflection coefficients now depend on the magnitude and phase of the ratio of the amplitudes of the third to first harmonic incident waves $\alpha_{3}$. It was seen that the reflection coefficients depend significantly on the incident third harmonic, as described in Sects. 6.3 and 6.4.3. There are qualitative differences in the dependencies of the reflection coefficients on the dimensionless frequency for the rod and beam. For example, for the beam, there can be two local maximums and one minimum (or one maximum and two local minimums), while for the rod only one maximum and one minimum were observed. A numerical study to show the minimum and maximum reflection coefficients of the first harmonic with two incident waves was done. When both incident waves are pure real, $\left| {r_{1} } \right|$ has a maximum value significantly larger than 1, while when the phase difference of incident waves is $\pi$, $\left| {r_{1} } \right|_{min}$ is smaller than the case with only one incident wave.

• (7) Multiple solutions for reflection coefficients It was seen that for certain values of $\left| {\alpha_{3} } \right|$ and $\Phi_{3}$ there can be two solutions for the reflection coefficients of flexural waves: jump phenomena occur as $\gamma$ increases or decreases. Because energy is conserved, when |r₁| jumps up from the lower branch to the upper branch, |r₃| jumps down. Numerical studies were performed and the region in which the system becomes multi-valued was determined. No jump phenomenon was found for the reflection of axial waves.

Appendices

Appendix A: Equations for the reflection coefficients of flexural waves with a higher number of harmonics

Equation (27) is truncated at N = 9, and harmonics are collected by using the harmonic balance method. The equations for r₅, r₇, and r₉ are

$$ \begin{gathered} \left[ {5\sqrt 5 \Omega ^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} r_{5} \left( {1 - i} \right) - 2Kr_{5} } \right] \hfill \\ + ( - 24A)\left\{ {r_{3} \left[ {\left( {r_{1} + 1} \right)^{2} + r_{3} \left( {\bar{r}_{1} + 1} \right)} \right]} \right. \hfill \\ + r_{5} \left[ {2\left( {r_{1} + 1} \right)\left( {\bar{r}_{1} + 1} \right) + 2r_{3} \bar{r}_{3} + r_{5} \bar{r}_{5} } \right] \hfill \\ + r_{7} \left[ {\left( {\bar{r}_{1} + 1} \right)^{2} + 2\bar{r}_{3} \left( {r_{1} + 1} \right) + 2r_{3} \bar{r}_{5} + 2r_{5} \bar{r}_{7} + r_{7} \bar{r}_{9} } \right] \hfill \\ \left. { + 2r_{9} \left[ {\bar{r}_{3} \left( {\bar{r}_{1} + 1} \right) + \bar{r}_{5} \left( {r_{1} + 1} \right) + r_{3} \bar{r}_{7} + r_{5} \bar{r}_{9} } \right]} \right\} = 0, \hfill \\ \end{gathered} $$

(A.1)

$$ \begin{gathered} \left[ {7\sqrt 7 \Omega ^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} r_{7} \left( {1 - i} \right) - 2Kr_{7} } \right] + \hfill \\ + ( - 24A)\left\{ {r_{3}^{2} \left( {r_{1} + 1} \right)} \right. \hfill \\ + r_{5} \left[ {\left( {r_{1} + 1} \right)^{2} + 2r_{3} \left( {\bar{r}_{1} + 1} \right) + r_{5} \bar{r}_{3} } \right] \hfill \\ + r_{7} \left[ {2\left( {r_{1} + 1} \right)\left( {\bar{r}_{1} + 1} \right) + 2r_{3} \bar{r}_{3} + 2r_{5} \bar{r}_{5} + r_{7} \bar{r}_{7} } \right] \hfill \\ \left. { + r_{9} \left[ {\left( {\bar{r}_{1} + 1} \right)^{2} + 2\bar{r}_{3} \left( {r_{1} + 1} \right) + 2\left( {r_{3} \bar{r}_{5} + r_{5} \bar{r}_{7} + r_{7} \bar{r}_{9} } \right)} \right]} \right\} = 0, \hfill \\ \end{gathered} $$

(A.2)

$$ \begin{gathered} \left[ {9\sqrt 9 \Omega ^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} r_{9} \left( {1 - i} \right) - 2Kr_{9} } \right] \hfill \\ + ( - 8A)\left\{ {r_{3} ^{3} } \right. \hfill \\ + 3r_{5} \left[ {2r_{3} \left( {r_{1} + 1} \right) + r_{5} \left( {\bar{r}_{1} + 1} \right)} \right] \hfill \\ + 3r_{7} \left[ {\left( {r_{1} + 1} \right)^{2} + 2r_{3} \left( {\bar{r}_{1} + 1} \right) + 2r_{5} \bar{r}_{3} + r_{7} \bar{r}_{5} } \right] \hfill \\ \left. { + 3r_{9} \left[ {2\left( {r_{1} + 1} \right)\left( {\bar{r}_{1} + 1} \right) + 2r_{3} \bar{r}_{3} + 2r_{5} \bar{r}_{5} + 2r_{7} \bar{r}_{7} + r_{9} \bar{r}_{9} } \right]} \right\} = 0. \hfill \\ \end{gathered} $$

(A.3)

Appendix B: Equations for the reflection coefficients of axial waves

The equivalent equations for axial waves are presented here. First, it is assumed that only $a_{1}^{ + }$ is incident on the boundary so that $\alpha_{n} = 0,\,\,n > 1$. Hence, Eq. (24) becomes:

$$ \begin{gathered} \left[ {i\Omega \,\left( {e^{i\omega t} - \sum\limits_{n = 1,3,5,...}^{\infty } {nr_{n} e^{in\omega t} } } \right)} \right] + CC \hfill \\ = K\left[ {e^{i\omega t} + \sum\limits_{n = 1,3,5,...}^{\infty } {r_{n} e^{in\omega t} } + CC} \right] + A\left[ {e^{i\omega t} + \sum\limits_{n = 1,3,5,...}^{\infty } {r_{n} e^{in\omega t} } + CC} \right]^{3} . \hfill \\ \end{gathered} $$

(B.1)

The resulting set of equations can then be solved using the harmonic balance method. For example, taking N = 9, the equation for the first harmonic is:

$$ \begin{gathered} \left[ {i\Omega \left( {r_{1} - 1} \right) + K\left( {r_{1} + 1} \right)} \right] \hfill \\ + 3A\left\{ {\left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)^{2} + } \right. \hfill \\ r_{3} \left[ {\left( {\overline{r}_{1} + 1} \right)^{2} + 2\overline{r}_{3} \left( {r_{1} + 1} \right)} \right] + \hfill \\ r_{5} \left[ {2\overline{r}_{3} \left( {\overline{r}_{1} + 1} \right) + 2\overline{r}_{5} \left( {r_{1} + 1} \right)} \right] + r_{3}^{2} \overline{r}_{5} + \hfill \\ r_{7} \left[ {\overline{r}_{3}^{2} + 2\overline{r}_{5} \left( {\overline{r}_{1} + 1} \right)2\overline{r}_{7} \left( {r_{1} + 1} \right)} \right] + 2r_{3} r_{5} \overline{r}_{7} + \hfill \\ \left. {r_{9} \left[ {2\overline{r}_{3} \overline{r}_{5} + 2\overline{r}_{7} \left( {\overline{r}_{1} + 1} \right) + 2\overline{r}_{9} \left( {r_{1} + 1} \right)} \right] + 2r_{3} r_{7} \overline{r}_{9} + r_{5}^{2} \overline{r}_{9} } \right\} = 0. \hfill \\ \end{gathered} $$

(B.2)

In a similar way, collecting terms of frequency $3\omega$ gives

$$ \begin{gathered} \left[ {3r_{3} i\Omega + Kr_{3} } \right]+ \hfill \\ A\left\{ {\left( {r_{1} + 1} \right)^{3} + } \right. \hfill \\ r_{3} \left[ {3\overline{r}_{3} r_{3} + 6\left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)} \right] + \hfill \\ r_{5} \left[ {3\left( {\overline{r}_{1} + 1} \right)^{2} + 6\left( {\overline{r}_{3} \left( {r_{1} + 1} \right) + r_{3} \overline{r}_{5} } \right)} \right] + \hfill \\ 6r_{7} \left[ {\overline{r}_{3} \left( {\overline{r}_{1} + 1} \right) + \overline{r}_{5} \left( {r_{1} + 1} \right) + r_{3} \overline{r}_{7} } \right] + 3\overline{r}_{7} r_{5}^{2} + \hfill \\ \left. {6r_{9} \left[ {\overline{r}_{5} \left( {\overline{r}_{1} + 1} \right) + \overline{r}_{7} \left( {r_{1} + 1} \right) + r_{3} \overline{r}_{9} } \right] + 3r_{9} \overline{r}_{3}^{2} + 6r_{5} r_{7} \overline{r}_{9} } \right\} = 0. \hfill \\ \end{gathered} $$

(B.3)

Similarly, equations can be found for higher harmonics:

$$ \begin{gathered} \left[ {5r_{5} i\Omega + Kr_{5} } \right] \hfill \\ + 3A\left\{ {r_{3} \left[ {\left( {r_{1} + 1} \right)^{2} + r_{3} \left( {\bar{r}_{1} + 1} \right)} \right]} \right. \hfill \\ + r_{5} \left[ {2\left( {r_{1} + 1} \right)\left( {\bar{r}_{1} + 1} \right) + 2r_{3} \bar{r}_{3} + r_{5} \bar{r}_{5} } \right] \hfill \\ + r_{7} \left[ {\left( {\bar{r}_{1} + 1} \right)^{2} + 2\bar{r}_{3} \left( {r_{1} + 1} \right) + 2r_{3} \bar{r}_{5} + 2r_{5} \bar{r}_{7} + r_{7} \bar{r}_{9} } \right] \hfill \\ \left. { + 2r_{9} \left[ {\bar{r}_{3} \left( {\bar{r}_{1} + 1} \right) + \bar{r}_{5} \left( {r_{1} + 1} \right) + r_{3} \bar{r}_{7} + r_{5} \bar{r}_{9} } \right]} \right\} = 0, \hfill \\ \end{gathered} $$

(B.4)

$$ \begin{gathered} \left[ {7r_{7} i\Omega + Kr_{7} } \right] \hfill \\ + 3A\left\{ {r_{3}^{2} \left( {r_{1} + 1} \right)} \right. \hfill \\ + r_{5} \left[ {\left( {r_{1} + 1} \right)^{2} + 2r_{3} \left( {\bar{r}_{1} + 1} \right) + r_{5} \bar{r}_{3} } \right] \hfill \\ + r_{7} \left[ {2\left( {r_{1} + 1} \right)\left( {\bar{r}_{1} + 1} \right) + 2r_{3} \bar{r}_{3} + 2r_{5} \bar{r}_{5} + r_{7} \bar{r}_{7} } \right] \hfill \\ \left. { + r_{9} \left[ {\left( {\bar{r}_{1} + 1} \right)^{2} + 2\bar{r}_{3} \left( {r_{1} + 1} \right) + 2\left( {r_{3} \bar{r}_{5} + r_{5} \bar{r}_{7} + r_{7} \bar{r}_{9} } \right)} \right]} \right\} = 0, \hfill \\ \end{gathered} $$

(B.5)

$$ \begin{gathered} \left[ {9r_{9} i\Omega + Kr_{9} } \right] \hfill \\ + A\left\{ {r_{3} ^{3} } \right. \hfill \\ + 3r_{5} \left[ {2r_{3} \left( {r_{1} + 1} \right) + r_{5} \left( {\bar{r}_{1} + 1} \right)} \right] \hfill \\ + 3r_{7} \left[ {\left( {r_{1} + 1} \right)^{2} + 2r_{3} \left( {\bar{r}_{1} + 1} \right) + 2r_{5} \bar{r}_{3} + r_{7} \bar{r}_{5} } \right] \hfill \\ \left. { + 3r_{9} \left[ {2\left( {r_{1} + 1} \right)\left( {\bar{r}_{1} + 1} \right) + 2r_{3} \bar{r}_{3} + 2r_{5} \bar{r}_{5} + 2r_{7} \bar{r}_{7} + r_{9} \bar{r}_{9} } \right]} \right\} = 0. \hfill \\ \end{gathered} $$

(B.6)

The case of N = 3 in Eq. (B.1) is now considered so that only the first and third reflected harmonics are taken into account. Equations (B.2) and (B.3) become

$$ \left[ {i\Omega \left( {r_{1} - 1} \right) + K\left( {r_{1} + 1} \right)} \right] + 3A\left[ {\left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)^{2} + r_{3} \left( {\overline{r}_{1} + 1} \right)^{2} + 2r_{3} \overline{r}_{3} \left( {r_{1} + 1} \right)} \right] = 0, $$

(B.7)

$$ \left[ {3r_{3} i\Omega + Kr_{3} } \right] + A\left[ {\left( {r_{1} + 1} \right)^{3} + 3\overline{r}_{3} r_{3}^{2} + 6r_{3} \left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)} \right] = 0. $$

(B.8)

When A = 0, the equations reduce to those of a linear system, with $r_{lin} = - \frac{{1 - {{i\Omega } \mathord{\left/ {\vphantom {{i\Omega } K}} \right. \kern-\nulldelimiterspace} K}}}{{1 + {{i\Omega } \mathord{\left/ {\vphantom {{i\Omega } K}} \right. \kern-\nulldelimiterspace} K}}}$ and $r_{3} = 0$. In this case, $\left| {r_{1} } \right| = 1$ because of energy conservation. Putting K = 0 in equations (B.7) and (B.8), it is seen that the reflection coefficients depend only on the nondimensional parameter $\gamma = \frac{A}{\Omega }.$ Equations (B.7) and (B.8) can be rewritten in terms of $\gamma$ as

$$ \left[ {i(r_{1} - 1)} \right] + 3\gamma \left[ {\left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)^{2} + r_{3} \left( {\overline{r}_{1} + 1} \right)^{2} + 2r_{3} \overline{r}_{3} \left( {r_{1} + 1} \right)} \right] = 0, $$

(B.9)

$$ \left[ {3r_{3} i} \right] + \gamma \left[ {\left( {r_{1} + 1} \right)^{3} + 3\overline{r}_{3} r_{3}^{2} + 6r_{3} \left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)} \right] = 0. $$

(B.10)

To find an approximate solution to Eqs. (B.7) and (B.9), the same method given in Sect. 4.2 is utilized. Expressions for $r_{1}$ and $r_{3}$ are

$$ \begin{gathered} r_{01} = r_{lin} = - \frac{{1 - i{\Omega \mathord{\left/ {\vphantom {\Omega K}} \right. \kern-\nulldelimiterspace} K}}}{{1 + i{\Omega \mathord{\left/ {\vphantom {\Omega K}} \right. \kern-\nulldelimiterspace} K}}};\,\,\,r_{11} = - {\left( {\frac{3A}{{i\Omega + K}}} \right)\left( {1 + r_{01} } \right)^{2} \left( {1 + \overline{r}_{01} } \right)}, \\ r_{21} = - {\left( {\frac{3A}{{i\Omega + K}}} \right)(\overline{r}_{11} (r_{01} + 1)^{2} + r_{13} (\overline{r}_{01} + 1)^{2} + 2r_{11} (r_{01} + 1)(\overline{r}_{01} + 1))}, \\ \end{gathered} $$

(B.11)

$$ \begin{gathered} r_{03} = 0;\,\,\,\,\,r_{13} = - {\left( {\frac{A}{3i\Omega + K}} \right)\left( {r_{01} + 1} \right)^{3} },\,\,\,\,\, \\ r_{23} = - {\left( {\frac{A}{3i\Omega + K}} \right)\left( {3r_{11} (r_{01} + 1)^{2} + 6r_{13} (r_{01} + 1)(\overline{r}_{01} + 1)} \right)}, \\ \end{gathered} $$

(B.12)

The second incident wave with frequency $3\omega$ is now considered so that $\alpha_{3} \ne 0$. Truncating Eq. (24) at N = 3 and collecting harmonics results in

$$ \begin{gathered} \left[ {i\Omega \left( {r_{1} - 1} \right) + K\left( {r_{1} + 1} \right)} \right] + \hfill \\ 3A\left[ {\left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)^{2} + 2\left( {r_{1} + 1} \right)\left( {\alpha_{3} \overline{\alpha }_{3} + r_{3} \overline{r}_{3} + \alpha_{3} \overline{r}_{3} + \overline{\alpha }_{3} r_{3} } \right) + \left( {\alpha_{3} + r_{3} } \right)\left( {\overline{r}_{1} + 1} \right)^{2} } \right] = 0, \hfill \\ \end{gathered} $$

(B.13)

$$ \begin{gathered} 3i\Omega \left[ {r_{3} - \alpha_{3} } \right] + K\left[ {r_{3} + \alpha_{3} } \right] + \hfill \\ A\left[ {\left( {r_{1} + 1} \right)^{3} + 3\left( {r_{3} + \alpha_{3} } \right)^{2} \left( {\overline{r}_{3} + \overline{\alpha }_{3} } \right) + 6\left( {r_{1} + 1} \right)\left( {\overline{r}_{1} + 1} \right)\left( {r_{3} + \alpha_{3} } \right)} \right] = 0, \hfill \\ \end{gathered} $$

(B.14)

and for the case of essential nonlinearity

$$ \begin{gathered} i\left( {r_{1} - 1} \right) + \hfill \\ 3\gamma \left[ {\left( {\overline{r}_{1} + 1} \right)\left( {r_{1} + 1} \right)^{2} + 2\left( {r_{1} + 1} \right)\left( {\alpha_{3} \overline{\alpha }_{3} + r_{3} \overline{r}_{3} + \alpha_{3} \overline{r}_{3} + \overline{\alpha }_{3} r_{3} } \right) + \left( {\alpha_{3} + r_{3} } \right)\left( {\overline{r}_{1} + 1} \right)^{2} } \right] = 0, \hfill \\ \end{gathered} $$

(B.15)

$$ 3i\left[ {r_{3} - \alpha_{3} } \right] + \gamma \left[ {\left( {r_{1} + 1} \right)^{3} + 3\left( {r_{3} + \alpha_{3} } \right)^{2} \left( {\overline{r}_{3} + \overline{\alpha }_{3} } \right) + 6\left( {r_{1} + 1} \right)\left( {\overline{r}_{1} + 1} \right)\left( {r_{3} + \alpha_{3} } \right)} \right] = 0. $$

(B.16)