Introduction

Motivations and State of the Art

Vibratory feeders are widely used in the industry to convey products in manufacturing plants by exploiting mechanical vibrations [1]. Linear vibratory feeders convey the products along a linear path [2] and the flexibility of these devices is exploited to achieve a large amplitude of vibration through a low actuation effort [3]. In general, the number of actuators is smaller than the number of degrees of freedom (DOFs) arising in the system due to its flexibility, leading to an underactuated system. It is well known in the literature that the control of underactuated systems is not trivial, in particular when they are operated in open loop, as it is usually done for linear vibratory feeders. Hence, it is fundamental to carefully plan a-priori the actuation forces to achieve high performances [4]. Open loop control is usually adopted in feeders (as well as other resonators or vibration generators), because these systems, with the goal of reducing their cost, are typically not equipped with sensors, with microprocessors implementing feedback control, or with actuators whose forces can be modified with a high rate and in real-time control as commanded by a controller.

Vibratory feeding is often performed by means of a sinusoidal vibration of the surface employed to convey the products (see, e.g., [5, 6]); however, harmonic excitation does not always allow achieving high conveying velocity [7]. It has been proved that non-sinusoidal vibrations might provide high conveying speed as well as other beneficial features such as reliable sorting and orientating motion [8].

The development of feedforward and motion planning algorithms for underactuated multibody systems is not trivial due to the presence of a rectangular force distribution matrix that exacerbates the difficulties in model inversion. In the case of non-minimum phase systems, model inversion is not trivial; indeed, zeros with positive real part arise, and once the model is inverted, those become right-half complex plane poles leading to unstable internal dynamics that does not enable to compute the actuation forces, since they diverge.

Trajectory tracking is tackled in [9] through an inverse dynamics approach together with the Byrnes–Isidori regulator, a non-causal solution is obtained, i.e., pre-actuation is required, to track the desired trajectory. More recently, the servo-constraint method has been introduced in [10] and applications to meaningful test cases have been proposed in [11, 12]. Such technique represents the trajectory to be tracked as an algebraic constraint that transforms the system model into a set of differential algebraic equations. Optimization-based approaches have been proposed in [4] where the model inversion approach through the non-linear input–output normal form and the servo-constraints are analyzed. Other formulations based on the solution of two-point boundary value optimization problems are proposed to tackle both the inverse dynamics and motion planning; see, e.g., [13,14,15] and the references therein. Recently, an inverse dynamics method for non-linear systems that exploits the non-linear output redefinition has been proposed by the authors in [16] to compute the actuation forces, and the method has been adopted in [17] to perform the motion planning.

In the case of highly underactuated systems, the number of non-actuated coordinates is much larger with respect to the number of independent actuators. In this scenario, achieving satisfying results is not trivial. This is the typical scenario of long and flexible linear vibratory feeders employed in manufacturing plants where several coordinates are adopted to model the flexible tray over which products flow, while a limited number of actuators are installed. In this case, dynamic structural modification (DSM) can be employed to improve the system performances. DSM methods compute the optimal structural modifications (mass, damping and stiffness system parameter modifications) that enable to achieve the desired specifications. Traditionally, structural modification has been widely adopted over the decades to assign natural frequencies [18,19,20], mode shapes [21, 22] and antiresonance frequencies [23,24,25]. Recently, DSM has been adopted also to increase the robustness against the system uncertainties in motion planning [26] and to improve the subspace of the allowable motion in linear vibratory feeders excited through harmonic excitation [27]. In addition, a mechanical design approach to convert non-minimum phase systems into minimum phase has been proposed in [4].

Contributions of the Paper

This paper proposes the general mathematical formulation for the inverse dynamics of non-minimum phase underactuated mechanical systems, where QR decomposition is exploited to transform the system into the actuated-unactuated model. Then, the internal dynamics is characterized exploiting the definition of the output reference in terms of the actuated and unactuated coordinates. Further, since the system is non-minimum phase, a strategy to stabilize the internal dynamics (relating the desired output trajectory and the unactuated coordinates) is proposed through the output redefinition method. In particular, the paper extends the inverse dynamics method for linear vibratory feeders proposed by the authors in [27] and [28] in the simpler case of a sinusoidal trajectory reference, to the more general case of a generic periodic reference trajectory. Conversely to the above-mentioned papers where an algebraic problem was solved to compute the actuation forces, here, a differential–algebraic problem is adopted because of the presence of the internal dynamics that is governed by ordinary differential equations.

The manuscript also provides a novel structural modification strategy compared to the usual DSM approaches proposed in the literature, that is therefore another novelty introduced by this paper. Indeed, the proposed approach directly exploits the internal dynamics (formulated for the undamped system, and in the presence of harmonic excitations), thus considering the forced response in the presence of the reference trajectories, to compute the optimal mechanical design for the system that enables to increase the tracking error performances of the whole system.

The proposed method is applied to the challenging case of a non-minimum phase underactuated linear vibratory feeder employed in manufacturing plants to convey products and the results confirm the effectiveness of the inverse dynamics algorithm, of the DSM approach, and of the overall approach proposed in this paper.

The proposed method is of interest under a theoretical point of view, because of the challenges in controlling underactuated systems that are here exacerbated by the presence of more unactuated variables than the actuated ones and because of the unstable internal dynamics. Additionally, it is of interest for several practical applications: the overall approach is an effective tool for the optimal concurrent mechanical design of the feeders (through the DSM) and of the actuation forces (through the inverse dynamics) to improve the feeding capabilities of these widely adopted devices, as well as for other vibration generators sharing similar dynamic models.

Dynamic Model

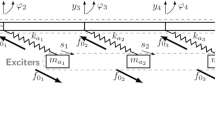
Let us consider the linear vibratory feeder, like the one sketched in Fig. 1, employed in manufacturing plants to convey products (see, e.g., [3]). The tray of the feeder is modeled as a flexible beam through Nb Euler–Bernoulli planar beam elements, as proposed in [28]. The vertical displacements and the nodal rotations of the tray are denoted as \(y_{i}\) and \(\varphi_{i}\), respectively (i = 1,…,Nb + 1). The horizontal displacement of the tray is xt, and the beam is assumed as axially stiff, thus just one coordinate is needed in this direction. Translations that are orthogonal to the xy plane of motion are not considered. The tray is actuated through NA independent actuators modeled as suspended masses (as usually done in linear feeder [28]), whose absolute translations are \(x_{{a_{i} }} = x_{t} + s_{i} \cos \theta_{{\text{f}}}\) and \(y_{{a_{i} }} = y_{i} + s_{i} \sin \theta_{{\text{f}}}\) (i = 1,…,NA). \(y_{i}\) is the tray vertical translation in the point of attachment of the actuators and si is the tray-actuator relative displacement along the direction defined by the angle \(\theta_{{\text{f}}} = 2\pi - \alpha_{{\text{f}}}\), with \(\alpha_{{\text{f}}}\) being the throw angle, that is a key parameter in the feeder design to ensure the desired flow. The model of the actuators, whose mass is \(m_{{a_{i} }}\) and \(k_{{a_{i} }}\) is the stiffness of the leaf spring connecting it to the tray, is here omitted for brevity (for more details about the system model, please refer to [3, 27, 28]).

Fig. 1
figure 1

Simplified scheme of the linear vibratory feeder assumed as the test case

Full size image

The equations of motion of the tray and of the actuators can be merged together and a second-order model of the N-DOFs system is obtained, with N = 2(Nb + 1) + NA + 1

$${\mathbf{M}}{\ddot{{\varvec{z}}}}\left( t \right) + {\mathbf{C}}\dot{\varvec{z}}\left( t \right) + {\mathbf{K}}{\varvec{z}}\left( t \right) = {\mathbf{B}}{\varvec{f}}\left( t \right),$$
(1)

where \({\mathbf{M}},{\mathbf{C}},{\mathbf{K}} \in {\mathbb{R}}^{N \times N}\) are the mass, damping and stiffness matrices of the overall system, respectively. The displacements, velocities and accelerations are collected in vectors \({\varvec{z}}\left( t \right) \in {\mathbb{R}}^{N}\), \(\dot{\varvec{z}}\left( t \right) \in {\mathbb{R}}^{N}\) and \({\ddot{\varvec{z}}}\left( t \right) \in {\mathbb{R}}^{N}\), with \({\varvec{z}}\left( t \right) = \left\{ {\begin{array}{*{20}c} {y_{1} } & {\varphi_{1} } & \ldots & {y_{{N_{{\text{b}}} + 1}} } & {\varphi_{{N_{{\text{b}}} + 1}} } & {x_{t} } & {s_{1} } & \ldots & {s_{{N_{{\text{A}}} }} } \\ \end{array} } \right\}^{T} \in {\mathbb{R}}^{N}\). \({\varvec{f}}\left( t \right)\) collects the NA independent forces exerted by the actuators that are distributed along the system through the actuator influence matrix \({\mathbf{B}} \in {\mathbb{R}}^{{N \times N_{{\text{A}}} }}\).

As it will be shown in the section "System Description and Performance Specifications", B is a dense matrix, i.e., it has more than NA not-null entries. The partition of the coordinates into actuated and unactuated ones, to perform inverse dynamics, is not straightforward. In this work, coordinate transformation based on QR decomposition of B is performed. This approach leads to an orthonormal matrix \({\mathbf{Q}}\) (satisfying \({\mathbf{Q}}^{T} {\mathbf{Q}} = {\mathbf{QQ}}^{T} = {\mathbf{I}}\), where I is the identity matrix) and an upper triangular nonsingular matrix \({\mathbf{B}}_{{\mathbf{A}}}\), with \({\text{rank}}\left( {{\mathbf{B}}_{{\mathbf{A}}} } \right) = {\text{rank}}\left( {\mathbf{B}} \right) = N_{{\text{A}}}\), such that: \({\mathbf{B}} = {\mathbf{QB}}_{{\mathbf{A}}}\). By defining a new coordinate vector \({\varvec{q}} = \left\{ {\begin{array}{*{20}c} {{\varvec{q}}_{{\varvec{A}}} } \\ {{\varvec{q}}_{{\varvec{U}}} } \\ \end{array} } \right\}\),

$${\varvec{z}} = {\mathbf{Q}}\left\{ {\begin{array}{*{20}c} {{\varvec{q}}_{{\varvec{A}}} } \\ {{\varvec{q}}_{{\varvec{U}}} } \\ \end{array} } \right\},$$
(2)

and then by performing the pre multiplication of the left-hand side and of the right-hand side of Eq. (1) by \({\mathbf{Q}}^{T}\), then a partitioned form of the equations of motion is obtained (for more details, refer to [27])

$$\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{{{\mathbf{AA}}}} } & {{\mathbf{M}}_{{{\mathbf{AU}}}} } \\ {{\mathbf{M}}_{{{\mathbf{AU}}}}^{T} } & {{\mathbf{M}}_{{{\mathbf{UU}}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\ddot{\varvec{q}}}_{{\varvec{A}}} \left( t \right)} \\ {{\ddot{\varvec{q}}}_{{\varvec{U}}} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{{{\mathbf{AA}}}} } & {{\mathbf{C}}_{{{\mathbf{AU}}}} } \\ {{\mathbf{C}}_{{{\mathbf{AU}}}}^{T} } & {{\mathbf{C}}_{{{\mathbf{UU}}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{{\varvec{q}}}_{{\varvec{A}}} \left( t \right)} \\ {\dot{{\varvec{q}}}_{{\varvec{U}}} \left( t \right)} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{{\mathbf{AA}}}} } & {{\mathbf{K}}_{{{\mathbf{AU}}}} } \\ {{\mathbf{K}}_{{{\mathbf{AU}}}}^{T} } & {{\mathbf{K}}_{{{\mathbf{UU}}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\varvec{q}}_{{\varvec{A}}} \left( t \right)} \\ {{\varvec{q}}_{{\varvec{U}}} \left( t \right)} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{\mathbf{B}}_{{\mathbf{A}}} } \\ {{\mathbf{0}}_{{\left( {N - N_{{\text{A}}} } \right) \times N_{{\text{A}}} }} } \\ \end{array} } \right]{\varvec{f}}\left( t \right).$$
(3)

The coordinate vector is partitioned into actuated qA \(\in {\mathbb{R}}^{{N_{{\text{A}}} }}\) and unactuated qU \(\in {\mathbb{R}}^{{N - N_{{\text{A}}} }}\) coordinates, and the system submatrices are consistently defined: \({\mathbf{M}}_{{{\mathbf{AA}}}} ,{\mathbf{C}}_{{{\mathbf{AA}}}} ,{\mathbf{K}}_{{{\mathbf{AA}}}} \in {\mathbb{R}}^{{N_{{\text{A}}} \times N_{{\text{A}}} }}\), \({\mathbf{M}}_{{{\mathbf{AU}}}} ,{\mathbf{C}}_{{{\mathbf{AU}}}} ,{\mathbf{K}}_{{{\mathbf{AU}}}} \in {\mathbb{R}}^{{N_{{\text{A}}} \times \left( {N - N_{{\text{A}}} } \right)}}\), \({\mathbf{M}}_{{{\mathbf{UU}}}} ,{\mathbf{C}}_{{{\mathbf{UU}}}} ,{\mathbf{K}}_{{{\mathbf{UU}}}} \in {\mathbb{R}}^{{\left( {N - N_{{\text{A}}} } \right) \times \left( {N - N_{{\text{A}}} } \right)}}\) and \({\mathbf{B}}_{{\mathbf{A}}} \in {\mathbb{R}}^{{N_{{\text{A}}} \times N_{{\text{A}}} }}\).

The dynamics of the actuated sub-system is defined through the first NA equations in Eq. (3), by showing how it is directly affected by the actuation forces f  through the input matrix BA. In contrast, the unactuated coordinates are just indirectly controlled by the evolution of the actuated coordinates through the remaining N – NA equations

$${\mathbf{M}}_{{{\mathbf{UU}}}} {\ddot{\varvec{q}}}_{{\varvec{U}}} \left( t \right) + {\mathbf{C}}_{{{\mathbf{UU}}}} \dot{{\varvec{q}}}_{{\varvec{U}}} \left( t \right) + {\mathbf{K}}_{{{\mathbf{UU}}}} {\varvec{q}}_{{\varvec{U}}} \left( t \right) = - {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {\ddot{\varvec{q}}}_{{\varvec{A}}} \left( t \right) - {\mathbf{C}}_{{{\mathbf{AU}}}}^{T} \dot{{\varvec{q}}}_{{\varvec{A}}} \left( t \right) - {\mathbf{K}}_{{{\mathbf{AU}}}}^{T} {\varvec{q}}_{{\varvec{A}}} \left( t \right).$$
(4)

Hereafter, the dependence with respect to time will be avoided, if not necessary, for brevity. Equation (4) defines constraints on the allowable state trajectories, and depends on both positions, speeds and accelerations. Thus, it is a set of second-order nonholonomic constraints [29], and any commanded trajectory should satisfy such constraints at any time. For this reason, the number of independent outputs to be imposed for the inverse dynamics is assumed to be equal to the number of independent actuation forces  f.

Inverse Dynamics

The Algebraic-Differential Scheme of Model Inversion for Generic Periodic References

The inverse dynamics problem is aimed at computing the NA actuation forces collected in \({\varvec{f}}\), so that NA output coordinates, collected in the output vector \({\varvec{\eta}}\), track the prescribed periodic desired displacement \({\varvec{\eta}}^{{{\varvec{des}}}} \left( t \right)\). In particular, the chosen coordinates should be defined to impose the desired tray motion, and therefore are defined as NA absolute tray displacements. A common requirement is to get uniform displacement along the tray, with a prescribed throw angle [27], thus imposing a relationship between the horizontal and the vertical displacements of the tray.

While the problem of dynamic inversion for undamped feeders tracking harmonic \({\varvec{\eta}}^{{{\varvec{des}}}}\) has been solved by the authors in [27] through a purely algebraic scheme, the use of generic periodic (and hence non-harmonic) references and in the presence of damping is not straightforward, as briefly outlined in [16], and requires an algebraic-differential scheme. Additionally, the possibility to impose just NA coordinates might severely affect the uniformity of the tray displacement, thus reducing the overall feeding capability of the device [3].

If \({\varvec{z}}\) is adopted in the dynamic model, the definition of such output coordinates would be straightforward, since they are xt and two vertical tray displacements that belong to the set of coordinates yi (i = 1,…,Nb + 1). Because of the coordinate partitioning introduced in Eq. (2), \({\varvec{\eta}}\) becomes a linear combination of the actuated–unactuated coordinates

$${\varvec{\eta}} = {{\varvec{\Gamma}}}_{{\mathbf{A}}} {\varvec{q}}_{{\varvec{A}}}^{{}} + {{\varvec{\Gamma}}}_{{\mathbf{U}}} {\varvec{q}}_{{\varvec{U}}}^{{}} ,$$
(5)

where \({{\varvec{\Gamma}}}_{{\mathbf{A}}} \in {\mathbb{R}}^{{N_{{\text{A}}} \times N_{{\text{A}}} }}\) and \({{\varvec{\Gamma}}}_{{\mathbf{U}}} \in {\mathbb{R}}^{{N_{{\text{A}}} \times \left( {N - N_{{\text{A}}} } \right)}}\) are two full-rank, constant matrices related to the choice of the three physical coordinates and to Q. It is possible to exploit Eq. (5) together with the desired output trajectory \({\varvec{\eta}}^{{{\varvec{des}}}}\) to express the position \({\varvec{q}}_{{\varvec{A}}}\), speed \(\dot{{\varvec{q}}}_{{\varvec{A}}}\) and acceleration \({\ddot{\varvec{q}}}_{{\varvec{A}}}\) of the actuated coordinates as follows:

$$\begin{aligned} {\varvec{q}}_{{\varvec{A}}} & = {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} \left( {{\varvec{\eta}}^{{{\varvec{des}}}} - {{\varvec{\Gamma}}}_{{\mathbf{U}}} {\varvec{q}}_{{\varvec{U}}} } \right) \\ \dot{{\varvec{q}}}_{{\varvec{A}}} & = {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} \left( {\dot{\boldsymbol{\eta }}^{{{\varvec{des}}}} - {{\varvec{\Gamma}}}_{{\mathbf{U}}} \dot{{\varvec{q}}}_{{\varvec{U}}} } \right) \\ {\ddot{\varvec{q}}}_{{\varvec{A}}} & = {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} \left( {{\ddot{\boldsymbol{\eta}}}^{{{\varvec{des}}}} - {{\varvec{\Gamma}}}_{{\mathbf{U}}} {\ddot{\varvec{q}}}_{{\varvec{U}}} } \right). \\ \end{aligned}$$
(6)

Equation (6) allows the second-order nonholonomic constraint in Eq. (4) to be written as a function of \({\varvec{q}}_{{\varvec{U}}}^{{}}\), \({\varvec{\eta}}^{{{\varvec{des}}}}\) and their derivatives, leading to the so-called “internal dynamics”

$$\begin{aligned} & \left( {{\mathbf{M}}_{{{\mathbf{UU}}}} - {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {{\varvec{\Gamma}}}_{{\mathbf{U}}} } \right){\ddot{\varvec{q}}}_{{\varvec{U}}} + \left( {{\mathbf{C}}_{{{\mathbf{UU}}}} - {\mathbf{C}}_{{{\mathbf{AU}}}}^{T} {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {{\varvec{\Gamma}}}_{{\mathbf{U}}} } \right)\dot{{\varvec{q}}}_{{\varvec{U}}} + \left( {{\mathbf{K}}_{{{\mathbf{UU}}}} - {\mathbf{K}}_{{{\mathbf{AU}}}}^{T} {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {{\varvec{\Gamma}}}_{{\mathbf{U}}} } \right){\varvec{q}}_{{\varvec{U}}} \\ & \quad = - {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {\ddot{\boldsymbol{\eta} }}^{{{\varvec{des}}}} - {\mathbf{C}}_{{{\mathbf{AU}}}}^{T} {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} \dot{\boldsymbol{\eta }}^{{{\varvec{des}}}} - {\mathbf{K}}_{{{\mathbf{AU}}}}^{T} {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {\varvec{\eta}}^{{{\varvec{des}}}} . \\ \end{aligned}$$
(7)

It should be noted that the internal dynamics depends on the chosen output to be controlled, and this choice affects its poles because of the term \({{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {{\varvec{\Gamma}}}_{{\mathbf{U}}}\).

Stabilization of the Internal Dynamics

In the feeder under investigation, as it will be shown in the section "Application Example" through the numerical example, and in similar cases as well, the system in Eq. (7) is unstable because of poles with positive real parts. Hence, the numerical integration of the internal dynamics leads to divergent solutions even when forced by bounded input (\({\varvec{\eta}}^{{{\varvec{des}}}}\), \(\dot{\boldsymbol{\eta }}^{{{\varvec{des}}}}\), \({\ddot{\boldsymbol{\eta}}}^{{{\varvec{des}}}}\)). Stabilization should be therefore performed. An effective approach is the output redefinition, that is approximating y through a proper fictitious output \(\tilde{\boldsymbol{\eta }}\) so that Eq. (7) is approximated through a stabilized internal dynamics. \(\tilde{\boldsymbol{\eta }}\) is, again, written as a linear combination of the actuated and unactuated coordinates, through proper matrices \({\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}} \in {\mathbb{R}}^{{N_{{\text{A}}} \times N_{{\text{A}}} }}\) and \({\tilde{\mathbf{\Gamma }}}_{{\mathbf{U}}} \in {\mathbb{R}}^{{N_{{\text{A}}} \times \left( {N - N_{{\text{A}}} } \right)}}\)

$$\tilde{\boldsymbol{\eta }} = {\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}} {\varvec{q}}_{{\varvec{A}}}^{{}} + {\tilde{\mathbf{\Gamma }}}_{{\mathbf{U}}} {\varvec{q}}_{{\varvec{U}}}^{{}} .$$
(8)

Provided that a proper choice of stabilizing \({\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}}\) and \({\tilde{\mathbf{\Gamma }}}_{{\mathbf{U}}}\) is done, the following stabilized internal dynamics is finally obtained:

$$\begin{aligned} & \left( {{\mathbf{M}}_{{{\mathbf{UU}}}} - {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}}^{ - 1} {\tilde{\mathbf{\Gamma }}}_{{\mathbf{U}}} } \right){\ddot{\varvec{q}}}_{{\varvec{U}}} + \left( {{\mathbf{C}}_{{{\mathbf{UU}}}} - {\mathbf{C}}_{{{\mathbf{AU}}}}^{T} {\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}}^{ - 1} {\tilde{\mathbf{\Gamma }}}_{{\mathbf{U}}} } \right)\dot{\varvec{q}}_{{\varvec{U}}} + \left( {{\mathbf{K}}_{{{\mathbf{UU}}}} - {\mathbf{K}}_{{{\mathbf{AU}}}}^{T} {\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}}^{ - 1} {\tilde{\mathbf{\Gamma }}}_{{\mathbf{U}}} } \right){\varvec{q}}_{{\varvec{U}}} \\ & \quad = - {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}}^{ - 1} {\ddot{\boldsymbol{\eta} }}^{{{\varvec{des}}}} - {\mathbf{C}}_{{{\mathbf{AU}}}}^{T} {\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}}^{ - 1} \dot{\boldsymbol{\eta }}^{{{\varvec{des}}}} - {\mathbf{K}}_{{{\mathbf{AU}}}}^{T} {\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}}^{ - 1} {\varvec{\eta}}^{{{\varvec{des}}}} . \\ \end{aligned}$$
(9)

The choice of \({\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}}\) and \({\tilde{\mathbf{\Gamma }}}_{{\mathbf{U}}}\) is not trivial and should pursue a twofold goal: on the one hand, \(\tilde{\boldsymbol{\eta }}\) should ensure negative real parts of the poles of the approximated internal dynamics; on the other hand, it should lead to a negligible perturbation of the stable poles of the internal dynamics to limit the tracking error.

Forward numerical integration of the ODEs in Eq. (9) is adopted to compute \({\ddot{\varvec{q}}}_{{\varvec{U}}}\), \(\dot{\varvec{q}}_{{\varvec{U}}}\) and \({\varvec{q}}_{{\varvec{U}}}\). The numerical integration scheme employed, and the choice of the discretization time step, rely on the usual practices adopted in the numerical simulations of multibody systems (see, e.g., [30]).

Computation of the Actuation Forces

Once the unactuated coordinates accelerations, speeds and displacements are obtained, and will be henceforth denoted as \({\varvec{q}}_{{\varvec{U}}}^{{{\varvec{des}}}}\), \(\dot{\varvec{q}}_{{\varvec{U}}}^{{{\varvec{des}}}}\) and \({\ddot{\varvec{q}}}_{{\varvec{U}}}^{{{\varvec{des}}}}\), it is possible to compute the reference trajectory for the actuated coordinates \({\varvec{q}}_{{\varvec{A}}}^{{{\varvec{des}}}}\), \(\dot{\varvec{q}}_{{\varvec{A}}}^{{{\varvec{des}}}}\), \({\ddot{\varvec{q}}}_{{\varvec{A}}}^{{{\varvec{des}}}}\) by inverting the actual maps in Eq. (6), i.e., using the actual values of \({{\varvec{\Gamma}}}_{{\mathbf{A}}}\) and \({{\varvec{\Gamma}}}_{{\mathbf{U}}}\); indeed, the method just relies on algebraic computations in the subsequent steps.

Finally, the actuation forces collected in \({\varvec{f}}\) are obtained through the solution of the first NA algebraic equations of the system in Eq. (3) that represent the invertible inverse dynamics of the actuated sub-system for imposed values of the motion of all the coordinates

$${\varvec{f}} = {\mathbf{B}}_{{\mathbf{A}}}^{ - 1} \left( {{\mathbf{M}}_{{{\mathbf{AA}}}} {\ddot{\varvec{q}}}^{{{\varvec{des}}}}_{{\varvec{A}}} \,\,\, + \,\,{\mathbf{M}}_{{{\mathbf{AU}}}} {\ddot{\varvec{q}}}^{{{\varvec{des}}}}_{{\varvec{U}}} \,\,\, + \,\,{\mathbf{C}}_{{{\mathbf{AA}}}} \dot{\varvec{q}}_{{\varvec{A}}}^{{{\varvec{des}}}} \,\, + \,\,{\mathbf{C}}_{{{\mathbf{AU}}}} \dot{\varvec{q}}_{{\varvec{U}}}^{{{\varvec{des}}}} \,\, + \,\,{\mathbf{K}}_{{{\mathbf{AA}}}} {\varvec{q}}_{{\varvec{A}}}^{{{\varvec{des}}}} \,\, + \,\,{\mathbf{K}}_{{{\mathbf{AU}}}} {\varvec{q}}_{{\varvec{U}}}^{{{\varvec{des}}}} \,\,} \right).$$
(10)

Dynamic Structural Modification

Aims of Dynamic Structural Modification

Although the presence of the second-order nonholonomic constraints in Eq. (4) imposes to assign the motion of just NA outputs, the proper functioning of long-tray feeders needs the correct assignment of more coordinates of interest. Indeed, a uniform motion of the conveyed parts is obtained if uniform oscillations are achieved all along the tray, not just in the (NA − 1) positions whose vertical displacements belong to \({\varvec{\eta}}\). It should be noted that also the use of feedback control is not effective in imposing the correct shape of vibration because of the limitation in assigning eigenvectors, and hence the vibrational mode shape, in underactuated systems [31, 32].

To overcome these difficulties and to obtain a correct feeding, this paper exploits the concepts of dynamic structural modification (DSM), i.e., the modification of elastic and inertial physical parameters, to achieve the desired displacements for all the Nd coordinates of interest (NA < Nd < N). DSM is usually adopted for assigning poles, mode shapes and antiresonances in vibrating systems, with particular regard to undamped ones. In this work, it is exploited in a slightly different manner, by considering the system forced response in the presence of the desired output \({\varvec{\eta}}^{{{\varvec{des}}}}\). The application of DSM for feeders is significantly simplified, and improved in term of solvability and solution reliability, by neglecting damping and by considering harmonic motion [27]. Under these circumstances, both the second-order nonholonomic constraint and the internal dynamics become algebraic equations (that define holonomic constraints relating the oscillation amplitudes of the unactuated coordinates), and the DSM problem can be solved as a purely algebraic optimization.

To apply this idea to the case under investigation, where the output reference \({\varvec{\eta}}^{{{\varvec{des}}}}\) is an arbitrary periodic function, the Fourier series is exploited together with the system linearity, that allows splitting the DSM problem into more subproblems, each one addressing one of the NH dominant harmonic components of \({\varvec{\eta}}^{{{\varvec{des}}}}\).

Let \({\varvec{\eta}}^{{{\varvec{des}}}} \left( t \right)\) be periodic with period \(T_{{\text{F}}} = {\raise0.7ex\hbox{${2\pi }$} \!\mathord{\left/ {\vphantom {{2\pi } {\omega_{{\text{F}}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{{\text{F}}} }$}}\), then its jth entry, j = 1,…,NA, can be approximated as the following truncated series (\(\phi_{j,k}\) and \(A_{j,k}\) denotes the phase and the amplitude, respectively, of each harmonic)

$$\eta_{j}^{des} \left( t \right) \simeq A_{j,0} + \sum\limits_{k = 1}^{{N_{\rm H} }} {A_{j,k} \cos \left( {k\omega_{{\text{F}}} t + \phi_{j,k} } \right)} .$$
(11)

The phase of each harmonic is not of interest for the DSM, and therefore can be discarded. The continuous component can be discarded as well.

The selection of NH should provide an accurate signal representation, also considering the actuators bandwidths, while trading off with the need of reducing the size of the DSM problem. It should be further stressed that such an approximation of \({\varvec{\eta}}^{{{\varvec{des}}}}\) is just used for the computation of the physical parameter modifications, to aid the inverse dynamics method proposed in the section "Inverse Dynamics" to get a quasi-uniform displacement along the tray, despite the high value of the degree of underactuation (i.e., N − NA). Once the system is modified through proper mass and stiffness modification, such a method will provide the almost-exact solution of the inverse dynamic problem; the sole approximation is the one required in stabilizing the internal dynamics.

DSM Problem Formulation for a Single Harmonic

In this section, the DSM problem is formulated and discussed for an arbitrary harmonic, indexed through k = 1,…, NH. The overall problem, considering all the dominant harmonics, is formulated in the section "DSM Problem Formulation for NH Harmonics".

The internal dynamics formulated in Eq. (7), under the hypotheses of neglecting damping and in the presence of harmonic reference, is written as follows:

$$\begin{aligned} & \left( { - \left( {k\omega_{{\text{F}}} } \right)^{2} {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} + {\mathbf{K}}_{{{\mathbf{AU}}}}^{T} } \right){{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {\varvec{\eta}}_{0,k}^{{{\varvec{des}}}} \\ & \quad + \left( { - \left( {k\omega_{{\text{F}}} } \right)^{2} {\mathbf{M}}_{{{\mathbf{UU}}}} + {\mathbf{K}}_{{{\mathbf{UU}}}} - \left( { - \left( {k\omega_{{\text{F}}} } \right)^{2} {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} + {\mathbf{K}}_{{{\mathbf{AU}}}}^{T} } \right){{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {{\varvec{\Gamma}}}_{{\mathbf{U}}} } \right){\varvec{q}}_{{{\varvec{U}}0,k}} = 0, \\ \end{aligned}$$
(12)

where \({\varvec{\eta}}_{0,k}^{{{\varvec{des}}}}\) collects the amplitudes \(A_{j,k}\) j = 1,…,NA, for the kth harmonic. Hereafter, subscript 0 denotes the amplitude of the signals. The inverse of the receptance matrices \({\mathbf{G}}_{{{\mathbf{AA}},k}} \in {\mathbb{R}}^{{N_{{\text{A}}} \times N_{{\text{A}}} }}\), \({\mathbf{G}}_{{{\mathbf{AU}},k}} \in {\mathbb{R}}^{{N_{{\text{A}}} \times \left( {N - N_{{\text{A}}} } \right)}}\) and \({\mathbf{G}}_{{{\mathbf{UU}},k}} \in {\mathbb{R}}^{{\left( {N - N_{{\text{A}}} } \right) \times \left( {N - N_{{\text{A}}} } \right)}}\), are introduced and defined as

$${\mathbf{G}}_{k} = \left[ {\begin{array}{*{20}c} {{\mathbf{G}}_{{{\mathbf{AA}},k}} } & {{\mathbf{G}}_{{{\mathbf{AU}},k}} } \\ {{\mathbf{G}}_{{{\mathbf{AU}},k}}^{T} } & {{\mathbf{G}}_{{{\mathbf{UU}},k}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{{\mathbf{AA}}}} - \left( {k\omega_{{\text{F}}} } \right)^{2} {\mathbf{M}}_{{{\mathbf{AA}}}} } & {{\mathbf{K}}_{{{\mathbf{AU}}}} - \left( {k\omega_{{\text{F}}} } \right)^{2} {\mathbf{M}}_{{{\mathbf{AU}}}} } \\ {{\mathbf{K}}_{{{\mathbf{AU}}}}^{T} - \left( {k\omega_{{\text{F}}} } \right)^{2} {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} } & {{\mathbf{K}}_{{{\mathbf{UU}}}} - \left( {k\omega_{{\text{F}}} } \right)^{2} {\mathbf{M}}_{{{\mathbf{UU}}}} } \\ \end{array} } \right].$$
(13)

Hence, Eq. (12) is therefore recast in the following more compact form:

$${\mathbf{G}}_{{{\mathbf{AU}},k}}^{T} {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {\varvec{\eta}}_{0,k}^{{{\varvec{des}}}} + \left( {{\mathbf{G}}_{{{\mathbf{UU}},k}} - {\mathbf{G}}_{{{\mathbf{AU}},k}}^{T} {{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {{\varvec{\Gamma}}}_{{\mathbf{U}}} } \right){\varvec{q}}_{{{\varvec{U}}0,k}} = 0.$$
(14)

Equation (14) can be exploited to modify the system internal dynamics, when forced by the desired output, such that all the Nd coordinates of interest track the desired reference. The following structural modification matrices are defined to represent the model changes due to the Np design variables collected in vector p:

$$\begin{aligned} {\mathbf{\Delta G}}_{{{\mathbf{AU}},k}}^{{}} \left( {\varvec{p}} \right) & = {\mathbf{\Delta K}}_{{{\mathbf{AU}}}}^{{}} \left( {\varvec{p}} \right) - \left( {k\omega_{{\text{F}}} } \right)^{2} {\mathbf{\Delta M}}_{{{\mathbf{AU}}}}^{{}} \left( {\varvec{p}} \right) \in {\mathbb{R}}^{{N_{{\text{A}}} \times \left( {N - N_{{\text{A}}} } \right)}} \\ {\mathbf{\Delta G}}_{{{\mathbf{UU}},k}}^{{}} \left( {\varvec{p}} \right) & = {\mathbf{\Delta K}}_{{{\mathbf{UU}}}} \left( {\varvec{p}} \right) - \left( {k\omega_{{\text{F}}} } \right)^{2} {\mathbf{\Delta M}}_{{{\mathbf{UU}}}} \left( {\varvec{p}} \right) \in {\mathbb{R}}^{{\left( {N - N_{{\text{A}}} } \right) \times \left( {N - N_{{\text{A}}} } \right)}} , \\ \end{aligned}$$
(15)

ΔKAU, ΔMAU, ΔKUU, ΔMUU are the mass and stiffness modification matrices obtained as

$$\begin{aligned} {\mathbf{Q}}^{T} {\mathbf{\Delta M}}\left( {\varvec{p}} \right){\mathbf{Q}} & = \left[ {\begin{array}{*{20}c} {{\mathbf{\Delta M}}_{{{\mathbf{AA}}}} \left( {\varvec{p}} \right)} & {{\mathbf{\Delta M}}_{{{\mathbf{AU}}}} \left( {\varvec{p}} \right)} \\ {{\mathbf{\Delta M}}_{{{\mathbf{AU}}}}^{T} \left( {\varvec{p}} \right)} & {{\mathbf{\Delta M}}_{{{\mathbf{UU}}}} \left( {\varvec{p}} \right)} \\ \end{array} } \right]\, \in {\mathbb{R}}^{N \times N} \,\,\, \\ {\mathbf{Q}}^{T} {\mathbf{\Delta K}}\left( {\varvec{p}} \right){\mathbf{Q}} & = \left[ {\begin{array}{*{20}c} {{\mathbf{\Delta K}}_{{{\mathbf{AA}}}} \left( {\varvec{p}} \right)} & {{\mathbf{\Delta K}}_{{{\mathbf{AU}}}} \left( {\varvec{p}} \right)} \\ {{\mathbf{\Delta K}}_{{{\mathbf{AU}}}}^{T} \left( {\varvec{p}} \right)} & {{\mathbf{\Delta K}}_{{{\mathbf{UU}}}} \left( {\varvec{p}} \right)} \\ \end{array} } \right] \in {\mathbb{R}}^{N \times N} . \\ \end{aligned}$$
(16)

The mass and stiffness modification matrices of the model with physical coordinates z, are denoted by ΔK, ΔM. The topology of the modification matrices is a-priori assumed and it represents the admissible choices in the system design, as usually done in the state of the art (see, e.g., [3, 27]).

Once structural modifications are considered, Eq. (14) is recast, in terms of the modified system, as follows:

$${\tilde{\mathbf{G}}}_{{{\mathbf{AU}},k}}^{T} \left( {\varvec{p}} \right){{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {\varvec{\eta}}_{0,k}^{{{\varvec{des}}}} + \left( {{\tilde{\mathbf{G}}}_{{{\mathbf{UU}},k}} \left( {\varvec{p}} \right) - {\tilde{\mathbf{G}}}_{{{\mathbf{AU}},k}}^{T} \left( {\varvec{p}} \right){{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {{\varvec{\Gamma}}}_{{\mathbf{U}}} } \right){\varvec{q}}_{{{\varvec{U}}0,k}} = 0,$$
(17)

with:

$${\tilde{\mathbf{G}}}_{{{\mathbf{AU}},k}}^{{}} \left( {\varvec{p}} \right) = {\mathbf{G}}_{{{\mathbf{AU}},k}}^{{}} + {\mathbf{\Delta G}}_{{{\mathbf{AU}},k}}^{{}} \left( {\varvec{p}} \right),\,\,\,\,\,\,{\tilde{\mathbf{G}}}_{{{\mathbf{UU}},k}} \left( {\varvec{p}} \right) = {\mathbf{G}}_{{{\mathbf{UU}},k}} + {\mathbf{\Delta G}}_{{{\mathbf{UU}},k}}^{{}} \left( {\varvec{p}} \right).$$
(18)

DSM Problem Formulation for N H Harmonics

Since the system is linear, the superposition principle can be applied. Therefore, for all the NH harmonics adopted to model the output reference signal in the frequency domain, the structural modification problem introduced in Eq. (17) becomes

$$\sum\limits_{k = 1}^{{N_{H} }} {{\tilde{\mathbf{G}}}_{{{\mathbf{AU}},k}}^{T} \left( {\varvec{p}} \right){{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {\varvec{\eta}}_{0,k}^{{{\varvec{des}}}} + \left( {{\tilde{\mathbf{G}}}_{{{\mathbf{UU}},k}} \left( {\varvec{p}} \right) - {\tilde{\mathbf{G}}}_{{{\mathbf{AU}},k}}^{T} \left( {\varvec{p}} \right){{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {{\varvec{\Gamma}}}_{{\mathbf{U}}} } \right){\varvec{q}}_{{{\varvec{U}}0,k}} = } 0.$$
(19)

Let us consider the scenario, introduced in the section "Aims of Dynamic Structural Modification", where a set \({\varvec{z}}_{{{\varvec{s}}_{0,k} }}^{{{\varvec{des}}}}\) of Nd coordinates of the system are of interest (k = 1,…,NH). The remaining N − Nd are unassigned coordinates, whose amplitudes are collected in vector zf0,k, k = 1,…,NH, as additional unknowns in the IDSM problem, together with the design parameters p. The desired displacement amplitude vector in the transformed coordinate q is obtained through the transformation matrix Q, thus making \({\varvec{q}}_{{{\varvec{A}}0,k}}^{{{\varvec{des}}}}\) and \({\varvec{q}}_{{{\varvec{U}}0,k}}^{{{\varvec{des}}}}\) functions of the unknown

$$\left\{ {\begin{array}{*{20}c} {{\varvec{q}}_{{{\varvec{A}}0,k}}^{{{\varvec{des}}}} } \\ {{\varvec{q}}_{{{\varvec{U}}0,k}}^{{{\varvec{des}}}} } \\ \end{array} } \right\} = {\mathbf{Q}}^{T} {\varvec{z}}_{0,k}^{{\varvec{d}}} = {\mathbf{Q}}^{T} \left\{ {\begin{array}{*{20}c} {{\varvec{z}}_{{{\varvec{s}}_{0,k} }}^{{{\varvec{des}}}} } \\ {{\varvec{z}}_{{{\varvec{f}}_{0} ,k}}^{{}} } \\ \end{array} } \right\},\,\,\,k = 1,...,N_{{\text{H}}} ,$$
(20)

where superscript des denotes the desired displacements.

The Np design variables are constrained to belong to a feasible domain defined through lower and upper bounds as follows \({\varvec{p}}_{{}}^{{\varvec{L}}} \le {\varvec{p}} \le {\varvec{p}}_{{}}^{{\varvec{U}}}\) (with element-wise inequalities), and \({\varvec{p}}_{{}}^{{\varvec{L}}} ,{\varvec{p}}_{{}}^{{\varvec{U}}} \in {\mathbb{R}}^{{N_{\rm p} }}\) are related to technological and economical constraints on the admissible system modifications. Constraints on the unassigned displacements are introduced as well to define their admissible values through the following element-wise inequalities, i.e., \({\varvec{z}}_{{{\varvec{f}}_{0} ,k}}^{{\varvec{L}}} \le {\varvec{z}}_{{{\varvec{f}}_{0} ,k}}^{{}} \le {\varvec{z}}_{{{\varvec{f}}_{0} ,k}}^{{\varvec{U}}}\) with \({\varvec{z}}_{{{\varvec{f}}_{0} ,k}}^{{\varvec{L}}} ,{\varvec{z}}_{{{\varvec{f}}_{0} ,k}}^{{\varvec{U}}} \in {\mathbb{R}}^{{N - N_{{\text{d}}} }}\), k = 1,…,NH. Such constraints provide several benefits in the development of an effective solution method for finding the optimal values of p, as explained in the section "Solution of the Minimization Problem". All the constraints on the unknowns are merged to define the feasible domain \({{\varvec{\Psi}}}\).

The IDSM problem is defined by recasting Eq. (19) into the following minimization:

$$\begin{gathered} \mathop {\min }\limits_{{{\varvec{p}},{\varvec{z}}_{{{\varvec{f}}_{{0}} }}^{{}} }} \left\{ {{{\varvec{\Omega}}}\left\| {\sum\limits_{k = 1}^{{N_{H} }} {{\tilde{\mathbf{G}}}_{{{\mathbf{AU}},k}}^{T} \left( {\varvec{p}} \right){{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {\varvec{\eta}}_{0,k}^{{{\varvec{des}}}} \left( {{\varvec{z}}_{{{\varvec{f}}_{{0}} ,k}}^{{}} } \right) + \left( {{\tilde{\mathbf{G}}}_{{{\mathbf{UU}},k}} \left( {\varvec{p}} \right) - {\tilde{\mathbf{G}}}_{{{\mathbf{AU}},k}}^{T} \left( {\varvec{p}} \right){{\varvec{\Gamma}}}_{{\mathbf{A}}}^{ - 1} {{\varvec{\Gamma}}}_{{\mathbf{U}}} } \right){\varvec{q}}_{{_{{{\varvec{U}}0,k}} }}^{{{\varvec{des}}}} \left( {{\varvec{z}}_{{{\varvec{f}}_{0} ,k}}^{{}} } \right)} } \right\|_{2}^{2} + \left\| {{{\varvec{\Lambda}}}{\varvec{p}}} \right\|_{2}^{2} ,\,\left\{ {\begin{array}{*{20}c} {\varvec{p}} \\ {{\varvec{z}}_{{{\varvec{f}}_{0} }}^{{}} } \\ \end{array} } \right\} \in {{\varvec{\Psi}}}} \right\}\,, \hfill \\ \hfill \\ \end{gathered}$$
(21)

where \({{\varvec{\Omega}}} \in {\mathbb{R}}^{{N_{{\text{H}}} \times N_{{\text{H}}} }}\) is a diagonal matrix that collects NH scalar coefficients that are introduced to reflect different levels of concern on each harmonic adopted to approximate the output reference signal. The cost function also includes a Tikhonov regularization term \({{\varvec{\Lambda}}} \in {\mathbb{R}}^{{N_{\rm p} \times N_{\rm p} }}\), i.e., a positive-definite diagonal matrix that collects Np scalar coefficients, introduced to improve numerical conditioning, and it is adopted to properly weigh the structural modification parameters [33].

Equation (21) features bilinear terms due to the products between the two unknowns, and hence, it yields to a non-linear and non-convex minimization problem. Handling non-convex optimization is cumbersome, and the main threat is related to the risk of attaining a local minimum instead of the desired global optimal solution. Hence, it requires a proper solving strategy, such as the one explained in the section "Solution of the Minimization Problem", to boost the attainment of the global optimum. Once the optimal values popt for the design variables are found, it is possible to compute the modified system matrices as follows:

$${\mathbf{M}}_{\bmod } = {\mathbf{M}} + {\mathbf{\Delta M}}\left( {{\varvec{p}}_{{{\text{opt}}}} } \right),\,\,\,\,{\mathbf{K}}_{\bmod } = {\mathbf{K}} + {\mathbf{\Delta K}}\left( {{\varvec{p}}_{{{\text{opt}}}} } \right).$$
(22)

Then, the actuation forces are computed through the procedure proposed in the section "Inverse Dynamics", by adopting the modified system matrices obtained by solving the DSM problem in Eq. (21).

Solution of the Minimization Problem

The minimization problem in Eq. (21) is solved through homotopy optimization. This technique has been widely adopted to solve structural modification problems [26, 27, 34]. Homotopy relies on the idea of solving a finite set of optimization problems fi, starting from a convex relaxation fc of the non-convex function to be solved and moving to the non-convex function fnc to be solved by means of a path, called the homotopy map defined as

$${\varvec{f}}_{{\varvec{i}}} = \left( {1 - \lambda } \right){\varvec{f}}_{{\varvec{c}}} + \lambda {\varvec{f}}_{{{\varvec{nc}}}} ,$$
(23)

where \(\lambda \in \left[ {0;1} \right]\) is a morphing parameter that varies discretely from 0 to 1. Since \(\lambda\) is monotonically increasing, fi varies from convexity to non-convexity.

In the last optimization step (\(\lambda = 1\)), the function fnc is solved and the solutions obtained at the last step (i.e., \({\mathbf{\Delta M}}_{{{\text{opt}}}} = {\mathbf{\Delta M}}\left( {{\varvec{p}}_{{{\text{opt}}}} } \right) = {\mathbf{\Delta M}}\left( {{\varvec{p}}_{\lambda = 1} } \right)\) and \({\mathbf{\Delta K}}_{{{\text{opt}}}} = {\mathbf{\Delta K}}\left( {{\varvec{p}}_{{{\text{opt}}}} } \right) = {\mathbf{\Delta K}}\left( {{\varvec{p}}_{\lambda = 1} } \right)\)) are the optimal structural modification matrices. It is worth to notice that homotopy procedures prescribe to exploit the solution of the previous optimization step as the initial guess of the following minimization. This feature is fundamental to boost the attainment of a global minima instead of a local one.

More details regarding homotopy optimization and its applications to DSM problems are provided in [27, 34] and here omitted for brevity.

Outline of the Method

The method proposed in this paper is outlined in Fig. 2, where the required equations are referenced. The method requires, as the input, the system dynamic model through matrices M, C, K, B, together with the required motion profile for the output coordinates \({\varvec{\eta}}^{{{\varvec{des}}}} \left( t \right)\); the method output are the actuation forces \({\varvec{f}}\left( t \right)\).

Fig. 2
figure 2

Outline of the proposed method

Full size image

Two decisions may be needed: first, once the desired outputs are defined, if the dynamic system features unstable internal dynamics, it is necessary to stabilize it as shown in the flowchart in Fig. 2; otherwise, stabilization is not required. For these systems, it is quite common experiencing a non-minimum phase behavior, and hence, stabilization is usually likely to be required. Second, if the tracking errors obtained in the coordinates not belonging to \({\varvec{\eta}}^{{{\varvec{des}}}}\) (and hence not imposed in the desired output) are larger than desired, it is possible to take advantage of the DSM modification algorithm to improve trajectory tracking in more than NA coordinates.

Application Example

System Description and Performance Specifications

Let us consider the linear vibratory feeder sketched in Fig. 1. It recalls a typical linear feeder adopted in packaging lines. The system properties and the performance requirements of the proposed test case are based on typical specifications set for proper operating these devices in industrial plants [3, 35].

The number of actuators is NA = 3 and the force distribution matrix is

$${\mathbf{B}} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\sin \theta_{{\text{f}}} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\cos \theta_{{\text{f}}} } & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\sin \theta_{{\text{f}}} } & 0 & 0 & 0 & 0 & 0 & {\cos \theta_{{\text{f}}} } & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\sin \theta_{{\text{f}}} } & 0 & 0 & 0 & {\cos \theta_{{\text{f}}} } & 0 & 0 & 1 \\ \end{array} } \right]^{T} .$$
(24)

The feeder is modeled through Nb = 4 Euler Bernoulli beam elements, and hence, \({\varvec{z}} = \left\{ {\begin{array}{*{20}c} {y_{1} } & {\varphi_{1} } & \ldots & {y_{5} } & {\varphi_{5} } & {x_{t} } & {s_{1} } & \ldots & {s_{3} } \\ \end{array} } \right\}^{T}\). It follows that N = 14, since 3 independent actuation forces are adopted, 3 coordinates are actuated, while the remaining 11 coordinates are unactuated. The tray length is L = 3.6 m and its damping matrix is obtained using the Rayleigh damping model [36] C = αM + βK, with α = 102 and β = 10–3. The remaining parameters are listed in Table 1.

Table 1 Original and modified system parameters
Full size table

To ensure a uniform flow of the conveyed parts, it is required that the tray behaves as a rigid body with uniform displacements ensuring a uniform throw angle αf = 20°. This requirement would impose assigning the 5 vertical displacements y1, y2, y3, y4, y5 and the horizontal one \(x_{{t_{{}} }}^{{}}\), and the nodal elastic rotations as well. All the vertical displacements should track the same references, while the elastic nodal rotations of the tray should be equal to zero, to ensure the rigid-like motion. These specifications yield to Nd = 11 coordinates of interest.

However, since NA = 3, just three outputs can be assigned. To boost the achievement of the desired goal, the output vector is defined as \({\varvec{\eta}} = \left\{ {\begin{array}{*{20}c} {y_{2} } & {y_{4} } & {x_{t} } \\ \end{array} } \right\}^{T}\): two vertical displacements in the attachment points of the first and third actuators, and the horizontal displacement to set the desired throw angle. \({\varvec{\eta}}^{{{\varvec{des}}}} \left( t \right)\) is defined as a periodic asymmetric reference profile, whose period is TF = 28.60 ms, i.e., ωF = 2π 35 rads−1, as often adopted in feeding of small parts [3, 27]. Each period of the wave signal consists of a rising phase lasting 0.4TF, followed by a drop phase of 0.6TF; both phases are performed through a fifth-degree polynomial motion law. The peak oscillation amplitude in the throw angle direction is \(s_{\max }^{d} = 5\;{\text{mm}}\), and hence, \(y_{\max }^{d} = s_{\max }^{d} \sin \left( {\pi - \alpha_{{\text{f}}} } \right)\) and \(x_{{t_{0} }}^{d} = s_{\max }^{d} \cos \left( {\pi - \alpha_{{\text{f}}} } \right)\). The required motion profiles for y2, y4, xt are shown in Fig. 3a.

Fig. 3
figure 3

Output reference for y2, y4, xt: time history (a) and their frequency spectrum (b)

Full size image

Application of the Inverse Dynamics on the Original System

The inverse dynamic approach proposed in the section "Inverse Dynamics" is applied to the system with the original parameters, to meet the motion requirements listed in the section "System Description and Performance Specifications". The linear vibratory feeder, for the chosen output coordinates \({\varvec{\eta}}\), has unstable internal dynamics, as shown in Fig. 4a, where a right-half complex plane pole appears. A proper selection of the tuning matrices \({\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}}\) and \({\tilde{\mathbf{\Gamma }}}_{{\mathbf{U}}}\) enables to stabilize its internal dynamics as evidenced in Fig. 4a; further, the original internal dynamics poles are only slightly perturbed in the approximate internal dynamics. The actuation forces are computed through the method outlined in the section "Outline of the Method" without applying structural modification, and the time history of the obtained actuation forces is shown in Fig. 5.

Fig. 4
figure 4

poles of the exact and the stabilized internal dynamics, for both the original (a) and the modified (b) systems

Full size image
Fig. 5
figure 5

Actuation forces f1 (a), f2 (b) and f3 (c) for the original and the modified systems

Full size image

The method implementation is not demanding under a computational point of view: the average computational time employed to compute the actuation forces for an interval of 0.3 s, by means of MATLAB/Simulink running on an i7 16 GB RAM laptop, is equal to 1.7 s. It is worth to notice, however, that open-loop control can be computed offline.

The multibody system is simulated with Ts = 0.01 ms, adopting the Runge–Kutta ODE4 solver for the numerical integration, and the time histories of the desired output coordinates y2, y4, xt are reported in Fig. 6, where it can be noticed that the reference signals and the simulated signals are almost overlapped. This aspect is confirmed by the tracking errors shown in Fig. 6, where \(e_{i} = y_{i}^{des} - y_{i}\) is the tracking error related to coordinate yi. Similarly, \(e_{x}\) is the tracking error related to xt. Figure 6 highlights the tracking errors achieved. The effectiveness of the proposed inverse dynamic method is corroborated by the root mean square (RMS) and maximum tracking errors, respectively, denoted through eRMS and eMAX = max(|ei|), whose values for the imposed coordinates are the following ones:

  • \(e_{2}^{RMS} = 2.51 \times 10^{ - 5} \,{\text{m}}\) and \(e_{2}^{MAX} = 3.74 \times 10^{ - 5} \,{\text{m}}\);

  • \(e_{4}^{RMS} = 9.76 \times 10^{ - 5} \,{\text{m}}\) and \(e_{4}^{MAX} = 1.92 \times 10^{ - 4} \,{\text{m}}\);

  • \(e_{x}^{RMS} = 1.26 \times 10^{ - 4} \,{\text{m}}\) and \(e_{x}^{MAX} = 2.74 \times 10^{ - 4} \,{\text{m}}\).

Fig. 6
figure 6

Comparison of the trajectory tracking responses (a, c, e) and tracking errors (b, d, f) of the desired output coordinates for the original and the modified systems

Full size image

Figure 10a shows the overall RMS error for the imposed coordinates, denoted as \(e_{{{\varvec{\eta}}^{{{\varvec{des}}}} }}^{RMS} = {\text{RMS}}\left( {{\varvec{\eta}}^{{{\varvec{des}}}} - {\varvec{\eta}}} \right)\). Its time history evidences that the inverse dynamic method proposed in this paper is effective and, indeed, it enables to achieve low tracking error values: the maximum value of \(e_{{{\varvec{\eta}}^{{{\varvec{des}}}} }}^{RMS}\) is equal to 0.16 mm.

This paper pursues a further goal that is to achieve a rigid-like motion of the entire tray, as already pointed out in the previous section. This aspect is analyzed by considering the remaining vertical displacements (y1, y3, y5) and comparing them with the reference signals for the desired vertical output displacements. The simulated time histories, together with the tracking errors, for these signals are reported in Fig. 7. Higher tracking errors with respect to the imposed output coordinates are obtained. This yields to an unsatisfying behavior for the feeder tray. These results are summarized by the following performance indexes:

  • \(e_{1}^{RMS} = 1.40 \times 10^{ - 3} \,{\text{m}}\) and \(e_{1}^{MAX} = 2.30 \times 10^{ - 3} \,{\text{m}}\);

  • \(e_{3}^{RMS} = 5.94 \times 10^{ - 4} \,{\text{m}}\) and \(e_{3}^{MAX} = 1.00 \times 10^{ - 3} \,{\text{m}}\);

  • \(e_{5}^{RMS} = 1.50 \times 10^{ - 3} \,{\text{m}}\) and \(e_{5}^{MAX} = 2.60 \times 10^{ - 3} \,{\text{m}}\).

Fig. 7
figure 7

Comparison of the trajectory tracking responses (a, c, e) and of the tracking errors (b, d, f), for the non-imposed tray vertical displacements: original and modified systems

Full size image

Additionally, the nodal rotations at each node of the tray are reported in Fig. 9, together with the desired nodal rotations that should be null to enforce uniform displacements all along the tray of the feeder. In this case

  • \(\varphi_{1}^{RMS} = 1.60 \times 10^{ - 3} \,^\circ\) and \(\varphi_{1}^{MAX} = 2.70 \times 10^{ - 3} \,^\circ\);

  • \(\varphi_{2}^{RMS} = 1.20 \times 10^{ - 3} \,^\circ\) and \(\varphi_{2}^{MAX} = 2.10 \times 10^{ - 3} \,^\circ\);

  • \(\varphi_{3}^{RMS} = 7.97 \times 10^{ - 5} \,^\circ\) and \(\varphi_{3}^{MAX} = 1.61 \times 10^{ - 4} \,^\circ\);

  • \(\varphi_{4}^{RMS} = 1.30 \times 10^{ - 3} \,^\circ\) and \(\varphi_{4}^{MAX} = 2.30 \times 10^{ - 3} \,^\circ\);

  • \(\varphi_{5}^{RMS} = 1.80 \times 10^{ - 3} \,^\circ\) and \(\varphi_{5}^{MAX} = 3.20 \times 10^{ - 3} \,^\circ\).

The behavior of the non-imposed coordinates is evaluated through two additional error vectors adopted as synthetizing performance indexes. The RMS error of the remaining vertical displacements: \(e_{{{\varvec{y}}_{{{\varvec{ni}}}} }}^{RMS} = {\text{RMS}}\left( {{\varvec{y}}_{{{\varvec{ni}}}}^{{{\varvec{des}}}} - {\varvec{y}}_{{{\varvec{ni}}}} } \right)\), where \({\varvec{y}}_{{{\varvec{ni}}}}^{{{\varvec{des}}}}\) collects the desired motions of the not imposed vertical displacements, which are equal to the displacements required for y2 and y4, and \({\varvec{y}}_{{{\varvec{ni}}}} = \left[ {\begin{array}{*{20}c} {y_{1} } & {y_{3} } & {y_{5} } \\ \end{array} } \right]^{T}\). The time history of \(e_{{{\varvec{y}}_{{{\varvec{ni}}}} }}^{RMS}\) is shown in Fig. 10b and its maximum value is equal to 2.0 mm. Additionally, the error vector \({\varvec{e}}_{\boldsymbol{\varphi }} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varphi_{1} } & {\varphi_{2} } \\ \end{array} } & {\begin{array}{*{20}c} {\varphi_{3} } & {\varphi_{4} } & {\varphi_{5} } \\ \end{array} } \\ \end{array} } \right]^{T}\) is also considered, which contains all the nodal rotations, allowing for a concise evaluation of the rotations at each node of the tray. Its RMS value is reported in Fig. 10c and the maximum value of \(e_{\varphi }^{RMS}\) is equal to 0.13°.

An overall performance index is adopted to evaluate the tracking error between the desired and the obtained vertical displacements of the tray: it is computed as \({\varvec{e}}_{{{\varvec{y}}_{{\varvec{t}}} }} = {\varvec{y}}_{{\varvec{t}}}^{{{\varvec{des}}}} - {\varvec{y}}_{{\varvec{t}}}\), where \({\varvec{y}}_{{\varvec{t}}}^{{{\varvec{des}}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {y_{1}^{des} } & {y_{2}^{des} } \\ \end{array} } & {\begin{array}{*{20}c} {y_{3}^{des} } & {y_{4}^{des} } & {y_{5}^{des} } \\ \end{array} } \\ \end{array} } \right]^{T}\) with \(y_{1}^{des} = y_{2}^{des} = y_{3}^{des} = y_{4}^{des} = y_{5}^{des}\), and \({\varvec{y}}_{{\varvec{t}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {y_{1} } & {y_{2} } \\ \end{array} } & {\begin{array}{*{20}c} {y_{3} } & {y_{4} } & {y_{5} } \\ \end{array} } \\ \end{array} } \right]^{T}\). The time history of the RMS value of \({\varvec{e}}_{{{\varvec{y}}_{{\varvec{t}}} }}\) is shown in Fig. 10d and the maximum value of \(e_{{{\varvec{y}}_{{\varvec{t}}} }}^{RMS}\) is equal to 1.6 mm.

The results here discussed highlight that the error in the trajectory tracking of the imposed coordinates approaches zero. Conversely, for the remaining non-imposed coordinates, the tracking errors are larger and these should be reduced to achieve a more uniform and rigid-like behavior of the tray. In this light and following the outline of the proposed method provided in Fig. 2, it is possible to exploit structural modification to improve the performances of the system.

Application of the Dynamic Structural Modification

The required motion profile is decomposed through Fourier Series and its dominant harmonics are: 35, 70 and 105 Hz, as evidenced in Fig. 3b. These harmonics are adopted to define the DSM problem in Eq. (21) with \({{\varvec{\Omega}}} = {\text{diag}}\left( {\left[ {10^{5} ;10^{3} ;1} \right]} \right)\), which reflects the relative importance of the three harmonics.

The following system parameters are assumed to be modifiable: the actuator masses and the leaf spring stiffnesses, respectively, mai and kai, i = 1,…3, the tray support stiffnesses in the vertical (kl and kr) and horizontal directions (kx). In addition, 5 nodal lumped masses mi, i = 1,…,5, to be placed to the tray, are introduced in the DSM problem. Modifications of the tray flexural stiffness EI and linear mass density ρA are not allowed, although the method can handle their modifications too. Indeed, for an existing feeder, it is very difficult to modify its tray. Conversely, including these parameters would allow for better results. The Tikhonov regularization matrix adopted is \({{\varvec{\Lambda}}} = {\text{diag}}\left( {\left[ {1;1;1;1;1;10^{ - 3} ;10^{ - 3} ;10^{ - 3} ;5 \cdot 10^{ - 3} ;5 \cdot 10^{ - 3} ;5 \cdot 10^{ - 3} ;10^{3} ;10^{3} ;10^{3} } \right]} \right)\), and these weights are chosen to penalize modifications of the lumped masses and of the leaf springs of the actuators. The optimal values of the modified variables together with the structural modification constraints adopted are listed in Table 1. The average computational time needed to compute the optimal structural modifications in MATLAB running on a laptop with an i7 16 GB RAM is equal to 5.2 s.

Inverse Dynamics on the Modified System

The modified parameters reported in Table 1 are adopted to update the mass and stiffness matrices accordingly to Eq. (22). The same motion specifications listed in the section "System Description and Performance Specifications" are required. For the chosen output coordinates \({\varvec{\eta}}\), the internal dynamics is unstable once again, as shown through the pole map in Fig. 4b, where it is evident the presence of a right-half complex plane pole. Once \({\tilde{\mathbf{\Gamma }}}_{{\mathbf{A}}}\) and \({\tilde{\mathbf{\Gamma }}}_{{\mathbf{U}}}\) are chosen, the internal dynamics is stable, as shown in Fig. 4b, indeed the right-half complex plane pole migrates beyond the imaginary axis and its real part becomes negative; further, only a negligible spillover is obtained on the remaining stable poles.

The inverse dynamic approach proposed in the section "Inverse Dynamics" is exploited once again for the modified system, to compute the actuation forces through the procedure outlined in the section “Outline of the Method". The time history of the obtained actuation forces is shown in Fig. 5 and compared with the actuation forces computed for the original system. It shows that the adoption of DSM does not increase the average RMS value of the actuation forces, that is 1.15e5 N for the original system, and 1.14e5 N for the one modified with the optimal structural modification. While f1 and f3 decrease (both in term of RMS and maximum values), f2 increases. Indeed, the actuation forces of the original system are

  • \(f_{1}^{RMS} = 1.05{\text{e}}5\,{\text{N}}\), \(f_{2}^{RMS} = 1.21{\text{e}}5\,{\text{N}}\) and \(f_{3}^{RMS} = 1.15{\text{e}}5\,{\text{N}}\);

  • \(f_{1}^{MAX} = 4.30{\text{e}}5\,{\text{N}}\), \(f_{2}^{MAX} = 3.40{\text{e}}5\,{\text{N}}\) and \(f_{3}^{MAX} = 3.40{\text{e}}5\,{\text{N}}\).

Those of the modified system are

  • \(f_{1}^{RMS} = 7.94{\text{e4}}\,{\text{N}}\), \(f_{2}^{RMS} = 1.81{\text{e}}5\,{\text{N}}\) and \(f_{3}^{RMS} = 8.17{\text{e4}}\,{\text{N}}\);

  • \(f_{1}^{MAX} = 3.34{\text{e}}5\,{\text{N}}\), \(f_{2}^{MAX} = 4.92{\text{e}}5\,{\text{N}}\) and \(f_{3}^{MAX} = 2.52{\text{e}}5\,{\text{N}}\).

It should be clearly stated that there is no a-priori control on the changes in the actuation forces, that can either increase or decrease, since DSM is focused on just reducing the tracking error.

The same sample time and numerical integrator adopted for the original system (see the section "Application of the Inverse Dynamics on the Original System") are used for the modified system to provide a fair comparison. The application of the actuation forces to the dynamic model of the modified vibratory feeder yields to the response of the imposed coordinates y2, y4, xt shown in Fig. 6. Once again, the reference signals and the simulated ones are almost overlapped, as corroborated by the small values of the tracking errors reported in Fig. 6. Hence, the proposed inverse dynamics approach is effective. Additionally, the RMS and maximum values of the tracking errors for the imposed coordinates are the following:

  • \(e_{2}^{RMS} = 1.43 \times 10^{ - 5} \,{\text{m}}\) and \(e_{2}^{MAX} = 2.86 \times 10^{ - 5} \,{\text{m}}\);

  • \(e_{4}^{RMS} = 9.92 \times 10^{ - 5} \,{\text{m}}\) and \(e_{4}^{MAX} = 2.50 \times 10^{ - 4} \,{\text{m}}\);

  • \(e_{x}^{RMS} = 1.00 \times 10^{ - 4} \,{\text{m}}\) and \(e_{x}^{MAX} = 2.37 \times 10^{ - 4} \,{\text{m}}\).

These results evidence that the adoption of DSM does not alter the trajectory tracking performances for the desired output coordinates. Indeed, the tracking error is smaller for y2 and xt, in the modified system and only an increase of the RMS and maximum values of the tracking error is obtained for the output coordinate y4. Table 2 summarizes the obtained errors together with the percentage variation of these parameters with respect to those obtained for the original system.

Table 2 Comparison of the tracking errors for the original and the modified systems
Full size table

The time history of the overall RMS error for the desired output coordinates is reported in Fig. 10a. It confirms the effectiveness of the inverse dynamics method proposed in this paper and it shows, once again, that the mechanical redesign of the feeder is almost negligible for the desired output coordinates. Indeed, the maximum value of \(e_{{{\varvec{\eta}}^{{{\varvec{des}}}} }}^{RMS}\) is equal to \(1.94 \times 10^{ - 4} \,{\text{m}}\).

The increase of performances provided by the adoption of structural modifications is shown in Fig. 7, where the trajectory tracking responses for the non-imposed vertical displacements (y1, y3, y5) are reported together with their tracking errors. An improvement of the motion of the entire tray is obtained with the goal of achieving the desired rigid-like motion. This result is confirmed by the following values for the RMS and maximum tracking errors:

  • \(e_{1}^{RMS} = 5.87 \times 10^{ - 4} \,{\text{m}}\) and \(e_{1}^{MAX} = 1.20 \times 10^{ - 3} \,{\text{m}}\);

  • \(e_{3}^{RMS} = 1.24 \times 10^{ - 4} \,{\text{m}}\) and \(e_{3}^{MAX} = 3.02 \times 10^{ - 4} \,{\text{m}}\);

  • \(e_{5}^{RMS} = 6.07 \times 10^{ - 4} \,{\text{m}}\) and \(e_{5}^{MAX} = 1.30 \times 10^{ - 3} \,{\text{m}}\).

The percentage variations with respect to the original system are summarized in Table 2 and confirm the benefits obtained through the adoption of the DSM.

The Cartesian displacements of each tray node for the original and modified system are reported in Fig. 8, together with the desired reference signals. It can be noticed that the inverse dynamic algorithm is effective in obtaining the desired throw angle for the imposed coordinates, i.e., y2, y4 and xt. Further, structural modification allows to significantly improve the throw angle for the non-imposed nodes, i.e., those denoted through y1, y3 and y5.

Fig. 8
figure 8

Cartesian displacements of the tray nodes for the original and the modified systems

Full size image

The effectiveness of the proposed method is assessed by the elastic rotations at each node of the tray, which are shown in Fig. 9 and take the following values for the modified system:

  • \(\varphi_{1}^{RMS} = 7.57 \times 10^{ - 4} \,^\circ\) and \(\varphi_{1}^{MAX} = 1.60 \times 10^{ - 3} \,^\circ\);

  • \(\varphi_{2}^{RMS} = 3.89 \times 10^{ - 4} \,^\circ\) and \(\varphi_{2}^{MAX} = 8.61 \times 10^{ - 4} \,^\circ\);

  • \(\varphi_{3}^{RMS} = 9.22 \times 10^{ - 5} \,^\circ\) and \(\varphi_{3}^{MAX} = 2.30 \times 10^{ - 4} \,^\circ\);

  • \(\varphi_{4}^{RMS} = 4.12 \times 10^{ - 4} \,^\circ\) and \(\varphi_{4}^{MAX} = 9.36 \times 10^{ - 4} \,^\circ\);

  • \(\varphi_{5}^{RMS} = 8.65 \times 10^{ - 4} \,^\circ\) and \(\varphi_{5}^{MAX} = 2.00 \times 10^{ - 3} \,^\circ\).

Fig. 9
figure 9

Elastic rotations for the tray nodes for the original and the modified systems

Full size image

The time history of \(e_{{{\varvec{y}}_{{{\varvec{ni}}}} }}^{RMS}\) is reported in Fig. 10b: it clearly shows that the tracking error for the non-imposed coordinates is remarkably reduced for the modified system. Indeed, it is characterized by a maximum value equal to 1.00 mm which yields to a percentage reduction of the 50% with respect to the original system. The tracking error related to the nodal elastic rotations, whose reference is imposed to be null to enforce the uniformity requirement for the tray displacements, is shown in Fig. 10c. The maximum value of \(e_{\boldsymbol{\varphi }}^{RMS}\) is equal to 0.07°, i.e., it is 45.2% smaller if compared with the original system. The time history of the overall performance index \(e_{{{\varvec{y}}_{{\varvec{t}}} }}^{RMS}\) is reported in Fig. 10d and it shows that the tracking error for the vertical coordinates of the tray remarkably decreases; indeed, its maximum value is equal to 0.81 mm leading to a percentage reduction equal to 49.1% with respect to the original system.

Fig. 10
figure 10

Comparison of the RMS tracking errors for the original and the modified systems: \(e_{{{\varvec{\eta}}^{{{\varvec{des}}}} }}^{RMS}\) (a), \(e_{{{\varvec{y}}_{{{\varvec{ni}}}} }}^{RMS}\) (b), \(e_{\varphi }^{RMS}\) (c), and \(e_{{{\varvec{y}}_{{\varvec{t}}} }}^{RMS}\) (d)

Full size image

These results, together with those summarized in Table 2, evidence that the concurrent usage of the proposed inverse dynamics approach together with the optimized mechanical design obtained through the DSM algorithm is effective. Indeed, both the imposed output coordinates and the remaining non-imposed coordinates of interest lead to a uniform rigid-like behavior of the tray.

Conclusions

This paper proposes an integrated method for ensuring uniform motion of the tray of linear vibratory feeders, operated in open-loop control with generic periodic references, by means of the integrated use of inverse dynamics and dynamic structural modification. The goal is challenging, since these systems are underactuated and non-minimum phase. Additionally, although inverse dynamics enables to impose just a number of desired outputs equal to the number of independent actuation forces, specifications on the motion of the whole tray is usually set to ensure proper motion. This problem cannot be therefore solved if internal dynamics is used alone. To overcome this limitation, this paper exploits DSM.

The inverse dynamics technique exploits the QR decomposition to transform the model of the system into a representation featuring actuated and unactuated coordinates. Then, the output reference coordinates are defined, and the system internal dynamics is analyzed. Since unstable internal dynamics occurs for non-minimum phase systems, the output redefinition method is exploited to stabilize it. The stabilized internal dynamics ordinary differential equations are then integrated to obtain the reference values for the unactuated coordinates and, finally through algebraic calculations, the actuation forces. The proposed approach leads to a causal, almost-exact solution of the inverse dynamics problem, thanks to the use of the actual output map in the computation of the forces.

The formulation of the internal dynamics with the actual output map is then exploited to perform structural modification, by considering the undamped system in the presence of harmonic excitations, thus leading to a straightforward problem formulation. Hence, the periodic output reference is decomposed through the Fourier Series truncated to a subset of harmonics of interest. Then, a DSM problem for the internal dynamics is formulated to improve the system performances by properly shaping such a constraint on the allowable motion. The solvability of the DSM problem for all the choices of the design parameters is ensured by recasting it into a non-linear non-convex optimization solved through the homotopy optimization technique.

To summarize, the main novel contributions of this integrated method for optimal control and design of feeders are:

  • Generic periodic references are handled both in the inverse dynamics and in the DSM;

  • The presence of viscous damping is considered in the inverse dynamics problem;

  • The second-order nonholonomic constraints, representing the motion of the unactuated coordinates leads to unstable internal dynamics, that is coped with in this paper through an output redefinition strategy;

  • DSM is performed by considering the internal dynamics, to better represent the effect of the desired reference on the desired output.

The effectiveness of the proposed method is assessed by its application to the challenging test case of a 14-DOFs industrial linear vibratory feeder employed in packaging plants. The system is excited through 3 independent actuators and its tray, over which products flow, is modeled through 11 coordinates. To ensure a uniform flow of the transported parts over the tray, it is required that the tray behaves as a rigid-like beam even if it is flexible. Underactuation exacerbates the problem, since only 3 tray coordinates can be imposed through the inverse dynamics algorithm, while an effective achievement of the remaining 8 coordinates of the tray relies on the DSM algorithm. The results proposed in the paper highlight the effectiveness of the proposed method. Indeed, the proposed inverse dynamics technique enables to obtain low tracking error for the imposed coordinates. Further, the optimized mechanical design obtained through structural modification enables to drastically reduce the tracking error also for the non-imposed coordinates of interest.