1 Introduction

1.1 Motivations

Vibration generators are widely employed in manufacturing plants to exert vibrations with prescribed frequency, amplitude, and spatial shape, as required by the process. Meaningful examples are vibratory feeders, often adopted to convey small parts in manufacturing plants, packaging lines, or flexible assembly cells [1,2,3,4] by exploiting the forced vibrations of a surface (named tray or trough) where the conveyed objects are placed. The vibration frequency should be consistent with the features of the conveyed objects [5, 6]. On the other hand, the shape of the vibration of the trough should be consistent with the requirements on the conveying velocity. For example, a uniform flow of the product can be obtained by ensuring uniform vibrations of the trough. Actually, bending of the trough at the frequency of excitation might cause large elastic deformation that severely compromise the part flow, if the design and the control of the feeder do not account for this issue [1]. Other examples are ultrasonic sonotrodes (horns) adopted for welding, atomizing, deagglomerating, machining, cleaning, or cutting [7,8,9,10]. These devices should be designed and excited to vibrate at the prescribed ultrasonic frequency with the proper shape and amplitude [10]. For example, plastic welding and solid-state bonding usually need high uniformity of the tip vibration of the sonotrode to ensure an effective process due to uniform heating and to prevent damage of the sonotrode itself and the products too [8].

These examples show that both a proper excitation force and a proper design of the mechanical part should be adopted to achieve the desired behavior. The difficulties in achieving the desired vibration are exacerbated in the presence of large and flexible devices, such as the long tray of linear feeders, which are excited by just few actuators. This problem has been up to now tackled in the literature through the optimal design of the elastic and inertial properties of the system, in the frame of the “dynamic structural modification” (DSM), by considering the free response of the system, i.e., without considering the excitation forces. A rich literature on DSM has been recently proposed, and several methods to assign the desired modal properties are available (see [11,12,13,14]). In contrast, the optimal shaping of the excitation forces in this kind of systems, as well as its relationship with the mechanical design, has not been investigated.

The optimal force shaping is an open-loop feedforward control. Feedforward control has been usually exploited in the literature in different fields of motion control, especially to overcome bandwidth limitations. The idea of feedforward is to invert the input–output map to compute the input profile leading to the desired output trajectory, by exploiting the system dynamic model. Feedforward is usually developed to track the desired trajectory of the end effector of flexible multibody systems (see [15,16,17,18]), which is defined through just few coordinates. The difficulties in the inversion of such a model are significantly exacerbated in the case of underactuated systems, i.e., when the number of independent actuators is smaller than the number of degrees of freedom (DOFs) of the system, and when the number of prescribed outputs is greater than the number of the actuators. These two situations are typical occurrences in vibration generators, where the response is set to many DOFs that represent different positions of the flexible system, while few actuators are employed.

1.2 Contributions of this paper

The analysis of the state-of-the-art highlights that developing a method for shaping the force to be exerted by the actuators is crucial, since the methods in the literature of feedforward control are not appropriate for the case under investigation. On the other hand, the presence of more output specifications than the number of independent control forces restricts the achievable time trajectories of the coordinates of interest, thus often preventing the achievement of the desired system response. Therefore, it is necessary to evaluate the set of allowable responses and to define the best feasible approximation of such a requirement. As for the use of DSM, it is usually addressed by neglecting the forces and are focused on the eigenstructure.

In the light of these needs and of the limitations of the existing literature, this paper proposes four novel approaches for improving the harmonic response of underactuated vibration generators under harmonic open-loop excitations. The goal is to approximate, as much as possible, the desired forced response for all or some coordinates (whose number is greater than the number of actuators), to meet the requirements of the manufacturing process. The first strategy investigated is the proper shaping of the harmonic excitation provided by the actuators. This technique, denoted “force shaping” (FS), computes the best achievable response and the suitable force by solving an inverse dynamic problem through a coordinate transformation and projection of the desired response onto the subspace of the allowable motion. The formulation of such a subspace reveals its relationship with the physical parameters of the system. Hence, a new concurrent approach involving the FS and the mechanical design is proposed. The idea of this approach is to exploit the modification of the elastic and inertial parameters to properly shape the allowable subspace in such a way that it spans the desired response. The benefit of concurrent approaches that handle the design of both the mechanical part and of the feedback control has been already shown to be very effective in the field of eigenstructure assignment together with state feedback control [19,20,21]. This idea is often denoted as “hybrid approach,” since the design problem is tackled with a multi-domain perspective and can be interpreted as a model-based mechatronic design [22]. In this work, a novel formulation is proposed, to solve a new problem that is optimizing the forced response through the structural modification and the feedforward control.

All the approaches proposed in this paper, both involving just FS and FS with DSM, are original. The effectiveness and the comparison of the results they provide is proposed through a meaningful test case taken from the literature, that is, the optimization of the response of an industrial vibratory feeder employed in manufacturing plant proposed in [1].

2 Definitions and statements of the problems

Let us model the vibration generator as an N DOF undamped linear system whose equations of motion are:

$$ \mathbf{M}\ddot{\mathbf{x}}(t)+\mathbf{Kx}(t)=\mathbf{Bf}(t) $$
(1)

M ∈ ℝN × Nand K ∈ ℝN × N are the mass and stiffness matrices, respectively. x ∈ ℝN is the vector of the displacement of the independent coordinates, and \( \mathbf{B}\in {\mathrm{\mathbb{R}}}^{N\times {N}_F} \) is the force distribution matrix, that is, assumed to be full column rank. The independent external forces are collected in vector\( \mathbf{f}(t)\in {\mathbb{R}}^{N_F} \), with NF ≤ N. Damping can be neglected, since vibration generators are usually built with low damping to ensure large vibration with reduced actuation effort.

Let us assume that the system is excited by in-phase harmonic forces f(t) = f0 cos(ωft) (f0 is the amplitude vector, ωf the radian excitation frequency) to obtain the harmonic vibratory motion required by the process. Hence, the steady-state response is x(t) = x0 cos(ωft), (x0 is the amplitude vector). The relation between the amplitude vectors is written in the frequency domain as follows:

$$ \left(-{\omega_f}^2\mathbf{M}+\mathbf{K}\right){\mathbf{x}}_{\mathbf{0}}=\mathbf{B}{\mathbf{f}}_{\mathbf{0}} $$
(2)

As briefly mentioned in Section 1.2, two different strategies are adopted in this paper to optimize the system response, in such a way that it feats the desired one:

  1. 1.

    the optimal shaping of the amplitude of the excitation force f0 to ensure the attainment of the desired displacements for all the DOFs or just a reduced subset of meaningful coordinates of interest. This strategy is denoted “FS.”

  2. 2.

    the simultaneous shaping of the amplitude of the excitation force f0 and modification of the inertial and elastic properties of the system (i.e., of matrices M and K) to ensure the attainment of the desired displacements for all the DOFs or just a reduced subset of meaningful coordinates of interest.

Each strategy, in turn, can be devoted to two different goals:

  1. a.

    the achievement of the desired response for all the coordinates

  2. b.

    the achievement of the desired response for a reduced subset of coordinates.

Combining strategies “1” and “2” together with the goals “a” and “b” leads to four problems solved in the paper:

  • Problem 1.a (Section 3.1): shaping the force amplitude vector to obtain the desired displacements for all the N DOFs of the system.

  • Problem 1.b (Section 3.2): shaping the force amplitude vector to obtain the desired displacements for a reduced subset of coordinates.

  • Problem 2.a (Section 4.2): simultaneous shaping the force amplitude vector and modification of the inertial and elastic properties of the system to obtain the desired displacements for all the N DOFs of the system.

  • Problem 2.b (Section 4.3): simultaneous shaping the force amplitude vector and modification of the inertial and elastic properties of the system to obtain the desired displacements for a reduced subset of coordinates.

3 Optimal shaping of the excitation forces

3.1 FS with fully assigned displacements: the “full force shaping”

3.1.1 Problem statement

The problem consists in shaping the vector of the force amplitudes, f0, to ensure the attainment of the desired displacements \( {\mathbf{x}}^{\mathbf{d}}(t)={\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}}\cos \left({\omega}_ft\right) \), which is defined for all the N DOFs of the system. The problem is therefore finding f0, ensuring that:

$$ \mathbf{B}{\mathbf{f}}_{\mathbf{0}}=\left(-{\omega}_f^2\mathbf{M}+\mathbf{K}\right){\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} $$
(3)

All along the paper, superscript d denotes the desired values, while subscript 0 denotes the vector of amplitudes.

3.1.2 Subspace of the allowable motions

If the system is fully actuated (i.e., NF = N), the solution is straightforward since B ∈ ℝN × N is an invertible matrix:

$$ {\mathbf{f}}_{\mathbf{0}}={\mathbf{B}}^{-\mathbf{1}}\left(-{\omega}_f^2\mathbf{M}+\mathbf{K}\right){\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} $$
(4)

An exact solution exists for any \( {\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} \). Hence, any displacement vector can be achieved, provided that f0 belongs to the characteristic curves of the actuators and the actuator bandwidths are greater than ωf.

If the system is underactuated (i.e., NF < N), two critical issues should be tackled. First, B is rectangular, and therefore, it is not possible to calculate its inverse. On the other hand, using the pseudoinverse of B (denoted as B†) in lieu of B−1, i.e., calculating the force vector as \( {\mathbf{f}}_{\mathbf{0}}={\mathbf{B}}^{\dagger}\left(-{\omega}_f^2\mathbf{M}+\mathbf{K}\right){\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} \), just leads to a rough approximation of \( {\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} \). Second, it should be observed that the motion of the coordinates is constrained to lie on a NF-dimensional subspace, the so-called allowable subspace. These issues impose to develop a proper way to compute f0 that provides the best approximation of \( {\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} \) among the allowable ones.

In the general case, where B is a sparse matrix with more than NF not-null entries, let us perform the QR decomposition of B as follows:

$$ \mathbf{B}=\mathbf{Q}\mathbf{R}=\mathbf{Q}\left[\begin{array}{c}{\mathbf{B}}_{\mathbf{A}}\\ {}\mathbf{0}\end{array}\right] $$
(5)

where Q ∈ ℝN × N is an orthonormal matrix (QTQ = QQT = I, I is the identity matrix) and \( \mathbf{R}\in {\mathbb{R}}^{N\times {N}_F} \) is upper triangular. R, in turn, can be written by highlighting its upper-triangular, invertible sub-matrix \( {\mathbf{B}}_{\mathbf{A}}\in {\mathbb{R}}^{N_F\times {N}_F} \) which collects all its non-null entries, rank (BA) = NF.

By substituting Eq. (5) into Eq. (2), pre-multiplying it by QT, and finally introducing the new coordinate vector y = QTx, Eq. (2) is transformed into the following one:

$$ \left(-{\omega}_f^2{\mathbf{Q}}^{\mathbf{T}}\mathbf{MQ}+{\mathbf{Q}}^{\mathbf{T}}\mathbf{KQ}\right){\mathbf{y}}_{\mathbf{0}}=\left[\begin{array}{c}{\mathbf{B}}_{\mathbf{A}}\\ {}\mathbf{0}\end{array}\right]{\mathbf{f}}_{\mathbf{0}} $$
(6)

Although y has no physical meaning, it simplifies the problem solution. Indeed, y can be partitioned into NF actuated coordinates, \( {\mathbf{y}}_{\mathbf{A}}\in {\mathbb{R}}^{N_F} \), and N − NF unactuated coordinates, \( {\mathbf{y}}_{\mathbf{U}}\in {\mathrm{\mathbb{R}}}^{N-{N}_F} \) and \( \mathbf{y}=\left\{\begin{array}{c}{\mathbf{y}}_{\mathbf{A}}\\ {}{\mathbf{y}}_{\mathbf{U}}\end{array}\right\} \). The model in Eq. (6) is written accordingly, by defining the following partitions of M and K:\( {\mathbf{M}}_{\mathbf{AA}}\in {\mathbb{R}}^{N_F\times {N}_F} \), \( {\mathbf{K}}_{\mathbf{AA}}\in {\mathbb{R}}^{N_F\times {N}_F} \), \( {\mathbf{M}}_{\mathbf{UU}}\in {\mathbb{R}}^{\left(N-{N}_F\right)\times \left(N-{N}_F\right)} \), \( {\mathbf{K}}_{\mathbf{UU}}\in {\mathbb{R}}^{\left(N-{N}_F\right)\times \left(N-{N}_F\right)} \), \( {\mathbf{M}}_{\mathbf{AU}}\in {\mathbb{R}}^{N_F\times \left(N-{N}_F\right)} \),\( {\mathbf{K}}_{\mathbf{AU}}\in {\mathbb{R}}^{N_F\times \left(N-{N}_F\right)} \).

$$ \left(-{\omega}_f^2\left[\begin{array}{cc}{\mathbf{M}}_{\mathbf{A}\mathbf{A}}& {\mathbf{M}}_{\mathbf{A}\mathbf{U}}\\ {}{\mathbf{M}}_{\mathbf{A}\mathbf{U}}^{\mathbf{T}}& {\mathbf{M}}_{\mathbf{U}\mathbf{U}}\end{array}\right]+\left[\begin{array}{cc}{\mathbf{K}}_{\mathbf{A}\mathbf{A}}& {\mathbf{K}}_{\mathbf{A}\mathbf{U}}\\ {}{\mathbf{K}}_{\mathbf{A}\mathbf{U}}^{\mathbf{T}}& {\mathbf{K}}_{\mathbf{U}\mathbf{U}}\end{array}\right]\right)\left\{\begin{array}{c}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}\\ {}{\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}\end{array}\right\}=\left[\begin{array}{c}{\mathbf{B}}_{\mathbf{A}}\\ {}\mathbf{0}\end{array}\right]{\mathbf{f}}_{\mathbf{0}} $$
(7)

\( {\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}\in {\mathbb{R}}^{N_F} \)and \( {\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}\in {\mathbb{R}}^{N-{N}_F} \) denote the amplitudes.

Equation (7) can be written in term of the inverse of the receptance matrices \( {\mathbf{G}}_{\mathbf{AA}}\in {\mathbb{R}}^{N_F\times {N}_F} \), \( {\mathbf{G}}_{\mathbf{AU}}\in {\mathbb{R}}^{N_F\times \left(N-{N}_F\right)} \), and\( {\mathbf{G}}_{\mathbf{UU}}\in {\mathbb{R}}^{\left(N-{N}_F\right)\times \left(N-{N}_F\right)} \), defined as:

$$ \mathbf{G}=\left[\begin{array}{cc}{\mathbf{G}}_{\mathbf{AA}}& {\mathbf{G}}_{\mathbf{AU}}\\ {}{\mathbf{G}}_{\mathbf{AU}}^{\mathbf{T}}& {\mathbf{G}}_{\mathbf{UU}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{K}}_{\mathbf{AA}}-{\omega}_f^2{\mathbf{M}}_{\mathbf{AA}}& {\mathbf{K}}_{\mathbf{AU}}-{\omega}_f^2{\mathbf{M}}_{\mathbf{AU}}\\ {}{\mathbf{K}}_{\mathbf{AU}}^{\mathbf{T}}-{\omega}_f^2{\mathbf{M}}_{\mathbf{AU}}^{\mathbf{T}}& {\mathbf{K}}_{\mathbf{UU}}-{\omega}_f^2{\mathbf{M}}_{\mathbf{UU}}\end{array}\right] $$
(8)

It follows that:

$$ \left\{\begin{array}{c}{\mathbf{G}}_{\mathbf{A}\mathbf{A}}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}+{\mathbf{G}}_{\mathbf{A}\mathbf{U}}{\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}={\mathbf{B}}_{\mathbf{A}}{\mathbf{f}}_{\mathbf{0}}\\ {}{\mathbf{G}}_{\mathbf{A}\mathbf{U}}^{\mathbf{T}}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}+{\mathbf{G}}_{\mathbf{U}\mathbf{U}}{\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}=\mathbf{0}\end{array}\right. $$
(9)

The second matrix equation in Eq. (9) reveals that the motion of the unactuated DOFs is fully imposed by the motion of the actuated ones:

$$ {\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}=-{\mathbf{G}}_{\mathbf{U}\mathbf{U}}^{-\mathbf{1}}{\mathbf{G}}_{\mathbf{A}\mathbf{U}}^{\mathbf{T}}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}} $$
(10)

The following transmission matrix can be therefore defined:

$$ \left\{\begin{array}{c}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}\\ {}{\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}^{\mathbf{d}}\end{array}\right\}=\left[\begin{array}{c}{\mathbf{I}}_{N_F\times {N}_F}\\ {}-{\mathbf{G}}_{\mathbf{U}\mathbf{U}}^{-\mathbf{1}}{\mathbf{G}}_{\mathbf{A}\mathbf{U}}^{\mathbf{T}}\end{array}\right]{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} $$
(11)

Equation (11) shows that the feasible displacement vectors are constrained to belong to a subspace spanned by the NF columns of \( \mathbf{L}=\left[\begin{array}{c}{\mathbf{I}}_{N_F\times {N}_F}\\ {}-{\mathbf{G}}_{\mathbf{UU}}^{-\mathbf{1}}{\mathbf{G}}_{\mathbf{AU}}^{\mathbf{T}}\end{array}\right]\in {\mathbb{R}}^{N\times {N}_F} \):

$$ \left[\begin{array}{c}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}\\ {}{\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}\end{array}\right]\in \mathrm{span}\left(\left[\begin{array}{c}{\mathbf{I}}_{N_F\times {N}_F}\\ {}-{\mathbf{G}}_{\mathbf{U}\mathbf{U}}^{-\mathbf{1}}{\mathbf{G}}_{\mathbf{A}\mathbf{U}}^{\mathbf{T}}\end{array}\right]\right) $$
(12)

The allowable subspace depends on the inertial and elastic properties of the underactuated subsystem and of the frequency of the excitation force. Additionally, it implicitly depends on matrix B. Indeed, not only the rank of the force distribution matrix imposes the dimension of the allowable subspace but also B itself sets the transformation from the physical coordinates x to the auxiliary ones y, and hence the partitioning into yA and yU. Clearly, the possibility to achieve the desired response is strongly related to the number of independent external forces compared with the number of DOFs (i.e., the so-called degree of underactuation).

By taking advantage of Eq. (10), the first matrix equation in Eq. (9) can be written as a fully actuated NF-DOF subsystem:

$$ \left({\mathbf{G}}_{\mathbf{A}\mathbf{A}}-{\mathbf{G}}_{\mathbf{A}\mathbf{U}}{\mathbf{G}}_{\mathbf{UU}}^{-\mathbf{1}}{\mathbf{G}}_{\mathbf{A}\mathbf{U}}^{\mathbf{T}}\right){\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}={\mathbf{B}}_{\mathbf{A}}{\mathbf{f}}_{\mathbf{0}} $$
(13)

Since the input matrix BA computed through the QR decomposition is square and full rank, Eq. (13) can be easily inverted, and therefore, any arbitrary desired motion of the actuated DOFs, \( {\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \), can be obtained through the following forces:

$$ {\mathbf{f}}_{\mathbf{0}}={\mathbf{B}}_{\mathbf{A}}^{-\mathbf{1}}\left({\mathbf{G}}_{\mathbf{A}\mathbf{A}}-{\mathbf{G}}_{\mathbf{A}\mathbf{U}}{\mathbf{G}}_{\mathbf{UU}}^{-\mathbf{1}}{\mathbf{G}}_{\mathbf{A}\mathbf{U}}^{\mathbf{T}}\right){\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} $$
(14)

3.1.3 Solving strategy

Let us assume that all the N entries of x0 are required to assume the prescribed values \( {\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} \). The desired displacement vector is transformed from x to y, leading to the desired amplitudes of the actuated and unactuated DOFs:

$$ \left\{\begin{array}{c}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}\\ {}{\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}^{\mathbf{d}}\end{array}\right\}={\mathbf{Q}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} $$
(15)

Imposing \( {\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) in Eq. (14) does not ensure that \( {\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}} \) equals \( {\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}^{\mathbf{d}} \) too. Therefore, \( \left\{\begin{array}{c}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}\\ {}{\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}^{\mathbf{d}}\end{array}\right\} \)should be projected onto the subspace of the allowable motion spanned by the columns of L to compute the modified desired displacements of the actuated DOFs, denoted \( {\overset{\sim }{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \), that should be imposed in Eq. (14) in lieu of \( {\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) to provide the best approximation of \( {\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} \):

$$ {\tilde{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}={\left({\mathbf{L}}^{\mathbf{T}}\mathbf{L}\right)}^{-\mathbf{1}}{\mathbf{L}}^{\mathbf{T}}\left\{\begin{array}{c}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}\\ {}{\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}^{\mathbf{d}}\end{array}\right\} $$
(16)

Weighed projections can be also performed to reflect differing levels of concern about each entry, i.e., to boost the achievement of the desired displacements for some meaningful coordinates. Additionally, numerical methods for improving the calculation of (LTL)−1LT can be exploited.

The approach proposed in this section will be denoted for brevity in the following of the paper as full force shaping (FFS).

3.2 FS with partial assignment of the displacements: the “partial force shaping”

3.2.1 Problem statement

In large-scale systems, it is common that the desired displacements are imposed on just some coordinates [10, 11]. A different solution of the FS problem should be therefore developed, compared with the one in Section 3.1, leading to the partial force shaping (PFS).

Let us assume that only nd < N harmonic in-phase DOF displacements, \( {\mathbf{x}}_{\mathbf{s}}^{\mathbf{d}}\in {\mathrm{\mathbb{R}}}^{n_d} \) (\( {\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}} \) is the amplitude vector), are “set” to assume desired values. In contrast, the remaining N − nd coordinate displacements are “free” to assume arbitrary values and are collected into \( {\mathbf{x}}_{\mathbf{f}}\in {\mathrm{\mathbb{R}}}^{N-{n}_d} \) (\( {\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}} \) is the amplitude vector).

Matrix Q is partitioned into \( {\mathbf{Q}}_{\mathbf{s}}\in {\mathbb{R}}^{{\mathrm{n}}_{\mathrm{d}}\times \mathrm{N}} \) and \( {\mathbf{Q}}_{\mathbf{f}}\in {\mathbb{R}}^{\left(\mathrm{N}-{\mathrm{n}}_{\mathrm{d}}\right)\times \mathrm{N}} \) according to the coordinate partitioning \( \mathbf{x}=\left\{\begin{array}{c}{\mathbf{x}}_{\mathbf{s}}\\ {}{\mathbf{x}}_{\mathbf{f}}\end{array}\right\} \). The goal is to properly define \( {\tilde{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) that should be imposed in Eq. (14) in lieu of \( {\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) to provide the best approximation of \( {\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}} \).

3.2.2 Subspace of the allowable motions for underactuated systems

By exploiting the coordinate transformation, such as the one in Eq. (15) and Eq. (11), it is possible to write:

$$ {{\mathbf{Q}}_{\mathbf{s}}}^{\mathbf{T}}{\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}}=\left[\mathbf{L}\kern0.5em -{{\mathbf{Q}}_{\mathbf{f}}}^{\mathbf{T}}\right]\left\{\begin{array}{c}{\overset{\sim }{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}\\ {}{\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\end{array}\right\} $$
(17)

Equation (17) shows that the allowable \( {\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}} \) are constrained to belong to a reduced subspace spanned by the column of the full-rank matrix \( \mathbf{P}=\left[\mathbf{L}\kern0.5em -{\mathbf{Q}}_{\mathbf{f}}^{\mathbf{T}}\right]\in {\mathrm{\mathbb{R}}}^{N\times \left({N}_F+N-{n}_d\right)} \):

$$ {{\mathbf{Q}}_{\mathbf{s}}}^{\mathbf{T}}{\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}}\in \mathrm{span}\left(\left[\mathbf{L}\kern0.5em -{{\mathbf{Q}}_{\mathbf{f}}}^{\mathbf{T}}\right]\right) $$
(18)

This proves that reducing the number of imposed coordinates enlarges the dimension of the achievable subspace and hence boosts the achievement of the desired response for the nd DOFs of interest.

3.2.3 Solving strategy

In accordance with Eq. (18), \( {\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}} \) should be projected onto the subspace of the allowable motion spanned by the columns of P. Hence, the following \( {\tilde{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) should be imposed:

$$ {\tilde{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}=\left[{\mathbf{I}}_{N_F\times {N}_F}\kern1em {\mathbf{0}}_{N_F\times \left(\mathrm{N}-{\mathrm{n}}_{\mathrm{d}}\right)}\right]{\left({\mathbf{P}}^{\mathbf{T}}\mathbf{P}\right)}^{-1}{\mathbf{P}}^{\mathbf{T}}{\mathbf{Q}}_{\mathbf{s}}^{\mathbf{T}}{\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}} $$
(19)

Again, the optimal excitation forces f0 are obtained exploiting Eq. (14), introducing \( {\tilde{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) provided by Eq. (19) in lieu of \( {\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \).

Constraints on the admissible values of the unassigned displacements can be also set. In this case, no analytical solution for \( {\tilde{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) can be found. In contrast, a numerical least-square solution of the following problem should be computed (Γ denotes the set of constraints on the feasible displacements for the unassigned DOFs):

$$ \underset{{\overset{\sim }{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}},{\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}}{\min}\left\{{\left\Vert \left[\mathbf{L}\kern0.5em -{{\mathbf{Q}}_{\mathbf{f}}}^{\mathbf{T}}\right]\left\{\begin{array}{c}{\overset{\sim }{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}\\ {}{\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\end{array}\right\}-{{\mathbf{Q}}_{\mathbf{s}}}^{\mathbf{T}}{\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}}\right\Vert}_2^2,\left\{\begin{array}{c}{\overset{\sim }{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}\\ {}{\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\end{array}\right\}\in \boldsymbol{\Gamma} \right\} $$
(20)

If Γ is a convex set, Eq. (20) is a convex minimization problem.

4 Concurrent DSM and shaping of the excitation forces

4.1 Definitions and problem statement

Both the FS approaches proposed in Section 3 look for the closest approximation of the desired displacement vector by projecting it onto the allowable subspace. This approximation might be inadequate. This limitation can be overcome by modifying the allowable subspace in such a way that it leads to a closer approximation of the desired system response, or, in the best case, it spans such a vector. Whenever the number and the locations of the external forces cannot be modified (i.e., matrix B is not modified), as it often happens in practice, the modification of the elastic and inertial parameters should be exploited.

The DSM problem can be formulated by taking advantage of the relation stated in the second equation in Eq. (9) that shows how the motion of the unactuated DOFs is imposed by the motion of the actuated ones. By defining the following structural modification matrices:

$$ {\displaystyle \begin{array}{c}\boldsymbol{\Delta} {\mathbf{G}}_{\mathbf{AU}}=\boldsymbol{\Delta} {\mathbf{K}}_{\mathbf{AU}}-{\omega}_f^2\boldsymbol{\Delta} {\mathbf{M}}_{\mathbf{AU}}\in {\mathbb{R}}^{N_F\times \left(N-{N}_F\right)}\\ {}\boldsymbol{\Delta} {\mathbf{G}}_{\mathbf{UU}}=\boldsymbol{\Delta} {\mathbf{K}}_{\mathbf{UU}}-{\omega}_f^2\boldsymbol{\Delta} {\mathbf{M}}_{\mathbf{UU}}\in {\mathbb{R}}^{\left(N-{N}_F\right)\times \left(N-{N}_F\right)}\end{array}} $$
(21)

then, such a relation can be written for the modified system as follows:

$$ {\left({\mathbf{G}}_{\mathbf{A}\mathbf{U}}+\boldsymbol{\Delta} {\mathbf{G}}_{\mathbf{A}\mathbf{U}}\right)}^{\mathbf{T}}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}+\left({\mathbf{G}}_{\mathbf{U}\mathbf{U}}+\boldsymbol{\Delta} {\mathbf{G}}_{\mathbf{U}\mathbf{U}}\right){\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}=\mathbf{0} $$
(22)

The DSM problem exploits Eq. (22). Two different formulations should be adopted for the cases of full or partial assignment of the response.

The mass and stiffness modification matrices, ΔKAU, ΔMAU, ΔKUU, ΔMUU, are obtained by transforming and partitioning the mass and stiffness modification matrices of the model with physical coordinates x, denoted as ΔM and ΔK, through matrix Q:

$$ {\mathbf{Q}}^{\mathbf{T}}\boldsymbol{\Delta} \mathbf{MQ}=\left[\begin{array}{cc}\boldsymbol{\Delta} {\mathbf{M}}_{\mathbf{AA}}& \boldsymbol{\Delta} {\mathbf{M}}_{\mathbf{AU}}\\ {}\boldsymbol{\Delta} {\mathbf{M}}_{\mathbf{AU}}^{\mathbf{T}}& \boldsymbol{\Delta} {\mathbf{M}}_{\mathbf{UU}}\end{array}\right]\in {\mathbb{R}}^{N\times N}\kern0.24em \;\kern0.24em \;\kern0.24em {\mathbf{Q}}^{\mathbf{T}}\boldsymbol{\Delta} \mathbf{KQ}=\left[\begin{array}{cc}\boldsymbol{\Delta} {\mathbf{K}}_{\mathbf{AA}}& \boldsymbol{\Delta} {\mathbf{K}}_{\mathbf{AU}}\\ {}\boldsymbol{\Delta} {\mathbf{K}}_{\mathbf{AU}}^{\mathbf{T}}& \boldsymbol{\Delta} {\mathbf{K}}_{\mathbf{UU}}\end{array}\right]\in {\mathbb{R}}^{N\times N} $$
(23)

It is assumed, as usually done in the literature on DSM, that the topology of the modification matrices is a-priori assumed, to represent design choices on the admissible modifications. The values of these modifications are, instead, unknowns and are the design variables.

4.2 Full FS and dynamic structural modification

If both \( {\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) and \( {\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}^{\mathbf{d}} \) are prescribed, the DSM problem is formulated starting from the following equation:

$$ {\left({\mathbf{G}}_{\mathbf{A}\mathbf{U}}+\boldsymbol{\Delta} {\mathbf{G}}_{\mathbf{A}\mathbf{U}}\left(\mathbf{p}\right)\right)}^{\mathbf{T}}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}+\left({\mathbf{G}}_{\mathbf{U}\mathbf{U}}+\boldsymbol{\Delta} {\mathbf{G}}_{\mathbf{U}\mathbf{U}}\left(\mathbf{p}\right)\right){\mathbf{y}}_{{\mathbf{U}}_0}^{\mathbf{d}}=\mathbf{0} $$
(24)

Vector \( \mathbf{p}\in {\mathrm{\mathbb{R}}}^{n_p} \) collects the np design variables, i.e., the structural modification parameters, which are constrained to belong to a feasible domain Ψp.

Since the exact solvability of Eq. (24) is not always ensured, it is convenient to formulate the DSM problem in Eq. (24) as a constrained least-square minimization:

$$ \underset{\mathbf{p}}{\min}\left\{{\left\Vert {\left({\mathbf{G}}_{\mathbf{A}\mathbf{U}}+{\boldsymbol{\Delta} \mathbf{G}}_{\mathbf{A}\mathbf{U}}\left(\mathbf{p}\right)\right)}^{\mathbf{T}}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}+\left({\mathbf{G}}_{\mathbf{U}\mathbf{U}}+{\boldsymbol{\Delta} \mathbf{G}}_{\mathbf{U}\mathbf{U}}\left(\mathbf{p}\right)\right){\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}^{\mathbf{d}}\right\Vert}_2^2,\mathbf{p}\in {\boldsymbol{\Psi}}_{\mathbf{p}}\right\} $$
(25)

Equation (25) is a convex optimization problem whenever Ψp is convex. Hence, the global optimal solution can be found regardless of the initial guess.

Once the optimal values of the design variables, popt, are found, it is possible to apply the method outlined in Section 3.1 to compute the optimal excitation forces for the modified system. First, \( {\tilde{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) is find out for the modified system through Eq. (16). Then, f0 is computed as follows:

$$ {\mathbf{f}}_{\mathbf{0}}={\mathbf{B}}_{\mathbf{A}}^{-\mathbf{1}}\left({\overline{\mathbf{G}}}_{\mathbf{A}\mathbf{A}}-{\overline{\mathbf{G}}}_{\mathbf{A}\mathbf{U}}{\overline{\mathbf{G}}}_{\mathbf{UU}}^{-\mathbf{1}}{\overline{\mathbf{G}}}_{\mathbf{A}\mathbf{U}}^{\mathbf{T}}\right){\tilde{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} $$
(26)

where:

$$ {\displaystyle \begin{array}{l}{\overline{\mathbf{G}}}_{\mathbf{AA}}={\mathbf{G}}_{\mathbf{AA}}+{\boldsymbol{\Delta} \mathbf{G}}_{\mathbf{AA}}\left({\mathbf{p}}_{\mathrm{opt}}\right)\\ {}{\overline{\mathbf{G}}}_{\mathbf{AU}}={\mathbf{G}}_{\mathbf{AU}}+{\boldsymbol{\Delta} \mathbf{G}}_{\mathbf{AU}}\left({\mathbf{p}}_{\mathrm{opt}}\right)\\ {}{\overline{\mathbf{G}}}_{\mathbf{UU}}={\mathbf{G}}_{\mathbf{UU}}+{\boldsymbol{\Delta} \mathbf{G}}_{\mathbf{UU}}\left({\mathbf{p}}_{\mathrm{opt}}\right)\end{array}} $$
(27)

Hereafter, the concurrent FFS enhanced through DSM will be denoted for brevity as FFS-DSM.

4.3 Partial FS and dynamic structural modification

Let us consider the case of Section 3.2, and therefore, let us regard the N − nd unassigned coordinates, whose amplitudes are collected in vector \( {\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}} \), as additional unknowns in the DSM problem, together with the design parameters p. This concurrent use of PFS together with DSM is denoted henceforth as PFS-DSM. The desired displacement amplitude vector in the transformed coordinate y is obtained through matrix Q, thus making \( {\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) and \( {\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}^{\mathbf{d}} \) functions of the unknown:

$$ \left\{\begin{array}{c}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}\left({\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\right)\\ {}{\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}^{\mathbf{d}}\left({\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\right)\end{array}\right\}={\mathbf{Q}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}}={\mathbf{Q}}^{\mathbf{T}}\left\{\begin{array}{c}{\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}}\\ {}{\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\end{array}\right\} $$
(28)

The unassigned displacement amplitudes are bounded by means of upper and lower element-wise inequalities, i.e., \( {\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}^L\le {\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\le {\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}^U \)with \( {\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}^L,{\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}^U\in {\mathbb{R}}^{N-{n}_d} \) representing constraints on their admissible values. The definition of these constraints is helpful for developing an effective solution method of the minimization problem, as explained in Section 4.3.1. By collecting all the constraints on the problem unknowns \( \left\{\begin{array}{c}\mathbf{p}\\ {}{\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\end{array}\right\} \) within the definition of a feasible domain Ψ, the DSM problem in Eq. (25) is recast into Eq. (29):

$$ \underset{\mathbf{p},{\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}}{\min}\left\{{\left\Vert {\left({\mathbf{G}}_{\mathbf{A}\mathbf{U}}+\boldsymbol{\Delta} {\mathbf{G}}_{\mathbf{A}\mathbf{U}}\left(\mathbf{p}\right)\right)}^{\mathbf{T}}{\mathbf{y}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}\left({\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\right)+\left({\mathbf{G}}_{\mathbf{U}\mathbf{U}}+\boldsymbol{\Delta} {\mathbf{G}}_{\mathbf{U}\mathbf{U}}\left(\mathbf{p}\right)\right){\mathbf{y}}_{{\mathbf{U}}_{\mathbf{0}}}^{\mathbf{d}}\left({\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\right)\right\Vert}_2^2,\left\{\begin{array}{c}\mathbf{p}\\ {}{\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}}\end{array}\right\}\in \boldsymbol{\Psi} \right\} $$
(29)

Equation (29) is non-linear and non-convex, due to the presence of some products of two unknowns. Therefore, a proper solving strategy, such as the one proposed in Section 4.3.1, should be adopted to boost the convergence to a global optimal solution. Once Eq. (29) has been solved and the optimal values of the parameter modifications, popt, and of the unassigned displacements \( {\mathbf{x}}_{{\mathbf{f}}_{\mathbf{0}}} \) are found, then the solving strategy proposed in Section 3.2.3 is exploited. First, \( {\tilde{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}} \) is computed through Eq. (19) with matrix P (and hence L) of the modified system (i.e., adopting the modified system matrices introduced in Eq. (27)). Then, the optimal excitation forces is computed through Eq. (26), by adopting once again the modified system matrices introduced in Eq. (27).

4.3.1 Homotopy optimization

The proposed solution method for Eq. (29) exploits homotopy optimization and is here briefly described. The proposed technique takes advantage of two methods developed by the Authors of this paper for assigning eigenfrequencies and partial mode shapes [11] or antiresonances [23,24,25,26] in vibrating systems. Homotopy is an optimization technique for non-convex functions that boosts the convergence to a global minimum by solving a sequence of optimization problems that starts with a convex relaxation of the original problem and then morphs it back to the original non-convex one through a path of solutions.

Variable lifting is here exploited to obtain the convex approximation of the bilinear terms in the form \( {p}_i{x}_{f_0,j} \) (for some indexes i and j). The problem can be, however, written as a convex function of the auxiliary variables bn (for some indexes n), \( {b}_n={p}_i{x}_{f_0,j} \). This approach is denoted as variable lifting.

The homotopy map that morphs back to the original problem of Eq. (29) is defined by replacing each bilinear term \( {p}_i{x}_{f_0,j} \) with an affine combination of itself and its related auxiliary variable bn, i.e., \( \lambda {p}_i{x}_{f_0,j}+\left(1-\lambda \right){b}_n \). The scalar λ ∈ [0; 1] that grows in a discrete way from 0 to 1 is the morphing parameter. In this way, the first problem (λ = 0) consists in solving the convex approximation fc, while the final one (λ = 1) is Eq. (29). In practice, homotopy is adopted to set effective initial guesses for the intermediate non-convex problems. Indeed, at any step of the homotopy transformation, the initial guess is set as the optimal solution of the previous step. The solution obtained at the last step (i.e., ΔGAU(pλ = 1) = ΔGAUopt and ΔGUU(pλ = 1) = ΔGUUopt) is the optimal modification of the system parameters.

To provide an effective approximation of the bilinear terms \( {p}_i{x}_{f_0,j} \) in all the intermediate steps, the McCormick envelopes are adopted too [27], by imposing upper and lower bounds to pi and \( {x}_{f_0,j} \).

4.3.2 Sensitivity analysis on the system displacements

The numerical efficiency and reliability of DSM algorithms can be increased by removing the design parameters whose variations have a weak effect on the system response (see [28, 29]). Sensitivity analysis is often formulated in DSM as the sensitivity of eigenfrequencies or mode shapes with respect to the design parameters. In contrast, this paper proposes the sensitivity analysis of the response of the DOFs of interest with respect to the design parameters. By denoting as p an arbitrary parameter belonging to p (either a mass or a stiffness), sensitivity Sp is:

$$ {S}_p={\left\Vert \frac{\partial {\mathbf{x}}_{\mathbf{0}}}{\partial p}\right\Vert}_2{p}_0 $$
(30)

where p0 is the nominal value. By exploiting Eq. (10), the following relation is obtained:

$$ \frac{\partial {\mathbf{x}}_{\mathbf{0}}}{\mathrm{\partial p}}=\mathbf{Q}\left\{\begin{array}{c}\frac{\partial {\tilde{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}}{\partial p}\\ {}-\left(\mathbf{D}{\overset{\sim }{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}^{\mathbf{d}}+{\mathbf{G}}_{\mathrm{UU}}^{-1}{\mathbf{G}}_{\mathrm{AU}}^{\mathrm{T}}\frac{\partial {\overset{\sim }{\mathbf{y}}}_{{\mathbf{A}}_{\mathbf{0}}}}{\partial \mathbf{p}}\right)\end{array}\right\} $$
(31)

The demonstration of Eq. (31) is proposed in Appendix 1, with the analytical expression of\( \mathbf{D}\in {\mathbb{R}}^{\left(N-{N}_F\right)\times {N}_F} \).

5 Test case

5.1 Model of the system

This section applies the proposed methods to a meaningful test case: an industrial linear vibratory feeder. The main part concerning the operations of a linear vibratory feeders is the oscillating tray, where the conveyed products flow. Uniform flow along the tray is obtained by imposing uniform vibration of the tray, despite its flexibility. Vibratory feeders are usually driven by electromagnetic actuators [1, 30, 31], linear actuators [32, 33], and rotating motor with eccentric masses [34], although some new promising techniques are being investigated in the literature, such as actuators based on dielectric elastomers [35]. Regardless of the technology adopted for actuation, it is here assumed that the force amplitude of each actuator can be set to the desired one.

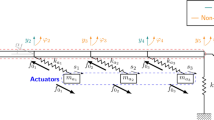
The linear vibratory feeder assumed for validation is sketched in Fig. 1, and its parameters are taken from [1] and summarized in Table 1. Small vibratory feeders are often modeled in the literature as single-DOF [35, 36] or two-mass [7] systems. In the case under investigation, due to the presence of more actuators and of a long and flexible tray, such a model is not adequate [1]. Therefore, a multi-DOF model with finite elements to model the continuum masses and elasticity should be adopted.

Fig. 1
figure 1

Sketch of the linear vibratory feeder

Full size image
Table 1 Original system parameters
Full size table

The tray is a flexible beam supported by two vertical grounding springs (whose stiffnesses are kl, kr respectively) and an horizontal grounding spring (kx). The feeder is excited by three actuators that are represented in the model as three lumped masses (with the same value\( {m}_{a_1}={m}_{a_2}={m}_{a_3} \)) connected to the tray by means of springs whose stiffnesses are\( {k}_{a_1}={k}_{a_2}={k}_{a_3} \). These springs are adopted and tuned to create a resonance frequency where the tray should vibrate in a quasi-rigid way in the direction of the desired throw angle, i.e., the angle between the speed vector and the tray longitudinal direction. For the same reason, the actuators are linked to the tray with an inclination equal to αf, which is the desired throw angle. In practice, tray flexibility does not allow for this rigid-body ideal behavior, and hence, both the vibration amplitude and the throw angle change along the tray. This is the main cause of non-uniform flow. The problem is exacerbated for long trays. To account for this issue, the tray is modeled through four Euler–Bernoulli finite elements with equal length. In contrast, the beam is assumed to be infinitely rigid in the axial direction; hence, it behaves as a lumped mass mB = ρAl whose horizontal displacement is defined through coordinate xt. The resulting mass and stiffness matrices of the subsystem made by the tray are denoted MB, KB ∈ ℝ11 × 11. Three independent coordinates are adopted to model the relative motion of the actuators and the tray: s1, s2, and s3 along a direction tilted as the throw angle. These assumptions lead to a 14-dimensional model which includes the 5 nodal translational coordinates of the beam (y), 5 nodal elastic rotations (φ), the horizontal translation of the tray (xt), and the 3 relative displacements of the actuators (s): x = {y1, φ1, y2, φ2, y3, φ3, y4, φ4, y5, φ5, xt, s1, s2, s3 }T.

Three independent control forces, \( {f}_{0_i} \), are applied. The mass and stiffness matrices (\( {\mathbf{M}}_{{\mathbf{a}}_{\mathbf{i}}}\in {\mathrm{\mathbb{R}}}^{3\times 3} \) and \( {\mathbf{K}}_{{\mathbf{a}}_{\mathbf{i}}}\in {\mathrm{\mathbb{R}}}^{3\times 3} \), respectively) of the ith actuator (i = 1, 2, 3), developed in Appendix 2, are:

(32)

yi denotes the ith coordinate of the beam at the respective actuator attachment point.

The mass and stiffness matrices of the full system, respectively M ∈ ℝ14 × 14 and K ∈ ℝ14 × 14, are obtained by assembling the mass and stiffness matrices of the beam, MB, KB, with those of each actuator.

Finally, the force distribution matrix B is obtained by considering the left-hand side of Eq. (32):

$$ \mathbf{B}={\left[\begin{array}{cccccccccccccc}0& 0& \sin {\theta}_f& 0& 0& 0& 0& 0& 0& 0& 1& 0& 0& \cos {\theta}_f\\ {}0& 0& 0& 0& \sin {\theta}_f& 0& 0& 0& 0& 0& 0& 1& 0& \cos {\theta}_f\\ {}0& 0& 0& 0& 0& 0& \sin {\theta}_f& 0& 0& 0& 0& 0& 1& \cos {\theta}_f\end{array}\right]}^{\mathrm{T}} $$
(33)

5.2 Specifications

In accordance with the typical requirement set for feeders, the beam should have uniform displacement in the direction of the desired throw angle αf, when excited with a 35-Hz harmonic force.

By assuming an oscillation with prescribed amplitude \( {z}_0^d \) in the throw angle direction, i.e., parallel to the actuators in the rest configuration, equal displacements are imposed for all the nodes:

$$ {\displaystyle \begin{array}{c}{x}_{t_0}^d={z}_0^d\cos \left(\pi -{\alpha}_f\right)\\ {}{y}_0^d={z}_0^d\sin \left(\pi -{\alpha}_f\right)\end{array}} $$
(34)

Uniformity is enforced by imposing a rigid motion of the beam with null elastic nodal rotations, i.e., \( {\varphi}_0^d=0 \).

In the case of FFS, the actuator oscillation amplitude should be assigned too. A reasonable choice is imposing the relative motion \( {s}_0^d \) to be scaled with respect to \( {z}_0^d \) in accordance with a simplified rigid-body model (i.e., a four-mass system). It follows that the amplitudes of the desired displacements at the frequency of operations are collected in \( {\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} \):

$$ {\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}}={\left\{{y}_0^d\kern0.5em 0\kern0.5em {y}_0^d\kern0.5em 0\kern0.5em {y}_0^d\kern0.5em 0\kern0.5em {y}_0^d\kern0.5em 0\kern0.5em {y}_0^d\kern0.5em 0\kern0.5em {x}_{t_0}^d\kern0.5em {s}_0^d\kern0.5em {s}_0^d\kern0.5em {s}_0^d\right\}}^{\mathbf{T}} $$
(35)

It should be noted that changing \( {z}_0^d \) leads to the same scaling of f0, since the same scaling of \( {\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} \) is obtained and the system is linear time-invariant. In this test case, let us assume \( {z}_0^d=5\;\mathrm{mm} \) and \( {s}_0^d=13.70\;\mathrm{mm} \), which lead to \( {\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} \) stated in the first column of Table 2. A sketch of the system undergoing such desired displacements is reported in Fig. 2 (different scaling are adopted to represent the X and Y axis).

Table 2 Desired and obtained displacements with the methods proposed
Full size table
Fig. 2
figure 2

Sketch of the desired displacement amplitudes in the case of FFS

Full size image

In the case of PFS, the desired coordinates are just those of the tray, while arbitrary motion is allowed for the actuators:

$$ {\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}}={\left\{{y}_0^d\kern0.5em 0\kern0.5em {y}_0^d\kern0.5em 0\kern0.5em {y}_0^d\kern0.5em 0\kern0.5em {y}_0^d\kern0.5em 0\kern0.5em {y}_0^d\kern0.5em 0\kern0.5em {x}_{t_0}^d\right\}}^{\mathbf{T}} $$
(36)

5.3 Modal analysis

The modal analysis reveals that there are some vibrational modes close to the excitation frequency ωf, in which the beam undergoes large elastic deformations. The mode shapes ui ∈ ℝN and the natural frequencies ωi of the 9 lowest-frequency ones are shown in Fig. 3 (by assuming mass normalization). These modes are excited by the actuator, by perturbing the desired shape of the tray vibration. Attention should be paid to the 6th and the 7th vibrational. In particular, if the tray is rigid, the 6th mode shape is the one that best describes the motion of interest, i.e., the relative opposite motion between the tray and the actuators in the throw angle direction.

Fig. 3
figure 3

Lowest-frequency mode shapes of the original system

Full size image

In the light of the results of the modal analysis, the basic idea of the proposed force shaping can be therefore interpreted as finding the optimal force vector that optimally compensates for these unwanted elastic behaviors, leading to the best achievable response. As for the hybrid approaches involving FS and DSM, they can be interpreted in finding the optimal feasible modifications that allow the force to properly compensate for these elastic behaviors.

5.4 Application of FFS and PFS

FFS and PFS are here applied to the test case and compared with the results provided by the application of three equal forces, as often done by practitioners in commanding vibratory feeders whenever a uniform response along the tray is wanted [1]. It should be noted that equal forces are also the ones computed by solving Eq. (3) through the pseudoinverse of B, \( {\mathbf{f}}_{\mathbf{0}}={\mathbf{B}}^{\dagger}\left(-{\omega}_f^2\mathbf{M}+\mathbf{K}\right){\mathbf{x}}_{\mathbf{0}}^{\mathbf{d}} \), and are optimal in the case of rigid beams. This widespread benchmark approach will be named “PsI method” (PsI) in tables and in figures.

Performances are evaluated through these parameters, listed in Table 2 and Table 3:

  • the cosine between the obtained displacements and the desired ones that should approach 1. Such a value is computed for just the tray displacements, i.e.,\( \cos \left({\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}},{\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}\right) \);

  • the maximum difference among the vertical displacements of the tray, \( \left|\max \left({y}_{0_i}\right)-\min \left({y}_{0_i}\right)\right| \), and the maximum elastic rotations\( \max \left(\left|{\varphi}_{0_i}\right|\right) \) that provide two measures of the elastic deformations;

  • the throw angles for each node of the tray\( {\alpha}_{f_i}={\tan}^{-1}\left({y}_{0_i}/\left|{x}_{t_0}\right|\right) \) that should be 20°, as well as the maximum difference among the throw angles of the tray, \( \left|\max \left({\alpha}_{f_i}\right)-\min \left({\alpha}_{f_i}\right)\right| \)

Table 3 Comparison of the throw angles obtained with the methods proposed
Full size table

The steady-state forced responses obtained by using the methods discussed in this section are reported in Table 2 and depicted in Fig. 4. It is evident, by comparing all the evaluation parameters, that PFS closely approximates the desired response, which is instead very roughly approximated if the benchmark is adopted. The displacement of the tray is a quasi-rigid motion, with negligible elastic rotations and high uniformity. A minor improvement is obtained through FFS, which exploits the simplified rigid-body model as a heuristic rule to set \( {s}_0^d \). The comparison of the throw angles in Table 3 confirms the results, since just small variations about the target are obtained through PFS.

Fig. 4
figure 4

Comparison of the feeder displacements with different shaping methods

Full size image

The force vectors leading to such results are listed in Table 4, by also normalizing the harmonic excitation amplitudes with respect to their maximum value, i.e., \( {f}_{0_M}=\max \left({f}_{0_1},{f}_{0_2},{f}_{0_3}\right) \). While the PsI method employs three equal forces, the two proposed methods lead to different amplitudes. In the case of PFS, forces with 180-degree relative phases are obtained too, to compensate for the beam flexibility. Clearly, it causes a higher control effort, as corroborated by ‖f0‖2.

Table 4 Analysis of the forces obtained with the methods proposed
Full size table

The results are analyzed through the modal participation factor (MPF) of each vibrational mode in the forced response. Indeed, when a linear system is excited by harmonic forces at the frequency ωf and whose amplitudes is \( {\mathbf{f}}_{\mathbf{0}}\in {\mathrm{\mathbb{R}}}^{N_F} \), its displacements are a linear combination of the mode shapes ui. The coefficients of this linear combination are the MPFs:

$$ {\mathrm{MPF}}_i\left(\omega \right)=\frac{{\mathbf{u}}_{\mathbf{i}}^{\mathbf{T}}\mathbf{B}{\mathbf{f}}_{\mathbf{0}}}{\omega_i^2-{\omega}_f^2} $$
(37)

The MPFs of the three methods are reported in Fig. 5, where each value has been normalized through the maximum participation factor for ease of comparison: the 6th and the 7th modes are those that mainly contributes in the case of PsI and FFS. These mode shapes involve large elastic deformations of the tray (see Fig. 3), thus causing the non-uniform displacement. In contrast, PFS excites remarkably other vibrational modes, where the tray experiences a quasi-rigid motion, such as the 4th and the1st modes. The higher contributions of these modes partially compensate for the large displacement at the central point of the beam due to the 6th mode. This new mix of mode shapes ensures therefore the desired quasi-rigid motion of the tray.

Fig. 5
figure 5

Absolute values of the modal participation factors

Full size image

5.5 FS with structural modification

Fourteen design variables are initially chosen (p ∈ ℝ14), including the actuator masses that can be modified by adding or removing counterweight masses [1]; 5 additional nodal lumped masses mi, i = 1, …, 5, to be placed to the tray; and the modification of all the lumped springs:

$$ \mathbf{p}={\left\{{m}_{a_1}\kern0.5em {m}_{a_2}\kern0.5em {m}_{a_3}\kern0.5em {m}_1\kern0.5em {m}_2\kern0.5em {m}_3\kern0.5em {m}_4\kern0.5em {m}_5\kern0.5em {k}_{a_1}\kern0.5em {k}_{a_2}\kern0.5em {k}_{a_3}\kern0.5em {k}_l\kern0.5em {k}_r\kern0.5em {k}_x\right\}}^{\mathbf{T}} $$
(38)

In contrast, it is assumed that the tray flexural stiffness and linear mass density cannot be modified, although the method can handle their modifications, too. Clearly, in the case of an existing tray, it is very difficult modifying such parameters. On the other hand, including these parameters would allow for better results. A sketch of the feeder highlighting the chosen design variables is reported in Fig. 6. Constraints on the feasible modifications are imposed, as stated in the first column of Table 6. Additionally, a constraint on the overall mass increase to be lower than 15 kg is set.

Fig. 6
figure 6

Sketch of the feeder with a highlight on the design variables

Full size image

5.5.1 Sensitivity analysis

The sensitivity analysis is here applied to discard the design variables with the lowest sensitivity. In the case of the nodal masses mi, i = 1, …, 5 whose initial values are 0, the value adopted for normalization p0 is assumed as the upper bound of the feasible modification. The sensitivity analysis for PFS is reported in Table 5.

Table 5 Sensitivities
Full size table

To show the correctness and the usefulness of the sensitivity analysis, PFS-DSM will be evaluated considering both the complete set of available structural modifications reported in Eq. (38) and a reduced set not including \( {m}_{a_1} \), \( {m}_{a_3} \), and kx, which are the masses and stiffness with the smallest sensitivities. The test with a lower number of design parameters will be denoted as PFS-DSM 2 (Table 6).

Table 6 Parameter modifications
Full size table

5.5.2 Application of FFS-DSM and PFS-DSM

The methods have been applied with the same requirements given for the FS alone. Additionally, as required by the use of the McCormick envelopes, the actuator displacements \( {s}_{0_i} \) are constrained as follows: \( -20\;\left(\mathrm{mm}\right)\le {s}_{0_i}\le 20\;\left(\mathrm{mm}\right) \). Columns from the 3rd to the 5th ones report the optimal modifications computed through FFS-DSM, PFS-DSM, and PFS-DSM 2. The displacements obtained are listed in Table 2.

In the case of FFS, the concurrent use of DSM leads to a considerable improvement, as corroborated by the increase of \( \cos \left({\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}},{\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}\right) \) from 0.6526 to 0.9873, the decrease of \( \left|\max \left({y}_{0_i}\right)-\min \left({y}_{0_i}\right)\right| \) from 3.29 to 0.62 (mm), and the decrease of \( \max \left(\left|{\varphi}_{0_i}\right|\right) \) from 0.0023 to 0.0005 (rad).

In the case of PFS, the concurrent use of DSM leads to a smaller improvement compared with FFS, since PFS alone provides very good performances. Nonetheless, the improvement is evident by the cosine that approaches 1 and by comparing \( \left|\max \left({y}_{0_i}\right)-\min \left({y}_{0_i}\right)\right| \) that decreases from 0.38 to 0.05 (mm) and \( \max \left(\left|{\varphi}_{0_i}\right|\right) \) that decreases from 0.0003 to 0.0001 (rad). In practice, the tray behaves as a rigid beam under the excitation of the computed optimal force, despite its flexibility.

In the case of PFS-DSM 2, i.e., with reduced design variables, just a negligible reduction of the performances is obtained, as expected: the partial cosine decreases from 0.9998 to 0.9990. The elastic rotations are almost unchanged, while the maximum variation of the vertical displacements along the tray increases for just 5%. On the other hand, a simpler set of modification has been employed. Figure 7 corroborates the results showing the system displacements obtained in the cases of concurrent DSM and FS.

Fig. 7
figure 7

Comparison of the feeder displacements obtained with FFS-DSM and PFS-DSM

Full size image

The analysis of the throw angles along the tray, proposed in Table 3, confirms these results. High uniformity is obtained in both the strategies of partial FS with DSM, with negligible differences between the maximum and minimum angles (0.6° and 0.7° for PFS-DSM and PFS-DSM2 respectively).

The analysis of the optimal forces in Table 4 reveals that FFS-DSM and PFS-DSM employ three forces having equal phases and different amplitudes. In contrast, PFS-DSM 2 leads to forces with different amplitudes and 180-degree relative phases. FFS-DSM leads to higher actuation forces, as corroborated by ‖f0‖2, while PFS-DSM 2 enables the lowest actuator effort among the hybrid strategies.

Finally, it should be noted that all the constraints on the design variables are satisfied. The possibility to handle different constraints is another strength of the proposed methods.

5.5.3 Eigenstructure and modal participation factors in the modified systems

The modal participation factors of the mode shapes of the modified systems, excited with the optimal forces, are shown in Fig. 8. It highlights that DSM notably alters the participation of each mode. It is interesting to notice that elimination of some design variables in PFS-DSM 2 leads to a significantly different mix of mode shapes involved in the forced response.

Fig. 8
figure 8

Absolute values of the modal participation factors with FFS-DSM and PFS-DSM

Full size image

Finally, the presence of several vibrational modes that significantly contribute to the forced response confirms that the formulation of DSM problem through the subspace of the allowable motions of the forced response, in lieu of the traditional assignment of the vibrational modes, is more straightforward.

5.5.4 Response of the modified system to three equal forces

Finally, it should be noted that these structural modifications are not enough to obtain the desired response when used alone. Indeed, if three equal forces are applied to the modified systems, as those of the PsI method, a bad uniformity is obtained, as summarized by the following values of \( \cos \left({\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}^{\mathbf{d}},{\mathbf{x}}_{{\mathbf{s}}_{\mathbf{0}}}\right) \):

  • 0.6724 in the case of FFS-DSM

  • 0.5825 in the case of PFS-DSM

  • 0.7373 in the case of PFS-DSM 2.

These results corroborate the benefits of a hybrid approach that combines feedforward control and optimal design.

6 Conclusions

This paper proposes four novel strategies for improving the response of underactuated vibration generators operating under harmonic, open-loop excitation. The goal is to assign the desired steady-state response to all the coordinates (the “full assignment”) or to a subset of meaningful ones of interest (the “partial assignment”) to accomplish the requirements of the manufacturing process. Two strategies are exploited, leading to 4 methods: the optimal shaping of the excitation force (FS) and the simultaneous use of FS and the modification of the inertial and elastic properties of the system (DSM). Underactuated systems are investigated, where the number of specifications is greater than the number of independent control forces.

Since the input matrix can be sparse, its QR decomposition is employed to transform the model in a convenient set of coordinates. Although this representation loses physical meaning, it defines the subspace of the allowable motions. The dimension of the basis of such a space depends on the number of actuators and of coordinates whose motion is not imposed. Consequently, partial assignment solved through the proposed PFS enables a better approximation for the coordinate of interest, compared with the FFS where the motion of all the coordinates is imposed.

An even closer approximation of the desired response is obtained by modifying the subspace of the allowable motions, in such a way that it could span the desired response or, at least, provide a closer approximation of it. Two “hybrid” approaches are proposed: FFS-DSM and PFS-DSM. A strategy to solve the concurrent design of the control forces and of the modifications of the inertial and elastic parameters is proposed for both the full and the partial assignments. Constraints on the design variables can be introduced. Analytical formulation of the sensitivity analysis is proposed too, to discard the parameters that weakly affect performances.

The method validation is proposed through a linear vibratory feeder, taken from the literature, whose 14 DOFs are controlled through 3 independent forces, and where specifications are set on the motion of the flexible tray. The application of the 4 techniques that are compared with a common benchmark used by practitioners shows the benefits of the proposed methods. In particular, PFS-DSM provides the best approximation of the desired response and makes the system behave as a “quasi-rigid” system, despite the presence of relevant flexible dynamics of the tray.