Introduction

Pendulum prototypes are very convenient for investigation explanations in practical engineering. They represent a physical process, which can be thought of as condensed educational models; on behalf of instance, see manufacturing and spaceships [1]. Additionally, they contribute to demonstrating the essential nonlinear dynamic approaches. Therefore, pendulum models have provided a large number of applications in dynamic systems and, more recently, nonlinear controlling. For these aspects, see Beruno [2] and references cited therein for the historical background. Beruno [2] introduced novel nonlinear problem-solving methodologies and techniques and they are used to solve the fundamental issue of a massive solid rotating around a fixed rotation, i.e. the set of Poisson-Euler equations. The magnetic spherical pendulum in this paper is represented by a mechanical system that consists of a spherical pendulum, whereas its bob is electrically charged as a point charge. Simultaneously, it moves under the influence of the gravitational force along through a constant magnetic field. The concept of the magnetic spherical pendulum in the literature of classical mechanics stands for the configuration of a charged particle. It is suspended by a weightless rigid rod from a fixed point, moving in a sphere, and subjected to constant uniform gravity together with a uniform magnetic field, see Refs. [3] and [4]. Actually, this is an old topic since it was established throughout the problems of classical mechanics, which has been constructed in a number of textbooks [5] and [6]. This literature proved that the full quantitative solutions of the governing equation require the use of the elliptic functions. Porta and Montiel [7] obtained a solution for the equation of motion of the spherical pendulum with magnetic monopolies located at the origin of the coordinates. Generally, they applied the simplest contemporary methodology for the magnetic spherical pendulum. Yildirim [8] worked on a master thesis on the same topic. He concluded that the Poisson formalism represents the most efficient category for classical mechanics. Cushman and Bates [9] showed that the mechanically magnetic spherical pendulum is situated in the center of the sphere and acted upon by gravitational forces just on the particle as well as a homogeneous force owing to magnetic monopolies.

Linear/nonlinear differential equations have gained considerable interest given their wide-ranging applications. They have an important influence on many branches of pure and applied mathematics, applied mechanics, engineering, analytical chemistry, biology, quantum physics, astronomy, and many other applications. For many decades, researchers paid attention to the analytical solutions of these equations. Therefore, it has become increasingly important in all traditional and recently developed methods for solving these equations. There are many numerical and analytical methods used in solving nonlinear oscillator equations. Kyzioł and Okniński [10] examined such approximate solutions using the theory of algebraic curves. Precisely, they determined periodic steady-state solutions for the Duffing-Van der Pol oscillator (DVdP) to determine the amplitude’s dependence on the forcing frequency. Rawashdeh and Maitama [11] proposed the natural decomposition method (NDM) for solving the Riccati differential equation together with two nonlinear differential equations. This method gave a more significant improvement over the existing techniques. Zeghdoudi et al. [12] gave a brief description and some examples of the concept of symmetry classification of the Liénard equation. Beléndez et al. [13] examined a one-dimensional, undamped, and unforced cubic-quintic Duffing oscillator. In view of comprehensive elliptic integral, of first and second kinds involving the Jacobian functions, they obtained a solution. Mosta and Sibanda [14] presented an original presentation of a continuous linearization technique to the traditional Van der Pol (VdP) and Duffing oscillator. They demonstrated a planned scheme may be employed to attain limit cycle and bifurcation figures of the controlling equation of motion. Cui et al. [15], based on the Homotopy analysis method, obtained and examined the stable and unstable bounded solutions of VdP. By means of the Floquet theory, they analyzed the stability analysis. Moreover, their consequences are authorized to view the spectral analysis. Kudryashov [16] examined the force-free Duffing-Van der Pol equation. He used Painlevé’s test for the considered equation. Furthermore, he demonstrated the effectiveness of the technique by obtaining the first integral and the complete solution of the second-order differential equation. Chandrasekhar et al. [17] displayed that the force-free DVdP, under certain restrictions, is completely integrable. Furthermore, they described a method for constructing a conversion that eliminates the time-dependent element of the first integral and yields a coherent approach. Cherevko et al. [18] examined a comprehensive prototypical of DVdP that describes the relaxation oscillation in the limited mind hemodynamics. They investigated the equation for diverse patients seeing the individualities of their container schemes. In a study on oscillatory systems with pure cubic nonlinearity, chains with two and more degrees of freedom are the main focus before elastic systems were discussed [19]. A periodic force was used to activate a purely nonlinear and damped two-mass oscillator [20]. When numerical solutions were checked with analytically generated ones, they agreed well.

Characteristically, many problems arising in a wide array of technical grounds involving models of computational chemistry, hydrodynamics, and theoretical physics have been all effective in utilizing ordinary/partial differential equations. Unfortunately, few of these problems may have exact solutions. Consequently, the other methods may be solved in the light of the numerical techniques or along with the analytical perturbation ones. Generally, the analytical solutions are preferred, where all the classical perturbation methods depend upon the presence of minor parameters in the given problem. Really, the absence of this parameter yields more restrictions in the phenomenon in question. Consequently, a novel perturbation procedure has been proposed by He [21,22,23,24,25]. This technique is addressed by the Homotopy perturbation method (HPM). The straightforwardness of this approach is attributed to the fact that it needs no small parameter. Therefore, it is a promising and powerful approach, and it can remain utilized in various classes in the field of differential equations. The procedure for considering the HPM is as follows. The problem is divided into two portions. They are divided by an embedding restriction, which is called the embedded Homotopy parameter. Ayati and Biazar [23] used the HPM to find an exact solution or a closed approximate solution for some problems. They showed that the convergence of this approach has been briefly elaborated. El-Dib and Moatimid [24] modified the HPM to obtain perfect explanations for linear as well as nonlinear differential equations. The main concept in the process depends on guessing an appropriate guessing function, regularly, like a power series. All subsequent orders, because of the cancelation of the first order, are likewise neglected. Consequently, the residual zero-order solution will be confirmed to become a precise one. Moatimid [28] utilized the HPM to attain analytical bounded solutions, in a smoothly vertically rotated parabola, a sliding bead moves. In [29,30,31], the authors investigated the vibrating motion of two different dynamical systems using the HPM. Once more, in view of the importance of the Duffing oscillator in numerous occurrences in practical engineering, Moatimid [32] examined the stability analysis of a parametric Duffing oscillator. Utilizing the HPM, an analytical bounded solution of motion is attained.

Considering the foregoing consideration and the possible uses in sciences, technology, biological issues, and applied mechanics, the present study focuses on analyzing the magnetic spherical pendulum. Therefore, the current work focuses on examining this problem. To facilitate the presentation, the remaining of the manuscript is systematized as follows: Sect. 2 emphasizes on the methodology of the controlling equation. In Sect. 3, a modified analytical bounded approximate solution originating from the knowledge of the nonlinear extended frequency is introduced. In addition to the representation of the time history of this solution, the accompanying phase plane plots are used to highlight the influence of the affecting factors of the motion behavior. The evaluation of this solution and the numerical one reveals a good matching, indicating that the chosen approach is accurate. For various values of the azimuthal angular velocity, the relationship between the expanding frequency and the cyclotron one is plotted to show the possible values of the expanding frequency. The linearized stability analysis is depicted throughout Sect. 4. The phase portraits are drawn in this Section. The findings of the whole examination are summarized as concluding remarks in Sect. 5.

Methodology of the Problem

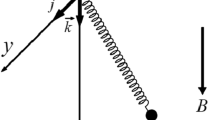
A magnetic spherical pendulum is considered a mechanical system; whereas its bob is electrically charged as a point of mass \(m\) and carries a positive charge \(e\). It is attached to a weightless rigid rod of length \(a\), simultaneously, the other end is hanged at a fixed point \(o\). It moves under the action of a constant gravitational field \(\underline{g}\) together with a constant magnetic field \(\underline{B}\) that acts in the negative \(z -\) direction. This uniform magnetic field comes from the magnetic monopole, which is located at the center of the sphere. The physical model is drawn as in Fig. 1

Fig. 1
figure 1

Sketch of the model under consideration

Full size image

The Cartesian coordinates \((x,\,y,\,z)\) are used for clarity in such a way that the position vector of the pendulum is given as follows:

$$\underline{r} = a\sin \theta \cos \varphi \,\underline{i} + a\sin \theta \sin \varphi \,\underline{j} - a\cos \theta \,\underline{k}$$
(1)

The velocity is given in the following form:

$$\underline{V} = a\left( {\dot{\theta }\cos \varphi \cos \theta - \dot{\varphi }\sin \theta \sin \varphi } \right)\,\underline{i} + a\left( {\dot{\theta }\sin \varphi \cos \theta + \dot{\varphi }\sin \theta \cos \varphi } \right)\,\underline{j} + a\dot{\theta }\sin \theta \,\underline{k}$$
(2)

Therefore, the kinetic energy \(K.E.\) of the pendulum produces

$$K.E. = \frac{{ma^{2} }}{2}\left( {\dot{\theta }^{2} + \dot{\varphi }^{2} \sin^{2} \theta } \right)$$
(3)

Because the charged pendulum moves in a uniform magnetic field \(\underline{B} = - B\,\underline{k}\), the Lagrangian function of the problem must include the magnetic term \(\frac{{\underline{V} \,.\,e\underline{A} }}{c}\), where \(\underline{A}\) is the magnetic potential and \(c\) is the light speed in the medium under consideration. In other words, the potential energy due to the magnetic field is given by \(\frac{{\underline{V} \,.\,e\underline{A} }}{c}\); for instance, see Eyal and Goldstein [33]. Keep in mind that the following relationship between both the magnetic field \(\underline{B}\) and the magnetic potential \(\underline{A}\) is given by: \(\underline{B} = \nabla \wedge \underline{A}\). As known, the uniform magnetic field has a practical importance. One may show that one of the possibilities of the vector potential is \(\underline{A} = \frac{1}{2}\left( {\underline{B} \wedge \underline{r} } \right)\). It follows that \(\underline{A}\) may be written as follows:

$$\underline{A} = \frac{1}{2}Ba\left( {\sin \varphi \,\underline{i} - \cos \varphi \,\underline{j} } \right)\sin \theta$$
(4)

From Eqs. (2) and (4), one gets the value of \({{(\underline{V} \,.\,e\underline{A} )} \mathord{\left/ {\vphantom {{(\underline{V} \,.\,e\underline{A} )} c}} \right. \kern-\nulldelimiterspace} c}\) as

$$\frac{{\underline{V} \,.\,e\underline{A} }}{c} = - \frac{1}{2c}eBa^{2} \dot{\varphi }\sin^{2} \theta$$
(5)

At this end, the charged pendulum is affected by two potential energies; namely, the gravitational potential energy, which is represented by the term \(- mga\cos \theta\) and the magnetic potential energy, which is exemplified by the term \(- \underline{\mu } \,.\,\,\underline{B}\), where \(\underline{\mu } = \frac{e}{2c}\left( {\underline{r} \wedge \underline{V} } \right)\).

From Eqs. (1) and (2), one finds

$$(\underline{\mu } )_{z} = \frac{{ea^{2} \sin^{2} \theta }}{2c}\dot{\varphi }$$
(6)

Therefore, the magnetic potential energy is given by the term \(- \frac{{ea^{2} B\sin^{2} \theta }}{2c}\dot{\varphi }\).

The total energy of the charged pendulum is then specified as:

$$\left( {K.\,E.} \right)_{T} = \frac{{ma^{2} }}{2}\left( {\dot{\theta }^{2} + \dot{\varphi }^{2} \sin^{2} \theta } \right) - \frac{{ea^{2} B\sin^{2} \theta }}{c}\dot{\varphi }$$
(7)

Finally, the Lagrangian of the pendulum is then given by:

$$L\left( {\theta ,\dot{\theta },\dot{\varphi }} \right) = ma^{2} \left[ {\frac{{\dot{\theta }^{2} }}{2} + \sin^{2} \theta \left( {\frac{{\dot{\varphi }^{2} }}{2} - \dot{\varphi }\omega_{c} } \right)} \right] + mga\cos \theta$$
(8)

where, the cyclotron frequency \(\omega_{C}\) is defined as: \(\omega_{C} = \frac{eB}{{mc}}\).

It should be noted that \(1/c\) appears in the Gauss system of units, meanwhile, it will be absent in \(SI\) System. Therefore, the system having two degrees of independence. Therefore, the governing equations of motion along the coordinates \(\theta\) and \(\varphi\), respectively, may be written as:

$$\ddot{\theta } + \frac{g}{a}\sin \theta - \left( {\dot{\varphi }^{2} - 2\omega_{C} \dot{\varphi }} \right)\sin \theta \cos \theta = 0$$
(9)

and

$$ma^{2} \sin^{2} \theta \left( {\dot{\varphi } - \omega_{C} } \right) = h$$
(10)

where \(h\) is a constant of integration to really be established based on the initial conditions.

As seen, Eq. (8) shows that the system movement is unaffected by the surroundings of the azimuthal angle \(\varphi\).

On the contrary, Eq. (10) reads \(\dot{\varphi } = \omega_{C} + \frac{h}{{ma^{2} \sin^{2} \theta }}\), therefore, Eq. (9) then becomes

$$\ddot{\theta } + \frac{g}{a}\sin \theta - \left[ {\left( {\frac{h}{{ma^{2} \sin^{2} \theta }}} \right)^{2} - \omega_{C}^{2} } \right]\sin \theta \cos \theta = 0$$
(11)

To facilitate the current investigation, one may consider that the horizontal angular velocity may be uniform, namely, \(\dot{\varphi } = \sigma\). In this case, Eq. (9) then becomes

$$\ddot{\theta } + \frac{g}{a}\sin \theta - \left( {\sigma^{2} - 2\sigma \omega_{C} } \right)\sin \theta \cos \theta = 0$$
(12)

To simplify the governing equation of motion (12), for more convenience, it needs to be interpreted in a non-dimensional manner. To achieve this goal, consider \(a\) as a characteristic length and \(\sqrt {a/g}\) equally as a characteristic time. It follows that Eq. (12) may be written as follows:

$$\ddot{\theta } + \sin \theta - \left( {\sigma^{2} - 2\sigma \omega_{C} } \right)\sin \theta \cos \theta = 0$$
(13)

On using the Taylor expansion, for small values of \(\theta\), one may consider \(\sin \theta \cong \theta - \theta^{3} /3!\),\(\cos \theta \cong 1 - \theta^{2} /2!\). Equation (13) then becomes

$$\ddot{\theta } + \omega^{2} \theta - \alpha \theta^{3} + \beta \theta^{5} = 0$$
(14)

where \(\omega^{2} = 1 + \sigma (2\omega_{C} - \sigma ),\)\(\alpha = \frac{1}{3}\left( {\sigma (2\omega_{C} - \sigma ) + \frac{1}{2}} \right),\) and \(\beta = \frac{\sigma }{12}(2\omega_{c} - \sigma )\).

To the real natural frequency, it should be considered that: \(\sigma \le 2\omega_{C}\). The parameters ω, α and β are specified as the natural frequency, cubic stiffness, and quintic stiffness parameters, respectively.

All terms in the governing equation that is given in (14) may be treated as non-dimensional ones, and all these coefficients are of a positive nature. Equation (14) is known as a free force undamped cubic-quintic Duffing oscillator. It is important to note that the nonlinear behaviors of a flexible elastic are modeled using a cubic-quintic Duffing oscillator, see Lenci et al. [34]. For nonlinear wave systems, see Huang and Zhang [35]. On behalf of the transmission of a small electromagnetic pulsate in a nonlinear medium, see Maimistov [36], then for the Duffing temporal oscillator, see Hamdan and Shabaneh [37].

A Periodic Analytical Approximate Solution

As aforementioned, the governing equation of motion (14) is a nonlinear one. Essentially, it does not have any exact solution. Consequently, it must be examined by a perturbation technique. As seen in our previous works [28] and [32], the traditional HPM yields secular terms, which are unfortunately physically undesired, and we do not have any authority to cancel them. Therefore, a modification of the classical HPM, namely the expanded nonlinear frequency, is needed. For this purpose, the Homotopy equation in this case may be formulated as follows:

$$\ddot{\theta } + \omega^{2} \theta + \rho \left( { \beta \theta^{5} - \alpha \theta^{3} } \right) = 0,\,\rho \in \left[ {0,\,1} \right]$$
(15)

To achieve a special solution, for a sake of simplicity, one may be based on the initial criteria as follows:

$$\theta (0) = 0\;{\text{and }}\theta (0) = 1$$
(16)

By means of the previous comprehended works [28] and [32], the natural frequency \(\omega^{2}\) may be expanded as follows:

$$\Omega^{2} = \omega^{2} + \sum\limits_{i = 1}^{n} {\rho^{i} } \omega_{i}$$
(17)

In accordance with the systematic HPM, the dominant function \(\theta (t)\) may be extended in the following way:

$$\theta (t;\rho ) = \sum\limits_{i = 1}^{n} {\rho^{i} } \theta_{i} (t)$$
(18)

Taking Laplace transforms (LT) of the combinations of Eqs. (15–17), one gets

$$L_{T} \left\{ {\theta (t;\rho )} \right\} = \frac{1}{{s^{2} + \Omega^{2} }} - \frac{\rho }{{s^{2} + \Omega^{2} }}L_{T} \left\{ {\alpha \theta^{3} (t;\rho ) - \beta \theta^{5}(t;\rho ) - \left( {\omega_{1} + \rho \omega_{2} } \right)\theta (t;\rho )} \right\}$$
(19)

Employing the inverse Laplace transforms to Eq. (19), one finds

$$\theta (t;\rho ) = \frac{1}{\Omega }\sin \,\Omega t - \rho L_{T}^{ - 1} \left[ {\frac{1}{{s^{2} + \Omega^{2} }}L_{T} \left\{ {\alpha \theta^{3}(t;\rho ) - \beta \theta^{5}(t;\rho ) - \left( {\omega_{1} + \rho \omega_{2} } \right)\theta (t;\rho )} \right\}} \right]$$
(20)

Consequently, the nonlinear part may be formulated by way of:

$$N\left( {\sum\limits_{i}^{n} {\rho^{i} \theta_{i} } } \right) = N_{0} (\theta_{0} ) + \rho N_{1} (\theta_{0} ,\,\theta_{1} ) + \rho^{2} N_{2} (\theta_{0} ,\,\theta_{1} ,\,\theta_{2} ) + ... + \rho^{n} N_{n} (\theta_{0} ,\,\theta_{1} ,\,\theta_{2} ,\,...\theta_{n} )$$
(21)

where

$$N_{n} (\theta_{0} ,\,\theta_{1} ,\,\theta_{2} ,\,...\theta_{n} ) = \frac{1}{n!}\mathop {\lim }\limits_{\rho \to 0} \frac{\partial }{{\partial \rho^{n} }}N\left( {\sum\limits_{i}^{n} {\rho^{i} \theta_{i} } } \right)$$
(22)

Exploiting the development of the dominant function \(\theta (t;\rho )\) that is given in Eq. (18), then associating the coefficient of like initial \(\rho\) on both borders, we catch the following orders:

$$\rho^{0} :\theta_{0} (t) = \frac{1}{\Omega }\sin \,\Omega t$$
(23)
$$\rho :\,\theta_{1} (t) = - L_{T}^{ - 1} \left[ {\frac{1}{{s^{2} + \Omega^{2} }}L_{T} \left\{ {\alpha \theta_{0}^{3} - \beta \theta_{0}^{5} - \omega_{1} \theta_{0} } \right\}} \right]$$
(24)

Inserting Eq. (23) into Eq. (24), the uniform effective development needs a withdrawal of the secular relationships. Actually, because of the nature of the initial conditions, the coefficient of the function \(\cos \,\Omega t\) is identical. By contrast, the elimination of the coefficient of the function \(\sin \,\Omega t\) yields

$$\omega_{1} = \frac{{ 10\beta - 12\alpha \Omega^{2}}}{{16\Omega^{4} }}$$
(25)

The conclusion is that the uniform expression of \(\theta_{1} (t)\) becomes

$$\theta_{1} (t) = \frac{1}{{384\Omega^{7} }}\left\{ {4\left( { 9\alpha \,\Omega^{2} - 10\beta} \right)\sin \,\Omega t + 3\left( {5\beta - 4\alpha \Omega^{2} } \right)\sin \,3\Omega t - \beta \sin \,5\Omega t} \right\}.$$
(26)

Once more, using Eqs. (23) and (26) as a starting point in the second order of Eq. (20), one finds that the elimination of the secular term results in

$$\omega_{2} = \frac{1}{{6144\Omega^{10} }}(1980\beta^{2} - 2880\alpha \beta \Omega^{2} + 1008\alpha^{2} \Omega^{4} )$$
(27)

Therefore, the suitable solution \(\theta_{2} (t)\) then becomes

$$\begin{gathered} \theta_{2} (t) = \frac{1}{{12288\Omega^{13} }}\{ \frac{1}{12}(9599\beta^{2} - 13500\alpha \beta \Omega^{2} + 4464\alpha^{2} \Omega^{4} )\sin \Omega t \hfill \\ \,\,\,\,\,\,\,\,\,\,\, - 3(110\beta^{2} - 151\alpha \beta \Omega^{2} + 48\alpha^{2})\Omega^{4} \sin3\Omega t + \frac{1}{3}(130\beta^{2} - 153\alpha \beta \Omega^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\, + 36\alpha^{2} \Omega^{4} )\sin 5\Omega t + \frac{1}{24}( 72\alpha \beta \Omega^{2} - 95\beta^{2})\sin 7\Omega t + \frac{{\beta^{2} }}{8}\sin 9\Omega t\} . \hfill \\ \end{gathered}$$
(28)

Considering the HPM, the approximate bounded expansion of the cubic-quintic Duffing problem that is given in Eq. (14) may be written as follows:

$$\theta (t) = \mathop {\lim }\limits_{\rho \to 1} \left( {\theta_{0} (t) + \rho \theta_{1} (t) + \rho^{2} \theta_{2} (t) + ...} \right)$$
(29)

where the functions \(\theta_{0} (t),\,\theta_{1} (t)\) and \(\theta_{2} (t)\) are dominant functions given by Eqs. (23), (26) and (28), correspondingly. This approximate solution (29) demands that the mathematical function arguments remain of actual real nature. For this objective, and by putting Eqs. (17), (25) and (27) together, one obtains a sixth-order equation in \(\Omega^{2}\) as follows:

$$\,\Omega^{12} - \omega^{2} \Omega^{10} + \frac{3\,\alpha }{4}\Omega^{8} + \frac{5\,\beta }{8}\Omega^{6} - \frac{{21\,\alpha^{2} }}{128}\Omega^{4} + \frac{15\,\alpha \beta }{{32}}\Omega^{2} - \frac{165}{{512}}\beta^{2} = 0$$
(30)

The necessary stability requirements need that \(\Omega^{2}\) is real and positive. This equation has three positive roots with values \((\Omega =\mathrm{0.259951,0.41857,1.00879})\).

Now, we are going to represent the time history of acquired analytical solution (AS) in (29) graphically to reveal the behavior of the examined problem. Therefore, Fig. 2 Is graphed for one of the roots of the Eq. (30) i.e. \(\Omega = 1.00879\) and when \(\omega_{c} = 1\) and \(\sigma = 0.1\) using our computer codes of Mathematica software (12.0.0.0). An inspection of a part (a) of this figure shows that the behavior of the attained solution has the form of periodic wave, which yields an induction about the steady-state manner of this solution. On the other hand, the phase plane diagram of the expression \(\theta (t)\) versus the function \(\theta^{\prime}(t)\) is plotted in part (b) of Fig. 2, to obtain a symmetric closed curve, which asserts that the solution has a stable manner.

Fig. 2
figure 2

Represents a the AS and b the phase plane of the AS at \(\sigma = 0.1,\omega_{c} = 1\) and \(\Omega = 1.00879\)

Full size image

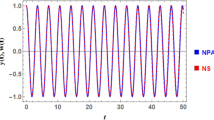
On the other hand, the numerical solution (NS) of the governing Eq. (14) and the corresponding phase plane plot, at the same considered values of \(\omega_{c}\), are represented graphically in parts (a) and (b) of Fig. 3 respectively. The comparison between AS and NS is graphed in parts of Fig. 4 to explore the consistency between them, which exhibits better accuracy of the utilized modified HPM. Moreover, the effects of other values of \(\sigma\) on the behavior of both solutions are presented in the parts (a) and (b) of Fig. 5 when \(\sigma = 0.01\)and \(\sigma = 0.2\), respectively. Figure 6 is calculated from the same preceding values of \(\sigma\) and \(\omega_{c}\) when \(\Omega = (0.259951,0.41857,1.00879)\) to examine the behavior of the AS with the various values of \(\Omega\). It's worthy to mention that the time histories of the AS with various values of \(\Omega\) having periodic waves. For the plotted waves, one can observe that the frequency of oscillations rises, the amplitudes of the waves decrease, and the wavelengths decrease with the increase of \(\Omega\) values, as seen in part (a). The corresponding phase plane curves are plotted in part (b) to detect the steady-state behavior of the obtained results. Therefore, the energy of the system depends on the value of the amplitude that change with the frequency. Consequently, it can be utilized in engineering applications that use the spherical pendulum.

Fig. 3
figure 3

Represents a the NS and b the phase plane of the NS at \(\sigma = 0.1,\omega_{c} = 1\) and \(\Omega = 1.00879\)

Full size image
Fig. 4
figure 4

Reveals the comparison between the AS and NS when \(\sigma = 0.1,\omega_{c} = 1\) and \(\Omega = 1.00879\): a time histories of both solutions and b the phase plane of both solutions

Full size image
Fig. 5
figure 5

Describes the comparison between the AS and NS when \(\omega_{c} = 1\) and \(\Omega = 1.00879\): a at \(\sigma = 0.01\) and b at \(\sigma = 0.2\)

Full size image
Fig. 6
figure 6

a Illustrates the AS and b describes the phase plane of the AS at \(\sigma = 0.1\) and \(\omega_{c} = 1\) when \(\Omega ( = 0.259951,0.41857,1.00879)\)

Full size image

Figure 7 examines the influence of the values of \(\sigma ( = 0.01,0.1,0.2)\) on the curves of the plane \(\omega_{c} \,\Omega\) in accordance with Eq. (30). We have two curves coinciding with each other at \(\Omega = 0\) for each value of \(\Omega\) to yield three positive roots plus their additive inverses. The intersection of these curves with \(\omega_{c}\) axis \(\sigma = 0.01,\sigma = 0.1\) and \(\sigma = 0.2\) will satisfy the equality \(\omega_{c} = {\sigma \mathord{\left/ {\vphantom {\sigma 2}} \right. \kern-\nulldelimiterspace} 2}\) to gain the values \(\omega_{c} = 0.005,\omega_{c} = 0.05\) and \(\omega_{c} = 0.1\), respectively.

Fig. 7
figure 7

Presents \(\omega_{c} \,\Omega\) plane at \(\sigma ( = 0.01,0.1,0.2)\)

Full size image

Linearization of Stability

The generalized linear methodology has utilized the autonomous system of the Duffing cubic-quintic equation that is given by (14). Through this whole Section, the linearized approach, using the expression correlates \(\dot{\theta } = \varphi\) Eq. (14) is transformed to the subsequent organization:

$$\dot{\theta } = f(\theta ,\varphi )\;\,\quad {\text{and}}\quad \,\, \dot{\varphi} = h \left( {\theta ,\varphi } \right)$$
(31)

where

$$\;f\left( {\theta ,\varphi } \right) = \varphi\;\quad {\text{and}}\quad \;h(\theta ,\varphi ) = - \omega^{2} \theta + \alpha \theta^{3} - \beta \theta^{5}$$
(32)
$$f(\theta_{0} ,\varphi_{0} ) = 0\quad {\text{and}}\quad h(\theta_{0} ,\varphi_{0} ) = 0$$
(33)

It follows that

$$\left. {\begin{array}{*{20}c} {\varphi_{0} = 0} \\ {\omega^{2} \theta_{0} - \alpha \theta_{0}^{3} + \beta \theta_{0}^{5} = 0} \\ \end{array} } \right\}$$
(34)

Therefore, the following five fixed points exist:

$$\left. {\begin{array}{*{20}c} {\theta_{0} = 0} \\ {\theta_{0} = \pm \sqrt {\frac{{\alpha \pm \sqrt {\alpha^{2} - 4\beta \omega^{2} } }}{2\beta }} } \\ \end{array} } \right\}$$
(35)

The second equation of (34) is represented graphically in parts (a), (b) and (c) of Fig. 8 to show the relation between \(\theta_{0}\) and \(\omega\) for different values of \(\sigma ( = 0.01,0.1,0.2)\) when \(\omega_{c} = 1,\omega_{c} = 2\) and \(\omega_{c} = 3\), correspondingly. It remains clear that there are three roots of this equation for each value of \(\sigma\), in which one of them is zero that corresponds to the trivial solution of this equation and the other two roots are equal with different signs at any value of \(\omega\).

Fig. 8
figure 8

Shows \(\omega \theta_{0}\) plane when \(\sigma ( = 0.01,0.1,0.2)\): a at \(\omega_{c} = 1\), b at \(\omega_{c} = 2\), and c at \(\omega_{c} = 3\)

Full size image

It follows from (35) that nearby are equilibrium points, if the following circumstances are met:

$$\left. {\begin{array}{*{20}c} {\alpha^{2} - 4\beta \omega^{2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \ge 0} \\ {\frac{{\alpha \pm \sqrt {\alpha^{2} - 4\beta \omega^{2} } }}{2\beta } > 0} \\ \end{array} } \right\}$$
(36)

The accompanying Jacobian matrix is obtained by expanding the functions \(f(\theta ,\varphi )\) and \(h(\theta ,\varphi )\) as well as around the fixed points with the Taylor series, keeping just the linear term in mind as follows:

$$J = \left( {\begin{array}{*{20}c} 0 & 1 \\ { - \omega^{2} + 3\alpha \theta_{0}^{2} - 5\beta \theta_{0}^{4} } & 0 \\ \end{array} } \right)$$
(37)

The determinant of the Jacobian matrix must be vanished at the fixed points:

$$\left| {\begin{array}{*{20}c} { - \Lambda } & 1 \\ { - \omega^{2} + 3\alpha \theta_{0}^{2} - 5\beta \theta_{0}^{4} } & { - \Lambda } \\ \end{array} } \right| = 0$$
(38)

From the above matrix, the eigenvalues are as follows:

$$\Lambda_{1,2} = \pm \sqrt { - \omega^{2} + 3\alpha \theta_{0}^{2} - 5\beta \theta_{0}^{4} }$$
(39)

Clearly, when all eigen values of the Jacobian which is computed near the fixed points possess negative real components, it follows that the equilibrium is stable. On the contrary, the equilibrium point becomes unstable, if at least one root of the eigen values has a positive real portion. To characterize the stability and instability maps, it is much more useful to study a set of randomly selected systems. The details may be found in our previous work [38]. The numerical calculations are carried out throughout Table 1.

Table 1 Summarizes the fixed points, nature of the eigenvalues as well as the stability/instability behaviors
Full size table
Fig. 9
figure 9

Shows a stable center

Full size image
Fig. 10
figure 10

Shows a stable node

Full size image

Concluding Remarks

Numerous academics who interested in analyzing nonlinear differential equations really would like to attain analytic as well as numerical approaches. Certain approaches such as Pade’ approximations, differential transformation technique, Adomian decomposition process, harmonic balancing procedure, and so on, are deeply used by these authors. In fact, the cubic-quintic Duffing oscillator is among the most advanced mathematical models for understanding a mechanical system with only one degree of freedom. Aimed at these foundations, the existing research looks at analytic approximation as well as stability configuration. Undesirably, the classical HPM fails to ignore the existence of the source of the secular terms. Therefore, to arrive this objective, a mixture of a modified HPM and Laplace transforms has been provided. Consequently, the attained approximate solution takes on a periodic structure as time passes. For different values of the azimuthal angular velocity, numerical validations are done to verify the analytical approximation result. With the rise of these values, the distinction among them becomes evident. A regular solution, on the other hand, is achieved using the concept of the nonlinear expanded frequency examination, in which it is graphically displayed versus the cyclotron one to illustrate the positive effect of the specified rotational velocity on its behavior. Indeed, this strategy is characterized by its simplicity, power, and clarity. Along with this method, a characterized equation is attained and numerically solved. Additionally, the stability behavior neighboring the fixed points is examined. The phase portraits are planned for suitability to guarantee the mechanisms of stability and instability near the fixed points. Generally, the present work final observations may be described as follows:

  • The mathematical procedure of the expanded frequency results in

    • The periodic, regular expansion via an adapted, expanded frequency is given in Eq. (17) and plotted through some various representations to show the action of the different parameters on the motion.

    • The bounded approximate solution given in Eq. (29).

    • The estimated importance of the nonlinear expanded frequency given in Eq. (30) and is graphed versus the cyclotron one to demonstrate the positive impact of the specified values of angular velocity on its behavior.

  • Lengthways the linearization stability theory, one gets

    • The equilibrium points are attained from Eqs. (34) and (39). Furthermore, the standards of the eigenvalues are found in Eq. (39).

    • Table 1 illustrates the different types of the values of the eigenvalues, and hence the nature of stability/instability.

    • Two figures of the phase portraits, conforming to the diverse nature of the eigenvalues, are plotted.