Analytical Scheme of Stability Analysis for 4-DoF Mechanical System Subjected to Friction-Induced Vibrations

Abstract

Purpose:

The stability problem for non-conservative multi-parameter dynamical system is usually associated with labor-intensive calculations, and numerical methods do not always allow one to obtain the desired information. The presence of circulatory forces often leads to the so-called ”destabilization effect” of the system under the influence of small dissipative forces. In this regard, it seems important to develop analytical approaches that make it possible to use a simplified scheme for checking the stability conditions.

Methods:

When obtaining and analyzing stability conditions, the algebra of polynomials and elements of mathematical analysis are applied. To obtain a simplified scheme for checking the stability conditions, an asymptotic method is used.

Results and Conclusion:

A mechanical system with four degrees of freedom which is under the action of dissipative, potential and non-conservative potential (circulatory) forces is considered. The stability problem of friction-induced vibrations is studying. In the case of weak damping an analytical approach is proposed that makes it possible to simplify the analysis of stability conditions, which, due to the presence of many uncertain parameters, are very cumbersome. With the help of numerical testing, the adequacy of the results obtained for the reduced conditions and full stability conditions was established. The results of the analysis make it possible to single out the ”advantageous” regions in the space of dimensionless parameters, which makes it possible to improve the design of the system to increase its reliability.

Introduction

The history of research on the stability of systems with nonconservative positional (circulatory) forces dates back to Euler, who analyzed the static buckling of elastic compressed rods and formulated a theory of buckling, which can be regarded as the first approximation in solving the stability problem of lightweight load-bearing structures. The problem was updated and attracted much attention of scientists in the field of structural mechanics in the second half of the last century, when flutter was theoretically discovered as a result of the action of so-called follower forces.

In 1952, Hans Ziegler investigated the flutter problem in aerodynamics and considered the model of a double pendulum fixed at one end and loaded with a tangential load at the other end [1]. He discovered a phenomenon with an unexpected property: there is a gap between the stability regions in the case of vanishingly small damping compared to the case when there is no damping. This problem attracted great attention of scientists in the field of structural mechanics in the second half of the last century, and numerous studies were devoted to the theoretical analysis of this problem [2,3,4,5,6]. Circulatory forces are present in many mechanical systems and often lead to undesirable effects such as self-excited vibrations in rotor dynamics [7, 8], friction-induced vibrations [9, 10], squeal vibration in drum brakes [11, 12], flutter in aeroelastic systems [13, 14], the Levitron system [15] and others.

A wide variety of works has been devoted to studying the different aspects of this phenomena. The paper [16] proposed a physical explanation of the mechanism behind the destabilizing effect of small internal damping in the dynamic stability of Beck’s column. Several theorems related to the stability problem of non-conservative linear systems were presented in a paper [17]. In paper [18], some paradoxical phenomena that arise in the study of the dynamic stability of finite-dimensional autonomous mechanical systems were discussed. In [6], systems with two neutrally stable damping levels were considered, at which the system firstly acquires stability and then loses it as the damping level increases. In [19], the Brouwer problem of a heavy particle in a rotating vessel was considered. This problem highlights some important effects that arise in the study of the dynamics of systems with dissipation-induced instabilities. In paper [20] some optimized algorithms for stability analysis of systems with circulatory forces were suggested.

Despite the extensive literature on the stability of mechanical systems with circulatory forces, the analytical approaches that may be applied to multi-parameter systems with several degrees of freedom are not well developed. Usually, the problem is solved using numerical analysis, which gives a very limited understanding on the dynamics of the system: in particular, research using grid search is ineffective due to the presence of a large number of unknown parameters. These unknown parameters may arise at the design stage, in the process of optimization the tuned parameters (stiffness and damping of the dynamic absorber for instance), unknown excitations etc. Besides, such methods are unreliable and too expensive in terms of computation time. The problem is complicated by the fact that there are no universal criteria for making a conclusion based on the general structure of the circulatory forces—a kind of analogs of the Kelvin—Chetaev theorems [21, 22].

Many theoretical models have been presented in the literature to describe and predict friction-induced vibrations [15, 23,24,25,26]. Along with the use of very simple models with lumped parameters, more complex finite element models are considered, but experimental verification turns out to be ambiguous. One of the main reasons for this is the high sensitivity of such systems to changes in parameters which can occur under certain conditions and that predictions can be sensitive to parameters that are often neglected as irrelevant [27, 28].

In the present paper, we consider the system with four degrees of freedom, which can be considered as a phenomenological model of multi-parameter multi-DoF system [25, 26]. Our aim is to suggest an effective approach for analyzing stability conditions for such systems and elicit the mechanical parameters more important in order to enlarge the stability region in parameter space.

The paper is organized as follows. In the next section, some auxiliary notes from algebra are presented. In the following section, the mechanical system under study is described and a general form of stability conditions is given. The next section analyzes the case when the damping in joints is neglected and reduces the system of stability conditions to a single inequality. Finally, in the last section these results are expanded for a case of a weakly damped system, and numerical testing is provided.

Mathematical Annex

In 1914, Lienard and Shipard proposed a criterion [29] that simplifies the well-known Hurwitz criterion. It reads:

The necessary and sufficient conditions for a real polynomial

$$\begin{aligned} f(z) = a_n z^n + a_{n-1} z^{n-1} + \cdots + a_1 z + a_0 \ (a_0 > 0) \end{aligned}$$

(1)

to have all roots with negative real parts can be presented in one of the following forms:

$$\begin{aligned}&a_0> 0, a_2> 0, a_4> 0, \cdots , \Delta _1> 0, \Delta _3 > 0, \cdots , \end{aligned}$$

(2)

$$\begin{aligned}&a_0> 0, a_2> 0, a_4> 0, \cdots , \Delta _2> 0, \Delta _4 > 0, \cdots , \end{aligned}$$

(3)

$$\begin{aligned}&a_0> 0, a_1> 0, a_3> 0, \cdots , \Delta _1> 0, \Delta _3 > 0, \cdots , \end{aligned}$$

(4)

$$\begin{aligned}&a_0> 0, a_1> 0, a_3> 0, \cdots , \Delta _2> 0, \Delta _4 > 0, \cdots . \end{aligned}$$

(5)

Here

$$\begin{aligned} \Delta _j = det \left( \begin{array}{cccccc} a_1 &{} a_3 &{} a_5 &{} \cdots &{} &{} \vdots \\ a_0 &{} a_2 &{} a_4 &{} \cdots &{} &{} \vdots \\ 0 &{} a_1 &{} a_3 &{} \cdots &{} &{} \vdots \\ 0 &{} a_0 &{} a_2 &{} a_4 &{} &{} \vdots \\ &{} \cdots &{} &{} &{} \ddots &{} \\ &{} \cdots &{} &{} &{} &{} a_j \\ \end{array} \right) . \end{aligned}$$

(6)

Conditions (2)–(5) have a certain advantage over the Hurwitz criterion, since they contain approximately half as many determinant inequalities as the Hurwitz conditions. Conditions (2) were presented in original paper [29], and conditions (3)–(5) were proved by Gantmakher [30] and may be applied depending on the form of the polynomial f(z). For instance, if the last has the even degree, then conditions (2), (4) are more easy than conditions (3), (5) (there is no need to compute the determinants of highest degree n).

We will also use the criterion for the absence of complex roots in the fourth-degree polynomial.

Pokrovsky criterion [31, 32]. For a real polynomial

$$\begin{aligned} P(z) = c_4 z^4 + 4 c_3 z^3 + 6 c_2 z^2 + 4 c_1 z + c_0 \end{aligned}$$

(7)

had four different real roots, it is necessary and sufficient to satisfy the inequalities

$$\begin{aligned}&c_3^2 - c_4 c_2> 0, \ 12 c_3^4 - 24c_4 c_3^2 c_2 \nonumber \\&\quad + 4 c_4^2 c_3 c_1 + 9 c_4^2 c_2^2 -c_4^3 c_0> 0, \ \mathrm {dis}(P) > 0, \end{aligned}$$

(8)

where $\mathrm {dis} (P)$ is discriminant of the polynomial P(z).

In the case of multiple roots, the last inequality becomes the equality.

The above two criteria lead to the following consequence:

Statement 1. The polynomial (7) has four different negative roots if and only if the inequalities (8) supplemented by inequalities

$$\begin{aligned} 6 c_3 c_2 c_1 - c_3^2 c_0 - c_4 c_1^2> 0, c_0>0, c_2>0, c_4>0 \end{aligned}$$

(9)

hold.

Mechanical Model and Motion Equations

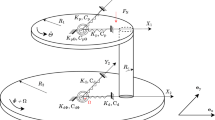
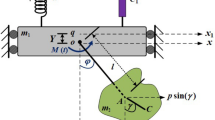
The model consists of two mass blocks $m_1$ and $m_2$ which are coupled by viscoelastic spring, its damping and stiffness coefficients are denoted as $d_a$ and $k_a$ respectively. These blocks are held against three moving bands as it is shown in Fig. 1.

Fig. 1

Mechanical system (adopted from [25])

It is assumed that the belts move at a constant speed, and the coefficient of friction ${\tilde{\mu }}$ on the contacting surfaces is constant; for the sake of simplicity, this coefficient is supposed to be the same for all friction surfaces. Due to the pre-load applied to the system, it is assumed that the masses and bands are always in contact. The classical Coulomb’s law is used. In addition, it is assumed that the directions of the tangential frictional forces $F_t$ do not change, since the relative velocities between the blocks and the belt are considered to be positive. Thus, the tangential friction forces are proportional to the normal forces $F_n$, namely $F_t = {\tilde{\mu }} F_n.$

The linearized equations of motion have the following view [25]

$$\begin{aligned} \varvec{M \ddot{x} + D \dot{x} + (K + K_{\mu }) x = 0}. \hbox {} \end{aligned}$$

(10)

Here ${\varvec{x}} = (x_1, x_2, x_3, x_4)^T$ describes the displacement vector, symmetric matrices $\varvec{M, D, K}$ represent the mass, damping and structural stiffness matrices, respectively; the matrix ${\varvec{K}}_{\mu }$ represents the influence of frictional forces. These matrices have the following form

$$\begin{aligned}&{\varvec{M}} = \left( \begin{array}{cccc} m_1 &{} 0 &{} 0 &{} 0 \\ 0 &{} m_1 &{} 0 &{} 0 \\ 0 &{} 0 &{} m_2 &{} 0 \\ 0 &{} 0 &{} 0 &{} m_2 \\ \end{array} \right) , \nonumber \\&{\varvec{D}} = \left( \begin{array}{cccc} d_{12} + d_a &{} 0 &{} - d_a &{} 0 \\ 0 &{} d_{11} &{} 0 &{} 0 \\ - d_a &{} 0 &{} d_{22} + d_a &{} 0 \\ 0 &{} 0 &{} 0 &{} d_{21} \\ \end{array} \right) , \nonumber \\&{\varvec{K}} = \left( \begin{array}{cccc} k_{12} + k_a &{} 0 &{} - k_a &{} 0 \\ 0 &{} k_{11} &{} 0 &{} 0 \\ - k_a &{} 0 &{} k_{22} + k_a &{} 0 \\ 0 &{} 0 &{} 0 &{} k_{21} \\ \end{array} \right) , \nonumber \\&{\varvec{K}}_{\mu } = {\tilde{\mu }} \left( \begin{array}{cccc} 0 &{} k_{11} &{} 0 &{} 0 \\ - k_{12} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} k_{21} \\ 0 &{} 0 &{} - k_{22} &{} 0 \\ \end{array} \right) . \end{aligned}$$

(11)

One can see that matrix ${\varvec{K}}_{\mu }$ is non-symmetric neither skew-symmetric matrix and in terms of so-called MDGKN structuring [17] may be presented in the form $\varvec{K}_{\mu } = {\tilde{\mu }} (\varvec{K + N})$ where matrix ${\tilde{\mu }} {\varvec{K}}$ is classified as a part of positional forces influence, and ${\tilde{\mu }} {\varvec{N}}$ represents the non-conservative positional or circulatory forces.

For the sake of simplicity, we consider the case of identical masses and two pairs of identical joints, namely

$$\begin{aligned} m_2= & \, m_1 = m, k_{21} = k_{11}, k_{22} = k_{12}, \nonumber \\ d_{21}= & \, d_{12} = d_{22} = d_{11}. \end{aligned}$$

(12)

Introducing the dimensionless parameters $\kappa , p, q, \varepsilon , \mu$ and time $\tau$ according to formulas

$$\begin{aligned} k_{12}= & \, \kappa k_{11}, k_a = p k_{11}, d_a = q d_{11}, \omega _1 = \sqrt{\frac{k_{11}}{m}}, \nonumber \\ d_{11}= & \, \varepsilon \omega _1, t = \frac{\tau }{\omega _1}, {\tilde{\mu }} = \sqrt{\mu }, \end{aligned}$$

(13)

we can write down the characteristic polynomial

$$\begin{aligned} P (\lambda ) = a_8 \lambda ^8 + \cdots + a_1 \lambda + a_0. \end{aligned}$$

(14)

Here

$$\begin{aligned} a_8= & \, 1, \ a_7 = 2 \varepsilon (2 + q), a_6 = 2 + 3 \kappa + 2 p \nonumber \\&+ 6 \varepsilon ^2 (1 + q), a_5 = \varepsilon [ 6 + 9 \kappa \nonumber \\&+ 6 p + q (4 + 3 \kappa ) + 2 \varepsilon ^2 (2 + 3 q)], \ a_4 = 1 \nonumber \\&+ 6 \kappa + 2 \kappa ^2 + p (4 + 3 \kappa ) \nonumber \\&+ 3 \mu \kappa + \varepsilon ^2 [ 3 (2 + 3 \kappa + 2 p) \nonumber \\&+ 2 q (4 + 3 \kappa )] + \varepsilon ^4 (1 + 2 q), \nonumber \\ a_3= & \, \varepsilon \{ 2 [1 + 6 \kappa + 2 \kappa ^2 \nonumber \\&+ p (4 + 3 \kappa ) + q (1 + 3 \kappa )] + 3 \mu \kappa (2 + q) \nonumber \\&+ \varepsilon ^2 [2 + 3 \kappa + 2 p + q (4 + 3 \kappa )] \}, \nonumber \\ a_2= & \, \kappa (3 + 4 \kappa ) + 2 p (1 + 3 \kappa ) \nonumber \\&+ \mu \kappa (3 + 4 \kappa + 3 p) + \varepsilon ^2 [1 + 6 \kappa \nonumber \\&+ 2 \kappa ^2 + p (4 + 3 \kappa ) + 2 q (1 + 3 \kappa ) \nonumber \\&+ 3 \mu \kappa (1 + q)], \ a_1 = \varepsilon [\kappa (3 \nonumber \\&+ 4 \kappa ) + 2 p (1 + 3 \kappa ) + 3 \kappa q \nonumber \\&+ \mu \kappa ( 3 + 4 \kappa +3 p + 3 q)], \nonumber \\ a_0= & \, \kappa [2 \kappa + 3 p + \mu (4 \kappa + 3 p) + 2 \mu ^2 \kappa ]. \end{aligned}$$

(15)

All coefficients of characteristic polynomial (14) are positive, and stability conditions are

$$\begin{aligned} \Delta _j > 0 \ (j = 3, 5, 7), \end{aligned}$$

(16)

where

$$\begin{aligned} \Delta _3= & \, \varepsilon ^2 \{ - 6 \kappa \mu (q + 2)^2 + \kappa ^2 (q^2 + 12 q + 11) \nonumber \\&+ 12 \kappa (2 p q + p - q - 1) \nonumber \\&+ 4 (3 p^2 - 2 p + 1 ) + 4 q (6 p^2 \nonumber \\&- 4 p + 1) + 64 (q + 1)^3 \nonumber \\&+ \varepsilon ^2 [ 6 \kappa (q + 1) (2 q^2 + 13 q + 10) \nonumber \\&+ 4 p (18 q^2 + 29 q + 10) + 4 (4 q^3 + 12 q^2 \nonumber \\&+ 17 q + 10)] \}, \ \Delta _5 = \varepsilon ^3 [\Delta _{50} + O_1 (\varepsilon ^2)], \nonumber \\ \Delta _7= & \, \varepsilon ^4 [\Delta _{70} + O_2 (\varepsilon ^2)]. \end{aligned}$$

(17)

Expressions for $\Delta _{50}$ and $\Delta _{70}$ are much more cumbersome and are presented in Appendix.

Stability Conditions for the Case $\varepsilon = 0$

Even in considered particular case (12), the expression for $\Delta _7$ is extremely huge. For this reason, we shall use the asymptotic expansion on the small parameter $\varepsilon .$ First of all let us discuss the stability conditions for ”generative” system (in mathematical meaning), i.e. we take $\varepsilon = 0.$ With such assumption the characteristic polynomial $P (\lambda )$ becomes biquartic polynomial. The system is marginally stable if all eigenvalues are purely imaginary, in other words, with respect to variable $\Lambda = \lambda ^2$ this polynomial has four negative roots.¹ We write the stability conditions according to Statement 1.

$$\begin{aligned} U_1= & \, \frac{1}{144} [(3 \kappa + 6 p - 2)^2 + 8 (1 - 3 \kappa + 3 \kappa ^2) - 72 \mu \kappa ] > 0, \end{aligned}$$

(18)

$$\begin{aligned} U_2= & \, \frac{1}{64} \{ (\kappa ^2 + 4 p^2) [ 19 \kappa ^2 + 8 p (3 \kappa - 2) + 12 p^2 - 24 \kappa + 8 ] \nonumber \\&- 16 \mu \kappa [\kappa (3 \kappa - 1 + p) + 6 p^2 ] + 16 \mu ^2 \kappa ^2 \} > 0 \end{aligned}$$

(19)

$$\begin{aligned} U_3= & \, \frac{(\mu \kappa )^2}{256} [u_{30} + u_{31} \mu \kappa + u_{32} (\mu \kappa )^2 \nonumber \\&+ 12 u_{33}(\mu \kappa )^3 + 32 (\mu \kappa )^4 ] > 0, \end{aligned}$$

(20)

where

$$\begin{aligned} u_{30}= & \, (\kappa ^2 + 4 p^2)(1 - 2 p + 9 p^2) [1 - 3 \kappa + 2 \kappa ^2 + p (3 \kappa - 2)]^2, \nonumber \\ u_{31}= & \, 2 [ \kappa (1 - 12 \kappa + 29 \kappa ^2 - 24 \kappa ^3 + 4 \kappa ^4) + p \kappa (\kappa - 1) (5 - 43 \kappa \nonumber \\&+ 44 \kappa ^2 - 4 \kappa ^3) - p^2 ( 30 - 107 \kappa + 243 \kappa ^2 - 281 \kappa ^3 + 144 \kappa ^4) \nonumber \\&+ p^3 (120 - 301 \kappa + 390 \kappa ^2 - 223 \kappa ^3) - 3 p^4 (130 - 264 \kappa \nonumber \\&+ 201 \kappa ^2) + 54 p^5 (10 - 11 \kappa ) - 432 p^6 ], \nonumber \\ u_{32}= & \, 1 - 30 \kappa + 109 \kappa ^2 - 60 \kappa ^3 + 4 \kappa ^4 - 2 p (2 - 45 \kappa + 109 \kappa ^2 \nonumber \\&-30 \kappa ^3) + p^2 (274 - 474 \kappa + 645 \kappa ^2) - 18 p^3 (30 - 23 \kappa ) \nonumber \\&+ 1485 p^4, u_{33} = - [1 - 8 \kappa + 2 \kappa ^2 + 2 p (4 \kappa - 1) + 33 p^2 ]. \end{aligned}$$

(21)

The inequalities (9) are satisfied for all admissible values of incoming parameters.

Inequalities (18)–(20) determine the region of stability in the space of dimensionless parameters (the region below the surface shown in Fig. 2). Physically, these conditions determine the range of safe values for friction coefficient $\mu .$ This interval can be significantly increased with a suitable choice of coefficients characterizing the stiffness and damping of the hinge connecting the masses $m_1$ and $m_2.$

To analyze system of inequalities (18)–(20), we need first clarify some properties of the polynomials $U_j (j = 1, 2, 3).$

Lemma 1

The polynomial $U_2(\mu )$ has two positive roots if its discriminant

$$\begin{aligned} \mathrm {dis}_2= & \, \frac{1}{64} [17 \kappa ^4 + 4 \kappa ^2 (15 p^2 + 2 p - 1) \nonumber \\&- 48 p^2 \kappa (p - 1) + 32 p^2 (3 p^2 + 2 p - 1)] \end{aligned}$$

(22)

is non-negative.

Lemma 2

In special case

$$\begin{aligned} p = {\tilde{p}} \triangleq \frac{2 \kappa ^2 - 3 \kappa + 1}{2 - 3 \kappa } , \quad \kappa \ne \frac{2}{3} \end{aligned}$$

(23)

the system of inequalities (18)–(20) is inconsistent (the equilibrium is unstable for any value of $\mu$).

Lemma 3

For any positive values of $\kappa , p$ the polynomial $U_3 (\mu )$ has a pair of complex conjugate roots and two real roots. A single exception is the case $p = p^{+} = 1 + \sqrt{2} \kappa ,$ in which there are four positive roots.

Remark 1

In fact, if $p \ne p^{+}, {\tilde{p}},$ then two real roots of polynomial $U_3 (\mu )$ are positive. This fact may be proven thoroughly using Sturm theorem or similar mathematical tools, although, technically, such proof is tedious enough and we refer here to image of 3-D surface $U_3 (\mu , \kappa , p) = 0$ presented in Fig. 2.

Fig. 2

The 3-D surface $U_3 (\mu , \kappa , p) = 0$

Consider now three resultants for each pair of polynomials $U_j (\mu ) \ (j = 1, 2, 3).$ The corresponding expressions are given by the following formulas

$$\begin{aligned} \mathrm {res}_{12}= & \, 17 \kappa ^4 + 4 \kappa ^2 (15 p^2 + 4 p - 1) \nonumber \\&+ 48 \kappa p^2 (1 - p) + 32 p^2 (3 p^2 + 2 p - 1)\end{aligned}$$

(expressions for two others are presented in Appendix). The equality of each resultant to zero may be interpreted geometrically as part of the line belonging to the first quadrant of the parametrical plane $\kappa p$ (the curve of fourth order and two curves of eighth order). These curves are shown in Fig. 3.

Fig. 3

Partition of the parametric plane $\kappa p$ by curves $\mathrm {res}_{js} = 0, j, s = 1, 2, 3, \ j < s.$ The dash lines correspond to instability case $p = {\tilde{p}}$

Let us take a look at Fig. 3a. Inside each of the open domains Ia, IIa, IIIa the hierarchy of values of the roots $\mu _1, \mu _{31}, \mu _{32}$ is preserved. Indeed, let us assume the contrary—let, for instance, within the domain Ia exist two points $M_1$ and $M_2$ with different hierarchies. Then there exists a path $M_1 M_2$ which belongs to this domain, and at some point $M_3$ of this path we have relation $rez_{13} = 0,$ because $rez_{13}(\kappa , p)$ is the continuous function on its arguments. However, this equality may happen only on the boundary of the domain, and point $M_3$ does not belong to this boundary. The same argumentation is valid also for domains IIa and IIIa. Now, taking arbitrary points at each of the domains we can reveal the corresponding hierarchy. Namely, we have $\mu _{31}< \mu _1 < \mu _{32}$ in the domains Ia, IIIa and $\mu _{31}< \mu _{32} < \mu _1$ in the domain IIa. With the similar reasoning we have the following results for Fig. 3b, c: $\mu _{32} < \mu _{21}$ in domain IIb; $\mu _{31}< \mu _{21}< \mu _{32} < \mu _{22}$ in domain IIIb; $\mu _1 < \mu _{21}$ in the domain IIc; $\mu _{21}< \mu _1 < \mu _{22}$ in the domain IIIc and $\mu _1 < \mu _{21}$ in the domain IVc. (In the domains Ib, Ic the expression $\mathrm {dis}_2 (\kappa , p)$ is negative.) Now, bringing together these results, we can make a conclusion about hierarchy of all six roots of polynomials $U_j (\mu )$ with the aim to find the solution of system (18)–(20). Results are presented in Table 1 and Fig. 4.

Table 1 Hierarchy of roots of the polynomials $U_j (p)$ depending on values $\kappa , p$

Fig. 4

Zones which specify the hierarchy of the roots $\mu _{js}.$ The dash lines correspond to instability case $p = {\tilde{p}}$

Let’s take a look at the situation in zone 4 for example. Remind, that inequality $U_1 > 0$ is equivalent to restriction $\mu < \mu _1.$ The inequality $U_2 > 0$ is equivalent to condition $\mu \in (0, \mu _{21}) U (\mu _{22},0)$ if $\mathrm {dis}_2 (\kappa , p) > 0$² and is fulfilled otherwise. Finally, the inequality $U_3 > 0$ is equivalent to condition $\mu \in (0, \mu _{31}) U (\mu _{32}, +\infty ).$ Hence, in zone 4 in order to satisfy all three inequalities (18)–(20) we have restriction $\mu < \mu _1.$ But on subinterval $[\mu _{21}, \mu _1)$ the second inequality is broken, and on subinterval $[\mu _{31}, \mu _{21})$ the third inequality is not valid. At the same time, all three inequalities are fulfilled if $\mu \in (0, \mu _{31}).$ In the same manner one can see that in all other zones we also have this limitation on $\mu .$ In other words, system (18)–(20) is equivalent to a single inequality $\mu < \mu _{31}.$

Numerical Testing and Discussion

Now let us consider the case when the weak damping in the joints between the masses is present. Let us turn to the condition $\Delta _7 > 0.$ For small values of $\varepsilon$, its sign is determined by the sign of the expression $\Delta _{70},$ which for $q = 0$ coincides with the sign of $U_3 (\mu ).$ As one can see from Fig. 5, the fulfillment of condition $\Delta _7 > 0$ entails the fulfillment of two other conditions (16) In addition, numerical experiments show that varying the parameter q within a fairly wide range has a rather weak effect on the boundary of permissible values of $\mu$ (Fig. 6). Thereby, we shall give our conclusion based on the analysis of inequality (20) and thereafter shall verify its correspondence to the stability conditions (16).

Fig. 5

Schematic view of surfaces $\Delta _3 = 0$ (green), $\Delta _5 = 0$ (red), $\Delta _7 = 0$ (blue)

Fig. 6

Affinity of the surfaces $U_3 = 0$ (blue) and $\Delta _7 = 0$ (green): a $\varepsilon =0.03, \ q=0.02;$ b $\varepsilon =0.03, \ q=1;$ c $\varepsilon =0.01, \ q=0.5; \$ d $\varepsilon =0.1, \ q=0.5$

Let us set a task of finding the optimal values for stiffness ratios $\kappa , p$ and damping ratio q which allow to maximize the range of dimensionless parameter $\mu$.³ We shall use the asymptotical expansion for $\Delta _7$ on $\varepsilon ,$ and as a first step we consider the generating case, i.e. stability conditions for $\varepsilon = 0$ which are governed by value $\mu _{31} (\kappa , p).$ Remind that this is the least root of the quartic polynomial $U_3 (\mu ).$ Actually, it can be written in explicit form using, for instance, Ferrari’s method, but this way is completely impractical, because the resulting expressions are extremely bulky (and strongly irrational), and there is a negligible chance to extract some information from their analysis. For this reason, we consider $\mu _{31}$ as implicit function $U_3 (\mu , \kappa , p) = 0.$ At the moment, we cannot separate the least root of this equation, but we can consider a general problem of extremum for this implicit function with respect to variable $\mu .$ Thus, we can find all points $(\kappa , p)$ satisfying relations

$$\begin{aligned} \frac{\partial U_3}{\partial \kappa } = 0, \quad \frac{\partial U_3}{\partial p} = 0, \quad U_3 = 0 \end{aligned}$$

(24)

and then verify which of them correspond to the root $\mu _{31}.$

The possibility of a direct finding the solutions of system (24) is questionable because of high degrees of incoming polynomials. From the other side, the necessary conditions for system equalities (24) be consistent are the equalities to zero two pairs of resultants of these three polynomials. Both resultants taken on variable $\mu _\kappa = \mu \kappa$ are huge enough (polynomial of 28th order on variables $\kappa , p$), but allow the factorization with the following multipliers

$$\begin{aligned}&p^2> 0, \ (3 \kappa ^2 + 2)^2> 0, \ 9 p^2 - 2 p + 1> 0, \nonumber \\&\psi _1 (\kappa , p)^3 > 0,\ (3 \kappa - 2) p + 2 \kappa ^2 - 3 \kappa + 1, \ [2 \kappa ^2 - (p - 1)^2]^2, \end{aligned}$$

(25)

and only two last of them may be equal to zero (both are present in the decomposition of resultants). According to Lemma 2, if $(3 \kappa - 2) p + 2 \kappa ^2 - 3 \kappa + 1 = 0,$ then the motion is unstable (flutter instability), hereby this case may be excluded from further consideration. Finally, we have two candidates for extremum $p = 1 \pm \sqrt{2} \kappa .$

Generally, now we have to calculate the second derivatives in order to check if the found stationary points of implicit function $U_3 (\mu , \kappa , p ) = 0$ are extremum points for $\mu _{31}.$ However, taking into account results of Lemma 3, we can straight away take the variations of the values $p = 1 \pm \sqrt{2} \kappa$ which are candidates for extremum points and analyze the behaviour of the function $U_3 (\mu )$ in the vicinity of each point. Namely, substituting $p = 1 - \sqrt{2} \kappa + \delta _p,$ and seeking the value of $\mu$ in the form of power series $\mu ^{(0)} + \mu ^{1} \delta _p + \cdots ,$ we have the following expansion

$$\begin{aligned} U_3= & \, \frac{2321 - 204 \sqrt{2}}{8} [2303 \kappa ^2 - 64 (34 \sqrt{2} - 3) \kappa + \nonumber \\&+ 16 (68 - 3 \sqrt{2})]^2 \psi _4 (\mu ^{(1)}, \kappa ) \delta _p^2 + O (\delta _p^3). \end{aligned}$$

(26)

Here

$$\begin{aligned} \mu ^{(0)}= & \, \frac{3 - 2 \sqrt{2}}{4 \kappa } (9 \kappa ^2 - 8 \sqrt{2} \kappa + 4), \ \psi _4 = \kappa ^2 (\mu ^{(1)}) ^2 \nonumber \\&+ \left( \frac{3 \sqrt{2}}{4} - 1\right) \kappa (17 \kappa - 8 \sqrt{2}) \mu ^{(1)} \nonumber \\&- \frac{\sqrt{2}}{8} (99 - 70 \sqrt{2}) (3 \kappa + 2)^2. \end{aligned}$$

(27)

Two first multipliers in formula (26) are positive, hence we have condition $\psi _4 = 0$ which defines two values for $\mu ^{(1)}.$ Taking into account that $(99 - 70 \sqrt{2}) = 1 / (99 + 70 \sqrt{2}) > 0,$ one can see that these values have opposite signs. If $\delta _p > 0,$ then negative root of $\psi _4$ corresponds to $\mu _{31},$ and positive root corresponds to $\mu _{32}$ (as $\mu _{31} \le \mu _{32}$ according to our nomenclature). In case $\delta _p < 0$ the correspondence is on the contrary.

The key moment here is that point $p = 1 - \sqrt{2} \kappa$ is not the point of extremum, because both branches $B_{\mu }^1, \ B_{\mu }^2$ of the curve $U_3 (\mu , p) = 0$ are monotonic in the vicinity of this point. Moreover, there are no other points of extremum, thus these branches are monotonic for any value of p (Fig. 7). Thereby, the curve $\mu = \mu _{31}$ is composed of two semi-branches—semi-branch $B_{\mu }^1$ for $p \le 1 - \sqrt{2} \kappa$ and semi-branch $B_{\mu }^2$ for $p > 1 - \sqrt{2} \kappa ,$ and the maximal possible value for $\mu _{31}$ is defined according to formula (27).

Remark 2

There is no need to do such verification for point $p = 1 + \sqrt{2} \kappa ,$ because, according to Lemma 3, this case is related to the roots $\mu _{33}, \mu _{34}$ which are complex everywhere except this point (the imaginary part turns to zero here). The branches $B_{\mu }^1, \ B_{\mu }^2$ are still monotonic (Fig. 8d–f).

Fig. 7

Intersections of surfaces $U_3 = 0$ and $\Delta _7 = 0$ with planes $\kappa = 0.3$ for different values of parameters

Fig. 8

Different kinds of formation the curve $\mu = \mu _{31}$

Expression for $\mu ^{(0)}$ from formula (27) has a minimum at $\kappa = 2/3,$, respectively, taking into account the constraint $\kappa < \sqrt{2} / 2,$ we see that the limit value for $\mu$ increases with decreasing value of $\kappa .$ Due to the design features of the system, the value for $\kappa$ has some lower constraint $\kappa \ge \kappa _0$ ($\kappa$ cannot be ”too” small), therefore, the optimal choice will be $\kappa = \kappa _0, \ p = p_{-} = 1 - \sqrt{2} \kappa _0.$ On the other hand, if the parameter p is ”moderately tunable”, that is, due to the features of design may take values from some limited range $[p_1, p_2 ]$ which does not contain point $p_{-},$ then, the optimal choice depends on whether the value of $\kappa$ exceed $\sqrt{2} / 2$ or not. If $\kappa < \sqrt{2} / 2$ and $p_{-} < p_1,$ then values which are close to $p_1$ are preferable—the line $\mu = \mu _{31} (p)$ decreases slowly (Fig. 8). If $p_{-}> p_2, \ p_1 > p_Q,$ then the value $p = p_2$ is our choice. If $p_1< p_Q< p_2 < p_{-},$ then quantities $\mu _{31} (p_1)$ and $\mu _{31} (p_2)$ should be compared.

In case $\kappa \ge \sqrt{2} / 2$ the choice is more evident, because the function $\mu = \mu _{31} (p)$ is monotonic, thus values from the right side of interval $[p_1, p_2 ]$ are likely to apply (Fig. 8f). Of course, it is necessary to take into account, that this is true for values of $\kappa$ which are not close to the value 2/3,  because in the vicinity of this point the threshold for $\mu$ is drastically lower comparatively to values $\kappa \ge 2$ (Fig. 8d, e).

Thus, to increase the range of permissible values for friction coefficient ${\tilde{\mu }},$ we can offer two options for the structure of the matrix ${\varvec{K}}:$ (a) the stiffness of the hinges 12, 22 (Fig. 1) is 3–5 times less than the stiffness of the hinges 11, 21, and the stiffness in the joint between the masses is approximately equal to the last one ($p \approx 1$); (b) ”reverse” distribution—the stiffness of the hinges 12, 22 (Fig. 1) is 3–5 times higher than the stiffness of the hinges 11, 21, and $p \ge 1$). At the same time, choosing the values for $\kappa$ from interval $\approx [0.7, 1.3]$ is a bad choice, because the threshold for $\mu$ is about ten times lower.

Conclusions

The article considers the stability problem for a multi-parameter mechanical system with four degrees of freedom, considered earlier in works [25, 26]. On the basis of the algebraic Lienard–Shipard criterion, stability conditions are obtained and analyzed. In the case of weak damping, these conditions can be significantly simplified, which makes it possible to give recommendations about convenient and inconvenient system configurations. In particular, the ratios between the components of the stiffness matrix are indicated, which make it possible to significantly expand the range of permissible values for friction coefficient ${\tilde{\mu }}.$

As numerical calculations show, the moderate variation of the damping ratio q has little effect on the maximum allowable value of the parameter $\mu .$ At the same time, the weakening of the friction coefficient in the joint between the masses increases the rate of damping of system oscillations. For instance, at $q = 1$ the maximum Lyapunov exponent in dimensionless time is $- 0.0123 \ (\kappa = 0.2, p = 1, \mu = 0.4),$ and at $q = 0.1$ it is equal to $- 0.0147,$ i.e. the damping rate is 20 percent higher. In this regard, the future work will be related to the assessment of the Lyapunov exponents of the system (10) and the study of the influence the structure of the matrix ${\varvec{D}}$ on the rate of damping of system oscillations.

Appendices

Appendix A

Proof of Lemma 1

Note, that expression $19 \kappa ^2 + 24 (p - 1) \kappa + 12 p^2 - 16 p + 8$ is positive for any positive values of parameters $\kappa , p.$ Indeed, this function of two variables has absolute minimum $\frac{8}{27}$ at $\kappa = \frac{4}{7}, \ p = \frac{2}{21}.$ Therefore, if $\mathrm {dis}_2 \ge 0,$ both roots of polynomial $U_2 (\mu )$ has the same signs. However, if the expression

$$\begin{aligned} u_{21} = - \frac{1}{4} \kappa [\kappa (3 \kappa - 1 + p) + 6 p^2] \end{aligned}$$

(a1)

is positive, then $\mathrm {dis}_2$ is negative. This fact may be proven by finding the maximal value of function $\mathrm {dis}_2(\kappa , p)$ in the domain $\kappa> 0, p> 0, u_{21}(\kappa , p) > 0.$ However, it is easier to write down the resultant of polynomials $\mathrm {dis}_2, u_{21}$ (either on variable $\kappa$ or p ). Such resultant on variable $\kappa$ reads

$$\begin{aligned}&p^2 (32700 p^6 - 20680 p^5 + 14688 p^4 \\&\quad - 4652 p^3 + 1543 p^2 - 228 p + 38), \end{aligned}$$

which is strictly positive, because the expression in parenthesis has only complex roots

$$\begin{aligned} \frac{1}{327} (38 \pm \sqrt{38} i), \ \frac{1}{10} (1 \pm 3 i) (\mathrm {multiple \ roots}). \end{aligned}$$

This means that boundaries of two domains have no intersection. Taking into account that the closure of the set $S_1 = \{ (\kappa , p): u_{21} < 0 \}$ has common point (0, 0) with the closure of the set $S_2 = \{ (\kappa , p): \mathrm {dis}_2 < 0 \} ,$ we conclude that one of these sets is the subset of another one. To determine which one is smaller, let us take the point belonging to the boundary of one of these sets. We take $\partial S_1,$ because it determines the part of ellipse (more simple then curve of fourth order $\partial S_2$). For instance, let it be point $M_1 (0.1, 0.1).$ Calculating the corresponding value for $\mathrm {dis}_2,$ we have $- 0.2275 < 0.$ In addition, along the line segment $\kappa = p, \ p \in (0, 0.1)$ the sign of $u_{21}$ is opposite to the sign of expression $p (3 p - 1 + p ) + 6 p^2 = 10 p^2 - 1 < 0.$ As a consequence, the boundary of set $S_1$ as well as the set itself belong to the closure of the set $S_2.$ $\square$

Eventually, if the polynomial $U_2 (\mu )$ has real roots $\mu _{21} < \mu _{22},$ then the coefficient $u_{21}$ is negative, hence both these roots are positive.

It is obvious, that in the domain $\mathrm {dis}_2 < 0$ the condition (19) is fulfilled for any values of the parameter $\mu .$

Proof of Lemma 2

To prove the statement of the Lemma 2 it is sufficient to show that fulfillment of the condition $U_1 > 0$ leads to inequality $U_3 < 0.$ Since parameter p is positive, possible values for $\kappa$ are limited by intervals (0, 1/2) and (2/3, 1). Substituting relation (a1) into expressions for $U_1, U_3$ and introducing an auxiliary parameter $\mu _1 = \mu \kappa (2 - 3 \kappa )^2$ we have

$$\begin{aligned} U_{10}= & \, \frac{1}{8} ( 25 \kappa ^4 - 60 \kappa ^3 + 56 \kappa ^2 - 24 \kappa + 4 - 8 \mu _1), \nonumber \\ U_{30}= & \, 32 \mu _1^3 - 12 \mu _1^2 (102 \kappa ^4 - 376 \kappa ^3 + 444 \kappa ^2 \nonumber \\&- 208 \kappa + 33) + 3 \mu _1 (11376\kappa ^8 - \nonumber \\&- 59520 \kappa ^7 + 137648 \kappa ^6 - 183624 \kappa ^5 \nonumber \\&+ 154483 \kappa ^4- 83916 \kappa ^3 + 28742 \kappa ^2 - \nonumber \\&- 5676 \kappa + 495) - 4 (6 \kappa ^2 - 8 \kappa + 3)^3 (5 \kappa ^2 - 6 \kappa + 2)^3. \end{aligned}$$

(a2)

Condition $U_{10} > 0$ is valid if and only if $\mu _1 \in (0, \mu _{10})$ where

$$\begin{aligned} \mu _{10} = \frac{1}{8} ( 25 \kappa ^4 - 60 \kappa ^3 + 56 \kappa ^2 - 24 \kappa + 4). \end{aligned}$$

So far as $U_{30} (0) < 0,$ it is sufficient to show that polynomial $U_{30} (\mu _1)$ has no roots on this interval. Let us consider first the expression for discriminant of $U_{30}(\mu _1)$ which is polynomial of 24 order on $\kappa$ and may be given in the following form

$$\begin{aligned} \mathrm {dis} (U_{30})= & \, - (\kappa - 1)^2 (2 \kappa - 1)^2 \psi _1^2 (\kappa ) \psi _2 ^3 (\kappa ), \ \psi _1(\kappa ) \nonumber \\= & \, 14 \kappa ^4 - 24 \kappa ^3 + 12 \kappa ^2 - 1, \nonumber \\ \psi _2 (\kappa )= & \, 196 \kappa ^4 - 476 \kappa ^3 + 457 \kappa ^2 - 206 \kappa + 37. \end{aligned}$$

(a3)

The polynomial $\psi _2 (\kappa )$ has two pairs of complex conjugate roots, thus takes positive values only, as well as two first multipliers in right-hand side of formula (a3) (since $p > 0,$ then $\kappa \ne 0.5, 1$ according to formula (a1)). The polynomial $\psi _1 (\kappa )$ has single positive root $\kappa \approx 0.6864,$ and this is a single value for $\kappa$ when the discriminant is equal to zero. However, for this value the roots of $U_{30}(\mu _1)$ are 0.0111, 0.0703, 0.0922 and the least of them exceed the value $\mu _{10} \approx 0.0070$ (remind that $\mu _1 < \mu _{10}$ is the necessary condition of stability).

Now composing the Sturm polynomials $P_0 (\mu _1), \ P_1 (\mu _1), \ P_2 (\mu _1), \ P_3 = \mathrm {dis}(U_{30}),$ and substituting subsequently values 0 and $\mu _{10}$ we have the expressions which determine the signs of polynomials $P_j.$ These expressions are presented in Appendix and lead to the following combinations of signs: $(- + ? -)$ for $\mu _1 = 0$ and $(- + ?? -)$ for $\mu _1 = \mu _{10}.$ Here symbols ? and ?? mean either plus or minus depending on the exact value of $\kappa .$ Nevertheless, in spite of exact value for the signs $? , ?? -$ plus, minus or zero, we have two changes of the sign in both combinations. Hence, there are no roots of polynomial $U_{30} (\mu _1)$ in interval $(0, \mu _{10}),$ and the system of inequalities $U_{10}> 0, \ U_{30} > 0$ is inconsistent. $\square$

Proof of Lemma 3. Let us calculate the discriminant⁴ of the quartic polynomial $U_3 (\mu ).$ The direct expression itself is bulky enough, but it allows the following factorization

$$\begin{aligned} \mathrm {dis}(U_3) = - p^2 [2 \kappa ^2 - (p - 1)^2 ]^2 \psi _3^3 (\kappa , p), \end{aligned}$$

(4)

where

$$\begin{aligned} \psi _3= & \, 8 \kappa ^6 + 36 \kappa ^5 (1 - p) \\&+ 6 \kappa ^4 (93 p^2 - 22 p + 11) - 9 \kappa ^3 (135 p^3 - 149 p^2 + \\&+ 21 p - 7) + 3 \kappa ^2 (2439 p^4 - 804 p^3 \\&+ 446 p^2 - 44 p + 11) - \\&- 9 \kappa (1089 p^5 - 1221 p^4 + 202 p^3 - 74 p^2 + 5 p - 1) + \\&+ 35964 p^6 - 6642 p^5 + 3825 p^4 \\&- 512 p^3 + 138 p^2 - 6 p + 1. \end{aligned}$$

Function (a2) does not have any extremum, because the system $\partial \psi _3 / \partial \kappa = 0, \ \partial \psi _3 / \partial \kappa = 0$ is inconsistent. Indeed, the resultant of these partial derivatives may be presented in the form

$$\begin{aligned}&(\kappa + 1)^2 (2 \kappa + 1)^2 (1538793207 \kappa ^9 + 4223446200 \kappa ^8\\&+3947948235 \kappa ^7 + 1054641888 \kappa ^6 \\&- 344293764 \kappa ^5 - 86587520 \kappa ^4 \\&+ 68767104 \kappa ^3 + 3530752 \kappa ^2 - 5116416 \kappa + 884736), \end{aligned}$$

and is positive (thereby, not equal to zero), because the polynomial of ninth order has four pairs of complex conjugate roots and one negative root. Thus, if the expressions in brackets in formula (a4) is not equal to zero, then $\mathrm {dis} (U_3) < 0,$ and the statement of the Lemma takes place.

Now, suppose that $p = 1 \pm \sqrt{2} \kappa .$ Substituting

$$\begin{aligned} p = p^{-}(\kappa ) \triangleq 1 - \sqrt{2} \kappa > 0 \end{aligned}$$

into expression for $U_3 ,$ we can directly find the roots. There is a double positive root

$$\begin{aligned} \frac{3 - 2 \sqrt{2}}{4 \kappa } (9 \kappa ^2 - 8 \sqrt{2} \kappa + 4) \end{aligned}$$

and a pair of complex conjugate roots

$$\begin{aligned} \frac{1 + \sqrt{2}}{\kappa } \left\{ (1 + \sqrt{2}) \left[ 3 (2 - \sqrt{2}) \kappa ^2 - 2 \sqrt{2} \kappa + 1\right] \pm 2^{1/4} \kappa (1 - \sqrt{2} \kappa ) \imath \right\} . \end{aligned}$$

In the particular case $p = p^{+}(\kappa ) \triangleq 1 + \sqrt{2}$ there are four positive roots

$$\begin{aligned}&\frac{(\sqrt{2} - 1)}{\kappa } \left[ \sqrt{2} (3 - 2 ^{5/4}) \kappa ^2 - 2^{5/4 } (1 + 2^{1/4} - 2^{3/4}) \kappa + \sqrt{2} - 1\right] \\&\frac{(\sqrt{2} - 1)}{\kappa } \left[ \sqrt{2} (3 + 2 ^{5/4}) \kappa ^2 - 2^{5/4 } (1 - 2^{1/4} + 2^{3/4}) \kappa + \sqrt{2} - 1\right] \\&\frac{(3 + 2 \sqrt{2})}{4 \kappa } \left( 9 \kappa ^2 + 8 \sqrt{2} \kappa + 4\right) \end{aligned}$$

(the last root is of multiplicity two).

Appendix B

• (1) Expressions for $\Delta _{50}, \Delta _{70}:$

  $$\begin{aligned} \Delta _{50} = - 3 (q + 2)^3 (\mu \kappa )^3 + \delta _{502} (\mu \kappa )^2 + \delta _{501} \mu \kappa + \delta _{500} , \end{aligned}$$

  where

  $$\begin{aligned}&\delta _{502} = (q + 2) \{ \kappa ^2 (12 q^2 + 45 q + 37) - 6 \kappa [q^2 \\&+ (1 - p)(4 q + 3)] + 2 [q (42 p^2 - 4 p + 1) + 39 p^2 - 2 p + 1] \},\\&\delta _{501} = - 6 \kappa ^4 (q + 1) (q^2 + 7 q + 8) + 2 \kappa ^3 [(1 - p) (33 q^2 + 74 q \\&+37) + 4 q (q^2 + q - 1)] - 3 \kappa ^2 [q^3 + 4 q^2 (8 p^2 - 6 p + 3) \\&+q (120 p^2 - 48 p + 23) + 4 (16 p^2 - 6 p + 3)] + 4 \kappa [q^2 (20 p^2 \\&- 4 p + 1) - 2 q (48 p^3 - 46 p^2 + 3 p - 1) - 48 p^3 \\&+(1 - p) (48 p^2 - 2 p + 1)] - 12 p^2 [ 2 q^2 + q (24 p^2 - 24 p + 11) \\&+ 6 (2 p^2 - 2 p + 1)],\\&\delta _{500} = 2 [(q + 1)^2 \kappa ^2 + 4 p^2 (2 q + 1)] [2 \kappa ^2 - 3 (1 - p) \kappa + 1 - 2 p]^2,\\&\Delta _{70} = (\mu \kappa )^2 [ \delta _{704} (\mu \kappa )^4 + \cdots + \delta _{701} (\mu \kappa ) + \delta _{700}],\\&\delta _{704} = 2 (q + 2)^4, \ \delta _{703} = - (q + 2)^2 \{ 6 \kappa ^2 (q + 1) - 4 \kappa [q^2 \\&+ 6 (q + 1) (1 - p)] + 3 (q + 1) (33 p^2 - 2 p + 1) \}, \\&\delta _{702} = 4 \kappa ^4 (q + 1)^2 + 12 \kappa ^3 (p - 1) (q + 1) ( q^2 + 5 q + 5) \\&+\kappa ^2 [2 q^4 + 4 q^3 (45 p^2 - 10 p + 8) + q^2 (819 p^2 - 254 p + 141) \\&+ (2 q + 1) (645 p^2 - 218 p + 109)] + 6 \kappa [- q^3 ( 9 p^2 - 2 p + 1) \\&+ q^2 (45 p^3 - 72 p^2 + 17 p - 6) + (2 q + 1) (69 p^3 - 79 p^2 + 15 p \\&-5)] + 16 p^2 q^3 + q^2 (1296 p^4 - 540 p^3 + 274 p^2 - 4 p + 1) \\&+(2 q + 1) (1485 p^4 - 540 p^3 + 274 p^2 - 4 p + 1), \\&\delta _{701} = 8 \kappa ^5 (1 - p) (q + 1)^2 - 6 \kappa ^4 [q^3 (9 p^2 - 2 p + 1) \\&+3 q^2 (19 p^2 - 6 p + 3) + 8 (2 q+ 1) (6 p^2 - 2 p + 1)] \\&+ 2 \kappa ^3 [4 q^3 (9 p^2 - 2 p + 1) - 3 q^2 (63 p^3 - 99 p^2 + 31 p - 11) \\&-(2 q + 1) (223 p^3 - 281 p^2 + 87 p - 29)] - 3 \kappa ^2 [q^3 (9 p^2 \\&- 2 p + 1)+q^2 (234 p^4 - 180 p^3 + 131 p^2 - 34 p + 9) \\&+ 2 (2 q + 1) (201 p^4 - 130 p^3 + 81 p^2 - 16 p + 4)] + 2 \kappa [q^2 (9 p^2 \\&- 2 p + 1) (36 p^2 - 4 p + 1) -2 (2 q + 1)) (p - 1) (594 p^4 - 198 p^3 \\&+103 p^2 - 4 p + 1)] - 12 p^2 [2 q^2 (9 p^2 - 2 p + 1) \\&+(2 q + 1) (72 q^4 - 90 p^3 + 65 p^2 - 20 p + 5)], \\&\delta _{700} = (9 p^2 - 2 p + 1) \{ 4 \kappa ^6 (q + 1)^2 + 12 \kappa ^5 (p - 1) (q + 1)^2 \\&+ \kappa ^4 [(q + 1)^2 (9 p^2 - 26 p + 13) + 16 p^2 (2 q + 1)] \\&+ 6 \kappa ^3 (p - 1) [(q + 1)^2 (1 - 2 p) + 8 p^2 (2 q + 1)] + \kappa ^2 [q^2 (2 p - 1)^2 \\&+(2 q + 1)(36 p^4 - 104 p^3 + 56 p^2 - 4 p + 1)] \\&- 24 \kappa p^2 (2 q + 1) (p - 1) (2 p - 1) + 4 p^2 (2 q + 1) (2 p - 1)^2 \}. \end{aligned}$$

• (2) Verification the signs for Sturm polynomials in Lemma 2. For $\mu _1 = 0$: $p_0(\kappa )= - (6 \kappa ^2 - 8 \kappa + 3)^3 (5 \kappa ^2 - 6 \kappa + 2)^3,$ $p_1(\kappa ) = 11376 \kappa ^8 - 59520 \kappa ^2 + 137648 \kappa ^6 - 183624 \kappa ^5 + 154483 \kappa ^ 4 -$ $- 83916 \kappa ^3 + 28742 \kappa ^2 - 5676 \kappa + 495 > 0$ (has no real roots). The polynomial $p_2 (\kappa )$ is of 12th order on $\kappa ,$ has four different real roots (thus, may be positive, negative or takes zero value). For $\mu _1 = \mu _{10}$: $p_0 (\kappa ) = - (\kappa - 1)^2 (5 \kappa ^2 - 6 \kappa + 2)^2 (7889 \kappa ^6 - 30086 \kappa ^5 +$ $+ 49511 \kappa ^4 - 44956 \kappa ^3 + 23738 \kappa ^2 - 6908 \kappa + 866) < 0$ (the polynomial of 6th order has no real roots).$p_1 (\kappa ) = 18277 \kappa ^8 - 91000 \kappa ^7 + 202952 \kappa ^6 - 264480 \kappa ^5 + 219980 \kappa ^4 - 119424 \kappa ^3 +$ $+ 41276 \kappa ^2 - 8296 \kappa + 742 > 0,$ because all roots are complex. The polynomial $p_2 (\kappa )$ is of 11th order on $\kappa ,$ has five different real roots other then roots of $p_2 (\kappa , 0)$.

• (3) Resultants for pairs of polynomials $U_j (\mu _\kappa ).$

  $$\begin{aligned}&\mathrm {res}_{13} = - 605 \kappa ^8 + 1320 \kappa ^7 (p - 1) - \kappa ^6 (21945 p^2 - 626 p \\&+ 313) + 72 \kappa ^5 (p - 1) (381 p^2 + 38 p - 19) \\&- 6 \kappa ^4 (47079 p^4 + 7140 p^3 - 4438 p^2 + 868 p - 217) \\&+ 144 \kappa ^3 (p - 1) (225 p^4 + 576 p^3 - 292 p^2 + 4 p - 1) \\&- 32 \kappa ^2 (49626 p^6 + 32130 p^5 - 16641 p^4 + 488 p^3 - 12 p^2 \\&-66 p + 11) - 64 \kappa (p - 1) (3 p + 1) (5 p - 1) (21 p^2 - 2 p + 1)\\&\times (57 p^2 - 2 p + 1) - 32 (35073 p^8 - 95472 p^7 + 66096 p^6 \\&-19320 p^5 + 6046 p^4 - 752 p^3 + 144 p^2 - 8 p + 1), \\&\mathrm {res}_{23} = - 2888 \kappa ^8 + 7296 \kappa ^7 (p - 1) - 2 \kappa ^6 ( 32313 p^2 - 7762 p \\&+3881) + 144 \kappa ^5 (p - 1) (1002 p^2 - 68 p + 34) \\&- 3 \kappa ^4 (180189 p^4 - 101940 p^3 + 53518 p^2 - 2548 p + 637) \\&+144 \kappa ^3 (p - 1) (8775 p^4 - 1164 p^3 + 578 p^2 + 4 p - 1) \\&- 8 \kappa ^2 (186003 p^6 - 338688 p^5 + 167868 p^4 + 2228 p^3 \\&-1497 p^2 + 564 p - 94) + 192 \kappa (p - 1) (33 p^2 - 2 p + 1) (1629 p^4 \\&+138 p^3 - 77 p^2 + 8 p - 2) - 16 (312903 p^8 + 461484 p^7 \\&-310122 p^6 + 83316 p^5 - 25813 p^4 + 3080 p^3 - 588 p^2 + 32 p - 4). \end{aligned}$$