Skip to main content
SpringerLink
Log in

Experimental and Analytical Approach to Study the Effect of Large Vibration Amplitude of Rectangular Plates

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

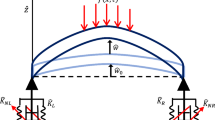
The effect of geometrical non-linearities of thin clamped and simply supported rectangular plates is considered in this paper. The formulation is made basing on Von Kármán theory, Lagrange equations, and the harmonic balance method. In addition, the calculations are made and allowed the application of the semi-analytical model which involved three tensors (mass (\(m_{ij}\)), linear (\(k_{ij}\)) and non-linear rigidity (\(b_{ijkl}\))) which are reduced from the potential and kinetic energy. The solution of non-linear algebraic equations is derived through an approximation solution which is obtained explicitly. The stability of forced vibration is studied for different degrees of freedom (dof) which is reached at four dof using the multimode approach. To valid our numerical results we made the experimental measurements. First, the geometric imperfections are investigated experimentally intending to measure the deviation of our plate. Second, our structure is investigated on a test rig with heavy boundaries conditions which are made from steel alloy, to avoid the external auto-excitation. The harmonic excitation force is generated by an electrodynamic exciter which is applied at a point of the examined plate. The geometric imperfection parameter does not take into account in the formulation of the problem. This assumption is based on the reasons that are cited in this paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. Fully free (FFFF), simply supported plates with immovable and movable edges (SSSS), and fully clamped (CCCC) rectangular plates.

References

  1. Szilard R (2004) Theories and applications of plate analysis. Wiley, Hoboken

    Book  Google Scholar 

  2. Amabili M (2008) Nonlinear vibrations and stability of shells and plates. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  3. Salvatore LL, Dale MP, Michael JT, Nicholas G (2011) Air Vehicle Integration and Technology Research (AVIATR). In: Delivery Order 0013: nonlinear, low-order/reduced-order modeling applications and demonstration 45433-7542

  4. Dossogne T, Noël J, Grappasonni C, Kerschen G, Peeters B, Debille J, Vaes M, Schoukens J (2015) Nonlinear ground vibration identification of an F-16 aircraft—part II: understanding nonlinear behaviour in aerospace structures using sine-sweep testing, Vol. 16th of international forum on aeroelasticity and structural dynamics, IFASD, Sokos Hotel Palace BridgeSaint Petersburg; Russian Federation

  5. Ribeiro P, Petyt M (2000) Non-linear free vibration of isotropic plates with internal resonance. Int J Non-Linear Mech 35(2):263–278

    Article  MATH  Google Scholar 

  6. El Kadiri M, Benamar R (2002) Improvement of the semi-analytical method, based on Hamilton’s principle and spectral analysis, for determination of the geometrically non-linear response of thin straight structures. Part III: steady state periodic forced response of rectangular plates. J Sound Vibr 264(1):1–35

    Article  Google Scholar 

  7. El Bikri K, Benamar R, Bennouna M (2003) Geometrically non-linear free vibrations of clamped simply supported rectangular plates. Part I: the effects of large vibration amplitudes on the fundamental mode shape. Comput Struct 81(20):2029–2043

    Article  Google Scholar 

  8. Amabili M (2004) Nonlinear vibrations of rectangular plates with different boundary conditions: theory and experiments. Comput Struct 82(31–32):2587–2605

    Article  Google Scholar 

  9. Beidouri Z, Benamar R, El Kadiri M (2006) Geometrically non-linear transverse vibrations of C-S-S-S and C-S-C-S1 rectangular plates. Int J Non-Linear Mech 41(1):57–77

    Article  MATH  Google Scholar 

  10. Alijani F, Amabili M, Balasubramanian P, Carra S, Ferrari G, Garziera R (2016) Damping for large-amplitude vibrations of plates and curved panels, part 1: modeling and experiments. Int J Non-Linear Mech 85:23–40

    Article  Google Scholar 

  11. Gunda J (2013) Large amplitude free vibration analysis of square plates resting on elastic foundation: a simple closed-form solutions. ZAMM J Appl Math Mech 93(8):597–608

    Article  MathSciNet  MATH  Google Scholar 

  12. Breslavsky ID, Amabili M, Legrand M (2014) Physically and geometrically non-linear vibrations of thin rectangular plates. Int J Non-Linear Mech 58:30–40

    Article  Google Scholar 

  13. Panda S, Barik M (2017) Large amplitude free flexural vibration of arbitrary thin plates using superparametric element. Int J Dyn Control 5(4):982–998

    Article  MathSciNet  Google Scholar 

  14. Chaari F, Barkallah M, Bouguecha A, Zouari B, Khabou MT, Kchaou M, Haddar M(2020) Advances in materials mechanics and manufacturing: proceedings of the second international conference on advanced materials, mechanics and manufacturing (A3M’2018), December 166–174, 2018 Hammamet, Tunisia, Lecture Notes in Mechanical Engineering. Springer International Publishing, Cham

  15. Leissa AW (1969) Vibrations of plates, NASA SP-160, U.S. Government Printing Office, Washington D.C.

  16. Nayfeh AH (2000) Perturbation methods, Wiley classics, library. Wiley, New York

    Book  Google Scholar 

  17. Benamar R, Bennouna M, White R (1992) The effects of large vibration amplitudes on the mode shapes and natural frequencies of thin elastic structures. Part II: fully clamped rectangular isotropic plates. J Sound Vib 175(3):377–395

    Article  MATH  Google Scholar 

  18. Benamar R, Bennouna M, White R (1993) The effects of large vibration amplitudes on the mode shapes and natural frequencies of thin elastic structures, part III: fully clamped rectangular isotropic plates-measurements of the mode shape amplitude dependence and the spatial distribution of harmonic distortion. J Sound Vib 175(3):377–395

    Article  Google Scholar 

  19. Benamar R, Bennouna M, White R (1991) The effects of large vibration amplitudes on the mode shapes and natural frequencies of thin elastic structures part I: Simply supported and clamped-clamped beams. J Sound Vib 149(2):179–195

    Article  Google Scholar 

  20. Azrar L, Benamar R, White R (1998) Semi-analytical approach to the non-linear dynamic response problem of S-S and C-C beams at large vibration amplitudes part I: general theory and application to the single mode approach to free and forced vibration analysis. J Sound Vib 224(2):183–207

    Article  Google Scholar 

  21. Adri A, Beidouri Z, Benamar R (2011) Geometrically non linear mode shapes and resonant frequencies of multi-span beams. In: \(8^{th}\) International Conference on Structural Dynamics, EURODYN 2011, Leuven; Belgium

  22. Majid A, Abdeddine EM, Zarbane K, Beidouri Z (2020) Geometrically non-linear free and forced vibration of C-F-C-F rectangular plate at large transverse amplitudes, XI International Conference on Structural Dynamics, Athens, Greece, pp 225–238

  23. Abdeddine EM, Majid A, Beidouri Z, Zarbane K (2020) Nonlinear longitudinal free vibration of uniform rods and rods with sections varying exponentially, XI International Conference on Structural Dynamics, Athens, Greece, pp 239–251

  24. Majid A, Abdeddine E, Zarbane K, Beidouri Z (2021) Geometrically nonlinear forced transverse vibrations of C-S-C-S rectangular plate: Numerical and experimental investigations. J Appl Nonlinear Dyn 10(4):755–773

    MathSciNet  Google Scholar 

  25. Amabili M (2004) Nonlinear vibrations of rectangular plates with different boundary conditions: theory and experiments. Comput Struct 82:2587–2605

    Article  Google Scholar 

  26. Amabili M, Farhadi S (2009) Shear deformable versus classical theories for nonlinear vibrations of rectangular isotropic and laminated composite plates. J Sound Vib 320(3):649–667

    Article  Google Scholar 

  27. Amabili M (2006) Theory and experiments for large-amplitude vibrations of rectangular plates with geometric imperfections. J Sound Vib 291(3–5):539–565

    Article  Google Scholar 

  28. Amabili M (2016) Nonlinear vibrations of viscoelastic rectangular plates. J Sound Vib 362:142–156

    Article  Google Scholar 

  29. Eftekhari S, Jafari A (2012) A mixed method for free and forced vibration of rectangular plates. Appl Math Model 36(6):2814–2831

    Article  MathSciNet  MATH  Google Scholar 

  30. Rui L, Bo W, Gang L, Bin T (2016) Hamiltonian system-based analytic modeling of the free rectangular thin plates’ free vibration, Applied Mathematical Modelling, pp 984-992

  31. Formosa F (2009) Nonlinear dynamics analysis of a membrane Stirling engine: starting and stable operation. J Sound Vib 326(3–5):794–808

    Article  Google Scholar 

  32. Breslavsky I (2012) Stress distribution over plates vibrating at large amplitudes. J Sound Vib 331(12):2901–2910

    Article  Google Scholar 

  33. Ducceschi M, Touzé C, Bilbao S, Webb CJ (2014) Nonlinear dynamics of rectangular plates: investigation of modal interaction in free and forced vibrations. Acta Mech 225(1):213–232

    Article  MathSciNet  MATH  Google Scholar 

  34. Harras B, Benamar R, White R (2001) Experimental and theoretical investigation of the linear and non-linear dynamic behaviour of a glare 3 hybrid composite panel. J Sound Vib 252(2):281–315

    Article  Google Scholar 

  35. Amabili M, Alijani F, Delannoy J (2016) Damping for large-amplitude vibrations of plates and curved panels part 2: Identification and comparisons. Int J Non-Linear Mech 85:226–240

    Article  Google Scholar 

  36. Alijani F, Amabili M (2013) Theory and experiments for nonlinear vibrations of imperfect rectangular plates with free edges. J Sound Vib 332(14):3564–3588

    Article  Google Scholar 

  37. Thomas O, Touzé C, Chaigne A (2003) Asymmetric non-linear forced vibrations of free-edge circular plates. Part II: experiments. J Sound Vib 265(5):1075–1101

    Article  Google Scholar 

  38. Leissa A (1973) The free vibration of rectangular plates. J Sound Vib 31(3):257–293

    Article  MATH  Google Scholar 

  39. Hosseini-Hashemi S, Fadaee M, Taher HRD (2011) Exact solutions for free flexural vibration of Lévy-type rectangular thick plates via third-order shear deformation plate theory. Appl Math Model 35(2):708–727

    Article  MathSciNet  MATH  Google Scholar 

  40. Harras B, Benamar R, White RG (2001) Experimental and theoretical investigation of the linear and non-linear dynamic behaviour of a glare 3 hybrid composite panel. J Sound Vib 252:281–315

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Centre d’Etude Doctorale, École Nationale Supérieure de l’Electricité et de Mécanique, Hassan II University of Casablanca, Casablanca, 8118, Morocco

    A. Majid & E. Abdeddine

  2. Laboratoire Mécanique, Productique et Génie Industriel, École Supérieure Technologie, Hassan II University of Casablanca, Casablanca, 8012, Morocco

    A. Majid, E. Abdeddine, Kh. Zarbane & Z. Beidouri

Authors
  1. A. Majid
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. Abdeddine
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kh. Zarbane
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Z. Beidouri
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Majid.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A Numerical Details of CSSS Rectangular Plates (Boundaries Conditions)

Appendix A Numerical Details of CSSS Rectangular Plates (Boundaries Conditions)

A.1 C-SS Beam Functions in x Direction

The function of C-SS beam are given below:

$$\begin{aligned} {w}_{j}(x)=\frac{\mathrm{ch}(\beta _{j}x)-\mathrm{cos}(\beta _{j}x)}{\mathrm{ch}(\beta _{j})-\mathrm{cos}(\beta _{j})}-\frac{\mathrm{sh}(\beta _{j}x)-\mathrm{sin}(\beta _{j}x)}{\mathrm{sh}(\beta _{j})-\mathrm{sin}(\beta _{j})} \end{aligned}$$

where the eigenvalue parameters (\(\beta _{j}\)) are obtained from solution of the transcendental equation tg\((\beta )- \mathrm{th}(\beta )\) and are given in Table 3, Figs. 10, 11.

Table 3 Symmetric (a) and antisymmetric (b) eigenvalue parameters for a C-SS beam
Full size table
Fig. 10
figure 10

C-SS beams functions for i = 1, 2, 3, 4, 5, and 6

Full size image

where \({w}_{i}\) for \(i=1, 2,\ldots \) are the mode shapes for a \(C-SS\) beams.

A.2 SS–SS Beam Functions in y Direction

$$\begin{aligned} {w}_{j}(y)=\mathrm{sin}\left( \frac{j\pi y}{b}\right) \end{aligned}$$

where \({w}_{j}\) for \(j=1,2,\ldots \) are the mode shapes for a SS–SS beams.

Fig. 11
figure 11

SS–SS beams functions for j=1, 2, 3, 4, 5, and 6

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Majid, A., Abdeddine, E., Zarbane, K. et al. Experimental and Analytical Approach to Study the Effect of Large Vibration Amplitude of Rectangular Plates. J. Vib. Eng. Technol. 10, 3011–3023 (2022). https://doi.org/10.1007/s42417-022-00533-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00533-9

Keywords

Search

Navigation