Skip to main content
SpringerLink
Log in

Modeling and flexural vibration analysis of a double-thin-plate coupling system connected by nonlinear elements

  • Research
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

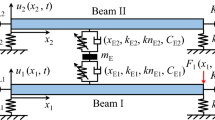
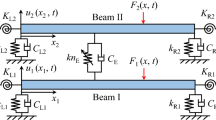
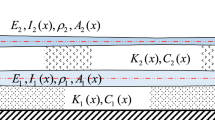
Abstract

As one of the most common structural units, plates are broadly employed in various engineering fields. However, the vibration prediction model in most studies was built as the single-plate system, causing few studies to investigate the potential application of nonlinear coupling elements on the vibration control of the coupled plate system. Based on the above background, this work concentrates on the impact of nonlinear coupling elements on the vibration responses of the coupled plate system. A vibration prediction model for the double-thin-plate coupling system connected through nonlinear elements is established. Meanwhile, the improved Galerkin truncation method (IGTM) is proposed to quickly predict vibration responses of the double-thin-plate coupling system. Based on the correctness of numerical results gained by the IGTM, vibration responses of the double-thin-plate coupling system connected by nonlinear elements are deeply studied. According to numerical results, it can be found that complex responses of the double-thin-plate coupling system are motivated by nonlinear elements. Under complex responses, the vibration kinetic energy of the double-thin-plate coupling system presents the targeted energy transfer character. Adjusting parameters of nonlinear elements can effectively adjust the vibration energy and vibration behavior of the double-thin-plate coupling system. The variation of nonlinear force is the root reason for the appearance and disappearance of complex responses belonging to the double-thin-plate coupling system. The study of the parameter changes belonging to nonlinear elements provides a way for vibration control of the double-thin-plate coupling system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.

References

  1. Tarnóczy, T.: Vibration of metal plates covered with vibration damping layers. J. Sound Vib. 11(3), 299–307 (1970)

    Article  Google Scholar 

  2. Leissa, A.W.: The free vibration of rectangular plates. J. Sound Vib. 31(3), 257–293 (1973)

    Article  Google Scholar 

  3. Zhao, Y.B., Wei, G.W., Xiang, Y.: Plate vibration under irregular internal supports. Int. J. Solids Struct. 39, 1361–1383 (2002)

    Article  Google Scholar 

  4. Wu, J.J.: Free vibration characteristics of a rectangular plate carrying multiple three-degree-of-freedom spring–mass systems using equivalent mass method. Int. J. Solids Struct. 43, 727–746 (2006)

    Article  Google Scholar 

  5. Kerboua, Y., Lakis, A.A., Thomas, M., Marcouiller, L.: Vibration analysis of rectangular plates coupled with fluid. Appl. Math. Model. 32, 2570–2586 (2008)

    Article  Google Scholar 

  6. Abolghasemi, S., Eipakchi, H.R., Shariati, M.: An analytical procedure to study vibration of rectangular plates under non-uniform in-plane loads based on first-order shear deformation theory. Arch. Appl. Mech. 86, 853–867 (2015)

    Article  Google Scholar 

  7. Chen, H., Wu, R., Xie, L., Du, J., Yi, L., Huang, B., Zhang, A., Wang, J.: High-frequency vibrations of circular and annular plates with the Mindlin plate theory. Arch. Appl. Mech. 90, 1025–1038 (2020)

    Article  Google Scholar 

  8. Songong, E.F., Djanan, A.A.N., Nbendjo, B.R.N.: Vibration absorption of a rectangular plate supporting a DC motor with a TLCD. Nonlinear Dyn. 105, 1357–1372 (2021)

    Article  Google Scholar 

  9. Bozyigit, B., Yesilce, Y.: Dynamic stiffness formulations for harmonic response of infilled frames. Struct. Eng. Mech. 68(2), 183–191 (2018)

    Google Scholar 

  10. Bozyigit, B., Yesilce, Y., Wahab, M.A.: Single variable shear deformation theory for free vibration and harmonic response of frames on flexible foundation. Eng. Struct. 208, 110268 (2020)

    Article  Google Scholar 

  11. Bozyigit, B., Yesilce, Y., Wahab, M.A.: Free vibration and harmonic response of cracked frames using a single variable shear deformation theory. Struct. Eng. Mech. 74(1), 33–54 (2020)

    Google Scholar 

  12. Chen, Y., Jin, G., Liu, Z.: Flexural and in-plane vibration analysis of elastically restrained thin rectangular plate with cutout using Chebyshev–Lagrangian method. Int. J. Mech. Sci. 89, 264–278 (2014)

    Article  Google Scholar 

  13. Li, W.L., Zhang, X., Du, J., Liu, Z.: An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports. J. Sound Vib. 321, 254–269 (2009)

    Article  Google Scholar 

  14. Yang, C., Jin, G., Ye, X., Liu, Z.: A modified Fourier-Ritz solution for vibration and damping analysis of sandwich plates with viscoelastic and functionally graded materials. Int. J. Mech. Sci. 106, 1–18 (2016)

    Article  Google Scholar 

  15. Takahashi, D.: Sound radiation from periodically connected double-plate structures. J. Sound Vib. 90(4), 541–557 (1983)

    Article  Google Scholar 

  16. Hedrih, K.S.: Transversal vibrations of double-plate systems. Acta Mech. Sin. 22, 487–501 (2006)

    Article  Google Scholar 

  17. Hedrih, K.S., Simonović, J.: Transversal vibrations of a double circular plate system with visco-elastic layer excited by a random temperature field. Int. J. Nonlinear Sci. Numer. Simul. 9(1), 47–50 (2008)

    Article  Google Scholar 

  18. Rosa, M.A.D., Lippiello, M.: Free vibrations of simply supported double plate on two models of elastic soils. Int. J. Numer. Anal. Meth. Geomech. 33, 331–353 (2009)

    Article  Google Scholar 

  19. Du, J., Li, W., Liu, Z., Yang, T., Jin, G.: Free vibration of two elastically coupled rectangular plates with uniform elastic boundary restraints. J. Sound Vib. 330, 788–804 (2011)

    Article  Google Scholar 

  20. Pereira, V.S., Santos, J.M.C.D.: Coupled plate energy models at mid- and high-frequency vibrations. Comput. Struct. 134, 48–61 (2014)

    Article  Google Scholar 

  21. Zhang, Y., Shi, D., He, D., Shao, D.: Free vibration analysis of laminated composite double-plate structure system with elastic constraints based on improved Fourier series method. Shock. Vib. 3(2021), 1–25 (2021)

    Google Scholar 

  22. Wen, S., Chen, M., Zhou, Z., Jia, W.: Analytical and experimental studies for the vibration transmission of the double-plated structure containing the inner fluid and elastic connections. Thin-Walled Struct. 188, 110806 (2023)

    Article  Google Scholar 

  23. Mirian, A., Ariaei, A.: Free and forced vibrations of an elastically interconnected annular plates system. Arch. Appl. Mech. 93, 3025–3043 (2023)

    Article  Google Scholar 

  24. Hosseini, M., Bemanadi, N., Mofidi, M.: Free vibration analysis of double-viscoelastic nano-composite micro-plates reinforced by FG-SWCNTs based on the third-order shear deformation theory. Microsyst. Technol. 29, 71–89 (2023)

    Article  Google Scholar 

  25. Sathyamoorthy, M.: Nonlinear vibrations of plates: An update of recent research developments. Appl. Mech. Rev. 49(10S), S55–S62 (1996)

    Article  Google Scholar 

  26. Cheng, Z.Q., Wang, X.X., Huang, M.G.: Nonlinear flexural vibration of rectangular moderately thick plates and sandwich plates. Int. J. Mech. Sci. 35(10), 815–827 (1993)

    Article  Google Scholar 

  27. Amabili, M.: Nonlinear vibrations of rectangular plates with different boundary conditions: theory and experiments. Comput. Struct. 82, 2587–2605 (2004)

    Article  Google Scholar 

  28. Amabili, M.: Nonlinear vibrations of viscoelastic rectangular plates. J. Sound Vib. 362, 142–156 (2016)

    Article  Google Scholar 

  29. Chen, C.F., Chen, J.H.: Nonlinear study of large deflection of simply supported piezoelectric layered-plate under initial tension. Int. J. Mech. Sci. 53, 485–493 (2011)

    Article  Google Scholar 

  30. Hedrih, K.R.S., Simonović, J.D.: Non-linear dynamics of the sandwich double circular plate system. Int. J. Non-Linear Mech. 45, 902–918 (2010)

    Article  Google Scholar 

  31. Hedrih, K.R.S., Simonović, J.D.: Multi-frequency analysis of the double circular plate system non-linear dynamics. Nonlinear Dyn. 67, 2299–2315 (2012)

    Article  MathSciNet  Google Scholar 

  32. Breslavsky, I.D., Amabili, M., Legrand, M.: Nonlinear vibrations of thin hyperelastic plates. J. Sound Vib. 333, 4668–4681 (2014)

    Article  Google Scholar 

  33. Valeev, A.: Vibration isolating plate with quasi-zero effect. International Conference on Processing of Materials, Minerals and Energy (July 29th-30th) 2016, Ongole, Andhra Pradesh, India (2016)

  34. Ma, N.J., Gu, L.X., Piao, L.: Nonlinear dynamic response of elastically supported stiffened plates with initial stresses and geometric imperfections under impact loads. Int. J. Struct. Stab. Dyn. 20(4), 2050053 (2020)

    Article  MathSciNet  Google Scholar 

  35. Xu, P., Wellens, P.: Effects of static loads on the nonlinear vibration of circular plates. J. Sound Vib. 504, 116111 (2021)

    Article  Google Scholar 

  36. Yao, G., Xie, Z., Zhu, L., Zhang, Y.: Nonlinear vibrations of an axially moving plate in aero-thermal environment. Nonlinear Dyn. 105, 2921–2933 (2021)

    Article  Google Scholar 

  37. Zhang, Y.W., Shang, H., Hou, S., Xu, K.F., Chen, L.Q.: Vibration suppression of composite laminated plate with nonlinear energy sink. Acta Astronaut. 123, 109–115 (2016)

    Article  Google Scholar 

  38. Tian, W., Li, Y., Yang, Z., Li, P., Zhao, T.: Suppression of nonlinear aeroelastic responses for a cantilevered trapezoidal plate in hypersonic airflow using an energy harvester enhanced nonlinear energy sink. Int. J. Mech. Sci. 172, 105417 (2020)

    Article  Google Scholar 

  39. Li, H., Li, A., Kong, X.: Design criteria of bistable nonlinear energy sink in steady-state dynamics of beams and plates. Nonlinear Dyn. 103, 1475–1497 (2021)

    Article  Google Scholar 

  40. Peikkhosh, S.P., Dardel, M., Ghasemi, M.H.: Enhancing bandwidth of metamaterial plate with linear and nonlinear passive absorbers. Int. J. Non-Linear Mech. 135, 103769 (2021)

    Article  Google Scholar 

  41. Kumar, R.K., Kumar, A.: NES-based multi-mode vibration absorber for a sandwich plate in thermal environment. J. Vib. Eng. Technol. (2023). https://doi.org/10.1007/s42417-023-01079-0

    Article  Google Scholar 

  42. Ye, S.Q., Mao, X.Y., Ding, H., Ji, J.C., Chen, L.Q.: Nonlinear vibrations of a slightly curved beam with nonlinear boundary conditions. Int. J. Mech. Sci. 168, 105294 (2020)

    Article  Google Scholar 

  43. Hao, R.B., Lu, Z.Q., Ding, H., Chen, L.Q.: A nonlinear vibration isolator supported on a flexible plate: analysis and experiment. Nonlinear Dyn. 108, 941–958 (2022)

    Article  Google Scholar 

Download references

Funding

This work is supported by the Fund of Natural Science Special (Special Post) Research Foundation of Guizhou University [Grant No. 2023–060].

Author information

Authors and Affiliations

  1. Key Laboratory of Advanced Manufacturing Technology of the Ministry of Education, Guizhou University, Guiyang, 550025, People’s Republic of China

    Yuhao Zhao

  2. College of Power and Energy Engineering, Harbin Engineering University, Harbin, 150001, People’s Republic of China

    Fanhao Guo

  3. Nuclear Power Institute of China, Chengdu, 610005, People’s Republic of China

    Deshui Xu

Authors
  1. Yuhao Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fanhao Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Deshui Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Yuhao Zhao wrote the main manuscript text and prepared all figures. All authors reviewed the manuscript.

Corresponding author

Correspondence to Yuhao Zhao.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, Y., Guo, F. & Xu, D. Modeling and flexural vibration analysis of a double-thin-plate coupling system connected by nonlinear elements. Nonlinear Dyn (2024). https://doi.org/10.1007/s11071-024-09697-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11071-024-09697-3

Keywords

Search

Navigation