1 Introduction

The problem to find a sequence of trajectories to visit a given set of space objects with known orbital data, while keeping a target function (e.g., propellant expenditure) at a minimum, is usually treated as a Multi-Target Optimization Problem (MTOP). This class of optimization problems is of interest for space missions of various nature, such as active debris removal (ADR), on-orbit servicing, and exploration. The possibility of a multi-target mission to main-belt asteroids was first mentioned in [1], proving that it is possible to reach at least five or six asteroids during a 3-year tour. Different scenarios for low-cost missions to four main-belt asteroids were also proposed by [2, 3], considering a combination of impulsive maneuvers and multiple gravity-assists at Venus, Earth and Mars. Izzo et al. [4] and Di Carlo et al. [5] focus their attention on a low-thrust propulsion ADR mission: the former splits the problem in three optimization sub-problems: combinatorial, global and local, while the latter selects the target by considering the minimum orbit intersection distance. Barbee et al. [6] proposes a series method able to find a good visiting sequence—up to 42 pieces of debris—with low computational cost. Both [7, 8] formulate an interesting strategy for ADR missions, introducing a “drift orbit” to control the right ascension of the ascending node drift velocity, and splitting the problem in two levels, i.e., target sequence and transfer orbits, with an integrated branch-and-bound algorithm (B &B). This strategy is improved in [9], where the transfer problem is solved for every pair of targets, the best sequence is calculated by a simulated annealing algorithm and then the transfer orbits are optimized again. Chen et al. [10] instead introduces the Particle Swarm Optimization method (PSO) for a multi-objective optimization regarding asteroid rendezvous missions. Conway et al. [11], Wall and Conway [12] and Yu et al. [13] exploit a combination of Hybrid Optimal Control based on genetic algorithms and others methods for asteroid exploration and ADR missions. Bang and Ahn [14] defines a two-phase framework for ADR missions, that initially solves all the possible Lambert problems and then develops a variant of the traveling salesman problem to find the best combination. Another strategy is the automatic planning and scheduling algorithm introduced by [15] and named Physarum Algorithm (PA), after the unicellular organism Physarum Polycephalum. This method is very reminiscent of B &B algorithms, since it is inspired by the “intelligent” behavior shown by Physarum Polycephalum, but the bounding phase is heuristic in this case. Finally, [16, 17] analyze a multiple rendezvous mission to near-Earth asteroids with a solar sail propulsion system.

The MTOP methods and results are very dependent on the related mission concept and assumptions. Indeed, a “standard” form of both problem and resolution does not exist in literature. Most previous studies focus on sequence elements rather than on a mission-level performance figure of merit (such as, e.g., propellant consumption), utilizing heuristic or hybrid algorithms with widely different assumptions and, sometimes, with little or no discussion about trajectory determination. Heuristic methods may also suffer from early convergence, thus not ensuring that the optimal global solution will be actually identified.

In a previous work by our team [18], a 2-D algorithm for multi-target exploration missions at NEAs is formulated, attempting to create a deterministic direct method for asteroid target sequence selection as a function of the mission parameters (e.g., propellant consumption, spacecraft-Sun distance, etc.). A MATLAB® software package was implemented and successfully tested that provides a useful tool for preliminary analysis of multi-target missions. The reader is referred to [18] for a detailed discussion of the fundamentals and motivations underlying the structure of the algorithm. The present work builds on the method illustrated in [18] to develop a substantially enhanced version of the procedure, with extension of the algorithm to full 3-D trajectories and with detailed modeling of specific phases of the trajectories, such as escape from a parking orbit and asteroid fly-by.

The method here presented does not aim at solving a MTOP, nor does it perform a proper mathematical optimization, other than by selecting among discrete sets of alternative possibilities at various phases in the procedure. This direct procedure, however, allows the mission planner to quickly identify practical, viable trajectories allowing for multiple asteroid flyby’s under realistic constraints. In this paper we introduce the algorithm, present several series of tests and discuss the relevant results.

2 Main assumptions

The algorithm is designed as a tool to find an efficient asteroid visit sequence for a spacecraft equipped with a propulsion system. The goal of the algorithm we seek to build is to determine a trajectory that encounters the largest possible number of asteroids with the lowest possible propellant consumption. It is understood and accepted that the resulting trajectories are, generally speaking, not the optimal ones in a strict mathematical sense; they are however selected so to meet the needs of the mission planner during preliminary mission design. For this purpose, our earlier 2-D work [18] defined a “mission area” constrained by a minimum and a maximum distance from the Sun (\(d_{{\min }}\) and \(d_{{\max }}\)) where the spacecraft’s trajectory takes place during a period of time defined by a starting and a final date (\(t_0\) and \(t_{\mathrm{end}}\)). That choice was motivated by the fact that most of the asteroids pass through the ecliptic plane at a distance from the Sun between 1 and 1.2 AU, in the so-called high-density transit zone (HDTZ). The spacecraft was bound to move in a 2-D trajectory on the ecliptic plane, trying to intercept the asteroids during their transit. Therefore each asteroid could only be passed by at the nodes of its orbit, thus providing limited opportunities of visiting it.

However, most Apollo asteroids have low orbit inclinations (\(<10\,\text {deg}\)), so that they stay relatively close to the ecliptic plane during large portions of their orbit. It is therefore reasonable to extend the mission area to a three-dimensional volume of space in the vicinity of the plane of the ecliptic. In this work the mission area is thus assumed to be a torus that provides the spacecraft a track on the ecliptic plane from which to depart, or towards which to aim for approach, to reach asteroids. In particular, as described later in Sect. 3, the Sun-centered torus area can be defined by means of Sun-spacecraft’s maximum and minimum distances, respectively \(d_{{\min }}\) and \(d_{{\max }}\) (Eq. 5). This feature allows to manage the size of solar system’s belt to be explored and to consider the planning of various simultaneous prospecting missions in different areas.

Table 1 Commented list of algorithm starting assumptions
Full size table

Since we are interested in a multi-target mission, orbital maneuvers will be needed to guide the spacecraft in chasing the asteroids. To minimize the delay between successive asteroid visits, we assume to use impulsive maneuvers only, such as can be provided by a restartable liquid rocket engine. The quantity of propellant needed can be defined in terms of the total velocity change \(\Delta v_{\mathrm{tot}}\). Since the spacecraft will have to perform multiple maneuvers, it is also reasonable to set a maximum consumption per maneuver \(\Delta v_{{\max }}\), so to preserve enough propellant for the final phases of the mission.

The asteroid orbital elements \(\left\{ a,e,i,\Omega ,\omega \right\} \) with respect to the heliocentric-ecliptic reference frame are assumed known and constant over time. In this scenario, perturbations due to close encounters with planets are neglected. This issue must be taken into account when using the method for the preliminary design of long duration missions; in such case, a parallel check of the selected asteroid trajectories should be performed. The Earth’s orbital elements \(\left\{ a_\oplus ,e_\oplus ,i_\oplus ,\Omega _\oplus ,\omega _\oplus \right\} \) are also known and constant. The initial position of the spacecraft, from which the search for target asteroids begins, is assumed at the Earth.

The algorithm provides the possibility to take into account the escape phase from any initial parking orbit around the Earth. This feature has been introduced for those missions where it is impossible to escape from the Earth by means of the launcher vehicle only. The escape maneuver is assumed impulsive and requires the user to input the parking orbit elements \(\left\{ a_{\mathrm{par}},e_{\mathrm{par}},i_{\mathrm{par}},\Omega _{\mathrm{par}},\omega _{\mathrm{par}}\right\} \) with respect to a geocentric-equatorial reference frame. Earth gravity assists, which might indeed be feasible given the near-Earth orbits, are not taken into consideration at this stage.

Table 2 Asteroid 4179 Toutatis estimated data
Full size table

In summary, the main inputs to the algorithm are as follows:

  • Mission time interval: \(\left[ t_0,t_{\mathrm{end}}\right] \);

  • Mission area boundaries: \(\left[ d_{{\min }},d_{{\max }}\right] \);

  • Maximum single maneuver consumption: \(\Delta v_{{\max }}\);

  • Total mission consumption: \(\Delta v_{\mathrm{tot}}\);

  • Spacecraft parking orbit elements (optional): \(\left\{ a_{\mathrm{par}},e_{\mathrm{par}},i_{\mathrm{par}},\Omega _{\mathrm{par}},\omega _{\mathrm{par}}\right\} \).

The assumptions discussed so far are summarized in Table 1.

2.1 Asteroid flyby analysis

As knowledge of size and mass of asteroids is very scarce, the gravitational effect on spacecraft trajectory during the flyby phase is mostly impossible to calculate. It is therefore interesting to assess whether such effect can actually be neglected. To this end, we take into consideration asteroid 4179 Toutatis as a representative example (Table 2).

We seek to demonstrate that, for a typical flyby, the gravitational effect of asteroid Toutatis (here assumed to be of spherical shape) on the spacecraft trajectory is negligible. Given the estimated size-frequency distribution of observed NEA’s reported in Fig. 1, a similar result will hold for most of Apollo asteroids.

Fig. 1
figure 1

Estimated size distribution of presently known NEAs [19]

Full size image

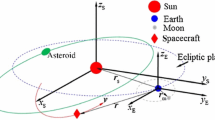
Regardless of the fact that flyby occurs upstream or downstream of the asteroid velocity vector, let \({\textbf {v}}_{\mathrm{S}}\) and \({\textbf {v}}_{\mathrm{AST}}\) be respectively the spacecraft and the asteroid velocities in the heliocentric reference frame (Fig. 2). The spacecraft velocity with respect to the asteroid is, therefore,

$$\begin{aligned} {\textbf {v}}_{\infty }={\textbf {v}}_{\mathrm{S}}-{\textbf {v}}_{\mathrm{AST}}. \end{aligned}$$

The quantity \({\textbf {v}}_\infty \) is the velocity at the border of asteroid’s sphere of influence (SOI). Using the superscripts (1) and (2) respectively for entry and exit conditions from the SOI, the module of velocity variation resulting on the spacecraft is:

$$\begin{aligned} \Delta {\textbf {v}}_{\mathrm{fb}}= & {} {\textbf {v}}_{\mathrm{S}}^{(2)}-{\textbf {v}}_{\mathrm{S}}^{(1)}={\textbf {v}}_{\infty }^{(2)}-{\textbf {v}}_{\infty }^{(1)}~\Rightarrow ~\Delta v_{\mathrm{fb}}=\left| \Delta {\textbf {v}}_{\mathrm{fb}}\right| \\= & {} \left| {\textbf {v}}_{\infty }^{(2)}-{\textbf {v}}_{\infty }^{(1)}\right| . \end{aligned}$$

As mass of the spacecraft does not change during the flyby, mechanical energy is conserved. Therefore, the module of the velocity vector relative to the asteroid at the boundary of the sphere of influence is the same both for the incoming leg of the trajectory and for the outgoing leg, with the flyby maneuver resulting in a change of the velocity vector direction only. Let’s indicate \(\delta \) for the flyby turning angle (see Fig. 2); for the conservation of specific mechanical energy we have:

$$\begin{aligned} \left| {\textbf {v}}_{\infty }^{(1)}\right| =\left| {\textbf {v}}_{\infty }^{(2)}\right| = v_\infty ~\Rightarrow ~\Delta v_{\mathrm{fb}}=2 v_\infty \sin \left( \frac{\delta }{2}\right) \end{aligned}$$
(1)
Fig. 2
figure 2

Asteroid flyby vector diagram

Full size image

Taking advantage of the properties of a hyperbolic trajectory, it is possible to determine eccentricity and semi-major axis of the flyby trajectory:

$$\begin{aligned} \frac{1}{e_{\mathrm{fb}}}=\sin \left( \frac{\delta }{2}\right) ;~~~a_{\mathrm{fb}}=-\frac{\mu }{{ v}^2_\infty } \end{aligned}$$
(2)

The maximum \(\Delta v_{\mathrm{fb}}\) is obtained with the largest value of turning angle \(\delta \), that is when the pericenter distance of the hyperbolic trajectory is equal to the asteroid radius:

$$\begin{aligned} r_p=a_{\mathrm{fb}}\left( 1-e_{\mathrm{fb}}\right) =-\frac{\mu }{{v}^2_\infty }\left[ 1-\frac{1}{\sin \left( \frac{\delta }{2}\right) }\right] =\frac{{\overline{D}}}{2}. \end{aligned}$$
(3)
Fig. 3
figure 3

Plot of the flyby-induced \(\Delta v\) with respect to the spacecraft approaching relative velocity \(v_\infty \). The graph illustrates the order of magnitude of the gravitational effect of the asteroid flyby

Full size image

Finally, obtaining the sine term from Eq. 2 and replacing it in Eq. 1, we have

$$\begin{aligned} \Delta v_{\mathrm{fb}}=\frac{2 v_\infty }{1+k v_\infty ^2}~~\text {with}~~k=\frac{{\overline{D}}}{2\mu }\simeq 1.136\times 10^6~\text {s}^2/\text {km}^2\nonumber \\ \end{aligned}$$
(4)

Equation 4 gives the spacecraft velocity variation as a function of the hyperbolic excess velocity at the border of SOI. To estimate a upper boundary to such change of velocity, let’s consider the following function:

$$\begin{aligned} f( v_\infty )=\Delta v_{\mathrm{fb}}=\frac{2 v_\infty }{1+k v_\infty ^2}~~\text {with}~~v_\infty \in \left[ 0;+\infty \right] . \end{aligned}$$

The denominator of f is always positive, so the function is positive in the domain considered. The derivative of f is

$$\begin{aligned} f'(v_\infty )=2\frac{1-kv_\infty ^2}{\left( 1+kv_\infty ^2\right) ^2}. \end{aligned}$$

The function derivative is positive for \(0<v_\infty \le 1/\sqrt{k}\), hence there is a global maximum for:

$$\begin{aligned} \left( v_\infty \right) _{{\max }}= & {} \frac{1}{\sqrt{k}}\simeq 9.382\times 10^{-4}\,\text {km}/\text {s}~\Rightarrow ~\left( \Delta v_{\mathrm{fb}}\right) _{{\max }}\\= & {} \left( v_\infty \right) _{{\max }}\simeq 9.382\times 10^{-4}\,\text {km}/\text {s}. \end{aligned}$$

Using Eqs. 2 and 3:

$$\begin{aligned} (\delta )_{{\max }}=30\,\text {deg};~~~(a_{\mathrm{fb}})_{{\max }}=-\frac{{\overline{D}}}{2};~~~(e_{\mathrm{fb}})_{{\max }}=2. \end{aligned}$$

Furthermore, as the hyperbolic excess velocity increases we get:

$$\begin{aligned} \left( \Delta v_{\mathrm{fb}}\right) _\infty =\lim _{v_\infty \rightarrow \infty }f\left( v_\infty \right) =0 \end{aligned}$$

and, therefore,

$$\begin{aligned} (\delta )_\infty =0;~~~(a_{\mathrm{fb}})_\infty =-\infty ;~~~(e_{\mathrm{fb}})_\infty =+\infty . \end{aligned}$$

The function f is represented in Fig. 3. As the relative velocity of the spacecraft increases, the gravitational influence of the asteroid vanishes and the trajectory tends to a straight line. Therefore, it is possible to neglect the flyby phase when the initial spacecraft relative velocity \(v_\infty \) is much larger than about \(10^{-2}\,\text {km/s}\), as will happen in all practical cases. The flyby phase at the asteroids will, therefore, not be considered in further analysis, with no detriment to the quality of the trajectory determination.

3 Preliminary phase

Since asteroids will be reachable only within the torus-shaped mission area (Fig. 4), it is necessary to calculate when they enter or leave this domain. To this end, let us consider a parametric definition of the torus surface:

$$\begin{aligned} {\left\{ \begin{array}{ll} x(\theta ,\phi )=(R_1+R_2\cos \theta )\cos \phi \\ y(\theta ,\phi )=(R_1+R_2\cos \theta )\sin \phi \\ z(\theta ,\phi )=R_2\sin \theta \end{array}\right. }~~~\text {with}~~~\theta \in \left[ 0,2\pi \right) ,~\phi \in \left[ 0,2\pi \right) , \end{aligned}$$

where \(R_1>0\) is the distance between the torus center and the tube center, while \(R_2>0\) is the tube radius.

Fig. 4
figure 4

Torus cross section passing through the asteroid position with main geometrical parameters indicated

Full size image

The torus geometric parameters are related to the maximum and minimum input distances through the following equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{{\min }}=R_1-R_2\\ d_{{\max }}=R_1+R_2 \end{array}\right. } ~\Rightarrow ~ {\left\{ \begin{array}{ll} R_1=\left( d_{{\max }}+d_{{\min }}\right) /2\\ R_2=\left( d_{{\max }}-d_{{\min }}\right) /2 \end{array}\right. } \end{aligned}$$
(5)

With reference to Fig. 4, let \({\textbf {r}}_{\mathrm{A}}=[x_{\mathrm{A}},y_{\mathrm{A}},z_{\mathrm{A}}]\) be a generic asteroid position vector and \(r_{\mathrm{A}}=\sqrt{x_{\mathrm{A}}^2+y_{\mathrm{A}}^2+z_{\mathrm{A}}^2}\) its modulus. The asteroid is on the surface of the torus when the asteroid-tube center distance \(d_{\mathrm{A}}\) is

$$\begin{aligned} d_{\mathrm{A}}=\sqrt{(\rho _{\mathrm{A}}-R_1)^2+z_{\mathrm{A}}^2}=\sqrt{r_{\mathrm{A}}^2+R_1^2-2R_1\rho _{\mathrm{A}}}=R_2 \end{aligned}$$

with \(\rho _{\mathrm{A}}^2=x_{\mathrm{A}}^2+y_{\mathrm{A}}^2\) the Sun-asteroid distance projected on the ecliptic plane. The asteroid is inside the torus when:

$$\begin{aligned} f_{\mathrm{tor}}({\textbf {r}}_{\mathrm{A}})=\left( r_{\mathrm{A}}\right) ^2+R_1^2-2R_1\rho _{\mathrm{A}}-R_2<0. \end{aligned}$$
(6)

An asteroid is defined as potentially observable, when

$$\begin{aligned} \exists ~t\in \left[ t_0,t_{\mathrm{end}}\right] :f_{\mathrm{tor}}({\textbf {r}}_{\mathrm{A}}(t))<0. \end{aligned}$$
(7)

Therefore, the asteroid will be selected only if it is already inside the mission area at the time \(t_0\), or if it is initially external to the torus but its entry is expected at time \(t<t_{\mathrm{end}}\); on the contrary, it will instead be discarded if is initially outside the torus but it will enter at time \(t>t_{\mathrm{end}}\), or if it will never enter.

Since the torus is not a simply connected domain, it is reasonable to assume that more than one orbital arc exists for which the asteroid is within the torus (usually there are two at maximum). Thus, there are time intervals in which the asteroid is within the mission area, alternating with intervals in which it is out. Determining the transit times \(t_{\mathrm{tor}}\) and related positions \({\textbf {r}}_{\mathrm{tor}}={\textbf {r}}(t_{\mathrm{tor}})\) on the torus surface involves the solution of a non-linear problem:

$$\begin{aligned} f_{\mathrm{tor}}({\textbf {r}}_{\mathrm{tor}})=0~~\text {with}~~ {\left\{ \begin{array}{ll} f'_{\mathrm{tor}}({\textbf {r}}_{\mathrm{tor}})<0~~\text {incoming}\\ f'_{\mathrm{tor}}({\textbf {r}}_{\mathrm{tor}})>0~~\text {outgoing}, \end{array}\right. } \end{aligned}$$
(8)

where the first equation expresses the condition that the asteroid is on the torus surface and the inequalities provide the necessary conditions on the time rate of change of distance from the torus surface.

The most direct strategy for deciding if an asteroid meets the condition expressed by Eq. 7 is to find the time of the first transit \(t_{\mathrm{tor}}^{\mathrm{(I)}}\). For this purpose, one needs to determine all the solutions of Problem 8, \(\left\{ {\textbf {r}}_{\mathrm{tor}}^{(1)},{\textbf {r}}_{\mathrm{tor}}^{(2)},\ldots \right\} \), and then to solve Direct Kepler Problems (DKPs) for each of them with initial conditions at \(t=t_0\), so to find the related times \(\left\{ t_{\mathrm{tor}}^{(1)},t_{\mathrm{tor}}^{(2)},\ldots \right\} \); the smallest solution is the next asteroid transit time \(t_{\mathrm{tor}}^{\mathrm{(I)}}\). Summing up, we have

  • Mission area transit positions

    $$\begin{aligned} f_{\mathrm{tor}}({\textbf {r}}_{\mathrm{tor},k})=0~\Rightarrow ~\left\{ {\textbf {r}}_{\mathrm{tor},k}^{(1)},{\textbf {r}}_{\mathrm{tor},k}^{(2)},\dots \right\} ~\text {for}~k=1:N_{\mathrm{tot}} \end{aligned}$$

  • Mission area transit times

    $$\begin{aligned} \text {DKP}= & {} {\left\{ \begin{array}{ll} \text {Initial conditions}:t_0,{\textbf {r}}_{0,k}\\ \text {Final conditions}:{\textbf {r}}_{\mathrm{tor},k}^{(n)} \end{array}\right. }\\\Rightarrow & {} ~~t_{\mathrm{tor},k}^{(n)}~~~\text {for}~ {\left\{ \begin{array}{ll} k=1:N_{\mathrm{tot}}\\ n=1,2,\ldots \end{array}\right. } \end{aligned}$$

  • Next transit time

    $$\begin{aligned} t_{\mathrm{tor},k}^{\mathrm{(I)}}=\min \left\{ t_{\mathrm{tor},k}^{(1)},t_{\mathrm{tor},k}^{(2)},\ldots \right\} ~~\text {for}~~k=1:N_{\mathrm{tot}} \end{aligned}$$

    This solution is related to an incoming transit if the asteroid is initially out, or to an outgoing transit if the asteroid is inside. So the first asteroid selection can be performed:

  • Potentially observable asteroids selection

    $$\begin{aligned}&f_{\mathrm{tor}}({\textbf {r}}_{0,k})<0~~~\vee ~~~\left( f_{\mathrm{tor}}({\textbf {r}}_{0,k})>0~~\wedge ~~t_{\mathrm{tor},k}^{\mathrm{(I)}}<t_{\mathrm{end}}\right) ~~~\\&\Rightarrow ~~~Asteroid selected \end{aligned}$$

    for \(k=1:N_{\mathrm{tot}}\).

After this first selection, the number of asteroids taken into consideration in the following phases will be:

  • Potentially observable asteroids number: \(N\le N_{\mathrm{tot}}\)

4 Search phase

4.1 Initial assumptions

Once the asteroids within the reach of the mission have been identified, attention is focused onto the target search phase. The goal is to derive a strategy to be used at any time during the mission to determine the next destination to visit and the relevant transfer orbit. The strategy must depend only on the current state of the spacecraft—i.e. mission time t, spacecraft position \({\textbf {r}}_{\mathrm{S}}(t)\) and velocity \({\textbf {v}}_{\mathrm{S}}(t)\)—and so a local selection of asteroids is made. Consequently, the mission profile will be shaped step-by-step with each new choice. The spacecraft final trajectory will be a segmented curve composed by transfer orbit arcs from an asteroid to the next one. For a n-asteroids sequence with indexes \(\left\{ k_1,k_2,\ldots ,k_n\right\} \) encountered at times \(\left\{ t_1,t_2,\ldots ,t_n\right\} \), we have:

  • Step-by-step trajectory

    $$\begin{aligned} {\textbf {r}}_{\mathrm{S}}(t_1)={\textbf {r}}_{k_1}(t_1);~~ {\textbf {r}}_{\mathrm{S}}(t_2)={\textbf {r}}_{k_2}(t_2);~~ ~~\cdots ~~~~{\textbf {r}}_{\mathrm{S}}(t_n)={\textbf {r}}_{k_n}(t_n). \end{aligned}$$

The search begins with the spacecraft positioned at the Earth:

  • Initial spacecraft state

    $$\begin{aligned} {\textbf {r}}_{\mathrm{S}}(t_0)={\textbf {r}}_{0,\oplus };~~~{\textbf {v}}_{\mathrm{S}}(t_0)={\textbf {v}}_{0,\oplus }. \end{aligned}$$

Propellant consumption for the escape maneuver will be determined later either by considering escape from the parking orbit (see Sect. 5) or by leaving it to the launcher to provide the necessary impulse:

  • First maneuver consumption

    $$\begin{aligned} \Delta v_1= {\left\{ \begin{array}{ll} 0~~~~~~~~\text {with launcher}\\ \Delta v_{\mathrm{esc}}~~~\text {with escape phase}. \end{array}\right. } \end{aligned}$$

As discussed in Sect. 2, flybys must take place within the mission area and the selected targets must be reached with a propellant consumption lower than the pre-defined maximum (\(\Delta v<\Delta v_{{\max }}\)). There may be situations in which multiple asteroids fulfill this requirement; in such case, selecting the target accessible with the lowest \(\Delta v\) is not necessarily a wise choice, as this does not necessarily lead to maximize the number of asteroids encountered during the mission. Instead, the preferred trajectory will be determined using a tree-structured strategy ([18]). During each search every selected asteroid is first taken into account and then new target searches are performed starting from each one of them. In this way we obtain a complex branching of possible paths that the spacecraft can travel. The branching will be stopped at those nodes where either the propellant is exhausted, or the end of mission time has been exceeded, or simply no further reachable targets are found. For a n-asteroids sequence with consumption values \(\left\{ \Delta v_1,\Delta v_2,\ldots ,\Delta v_n\right\} \), we have the following criterion:

  • Tree-structure branching stop criterion

    $$\begin{aligned} t_n>t_{\mathrm{end}}~~\vee ~~\sum _{h=1}^{n}\Delta v_h>\Delta v_{\mathrm{tot}}~~\vee ~~No reachable asteroids . \end{aligned}$$

Finally, a global selection of the best mission profile is made by selecting the sequence of branches that, starting from the Earth, passes by the largest number of asteroids with the lowest propellant consumption.

4.2 Asteroid transit observation area

To reduce the computational cost, the search is initially focused only on one part of the mission area. Since the mission has a finite duration, it is preferable to intercept the asteroids as close as possible to the spacecraft, to minimize transfer times between two targets and thus to maximize the number of asteroids encountered. To this end, we consider a spherical observation area centered at the spacecraft’s position within which the flyby must take place. The sphere must be large enough to hold a number of possible encounters and, at the same time, small enough to limit the transfer distance. To determine the sphere’s radius \(\delta \), we take as a reference a characteristic length of the system—namely, the distance between the spacecraft and the currently closest asteroid—and multiply it by a magnification factor \(c_1\) chosen at will:

  • Observation area radius

    $$\begin{aligned} \delta (t^*)=c_1\min \limits _{k}\left\{ \left| {\textbf {r}}_k(t^*)-{\textbf {r}}_{\mathrm{S}}(t^*)\right| \right\} , \end{aligned}$$

where \(t^*\) is the current mission time. In our case \(c_1=10\) is assumed.

It is necessary to select only those asteroids that transit within the observation area and to calculate when this happens. Let \({\textbf {r}}_{\mathrm{A}}\) be a generic asteroid position; the asteroid is on the surface of the sphere when the distance from the spacecraft \(d_{\mathrm{A}}\) is

$$\begin{aligned} d_{\mathrm{A}}=\left| {\textbf {r}}_{\mathrm{A}}-{\textbf {r}}_{\mathrm{S}}\right| =\delta . \end{aligned}$$

Therefore, it is inside the sphere when:

$$\begin{aligned} f_{\mathrm{sph}}({\textbf {r}}_{\mathrm{A}})=\left| {\textbf {r}}_{\mathrm{A}}-{\textbf {r}}_{\mathrm{S}}\right| -\delta <0. \end{aligned}$$
(9)

An asteroid must be intercepted when it is simultaneously inside the observation area (sphere) and the mission area (torus):

$$\begin{aligned} \exists ~ t\in \left[ t^*,t^*+T\right] :f_{\mathrm{sph}}({\textbf {r}}_{\mathrm{A}}(t))<0~\wedge ~f_{\mathrm{tor}}({\textbf {r}}_{\mathrm{A}}(t))<0.\nonumber \\ \end{aligned}$$
(10)

In the above formula, an interval of time equal to the asteroid period T has been set to include all the positions along a single orbit. Let \({\mathcal {S}}\) and \({\mathcal {T}}\) be respectively the sphere and torus three-dimensional domains; their intersection is defined as \({\mathcal {D}}={\mathcal {S}}\cap {\mathcal {T}}\). An asteroid will be selected only if it is already inside \({\mathcal {D}}\) at the time \(t^*\), or if it is initially external but its entry is expected at time \(t<t^*+T\); it will instead be discarded if is initially outside \({\mathcal {D}}\) but it will enter at time \(t>t^*+T\), or if it will never enter.

Determining the transit times \(t_{\mathcal {D}}\) and positions \({\textbf {r}}_{\mathcal {D}}(t_{\mathcal {D}})\) on \({\mathcal {D}}\) involves the solution of a non-linear problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} f_{\mathrm{sph}}({\textbf {r}}_{\mathcal {D}})=0~~\text {if}~~f_{\mathrm{tor}}({\textbf {r}}_{\mathcal {D}})<0~~\text {with}~~ {\left\{ \begin{array}{ll} f'_{\mathrm{sph}}({\textbf {r}}_{\mathcal {D}})<0~~\text {incoming}\\ f'_{\mathrm{sph}}({\textbf {r}}_{\mathcal {D}})>0~~\text {outgoing} \end{array}\right. }\\ f_{\mathrm{tor}}({\textbf {r}}_{\mathcal {D}})=0~~\text {if}~~f_{\mathrm{sph}}({\textbf {r}}_{\mathcal {D}})<0~~\text {with}~~ {\left\{ \begin{array}{ll} f'_{\mathrm{tor}}({\textbf {r}}_{\mathcal {D}})<0~~\text {incoming}\\ f'_{\mathrm{tor}}({\textbf {r}}_{\mathcal {D}})>0~~\text {outgoing}. \end{array}\right. } \end{array}\right. } \end{aligned}$$
(11)

To determine if an asteroid respects the condition in Eq. 10 it is necessary to find the time of the first transit \(t_{\mathcal {D}}^{\mathrm{(I)}}\). Then, all the solutions of Problem 11, \(\left\{ {\textbf {r}}_{\mathcal {D}}^{(1)},{\textbf {r}}_{\mathcal {D}}^{(2)},\ldots \right\} \), must be determined. For each of them a DKP is solved with initial conditions at \(t=t^*\) to find the related times \(\left\{ t_{\mathcal {D}}^{(1)},t_{\mathcal {D}}^{(2)},\ldots \right\} \). The smallest solution obtained is the next asteroid transit time \(t_{\mathcal {D}}^{\mathrm{(I)}}\). Summing up, we have

  • Observation area transit positions

    $$\begin{aligned} {\left\{ \begin{array}{ll} f_{\mathrm{sph}}({\textbf {r}}_{{\mathcal {D}},k})=0~~\text {if}~~f_{\mathrm{tor}}({\textbf {r}}_{{\mathcal {D}},k})<0\\ f_{\mathrm{tor}}({\textbf {r}}_{{\mathcal {D}},k})=0~~\text {if}~~f_{\mathrm{sph}}({\textbf {r}}_{{\mathcal {D}},k})<0 \end{array}\right. }\\ ~\Rightarrow ~ \left\{ {\textbf {r}}_{{\mathcal {D}},k}^{(1)},{\textbf {r}}_{{\mathcal {D}},k}^{(2)},\ldots \right\} ~\text {for}~k=1:N. \end{aligned}$$

  • Observation area transit times

    $$\begin{aligned} \text {DKP}= {\left\{ \begin{array}{ll} \text {Initial conditions}:t^*,{\textbf {r}}_k^*\\ \text {Final conditions}:{\textbf {r}}_{{\mathcal {D}},k}^{(n)} \end{array}\right. }\\ ~~\Rightarrow ~~t_{{\mathcal {D}},k}^{(n)}~~\text {for}~~ {\left\{ \begin{array}{ll} k=1:N\\ n=1,2,\cdots \end{array}\right. } \end{aligned}$$

  • Next transit time

    $$\begin{aligned} t_{{\mathcal {D}},k}^{\mathrm{(I)}}=\min \left\{ t_{{\mathcal {D}},k}^{(1)},t_{{\mathcal {D}},k}^{(2)},\ldots \right\} ~~~\text {for}~~~k=1:N. \end{aligned}$$

The obtained solution is related to an incoming asteroid if it is initially out of \({\mathcal {D}}\), or, on the contrary, to an outgoing asteroid if it is inside. Finally, the transiting asteroid can be selected:

  • Transiting asteroids selection

    $$\begin{aligned}&\left( f_{\mathrm{tor}}({\textbf {r}}_k^*)<0~\wedge ~f_{\mathrm{sph}}({\textbf {r}}_k^*)<0\right) ~\vee ~\\&\left[ \left( f_{\mathrm{tor}}({\textbf {r}}_k^*)>0~\vee ~f_{\mathrm{sph}}({\textbf {r}}_k^*)>0\right) ~\wedge ~t_{{\mathcal {D}},k}^{(1)}<\left( t^*+T_k\right) \right] \\~&\Rightarrow ~Asteroid selected \end{aligned}$$

    for \(k=1:N\).

After this step, the number of asteroids considered could decrease again:

  • Transiting asteroids number: \(N_1\le N\).

4.3 Flyby position

In this phase the previously calculated transit times \(\left\{ t_{{\mathcal {D}},k}^{(1)},t_{{\mathcal {D}},k}^{(2)},\ldots \right\} \) are used to set the temporal domain \({\mathcal {I}}\) in which the asteroids are reachable. Among them, an optimal time for flyby is selected, if possible. Finally, all the data concerning transfer orbits and maneuvers are calculated.

The transit time intervals are found by re-ordering the transit times in the form \(\left\{ t_{{\mathcal {D}},k}^{\mathrm{(I)}},t_{{\mathcal {D}},k}^{\mathrm{(II)}},\ldots \right\} \), and by considering the current asteroid position \({\textbf {r}}^*\). In particular, two different cases must be distinguished: (1) when the asteroid is initially inside the domain \({\mathcal {D}}\), and (2) when it is initially outside:

  • Transit time intervals statement

    $$\begin{aligned} {\mathcal {I}}_k={\left\{ \begin{array}{ll} \left[ t^*,t_{{\mathcal {D}},k}^{\text {(I)}}\right] ,\left[ t_{{\mathcal {D}},k}^{\text {(II)}},t_{{\mathcal {D}},k}^{\text {(III)}}\right] ,\ldots ,\left[ t_{{\mathcal {D}},k}^{\text {(end)}},t^*+T_k\right] \\ \text {if}~\left( f_{\mathrm{tor}}({\textbf {r}}_k^*)<0~\wedge ~f_{\mathrm{sph}}({\textbf {r}}_k^*)<0\right) \\ \left[ t_{{\mathcal {D}},k}^{\text {(I)}},t_{{\mathcal {D}},k}^{\text {(II)}}\right] ,\left[ t_{{\mathcal {D}},k}^{\text {(III)}},t_{{\mathcal {D}},k}^{\text {(IV)}}\right] ,\ldots ,\left[ t_{{\mathcal {D}},k}^{\text {(end-1)}},t_{{\mathcal {D}},k}^{\text {(end)}}\right] \\ \text {if}~\left( f_{\mathrm{tor}}({\textbf {r}}_k^*)>0~\vee ~f_{\mathrm{sph}}({\textbf {r}}_k^*)>0\right) \end{array}\right. } \end{aligned}$$

    for \(k=1:N_1\)

To minimize the transfer times, the search for optimal flyby conditions starts with the first of the aforementioned time intervals and moves on to the following ones if needed. To determine a transfer trajectory between two positions in a given time interval, a Lambert Problem (LP) must be solved. Let us consider the spacecraft position at current time \({\textbf {r}}_{\mathrm{S}}^*={\textbf {r}}_{\mathrm{S}}(t^*)\) and the asteroid position at a generic flyby time \({\textbf {r}}_f={\textbf {r}}(t_f)\). The goal is to determine \(t_f\in {\mathcal {I}}\) to find transfer trajectories from \({\textbf {r}}_{\mathrm{S}}^*\) to \({\textbf {r}}_f\) in a time interval equal to \(\left( \Delta t\right) _{\mathrm{tr}}=t_f-t^*\). Therefore, following [18], the following problem is solved:

  • Asteroid flyby position search

    $$\begin{aligned} {\left\{ \begin{array}{ll} \min \limits _{t_f\in {\mathcal {I}}_k}\left( \Delta v\right) _{\mathrm{tr},k}(t_f)\\ 0<\left( \Delta \nu \right) _{\mathrm{tr},k}<\pi \\ \left( t_p\right) _k<\left( \Delta t\right) _{\text {tr},k}<\left( t_m\right) _k\\ \left( \Delta v\right) _{\text {tr},k}<\Delta v_{{\max }} \end{array}\right. }~~\Rightarrow ~~t_{f,k}~~\Rightarrow ~~Asteroid selected ~~\text {for}~~k=1:N_1 \end{aligned}$$

The problem above and then a LP are solved for each asteroid, but only those that admit a solution are considered for tree-structure branching, so that the nodes in the tree-structure include only the reachable asteroids:

  • Reachable asteroids number: \(N_{\mathrm{fin}}\)

New search phases will be carried out for each of them considering the spacecraft state as shown in Sect. 4.1. On the other hand, if no asteroids can be reached according to the defined criteria, the size of the observation area is increased and the search phase restarts:

  • Observation area increase:

    $$\begin{aligned} \delta _{\mathrm{new}}=c_2\delta ~~\text {with}~~\delta _{\mathrm{new}}<2d_{{\max }} \end{aligned}$$

In our case, \(c_2=2\) is chosen; by considering a larger domain, the chances of finding favorable flyby positions are increased. The upper limit \(2d_{{\max }}\) represents the maximum distance between two points inside the torus mission area. If increasing the observation area radius does not allows to find reachable asteroids, the tree-structure branching is interrupted.

5 Escape phase

As anticipated in Sect. 1, if an initial parking orbit around the Earth is considered, the optimal escape trajectory is calculated for each generated trajectory. The escape hyperbolic excess velocity \({\textbf {v}}_\infty ^\oplus \) uniquely determines the escape direction and is determined by the initial velocity along the heliocentric transfer orbit \({\textbf {v}}_{\mathrm{tr}}^{\mathrm{in}}\) and the Earth’s velocity \({\textbf {v}}_\oplus \):

$$\begin{aligned} {\textbf {v}}_\infty ^\oplus ={\textbf {v}}_{\mathrm{tr}}^{\mathrm{in}}-{\textbf {v}}_\oplus \end{aligned}$$

The escape trajectory lies on the plane identified by the position over the parking orbit \({\textbf {r}}_{\mathrm{S}}\) where the maneuver occurs, the position of the Earth and the direction of the vector \({\textbf {v}}_\infty ^\oplus \) (Fig. 5).

Fig. 5
figure 5

Vector diagram of the generic conditions involved in the escape phase problem

Full size image

In particular, it is possible to have two escape maneuvers on this plane which are distinguished by the orbit travel direction—i.e. clockwise or anti-clockwise—and the true anomaly swept for escaping. To indicate the orbit travel direction, the angular momentum unit vector is calculated for both cases:

$$\begin{aligned} \hat{{\textbf {h}}}=\pm \frac{{\textbf {r}}_{\mathrm{S}}\times {\textbf {v}}_\infty ^\oplus }{\left| {\textbf {r}}_{\mathrm{S}}\times {\textbf {v}}_\infty ^\oplus \right| }. \end{aligned}$$
(12)

From now on the discussion will be valid for both cases, therefore no distinction will be made. First, the orbital elements of the escape hyperbola are determined. The escape orbit semi-major axis can be determined through conservation of mechanical energy:

$$\begin{aligned} a_{\mathrm{esc}}=-\frac{\mu _\oplus }{\left| {\textbf {v}}_\infty ^\oplus \right| ^2}. \end{aligned}$$

The escape orbit eccentricity can be calculated by solving a non-linear problem. Let’s consider the true anomaly \(\Delta \nu \) swept during escape:

$$\begin{aligned} \Delta \nu ={\left\{ \begin{array}{ll} \arccos \left( \frac{{\textbf {r}}_{\mathrm{S}}\cdot {\textbf {v}}_\infty ^\oplus }{\left| {\textbf {r}}_{\mathrm{S}}\right| \left| {\textbf {v}}_\infty ^\oplus \right| }\right) ~~~\text {if}~\left( {\textbf {r}}_{\mathrm{S}}\times {\textbf {v}}_\infty ^\oplus \right) \cdot \hat{{\textbf {h}}}\ge 0\\ 2\pi -\arccos \left( \frac{{\textbf {r}}_{\mathrm{S}}\cdot {\textbf {v}}_\infty ^\oplus }{\left| {\textbf {r}}_{\mathrm{S}}\right| \left| {\textbf {v}}_\infty ^\oplus \right| }\right) ~~~\text {if}~\left( {\textbf {r}}_{\mathrm{S}}\times {\textbf {v}}_\infty ^\oplus \right) \cdot \hat{{\textbf {h}}}<0. \end{array}\right. } \end{aligned}$$

This must be equal to the difference between the hyperbolic excess and the initial true anomaly, respectively \(\nu _\infty \) and \(\nu _{\mathrm{esc}}\):

$$\begin{aligned} \Delta \nu =\nu _\infty -\nu _{\mathrm{esc}} \end{aligned}$$
(13)

with

$$\begin{aligned} \nu _\infty= & {} \arccos \left( -\frac{1}{e_{\mathrm{esc}}}\right) \\ \nu _{\mathrm{esc}}= & {} {\left\{ \begin{array}{ll} \arccos \left[ \frac{1}{e_{\mathrm{esc}}}\left( \frac{a_{\mathrm{esc}}\left( 1-e_{\mathrm{esc}}^2\right) }{\left| {\textbf {r}}_{\mathrm{S}}\right| }-1\right) \right] ~~~\text {if}~~\nu _\infty \ge \Delta \nu \\ -\arccos \left[ \frac{1}{e_{\mathrm{esc}}}\left( \frac{a_{\mathrm{esc}}\left( 1-e_{\mathrm{esc}}^2\right) }{\left| {\textbf {r}}_{\mathrm{S}}\right| }-1\right) \right] ~~~\text {if}~~\nu _\infty <\Delta \nu . \end{array}\right. } \end{aligned}$$

In Eq. 13, the escape eccentricity \(e_{\mathrm{esc}}\) is the only unknown term:

$$\begin{aligned} f(e_{\mathrm{esc}})=\nu _\infty -\nu _{\mathrm{esc}}-\Delta \nu =0~~\Rightarrow ~~e_{\mathrm{esc}}. \end{aligned}$$

The remaining orbital elements are determined using their definition. Note that the unit vectors refer to a geocentric-equatorial reference system:

Table 3 Combined methods for the formulation of Brent’s algorithms
Full size table
$$\begin{aligned} i_{\mathrm{esc}}= & {} \arccos \left( \hat{{\textbf {k}}}\cdot \hat{{\textbf {h}}}\right) \\ \Omega _{\mathrm{esc}}= & {} {\left\{ \begin{array}{ll} \arccos \left( \hat{{\textbf {i}}}\cdot \hat{{\textbf {n}}}\right) ~~\text {if}~~\hat{{\textbf {n}}}\cdot \hat{{\textbf {j}}}\ge 0\\ 2\pi -\arccos \left( \hat{{\textbf {i}}}\cdot \hat{{\textbf {n}}}\right) ~~\text {if}~~\hat{{\textbf {n}}}\cdot \hat{{\textbf {j}}}<0 \end{array}\right. }~~~\text {with}~~~\hat{{\textbf {n}}}=\frac{\hat{{\textbf {k}}}\times \hat{{\textbf {h}}}}{\left| \hat{{\textbf {k}}}\times \hat{{\textbf {h}}}\right| }\\ \omega _{\mathrm{esc}}= & {} \alpha _\infty -\nu _\infty ~~~\text {with}~~~\alpha _\infty \\&= {\left\{ \begin{array}{ll} \arccos \left( \frac{{\textbf {v}}_\infty ^\oplus \cdot \hat{{\textbf {n}}}}{ v_\infty ^\oplus }\right) ~~\text {if}~~\left( \hat{{\textbf {h}}}\times \hat{{\textbf {n}}}\right) \cdot {\textbf {v}}_\infty ^\oplus \ge 0\\ 2\pi -\arccos \left( \frac{{\textbf {v}}_\infty ^\oplus \cdot \hat{{\textbf {n}}}}{ v_\infty ^\oplus }\right) ~~\text {if}~~\left( \hat{{\textbf {h}}}\times \hat{{\textbf {n}}}\right) \cdot {\textbf {v}}_\infty ^\oplus <0 \end{array}\right. } \end{aligned}$$

With the escape orbit parameters known, it is now possible to calculate the associated propellant consumption. Let \({\textbf {v}}_{\mathrm{par}}\) and \({\textbf {v}}_{\mathrm{esc}}\) be respectively the parking and escape orbit velocities in \({\textbf {r}}_{\mathrm{S}}\); the escape maneuver consumption is

$$\begin{aligned} \Delta v_{\mathrm{esc}}=\left| {\textbf {v}}_{\mathrm{esc}}-{\textbf {v}}_{\mathrm{par}}\right| . \end{aligned}$$

Therefore, the consumption for escape depends on two variables: the escape position \({\textbf {r}}_{\mathrm{S}}\) and the escape orbit travel direction (± in Eq. 12). To optimize \(\Delta v_{\mathrm{esc}}\), let’s consider the following two functions:

$$\begin{aligned} \Delta v_{\mathrm{esc}}\left( {\textbf {r}}_{\mathrm{S}}\right) ={\left\{ \begin{array}{ll} f_{+}\left( {\textbf {r}}_{\mathrm{S}}\right) ~~~\text {if}~~\hat{{\textbf {h}}}=+\frac{{\textbf {r}}_{\mathrm{S}}\times {\textbf {v}}_\infty ^\oplus }{\left| {\textbf {r}}_{\mathrm{S}}\times {\textbf {v}}_\infty ^\oplus \right| }\\ f_{-}\left( {\textbf {r}}_{\mathrm{S}}\right) ~~~\text {if}~~\hat{{\textbf {h}}}=-\frac{{\textbf {r}}_{\mathrm{S}}\times {\textbf {v}}_\infty ^\oplus }{\left| {\textbf {r}}_{\mathrm{S}}\times {\textbf {v}}_\infty ^\oplus \right| }. \end{array}\right. } \end{aligned}$$

The two functions are optimized independently of each other; at the end, the best value between the two optimal ones is chosen.

6 Numerical solvers

To solve the non-linear problems introduced in the previous sections two solver algorithms have been implemented, one for root-finding problems and the other for optimization problems, both derived from [20]. These algorithms are designed for single-variable functions and are derivative-free. Contrary to most iterative numerical methods, they are designed so to be both very convergent and very robust. Brent’s algorithms are a combination of a robust and a convergent method (see Table 3) that exploit the good properties of both to guarantee superlinear convergence independently from the starting values.

Let f(x) be the single-variable function inherent to the problem. There are four parameters that need to be defined as inputs to Brent’s algorithm. The tolerance tol is a combination of a relative tolerance \(\varepsilon \) and an absolute tolerance t:

$$\begin{aligned} tol=2\varepsilon \left| x^*\right| +t \end{aligned}$$

where \(x^*\) is the known best approximation of solution. The parameter \(\varepsilon \) is the machine precision—equal to \(2^{-23}\) or \(2^{-52}\) for a 32-bit or a 64-bit processor, respectively—while t must be arbitrarily assumed to have the desired tolerance. In our case, we set \(t=10^{-8}\). The remaining input parameters are the search interval edges, a and b, such that the solution is \(x^*\in \left[ a;b\right] \). To identify them, \((N+1)\) equidistant control points \(x_i\) (for \(i=0:N\)) are taken within the f(x) domain (edges included) and the function is evaluated for each of them. The search interval edges are chosen using the following criteria:

  • Root-finding problem

    $$\begin{aligned} f(x_i)f(x_{i+1})<0~~\Rightarrow ~~a=x_i,~b=x_{i+1}. \end{aligned}$$

  • Optimization problem

    $$\begin{aligned} f(x_i)=\min \limits _{i=0:N}f(x_i)~~\Rightarrow ~~a=x_{i-1},~b=x_{i+1}. \end{aligned}$$

As N increases, both accuracy and numerical effort grow. In our test cases (Sect. 7) it was assumed \(N=100\).

7 Test results

The software has been tested in two different ways to highlight how the trajectory depends on the mission start date. The first case includes a series of tests on 2-year missions spread over a period ranging from 2020 to 2040, while the second one includes 2-year missions in the period 2020 to 2025. In both cases only the mission time interval is changed, while the remaining input parameters are constant through the various executions; the escape maneuver is not considered. We focus here on the results obtained in a simple, constrained scenario. Investigation of the algorithm dependence on the input parameters is postponed to future works. Because of the limited computing power available and to prevent the generation of very large tree-structures with unacceptably long processing duration, the input values to the test case were arbitrarily selected to correspond to a 2-year mission with a modest quantity of propellant onboard (Table 4). The maximum maneuver consumption was chosen to obtain a significant, albeit small, number of encounters, i.e., 16 in our test case.

Table 4 List of constant input parameters during all the tests
Full size table

To get an idea of the amount of data produced, the following parameters have been recorded and compared for each test:

  • Generated nodes number: \(N_{\mathrm{nodes}}\);

  • Possible trajectories number: \(N_{\mathrm{traj}}\);

  • Maximum number of flyby’s: \(N_{\mathrm{ast}}\);

  • Trajectories with the maximum number of flyby’s: \(N_{\mathrm{traj}}^*\).

Testing was carried out on a computer equipped with an Intel® Core™ i7-3630QM processor. Software was compiled with the GNU FORTRAN compiler (GFortran), a free open source FORTRAN 95, FORTRAN 2003 and FORTRAN 2008 compiler. In all cases, each test run took not more than a few tens of minutes to complete. The results are reported and discussed in the following subsections. More complex mission cases can be addressed with acceptable computational time (tens of minutes or a few hours at most) by running the algorithm on present commonly available multi-core personal computers.

7.1 Test case 1

In this series of tests, twenty software runs were performed for mission epochs ranging from January 1, 2020, to January 1, 2040. The main results are shown in Table 5.

Table 5 Main results of 20 tests distributed along 20 years. Time is 12:00:00 UTC for all epochs
Full size table
Fig. 6
figure 6

Bar plot of the maximum number of asteroid generated (blue) and the related number of trajectories (orange) (color figure online)

Full size image

As can be seen from Fig. 6, the number of possible flybys has no clear dependence on the mission period. However, it can be noted that over a period of 20 years there are numerous opportunities for prospecting missions to nine or more asteroids, many of them even with the same launch. In particular, for a mission that starts on January 1, 2040, it is possible to have five different trajectories each of which intercepts twelve asteroids, for a total of 60 asteroids encounters in two years. The “best” of these, i.e. the one that exhibits the smaller total propellant consumption, is shown in Fig. 7 and the relative dates and consumptions are listed in Table 6. Figure 7 shows the projection of the 3-D trajectory on the plane of the ecliptic; deviations from planarity of the actual 3-D trajectory are not appreciable at scale of the drawing.

Fig. 7
figure 7

Plot of the projection on the plane of the ecliptic of the “best” interplanetary trajectory of a 2-year mission starting on January 1, 2040

Full size image
Table 6 List of asteroids encountered during the best mission generated in test case 1 with the relative transfer consumption
Full size table

7.2 Test case 2

Also, in this case twenty tests were carried out, for a period ranging from January 1, 2020, to January 1, 2025. The main results are shown in Table 7.

Table 7 Main results of 20 tests distributed along 5 years
Full size table

The maximum number of asteroids found in a trajectory and the number of sequences with this feature are shown in Fig. 8 as a function of the mission period. Unlike case 1, the frequency of negative results is higher, probably due to the shorter time span between missions.

Fig. 8
figure 8

Bar plot of the maximum number of asteroid generated (blue) and the related number of trajectories (orange) (color figure online)

Full size image

However, there are some cases of significant relevance for practical application to prospecting: e.g., it appears to be possible to perform a mission with nine spacecraft, each directed towards twelve asteroids, for a total of 108 asteroids prospected in two years. Considering a more basic mission architecture with the use of a single spacecraft, it is possible to fly a trajectory passing by 15 asteroids (Fig. 9, Table 8). Like Fig. 7, also Fig. 9 shows the projection of the trajectory on the ecliptic plane, the out-of-plane displacement being too small for the scale of the drawing.

Fig. 9
figure 9

Plot of the best interplanetary trajectory found for a 2-year mission starting on July 1, 2021

Full size image
Table 8 List of encountered asteroids during the best mission generated in test case 2 with the corresponding propellant consumption for transfer
Full size table

8 Conclusions

As expected, the 3-D algorithm yields better results than its 2-D predecessor [18], albeit at an increased computational cost due to the need to solve a larger number of non-linear problems. For the same \(\Delta v_{\mathrm{tot}}\) and the same mission area size, the 3-D version returned a flyby frequency of about 6 asteroids/year against the 4 asteroids/year obtained with the 2-D version. The number of possible trajectories with the same launch is also higher. In many cases, launch windows were found in which it was possible to travel more than 10 different trajectories with 10 asteroids each. We conclude that the procedure here presented provides a relatively simple method to determine trajectory sequences that allow for a substantial number of flyby’s.

Identifying asteroids that are potentially rich in raw materials requires a considerable effort. It has been estimated ([21]) that, if harvesting costs are taken into account, the cost of prospecting must be a small fraction (10%) of the material value in order for the mining venture to generate a profit. Therefore, considering an ideal asteroid with a size of 100 m rich in platinum group metals for an estimated value of US$ 5B, the prospecting mission cost should not exceed US$ 500M; this strongly suggests that small, relatively cheap satellites should be seriously considered for the task.

The results of this study show that a multi-asteroid prospecting mission with a fleet of small satellites is indeed an attractive possibility. According to [21], finding at least one rich asteroid with a probability of 99% requires the investigation of about 44 asteroids. In light of the results of this work we can confidently conclude that such target can be achieved with a reasonable number of small spacecraft, thus keeping launch cost and duration of the prospecting operations at a minimum.