1 Introduction

In view of the major consequences and huge expense are usually relevant to system failures, prognostics and health management (PHM) has received increasing attention in academia and industry. As a challenging task in PHM, prognostics aims to estimate how much time remains before a likely failure or in other words remaining useful life (RUL) to promote reliability and safety. Methods to evaluate RUL can be mainly grouped into three major categories: model-based methods, experience-based methods and data-driven methods [1]. The former requires extensive expert knowledge about systems to build a physical model [2,3,4], which is usually unavailable in practice, e.g. aircraft engines. Experience-based methods leverage historical failure cases to build hidden relationship among current system states, current lives and recorded failure instances. However, methods included in this category, e.g. instance-based methods [5, 6], require more calculations as reference cases increase and depend too much on run-to-failure cases.

Data-driven methods, especially deep learning techniques, have emerged as a research hotspot with the availability of sensor data from numerous systems. The clipped sensor readings and their corresponding RULs are used as inputs to train a deep neural network, and the network can discover intricate relations between them with powerful non-linear modeling capabilities. For example, Babu et al. [7] treated segmented sensor readings as 2-dimensional (2D) inputs and utilized 2D convolution to extract more informative feature. Li et al. [8] stacked 1-dimensional (1D) convolution layers for feature extraction of each sensor signals and predicted RUL by a fully-connected layer. Malhi et al. [9] proposed a learning-based method for long-term prognostics of rolling bearing with recurrent neural network (RNN). Wu et al. [10] combined a long short-term memory network (LSTM) based model with a dynamic difference method to get rid of operating condition influence.

However, methods mentioned above neglect spatial relationships between different sensors and RNN-based structures are possible to accumulate error by steps and difficult to capture long-term dependence. In this work, we adopt two crucial strategies to solve these two problems. First, we compute the weighted adjacency matrix of senor network with Pearson correlation coefficients (PCCs) among sensors. Second, graph convolutional networks (GCNs) and temporal convolutional networks (TCNs) constituted by stacked dilated casual convolutions work together to capture spatio-temporal dependencies followed by gating mechanism and skip connections.

The rest of the paper is organized as follows. Section 2 introduces the related work, including convolution on graph structure and spatio-temporal graph neural networks. Section 3 presents how to build graph structure of sensor network via PCCs and introduces the proposed framework. Section 4 shows the experimental results on C-MAPSS dataset. The last section draws the conclusion and discusses the future work.

2 Related work

2.1 Convolution on graph structure

Convolutions in the graph domain can be categorized as spatial approaches and spectral approaches [11]. The former defines convolutions directly on graph which is challenging to deal with differently sized neighborhoods [12,13,14]. Li et al. [12] model the spatial dependency based on diffusion process as:

$$ \begin{array}{*{20}c} {g_{\theta } *x = \mathop \sum \limits_{k = 0}^{K - 1} \left( {\theta_{k,1} A_{1}^{k} + \theta_{k,2} A_{2}^{k} } \right)x,} \\ \end{array} $$
(1)

where \(x \in {\mathbb{R}}^{N}\). is the input; \(g_{\theta }\) is a filter parameterized by \(\theta \in {\mathbb{R}}^{K \times 2}\).; \(A_{1}\) and \(A_{2}\) are the transition matrices of the diffusion process and the reverse one; \(k\) is the diffusion step and in [12] a finite \(K\)-step truncation of the diffusion process is adopted.

The latter operated convolutions based on Fourier domain [15], which is defined as:

$$ \begin{array}{*{20}c} {g_{\theta } *x = g_{\theta } \left( L \right)x = g_{\theta } \left( {U{\Lambda }U^{T} } \right)x = Ug_{\theta } \left( {\Lambda } \right)U^{T} x,} \\ \end{array} $$
(2)

where \(g_{\theta }\) is a filter parameterized by \(\theta \in {\mathbb{R}}^{N}\); \(x \in {\mathbb{R}}^{N}\) is the signal; \(L = I_{N} - D^{{ - \frac{1}{2}}} AD^{{ - \frac{1}{2}}}\) is the normalized graph Laplacian (\(D\) is the degree matrix and \(A\). is the adjacency matrix of the graph); \({\Lambda }\) is the diagonal matrix of eigenvectors of \(L\); \(U\) is the matrix of eigenvectors of \(L\).

Further to reduce the high computing consume of Eq. (2), many researchers proposed different methods. Hammond et al. [16] approximate the \(g_{\theta } \left( {\Lambda } \right)\). with a truncated expansion in terms of Chebyshev polynomials up to \(K{\text{th}}\) order:

$$ \begin{array}{*{20}c} {g_{\theta } *x \approx \mathop \sum \limits_{k = 0}^{K - 1} \theta_{k} T_{k} \left( {\tilde{L}} \right)x,} \\ \end{array} $$
(3)

where \(\tilde{L} = \frac{2}{{\lambda_{{{\text{max}}}} }}L - I_{N}\), \(\lambda_{{{\text{max}}}}\) is the rgest eigenvalue of \(L\); \(T_{k} \left( x \right) = 2xT_{k - 1} \left( x \right) - T_{k - 2} \left( x \right)\) with \(T_{0} \left( x \right) = 1\) and \(T_{1} \left( x \right) = x\).; \(\theta \in {\mathbb{R}}^{K}\) s a vector of Chebyshev coefficients.

More efforts are made to overcomthe problem of overfitting and numerical instabilities in [17], where a first-order approximation of Chebyshev polynomials and some normalization tricks are introduced:

$$ \begin{array}{*{20}l} g_{\theta } *x &\approx \theta_{0}^{^{\prime}} x + \theta_{1}^{^{\prime}} \left( {L - I_{N} } \right)x = \theta_{0}^{^{\prime}} x - \theta_{1}^{^{\prime}} D^{{ - \frac{1}{2}}} AD^{{ - \frac{1}{2}}} x \\ &= \theta \left( {I_{N} + D^{{ - \frac{1}{2}}} AD^{{ - \frac{1}{2}}} } \right)x = \theta \tilde{D}^{{ - \frac{1}{2}}} \tilde{A}\tilde{D}^{{ - \frac{1}{2}}} x, \end{array} $$
(4)

where \(\theta = \theta_{0}^{^{\prime}} = - \theta_{1}^{^{\prime}}\), \(\theta_{0}^{^{\prime}}\) and \(\theta_{1}^{^{\prime}}\) are two free parameters; \(\tilde{A} = A + I_{N}\) is the adjacency matrix with self-connections, \(I_{N}\) is the identity matrix; \(\tilde{D}_{ii} = \mathop \sum \limits_{j} \tilde{A}_{ij} .\)

2.2 Spatio-temporal graph neural networks

Spatio-temporal graph neural networks have a wide range of applications, e.g. traffic forecasting, action forecasting and wind speed forecasting [18,19,20,21,22]. In these tasks, the key is to determine the optimal combinations of spatial information and temporal dynamics under specific settings. Li et al. [12] replaced the matrix multiplications in gated recurrent units (GRU) with diffusion convolutions to extract spatio-temporal features of traffic flow, which was modeled as a directed graph. Seo et al. [19] combined convolutional neural network (CNN) on graphs to identify spatial structures and RNN to find dynamic patterns for predicting structured sequences of data, e.g. frames in videos.

However, RNN-based approaches are inefficient for long sequences and more likely to explode when they are combined with GCN [20]. Yu et al. [21] computed the distances among stations as the adjacency matrix of road graph, and then utilized complete convolutional structures to extract spatio-temporal features of traffic network. Yan et al. [22] designed a generic representation of skeleton sequences and extended graph neural networks with 1-D CNN to model dynamic skeletons effectively. Zhang et al. [23] used adaptive graph convolution to learn spatio-temporal features for RUL prediction. Different from their work, we explore a different graph convolution process and a different network structure.

3 RUL estimation based on spatio-temporal graph convolutional network

In this work, the graph structure of sensor network is constructed with PCCs and a method combining GCNs and TCNs is proposed to estimate RULs. Figure 1 shows the structure of our model where spatio-temporal convolutional blocks (ST-Conv blocks) are crucial components. Each ST-Conv block consists of two GCNs and two TCNs followed by gating mechanism to fuse both spatial and temporal features. Residual connections are applied in blocks and skip connections are utilized throughout the network to speed up convergence. The fully connected layer is utilized to get the final RUL result.

Fig. 1
figure 1

Structure of the proposed method

Full size image

3.1 Problem definition

Generally, RUL estimation is a typical time-series prediction problem that predicting the system will fail after \(\hat{y}^{t}\) time steps based on given \(T\) running observations:

$$ \begin{array}{*{20}c} {\left[ {x^{t - T + 1} , \ldots , x^{t} } \right]\to ^{h\left( \cdot \right)} \hat{y}^{t} .} \\ \end{array} $$
(5)

where \(\hat{y}^{t}\) is the estimated RUL; \( x^{i} \in {\mathbb{R}}^{N} \left( {i = t - T + 1, \ldots ,t} \right)\) is recorded sensor readings at time \(i\); \(h\left( \cdot \right)\) is a function that maps \(T\) running observations to the RUL at time \(t\).

Figure 2 shows a simplified diagram of engine. We can see various subroutines are assembled together and we can monitor its status by collecting data from different parts, such as pressure at fan inlet, HPC stall margin, temperature at LPT olet and so on. It is undoubtful that each part will be affected by other parts even operating environments rather than independent of each other. Considering the external and internal influences, graph structure is very suitable for this situation since it can aggregate information from neighboring nodes. In this work, we define the sensor network as a graph where sensors are nodes, their relations are edges, impact magnitude and its positive or negative represent weighted adjacency matrix. The schematic diagram is shown in Fig. 3.

Fig. 2
figure 2

Simplified diagram of engine [24]

Full size image
Fig. 3
figure 3

Graph structure of sensor network

Full size image

Combined with the graph structure, the original Eq. (5) can be expanded to:

$$ \begin{array}{*{20}c} {\left[ {x^{t - T + 1} , \ldots , x^{t} ;{\mathcal{G}}} \right]\to ^{h\left( \cdot \right)} \hat{y}^{t} ,} \\ \end{array} $$
(6)

where \({\mathcal{G}} = \left( {{\mathcal{V}}, { \mathcal{E}}, A } \right) \) is the graph structure of sensor network; \({\mathcal{V}}\) is the set of nodes or in other words sensors with a total of \(N\); \({\mathcal{E}}\). is the set of edges; \(A \in {\mathbb{R}}^{N \times N}\) is a weighted adjacency matrix derived from other nodes.

3.2 Graph convolution for spatial information

Different from traffic forecasting or action recognition where the adjacency matrix can be computed based on Euclidean distance among stations in traffic network or the intra-body connections of joints can be represented by distance according to partitioning strategies, relationships between sensors are not provided explicitly in RUL estimation tasks. Since the proximity of two sensors in Euclidean domain doesn’t mean they are closely related, Euclidean distance is not the optimal metric for relationship modeling. Hence, we construct the weighted adjacency matrix based on PCCs among sensors. The formulation of PCCs for sequence \(X\) nd \(Y\) is:

$$ \begin{array}{*{20}c} {\rho_{X,Y} = \frac{{{\text{cov}}\left( {X,Y} \right)}}{{\sigma_{X} \sigma_{Y} }} = \frac{{E\left( {\left( {X - \mu_{X} )(Y - \mu_{Y} } \right)} \right)}}{{\sigma_{X} \sigma_{Y} }} = \frac{{E\left( {XY} \right) - E\left( X \right)E\left( Y \right)}}{{\sqrt {E\left( {X^{2} } \right) - E^{2} \left( X \right)} \sqrt {E\left( {Y^{2} } \right) - E^{2} \left( Y \right)} }},} \\ \end{array} $$
(7)

where \({\text{cov}}\left( {X,Y} \right)\). is the covariancof \(X\) and \(Y\);\( \sigma_{X}\) and \(\sigma_{Y}\) are the standard deviations of \(X\) and \(Y\); \(\mu_{X}\) and \(\mu_{Y}\) are the means of \(X\) and \(Y\); \(\rho_{X,Y}\) is a number between -1 and 1 that indicates the extent to which two variables are related. Then the weighted adjacency matrix is defined as:

$$ \begin{array}{*{20}c} {A_{ij} = e^{{\rho_{{X_{i} X_{j} }} }} .} \\ \end{array} $$
(8)

Further based on the research of Li et al. [12] and Eq. (4), GCN on sensor readings can be represented as:

$$ \begin{array}{*{20}c} {Z = \mathop \sum \limits_{k = 0}^{K - 1} P^{k} XW_{k} ,} \\ \end{array} $$
(9)

where \(P = \frac{A}{{\mathop \sum \nolimits_{j} A_{ij} }}\) is the transition mrix; \(W_{k}\) are trainable weights.

3.3 Spatio-temporal convolutional block

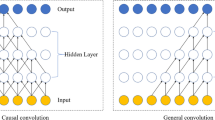
The ST-Conv block takes advantages of CNNs and RNNs as well as prevents their disadvantages. Due to the defects of RNN-based structure, here we choose dilated causal convolution [25] as temporal convolutional layer to extract temporal dynamics. Dilated causal convolution can learn long-term dependency properly in a non-recursive manner and increase the receptive field without greatly increasing computational cost or stacking many layers [26]. The formulation of dilated causal convolution is:

$$ \begin{array}{*{20}c} {x*f\left( t \right) = \mathop \sum \limits_{s = 0}^{K - 1} f\left( s \right)x\left( {t - d \times s} \right),} \\ \end{array} $$
(10)

where \(x \in {\mathbb{R}}^{T}\) is a 1D sequence input; \(f\left( \cdot \right) \in {\mathbb{R}}^{K}\) is a filter; \(d\) is the dilation factor which controls the skipping distance.

LSTM outperforms than basic RNN in sequences modeling thanks to the gating mechanism which can effectively control the flow of information. Learning from the success of LSTM and to enrich convolution operations with nonlinearity, 1-D dilated causal convolution and gating mechanism work together to extract features on time axis [27]. Furthermore, to fuse information from both spatial and temporal domains simultaneously, we embed GCN into ST-Conv block. So, the formulation of ST-Conv block can be defined as follows:

$$ \begin{array}{*{20}c} {Y = {\text{tan}}h\left( {\theta_{1,1} *X + \theta_{1,2} *Z} \right) \odot \sigma \left( {\theta_{2,1} *X + \theta_{2,2} *Z} \right),} \\ \end{array} $$
(11)

where \(\odot\) is the Hadamard product; \(\sigma \left( \cdot \right)\) is the sigmoid activation function; \(\theta_{1,1}\), \(\theta_{1,2}\), \(\theta_{2,1}\) and \(\theta_{2,2}\) are convolution parameters; \(Z\) is the output of GCN; \(X\) is the output of TCN.

4 Experiment

4.1 Dataset description

Saxena et al. [24] modeled a series of turbofan engines by Commercial Modular Aero-Propulsion System Simulation and recorded their run-to-failure data as C-MAPSS dataset. As shown in Table 1, the dataset contains four subsets covering different operating conditions and fault modes and they are further divided into training and test subsets. Each record includes 26 channels, involving engine id, running time (in cycles), 3-dimensional operating condition settings and 21-dimensional sensor readings. During training, all available data points from all engines are used as training samples. And for testing, only one data point corresponding to the last recorded operational cycle for each engine is used as the test sample [8].

4.2 Data preprocess

In practical application, degradation of a system tends to be negligible in the initial stage and increases as it approaches run-to-failure. Hence, we utilize a piece-wise linear degradation model to obtain RUL labels with respect to each sample, whose maximum RUL is set as 130 according to the research of Zheng et al. [28].

Though each observation is 26-dimentional, some channels do not provide valuable information about degradation, i.e. records on sensor #1, #5, #10, #16, #18, #19 and setting3. Each selected channel is normalized by z-score normalization:

$$ \begin{array}{*{20}c} {z = \frac{x - \mu }{\sigma },} \\ \end{array} $$
(12)

where \(\mu\) is the mean; \(\sigma\) is the corresponding standard deviation.

4.3 Experimental setting and evaluation metrics

The experiments are conducted on a 64-bit windows server with one Intel Core i7-7800 × CPU, a 64G RAM and one Nvidia GTX 1080Ti GPU. The default length of sliding window is 30. The selected observations are setting1, setting2, sensor#2, #3, #4, #6, #7, #8, #9, #11, #12, #13, #14, #15, #17, #20, #21 and cycle in turn.

In some cases, predicting failure early is better than late. Late prediction may lead to accidents because condition-based maintenance is too late to perform, while early failure warning will not pose life threatening. So, an unbalanced evaluation indicator average score (AS) is employed to penalize late prediction. Its definition is denoted as:

$$ \begin{array}{*{20}c} {AS = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} s_{i} ,} \\ \end{array} $$
(13)

where \(n\) is the number of test samples; \(s_{i}\) is the computed score of \(i\) th sample:

$$ \begin{array}{*{20}c} {s_{i} = \left\{ {\begin{array}{*{20}c} {e^{{ - \left( {\frac{{d_{i} }}{{a_{1} }}} \right)}} - 1\, {\text{for}}\, d_{i} < 0} \\ {e^{{\frac{{d_{i} }}{{a_{1} }}}} - 1\, {\text{for}} d_{i} \ge 0} \\ \end{array} ,} \right.} \\ \end{array} $$
(14)

where \(d_{i} = {\text{RUL}}_{i}^{{{\text{true}}}} - {\text{RUL}}_{i}^{{{\text{pre}}}}\) is the RUL estimation error of the \(i\) th engine; \(a_{1} = 13\) and \(a_{2} = 10\) are default factors in two cases.

We can know from Eq. (14) that if there are some instances whose d is large enough, then the score will grow exponentially. Furthermore, we also adopt another fair evaluation index called Root Mean Square Error (RMSE), it is:

$$ \begin{array}{*{20}c} {{\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} d_{i}^{2} } ,} \\ \end{array} $$
(15)

where \(d_{i}\) is the estimation error of the \(i\) th engine; \(n\) is the number of test samples.

4.4 Experiment results

To show the effectiveness of our approach, we compare its performance with other methods which are conducted under the same data division way and same evaluation metrics. The Adam optimization algorithm and RMSE loss function are used during training. The comparison results are shown in Table 2. We can know from Table 2 that our proposed method has competitive performance in both RMSE and AS especially for those operating condition is more complex. Compared with previous approaches whose AS of FD002 and FD004 is fifteen times more than it in a single environment, our method reaches a more similar level in different environments. This proves GCN is effective for aggregating spatial information from different orders of neighboring nodes. Figure 4 shows RUL prediction samples of four subsets.

Table 1 Information of C-MAPSS dataset
Full size table
Table 2 Performance comparisons of different methods on C-MAPSS dataset
Full size table
Fig. 4
figure 4

RUL prediction samples of four subsets

Full size image

4.5 Graph structure analysis

4.5.1 Analysis of weighted adjacency matrix

Figure 5 shows weighted adjacency matrixes of FD001 and FD002 based on PCCs. Since data in FD001 is collected under single operating condition, 0th and 1st observations (i.e. setting1 and setting2) are unrelated with other sensor readings, while in FD002 sensors are influenced by them. So, the weighted adjacency matrixes can not only identify relations of running data but also model the influence of operating conditions.

Fig. 5
figure 5

Weighted adjacency matrixes of FD001 and FD002

Full size image

4.6 Analysis the effectiveness of GCN

To further prove the effectiveness of our approach, we compare our method with its non-GCN version. Figure 6 shows their performance differences with respect to RMSE and AS. We can see non-GCN method performs slightly worse on RMSE and AS in FD001 and FD003 but much worse in FD002 and FD004 where environments are more complex. This demonstrates that our method can cope with multiple operational conditions and RUL estimation tasks can benefit from spatial information.

Fig. 6
figure 6

Performance differences with respect to RMSE and AS

Full size image

4.7 Effects of sequence length on performance

To explore the effect of sequence length on model performance, here we take FD001 dataset as an example. Figure 7 shows the effect of sequence length on model performance. The histogram represents RMSE and the line is average training time. It can be observed that with the growth of sequence length, average training time tends to increase while the RMSE continues to decrease. Though the RMSE keeps going down, average training time grow rapidly when the sequence length greater than 30. So, we choose 30 as our default sequence length in experiments.

Fig. 7
figure 7

The effect of sequence length on model performance. The histogram represents RMSE and the line is average training time

Full size image

5 Conclusion

This paper constructs the graph structure of sensor network properly and proposes an effective method to estimate RUL, which combines GCN and Gated-TCN to substantially fuse spatial and temporal features. The experiments on C-MAPSS dataset prove that our method can extract spatio-temporal features adequately and improve the accuracy of RUL estimation. Analysis about weighted adjacency matrix indicates that the constructed graph is qualified for multi-environment tasks. Furthermore, the effects of sequence length on prognostic performance are investigated.

Further improvements are still available. For instance, more precise adjacency matrix and more effective spatio-temporal structure deserves more exploration.