Steady Radiating Gravity waves: An Exponential Asymptotics Approach

Abstract

The radiation of steady surface gravity waves by a uniform stream $U_{0}$ over locally confined (width $L$) smooth topography is analyzed based on potential flow theory. The linear solution to this classical problem is readily found by Fourier transforms, and the nonlinear response has been studied extensively by numerical methods. Here, an asymptotic analysis is made for subcritical flow $D/\lambda > 1$ in the low-Froude-number ($F^{2} \equiv \lambda /L \ll 1$) limit, where $\lambda = U_{0}^{2} /g$ is the lengthscale of radiating gravity waves and $D$ is the uniform water depth. In this regime, the downstream wave amplitude, although formally exponentially small with respect to $F$, is determined by a fully nonlinear mechanism even for small topography amplitude. It is argued that this mechanism controls the wave response for a broad range of flow conditions, in contrast to linear theory which has very limited validity.

1 Introduction

Free-surface flow past bottom topography has been studied widely in connection with geophysical flow modelling, for instance oceanic flows over sea mounts and underwater ridges. The standard way of tackling such steady wave problems analytically is by solving the linearized water-wave equations with appropriate radiation conditions, using Fourier transforms [19]. There exists also a large body of numerical work utilizing boundary-integral and related techniques to compute the nonlinear wave response (see e.g. [4, 7, 8, 12, 20]).

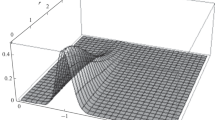
Here, we revisit the classical problem of straight-crested (1D) surface gravity waves in the 2D flow due to a uniform stream with velocity $U_{0}$ over localized bottom topography (Fig. 1), following an entirely different analytical approach. Our solution method formally applies in the weakly nonlinear ($\varepsilon = B/\lambda \ll 1$) and low Froude number ($F^{2} = \lambda /L \ll 1$) regime, where $B$ measures the amplitude and $L$ the width of the topography, and $\lambda = U_{0}^{2} /g$ is the characteristic lengthscale of radiating gravity waves. In addition, the flow is assumed to be subcritical, $D/\lambda > 1$, where $D$ is the uniform water depth. Under these flow conditions, the amplitude of the induced gravity wavetrain downstream is exponentially small relative to $F^{2}$ and thus lies beyond all orders of a perturbation expansion in powers of $F^{2}$. This situation is also known as the ‘low-speed paradox’, as a straightforward asymptotic analysis in the physical domain fails to capture the wave response at any order [6, 15].

Fig. 1

Sketch of free-surface flow due to a stream $U_{0}$ over bottom topography

In the present study we overcome this difficulty by an exponential-asymptotics methodology in the wavenumber domain. This approach was proposed by Akylas & Yang [2] and has recently been developed further by the authors [10] in the context of the forced Korteweg–de Vries (fKdV) equation. In this model problem, the dispersion parameter $\mu$ plays a role analogous to $F^{2}$ in the water wave problem and nonlinear effects are controlled by the amplitude of the forcing term of the fKdV equation.

The wavenumber approach in the fKdV problem exploits the fact that the (exponentially small with respect to $\mu \ll 1$) waves in the physical domain are tied to simple poles of the response Fourier transform on the real axis in the wavenumber domain. The focus then is on computing the residues of these poles which determine the wave amplitude upon inverting the Fourier transform. These residues naturally are exponentially small relative to $\mu$. Interestingly, however, they are also controlled by the nonlinear term of the fKdV equation: linearization is not appropriate in the limit $\mu \to 0$ for small but fixed forcing amplitude, and the radiated waves are governed by a nonlinear mechanism.

Earlier asymptotic analyses for $F^{2} \ll 1$ of free-surface flow past topography [5, 13], a submerged line source [14] and line vortices [16] were based on a WKB technique [5, 13, 14, 16,17,18], where the appearance of exponentially small terms is tied to the crossing of Stokes lines in the (complexified) physical space. For the fKdV equation with sech or sech² forcing term, it has been shown that the WKB technique and the wavenumber-domain approach used here give identical results [9].

Our asymptotic analysis of radiating gravity waves for $F^{2} ,\;\varepsilon \ll 1$ confirms the fully nonlinear wave generation mechanism found in the fKdV model. Furthermore, this mechanism controls the wave response for a broad range of flow conditions, as demonstrated by comparing asymptotic results against numerical computations for flow over topography with a sech profile. As a result, the validity of the classical linear solutions is extremely limited.

2 Problem Formulation

Consider the classical problem of surface gravity waves due to a uniform stream with velocity $U_{0}$ over localized bottom topography $z = b(x)$ of width $L$ (Fig. 1). The uniform water depth is $D$, and the effects of viscosity and surface tension are neglected. This two-dimensional steady flow is described by the well-known potential flow theory: the two-dimensional Laplace equation for the velocity potential subject to the kinematic and dynamic conditions on the free surface and the impermeable condition on the bottom. For the purpose of our analysis in the wavenumber domain, however, it is convenient to work with the non-local formulation of water waves presented by Ablowitz et al. [1] (see their (2.3), (2.4) and (1.8); note also that their $- H$ is our $b$):

$$ \left\{ \begin{gathered} \int_{ - \infty }^{\infty } {{\text{d}}x{\text{e}}^{{ - {\text{i}}kx}} \left\{ {(U_{0} + u)\sinh k(D + \eta ) - (U_{0} + w)\sinh kb(x)} \right\}} = 0, \hfill \\ \int_{ - \infty }^{\infty } {{\text{d}}x{\text{e}}^{{ - {\text{i}}kx}} \left\{ {(U_{0} + u)\cosh k(D + \eta ) - (U_{0} + w)\cosh kb(x)} \right\}} = 0, \hfill \\ \int_{ - \infty }^{\infty } {{\text{d}}x{\text{e}}^{{ - {\text{i}}kx}} \left\{ {g\eta + U_{0} u + \frac{{u^{2} }}{2} - \frac{{\left[ {(U_{0} + u)\eta_{x} } \right]^{2} }}{{2(1 + \eta_{x}^{2} )}}} \right\}} = 0, \hfill \\ \end{gathered} \right. $$

(2.1)

where $k$ is a (real) ‘Fourier-like’ parameter, $g$ is the gravitational acceleration and all the equations including the dynamic condition (third equation) are expressed in integral form. Here $U_{0} + u(x)$ is the tangential flow speed along the free surface (multiplied by $(1 + \eta_{x}^{2} )^{1/2}$), $U_{0} + w(x)$ is that along the bottom (multiplied by $(1 + b_{x}^{2} )^{1/2}$), and $\eta (x)$ is the surface displacement. Equations (2.1) form a closed system for the three unknowns $\left( {u(x),w(x),\eta (x)} \right)$. We also impose the radiation condition that waves appear downstream only:

$$ u(x),\;\;w(x),\;\;\eta (x) \to 0\quad \left( {x \to - \infty } \right). $$

(2.2)

Now we introduce dimensionless variables according to

$$ x \to Lx,\,k \to \frac{k}{L},\,(u,w) \to \varepsilon U_{0} \left( {u,w} \right),\,(\eta ,b) \to \varepsilon \lambda \left( {\eta ,b} \right),D \to \lambda D, $$

(2.3)

where $\lambda \left( { \equiv U_{0}^{2} /g} \right)$ is the characteristic lengthscale (~ wavelength) of radiating gravity waves and $\varepsilon$ measures the (dimensionless) amplitude of the topography. In addition, we define the Fourier transform in x

$$ \hat{u}(k) = \frac{1}{2\pi }\int_{ - \infty }^{\infty } {u(x){\text{e}}^{{ - {\text{i}}kx}} {\text{d}}x} , $$

(2.4)

with analogous expressions for $\hat{w}$, $\hat{\eta }$ and $\hat{b}$, and expand the sinh, cosh and $(1 + \eta_{x}^{2} )^{ - 1}$ functions in (2.1) in power series of $\varepsilon$. Thus, to leading order in $\varepsilon$, Eqs. (2.1) reduce to the linearized equations governing $\hat{u}$, $\hat{w}$ and $\hat{\eta }$, and the Fourier transforms of the higher-order (nonlinear) terms are expressed as convolution integrals. Specifically, after considerable manipulation, we find the following dimensionless equations in the wavenumber domain:

$$ \left\{ \begin{gathered} \left( {\frac{\tanh \mu kD}{{\mu k}} - 1} \right)\hat{u} = \frac{1}{\mu k\cosh \mu kD}\left( {\sum\limits_{j = 0}^{\infty } {\varepsilon^{2j} \hat{f}_{2j + 1} } + \sum\limits_{j = 1}^{\infty } {\varepsilon^{j} \hat{m}_{j} } } \right) - \sum\limits_{j = 1}^{\infty } {\varepsilon^{j} \hat{n}_{j} } , \hfill \\ \hat{u}\cosh \mu kD + \mu k(\sinh \mu kD)\hat{\eta } - \hat{w} = \sum\limits_{j = 1}^{\infty } {{\kern 1pt} \varepsilon^{2j - 1} \hat{f}_{2j} } + \sum\limits_{j = 1}^{\infty } {\varepsilon^{j} \overline{m}_{j} } , \hfill \\ \hat{\eta } + \hat{u} = \sum\limits_{j = 1}^{\infty } {\varepsilon^{j} \hat{n}_{j} } , \hfill \\ \end{gathered} \right. $$

(2.5a)

where $\mu \equiv F^{2} \left( { = \lambda /L} \right)$ is the Froude number squared. Regarding the right-hand side terms,

$$ \hat{f}_{j} (k) = \frac{{(\mu k)^{j} }}{j!\;}{\mathbb{F}}\left[ {b(x)^{j} } \right] $$

(2.5b)

accounts for the forcing due to the topography, and

$$ \hat{m}_{j} (k) = \frac{{(\mu k)^{j} }}{j!}\left\{ \begin{gathered} {\mathbb{F}}\left[ { - \cosh \mu kD\left( {u(x) + (\tanh \mu kD)\frac{\mu k\eta (x)}{{j + 1}}} \right)\eta (x)^{j} + w(x)b(x)^{j} } \right]\;\,(j:{\text{odd}}), \hfill \\ {\mathbb{F}}\left[ { - \cosh \mu kD\left( {(\tanh \mu kD)\,u(x) + \frac{\mu k\eta (x)}{{j + 1}}} \right)\eta (x)^{j} } \right] \, (j:{\text{even}}), \hfill \\ \end{gathered} \right. $$

(2.5c)

$$ \overline{m}_{j} (k) = \frac{{(\mu k)^{j} }}{j!}\left\{ \begin{gathered} {\mathbb{F}}\left[ { - \cosh \mu kD\left( {(\tanh \mu kD)\,u(x) + \frac{\mu k\eta (x)}{{j + 1}}} \right)\eta (x)^{j} } \right]\;\,(j:{\text{odd}}), \hfill \\ {\mathbb{F}}\left[ { - \cosh \mu kD\left( {u(x) + (\tanh \mu kD)\frac{\mu k\eta (x)}{{j + 1}}} \right)\eta (x)^{j} + w(x)b(x)^{j} } \right] \, (j:{\text{even}}), \hfill \\ \end{gathered} \right. $$

(2.5d)

$$ \hat{n}_{j} (k) = \left\{ \begin{gathered} {\mathbb{F}}\left[ {\frac{{ - u^{2} + \mu^{2} \eta_{x}^{2} }}{2}\left( { - \mu^{2} \eta_{x}^{2} } \right)^{{\frac{j - 1}{2}}} } \right]\quad (j:{\text{odd}}), \hfill \\ {\mathbb{F}}\left[ { - u(x)\left( { - \mu^{2} \eta_{x}^{2} } \right)^{\frac{j}{2}} } \right] \, (j:{\text{even}}), \hfill \\ \end{gathered} \right. $$

(2.5e)

are nonlinear terms. It should be noted that $\overline{m}_{j}$ in (2.5d) represents $\hat{m}_{j}$ as defined in (2.5c) but with $j:{\text{odd}}$ and $j:{\text{even}}$ interchanged. Furthermore, ${\mathbb{F}}\left[ {\; \cdot \;} \right]$ denotes the Fourier transform (2.4) of the quantity in the square brackets.

Importantly, Eqs. (2.5) suggest the presence of simple-pole singularities in $\left( {\hat{u},\hat{w},\hat{\eta }} \right)$ at $k = \pm \kappa_{0} /\mu$, where $\kappa_{0}$ is determined from

$$ \frac{{\tanh \kappa_{0} D}}{{\kappa_{0} }} = 1 $$

(2.6)

for $D > 1$ (see Fig. 2). Upon inverting the Fourier integrals, the residues of these singularities contribute radiating waves downstream (in keeping with (2.2)), in the form

$$ u(x)\left( { = - \eta (x)} \right)\sim R\sin \left( {\frac{{\kappa_{0} }}{\mu }x + \theta } \right)\quad \left( {x \to \infty } \right). $$

(2.7)

Fig. 2

$\kappa_{0} {\text{ vs}}{. }D$ under the relation (2.6)

The goal of the ensuing analysis is to compute the wave amplitude R and the phase shift $\theta$, which generally depend on $\mu$, $D$ and the topography profile $b(x)$. It should be noted that at low Froude number ($\mu \ll 1$), the (dimensionless) response wavelength $2\pi \mu /\kappa_{0}$ is short relative to the width of the topography. Owing to this lengthscale disparity, $\left( {\hat{u}(k),\;\hat{w}(k),\;\hat{\eta }(k)} \right)$ at the response wavenumber $k = \pm \kappa_{0} /\mu$ are expected to be exponentially small with respect to $\mu$. This suggests that the response amplitude R is exponentially small as well, which necessitates the use of exponential asymptotics in order to capture it.

The following sections are devoted to an exponential asymptotics procedure in the wavenumber domain for computing $R$ and $\theta$ in the weakly nonlinear ($\varepsilon \ll 1$) and low Froude number ($\mu \ll 1$) regime for $D = O(1) > 1$. We also assume that the topography profile $b(x)$ is smooth and even in $x$. Furthermore, $\hat{b}(k)$ decays exponentially for large $k$ like

$$ \hat{b}(k)\sim A\left| k \right|^{\alpha } \exp \left( { - \beta \left| k \right|} \right)\quad \left( {\left| k \right| \to \infty } \right), $$

(2.8)

where $A$, $\alpha$ and $\beta \;( > 0)$ are real constants. As in the fKdV model [10], the details of the analysis differ depending on the value of α.

3 Scalings

Based on Eqs. (2.5), straightforward expansions of $\left( {\hat{u},\hat{w},\hat{\eta }} \right)$ in powers of $\varepsilon$ and $\mu$ (with $D = O(1) > 1$) yield

$$ \left\{ \begin{gathered} \hat{u}(k) = \frac{1}{D - 1}\left\{ {1 + \frac{{D^{3} }}{3(D - 1)}\mu^{2} k^{2} + \cdots } \right\}\hat{b}(k) + \frac{2D + 1}{{2(D - 1)^{3} }}\varepsilon \int_{ - \infty }^{\infty } {\hat{b}(l)\hat{b}(k - l){\text{d}}l} + \cdots , \hfill \\ \hat{w}(k) = \hat{u}(k) + \cdots ,\quad \quad \hat{\eta }(k) = - \hat{u}(k) + \cdots . \hfill \\ \end{gathered} \right. $$

(3.1)

Furthermore, making use of (2.8), the asymptotic behavior as $\left| k \right| \to \infty$ of the convolution integral above is found to be (see Appendix B in [11])

$$ \int_{ - \infty }^{\infty } {\hat{b}(l)\hat{b}(k - l){\text{d}}l} = \left\{ \begin{gathered} O\left( {\left| k \right|^{2\alpha + 1} \exp ( - \beta \left| k \right|)} \right)\quad \left( {\alpha > - 1} \right), \hfill \\ O\left( {\left| k \right|^{\alpha } \exp ( - \beta \left| k \right|)} \right)\quad \left( {\alpha < - 1} \right). \hfill \\ \end{gathered} \right. $$

(3.2)

Thus, for $\varepsilon \ll 1$ nonlinear terms can contribute to the disordering for $\left| k \right| \ll 1$ of expansions (3.1), only if

$$ \alpha > - 1. $$

(3.3)

Assuming this condition is satisfied and making use of (2.8) and (3.2), expansions (3.1) take the following form for $\left| k \right| \gg 1$

$$ \left\{ \begin{gathered} \hat{u}(k) = \frac{{A\left| k \right|^{\alpha } }}{D - 1}\left\{ {1 + O\left( {\mu^{2} k^{2} } \right) + O\left( {\varepsilon \left| k \right|^{\alpha + 1} } \right) + \cdots } \right\}\exp \left( { - \beta \left| k \right|} \right), \hfill \\ \hat{w}(k) = \hat{u}(k) + \cdots ,\quad \quad \hat{\eta }(k) = - \hat{u}(k) + \cdots . \hfill \\ \end{gathered} \right. $$

(3.4)

Based on (3.4), nonlinear terms are expected to come into play for k near the poles of $\left( {\hat{u},\hat{w},\hat{\eta }} \right)$ at $k = \pm \kappa_{0} /\mu$, if $\varepsilon = O(\mu^{\alpha + 1} )$. Accordingly, we set

$$ \varepsilon = \mu^{\alpha + 1} , $$

(3.5)

and $A\left( { = O(1)} \right)$ defined by (2.8) will serve as the forcing amplitude parameter in (2.5). Under these scalings, we now focus on computing the residues of the poles at $k = \pm \kappa_{0} /\mu$ which determine R and $\theta$ in the wave response (2.7).

4 Two-Scale Asymptotics in the Wavenumber Domain

4.1 Uniformly Valid Approximation of $(\widehat{u},\widehat{w},\widehat{\eta })$

The disordering of expansions (3.1) for $\left| k \right| \gg 1$ noted above suggests a uniformly valid approximation of $\left( {\hat{u},\hat{w},\hat{\eta }} \right)$ that combines: (i) the straightforward perturbation expansions (3.1), valid for $0 \le \left| k \right| \ll 1$, with (ii) the two-scale expansions

$$ \left( {\hat{u},\hat{w},\hat{\eta }} \right) = A\left( {U(\kappa ),W(\kappa ),{\rm H}(\kappa )} \right)\frac{{{\text{e}}^{ - \beta \left| k \right|} }}{{\mu^{\alpha } }} + \cdots , $$

(4.1)

valid for $\kappa = \mu k = O(1)$. In view of (3.4), we require that the amplitude functions $\left( {U,W,{\rm H}} \right)$ satisfy

$$ U(\kappa ) = W(\kappa ) = - {\rm H}(\kappa )\sim \frac{{A\left| \kappa \right|^{\alpha } }}{D - 1}\quad \left( {\kappa \to 0} \right). $$

(4.2)

Thus, taking $\delta$ to be a constant such that $\mu \ll \delta \ll 1$, expansions (i) and (ii) match for k in the intermediate range

$$ 1 \ll \left| k \right| = O(1/\delta ) \ll 1/\mu . $$

(4.3)

4.2 Integral Equations for $(U,W,\mathrm{\rm H})$

We now derive approximate governing equations for $\left( {U(\kappa ),W(\kappa ),{\rm H}(\kappa )} \right)$, $0 < \kappa = O(1)$. Following [10], the Fourier transforms of quadratic nonlinear terms in (2.5a) are evaluated as

$$ \begin{aligned} \varepsilon {\mathbb{F}}\left[ {u^{2} } \right] & \equiv \mu^{\alpha + 1} \int_{ - \infty }^{\infty } {\hat{u}(k - l)\hat{u}(l){\text{d}}l} \\ &\sim \frac{{{\text{e}}^{ - \beta k} }}{{\mu^{\alpha } }}\left\{ {A^{2} U_{2} (\kappa ) + 2\mu^{\alpha + 1} A\int_{ - \infty }^{1/\delta } {U(\kappa - \mu l)\hat{u}(l){\text{e}}^{\beta l} {\text{d}}l} } \right\}, \\ \end{aligned} $$

(4.4a)

where (3.5) and (4.1) have been used and

$$ U_{2} (\kappa ) = \int_{\mu /\delta }^{\kappa - \mu /\delta } {U(\kappa - \lambda )U(\lambda ){\text{d}}\lambda } . $$

(4.4b)

Formally the term including $U_{2} (\kappa )$ in (4.4a) dominates; however, for $- 1 < \alpha \le 0$, the second term also comes into play when $\kappa = \kappa_{0} + O(\mu )$ because $U(\kappa - \mu l)$ becomes $O(\mu^{ - 1} )$ or larger and then affects the pole residues. Similarly, for the j-th order ($j \ge 3$) nonlinear terms, we find

$$ \varepsilon^{j - 1} {\mathbb{F}}\left[ {u^{j} } \right]\sim \frac{{{\text{e}}^{ - \beta k} }}{{\mu^{\alpha } }}\left\{ {A^{j} U_{j} (\kappa ) + O\left( {\mu^{\alpha + 1} ,\mu^{(\alpha + 1)(j - 1)} U(\kappa )} \right)} \right\}\,\,(j \ge 3), $$

(4.4c)

where

$$ U_{j} (\kappa ) = \int_{(j - 1)\mu /\delta }^{\kappa - \mu /\delta } {U(\kappa - \lambda )U_{j - 1} (\lambda ){\text{d}}\lambda } \,\,(j \ge 3). $$

(4.4d)

Here, the error term $O( \cdots )$, which originates from dropping terms analogous to the second term in (4.4a), is not shown explicitly because it remains subdominant to (4.4a) even close to the pole singularities.

Making use of (2.8), (4.1) and (4.4) as well as expansions (3.1) valid for $k = O(1)$, it follows from (2.5) that $\left( {U(\kappa ),W(\kappa ),{\rm H}(\kappa )} \right)$ for $\kappa > 0$ are governed by the following approximate equations:

$$ \left\{ \begin{gathered} \left( {\frac{\tanh \kappa D}{\kappa } - 1} \right)U + \sum\limits_{j = 1}^{\infty } {A^{j} \left( { - {\text{M}}_{j} + {\text{N}}_{j} } \right)} - \mu^{\alpha + 1} S = \sum\limits_{j = 0}^{\infty } {A^{2j} F_{2j + 1} } , \hfill \\ U + \kappa (\tanh \kappa D){\rm H} - \frac{W}{\cosh \kappa D} = \kappa \left\{ {\sum\limits_{j = 1}^{\infty } {A^{2j - 1} F_{2j} } + \sum\limits_{j = 1}^{\infty } {A^{j} {\overline{\text{M}}}_{j} } } \right\}, \hfill \\ {\rm H} + U = \sum\limits_{j = 1}^{\infty } {A^{j} {\text{N}}_{j} } , \hfill \\ \end{gathered} \right. $$

(4.5a)

where

$$ S(\kappa ) = \left\{ \begin{gathered} \frac{{2 + D(1 - \kappa_{0}^{2} )}}{D - 1}\int_{ - \infty }^{1/\delta } {\hat{b}(l)U(\kappa - \mu l){\text{e}}^{\beta l} {\text{d}}l} \quad \left( {\kappa = \kappa_{0} + O(\mu )} \right), \hfill \\ O(1)\quad \quad ({\text{otherwise}}). \hfill \\ \end{gathered} \right. $$

(4.5b)

The formally subdominant term $\mu^{\alpha + 1} S$ is included in (4.5a) because it can be important close to the singularities as detailed below (Sect. 4.3). Specific expressions for the forcing term $F_{j}$ and the nonlinear terms ${\text{M}}_{j}$, ${\text{N}}_{j}$ and ${\overline{\text{M}}}_{j}$ are given in Appendix A.

4.3 Overview of Exponential Asymptotics

Equations (4.5) form the basis of the ensuing analysis. Although these are simultaneous equations for $(U,W,{\rm H})$, the first of Eqs. (4.5a) is similar to the (single) integral equation for $U(\kappa )$ derived in our earlier analysis of the fKdV equation [10] (see their (3.7)): the first term is linear, the second term comprises nonlinear convolution integrals, the third term is the formally subdominant integral that becomes important (when $- 1 < \alpha \le 0$) close to the singularities at $\kappa = \kappa_{0}$ given by (2.6), and the right-hand-side term is the forcing term. Accordingly, the basic results of our study of the fKdV equation apply here as well.

Specifically, based on the leading-order (outer) approximation to (4.5a) where the $O\left( {\mu^{\alpha + 1} } \right)$ integral is dropped, $(U,W,{\rm H})$ feature a singularity at $\kappa = \kappa_{0}$ given by (2.6). However, the extent to which this singularity differs from the simple pole predicted by linear theory hinges on the value of $\alpha$: (i) when $\alpha > 0$, $(U,W,{\rm H})$ still have a simple pole at $\kappa = \kappa_{0}$ but its residue is influenced by nonlinear terms via the forcing amplitude A (and the depth parameter D); (ii) for $\alpha = 0$, the singularity at $\kappa = \kappa_{0}$ becomes algebraic with power depending on A (as well as D); (iii) for $- 1 < \alpha < 0$, the situation is even more complicated as there is a singularity of exponential type at $\kappa = \kappa_{0}$ if $A > 0$, but otherwise there is no singularity at all. For simplicity, here $\alpha$ will be restricted to $\alpha \ge 0$ so only (i) and (ii) arise.

It should be noted that, in the case $\alpha = 0$, the algebraic singularity of $(U,W,{\rm H})$ at $\kappa = \kappa_{0}$ predicted by the outer approximation needs to be reconsidered because the term $\mu S$ in (4.5a), which is dropped in the outer analysis, becomes important as $\kappa \to \kappa_{0}$. This necessitates an ‘inner’ analysis when $\kappa = \kappa_{0} + O(\mu )$, which reveals that $(U,W,{\rm H})$ actually feature a simple pole at $\kappa = \kappa_{0}$. Matching the inner solution with the outer solution for $\kappa_{0} - \kappa \gg O(\mu )$ then determines the residue of this pole. Here, nonlinear terms affect the order of magnitude of the pole residue and thereby modify the generated wave amplitude (and phase shift) in a more serious way than in the case $\alpha > 0$.

Below (Sect. 5) we sketch the procedure of determining the pole residues for $\alpha > 0$ and $\alpha = 0$ and compute the radiating waves in the form (2.7). Finally, Sect. 6 shows a comparison of asymptotic against exact numerical results for the topography profile $b(x) = A{\text{sech}} x$ which corresponds to the case $\alpha = 0$.

5 Pole Residues and Radiating Waves

To leading order in $\mu$ and $\mu /\delta$, Eqs. (4.5a) reduce to

$$ \left\{ \begin{gathered} \left( {\frac{\tanh \kappa D}{\kappa } - 1} \right)U + \sum\limits_{j = 1}^{\infty } {A^{j} \left( { - {\text{M}}_{j} {\text{ + N}}_{j} } \right)} = \sum\limits_{j = 0}^{\infty } {A^{2j} F_{2j + 1} } , \hfill \\ U + \kappa (\tanh \kappa D){\rm H} - \frac{W}{\cosh \kappa D} = \kappa \left\{ {\sum\limits_{j = 1}^{\infty } {A^{2j - 1} F_{2j} } + \sum\limits_{j = 1}^{\infty } {A^{j} {\overline{\text{M}}}_{j} } } \right\}, \hfill \\ {\rm H} + U = \sum\limits_{j = 1}^{\infty } {A^{j} {\text{N}}_{j} } , \hfill \\ \end{gathered} \right. $$

(5.1)

where $F_{j}$ is given by (A.1) and ${\text{M}}_{j} ,\;{\text{N}}_{j} ,\;{\overline{\text{M}}}_{j}$ are the nonlinear integral terms given by (A.2)–(A.7) with integration ranges simplified to $0 < \lambda < \kappa$. The integral equations (5.1), referred to as the ‘outer equations’, are to be solved subject to conditions (4.2).

5.1 The Case α > 0

Under the condition $\alpha > 0$, the integral terms in (5.1) are subdominant as $\kappa \to \kappa_{0}$, and $(U,W,{\rm H})$ feature a simple pole at $\kappa = \kappa_{0}$ irrespective of A. Specifically,

$$ \left( {U(\kappa ),W(\kappa ),{\rm H}(\kappa )} \right)\sim \frac{C}{{\kappa_{0} - \kappa }}\left( {1,\;\;(1 - \kappa_{0}^{2} )\cosh \kappa_{0} D,\;\; - 1} \right)\quad \left( {\kappa \to \kappa_{0} } \right), $$

(5.2)

where $C$ is a (real) constant. Thus, using (4.1) we can express $\hat{u}(k)$ close to the simple pole $k \to \kappa_{0} /\mu$ as

$$ \hat{u}(k)\sim \frac{ - AC}{{\mu^{\alpha + 1} (k - \kappa_{0} /\mu )}}{\text{e}}^{ - \beta k} \quad \left( {k \to \frac{{\kappa_{0} }}{\mu }} \right). $$

(5.3)

Nonlinear effects are encapsulated in the value of the constant $C$, which depends on $A$, $D$ and $\alpha$.

Then, inverting the Fourier transform,

$$ u(x) = \int_{\Omega }^{{}} {\hat{u}(k){\text{e}}^{{{\text{i}}kx}} {\text{d}}k} , $$

(5.4)

where the integration path $\Omega$ extends along the real k-axis but passes below $k = \pm \kappa_{0} /\mu$ so as to observe the radiation condition (2.2), the residues in (5.3) contribute a radiating wave downstream in the form (2.7) with

$$ R = \frac{4\pi AC}{{\mu^{\alpha + 1} }}{\text{e}}^{{ - \,\frac{{\beta {\kern 1pt} \kappa_{0} }}{\mu }}} ,\quad \theta = 0. $$

(5.5)

Thus, nonlinear terms influence the wave amplitude R but not the phase shift $\theta$, and the only difference of the nonlinear from the linear wave response

$$ R_{{{\text{lin}}}} = \frac{{4\pi AC_{{{\text{lin}}}} }}{{\mu^{\alpha + 1} }}{\text{e}}^{{ - \,\frac{{\beta {\kern 1pt} \kappa_{0} }}{\mu }}} ,\quad \theta_{{{\text{lin}}}} = 0, $$

(5.6a)

with

$$ C_{{{\text{lin}}}}= \frac{{\kappa_{0}^{\alpha } }}{{\frac{{\cosh \kappa_{0} D}}{{\kappa_{0} }} - \frac{D}{{\sinh \kappa_{0} D}}}}, $$

(5.6b)

is the value of $C$, which depends on A as well as D and $\alpha$.

The constant $C$ in (5.5) can be computed numerically by integrating (5.1) as an initial-value problem, using (4.2) as initial condition and marching towards the simple pole of $(U,W,{\rm H})$ at $\kappa = \kappa_{0}$ according to (5.2). Figure 3 plots $\left| {R/R_{{{\text{lin}}}} } \right| = \left| {C/C_{{{\text{lin}}}} } \right|$, the ratio of the nonlinear to the linear response amplitude, as a function of $- \,4 \le A \le 4$ for $\alpha =$ 1 and 2 (at $D = 2$). Nonlinearity becomes more important as $\alpha$ is decreased, and the validity of linear theory is rather limited when $\alpha \lesssim 1$. Furthermore, in this range of $\alpha$, the polarity of the forcing is a significant factor, as the nonlinear response amplitude is greatly enhanced (reduced) for $A > 0\;\;\left( {A < 0} \right)$.

Fig. 3

Ratio of nonlinear to linear wave amplitude as a function of the forcing amplitude A for $\alpha =$ 1 (solid line) and 2 (dashed line) at $D = 2$

5.2 The Case α = 0

For $\alpha = 0$, the nonlinear integral terms ${\text{M}}_{j}$ and ${\text{N}}_{j}$ in (5.1) partake in the dominant balance as $\kappa \to \kappa_{0}$ and the singularity takes of the form

$$ \left( {U(\kappa ),W(\kappa ),{\rm H}(\kappa )} \right)\sim \frac{{C_{0} }}{{(\kappa_{0} - \kappa )^{\gamma } }}\left( {1,\;\;(1 - \kappa_{0}^{2} )\cosh \kappa_{0} D,\;\; - 1} \right)\quad \left( {\kappa \to \kappa_{0} } \right), $$

(5.7)

where $C_{0}$ is a constant. By substituting (5.7) in (5.1), we then find

$$ \gamma = 1 + \overline{A}, $$

(5.8)

where

$$ \overline{A} = A\frac{{2 + (1 - \kappa_{0}^{2} )D}}{{(D - 1)\left( {\frac{1}{{\kappa_{0} }} - \frac{D}{{\sinh \kappa_{0} D\cosh \kappa_{0} D}}} \right)}} $$

(5.9)

(see Fig. 4). Thus, the singularity at $\kappa = \kappa_{0}$ of the outer solution no longer is a simple pole.

Fig. 4

$\overline{A}/A$ as a function of D given by (5.9)

It should be noted that the asymptotic behavior (5.7) is valid only if $\gamma > 1$, i.e. $\overline{A} > 0$. For $\overline{A} \le 0$, the singularity of $(U,W,{\rm H})$ at $\kappa = \kappa_{0}$ is determined by further differentiating (5.1). Briefly, suppose $- n < \overline{A} \le - n + 1$, where $n \ge 1$ is integer. After differentiating (5.1) n times with respect to $\kappa$, dominant balance as $\kappa \to \kappa_{0}$ reveals that the appropriate singular behavior is

$$ \left( {U^{(n)} (\kappa ),W^{(n)} (\kappa ),{\rm H}^{(n)} (\kappa )} \right)\sim \frac{{C_{n} }}{{(\kappa_{0} - \kappa )^{{{n + 1 + \overline{A}{}} }} }}\left( {1,\;\;(1 - \kappa_{0}^{2} )\cosh \kappa_{0} D,\;\; - 1} \right)\quad \left( {\kappa \to \kappa_{0} } \right), $$

(5.10)

where $C_{n}$ is a constant. The constants $C_{n} \;(n \ge 0)$ can be computed numerically from (5.1).

As remarked earlier, in this instance the term $\mu S$ in (4.5) comes into play when $\kappa - \kappa_{0} = O(\mu )$ and the singularity at $\kappa = \kappa_{0}$ ends up being a simple pole. To compute the pole residue for $\overline{A} > 0$, we introduce the inner variables:

$$ \tilde{\kappa } = \frac{{\kappa_{0} - \kappa }}{\mu },\,\left( {U(\kappa ),W(\kappa ),{\rm H}(\kappa )} \right) = \frac{{\left( {\tilde{U}(\tilde{\kappa }),\tilde{W}(\tilde{\kappa }),\tilde{\rm H}(\tilde{\kappa })} \right)}}{{\mu^{{{1 + \overline{A}{}} }} }}, $$

(5.11)

in (4.5). Then, this leads to a single equation for $\tilde{U}(\tilde{\kappa })$:

$$ \tilde{\kappa }\,\tilde{U}(\tilde{\kappa }) = \int_{ - \infty }^{\infty } {\hat{f}(l)\tilde{U}(\tilde{\kappa } - l){\text{e}}^{ - \beta l} {\text{d}}l} , $$

(5.12a)

where

$$ \hat{f}(l) \equiv \frac{{\overline{A}}}{A}\hat{b}(l), $$

(5.12b)

and $\hat{b}( - l) = \hat{b}(l)$ is used because $b(x)$ was assumed to be even in x. Taking derivative of (5.12a) with respect to $\tilde{\kappa }$ leads to the same inner equation as that for the fKdV equation [10] (see their (6.3)). Thus, the rest of the inner analysis is the same as in [10] (except for $A \to \overline{A}$). Here we only quote the final results of the radiating wave solution, which takes the form (2.7) with

$$ R = \frac{{4\pi AC_{n} {\text{e}}^{{ - J_{r} }} }}{{\Gamma (n + 1 + \overline{A})}}\frac{{{\text{e}}^{{ - \;\frac{\beta }{\mu }\kappa_{0} }} }}{{\mu^{{{1 + \overline{A}{}} }} }},\quad \theta = - \frac{{\pi \overline{A}}}{2} - J_{i} , $$

(5.13)

where $\Gamma$ is the gamma function and $J = J_{r} + {\text{i}}J_{i}$ is defined by

$$ J = \int_{0}^{1} {\left[ {{\text{i}}f(s - {\text{i}}\beta ) + \frac{{\overline{A}}}{s}} \right]{\text{d}}s} + \int_{1}^{\infty } {{\text{i}}f(s - {\text{i}}\beta ){\text{d}}s} , $$

(5.14)

with $f(x) = \left( {\overline{A} /A} \right)b(x)$ being the inverse Fourier transform of $\hat{f}(l)$ in (5.12b). The integer $n \ge 0$ in (5.13) is specified by the modified forcing amplitude $\overline{A}$: $n = 0$ for $\overline{A} > 0$ and $n \ge 1$ for $- n < \overline{A} \le - n + 1$.

6 Wave Response for $b\left(x\right)=A{\text{sech}}x$

In order to assess the validity of the asymptotic theory, we made comparisons of the theoretical predictions with direct numerical computations of wave responses based on the full water wave equations, under various flow conditions. For these computations we used the numerical method of Belward and Forbes [3] for two-layer flow over topography (setting the upper-layer density to zero in their formulation). Overall, we find that the asymptotic results for the amplitude R and phase shift $\theta$ of the wave response (2.7) are in good agreement with numerical computations for a broad range of flow conditions, beyond the formal range of validity $\varepsilon ,\;F^{2} \ll 1$ assumed in the exponential asymptotics. Here, in the interest of brevity, we present detailed results only for the topography profile $b(x) = A{\text{sech}} x$ (where $J$ defined by (5.14) is $- \overline{A}\ln 2$). This topography adheres to the assumed asymptotic behavior (2.8) with $\alpha = 0$, $\beta = \pi /2$ and expressions (5.13) are the appropriate asymptotic results for R and $\theta$.

Figure 5 shows a comparison of the asymptotic with the numerical downstream wave profile for $F = 0.45$ ($\varepsilon = \mu = 0.2$) and four forcing amplitudes, $\varepsilon A = - 0.08,\,- 0.04$, 0.04 and 0.08. In addition, the corresponding linear solution based on (5.6) is plotted for reference. For this moderate value of F, the nonlinear asymptotic results show quite nice agreement with the numerical results for all four topography amplitudes, unlike the linear response which grossly underpredicts (overpredicts) the wave amplitudes for $A > 0$ ($A < 0$). Specifically, the linear response underpredicts the wave amplitude by a factor of 5 for $\varepsilon A =$ 0.04 and 20 for $\varepsilon A =$ 0.08,

Fig. 5

Downstream wave profiles $\varepsilon \eta (x)$ as a function of $x$ in free-surface flow over the topography $b(x) = A{\text{sech}} x$ for $F = 0.45$ $(\mu = \varepsilon = 0.2)$ and $D = 2$ with topography amplitude $\varepsilon A = - 0.08,\,- 0.04,$ 0.04 and 0.08 (from top). (Red line): asymptotic theory; (——): exact numerical solution; (-----): prediction of linear theory

while it overpredicts the wave amplitude by a factor of 8 for $\varepsilon A = - 0.04$ and 40 for $\varepsilon A = - 0.08$. In regard to the phase shift $\theta$, Fig. 5 indicates that the asymptotic theory captures the overall trend of the dependence of $\theta$ on the forcing amplitude (cf. (5.13)), in contrast to the linear result $\theta_{{{\text{lin}}}} = 0$ (cf. (5.6a)).

Figure 6 summarizes the asymptotic results in a linear and a semi-log plot of the wave amplitude $\varepsilon \left| R \right|$ vs. topography amplitude $\varepsilon A$. It is worth noting that the linear solution is reliable only for exceedingly small topography amplitudes ($\left| {\varepsilon A} \right| < 0.01$). This is in contrast to the broad validity of the asymptotic nonlinear theory which captures also the steep increase of the wave response when $\varepsilon A \ge 0.08$; in this nonlinear regime the (formally exponentially small) wave amplitude $\varepsilon \left| R \right|$ is comparable to the topography peak amplitude ($\varepsilon A\sim 0.1$). Such a broad applicability of nonlinear exponential asymptotics also was noted in free-surface flow over a step [5]. Furthermore, Fig. 6 reveals that the sign of the topography is an important factor in the nonlinear wave response: a bottom bump ($A > 0$) generally gives rise to much larger waves than a bottom trench ($A < 0$), whereas according to linear theory $A \to - A$ simply changes the sign of the response.

Fig. 6

Downstream wave amplitude $\varepsilon \left| R \right|$ as a function of topography amplitude $\varepsilon A$ in free-surface flow over the topography $b(x) = A{\text{sech}} x$ for $F = 0.45$ and $D = 2$. The right figure is the corresponding semi-log plot. (Red line): asymptotic theory; (○): exact numerical solution; (------): prediction of linear theory

7 Concluding Remarks

Motivated by our earlier study of the fKdV equation [10], we presented an asymptotic treatment of steady surface gravity waves due to a uniform stream over smooth localized topography in the weakly nonlinear ($\varepsilon \ll 1$) low-Froude-number ($F \ll 1$) limit. In this flow regime, the wave response has exponentially small amplitude with respect to F. Moreover, as $F \to 0$ linearization is not appropriate for small but finite topography amplitude ($\varepsilon \ll 1$). Our exponential-asymptotics analysis in the joint limit $\varepsilon,\,F \ll 1$ confirms that the generated waves downstream are governed by a fully nonlinear mechanism which depends on the shape of the topography profile, specifically the parameter $\alpha$ in (2.8), as well as the sign of the topography (bump vs. trench). Comparisons of the asymptotic results with direct numerical computations suggest that this mechanism is valid for a broad range of flow conditions, even when the (formally exponentially small) downstream wave amplitude becomes comparable to the topography peak amplitude. This is in sharp contrast to linear theory which has very limited validity.

The present analysis is based on an exponential-asymptotics methodology that focuses on the residues of the poles of the response Fourier transform on the real axis in the wavenumber domain. These residues determine the wave amplitude upon inverting the Fourier transform. An advantage of this wavenumber approach is that it can be readily extended to two-dimensional (2D) wave patterns, as illustrated by our recent treatment of a 2D model equation [11]. We are currently exploring the possibility of applying this methodology to 2D steady water waves in 3D flow, including the Kelvin surface-wave problem.

Appendix A Expressions for the Forcing and Nonlinear Terms in (4.5a)

Here we give specific expressions of the forcing term $F_{j}$ and nonlinear terms ${\text{M}}_{j}$, ${\text{N}}_{j}$ and ${\overline{\text{M}}}_{j}$ in (4.5a). The forcing term $F_{j}$ is

$$ F_{j} (\kappa ) = \frac{{\kappa^{j - 1} B_{j} (\kappa )}}{j!\cosh \kappa D}. $$

(A.1)

The nonlinear terms ${\text{M}}_{j}$ and ${\text{N}}_{j}$ are

$$ {\text{M}}_{j} (\kappa ) = \left\{ \begin{gathered} \frac{{\kappa^{j - 1} }}{j!}\left\{ { - \int_{j\mu /\delta }^{\kappa - \mu /\delta } {\left[ {U(\kappa - \lambda ) + \frac{\kappa \tanh \kappa D}{{j + 1}}{\rm H}(\kappa - \lambda )} \right]{\rm H}_{j} (\lambda ){\text{d}}\lambda } } \right. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \left. { + \frac{1}{\cosh \kappa D}\int_{j\mu /\delta }^{\kappa - \mu /\delta } {W(\kappa - \lambda )B_{j} (\lambda ){\text{d}}\lambda } } \right\} \, (j:{\text{odd}}), \hfill \\ - \frac{{\kappa^{j - 1} }}{j!}\int_{j\mu /\delta }^{\kappa - \mu /\delta } {\left[ {(\tanh \kappa D)U(\kappa - \lambda ) + \frac{\kappa }{j + 1}{\rm H}(\kappa - \lambda )} \right]{\rm H}_{j} (\lambda ){\text{d}}\lambda } \, (j:{\text{even}}), \hfill \\ \end{gathered} \right. $$

(A.2)

$$ {\text{N}}_{j} (\kappa ) = \left\{ \begin{gathered} - \frac{1}{2}\int_{j\mu /\delta }^{\kappa - \mu /\delta } {\left[ {U(\kappa - \lambda )Q_{j} (\lambda ) + (\kappa - \lambda ){\rm H}(\kappa - \lambda )P_{j} (\lambda )} \right]{\text{d}}\lambda } \quad (j:{\text{odd}}), \hfill \\ - \int_{j\mu /\delta }^{\kappa - \mu /\delta } {U(\kappa - \lambda )P_{j} (\lambda ){\text{d}}\lambda } \quad (j:{\text{even}}), \hfill \\ \end{gathered} \right. $$

(A.3)

and ${\overline{\text{M}}}_{j}$ is given by ${\text{M}}_{j}$ as defined in (A.2) but with $j:{\text{odd}}$ and $j:{\text{even}}$ interchanged. Here,

$$ {\rm H}_{j} (\kappa ) = \left\{ \begin{gathered} {\rm H}(\kappa )\quad (j = 1), \hfill \\ \int_{(j - 1)\mu /\delta }^{\kappa - \mu /\delta } {{\rm H}(\kappa - \lambda ){\rm H}_{j - 1} (\lambda ){\text{d}}\lambda } \quad (j \ge 2), \hfill \\ \end{gathered} \right. $$

(A.4)

$$ B_{j} (\kappa ) = \left\{ \begin{gathered} \kappa^{\alpha } \quad (j = 1), \hfill \\ \frac{{\Gamma (\alpha + 1)^{j} \kappa^{(\alpha + 1)j - 1} }}{{\Gamma \left( {(\alpha + 1)j} \right)}}\;\;(j \ge 2), \hfill \\ \end{gathered} \right. $$

(A.5)

$$ P_{j} (\kappa ) = \left\{ \begin{gathered} \kappa {\rm H}(\kappa )\quad (j = 1), \hfill \\ \int_{(j - 1)\mu /\delta }^{\kappa - \mu /\delta } {(\kappa - \lambda ){\rm H}(\kappa - \lambda )P_{j - 1} (\lambda ){\text{d}}\lambda } \;\;(j \ge 2), \hfill \\ \end{gathered} \right. $$

(A.6)

$$ Q_{j} (\kappa ) = \left\{ \begin{gathered} U(\kappa )\quad (j = 1), \hfill \\ \int_{(j - 1)\mu /\delta }^{\kappa - \mu /\delta } {U(\kappa - \lambda )P_{j - 1} (\lambda ){\text{d}}\lambda \;\;(j \ge 2).} \hfill \\ \end{gathered} \right. $$

(A.7)