Abstract
In the applied mathematics literature solitary gravity–capillary water waves are modelled by approximating the standard governing equations for water waves by a Korteweg-de Vries equation (for strong surface tension) or a nonlinear Schrödinger equation (for weak surface tension). These formal arguments have been justified by sophisticated techniques such as spatial dynamics and centre-manifold reduction methods on the one hand and variational methods on the other. This article presents a complete, self-contained account of an alternative, simpler approach in which one works directly with the Zakharov–Craig–Sulem formulation of the water-wave problem and uses only rudimentary fixed-point arguments and Fourier analysis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 The Main Results
The classical water-wave problem concerns the two-dimensional, irrotational flow of a perfect fluid of unit density subject to the forces of gravity and surface tension. We use dimensionless variables, choosing h as length scale, \((h/g)^\frac{1}{2}\) as time scale and introducing the Bond number \(\beta =\sigma /gh^2\), where h is the depth of the water in its undisturbed state, g is the acceleration due to gravity and \(\sigma >0\) is the coefficient of surface tension. The fluid thus occupies the domain \(D_\eta = \{(x,y): x \in {{\mathbb {R}}}, y \in (0,1+\eta (x,t))\}\), where (x, y) are the usual Cartesian coordinates and \(\eta >-1\) is a function of the spatial coordinate x and time t, and the mathematical problem is formulated in terms of an Eulerian velocity potential \(\varphi (x,y,t)\) which solves Laplace’s equation
and the boundary conditions
Travelling waves are solutions of (1.1)–(1.4) of the form \(\eta (x,t)=\eta (x-ct)\), \(\varphi (x,y,t)=\varphi (x-ct,y)\), while solitary waves are non-trivial travelling waves which satisfy the asymptotic conditions \(\eta (x-ct) \rightarrow 0\) as \(|x-ct| \rightarrow \infty \); they correspond to localised disturbances of permanent form which move from left to right with constant speed c.
It is instructive to review the formal weakly nonlinear theory for travelling waves. We begin with the linear dispersion relation for a two-dimensional periodic travelling wave train of wave number \(k\ge 0\) and speed \(c>0\), namely
(see Fig. 1). The function \(k \mapsto c(k)\) has a unique global minimum at \(k=\omega \), and one finds that \(\omega =0\) (with \(c(0)=1\)) for \(\beta >\frac{1}{3}\) and \(\omega >0\) for \(\beta <\frac{1}{3}\). We denote the minimum value of c by \(c_0\), so that \(c_0^2=1\) for \(\beta >\frac{1}{3}\) and \(c_0^2=2\omega /(2\omega f(\omega )-\omega ^2f^\prime (\omega ))\) for \(\beta <\frac{1}{3}\) (the formula \(\beta =f^\prime (\omega )/(2\omega f(\omega )-\omega ^2f^\prime (\omega ))\) defines a bijection between the values of \(\beta \in (0,\frac{1}{3})\) and \(\omega \in (0,\infty )\)). Using c as a bifurcation parameter, we expect branches of small-amplitude solitary waves to bifurcate at \(c=c_0\) (where the linear group and phase speeds are equal) into the region \(\{c<c_0\}\) where linear periodic wave trains are not supported (see Dias and Kharif [8, Sect. 3]).
In the case \(\beta >\frac{1}{3}\) (‘strong surface tension’), one writes \(c^2=1-\varepsilon ^2\), where \(\varepsilon \) is a small positive number, substitutes the Ansatz
where \(X=\varepsilon x\), into the travelling-wave version of Eqs. (1.1)–(1.4), and finds that \(\rho _1\) satisfies the stationary Korteweg-de Vries equation
this equation admits an explicit solitary wave of depression given by the formula
(see Benjamin [3]). In the case \(\beta <\frac{1}{3}\) (‘weak surface tension’), one writes \(c^2 =c_0^2(1-\varepsilon ^2)\), uses the Ansatz
and finds that \(\zeta _1\) satisfies the stationary nonlinear Schrödinger equation
where
and
with
and
(see Ablowitz and Segur [1]). This equation admits a family \(\{\mathrm {e}^{\mathrm {i}\theta _0} \zeta ^\star \}_{\theta _0 \in [0,2\pi )}\) of solitary-wave solutions, where
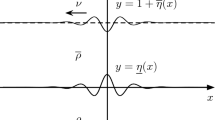
two of which, namely \(\pm \zeta ^\star \) (corresponding to \(\theta _0=0\) and \(\pi \)), are symmetric. (The positivity of \(a_3\) follows by elementary arguments after substituting the expressions for \(\beta \) and \(c_0^2\) as functions of \(\omega \).) The corresponding free-surface profiles are sketched in Fig. 2.
The results of these formal calculations have been rigorously confirmed by spatial dynamics and centre-manifold methods on the one hand (Kirchgässner [17], Amick and Kirchgässner [2], Sachs [20], Iooss and Kirchgässner [15], Iooss and Pérouème [16]) and variational techniques on the other (Buffoni [4, 5], Groves and Wahlén [11, 12]), the results of which are summarised in the following theorem.
Theorem 1.1
-
(i)
Suppose that \(\beta >\frac{1}{3}\) and \(c^2=1-\varepsilon ^2\). For each sufficiently small value of \(\varepsilon >0\) there exists a symmetric solitary-wave solution of (1.1)–(1.4) whose free surface is given by
$$\begin{aligned} \eta (x)=\varepsilon ^2 \rho ^\star (\varepsilon x) + o(\varepsilon ^2) \end{aligned}$$uniformly over \(x \in {{\mathbb {R}}}\).
-
(ii)
Suppose that \(\beta <\frac{1}{3}\) and \(c^2=c_0^2(1-\varepsilon ^2)\), where \(c_0=c(\omega )\) is the global minimum of the linear dispersion relation (see Fig. 1 (right)). For each sufficiently small value of \(\varepsilon >0\) there exist two symmetric solitary-wave solutions of (1.1)–(1.4) whose free surfaces are given by
$$\begin{aligned} \eta (x)=\pm \varepsilon \zeta ^\star (\varepsilon x)\cos \omega x + o(\varepsilon ) \end{aligned}$$uniformly over \(x \in {{\mathbb {R}}}\).
This article presents an alternative, simpler proof of Theorem 1.1 in which one works directly with the Zakharov–Craig–Sulem formulation of the travelling water-wave equations (see below) and uses only rudimentary fixed-point arguments and Fourier analysis. Some intermediate results are special cases of more general theorems available elsewhere; their proofs have been included here for the sake of a complete, self-contained exposition.
1.2 Methodology
We proceed by formulating the water-wave problem (1.1)–(1.4) in terms of the variables \(\eta \) and \(\Phi =\varphi |_{y=1+\eta }\) (see Zakharov [22] and Craig and Sulem [7]). The Zakharov–Craig–Sulem formulation of the water-wave problem is
where the velocity potential \(\varphi \) is recovered as the (unique) solution of the boundary-value problem
and the Dirichlet–Neumann operator \(G(\eta )\) is given by \(G(\eta )\Phi =\varphi _y -\eta _x\varphi _x\big |_{y=1+\eta }\). Travelling waves are solutions of the form \(\eta (x,t)=\eta (x-ct)\), \(\Phi (x,t)=\Phi (x-ct)\); they satisfy
It is possible to reduce Eqs. (1.11), (1.12) to a single equation for \(\eta \). Using (1.11), one finds that \(\Phi =-cG(\eta )^{-1}\eta _x\), and inserting this formula into (1.12) yields the equation
where
and
Note the equivalent definition
where \(\varphi \) is the solution of the boundary-value problem
(which is unique up to an additive constant).
We proceed by defining the Fourier transform \({\hat{u}}={{\mathcal {F}}}[u]\) of a function u of a real variable by the formula
and using the notation m(D) with \(D=-\mathrm {i}\partial _x\) for the Fourier multiplier-operator with symbol m, so that \(m(D)u = {{\mathcal {F}}}^{-1}[m {\hat{u}}]\). The Ansätze (1.5) and (1.9) suggest that the Fourier transform of a solitary wave is concentrated near the points \(k=\pm \omega \) (which coincide at \(k=0\) when \(\beta >\frac{1}{3}\)). Indeed, writing \(c^2=c_0^2(1-\varepsilon ^2)\), one finds that the linearisation of (1.13) at \(\varepsilon =0\) is
where
with equality precisely when \(k=\pm \omega \) (so that \(g(\omega )=g^\prime (\omega )=0\) and \(g^{\prime \prime }(\omega )>0\)). We therefore decompose \(\eta \) into the sum of functions \(\eta _1\) and \(\eta _2\) whose Fourier transforms \({\hat{\eta }}_1\) and \({\hat{\eta }}_2\) are supported in the region \(S=(-\omega -\delta ,-\omega +\delta ) \cup (\omega -\delta ,\omega +\delta )\) (with \(\delta \in (0,\frac{1}{3})\)) and its complement (see Fig. 3), so that \(\eta _1 = \chi (D)\eta \), \(\eta _2 = (1-\chi (D))\eta \), where \(\chi \) is the characteristic function of the set S. Decomposing (1.13) into
one finds that the second equation can be solved for \(\eta _2\) as a function of \(\eta _1\) for sufficiently small values of \(\varepsilon >0\); substituting \(\eta _2=\eta _2(\eta _1)\) into the first yields the reduced equation
for \(\eta _1\) (see Sect. 3).
Finally, the scaling
transforms the reduced equation into
for \(\beta >\frac{1}{3}\), while the scaling
transforms the reduced equation into
for \(\beta <\frac{1}{3}\); here \(\chi _0\) is the characteristic function of the set \((-\delta ,\delta )\), the symbol D now means \(-\mathrm {i}\partial _X\) and precise estimates for the remainder terms are given in Sect. 4. Eqs. (1.21) and (1.23) are termed full dispersion versions of (perturbed) stationary Korteweg-de Vries and nonlinear Schrödinger equations since they retain the linear part of the original equation (1.13); the fully reduced model equations (1.6) and (1.9) are recovered from them in the formal limit \(\varepsilon \rightarrow 0\).
Variational versions of this reduction procedure have previously been given by Groves and Wahlén [12]. Starting with the observation that (1.13) is the Euler–Lagrange equation for the functional
they use the decomposition \(\eta =\eta _1+\eta _2(\eta _1)\) and scaling of \(\eta _1\) described above to derive reduced variational functionals for \(\rho \) and \(\zeta \) whose Euler–Lagrange equations are given to leading order by (1.6) and (1.9). Critical points of the reduced functionals (and hence solitary-wave solutions of the reduced equations) are found by the direct methods of the calculus of variations. In the present paper we apply a more direct perturbative approach introduced by Stefanov and Wright [21] for another full dispersion Korteweg-de Vries equation, namely, the Whitham equation (see Ehrnström et al. [9] for a variational treatment of this equation).
The travelling-wave Whitham equation is
Noting that its linear dispersion relation has a unique global maximum at \(k=0\) (with \(c(0)=1\)), one writes \(c= 1 + \varepsilon ^2\) and seeks solitary waves of the form
so that
which can be rewritten as a fixed-point equation of the form
In the formal limit \(\varepsilon \rightarrow 0\) we recover the stationary Korteweg-de Vries equation
its (unique, symmetric) solitary-wave solution \(w^\star \) is nondegenerate in the sense that the only bounded solution of its linearisation at \(w^\star \) is \(w^\star _X\). Restricting to spaces of symmetric functions eliminates this antisymmetric solution of the linearised equation and a solution to (1.24) can be constructed as a perturbation of \(w^\star \) using the implicit-function theorem.
In Sect. 5 we apply the above argument to (1.21) and (1.23), first reformulating them as fixed-point equations. The functions \(\rho ^\star \) and \(\pm \zeta ^\star \) are nondegenerate solutions of (1.6) and (1.9) in the sense that the only bounded solutions of their linearisations at \(\rho ^\star \) and \(\pm \zeta ^\star \) are respectively \(\rho ^\star _X\) and \(\pm \zeta ^\star _X\), \(\pm \mathrm {i}\zeta ^\star \). Observe that equation (1.13) is invariant under the reflection \(\eta (x) \mapsto \eta (-x)\), and the reduction procedure preserves this property: the reduced equation for \(\eta _1\) is invariant under the reflection \(\eta _1(x) \mapsto \eta _1(-x)\), so that (1.21) and (1.23) are invariant under respectively \(\rho (x) \mapsto \rho (-x)\) and \(\zeta (x) \mapsto \overline{\zeta (-x)}\). Restricting to spaces of symmetric functions thus eliminates the antisymmetric solutions \(\rho ^{\star \prime }\) and \(\pm \zeta ^\star _X\), \(\pm \mathrm {i}\zeta ^\star \) of the linearised equations, and solutions to (1.21) and (1.23) can be constructed as perturbations of \(\rho ^\star \) and \(\pm \zeta ^\star \) using an appropriate version of the implicit-function theorem.
1.3 Function Spaces
We study the equation
in the basic space \({{\mathcal {X}}}=H^2({{\mathbb {R}}})\), where
are the usual Bessel-potential spaces. The decomposition \(\eta =\eta _1+\eta _2\), where \(\eta _1=\chi (D)\eta \), \(\eta _2=(1-\chi (D))\eta \), is accommodated by writing \({{\mathcal {X}}}\) as the direct sum of \({{\mathcal {X}}}_1 = \chi (D){{\mathcal {X}}}\) and \({{\mathcal {X}}}_2 = (1-\chi (D)){{\mathcal {X}}}\), where \({{\mathcal {X}}}_1\) and \({{\mathcal {X}}}_2\) are equipped with respectively the scaled norm
and the usual norm for \(H^2({{\mathbb {R}}})\). The norm for \({{\mathcal {X}}}_1\) is so chosen because the final scalings (1.20) and (1.22) transform \(|||\eta _1 |||\) into a multiple of the standard norm for \(H^1({{\mathbb {R}}})\), namely, \(|||\eta _1 |||= \varepsilon ^{3/2} \Vert \rho \Vert _1\) and \(|||\eta _1 |||= \varepsilon ^{1/2} \Vert \zeta \Vert _1\), and the reduced equations (1.21) and (1.23) are discussed in this space.
The following proposition yields in particular the estimate
for the supremum norm of \(\eta _1 \in {{\mathcal {X}}}_1\). We can also estimate higher-order derivatives of \(\eta _1 \in {{\mathcal {X}}}_1\) using the fact that the support of \({\hat{\eta }}_1\) is contained in the fixed bounded set S, so that, for example
for each \(n \in {{\mathbb {N}}}_0\).
Proposition 1.2
The estimate
holds for each \(\eta _1 \in {{\mathcal {X}}}_1\).
Proof
This estimate follows from the calculation
\(\square \)
It is also helpful to use the larger space
into which \(H^2({{\mathbb {R}}})\) is continuously embedded. In Sect. 2 we demonstrate that \(K(\cdot ) :{{\mathcal {Z}}}\rightarrow {{\mathcal {L}}}(H^{3/2}({{\mathbb {R}}}), H^{1/2}({{\mathbb {R}}}))\) is analytic at the origin and deduce that \({{\mathcal {K}}}\), \({{\mathcal {L}}}\) map the open neighbourhood
of the origin in \(H^2({{\mathbb {R}}})\) analytically into \(L^2({{\mathbb {R}}})\) for sufficiently small values of M. Moreover, we take advantage of the estimate
for \(\eta \in H^2({{\mathbb {R}}})\) to obtain estimates for \({{\mathcal {K}}}\) and \({{\mathcal {L}}}\) which are necessary for the reduction procedure described above (see Sect. 3). Note, however, that in the entirety of the existence theory we work in the fixed subset U of \(H^2({{\mathbb {R}}})\) (whose elements are ‘well-behaved’ functions).
2 Analyticity
In this section, we study the operator K given by (1.16) using basic results from the theory of analytic functions in Banach spaces (see the treatise by Buffoni and Toland [6] for a complete account). In particular, we present an elementary proof that \(K(\cdot ) :{{\mathcal {Z}}}\rightarrow {{\mathcal {L}}}(H^{3/2}({{\mathbb {R}}}), H^{1/2}({{\mathbb {R}}}))\), and hence \({{\mathcal {K}}}\), \({{\mathcal {L}}}: U \rightarrow L^2({{\mathbb {R}}})\), are analytic at the origin (see Sect. 1.3 above). A more comprehensive treatment of the analyticity of operators of Dirichlet–Neumann and Neumann–Dirichlet type in water-wave problems is given by Lannes [18, Ch. 3 and Appendix A] (see also Nicholls and Reitich [19] and Hu and Nicholls [14]).
We begin with the boundary-value problem (1.17)–(1.19), which is handled using the change of variable
to map \(\Sigma _\eta =\{(x,y):x \in {{\mathbb {R}}}, 0<y<1+\eta (x)\}\) to the strip \(\Sigma ={{\mathbb {R}}}\times (0,1)\). Dropping the primes, one finds that (1.17)–(1.19) are transformed into
where
and
We discuss (2.1)–(2.3) using the standard Sobolev spaces \(H^n(\Sigma )\), \(n \in {{\mathbb {N}}}\), together with \(H_\star ^{n+1}(\Sigma )\), \(n \in {{{\mathbb {N}}}}\), which is defined as the completion of
with respect to the norm
Proposition 2.1
For each \(F_1\), \(F_2 \in H^n(\Sigma )\) and \(\xi \in H^{n+1/2}({{\mathbb {R}}})\), \(n \in {{\mathbb {N}}}\), the boundary-value problem
admits a unique solution \(u=S(F_1,F_2,\xi )\) in \(H_\star ^{n+1}(\Sigma )\) given (with a slight abuse of notation, in that derivatives should be taken) by the explicit formula
in which
so that
Lemma 2.2
For each \(\xi \in H^{3/2}({{\mathbb {R}}})\) and each sufficiently small \(\eta \in {{\mathcal {Z}}}\) the boundary-value problem (2.1)–(2.3) admits a unique solution \(u \in H^2_\star (\Sigma )\). Furthermore, the mapping \({{\mathcal {Z}}}\rightarrow {{\mathcal {L}}}(H^{3/2}({{\mathbb {R}}}), H^2_\star (\Sigma ))\) given by \(\eta \mapsto (\xi \mapsto u)\) is analytic at the origin.
Proof
Define
by
and note that the solutions of (2.1)–(2.3) are precisely the zeros of \(T(\cdot ,\eta ,\xi )\). Using the estimates
(uniformly in n) and
one finds that the mappings \({{\mathcal {Z}}} \times H_\star ^2(\Sigma ) \rightarrow H^1(\Sigma )\) given by \((\eta ,u) \mapsto F_1(\eta ,u)\) and \((\eta ,u) \mapsto F_2(\eta ,u)\) are analytic at the origin; it follows that T is also analytic at the origin. Furthermore \(T(0,0,0)=0\) and
(because S is linear and \(F_1\), \(F_2\) are linear in their second arguments), so that \(\mathrm {d}_1T[0,0,0]=I\) is an isomorphism. By the analytic implicit-function theorem there exist open neighbourhoods \(N_1\) and \(N_2\) of the origin in \({{\mathcal {Z}}}\) and \(H^{3/2}({{\mathbb {R}}})\) and an analytic function \(v: N_1 \times N_2 \rightarrow H_\star ^2(\Sigma )\), such that
Since v is linear in \(\xi \) one can take \(N_2\) to be the whole space \(H^{3/2}({{\mathbb {R}}})\). \(\square \)
Corollary 2.3
The mapping \(K(\cdot ) :{{\mathcal {Z}}}\rightarrow {{\mathcal {L}}}(H^{3/2}({{\mathbb {R}}}), H^{1/2}({{\mathbb {R}}}))\) is analytic at the origin.
Corollary 2.4
The formulae (1.14), (1.15) define functions \(U \rightarrow L^2({{\mathbb {R}}})\) which are analytic at the origin and satisfy \({{\mathcal {K}}}(0)={{\mathcal {L}}}(0)=0\).
Proof
This result follows from Corollary 2.3 and the facts that \(H^1({{\mathbb {R}}})\) is a Banach algebra and \((u_1,u_2) \mapsto u_1 u_2\) is a bounded bilinear mapping \(H^{1/2}({{\mathbb {R}}}) \times H^{1/2}({{\mathbb {R}}}) \rightarrow L^2({{\mathbb {R}}})\) (see Hörmander [13, Theorem 8.3.1]). \(\square \)
In keeping with Lemma 2.2 and Corollaries 2.3 and 2.4 we write
where \(u_j\) is homogeneous of degree j in \(\eta \) and linear in \(\xi \), and
where \(K_j(\eta )\), \({{\mathcal {K}}}_j(\eta )\) and \({{\mathcal {L}}}_j(\eta )\) are homogeneous of degree j in \(\eta \) (and we accordingly abbreviate \(K_0(\eta )\) to \(K_0\)).
Remark 2.5
Note that \(K_j(\eta )=m_j(\{\eta \}^{(n)})\), where \(m_j\) is a bounded, symmetric, j-linear mapping \({{\mathcal {Z}}}^j \rightarrow {{\mathcal {L}}}(H^{3/2}({{\mathbb {R}}}), H^{1/2}({{\mathbb {R}}}))\).
We examine the first few terms
and
in the Maclaurin expansions of \({{\mathcal {K}}}\) and \({{\mathcal {L}}}\) in more detail since they play a prominent role in our subsequent calculations. We begin by computing explicit expressions for \(K_0\), \(K_1\) and \(K_2\).
Lemma 2.6
-
(i)
The operators \(K_0\) and \(K_1\) are given by the formulae
$$\begin{aligned} K_0\xi = f(D)\xi , \qquad K_1(\eta )\xi = -(\eta \xi _x)_x-K_0(\eta K_0 \xi ) \end{aligned}$$for each \(\eta \in H^2({{\mathbb {R}}})\) and \(\xi \in H^{3/2}({{\mathbb {R}}})\).
-
(ii)
The operator \(K_2\) is given by the formula
$$\begin{aligned} K_2(\eta )\xi = \tfrac{1}{2}(\eta ^2 K_0 \xi )_{xx} + \tfrac{1}{2}K_0(\eta ^2 \xi _{xx}) + K_0(\eta K_0(\eta K_0 \xi )) \end{aligned}$$under the additional regularity hypothesis that \(\eta \in H^3({{\mathbb {R}}})\) and \(\xi \in H^{5/2}({{\mathbb {R}}})\).
Proof
(i) The solution to the boundary-value problem
is
while the solution to the boundary-value problem
is
whence
(ii) Supposing that \(\xi \in H^{5/2}({{\mathbb {R}}})\), so that \(u^0 \in H_\star ^3(\Sigma )\), and \(\eta \in H^3({{\mathbb {R}}})\), so that \(u^1 \in H_\star ^3(\Sigma )\) (see Proposition 2.1), we find that the solution \(u^2 \in H_\star ^4(\Sigma )\) to the boundary-value problem
is
It follows that
\(\square \)
Remark 2.7
Explicit expressions for \(K_3\), \(K_4, \ldots \) can be computed in a similar fashion. However, computing an expansion in terms of Fourier-multiplier operators in this fashion leads a loss of one derivative at each order. It is therefore necessary to compensate by increasing the regularity of \(\xi \) and \(\eta \) by one derivative at each order.
Corollary 2.8
-
(i)
The function \({{\mathcal {L}}}_2\) is given by the formula
$$\begin{aligned} {{\mathcal {L}}}_2(\eta )=\tfrac{1}{2}\!\left( \eta _x^2 - (K_0 \eta )^2-(\eta ^2)_{xx}-2K_0(\eta K_0\eta ) \right) \end{aligned}$$for each \(\eta \in H^2({{\mathbb {R}}})\).
-
(ii)
The function \({{\mathcal {L}}}_3\) is given by the formula
$$\begin{aligned} {{\mathcal {L}}}_3(\eta )= & {} K_0\eta \, K_0(\eta K_0\eta )+K_0(\eta K_0(\eta K_0 \eta ))+\eta (K_0 \eta )\eta _{xx}\\&\qquad +\tfrac{1}{2}K_0(\eta ^2\eta _{xx})+\tfrac{1}{2}(\eta ^2K_0\eta )_{xx} \end{aligned}$$under the additional regularity hypothesis that \(\eta \in H^3({{\mathbb {R}}})\).
Finally, we record the representation \({{\mathcal {L}}}_2(\eta )=m(\eta ,\eta )\), where
which is helpful when performing calculations, and some straightforward estimates for the higher-order parts of \({{\mathcal {K}}}\) and \({{\mathcal {L}}}\).
Proposition 2.9
The estimate \(\Vert m(u,v)\Vert _0 \lesssim \Vert u\Vert _{{\mathcal {Z}}}\Vert v\Vert _2\) holds for each u, \(v\in H^2({{\mathbb {R}}})\).
Proposition 2.10
-
(i)
The quantities
$$\begin{aligned} {{\mathcal {K}}}_{\mathrm {c}}(\eta ):=\sum _{j=3}^\infty {{\mathcal {K}}}_j(\eta ), \qquad {{\mathcal {L}}}_{\mathrm {c}}(\eta ):=\sum _{j=3}^\infty {{\mathcal {L}}}_j(\eta ) \end{aligned}$$satisfy the estimates
$$\begin{aligned}&\Vert {{\mathcal {K}}}_{\mathrm {c}}(\eta )\Vert _0 \lesssim \Vert \eta \Vert _{{\mathcal {Z}}}^2 \Vert \eta \Vert _2, \qquad \Vert \mathrm {d}{{\mathcal {K}}}_{\mathrm {c}}[\eta ](v)\Vert _0 \lesssim \Vert \eta \Vert _{{\mathcal {Z}}}^2 \Vert v\Vert _2 + \Vert \eta \Vert _{{\mathcal {Z}}}\Vert \eta \Vert _2 \Vert v\Vert _{{\mathcal {Z}}}, \\&\Vert {{\mathcal {L}}}_{\mathrm {c}}(\eta )\Vert _0 \lesssim \Vert \eta \Vert _{{\mathcal {Z}}}^2 \Vert \eta \Vert _2, \qquad \Vert \mathrm {d}{{\mathcal {L}}}_{\mathrm {c}}[\eta ](v)\Vert _0 \lesssim \Vert \eta \Vert _{{\mathcal {Z}}}^2 \Vert v\Vert _2 + \Vert \eta \Vert _{{\mathcal {Z}}}\Vert \eta \Vert _2 \Vert v\Vert _{{\mathcal {Z}}}\end{aligned}$$for each \(\eta \in U\) and \(v \in H^2({{\mathbb {R}}})\).
-
(ii)
The quantities
$$\begin{aligned} {{\mathcal {K}}}_{\mathrm {r}}(\eta ):=\sum _{j=4}^\infty {{\mathcal {K}}}_j(\eta ), \qquad {{\mathcal {L}}}_{\mathrm {r}}(\eta ):=\sum _{j=4}^\infty {{\mathcal {L}}}_j(\eta )+\tfrac{1}{2}(K_1(\eta )\eta )^2 \end{aligned}$$satisfy the estimates
$$\begin{aligned}&\Vert {{\mathcal {K}}}_{\mathrm {r}}(\eta )\Vert _0 \lesssim \Vert \eta \Vert _{{{\mathcal {Z}}}}^4 \Vert \eta \Vert _2, \qquad \Vert \mathrm {d}{{\mathcal {K}}}_{\mathrm {r}}[\eta ](v)\Vert _0 \lesssim \Vert \eta \Vert _{{{\mathcal {Z}}}}^4 \Vert v\Vert _2 + \Vert \eta \Vert _{{{\mathcal {Z}}}}^3 \Vert \eta \Vert _2\Vert v\Vert _{{\mathcal {Z}}}, \\&\Vert {{\mathcal {L}}}_{\mathrm {r}}(\eta )\Vert _0 \lesssim \Vert \eta \Vert _{{{\mathcal {Z}}}}^3 \Vert \eta \Vert _2, \qquad \Vert \mathrm {d}{{\mathcal {L}}}_{\mathrm {r}}[\eta ](v)\Vert _0 \lesssim \Vert \eta \Vert _{{{\mathcal {Z}}}}^3 \Vert v\Vert _2 + \Vert \eta \Vert _{{{\mathcal {Z}}}}^2 \Vert \eta \Vert _2\Vert v\Vert _{{\mathcal {Z}}}\end{aligned}$$for each \(\eta \in U\) and \(v \in H^2({{\mathbb {R}}})\).
Proof
These estimates follow from the explicit formulae (2.5), (2.6), together with the calculations
and
where
\(\square \)
3 Reduction
In this section, we reduce the equation
to a locally equivalent equation for \(\eta _1\). Clearly \(\eta \in U\) satisfies (3.1) if and only if
and these equations can be rewritten as
in which
We proceed by writing (3.3) as a fixed-point equation for \(\eta _2\) using Proposition 3.1, which follows from the fact that \(g(k) \gtrsim |k|^2\) for \(k \not \in S\), and solving it for \(\eta _2\) as a function of \(\eta _1\) using Theorem 3.2, which is proved by a straightforward application of the contraction mapping principle. Substituting \(\eta _2=\eta _2(\eta _1)\) into (3.2) yields a reduced equation for \(\eta _1\). Note that the reduced equation is invariant under the reflection \(\eta _1(x) \mapsto \eta _1(-x)\), which is inherited from the invariance of (3.1) under the reflection \(\eta (x) \mapsto \eta (-x)\) (see below).
Proposition 3.1
The mapping \((1-\chi (D))g(D)^{-1}\) is a bounded linear operator \(L^2({{\mathbb {R}}}) \rightarrow {{\mathcal {X}}}_2\).
Theorem 3.2
Let \({{\mathcal {X}}}_1\), \({{\mathcal {X}}}_2\) be Banach spaces, \(X_1\), \(X_2\) be closed, convex sets in, respectively, \({{\mathcal {X}}}_1\), \({{\mathcal {X}}}_2\) containing the origin and \({{\mathcal {G}}}:X_1\times X_2 \rightarrow {{\mathcal {X}}}_2\) be a smooth function. Suppose that there exists a continuous function \(r:X_1\rightarrow [0,\infty )\), such that
for each \(x_2\in {\bar{B}}_r(0)\subseteq X_2\) and each \(x_1\in X_1\).
Under these hypotheses there exists for each \(x_1\in X_1\) a unique solution \(x_2=x_2(x_1)\) of the fixed-point equation \(x_2={{\mathcal {G}}}(x_1,x_2)\) satisfying \(x_2(x_1)\in {\bar{B}}_r(0)\). Moreover \(x_2(x_1)\) is a smooth function of \(x_1\in X_1\) and in particular satisfies the estimate
3.1 Strong Surface Tension
Suppose that \(\beta >\frac{1}{3}\). We write (3.3) in the form
and apply Theorem 3.2 with
the function \({{\mathcal {G}}}\) is given by the right-hand side of (3.4). Using Proposition 1.2 one can guarantee that \(\Vert {\hat{\eta }}_1\Vert _{L^1({{\mathbb {R}}}^2)} < \frac{1}{2}M\) for all \(\eta _1 \in X_1\) for an arbitrarily large value of \(R_1\); the value of \(R_2\) is constrained by the requirement that \(\Vert \eta _2\Vert _2 < \frac{1}{2}M\) for all \(\eta _2 \in X_2\).
Lemma 3.3
The estimates
-
(i)
\(\Vert {{\mathcal {G}}}(\eta _1,\eta _2)\Vert _2\lesssim \varepsilon ^{1/2} |||\eta _1|||^2+\varepsilon ^{1/2} |||\eta _1|||\Vert \eta _2\Vert _2 +|||\eta _1 |||\Vert \eta _2\Vert _2^2 +\Vert \eta _2\Vert _2^2 + \varepsilon ^2 \Vert \eta _2\Vert _2\),
-
(ii)
\(\Vert \mathrm {d}_1{{\mathcal {G}}}[\eta _1,\eta _2]\Vert _{{{\mathcal {L}}}({{\mathcal {X}}}_1,{{\mathcal {X}}}_2)}\lesssim \varepsilon ^{1/2} |||\eta _1|||+\varepsilon ^{1/2}\Vert \eta _2\Vert _2+ \Vert \eta _2\Vert _2^2\),
-
(iii)
\(\Vert \mathrm {d}_2{{\mathcal {G}}}[\eta _1,\eta _2]\Vert _{{{\mathcal {L}}}({{\mathcal {X}}}_1,{{\mathcal {X}}}_2)}\lesssim \varepsilon ^{1/2} |||\eta _1 |||+ |||\eta _1 |||\Vert \eta _2\Vert _2 + \Vert \eta _2\Vert _2+\varepsilon ^2\)
hold for each \(\eta _1\in X_1\) and \(\eta _2\in X_2\).
Proof
Observe that
and using Propositions 2.9 and 2.10(i), one finds that
and
part (i) follows from these estimates and inequality (1.25). Parts (ii) and (iii) are obtained in a similar fashion. \(\square \)
Theorem 3.4
Equation (3.4) has a unique solution \(\eta _2 \in X_2\) which depends smoothly upon \(\eta _1 \in X_1\) and satisfies the estimates
Proof
Choosing \(R_2\) and \(\varepsilon \) sufficiently small and setting \(r(\eta _1)=\sigma \varepsilon ^{1/2} |||\eta _1 |||^2\) for a sufficiently large value of \(\sigma >0\), one finds that
for \(\eta _1 \in X_1\) and \(\eta _2 \in {\overline{B}}_{r(\eta _1)}(0) \subset X_2\) (Lemma 3.3(i), (iii)). Theorem 3.2 asserts that equation (3.4) has a unique solution \(\eta _2\) in \({\overline{B}}_{r(\eta _1)}(0) \subset X_2\) which depends smoothly upon \(\eta _1 \in X_1\), and the estimate for its derivative follows from Lemma 3.3(ii). \(\square \)
Substituting \(\eta _2=\eta _2(\eta _1)\) into (3.2) yields the reduced equation
for \(\eta _1 \in X_1\). Observe that this equation is invariant under the reflection \(\eta _1(x) \mapsto \eta _1(-x)\); a familiar argument shows that it is inherited from the corresponding invariance of (3.2), (3.4) under \(\eta _1(x) \mapsto \eta _1(-x)\), \(\eta _2(x) \mapsto \eta _2(-x)\) when applying Theorem 3.2.
3.2 Weak Surface Tension
Suppose that \(\beta <\frac{1}{3}\). Since \(\chi (D){{\mathcal {L}}}_2(\eta _1)=0\) the nonlinear term in (3.2) is at leading order cubic in \(\eta _1\), so that this equation may be rewritten as
To compute the reduced equation for \(\eta _1\) we need an explicit formula for the leading-order quadratic part of \(\eta _2(\eta _1)\), which is evidently given by
It is convenient to write \(\eta _2 = F(\eta _1)+\eta _3\) and (3.3) in the form
(with the requirement that \(\eta _1+F(\eta _1)+\eta _3 \in U\)). We apply Theorem 3.2 to equation (3.8) with
the function \({{\mathcal {G}}}\) is given by the right-hand side of (3.8). (Here we write \(X_3\) rather than \(X_2\) for notational clarity.) Using Proposition 1.2 one can guarantee that \(\Vert {\hat{\eta }}_1\Vert _{L^1({{\mathbb {R}}})} < \frac{1}{2}M\) for all \(\eta _1 \in X_1\) for an arbitrarily large value of \(R_1\); the value of \(R_3\) is constrained by the requirement that \(\Vert F(\eta _1) + \eta _3\Vert _2 < \frac{1}{2}M\) for all \(\eta _1 \in X_1\) and \(\eta _3 \in X_3\), so that \(\eta _1+F(\eta _1)+\eta _3 \in U\) (Proposition 3.5 below asserts that \(\Vert F(\eta _1)\Vert _2 = O(\varepsilon ^{1/2})\) uniformly over \(\eta _1 \in X_1\)).
Proposition 3.5
The estimates
hold for each \(\eta _1\in X_1\).
Proof
This result follows from the formula
Proposition 2.9 and inequality (1.25). \(\square \)
Remark 3.6
Noting that
and that \(m(u_1,v_1)\) has compact support for all \(u_1\), \(v_1 \in {{\mathcal {X}}}_1\), one finds that \(K_0 F(\eta _1)\) satisfies the same estimates as \(F(\eta _1)\).
Lemma 3.7
The quantity
satisfies the estimates
-
(i)
\(\Vert {{\mathcal {N}}}_1(\eta _1,\eta _3)\Vert _0\lesssim \varepsilon |||\eta _1|||^3+\varepsilon ^{1/2} |||\eta _1|||^2\Vert \eta _3\Vert _2 +\varepsilon ^{1/2} |||\eta _1|||\Vert \eta _3\Vert _2+\Vert \eta _3\Vert _2^2\),
-
(ii)
\(\Vert \mathrm {d}_1{{\mathcal {N}}}_1[\eta _1,\eta _3]\Vert _{{{\mathcal {L}}}({{\mathcal {X}}}_1,L^2({{\mathbb {R}}}))}\lesssim \varepsilon |||\eta _1|||^2 +\varepsilon ^{1/2} |||\eta _1|||\Vert \eta _3\Vert _2+\varepsilon ^{1/2} \Vert \eta _3\Vert _2\),
-
(iii)
\(\Vert \mathrm {d}_2{{\mathcal {N}}}_1[\eta _1,\eta _3]\Vert _{{{\mathcal {L}}}({{\mathcal {X}}}_2,L^2({{\mathbb {R}}}))}\lesssim \varepsilon ^{1/2} |||\eta _1|||+\Vert \eta _3\Vert _2\)
for each \(\eta _1\in X_1\) and \(\eta _3\in X_3\).
Proof
We estimate
and its derivatives, which are computed using the chain rule, using Propositions 2.9 and 3.5 and inequality (1.25). \(\square \)
Lemma 3.8
The quantity
satisfies the estimates
-
(i)
\(\Vert {{\mathcal {N}}}_2(\eta _1,\eta _3)\Vert _0\lesssim (\varepsilon ^{1/2} |||\eta _1|||+\Vert \eta _3\Vert _2)^2(|||\eta _1|||+\Vert \eta _3\Vert _2)\),
-
(ii)
\(\Vert \mathrm {d}_1{{\mathcal {N}}}_2[\eta _1,\eta _3]\Vert _{{{\mathcal {L}}}({{\mathcal {X}}}_1,L^2({{\mathbb {R}}}))} \lesssim (\varepsilon ^{1/2} |||\eta _1|||+\Vert \eta _3\Vert _2)^2\),
-
(iii)
\(\Vert \mathrm {d}_2{{\mathcal {N}}}_2[\eta _1,\eta _3]\Vert _{{{\mathcal {L}}}({{\mathcal {X}}}_2,L^2({{\mathbb {R}}}))}\lesssim (\varepsilon ^{1/2}|||\eta _1|||+\Vert \eta _3\Vert _2)(|||\eta _1|||+\Vert \eta _3\Vert _2)\)
for each \(\eta _1\in X_1\) and \(\eta _3\in X_3\).
Proof
We estimate \({{\mathcal {N}}}_2\) and its derivatives, which are computed using the chain rule, using Propositions 2.10(i) and 3.5 and inequality (1.25). \(\square \)
Altogether we have established the following estimates for \({{\mathcal {G}}}\) and its derivatives (see Remark 3.6 and Lemmata 3.7 and 3.8).
Lemma 3.9
The estimates
-
(i)
\(\Vert {{\mathcal {G}}}(\eta _1,\eta _3)\Vert _2\lesssim (\varepsilon ^{1/2} |||\eta _1|||+\Vert \eta _3\Vert _2)^2(1+|||\eta _1|||+\Vert \eta _3\Vert _2)+\varepsilon ^2\Vert \eta _3\Vert _2\),
-
(ii)
\(\Vert \mathrm {d}_1{{\mathcal {G}}}[\eta _1,\eta _3]\Vert _{{{\mathcal {L}}}({{\mathcal {X}}}_1,{{\mathcal {X}}}_2)} \lesssim (\varepsilon ^{1/2} |||\eta _1|||+\Vert \eta _3\Vert _2) (\varepsilon ^{1/2}+\varepsilon ^{1/2} |||\eta _1|||+\Vert \eta _3\Vert _2)\),
-
(iii)
\(\Vert \mathrm {d}_2{{\mathcal {G}}}[\eta _1,\eta _3]\Vert _{{{\mathcal {L}}}({{\mathcal {X}}}_2,{{\mathcal {X}}}_2)}\lesssim (\varepsilon ^{1/2}|||\eta _1|||+\Vert \eta _3\Vert _2)(1+|||\eta _1|||+\Vert \eta _3\Vert _2)+\varepsilon ^2\)
hold for each \(\eta _1\in X_1\) and \(\eta _3\in X_3\).
Theorem 3.10
Equation (3.8) has a unique solution \(\eta _3 \in X_3\) which depends smoothly upon \(\eta _1 \in X_1\) and satisfies the estimates
Proof
Choosing \(R_3\) and \(\varepsilon \) sufficiently small and setting \(r(\eta _1)=\sigma \varepsilon |||\eta _1 |||^2\) for a sufficiently large value of \(\sigma >0\), one finds that
for \(\eta _1 \in X_1\) and \(\eta _3 \in {\overline{B}}_{r(\eta _1)}(0) \subset X_3\) (Lemma 3.9(i), (iii)). Theorem 3.2 asserts that equation (3.8) has a unique solution \(\eta _3\) in \({\overline{B}}_{r(\eta _1)}(0) \subset X_3\) which depends smoothly upon \(\eta _1 \in X_1\), and the estimate for its derivative follows from Lemma 3.9(ii). \(\square \)
Substituting \(\eta _2=F(\eta _1)+\eta _3(\eta _1)\) into (3.6) yields the reduced equation
for \(\eta _1 \in X_1\). This equation is also invariant under the reflection \(\eta _1(x) \mapsto \eta _1(-x)\); it is inherited from the invariance of (3.6), (3.8) under \(\eta _1(x) \mapsto \eta _1(-x)\), \(\eta _3(x) \mapsto \eta _3(-x)\) when applying Theorem 3.2.
4 Derivation of the Reduced Equation
In this section we compute the leading-order terms in the reduced equations (3.5) and (3.11) and hence derive the perturbed full dispersion Korteweg-de Vries and nonlinear Schrödinger equations announced in Sect. 1. The main steps are approximating the Fourier-multiplier operators appearing in lower-order terms by constants, estimating higher-order terms and performing the scalings (1.20) and (1.22).
It is convenient to introduce some additional notation to estimate higher-order ‘remainder’ terms.
Definition 4.1
-
(i)
The symbol \({{\mathcal {O}}}(\varepsilon ^\gamma |||\eta _1 |||^r)\) denotes a smooth function \({{\mathcal {R}}}: X_1 \rightarrow L^2({{\mathbb {R}}})\) which satisfies the estimates
$$\begin{aligned} \Vert {{\mathcal {R}}}(\eta _1)\Vert _0 \lesssim \varepsilon ^\gamma |||\eta _1 |||^r, \qquad \Vert \mathrm {d}{{\mathcal {R}}}[\eta _1]\Vert _{{{\mathcal {L}}}({{\mathcal {X}}}_1, L^2({{\mathbb {R}}}))}\lesssim \varepsilon ^\gamma |||\eta _1 |||^{r-1} \end{aligned}$$for each \(\eta _1 \in X_1\) (where \(\gamma \ge 0\), \(r \ge 1\)), and the underscored notation \({\underline{{{\mathcal {O}}}}}(\varepsilon ^\gamma |||\eta _1 |||^r)\) indicates additionally that the Fourier transform of \({{\mathcal {R}}}(\eta _1)\) lies in a fixed compact set (independently of \(\varepsilon \) and uniformly over \(\eta _1 \in X_1\)). Furthermore
$$\begin{aligned}&{\underline{{{\mathcal {O}}}}}_0(\varepsilon ^\gamma |||\eta _1 |||^r):=\chi _0(D){{\mathcal {O}}}(\varepsilon ^\gamma |||\eta _1 |||^r), \\&{\underline{{{\mathcal {O}}}}}_+(\varepsilon ^\gamma |||\eta _1 |||^r) := \chi ^+(D){{\mathcal {O}}}(\varepsilon ^\gamma |||\eta _1 |||^r), \end{aligned}$$where \(\chi _0\) and \(\chi ^+\) are the characteristic functions of the sets \((-\delta ,\delta )\) and \((\omega -\delta ,\omega +\delta )\) (for \(\omega >0\)).
-
(ii)
The symbol \({\underline{{{\mathcal {O}}}}}^\varepsilon _n(\Vert u \Vert _1^r)\) denotes \(\chi _0(\varepsilon D){{\mathcal {R}}}(u)\), where \({{\mathcal {R}}}\) is a smooth function \(B_R(0) \subseteq \chi _0(\varepsilon D)H^1({{\mathbb {R}}}) \rightarrow H^n({{\mathbb {R}}})\) or \(B_R(0) \subseteq H^1({{\mathbb {R}}}) \rightarrow H^n({{\mathbb {R}}})\) which satisfies the estimates
$$\begin{aligned} \Vert {{\mathcal {R}}}(u)\Vert _n \lesssim \Vert u \Vert _1^r, \quad \Vert \mathrm {d}{{\mathcal {R}}}[u]\Vert _{{{\mathcal {L}}}(H^1({{\mathbb {R}}}),H^n({{\mathbb {R}}}))}\lesssim \Vert u \Vert _1^{r-1} \end{aligned}$$for each \(u \in B_R(0)\) (with \(r \ge 1\), \(n \ge 0\)).
4.1 Strong Surface Tension
The leading-order terms in the reduced equation
derived in Sect. 3.1 are computed by approximating the operators \(\partial _x\) and \(K_0\) in the quadratic part of the equation by constants.
Proposition 4.2
The estimates
-
(i)
\(\eta _{1x} = {\underline{{{\mathcal {O}}}}}_0(\varepsilon |||\eta _1|||)\),
-
(ii)
\(K_0 \eta _1 = \eta _1 + {\underline{{{\mathcal {O}}}}}_0(\varepsilon |||\eta _1|||)\),
-
(iii)
\(K_0 \eta _1^2 = \eta _1^2 + {\underline{{{\mathcal {O}}}}}(\varepsilon ^{3/2}|||\eta _1|||)\)
hold for each \(\eta _1 \in X_1\).
Proof
Note that
and
the corresponding estimates for their derivatives are trivially satisfied since the operators are linear. The quantity to be estimated in (iii) is quadratic in \(\eta _1\); it therefore suffices to estimate the corresponding bilinear operator. The argument used above yields
for each \(u_1\), \(v_1 \in X_1\), where we have also used Young’s inequality. \(\square \)
Lemma 4.3
The estimate
holds for each \(\eta _1 \in X_1\).
Proof
Using Proposition 2.9 and Theorem 3.4, one finds that
and
because of (2.7) and Proposition 4.2. \(\square \)
Lemma 4.4
The estimate
holds for each \(\eta _1 \in X_1\).
Proof
This result follows from Proposition 2.10(i) and Theorem 3.4. \(\square \)
We conclude that the reduced equation for \(\eta _1\) is the perturbed full dispersion Korteweg-de Vries equation
and applying Proposition 4.2, one can further simplify it to
Finally, we introduce the Korteweg-de Vries scaling
so that \(\rho \in B_R(0) \subseteq \chi (\varepsilon D)H^1({{\mathbb {R}}})\), where \(R>0\) and \(\varepsilon \) is chosen small enough that \(\varepsilon ^{3/2} R \le R_1\), solves the equation
(note that \(|||\eta |||= \varepsilon ^{3/2} \Vert \rho \Vert _1\), the change of variable from x to \(X=\varepsilon x\) introduces an additional factor of \(\varepsilon ^{1/2}\) in the remainder term and the symbol D now means \(-\mathrm {i}\partial _X\)). The invariance of the reduced equation under \(\eta _1(x) \mapsto \eta _1(-x)\) is inherited by (4.1), which is invariant under the reflection \(\rho (X) \mapsto \rho (-X)\).
4.2 Weak Surface Tension
In this section we compute the leading-order terms in the reduced equation (3.11) derived in Sect. 3.2. To this end, we write
where \(\eta _1^+=\chi ^+(D)\eta _1\) and \(\eta _1^-=\overline{\eta _1^+}\), so that \(\eta _1^+\) satisfies the equation
(and \(\eta _1^-\) satisfies its complex conjugate). We again begin by showing how Fourier-multiplier operators acting upon the function \(\eta _1\) may be approximated by constants.
Lemma 4.5
The estimates
-
(i)
\(\partial _x \eta _1^+ = + \mathrm {i}\omega \eta _1^+ + {\underline{{{\mathcal {O}}}}}_+(\varepsilon |||\eta _1|||)\),
-
(ii)
\(\partial _x^2 \eta _1^+ =-\omega ^2\eta _1^++ {\underline{{{\mathcal {O}}}}}_+(\varepsilon |||\eta _1|||)\),
-
(iii)
\(K_0 \eta _1^+ = f(\omega )\eta _1^+ + {\underline{{{\mathcal {O}}}}}_+(\varepsilon |||\eta _1|||)\),
-
(iv)
\(K_0((\eta _1^+)^2) = f(2\omega )(\eta _1^+)^2 + {\underline{{{\mathcal {O}}}}}(\varepsilon ^{3/2}|||\eta _1|||^2)\),
-
(v)
\(K_0 (\eta _1^+\eta _1^-) = \eta _1^+ \eta _1^-+{\underline{{{\mathcal {O}}}}}(\varepsilon ^{3/2}|||\eta _1|||^2)\),
-
(vi)
\({{\mathcal {F}}}^{-1}[g(k)^{-1}{{\mathcal {F}}}[(\eta _1^+)^2]]=g(2\omega )^{-1}(\eta _1^+)^2+ {\underline{{{\mathcal {O}}}}}(\varepsilon ^{3/2}|||\eta _1|||^2)\),
-
(vii)
\({{\mathcal {F}}}^{-1}[g(k)^{-1}{{\mathcal {F}}}[ \eta _1^+\eta _1^- ]]=g(0)^{-1}\eta _1^+\eta _1^-+{\underline{{{\mathcal {O}}}}}(\varepsilon ^{3/2}|||\eta _1|||^2)\),
-
(viii)
\(K_0((\eta _1^+)^2\eta _1^-) = f(\omega )(\eta _1^+)^2\eta _1^- +{\underline{{{\mathcal {O}}}}}(\varepsilon ^2|||\eta _1|||^3)\)
hold for each \(\eta _1 \in X_1\).
Proof
Note that
and iterating this argument yields (ii); moreover
The corresponding estimates for their derivatives are trivially satisfied since the operators are linear.
Notice that the quantities to be estimated in (iv)–(vii) are quadratic in \(\eta _1\); it therefore suffices to estimate the corresponding bilinear operators. To this end we take \(u_1\), \(v_1\in {{\mathcal {X}}}_1\). The argument used for (iii) above yields
where we have also used Young’s inequality. Turning to (v), we note that
Estimates (vi) and (vii) are obtained in the same fashion.
To establish (viii) we similarly estimate the relevant trilinear operator. Take \(u_1\), \(v_1\), \(w_1 \in {{\mathcal {X}}}_1\) and observe that
\(\square \)
We proceed by approximating each term in the quadratic and cubic parts of equation (4.2) according to the rules established in Lemma 4.5, recalling that
where \(F(\eta _1)\), \({{\mathcal {N}}}_1(\eta _1,\eta _3)\) and \({{\mathcal {N}}}_1(\eta _1,\eta _3)\) are defined by respectively (3.7), (3.9) and (3.10).
Proposition 4.6
The estimate
where
holds for each \(\eta _1 \in X_1\).
Proof
Using equation (2.7) and the expansions given in Lemma 4.5, we find that
It follows that
because of Lemma 4.5(vi), (vii) and the facts that \(\chi (D){{\mathcal {L}}}_2(\eta _1)=0\) and
(since \((1-\chi (k))g(k)^{-1}\) is bounded). We conclude that
\(\square \)
Proposition 4.7
The estimate
holds for each \(\eta _1 \in X_1\).
Proof
Observe that
in which we have used the calculations
(see Propositions 2.9 and 3.5 and Theorem 3.10) and
(because of Propositions 2.9 and 4.6). Furthermore
and it follows from (2.7) and Lemma 4.5 that
\(\square \)
Proposition 4.8
The estimates
where
hold for each \(\eta _1 \in X_1\).
Proof
Using the estimates for \(F(\eta _1)\) and \(\eta _3(\eta _1)\) given in Proposition 3.5 and Theorem 3.10, we find that
and
(because of equation (2.5)). It similarly follows from the formula
(see equation (2.6) and Remark 2.5) that
and using Corollary 2.8(ii) twice yields
and
\(\square \)
Proposition 4.9
The estimates
hold for each \(\eta _1 \in X_1\).
Proof
This result follows from Propositions 2.10(ii) and 3.5 and Theorem 3.10. \(\square \)
Proposition 4.10
The estimate
holds for each \(\eta _1 \in X_1\).
Proof
Using Proposition 3.5 and Theorem 3.10 we find that
and furthermore
(see Lemma 2.6(i)). \(\square \)
Corollary 4.11
The estimate
holds for each \(\eta _1 \in X_1\).
We conclude that the reduced equation for \(\eta _1\) is the perturbed full dispersion nonlinear Schrödinger equation
where
and applying Lemma 4.5(iii), one can further simplify it to
Finally, we introduce the nonlinear Schrödinger scaling
so that \(\zeta \in B_R(0) \subseteq \chi _0(\varepsilon D)H^1({{\mathbb {R}}})\), where \(R>0\) and \(\varepsilon \) is chosen small enough that \(\varepsilon ^{1/2} R \le 2R_1\), solves the equation
(note that \(|||\eta _1 |||= \varepsilon ^{1/2}\Vert \zeta \Vert _1\), the change of variable from x to \(X=\varepsilon x\) introduces an additional factor of \(\varepsilon ^{1/2}\) in the remainder term and the symbol D now means \(-\mathrm {i}\partial _X\)). The invariance of the reduced equation under \(\eta _1(x) \mapsto \eta _1(-x)\) is inherited by (4.3), which is invariant under the reflection \(\zeta (X) \mapsto \overline{\zeta (-X)}\).
5 Solution of the Reduced Equation
In this section, we find solitary-wave solutions of the reduced equations
and
noting that in the formal limit \(\varepsilon \rightarrow 0\) they reduce to respectively the stationary Korteweg-de Vries equation
and the stationary nonlinear Schrödinger equation
which have explicit (symmetric) solitary-wave solutions \(\rho ^\star \) and \(\pm \zeta ^\star \) (Eqs. (1.7) and (1.10)). For this purpose we use a perturbation argument, rewriting (5.1) and (5.2) as fixed-point equations and applying the following version of the implicit-function theorem.
Theorem 5.1
Let \({{\mathcal {X}}}\) be a Banach space, \(X_0\) and \(\Lambda _0\) be open neighbourhoods of respectively \(x^\star \) in \({{\mathcal {X}}}\) and the origin in \({{\mathbb {R}}}\) and \({{\mathcal {G}}}: X_0 \times \Lambda _0 \rightarrow {{\mathcal {X}}}\) be a function which is differentiable with respect to \(x \in X_0\) for each \(\lambda \in \Lambda _0\). Furthermore, suppose that \({{\mathcal {G}}}(x^\star ,0)=0\), \(\mathrm {d}_1{{\mathcal {G}}}[x^\star ,0]: {{\mathcal {X}}}\rightarrow {{\mathcal {X}}}\) is an isomorphism,
and
uniformly over \(x \in X_0\).
There exist open neighbourhoods X of \(x^\star \) in \({{\mathcal {X}}}\) and \(\Lambda \) of 0 in \({{\mathbb {R}}}\) (with \(X \subseteq X_0\), \(\Lambda \subseteq \Lambda _0)\) and a uniquely determined mapping \(h: \Lambda \rightarrow X\) with the properties that
-
(i)
h is continuous at the origin (with \(h(0)=x^\star \)),
-
(ii)
\({{\mathcal {G}}}(h(\lambda ),\lambda )=0\) for all \(\lambda \in \Lambda \),
-
(iii)
\(x=h(\lambda )\) whenever \((x,\lambda ) \in X \times \Lambda \) satisfies \({{\mathcal {G}}}(x,\lambda )=0\).
5.1 Strong Surface Tension
Theorem 5.2
For each sufficiently small value of \(\varepsilon >0\) equation (5.1) has a small-amplitude, symmetric solution \(\rho _\varepsilon \) in \(\chi _0(\varepsilon D)H^1({{\mathbb {R}}})\) with \(\Vert \rho _\varepsilon -\rho ^\star \Vert _1 \rightarrow 0\) as \(\varepsilon \rightarrow 0\).
The first step in the proof of Theorem 5.2 is to write (5.1) as the fixed-point equation
and use the following result to ‘replace’ the nonlocal operator with a differential operator.
Proposition 5.3
The inequality
holds uniformly over \(|k| < \delta /\varepsilon \).
Proof
Clearly
furthermore
and
It follows that
\(\square \)
Using the above proposition, one can write equation (5.5) as
where
It is convenient to replace this equation with
where \({\tilde{F}}_\varepsilon (\rho ) = F_\varepsilon (\chi _0(\varepsilon D)\rho )\) and study it in the fixed space \(H^1({{\mathbb {R}}})\) (the solution sets of the two equations evidently coincide).
We establish Theorem 5.6 by applying Theorem 5.1 with
\(X=B_R(0)\), \(\Lambda _0=(-\varepsilon _0,\varepsilon _0)\) for a sufficiently small value of \(\varepsilon _0\), and
(here \(\varepsilon \) is replaced by \(|\varepsilon |\) so that \({{\mathcal {G}}}(\rho ,\varepsilon )\) is defined for \(\varepsilon \) in a full neighbourhood of the origin in \({{\mathbb {R}}}\)). Observe that
and noting that
because
that
and that \(H^{3/4}({{\mathbb {R}}})\) is a Banach algebra, we find that
uniformly over \(\rho \in B_R(0)\). The equation
has the (unique) nontrivial solution \(\rho ^\star \) in \(H_{\mathrm {e}}^1({{\mathbb {R}}})\) and it remains to show that
is an isomorphism.
Noting that \(\rho ^\star \in {{\mathcal {S}}}({{\mathbb {R}}})\), we obtain the following result by a familiar argument (see Kirchgässner [17, Proposition 5.1] or Friesecke & Pego [10, §4]).
Proposition 5.4
The formula \(\rho \mapsto 3\left( 1-(\beta -\tfrac{1}{3})\partial _X^2\right) ^{-1}(\rho ^\star \rho )\) defines a compact linear operator \(H^1({{\mathbb {R}}}) \rightarrow H^1({{\mathbb {R}}})\) and \(H^1_{\mathrm {e}}({{\mathbb {R}}}) \rightarrow H^1_{\mathrm {e}}({{\mathbb {R}}})\).
This proposition implies in particular that \(\mathrm {d}_1{{\mathcal {G}}}[\rho ^\star ,0]\) is a Fredholm operator with index 0. Its kernel coincides with the set of symmetric bounded solutions of the ordinary differential equation
and the next proposition shows that this set consists of only the trivial solution, so that \(\mathrm {d}_1{{\mathcal {G}}}[\rho ^\star ,0]\) is an isomorphism.
Proposition 5.5
Every bounded solution to the equation (5.6) is a multiple of \(\rho ^\star _X\) and is therefore antisymmetric.
Proof
Define
where \({\check{X}}=(\beta -\frac{1}{3})^{-1/2}X\), and observe that \(\{\rho _1,\rho _2\}\) is a fundamental solution set for (5.6). Its bounded solutions are therefore precisely the multiples of \(\rho _1\). \(\square \)
5.2 Weak Surface Tension
Theorem 5.6
For each sufficiently small value of \(\varepsilon >0\) equation (5.2) has two small-amplitude, symmetric solutions \(\zeta ^\pm _\varepsilon \) in \(\chi _0(\varepsilon D)H^1({{\mathbb {R}}})\) with \(\Vert \zeta ^\pm _\varepsilon \mp \zeta ^\star \Vert _1 \rightarrow 0\) as \(\varepsilon \rightarrow 0\).
We again begin the proof of Theorem 5.6 by ‘replacing’ the nonlocal operator in the fixed-point formulation
of equation (5.2) with a differential operator.
Proposition 5.7
The inequality
holds uniformly over \(|k| < \delta /\varepsilon \).
Proof
Clearly
while
and
It follows that
\(\square \)
Using the above proposition, one can write equation (5.2) as
where
or equivalently with
where \({\tilde{F}}_\varepsilon (\zeta ) = F_\varepsilon (\chi _0(\varepsilon D)\zeta )\), and studying it in the fixed space \(H^1({{\mathbb {R}}},{{\mathbb {C}}})\). We establish Theorem 5.2 by applying Theorem 5.1 with
\(X=B_R(0)\), \(\Lambda _0=(-\varepsilon _0,\varepsilon _0)\) for a sufficiently small value of \(\varepsilon _0\) and
Observe that
so that
uniformly over \(\zeta \in B_R(0)\).
The equation
has (precisely two) nontrivial solutions \(\pm \zeta ^\star \) in \(H_{\mathrm {e}}^1({{\mathbb {R}}},{{\mathbb {C}}})\), which are both real, and the fact that \(\mathrm {d}_1{{\mathcal {G}}}[\pm \zeta ^\star ,0]\) is an isomorphism is conveniently established by using real coordinates. Define \(\zeta _1={{\,\mathrm{Re}\,}}\zeta \) and \(\zeta _2={{\,\mathrm{Im}\,}}\zeta \), so that
where \({{\mathcal {G}}}_1: H_{\mathrm {e}}^1({{\mathbb {R}}}) \rightarrow H_{\mathrm {e}}^1({{\mathbb {R}}})\) and \({{\mathcal {G}}}_2: H_{\mathrm {o}}^1({{\mathbb {R}}}) \rightarrow H_{\mathrm {o}}^1({{\mathbb {R}}})\) are given by
and
Proposition 5.8
The formulae
define compact linear operators \(H^1({{\mathbb {R}}}) \rightarrow H^1({{\mathbb {R}}})\), \(H_{\mathrm {e}}^1({{\mathbb {R}}}) \rightarrow H_{\mathrm {e}}^1({{\mathbb {R}}})\) and \(H_{\mathrm {o}}^1({{\mathbb {R}}}) \rightarrow H_{\mathrm {o}}^1({{\mathbb {R}}})\).
The previous proposition implies in particular that \({{\mathcal {G}}}_1\), \({{\mathcal {G}}}_2\) are Fredholm operators with index 0. The kernel of \({{\mathcal {G}}}_1\) coincides with the set of symmetric bounded solutions of the ordinary differential equation
while the kernel of \({{\mathcal {G}}}_2\) coincides with the set of antisymmetric bounded solutions of the ordinary differential equation
and the next proposition shows that these sets consists of only the trivial solution, so that \({{\mathcal {G}}}_1\), \({{\mathcal {G}}}_2\) and hence \(\mathrm {d}_1{{\mathcal {G}}}[\zeta ^\star ,0]\) are isomorphisms.
Proposition 5.9
-
(i)
Every bounded solution to the equation (5.7) is a multiple of \(\zeta ^\star _X\) and is therefore antisymmetric.
-
(ii)
Every bounded solution to the equation (5.8) is a multiple of \(\zeta ^\star \) and is therefore symmetric.
Proof
Introducing the scaled variables
transforms Eqs. (5.7), (5.8) into
where \({\check{\zeta }}^\star ({\check{X}}) = \sqrt{2}{{\,\mathrm{sech}\,}}{\check{X}}\), and it obviously suffices to establish the corresponding results for these equations.
Define
and observe that \(\{\zeta _{1,1},\zeta _{1,2}\}\) is a fundamental solution set for (5.9), whose bounded solutions are therefore precisely the multiplies of \({\check{\zeta }}^\star _{{\check{X}}}\), while \(\{\zeta _{2,1},\zeta _{2,2}\}\) is a fundamental solution set for (5.10), whose bounded solutions are therefore precisely the multiples of \({\check{\zeta }}^\star \). \(\square \)
References
Ablowitz, M.J., Segur, H.: On the evolution of packets of water waves. J. Fluid Mech. 92, 691–715 (1979)
Amick, C.J., Kirchgässner, K.: A theory of solitary water waves in the presence of surface tension. Arch. Rat. Mech. Anal. 105, 1–49 (1989)
Benjamin, T.B.: The solitary wave with surface tension. Q. Appl. Math. 40, 231–234 (1982)
Buffoni, B.: Existence and conditional energetic stability of capillary-gravity solitary water waves by minimisation. Arch. Rat. Mech. Anal. 173, 25–68 (2004)
Buffoni, B.: Conditional energetic stability of gravity solitary waves in the presence of weak surface tension. Topol. Meth. Nonlinear Anal. 25, 41–68 (2005)
Buffoni, B., Toland, J.F.: Analytic theory of global bifurcation. Princeton University Press, Princeton (2003)
Craig, W., Sulem, C.: Numerical simulation of gravity waves. J. Comp. Phys. 108, 73–83 (1993)
Dias, F., Kharif, C.: Nonlinear gravity and capillary-gravity waves. Ann. Rev. Fluid Mech. 31, 301–346 (1999)
Ehrnström, M., Groves, M.D., Wahlén, E.: On the existence and stability of solitary-wave solutions to a class of evolution equations of Whitham type. Nonlinearity 25, 2903–2936 (2012)
Friesecke, G., Pego, R.L.: Solitary waves on FPU lattices: I. Qualitative properties, renormalization and continuum limit. Nonlinearity 12, 1601–1627 (1999)
Groves, M.D., Wahlén, E.: On the existence and conditional energetic stability of solitary water waves with weak surface tension. C. R. Math. Acad. Sci. Paris 348, 397–402 (2010)
Groves, M.D., Wahlén, E.: Existence and conditional energetic stability of solitary gravity-capillary water waves with constant vorticity. Proc. R. Soc. Edin. A 145, 791–883 (2015)
Hörmander, L.: Lectures on nonlinear hyperbolic differential equations. Springer, Heidelberg (1997)
Hu, B., Nicholls, D.P.: Analyticity of Dirichlet–Neumann operators on Hölder and Lipschitz domains. SIAM J. Math. Anal. 37, 302–320 (2006)
Iooss, G., Kirchgässner, K.: Bifurcation d’ondes solitaires en présence d’une faible tension superficielle. C. R. Acad. Sci. Paris, Sér. 1 311, 265–268 (1990)
Iooss, G., Pérouème, M.C.: Perturbed homoclinic solutions in reversible 1:1 resonance vector fields. J. Diff. Equ. 102, 62–88 (1993)
Kirchgässner, K.: Nonlinearly resonant surface waves and homoclinic bifurcation. Adv. Appl. Mech. 26, 135–181 (1988)
Lannes, D.: The water waves problem: mathematical analysis and asymptotics. Number 188 in Mathematical surveys and monographs. American Mathematical Society, Providence (2013)
Nicholls, D.P., Reitich, F.: A new approach to analyticity of Dirichlet–Neumann operators. Proc. R. Soc. Edin. A 131, 1411–1433 (2001)
Sachs, R.L.: On the existence of small amplitude solitary waves with strong surface-tension. J. Diff. Equ. 90, 31–51 (1991)
Stefanov, A., Wright, J.D.: Small amplitude traveling waves in the full-dispersion Whitham equation. J. Dyn. Diff. Equ. 32, 85–99 (2020)
Zakharov, V.E.: Stability of periodic waves of finite amplitude on the surface of a deep fluid. Zh. Prikl. Mekh. Tekh. Fiz. 9, 86–94 (1968). (English translation J. Appl. Mech. Tech. Phys. 9, 190–194.)
Funding
Open Access funding enabled and organised by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
In memory of Walter Craig.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Groves, M.D. An Existence Theory for Gravity–Capillary Solitary Water Waves. Water Waves 3, 213–250 (2021). https://doi.org/10.1007/s42286-020-00045-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42286-020-00045-7