A Variational Approach to Solitary Gravity–Capillary Interfacial Waves with Infinite Depth

Abstract

We present an existence and stability theory for gravity–capillary solitary waves on the top surface of and interface between two perfect fluids of different densities, the lower one being of infinite depth. Exploiting a classical variational principle, we prove the existence of a minimiser of the wave energy ${\mathcal {E}}$ subject to the constraint ${\mathcal {I}}=2\mu$, where ${\mathcal {I}}$ is the wave momentum and $0< \mu <\mu _0$, where $\mu _0$ is chosen small enough for the validity of our calculations. Since ${\mathcal {E}}$ and ${\mathcal {I}}$ are both conserved quantities a standard argument asserts the stability of the set $D_\mu$ of minimisers: solutions starting near $D_\mu$ remain close to $D_\mu$ in a suitably defined energy space over their interval of existence. The solitary waves which we construct are of small amplitude and are to leading order described by the cubic nonlinear Schrödinger equation. They exist in a parameter region in which the ‘slow’ branch of the dispersion relation has a strict non-degenerate global minimum and the corresponding nonlinear Schrödinger equation is of focussing type. The waves detected by our variational method converge (after an appropriate rescaling) to solutions of the model equation as $\mu \downarrow 0$.

1 Introduction

1.1 The Model

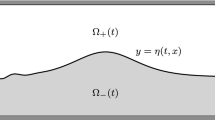
We consider a two-layer perfect fluid with irrotational flow subject to the forces of gravity, surface tension and interfacial tension. The lower layer is assumed to be of infinite depth, while the upper layer has finite asymptotic depth ${\overline{h}}$. We assume that density ${\underline{\rho }}$ of the lower fluid is strictly greater than the density ${\overline{\rho }}$ of the upper fluid. The layers are separated by a free interface $\{y={\underline{\eta }}(x,t)\}$, and the upper one is bounded from above by a free surface $\{y={\overline{h}}+{\overline{\eta }}(x,t)\}$. The fluid motion in each layer is described by the incompressible Euler equations. The fluid occupies the domain ${\underline{\Sigma }}({\underline{\eta }}) \cup {\overline{\Sigma }}(\varvec{\eta })$, where

$$\begin{aligned} {\underline{\Sigma }}({\underline{\eta }})&:=\left\{ (x,y)\in {\mathbb {R}}^2:-\infty< y<{\underline{\eta }}(x,t)\right\} ,\\ {\overline{\Sigma }}(\varvec{\eta })&:=\left\{ (x,y)\in {\mathbb {R}}^2:{\underline{\eta }}(x,t)< y< {\overline{h}}+ {\overline{\eta }}(x,t)\right\} , \end{aligned}$$

and $\varvec{\eta }=({\underline{\eta }}, {\overline{\eta }})$. Since the flow is assumed to be irrotational in each layer, there exist velocity potentials ${\underline{\phi }}$ and ${\overline{\phi }}$ satisfying

$$\begin{aligned} \Delta {\overline{\phi }}=0 \quad \text {in}\quad {\overline{\Sigma }}(\varvec{\eta }),\qquad \Delta {\underline{\phi }}=0 \quad \text {in}\quad {\underline{\Sigma }}({{\underline{\eta }}}). \end{aligned}$$

On the interface $\{y={\underline{\eta }}\}$ we have the kinematic boundary conditions

$$\begin{aligned} \partial _t {\underline{\eta }}={\overline{\phi }}_y-{\underline{\eta }}_x{\overline{\phi }}_x=(1+ {\underline{\eta }}_x^2)^{\frac{1}{2}} \partial _{\underline{\varvec{n}}} {\overline{\phi }}, \qquad \partial _t{\underline{\eta }} ={\underline{\phi }}_y-{\underline{\eta }}_x{\underline{\phi }}_x=(1+ {\underline{\eta }}_x^2)^{\frac{1}{2}}\partial _{\underline{\varvec{n}}} {\underline{\phi }}, \end{aligned}$$

where

$$\begin{aligned} \underline{\varvec{n}}=(1+{\underline{\eta }}_x^2)^{-\frac{1}{2}}(1, -{\underline{\eta }}_x) \end{aligned}$$

is the upward unit normal vector to the interface. In particular, this implies that the normal component of the velocity is continuous across the interface. At the free surface $\{y={\overline{h}}+{\overline{\eta }}\}$, the kinematic boundary condition reads

$$\begin{aligned} \partial _t {\overline{\eta }}&={\overline{\phi }}_y-{\overline{\eta }}_x{\overline{\phi }}_x=(1+ {\overline{\eta }}_x^2)^{\frac{1}{2}} \partial _{\overline{\varvec{n}}} {\overline{\phi }}, \end{aligned}$$

where

$$\begin{aligned} \overline{\varvec{n}}=(1+{\overline{\eta }}_x^2)^{-\frac{1}{2}}(1, -{\overline{\eta }}_x) \end{aligned}$$

is the outer unit normal vector at the surface. In addition, we have the Bernoulli conditions

$$\begin{aligned} {\overline{\rho }}\left( \partial _t{\overline{\phi }}+\frac{1}{2}|\nabla {\overline{\phi }}|^2+g{\underline{\eta }}\right) -{\underline{\rho }}\left( \partial _t{\underline{\phi }}+\frac{1}{2}|\nabla {\underline{\phi }}|^2+g{\underline{\eta }}\right) =-{\underline{\sigma }}\left( \frac{{\underline{\eta }}_x}{\sqrt{1+{\underline{\eta }}_x^2}}\right) _x, \end{aligned}$$

and

$$\begin{aligned} {\overline{\rho }}\left( \partial _t{\overline{\phi }}+\frac{1}{2}|\nabla {\overline{\phi }}|^2+g{\overline{\eta }}\right) ={\overline{\sigma }}\left( \frac{{\overline{\eta }}_x}{\sqrt{1+{\overline{\eta }}_x^2}}\right) _x \end{aligned}$$

at the interface and surface, respectively, where $g>0$ is the acceleration due to gravity, ${\overline{\sigma }}>0$ the coefficient of surface tension, and ${\underline{\sigma }}>0$ the coefficient of interfacial tension.

In order to obtain dimensionless variables we define

$$\begin{aligned}&(x',y'):=\frac{1}{{\overline{h}}}(x,y), \quad&t':=\left( \frac{g}{{\overline{h}}}\right) ^{\frac{1}{2}}t, \\&{\overline{\eta }}'(x',t'):=\frac{1}{{\overline{h}}}{\overline{\eta }}(x,t), \quad&{\underline{\eta }}'(x',t'):=\frac{1}{{\overline{h}}}{\underline{\eta }}(x,t), \\&{\overline{\phi }}'(x',y',t'):=\frac{1}{({\overline{h}})^{\frac{3}{2}}g^{\frac{1}{2}}}{\overline{\phi }}(x,y,t), \quad&{\underline{\phi }}'(x',y',t'):=\frac{1}{({\overline{h}})^{\frac{3}{2}}g^{\frac{1}{2}}}{\underline{\phi }}(x,y,t), \end{aligned}$$

and obtain the equations (dropping the primes for notational simplicity)

$$\begin{aligned}&\Delta {\underline{\phi }}=0,\qquad \qquad \qquad y<{\underline{\eta }}, \end{aligned}$$

(1.1)

$$\begin{aligned}&\Delta {\overline{\phi }}=0,\qquad \qquad \qquad {\underline{\eta }}<y<1+{\overline{\eta }}, \end{aligned}$$

(1.2)

with boundary conditions

$$\begin{aligned} \partial _t{\underline{\eta }}&={\underline{\phi }}_y-{\underline{\eta }}_x{\underline{\phi }}_x,&y={\underline{\eta }}, \end{aligned}$$

(1.3)

$$\begin{aligned} \partial _t{\underline{\eta }}&={\overline{\phi }}_y-{\underline{\eta }}_x{\overline{\phi }}_x,&y={\underline{\eta }}, \end{aligned}$$

(1.4)

$$\begin{aligned} \partial _t{\overline{\eta }}&={\overline{\phi }}_y-{\overline{\eta }}_x{\overline{\phi }}_x,&y=1+{\overline{\eta }}, \end{aligned}$$

(1.5)

$$\begin{aligned} \nabla {\underline{\phi }}&\rightarrow 0,&y\rightarrow -\infty , \end{aligned}$$

(1.6)

and

$$\begin{aligned}&\rho \left( \partial _t{\overline{\phi }}+\frac{1}{2}|\nabla {\overline{\phi }}|^2+{\underline{\eta }}\right) -\left( \partial _t{\underline{\phi }}+\frac{1}{2}|\nabla {\underline{\phi }}|^2+{\underline{\eta }}\right) =-{\underline{\beta }} \left( \frac{{\underline{\eta }}_x}{\sqrt{1+{\underline{\eta }}_x^2}}\right) _x, y={\underline{\eta }}, \end{aligned}$$

(1.7)

$$\begin{aligned}&\partial _t{\overline{\phi }}+\frac{1}{2}|\nabla {\overline{\phi }}|^2+{\overline{\eta }}={\overline{\beta }}\left( \frac{{\overline{\eta }}_x}{\sqrt{1+{\overline{\eta }}_x^2}}\right) _x, y=1+{\overline{\eta }}, \end{aligned}$$

(1.8)

in which $\rho :={\overline{\rho }}/{\underline{\rho }}\in (0,1)$, ${\underline{\beta }}:={\underline{\sigma }}/(g {\overline{h}}^2 {\underline{\rho }})>0$ and ${\overline{\beta }}:={\overline{\sigma }}/(g {\overline{h}}^2 {\overline{\rho }})>0$. The total energy

$$\begin{aligned} {\mathcal {E}}&=\frac{1}{2}\int _{{\overline{\Sigma }}(\varvec{\eta })}\rho |\nabla {\overline{\phi }}|^2\,\mathrm{d}x\, \mathrm{d}y+\frac{1}{2}\int _{{\underline{\Sigma }}({{\underline{\eta }}})}|\nabla {\underline{\phi }}|^2\,\mathrm{d}x\, \mathrm{d}y\\&\quad +\frac{1}{2}\int _{{\mathbb {R}}}(1-\rho ){\underline{\eta }}^2\,\mathrm{d}x\\&\quad +\frac{1}{2}\int _{{\mathbb {R}}}\rho \,{\overline{\eta }}^2\,\mathrm{d}x +\int _{{\mathbb {R}}}{\underline{\beta }} \left( \sqrt{1+{\underline{\eta }}_x^2}-1\right) \,\mathrm{d}x\\&\quad +\int _{{\mathbb {R}}}\rho {\overline{\beta }} \left( \sqrt{1+{\overline{\eta }}_x^2}-1\right) \,\mathrm{d}x \end{aligned}$$

and the total horizontal momentum

$$\begin{aligned} {\mathcal {I}}=\int _{{\mathbb {R}}} {\underline{\eta }}_x ({\underline{\phi }}|_{y={\underline{\eta }}}-\rho {\overline{\phi }}|_{y={\underline{\eta }}})\,\mathrm{d}x + \rho \int _{{\mathbb {R}}} {\overline{\eta }}_x {\overline{\phi }}|_{y=1+{\overline{\eta }}}\,\mathrm{d}x \end{aligned}$$

are conserved quantities.

Our interest lies in solitary-wave solutions of (1.1)–(1.8), that is, localised waves of permanent form which propagate in the negative x-direction with constant (dimensionless) speed $\nu >0$, so that ${\underline{\eta }}(x,t)={\underline{\eta }}(x+\nu t)$, ${\overline{\eta }}(x,t)={\underline{\eta }}(x+\nu t)$, ${\underline{\phi }}(x,y,t)={\underline{\phi }}(x+\nu t,y)$ and ${\overline{\phi }}(x,y,t)={\overline{\phi }}(x+\nu t,y)$, and ${\underline{\eta }}(x+\nu t), {\overline{\eta }}(x+\nu t) \rightarrow 0$ as $|x+\nu t|\rightarrow \infty$. Figure 1 contains a sketch of the physical setting.

Fig. 1

Sketch of the physical setting and the waves obtained in this paper (in dimensionless variables)

1.2 Heuristics

The existence of small-amplitude solitary waves can be predicted by studying the dispersion relation of the linearised version of (1.1)–(1.8). Instead of linearising (1.1)–(1.8) directly, we may derive the dispersion relation by using the fact that these waves are minimisers of an energy functional ${\mathcal {J}}_\mu (\varvec{\eta })={\mathcal {K}}(\varvec{\eta })+\mu ^2/{\mathcal {L}}(\varvec{\eta })$, where $\mu$ is the momentum (see Sect. 1.3 below). Writing the corresponding Euler–Lagrange equation in the form ${\mathcal {K}}'(\varvec{\eta })-\nu ^2 {\mathcal {L}}'(\varvec{\eta })=0$, where $\nu =\mu /{\mathcal {L}}(\varvec{\eta })$ is the wave speed, linearising and substituting the ansatz $\varvec{\eta }(x)=\cos (kx) \varvec{v}$, with $\varvec{v}$ a constant vector, leads to the equation

$$\begin{aligned} (P(k)-\nu ^2 F(k))\varvec{v}=0, \end{aligned}$$

where

$$\begin{aligned} P(k)= & {} \begin{pmatrix} 1-\rho +{\underline{\beta }}|k|^2 &{}\quad 0 \\ 0 &{}\quad \rho (1+{\overline{\beta }}|k|^2) \end{pmatrix} \quad \text {and} \nonumber \\ F(k)= & {} \begin{pmatrix} |k|+\rho |k| \coth |k|&{}\quad -\rho \frac{|k|}{\sinh |k|}\\ -\rho \frac{|k|}{\sinh |k|}&{}\quad \rho |k| \coth |k| \end{pmatrix}. \end{aligned}$$

(1.9)

(The formula for ${\mathcal {J}}_\mu '(\varvec{\eta })$ and its linearisation can be obtained from Lemmas A.27 and A.28.) Equivalently, $\nu ^2$ is an eigenvalue and $\varvec{v}$ an eigenvector of the matrix

$$\begin{aligned}&F(k)^{-1} P(k)= \frac{1}{|k| \coth |k|+\rho |k|}\\&\quad \begin{pmatrix} (1-\rho +{\underline{\beta }}|k|^2)\coth |k| &{}\quad (1+{\overline{\beta }}|k|^2)\frac{\rho }{\sinh |k|} \\ (1-\rho +{\underline{\beta }}|k|^2)\frac{1}{\sinh |k|}&{}\quad (1+{\overline{\beta }}|k|^2)\left( 1+ \rho \coth |k|\right) \end{pmatrix} \end{aligned}$$

(assuming that $k\ne 0$ so that F(k) is invertible). The eigenvalues are given by

$$\begin{aligned} \lambda _\pm (k) = \frac{(1-\rho +{\underline{\beta }}|k|^2)+(1+{\overline{\beta }}|k|^2)(\tanh |k|+\rho )}{2|k|(1+\rho \tanh |k|)} \pm \frac{1}{2|k|(1+\rho \tanh |k|)}\sqrt{D(k)}, \end{aligned}$$

with

$$\begin{aligned} D(k)&= \left( (1-\rho +{\underline{\beta }}|k|^2)-\left( \tanh |k|+\rho \right) (1+{\overline{\beta }}|k|^2)\right) ^2\\&\quad +\frac{4\rho }{\cosh ^2|k|}(1-\rho +{\underline{\beta }}|k|^2)(1+{\overline{\beta }}|k|^2) >0. \end{aligned}$$

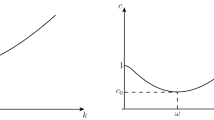
It follows that $\lambda _-(k)<\lambda _+(k)$ for all $k\ne 0$, meaning that for each wavenumber $k\ne 0$ there is an associated ‘slow’ speed $\sqrt{\lambda _-(k)}$ and a ‘fast’ speed $\sqrt{\lambda _+(k)}$ (see Fig. 2). Moreover,

$$\begin{aligned} \lambda _+(k) =\frac{1}{|k|}+O(|k|) \quad \text {and} \quad \lambda _-(k) =1-\rho -\rho (1-\rho )|k|+O(|k|^2) \end{aligned}$$

as $k\rightarrow 0$. As $|k|\rightarrow \infty$ we have that

$$\begin{aligned} \lambda _\pm (k) = \frac{{\underline{\beta }}+(1+\rho ){\overline{\beta }} \pm \left| {\underline{\beta }}- \left( 1+\rho \right) {\overline{\beta }}\right| }{2(1+\rho )} |k|+O(1). \end{aligned}$$

Since

$$\begin{aligned} \left| {\underline{\beta }}- \left( 1+\rho \right) {\overline{\beta }}\right| <{\underline{\beta }}+(1+\rho ){\overline{\beta }}, \end{aligned}$$

we have that $\lambda _\pm (k) \rightarrow \infty$ as $|k|\rightarrow \infty$. In view of the behaviour at 0, we conclude that $\lambda _-(k)$ is minimised at some $k=k_0>0$.

Fig. 2

Dispersion relation for the parameter values $\rho =0.5$, ${\underline{\beta }}=1$ and ${\overline{\beta }}=0.2$. The dispersion relation has a slow branch $\lambda _-(k)$ and a fast branch $\lambda _+(k)$

In order to find solitary waves we will assume the following non-degeneracy conditions.

Assumption 1.1

$$\begin{aligned} \lambda _-(k)>\lambda _-(k_0) \quad \text {for } k\ne \pm k_0 \end{aligned}$$

(1.10)

and

$$\begin{aligned} \lambda _-''(k_0)>0. \end{aligned}$$

(1.11)

The first part of the assumption is introduced in order to avoid resonances. The second part is introduced in order to obtain inequality (1.14) below. This in turn dictates the choice of model equation (the cubic nonlinear Schrödinger equation). We note that these conditions are satisfied for generic parameter values, but that there are exceptions; see Figs. 3 and 4.

Set $\nu _0=\sqrt{\lambda _-(k_0)}$ and note that $\varvec{v}_0=(1,-a)$ is an eigenvector to the eigenvalue $\nu _0^2$ of the matrix $F(k_0)^{-1}P(k_0)$, in which

$$\begin{aligned} a= \frac{\tfrac{1}{2}(1-\rho +{\underline{\beta }}|k_0|^2)- \tfrac{1}{2} (1+{\overline{\beta }}|k_0|^2)(\tanh |k_0|+\rho )+\tfrac{1}{2} \sqrt{D(k_0)}}{(\rho +{\overline{\beta }}|k_0|^2)\frac{1}{\cosh |k|} } >0.\nonumber \\ \end{aligned}$$

(1.12)

For future use we also introduce the matrix-valued function

$$\begin{aligned} g(k)&:=P(k)-\nu _0^2 F(k)\nonumber \\&= \begin{pmatrix} 1-\rho +{\underline{\beta }}|k|^2 &{}\quad 0 \\ 0 &{}\quad \rho +\rho {\overline{\beta }}|k|^2 \end{pmatrix} -\nu _0^2\begin{pmatrix} |k|+\rho |k| \coth |k|&{}\quad -\rho \frac{|k|}{\sinh |k|} \\ -\rho \frac{|k|}{\sinh |k|}&{}\quad \rho |k| \coth |k| \end{pmatrix}, \end{aligned}$$

(1.13)

which satisfies $g(k_0)\varvec{v}_0=0$ and (due to the second part of Assumption 1.1 and evenness)

$$\begin{aligned} g(k) \varvec{w} \cdot \varvec{w} \ge (\lambda _-(k)-\lambda _-(k_0)) F(k) \varvec{w} \cdot \varvec{w} \ge c(|k|-k_0)^2 |\varvec{w}|^2 \end{aligned}$$

(1.14)

for $||k|-k_0|\ll 1$, where c is a positive constant.

Fig. 3

Graphs of $\lambda _-(k)$ for $\rho =0.5$, ${\underline{\beta }}=1$ and three different values of ${\overline{\beta }}$. In cases (a) and (c) both conditions (1.10) and (1.11) are satisfied. In case (b) condition (1.10) is violated

Fig. 4

Numerical computations indicate that $\lambda _-(k)$ has a degenerate minimum at $k=1$ ($\lambda '(1)=\lambda ''(1)=\lambda '''(1)=0$, $\lambda ^{(iv)}(1)>0$) for $\rho \approx 0.063$, ${\underline{\beta }}\approx 0.939$, ${\overline{\beta }}\approx 0.232$, in violation of condition (1.11)

Bifurcations of nonlinear solitary waves are expected whenever the linear group and phase speeds are equal, so that $\nu ^\prime (k)=0$ [see Dias and Kharif (1999, Sect. 3)]. We therefore expect the existence of small-amplitude solitary waves with speed near $\nu _0$, bifurcating from a linear periodic wave train with frequency $k_0 \nu _0$. Making the ansatz

$$\begin{aligned} \eta= & {} \frac{1}{2}\mu (A(X,T)\mathrm {e}^{{i}k_0(x+\nu _0 t)}+\mathrm {c.c.}){\varvec{v}}_0+O(\mu ^2), \\ X= & {} \mu (x+\nu _0 t),\qquad T=2 k_0 (\nu _0 F(k_0)\varvec{v}_0\cdot \varvec{v}_0)^{-1} \mu ^2 t, \end{aligned}$$

where ‘$\mathrm {c.c.}$’ denotes the complex conjugate of the preceding quantity, and expanding in powers of $\mu$ one obtains the cubic nonlinear Schrödinger equation

$$\begin{aligned} 2{i}A_T -\tfrac{1}{4}A_2 A_{XX} + \tfrac{3}{2}\left( \tfrac{1}{2} A_3+A_4\right) |A|^2 A =0, \end{aligned}$$

(1.15)

for the complex amplitude A, in which

$$\begin{aligned} A_2=g''(k_0)\varvec{v}_0\cdot \varvec{v}_0 \end{aligned}$$

and $A_3$ and $A_4$ are functions of $\rho$, ${\underline{\beta }}$ and ${\overline{\beta }}$ which are given in Proposition 2.27 and Corollary  2.24. At this level of approximation a standing wave solution to Eq. (1.15) of the form $A(X,T)=\mathrm {e}^{i\nu _\mathrm {NLS}\,T}\phi (X)$ with $\phi (X) \rightarrow 0$ as $X \rightarrow \pm \infty$ corresponds to a solitary water wave with speed

$$\begin{aligned} \nu =\nu _0 + 2 (\nu _0 F(k_0)\varvec{v}_0\cdot \varvec{v}_0)^{-1} \mu ^2\nu _\mathrm {NLS}. \end{aligned}$$

Lemma 1.2

$A_2>0$ under Assumption 1.1.

Proof

Let $\varvec{v}(k)$ be a smooth curve of eigenvectors of $F(k)^{-1}P(k)$ corresponding to the eigenvalue $\lambda _-(k)$ with $\varvec{v}(0)=\varvec{v}_0$. Then

$$\begin{aligned} (P'(k)-\lambda _-(k) F'(k))\varvec{v}(k)+(P(k)-\lambda _-(k) F(k))\varvec{v}'(k)=\lambda _-'(k)F(k)\varvec{v}(k) \end{aligned}$$

and

$$\begin{aligned}&(P''(k)-\lambda _-(k) F''(k))\varvec{v}(k)+2(P'(k)-\lambda _-(k) F'(k))\varvec{v}'(k)\\&\qquad +(P(k)-\lambda _-(k) F(k))\varvec{v}''(k)\\&\quad =\lambda _-''(k) F(k)\varvec{v}(k)+2\lambda _-'(k)F'(k)\varvec{v}(k)+2\lambda _-'(k)F(k)\varvec{v}'(k). \end{aligned}$$

Evaluating the first equation at $k=k_0$ and using that $\lambda _-'(k_0)=0$, we find that

$$\begin{aligned} g'(k_0)\varvec{v}_0 =- g(k_0) \varvec{v}'(k_0). \end{aligned}$$

Taking the scalar product of the second equation with $\varvec{v}(k)$, evaluating at $k=k_0$ and using the previous equality, we therefore find that

$$\begin{aligned} g''(k_0) \varvec{v}_0\cdot \varvec{v}_0=\lambda _-''(k_0) F(k_0)\varvec{v}_0\cdot \varvec{v}_0+2g(k_0)\varvec{v}'(k_0)\cdot \varvec{v}'(k_0), \end{aligned}$$

where we have also used that $g(k_0)\varvec{v}_0=0$. This concludes the proof since $\lambda _-''(k_0)>0$ and $F(k_0)$ and $g(k_0)$ are positive definite. $\square$

It follows that a necessary and sufficient condition for Eq. (1.15) to possess solitary standing waves is that the coefficient in front of the cubic term is negative.

Assumption 1.3

$$\begin{aligned} \frac{1}{2} A_3+A_4<0. \end{aligned}$$

(1.16)

It seems difficult to give a general criterion for when this assumption is satisfied. In specific cases it can be verified numerically.

Example 1.4

Consider the two choices of parameter values in Fig. 3a, c, that is, $\rho =0.5$, ${\underline{\beta }}=1$ and (a) ${\overline{\beta }}=0.04$ or (c) ${\overline{\beta }}=0.07$. Numerical computations reveal that $k_0\approx 4.99$ and $\frac{1}{2} A_3 +A_4\approx -2.11 \times 10^{13}$ in case (a), while $k_0 \approx 0.245$ and $\frac{1}{2} A_3 +A_4\approx -50.7$ in case (c). Thus, Assumption 1.3 is satisfied in both cases.

Furthermore, in some cases it is possible to verify both Assumptions 1.1 and 1.3 using asymptotic analysis.

Example 1.5

Assume that ${\underline{\beta }}<1/4$ and ${\overline{\beta }}\ge 1/3$, and consider the limit $\rho \rightarrow 0$. Straightforward computations show that

$$\begin{aligned} \lambda _-(k) \rightarrow \lambda _-^\star (k):=\min \left\{ \frac{(1+{\overline{\beta }}|k|^2) \tanh |k|}{|k|}, \frac{1+{\underline{\beta }}|k|^2}{|k|}\right\} \end{aligned}$$

locally uniformly. Moreover, all derivatives also converge locally uniformly away from points where the two functions in the bracket are equal (that is, where $D^\star (k):=((1+{\underline{\beta }}|k|^2)-(1+{\overline{\beta }}|k|^2)\tanh |k|)^2=0$). Since $\lambda _-^\star (k)$ has a unique strict and non-degenerate positive global minimiser $k_0^\star =1/\sqrt{{\underline{\beta }}}$ with

$$\begin{aligned} \lambda _-^\star (k_0^\star )=2\sqrt{{\underline{\beta }}} <1 \end{aligned}$$

(note that $(1+{\overline{\beta }}|k|^2) \tanh |k|/|k| \ge 1$ under the assumption ${\overline{\beta }}\ge 1/3$) and $\lim _{|k|\rightarrow \infty } \lambda _-(k)=\infty$ uniformly in $\rho$, we find that $\lambda _-(k)$ has a unique strict and non-degenerate positive global minimiser $k_0$ for sufficiently small $\rho$, and that $k_0\rightarrow 1/\sqrt{{\underline{\beta }}}$ and $\lambda _-(k_0)\rightarrow 2\sqrt{{\underline{\beta }}}$ as $\rho \rightarrow 0$. Using the formulas in Propositions 2.23, 2.27 and Corollary 2.24 one now verifies that

$$\begin{aligned} \frac{1}{2} A_3+A_4\rightarrow -\frac{33}{72 {\underline{\beta }}}<0 \end{aligned}$$

as $\rho \rightarrow 0$. Thus, under the conditions ${\underline{\beta }}<1/4$ and ${\overline{\beta }}\ge 1/3$, Assumptions 1.1 and 1.3 are both satisfied if $\rho$ is sufficiently small.

Example 1.6

Consider next the limit ${\overline{h}} \rightarrow \infty$. Note that ${\overline{\beta }}, {\underline{\beta }}\rightarrow 0$ as $h \rightarrow \infty$. Moreover, we expect $k_0$ to diverge. Therefore, it is convenient to introduce the new length scale $h:=\sqrt{{\underline{\sigma }}/(g{\underline{\rho }})}$, the non-dimensional length parameter $H:={\overline{h}}/h$, the non-dimensional surface tension parameter $B:={\overline{\beta }} H^2={\overline{\beta }}/{\underline{\beta }}={\overline{\sigma }}/(\rho {\underline{\sigma }})$ (note that ${\underline{\beta }}=1/H^2$) and the new non-dimensional wavenumber $K:=k/H$. We then find that

$$\begin{aligned} H\lambda _\pm (k)&= \frac{(1-\rho +|K|^2)+(1+B|K|^2)(\tanh (|K|H)+\rho )}{2|K|(1+\rho \tanh (|K|H))}\\&\quad \pm \frac{1}{2|K|(1+\rho \tanh (|k|H))}\sqrt{D(k)}, \end{aligned}$$

with

$$\begin{aligned} D(k)&= \left( (1-\rho + |K|^2)-\left( \tanh (|K|H)+\rho \right) (1+B|K|^2)\right) ^2\\&\quad +\frac{4\rho }{\cosh ^2(|K|H)}(1-\rho +|K|^2)(1+B|K|^2). \end{aligned}$$

It follows that

$$\begin{aligned} H \lambda _{-}(k)\rightarrow \lambda _-^\star (K):=\min \left\{ \frac{1-\rho + |K|^2}{(1+\rho )|K|}, \frac{1 + B |K|^2}{|K|}\right\} \end{aligned}$$

uniformly for $|K|\ge \delta$, where $\delta >0$ is arbitrary, and that all derivatives converge uniformly on the same set away from points where the functions within the brackets coincide. On the other hand, $H\lambda _-(k)$ can be made arbitrarily large for $|K|\le \delta$ by first choosing $\delta$ sufficiently small and then H sufficiently large depending on $\delta$. Choosing $B>(1-\rho )/(1+\rho )^2$, we find that the function $\lambda _-^\star (K)$ has the unique strict and non-degenerate positive global minimiser $K_0^\star =\sqrt{1-\rho }$ with

$$\begin{aligned} \lambda _-^\star (K_0^\star )= \frac{2 \sqrt{1-\rho }}{1+\rho }. \end{aligned}$$

Therefore, $\lambda _-(k)$ has a unique strict and strict and non-degenerate positive global minimiser $k_0$ for large H with $k_0/H\rightarrow K_0^\star$ as $H\rightarrow \infty$. Straightforward computations now yield

$$\begin{aligned} \frac{\frac{1}{2} A_3+A_4}{H^2} \rightarrow -\frac{(1-\rho )^2}{24(1+\rho )^2}(11\rho ^2-42\rho +11) \end{aligned}$$

as $H\rightarrow \infty$. The right-hand side is negative for $\rho <\rho ^\star =(21-8\sqrt{5})/11\approx 0.28$ and positive for $\rho >\rho ^\star$. Thus, if $B>(1-\rho )/(1+\rho )^2$ and $\rho <\rho ^\star$ both Assumptions 1.1 and 1.3 are satisfied if ${\overline{h}}$ is sufficiently large, while if $\rho >\rho ^\star$ then Assumption 1.1 is satisfied but not Assumption 1.3.

The following lemma gives a variational description of the set of solitary waves of the nonlinear Schrödinger equation (1.15) [see Cazenave (2003, Sect. 8)].

Lemma 1.7

Assume that $A_2>0$ and $\frac{1}{2} A_3+A_4<0$. The set of complex-valued solutions to the ordinary differential equation

$$\begin{aligned} -\frac{1}{4}A_2\phi ^{\prime \prime }-2\nu _\mathrm {NLS}\phi +\frac{3}{2}\left( \frac{A_3}{2}+A_4\right) |\phi |^2\phi =0 \end{aligned}$$

satisfying $\phi (X) \rightarrow 0$ as $X \rightarrow \infty$ is $D_\mathrm {NLS} = \{\mathrm {e}^{{i}\omega }\phi _\mathrm {NLS}(\cdot + y):\omega \in [0,2\pi ), y \in {\mathbb {R}}\},$ where

$$\begin{aligned} \nu _\mathrm {NLS}&= -\frac{9\alpha _\mathrm {NLS}^2}{8A_2}\left( \frac{A_3}{2}+A_4\right) ^{\!\!2}, \\ \phi _\mathrm {NLS}(x)&= \alpha _\mathrm {NLS}\left( -\frac{3}{A_2}\left( \frac{A_3}{2}+A_4\right) \right) ^{\!\!\frac{1}{2}} \mathrm {sech}\,\left( -\frac{3\alpha _\mathrm {NLS}}{A_2}\left( \frac{A_3}{2}+A_4\right) x\right) . \end{aligned}$$

These functions are precisely the minimisers of the functional ${\mathcal {E}}_\mathrm {NLS}:H^1({\mathbb {R}}) \rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} {\mathcal {E}}_\mathrm {NLS}(\phi )=\int _{{\mathbb {R}}}\left\{ \frac{1}{8}A_2|\phi ^\prime |^2 +\frac{3}{8}\left( \frac{A_3}{2}+A_4\right) |\phi |^4\right\} \, \mathrm{d}x\end{aligned}$$

over the set $N_\mathrm {NLS} = \{\phi \in H^1({\mathbb {R}}): \Vert \phi \Vert _0^2=2\alpha _\mathrm {NLS}\}$, where $\alpha _\mathrm {NLS}=2(\nu _0 k_0+\nu _0\rho {\overline{F}}(k_0)\varvec{v}_0\cdot \varvec{v}_0)^{-1}$; the constant $2\nu _\mathrm {NLS}$ is the Lagrange multiplier in this constrained variational principle and

$$\begin{aligned} I_\mathrm {NLS}:=\inf \left\{ {\mathcal {E}}_\mathrm {NLS}(\phi ):\phi \in N_\mathrm {NLS}\right\} =-\frac{3\alpha _\mathrm {NLS}^3}{4A_2}\left( \frac{A_3}{2}+A_4\right) ^{\!\!2}. \end{aligned}$$

1.3 Main Results

The main result of this paper is an existence theory for small-amplitude solitary-wave solutions to Eqs. (1.1)–(1.8) under Assumptions 1.1 and 1.3. The waves are constructed by minimising the energy functional ${\mathcal {E}}$ subject to the constraint of fixed horizontal momentum ${\mathcal {I}}$; see Theorem 2.4 for a precise statement. As a consequence of the existence result we also obtain a stability result for the set of minimisers; see Theorem 2.5.

Before describing our approach in further detail, we note that the above formulation of the hydrodynamic problem has the disadvantage of being posed in a priori unknown domains. It is therefore convenient to reformulate the problem in terms of the traces of the velocity potentials on the free surface and interface. We denote the boundary values of the velocity potentials by ${\underline{\Phi }}(x):={\underline{\phi }}(x,{\underline{\eta }}(x))$ and $\overline{\varvec{\Phi }}(x)=({\overline{\Phi }}_i(x),{\overline{\Phi }}_s(x))$ where ${\overline{\Phi }}_i(x):={\overline{\phi }}(x,{\underline{\eta }}(x))$ and ${\overline{\Phi }}_s(x):={\overline{\phi }}(x,1+{\overline{\eta }}(x))$. Following Kuznetsov and Lushnikov (1995) and Benjamin and Bridges (1997) (see also Craig and Groves 2000; Craig et al. 2005) we set

$$\begin{aligned} {\underline{\xi }}(x):={\underline{\Phi }}(x)-\rho {\overline{\Phi }}_i(x),\qquad {\overline{\xi }}(x):=\rho {\overline{\Phi }}_s(x); \end{aligned}$$

(1.17)

the natural choice of canonical variables is $(\varvec{\eta },\varvec{\xi })$, where $\varvec{\eta }=({\underline{\eta }},{\overline{\eta }})$, $\varvec{\xi }=({\underline{\xi }},{\overline{\xi }})$. We formally define Dirichlet–Neumann operators ${\underline{G}}({\underline{\eta }})$ and ${\overline{G}}(\varvec{\eta })$ which map (for a given $\varvec{\eta }$) Dirichlet boundary data of solutions of the Laplace equation to the Neumann boundary data, i.e.

$$\begin{aligned} {\underline{G}}({\underline{\eta }}){\underline{\Phi }}&:=(1+{\underline{\eta }}_x^2)^{\frac{1}{2}}(\nabla {\underline{\phi }}\cdot \underline{\varvec{n}})|_{y={\underline{\eta }}},\\ {\overline{G}}(\varvec{\eta })\overline{\varvec{\Phi }}&:=\begin{pmatrix}{\overline{G}}_{11}(\varvec{\eta })&{}{\overline{G}}_{12}(\varvec{\eta })\\ {\overline{G}}_{21}(\varvec{\eta })&{}{\overline{G}}_{22}(\varvec{\eta })\end{pmatrix}\begin{pmatrix}{\overline{\Phi }}_i\\ {\overline{\Phi }}_s\end{pmatrix}:=\begin{pmatrix} -(1+{\underline{\eta }}_x^2)^{\frac{1}{2}}(\nabla {\overline{\phi }}\cdot \underline{\varvec{n}})|_{y={\underline{\eta }}}\\ (1+{\overline{\eta }}_x^2)^{\frac{1}{2}}(\nabla {\overline{\phi }}\cdot \overline{\varvec{n}})|_{y=1+{\overline{\eta }}}\end{pmatrix}; \end{aligned}$$

see Appendix A for the rigorous definition. Note that ${\underline{G}}$ only depends on ${\underline{\eta }}$, whereas ${\overline{G}}$ depends on ${\underline{\eta }}$ and ${\overline{\eta }}$. The boundary conditions (1.3)–(1.4) imply that

$$\begin{aligned} {\underline{G}}({\underline{\eta }}){\underline{\Phi }}=-({\overline{G}}_{11}(\varvec{\eta }){\overline{\Phi }}_i +{\overline{G}}_{12}(\varvec{\eta }){\overline{\Phi }}_s). \end{aligned}$$

(1.18)

If we define

$$\begin{aligned} B(\varvec{\eta }):={\overline{G}}_{11}(\varvec{\eta })+\rho {\underline{G}}({\underline{\eta }}), \end{aligned}$$

(1.19)

we can recover ${\underline{\Phi }}$ and ${\overline{\Phi }}$ from $\varvec{\xi }$ using the formulas

$$\begin{aligned} \begin{aligned} {\underline{\Phi }}&=B^{-1}{\overline{G}}_{11}{\underline{\xi }}-B^{-1}{\overline{G}}_{12}{\overline{\xi }},\\ {\overline{\Phi }}_i&=-B^{-1}{\underline{G}}{\underline{\xi }}-\frac{1}{\rho } B^{-1}{\overline{G}}_{12}{\overline{\xi }},\\ {\overline{\Phi }}_s&=\frac{1}{\rho } {\overline{\xi }}, \end{aligned} \end{aligned}$$

(1.20)

under assumption (1.18). Moreover, the total energy and horizontal momentum can be re-expressed as

$$\begin{aligned} {\mathcal {E}}(\varvec{\eta }, \varvec{\xi })= & {} \int _{{\mathbb {R}}} \left\{ \frac{1}{2}\varvec{\xi }\, G(\varvec{\eta })\varvec{\xi }+\frac{1-\rho }{2}{\underline{\eta }}^2+\frac{\rho }{2}\,{\overline{\eta }}^2\right. \nonumber \\&\left. +{\underline{\beta }} \left( \sqrt{1+{\underline{\eta }}_x^2}-1\right) +\rho {\overline{\beta }} \left( \sqrt{1+{\overline{\eta }}_x^2}-1\right) \right\} \,\mathrm{d}x \end{aligned}$$

(1.21)

and

$$\begin{aligned} {\mathcal {I}}(\varvec{\eta },\varvec{\xi })=\int _{{\mathbb {R}}} {\underline{\eta }}_x {\underline{\xi }}\,\mathrm{d}x + \int _{{\mathbb {R}}} {\overline{\eta }}_x {\overline{\xi }}\,\mathrm{d}x, \end{aligned}$$

(1.22)

respectively, where we have abbreviated

$$\begin{aligned} G(\varvec{\eta }):=\begin{pmatrix}{\underline{G}}({\underline{\eta }}) B(\varvec{\eta })^{-1}{\overline{G}}_{11}(\varvec{\eta }) &{}\quad -{\underline{G}}({\underline{\eta }})B(\varvec{\eta })^{-1}{\overline{G}}_{12}(\varvec{\eta })\\ -{\overline{G}}_{21}(\varvec{\eta })B(\varvec{\eta })^{-1}{\underline{G}}({\underline{\eta }})&{}\quad \tfrac{1}{\rho }{\overline{G}}_{22}(\varvec{\eta })-\tfrac{1}{\rho }{\overline{G}}_{21}(\varvec{\eta })B(\varvec{\eta })^{-1}{\overline{G}}_{12}(\varvec{\eta })\end{pmatrix}.\nonumber \\ \end{aligned}$$

(1.23)

Note that

$$\begin{aligned} G(\varvec{\eta })\varvec{\xi }=\begin{pmatrix}{\underline{G}}({\underline{\eta }}){\underline{\Phi }} \\ {\overline{G}}_{21}(\varvec{\eta }){\overline{\Phi }}_s+{\overline{G}}_{22}(\varvec{\eta }){\overline{\Phi }}_i\end{pmatrix}. \end{aligned}$$

We now give a brief outline of the variational existence method. We tackle the problem of finding minimisers of ${\mathcal {E}}(\varvec{\eta }, \varvec{\xi })$ under the constraint ${\mathcal {I}}(\varvec{\eta },\varvec{\xi })=2\mu$ in two steps.

• 1. Fix $\varvec{\eta }\ne 0$ and minimise ${\mathcal {E}}(\varvec{\eta },\cdot )$ over $T_\mu :=\left\{ \varvec{\xi }\in {{\tilde{X}}} :{\mathcal {I}}(\varvec{\eta },\varvec{\xi })=2\mu \right\}$, where the space ${{\tilde{X}}}$ is defined in Definition A.16. This problem (of minimising a quadratic functional over a linear manifold) admits a unique global minimiser $\varvec{\xi }$.

• 2. Minimise ${\mathcal {J}}_\mu (\varvec{\eta }):={\mathcal {E}}(\varvec{\eta },\varvec{\xi }_{\varvec{\eta }})$ over $\varvec{\eta }\in U{\setminus }\{0\}$ with $U:=B_M(0)\subset (H^2({\mathbb {R}}))^2$. Because $\varvec{\xi }_{\varvec{\eta }}$ minimises ${\mathcal {E}}(\varvec{\eta },\cdot )$ over $T_\mu$ there exists a Lagrange multiplier $\gamma _{\varvec{\eta }}$ such that

  $$\begin{aligned} G(\varvec{\eta })\varvec{\xi }_{\varvec{\eta }}=\gamma _{\varvec{\eta }} \varvec{\eta }_x. \end{aligned}$$

  Hence,

  $$\begin{aligned} \varvec{\xi }_{\varvec{\eta }}&=\gamma _{\varvec{\eta }}G(\varvec{\eta })^{-1}\varvec{\eta }_x. \end{aligned}$$

  Furthermore, we get

  $$\begin{aligned} \gamma _{\varvec{\eta }}=\frac{\mu }{{\mathcal {L}}(\varvec{\eta })}, \qquad {\mathcal {L}}(\varvec{\eta })=\frac{1}{2}\int _{{{\mathbb {R}}}}\varvec{\eta }K(\varvec{\eta })\varvec{\eta }\,\mathrm{d}x, \end{aligned}$$

  (1.24)

  where

  $$\begin{aligned} K(\varvec{\eta })=-\partial _x G(\varvec{\eta })^{-1}\partial _x = -\partial _x \begin{pmatrix} \rho {\overline{N}}_{11}(\varvec{\eta }) +{\underline{N}}({\underline{\eta }}) &{}\quad -\rho {\overline{N}}_{12}(\varvec{\eta })\ \\ -\rho {\overline{N}}_{21}(\varvec{\eta }) &{}\quad \rho {\overline{N}}_{22}(\varvec{\eta }) \end{pmatrix}\partial _x,\nonumber \\ \end{aligned}$$

  (1.25)

  with ${\underline{N}}({\underline{\eta }}):={\underline{G}}({\underline{\eta }})^{-1}$ and

  $$\begin{aligned} {\overline{N}}(\eta )= \begin{pmatrix} {\overline{N}}_{11}(\varvec{\eta })&{}\quad {\overline{N}}_{12}(\varvec{\eta })\\ {\overline{N}}_{21}(\varvec{\eta })&{}\quad {\overline{N}}_{22}(\varvec{\eta }) \end{pmatrix} :={\overline{G}}(\varvec{\eta })^{-1}; \end{aligned}$$

  see Proposition A.19. For ${\mathcal {J}}_\mu (\varvec{\eta })$ we obtain the representation

  $$\begin{aligned} {\mathcal {J}}_\mu (\varvec{\eta })={\mathcal {K}}(\varvec{\eta })+\frac{\mu ^2}{{\mathcal {L}}(\varvec{\eta })}, \end{aligned}$$

  (1.26)

  where

  $$\begin{aligned} \begin{aligned} {\mathcal {K}}(\varvec{\eta })&=\underline{{\mathcal {K}}}({\underline{\eta }})+\overline{{\mathcal {K}}}({\overline{\eta }}),\\ \underline{{\mathcal {K}}}({\underline{\eta }})&= \int _{{\mathbb {R}}} \left\{ \frac{(1-\rho )}{2}{\underline{\eta }}^2 + {\underline{\beta }}\sqrt{1+{\underline{\eta }}_x^2}-{\underline{\beta }} \right\} \, \mathrm{d}x, \\ \overline{{\mathcal {K}}}({\overline{\eta }})&= \rho \int _{{\mathbb {R}}} \left\{ \frac{1}{2}{\overline{\eta }}^2 + {\overline{\beta }}\sqrt{1+{\overline{\eta }}_x^2}-{\overline{\beta }} \right\} \, \mathrm{d}x. \end{aligned} \end{aligned}$$

  We address the problem of minimising ${\mathcal {J}}_\mu$ using the concentration-compactness method. The main difficulties are that the functional is quasilinear, non-local and non-convex. These difficulties are partly solved by minimising over a bounded set in the function space, but we then have to prevent minimising sequences from converging to the boundary of this set. This is achieved by constructing a suitable test function and a special minimising sequence with good properties using the intuition from the nonlinear Schrödinger equation above.

Our approach is similar to that originally used by Buffoni (2004) to study solitary waves with strong surface tension on a single layer of fluid of finite depth, and later extended to deal with weak surface tension (Buffoni 2005, 2009; Groves and Wahlén 2010), infinite depth (Buffoni 2004; Groves and Wahlén 2011), fully localised three-dimensional waves (Buffoni et al. 2013) and constant vorticity (Groves and Wahlén 2015). Our main interest is in investigating the non-trivial modifications needed to deal with multi-layer flows. We give detailed explanations when needed and refer to the above papers for the details of the proofs when possible. In particular, a new challenge is that we need to consider vector-valued Dirichlet–Neumann operators. This is discussed in detail in Appendix A. Another novelty is related to the special minimising sequence mentioned above. Since $\varvec{\eta }$ is vector-valued it is not sufficient to prove that the spectrum of the special minimising sequence concentrates around the wavenumbers $\pm k_0$. In addition, we need to identify a leading term related to the zero eigenvector $\varvec{v}_0$ of the matrix $g(k_0)$ and estimate the minimising sequence in a more refined way. Finally, as already discussed in Sect. 1.2, the multi-layer case allows for a much richer variety of scenarios in the weakly nonlinear regime. In particular, this means that we have to make some assumptions in order for the approach to work. We have, however, made these as weak as possible, and the examples in Sect. 1.2 show that they are satisfied in important special cases.

Note that we could also have considered a bottom layer with finite depth. This introduces an additional dimensionless parameter in the problem (the ratio between the depths of the two layers), which allows for other phenomena. (For example, the slow speed can have a minimum at the origin.) We refer to Woolfenden and Părău (2011) for a discussion of the dispersion relation and numerical computations of solitary waves in the finite depth case. One of the reasons why we chose to look at the infinite depth problem is that it entails some technical challenges which invalidates the use of certain methods which are widely used to find solitary waves in hydrodynamics. In particular, the idea originally due to Kirchgässner (1982) of formulating the steady water-wave problem as an ill-posed evolution equation and applying a centre-manifold reduction cannot be used. The variational method that we use is less sensitive to these issues. Note, however, that Kirchgässner’s method has been extended to deal with the issues due to infinite depth by several authors (see Barrandon and Iooss 2005 and references therein) and this could have been used in order to construct solitary waves also in our setting. These methods give no information about stability, however.

As far as we are aware, there are no previous existence results for solitary waves in our setting. However, Iooss (1999) constructed small-amplitude periodic travelling-wave solutions of problem (1.1)–(1.8) in two situations. The first situation is when the parameters are chosen so that $\nu ^2=\lambda _+(k)$ or $\nu ^2=\lambda _-(k)$ for some wavenumber $k\ne 0$ which is not in resonance with any other wavenumber (i.e. $\lambda _{\pm }(nk) \ne \nu ^2$ for all $n\in {\mathbb {Z}}$) and $\lambda _\pm '(k) \ne 0$ (where the sign is chosen such that $\lambda _{\pm }(k)=\nu ^2$). The second situation is the 1 : 1 resonance, that is when k is a non-degenerate critical point of $\lambda _{\pm }$. In both situations he proved the existence of small-amplitude waves with period close to $2\pi /k$ using dynamical systems techniques. The second situation includes our setting, but is somewhat more general. (The critical point is, for example, not assumed to be a minimum.) There are also a number of papers dealing with solitary or generalised solitary waves (asymptotic to periodic solutions at spatial infinity) in the related settings where either one or both of the surface and interfacial tension vanish (see Barrandon 2006; Barrandon and Iooss 2005; Dias and Iooss 2003; Iooss et al. 2002; Lombardi and Iooss 2003; Sun and Shen 1993 and references therein). The variational method presented in this paper does not work in those settings since it requires both surface tension and interfacial tension. Finally, let us conclude this section by mentioning that our assumptions exclude two possibilities which could be interesting for further study (by variational or other methods), that is when $\lambda _-$ has a degenerate global minimum at $k_0$ (see Fig. 4) or when the minimum value is attained at two distinct wavenumbers (Fig. 3). Also, when Assumption 1.1 is satisfied, but the corresponding nonlinear Schrödinger equation is of defocussing type (so that Assumption 1.3 is violated), one would expect the existence of dark solitary waves.

2 Existence and Stability

This section contains the main results of the paper. We begin by proving that the functional ${\mathcal {J}}_\mu$ has a minimiser in $U\!\setminus \!\{0\}$. This is done by using concentration-compactness and penalisation methods as in Buffoni (2004, 2005, 2009), Buffoni et al. (2013), Groves and Wahlén (2011, 2015), and we refer to those papers for the details of some of the proofs. The outcome is the following result.

Theorem 2.1

Suppose that Assumptions 1.1 and 1.3 hold.

• (i) The set $C_\mu$ of minimisers of ${\mathcal {J}}_\mu$ over $U \!\setminus \!\{0\}$ is non-empty.

• (ii) Suppose that $\{\varvec{\eta }_n\}$ is a minimising sequence for ${\mathcal {J}}_\mu$ on $U\!\setminus \!\{0\}$ which satisfies

  $$\begin{aligned} \sup _{n\in {{\mathbb {N}}}} \Vert \varvec{\eta }_n\Vert _2 < M. \end{aligned}$$

  (2.1)

  There exists a sequence $\{x_n\} \subset {{\mathbb {R}}}$ with the property that a subsequence of$\{\varvec{\eta }_n(x_n+\cdot )\}$ converges in $(H^r({\mathbb {R}}))^2$, $0 \le r < 2$ to a function $\varvec{\eta }\in C_\mu$.

The first statement of the theorem is a consequence of the second statement, once the existence of a minimising sequence satisfying (2.1) has been established. The existence of such a sequence can be proved using a penalisation method, cf. Buffoni (2004), Buffoni et al. (2013) and Groves and Wahlén (2011, 2015). A key part of the proof of Theorem 2.1 is the existence of a suitable ‘test function’ $\varvec{\eta }_\star$ which satisfies the inequality

$$\begin{aligned} {\mathcal {J}}_\mu (\varvec{\eta }_\star )<2\nu _0\mu -c\mu ^3. \end{aligned}$$

This implies in particular that any minimising sequence $\{\varvec{\eta }_n\}$ satisfies this property for n sufficiently large. We construct such a test function in Appendix B. Once the existence of the test function has been proved, the remaining steps in the construction of the special minimising sequence satisfying (2.1) are similar to Buffoni (2004), Buffoni et al. (2013) and Groves and Wahlén (2011, 2015), to which we refer for further details. In fact, this special minimising sequence satisfies further properties which will be used below. (Note that a general minimising sequence satisfies the weaker estimate $\Vert \varvec{\eta }_n\Vert _1^2 \le c\mu$ by Proposition A.29.)

Theorem 2.2

Suppose that Assumptions 1.1 and 1.3 hold. There exists a minimising sequence $\{\tilde{\varvec{\eta }}_n\}$ for ${\mathcal {J}}_\mu$ over $U\!\setminus \!\{0\}$ with the properties that $\Vert \tilde{\varvec{\eta }}_n\Vert _2^2 \le c \mu$ and ${\mathcal {J}}_\mu (\tilde{\varvec{\eta }}_n) < 2\nu _0\mu -c\mu ^3$ for each $n \in {{\mathbb {N}}}$, and $\lim _{n \rightarrow \infty }\Vert {\mathcal {J}}_\mu ^\prime (\tilde{\varvec{\eta }}_n)\Vert _0=0$.

The second statement of Theorem 2.1 is proved by applying the concentration-compactness principle (Lions 1984a, b) [a form suitable for the present situation can be found in Groves and Wahlén (2015, Theorem 3.7)] to the sequence $\{u_n\}$ defined by

$$\begin{aligned} u_n = |\varvec{\eta }_n^\prime |^{2} + |\varvec{\eta }_n|^2, \end{aligned}$$

where $\{\varvec{\eta }_n\}$ is a minimising sequence satisfying (2.1). Taking a subsequence if necessary, we may suppose that the limit $\ell :=\lim _{n \rightarrow \infty } \int _{-\infty }^\infty u_n(x) \, \mathrm{d}x> 0$ exists ($\ell =0$ would imply that $\lim _{n\rightarrow \infty } {\mathcal {J}}_\mu (\eta _n) =\infty$). Similar to Buffoni et al. (2013, Lemma 3.7) it is easy to show that the vanishing property

$$\begin{aligned} \lim _{n \rightarrow \infty }\left( \sup _{{\tilde{x}} \in {\mathbb {R}}} \int _{{\tilde{x}}-r}^{{\tilde{x}}+r}\!\!\! u_n(x) \, \mathrm{d}x\right) =0 \quad \text {for all } r>0 \end{aligned}$$

leads to a contradiction to the estimate $\Vert \varvec{\eta }_n\Vert _{1,\infty }\ge \,c\mu ^3$ which any minimising sequence has to satisfy because of the estimate ${\mathcal {J}}_\mu (\varvec{\eta }_n)<2\nu _0 \mu -c\mu ^3$ [see Lemma 2.29 and Buffoni et al. (2013, Lemma 3.4)]. We now comment on the more involved case ‘dichotomy’. Let us assume that there are sequences $\{x_n\} \subset {\mathbb {R}}$, $\{M_n^{(1)}\}, \{M_n^{(2)}\} \subset {\mathbb {R}}$ and a real number $\kappa \in (0,\ell )$ with the properties that $M_n^{(1)}$, $M_n^{(2)} \rightarrow \infty$, $M_n^{(1)}/M_n^{(2)} \rightarrow 0$,

$$\begin{aligned} \int _{-M_n^{(1)}}^{M_n^{(1)}} u_n(x+x_n) \, \mathrm{d}x\rightarrow \kappa , \qquad \int _{-M_n^{(2)}}^{M_n^{(2)}} u_n(x+x_n) \, \mathrm{d}x\rightarrow \kappa \end{aligned}$$

as $n \rightarrow \infty$. Furthermore,

$$\begin{aligned} \lim _{n \rightarrow \infty } \Bigg ( \sup _{{\tilde{x}} \in {\mathbb {R}}} \int _{{\tilde{x}}-r}^{{\tilde{x}}+r} \!\!\! u_n(x) \, \mathrm{d}x\Bigg ) \le \kappa \end{aligned}$$

for each $r>0$, and for each $\varepsilon >0$ there is a positive, real number R such that

$$\begin{aligned} \int _{-R}^R u_n(x+x_n) \, \mathrm{d}x\ge \kappa -\varepsilon \end{aligned}$$

for each $n \in {{\mathbb {N}}}$. We abbreviate the sequence $\{\varvec{\eta }_n(\cdot +x_n)\}$ to $\{\varvec{\eta }_n\}$ and define sequences $\{\varvec{\eta }_n^{(1)}\}$, $\{\varvec{\eta }_n^{(2)}\}$ by the formulas

$$\begin{aligned} \varvec{\eta }_n^{(1)}(x)=\varvec{\eta }_n(x)\chi \left( \frac{x}{M_n^{(1)}}\right) , \qquad \varvec{\eta }_n^{(2)}(x) = \varvec{\eta }_n(x) \left( 1-\chi \left( \frac{x}{M_n^{(2)}}\right) \right) , \end{aligned}$$

where $\chi \in C^\infty _c(-2,2)$ with $\chi =1$ in $[-1,1]$ and $0\le \chi \le 1$. The ‘splitting properties’

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert \eta _n^{(1)}\Vert _1^2 =\kappa , \quad \lim _{n\rightarrow \infty } \Vert \eta _n^{(2)}\Vert _1^2 =\ell - \kappa , \quad \lim _{n\rightarrow \infty } \Vert \eta _n-\eta _n^{(1)} - \eta _n^{(2)}\Vert _1^2=0, \end{aligned}$$

and hence

$$\begin{aligned} \lim _{n\rightarrow \infty } \left( {\mathcal {K}}(\varvec{\eta }_n)-{\mathcal {K}}(\varvec{\eta }_n^{(1)})-{\mathcal {K}}(\varvec{\eta }_n^{(2)})\right) =0, \end{aligned}$$

are straightforward consequences of these definitions [see Buffoni et al. (2013, Lemma 3.10 and Appendix C)]. The corresponding splitting property

$$\begin{aligned} \lim _{n\rightarrow \infty } \left( {\mathcal {L}}(\varvec{\eta }_n)-{\mathcal {L}}(\varvec{\eta }_n^{(1)})-{\mathcal {L}}(\varvec{\eta }_n^{(2)})\right) =0, \end{aligned}$$

for the non-local functional ${\mathcal {L}}$ is not as direct, but nevertheless follows using its ‘pseudo-local’ properties [see Appendix D, in particular Theorem D.6, in Buffoni et al. (2013) and Sect. 2.2.2, in particular Theorem 2.36, in Groves and Wahlén (2015)]. Taking subsequences, we can assume that all of the sequences $\{{\mathcal {K}}(\varvec{\eta }_n)\}$, $\{{\mathcal {K}}(\varvec{\eta }_n^{(1)})\}$, $\{{\mathcal {K}}(\varvec{\eta }_n^{(2)})\}$, $\{{\mathcal {L}}(\varvec{\eta }_n)\}$, $\{{\mathcal {L}}(\varvec{\eta }_n^{(1)})\}$ and $\{{\mathcal {L}}(\varvec{\eta }_n^{(2)})\}$ converge and that the limits are positive [see Buffoni et al. (2013, Lemma 3.10 and Appendix C)]. Setting

$$\begin{aligned} \mu _1=\mu \frac{\lim _{n\rightarrow \infty } {\mathcal {L}}(\varvec{\eta }_n^{(1)})}{\lim _{n\rightarrow \infty } {\mathcal {L}}(\varvec{\eta }_n)}, \quad \mu _2=\mu \frac{\lim _{n\rightarrow \infty } {\mathcal {L}}(\varvec{\eta }_n^{(2)})}{\lim _{n\rightarrow \infty } {\mathcal {L}}(\varvec{\eta }_n)} \end{aligned}$$

we obtain that $\mu =\mu _1+\mu _2$, $\mu _1, \mu _2>0$ and

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {J}}_\mu (\varvec{\eta }_n)&=\lim _{n\rightarrow \infty }\left( {\mathcal {K}}(\varvec{\eta }_n)+\frac{\mu ^2}{{\mathcal {L}}(\varvec{\eta }_n)}\right) \\&=\lim _{n\rightarrow \infty }\left( {\mathcal {K}}(\varvec{\eta }_n)+\frac{\mu ^2}{{\mathcal {L}}(\varvec{\eta }_n)^2} {\mathcal {L}}(\varvec{\eta }_n)\right) \\&=\lim _{n\rightarrow \infty }\left( {\mathcal {K}}(\varvec{\eta }_n^{(1)}) +\frac{\mu ^2}{{\mathcal {L}}(\varvec{\eta }_n)^2} {\mathcal {L}}(\varvec{\eta }_n^{(1)}) \right) \\&\quad +\lim _{n\rightarrow \infty } \left( {\mathcal {K}}(\varvec{\eta }_n^{(2)}) +\frac{\mu ^2}{{\mathcal {L}}(\varvec{\eta }_n)^2} {\mathcal {L}}(\varvec{\eta }_n^{(2)}) \right) \\&=\lim _{n\rightarrow \infty }\left( {\mathcal {K}}(\varvec{\eta }_n^{(1)}) +\frac{\mu _1^2}{{\mathcal {L}}(\varvec{\eta }_n^{(1)})} \right) +\lim _{n\rightarrow \infty } \left( {\mathcal {K}}(\varvec{\eta }_n^{(2)})+\frac{\mu _2^2}{{\mathcal {L}}(\varvec{\eta }_n^{(2)})} \right) \\&=\lim _{n\rightarrow \infty } {\mathcal {J}}_{\mu _1} (\varvec{\eta }_n^{(1)})+\lim _{n\rightarrow \infty } {\mathcal {J}}_{\mu _2} (\varvec{\eta }_n^{(2)}). \end{aligned}$$

The next key step in the analysis of dichotomy is to show that the function

$$\begin{aligned} \mu \mapsto I_\mu :=\inf \{ {\mathcal {J}}_\mu (\varvec{\eta }) :\varvec{\eta }\in U\!\setminus \!\{0\}\} \end{aligned}$$

is strictly sub-additive.

Theorem 2.3

Suppose that Assumptions 1.1 and 1.3 hold. The number $I_\mu$ has the strict sub-additivity property

$$\begin{aligned} I_{\mu _1+\mu _2}<I_{\mu _1}+I_{\mu _2},\quad 0<\mu _1,\mu _2,\mu _1+\mu _2<\mu _0. \end{aligned}$$

Theorem 2.3 is obtained using a careful analysis of the special minimising sequence from Theorem 2.2, which is postponed to the end of this section. With this at hand, the dichotomy assumptions lead to the contradiction

$$\begin{aligned} I_{\mu }<I_{\mu _1}+I_{\mu _2}\le \lim _{n\rightarrow \infty } {\mathcal {J}}_{\mu _1} (\varvec{\eta }_n^{(1)}) +\lim _{n\rightarrow \infty } {\mathcal {J}}_{\mu _1} (\varvec{\eta }_n^{(2)}) =\lim _{n\rightarrow \infty } {\mathcal {J}}_{\mu }(\varvec{\eta })= I_{\mu }. \end{aligned}$$

It follows that the sequence $\{u_n\}$ concentrates, that is, there is a sequence $\{x_n\} \subset {\mathbb {R}}$ with the property that for each $\varepsilon >0$ there exists a positive real number R with

$$\begin{aligned} \int _{-R}^R u_n(x+x_n) \, \mathrm{d}x\ge \ell -\varepsilon \end{aligned}$$

for each $n \in {{\mathbb {N}}}$. Arguing as in the proof of Lemma 3.9 of Buffoni et al. (2013), one finds that the sequence $\{\varvec{\eta }_n(\cdot + x_n)\}$ admits a subsequence which converges in $(H^r({\mathbb {R}}))^2$, $0 \le r < 2$, to a minimiser of ${\mathcal {J}}_\mu$ over $U{\setminus } \{0\}$. This concludes the proof of Theorem 2.1.

The next step is to relate the above result to our original problem of finding minimisers of ${\mathcal {E}}(\varvec{\eta },\varvec{\xi })$ subject to the constraint ${\mathcal {I}}(\varvec{\eta },\varvec{\xi }) = 2\mu$, where ${\mathcal {E}}$ and ${\mathcal {I}}$ are defined in Eqs. (1.21) and (1.22). The following result is obtained using the argument explained in Sect. 5.1 of Groves and Wahlén (2015). In fact, we first minimise ${\mathcal {E}}(\varvec{\eta },\cdot )$ over $T_\mu$ and then minimise ${\mathcal {J}}_\mu (\varvec{\eta })={\mathcal {E}}(\varvec{\eta },\varvec{\xi }_{\varvec{\eta }})$ over $B_M(0)\subset H^2({\mathbb {R}})$ (cf. Theorem 2.1) as indicated in Sect. 1.3.

Theorem 2.4

Suppose that Assumptions 1.1 and 1.3 hold.

• (i) The set $D_\mu$ of minimisers of ${\mathcal {E}}$ over the set

  $$\begin{aligned} S_\mu =\{(\varvec{\eta },\varvec{\xi }) \in U \times {{\tilde{X}}}:{\mathcal {I}}(\varvec{\eta },\varvec{\xi })=2\mu \} \end{aligned}$$

  is non-empty.

• (ii) Suppose that $\{(\varvec{\eta }_n,\varvec{\xi }_n)\} \subset S_\mu$ is a minimising sequence for ${\mathcal {E}}$ with the property that

  $$\begin{aligned} \sup _{n\in {{\mathbb {N}}}} \Vert \varvec{\eta }_n\Vert _2 < M. \end{aligned}$$

  There exists a sequence $\{x_n\} \subset {\mathbb {R}}$ with the property that a subsequence of$\{\varvec{\eta }_n(x_n+\cdot ),\varvec{\xi }_n(x_n+\cdot )\}$ converges in $(H^r({\mathbb {R}}))^2 \times {{\tilde{X}}}$, $0 \le r < 2$ to a function in $D_\mu$.

We obtain a stability result as a corollary of Theorem 2.4 using a contradiction argument as in Buffoni (2004), Theorem 19. Recall that the usual informal interpretation of the statement that a set V of solutions to an initial value problem is ‘stable’ is that a solution which begins close to V remains close to V at all subsequent times. The precise meaning of a solution in the theorem below is irrelevant, as long as it conserves the functionals ${\mathcal {E}}$ and ${\mathcal {I}}$ over some time interval [0, T] with $T>0$.

Theorem 2.5

Suppose that Assumptions 1.1 and 1.3 hold and that $(\varvec{\eta },\varvec{\xi }):[0,T] \rightarrow U \times {{\tilde{X}}}$ has the properties that

$$\begin{aligned} {\mathcal {E}}(\varvec{\eta }(t),\varvec{\xi }(t)) = {\mathcal {E}}(\varvec{\eta }(0),\varvec{\xi }(0)),\ {\mathcal {I}}(\varvec{\eta }(t),\varvec{\xi }(t))={\mathcal {I}}(\varvec{\eta }(0),\varvec{\xi }(0)), \qquad t \in [0,T] \end{aligned}$$

and

$$\begin{aligned} \sup _{t \in [0,T]} \Vert \varvec{\eta }(t)\Vert _2 < M. \end{aligned}$$

Choose $r \in [0,2)$, and let ‘${{\,\mathrm{dist}\,}}$’ denote the distance in $(H^r({\mathbb {R}}))^2 \times {{\tilde{X}}}$. For each $\varepsilon >0$ there exists $\delta >0$ such that

$$\begin{aligned} {{\,\mathrm{dist}\,}}((\varvec{\eta }(0),\varvec{\xi }(0)), D_\mu )< \delta \quad \Rightarrow \quad {{\,\mathrm{dist}\,}}((\varvec{\eta }(t),\varvec{\xi }(t)), D_\mu )<\varepsilon \end{aligned}$$

for $t\in [0,T]$.

This result is a statement of the conditional, energetic stability of the set $D_\mu$. Here energetic refers to the fact that the distance in the statement of stability is measured in the ‘energy space’ $(H^r({\mathbb {R}}))^2 \times {{\tilde{X}}}$, while conditional alludes to the well-posedness issue. At present there is no global well-posedness theory for interfacial water waves (although there is a large and growing body of literature concerning well-posedness issues for water-wave problems in general). The solution $t \mapsto (\varvec{\eta }(t),\varvec{\xi }(t))$ may exist in a smaller space over the interval [0, T], at each instant of which it remains close (in energy space) to a solution in $D_\mu$. Furthermore, Theorem 2.5 is a statement of the stability of the set of constrained minimisers $D_\mu$; establishing the uniqueness of the constrained minimiser would imply that $D_\mu$ consists of translations of a single solution, so that the statement that $D_\mu$ is stable is equivalent to classical orbital stability of this unique solution.

Let us finally discuss the relation to nonlinear Schrödinger waves and confirm the heuristic argument given in Sect. 1.2. Due to the relation

$$\begin{aligned} {\mathcal {J}}_\mu (\varvec{\eta }_\star )=2\nu _0\mu +I_\mathrm {NLS} \mu ^3 +o(\mu ^3), \end{aligned}$$

for the special test function $\varvec{\eta }_\star$ obtained in Lemma B.1 (constructed via the function $\phi _{\mathrm {NLS}}$ form Lemma 1.7) and the variational characterisation of $D_\mathrm{NLS}$ from Lemma 1.7 one can prove the following result by contradiction as in Groves and Wahlén (2011, Sect. 5; 2015, Sect. 5.2.2). Since the proof is similar, we omit the details.

Theorem 2.6

Under Assumptions 1.1 and 1.3, the set $D_\mu$ of minimisers of ${{\mathcal {E}}}$ over $S_\mu$ satisfies

$$\begin{aligned} \sup _{(\varvec{\eta },\varvec{\xi }) \in D_\mu } \inf _{\omega \in [0,2\pi ], x \in {{\mathbb {R}}}} \Vert {\varvec{\phi }}_{\varvec{\eta }}-e^{i\omega }\phi _\mathrm {NLS}(\cdot +x)\varvec{v}_0\Vert _1 \rightarrow 0 \end{aligned}$$

as $\mu \downarrow 0$, where we write ${\varvec{\eta }}_1^+(x) = \tfrac{1}{2}\mu {\varvec{\phi }}_{\varvec{\eta }}(\mu x)e^{i k_0 x}$ and $\varvec{\eta }_1^+={{\mathcal {F}}}^{-1}[\chi _{[k_0-\delta _0,k_0+\delta _0]}\hat{\varvec{\eta }}]$ with $\delta _0 \in (0,\tfrac{1}{3}k_0)$. Furthermore,

$$\begin{aligned} I_\mu =2\nu _0 \mu +I_\mathrm{NLS}\mu ^3 +o(\mu ^3) \end{aligned}$$

and the speed $\nu _\mu$ of the corresponding solitary wave satisfies

$$\begin{aligned} \nu _\mu = \nu _0 + 2(\nu _0F(k_0)\varvec{v}_0\cdot \varvec{v}_0)^{-1}\nu _\mathrm {NLS}\mu ^2 + o(\mu ^2) \end{aligned}$$

uniformly over $(\varvec{\eta },\varvec{\xi }) \in D_\mu$.

Note in particular that since $\varvec{v}_0=(1,-a)$ with $a>0$ (cf. Eq. (1.12)) the surface profile ${\overline{\eta }}$ is to leading order a scaled and inverted copy of the interface profile ${\underline{\eta }}$ (cf. Fig. 1). The fact that we do not know if the minimiser is unique up to translations is reflected by the lack of control over $\omega$; for the model equation, the minimiser is in fact not unique up to translations (see Lemma 1.7). Using dynamical systems methods (see, for example, Barrandon and Iooss 2005), we expect that one can prove the existence of two solutions corresponding to $\omega =0$ and $\omega =\pi$ above, but without any knowledge of stability. Since the proof of Theorem 2.6 follows Groves and Wahlén (2015, Sect. 5.2) closely, we shall omit it.

The goal of the rest of this section is to prove Theorem 2.3, which follows directly from the strict sub-homogeneity of $I_\mu$ (see Corollary 2.32). We will work under Assumptions 1.1 and 1.3 throughout the rest of the section, without explicitly mentioning when they are used. We begin by giving an outline of the proof. The heuristic argument in Sect. 1.2 (verified a posteriori in Theorem 2.6) suggests that the spectrum of minimisers should concentrate at wavenumbers $\pm k_0$ and that they should resemble the test function $\varvec{\eta }_\star$ identified in Lemma B.1 for small $\mu$. Consequently, $I_\mu$ should be well approximated by the upper bound $2\nu _0 \mu + I_\mathrm{NLS}\mu ^3 +o(\mu ^3)$, the first two terms of which define a strictly sub-homogeneous function. The strict sub-homogeneity property is rigorously established by proving results in this direction for a ‘near minimiser’ of ${\mathcal {J}}_\mu$ over $U\!\setminus \!\{0\}$, that is a function in $U \!\setminus \!\{0\}$ with

$$\begin{aligned} \Vert \tilde{\varvec{\eta }}\Vert _2^2 \le c\mu , \quad {\mathcal {J}}_\mu (\tilde{\varvec{\eta }}) < 2\nu _0\mu -c\mu ^3, \quad \Vert {\mathcal {J}}_\mu ^\prime (\tilde{\varvec{\eta }})\Vert _0 \le \mu ^N, \end{aligned}$$

for some $N\ge 3$. The existence of near minimisers is a consequence of Theorem 2.2. One of the main tools that we will use is the weighted norm

$$\begin{aligned} |{}|{}|\varvec{\eta }|{}|{}|_\alpha :=\left( \int _{{\mathbb {R}}} (1+\mu ^{-4\alpha }(|k|-k_0)^4) |\hat{\varvec{\eta }}(k)|^2 \, \mathrm{d}k\right) ^\frac{1}{2} \end{aligned}$$

and a splitting of $\tilde{\varvec{\eta }}$ in view of the expected wavenumber distribution. A difference compared to previous works is that $\tilde{\varvec{\eta }}$ is vector-valued and that we therefore have to identify a leading term related to the zero eigenvector $\varvec{v}_0$ of the matrix $g(k_0)$ in Sect. 1.2. We establish weighted and non-weighted estimates for the different components of $\tilde{\varvec{\eta }}$ in Lemma 2.19. These estimates allow us to identify the dominant term in the ‘nonlinear part’

$$\begin{aligned} {\mathcal {M}}_\mu (\tilde{\varvec{\eta }}):={\mathcal {J}}_\mu (\tilde{\varvec{\eta }})-\frac{\mu ^2}{{\mathcal {L}}_2(\tilde{\varvec{\eta }})}-{\mathcal {K}}_2(\tilde{\varvec{\eta }}) \end{aligned}$$

of ${\mathcal {J}}_\mu (\tilde{\varvec{\eta }})$ for near minimisers $\tilde{\varvec{\eta }}$, the key ingredients being a Modica–Mortola-type argument in the proof of Lemma 2.29 and the effect of the concentration of the Fourier modes, cf. Lemma 2.20. Finally, we can show in Proposition 2.31 monotonicity of the function $s\mapsto s^{-q}{\mathcal {M}}_{s^2\mu }(s\tilde{\varvec{\eta }})$ for a certain $q>2$. The strict sub-homogeneity follows easily from this (see Corollary 2.32).

Turning now to the details of the proof, it follows from Appendix A.3 that the functionals ${\mathcal {K}}$ and ${\mathcal {L}}$ are analytic on U with convergent power series expansions

$$\begin{aligned} {\mathcal {K}}(\varvec{\eta })=\sum _{k=2}^\infty {\mathcal {K}}_k(\varvec{\eta }), \qquad {\mathcal {L}}(\varvec{\eta })=\sum _{k=2}^\infty {\mathcal {L}}_k(\varvec{\eta }). \end{aligned}$$

Moreover, the gradients ${\mathcal {K}}'(\varvec{\eta })$ and ${\mathcal {L}}'(\varvec{\eta })$ exist in $(L^2({\mathbb {R}}))^2$ for each $\varvec{\eta }\in U$ and define analytic operators $U \rightarrow (L^2({\mathbb {R}}))^2$. Formulas for some of the terms in the power series and their gradients can be found in Appendix  A.3. In particular, the quadratic part ${\mathcal {L}}_2(\varvec{\eta })$ can be expressed as

$$\begin{aligned} {\mathcal {L}}_2(\varvec{\eta })=\frac{1}{2} \int _{{\mathbb {R}}} {\underline{\eta }} {\underline{K}}^0 {\underline{\eta }} \, \mathrm{d}x +\frac{\rho }{2} \int _{{\mathbb {R}}} \varvec{\eta }{\overline{K}}^0 \varvec{\eta }\, \mathrm{d}x, \end{aligned}$$

using the Fourier multiplier operators

$$\begin{aligned} {\underline{K}}^0 {\underline{\eta }}={\mathcal {F}}^{-1}(|k|\widehat{{\underline{\eta }}}) \quad \text {and} \quad {\overline{K}}^0 \varvec{\eta }={\mathcal {F}}^{-1}[{{\overline{F}}}(k)\hat{\varvec{\eta }}], \end{aligned}$$

with

$$\begin{aligned} {{\overline{F}}}(k)= \begin{pmatrix} |k| \coth |k|&{}\quad -\frac{|k|}{\sinh |k|}\\ -\frac{|k|}{\sinh |k|}&{}\quad |k| \coth |k| \end{pmatrix}. \end{aligned}$$

We will also use the notation ${\mathcal {K}}_\mathrm {nl}(\varvec{\eta }):={\mathcal {K}}(\varvec{\eta })-{\mathcal {K}}_2(\varvec{\eta })$, ${\mathcal {L}}_\mathrm {nl}(\varvec{\eta }):={\mathcal {L}}(\varvec{\eta })-{\mathcal {L}}_2(\varvec{\eta })$ for the superquadratic parts of the functionals. (The corresponding gradients are the nonlinear parts of ${\mathcal {K}}'$ and ${\mathcal {L}}'$, respectively.)

We next seek to split each $\varvec{\eta }\in U$ into the sum of a function $\varvec{\eta }_1$ with spectrum near $k=\pm k_0$ and a function $\varvec{\eta }_2$ whose spectrum is bounded away from these points. To this end we write the identity

$$\begin{aligned} {\mathcal {J}}_\mu ^\prime (\varvec{\eta })&= {\mathcal {K}}_2^\prime (\varvec{\eta }) + {\mathcal {K}}_\mathrm {nl}^\prime (\varvec{\eta }) -\left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^{\!\!2}{\mathcal {L}}_2^\prime (\varvec{\eta }) -\left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^{\!\!2} {\mathcal {L}}_\mathrm {nl}^\prime (\eta )\\&= {\mathcal {K}}_2^\prime (\varvec{\eta }) - \nu _0^2 {\mathcal {L}}_2^\prime (\varvec{\eta }) + {\mathcal {K}}_\mathrm {nl}^\prime (\varvec{\eta }) -\left( \left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^2 - \nu _0^2\right) {\mathcal {L}}_2^\prime (\eta ) -\left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^{\!\!2} {\mathcal {L}}_\mathrm {nl}^\prime (\varvec{\eta }) \end{aligned}$$

in the form

$$\begin{aligned} g(k)\hat{\varvec{\eta }} = {\mathcal {F}}\left[ {\mathcal {J}}_\mu ^\prime (\varvec{\eta }) - {\mathcal {K}}_\mathrm {nl}^\prime (\varvec{\eta }) + \left( \left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^2 - \nu _0^2\right) {\mathcal {L}}_2^\prime (\varvec{\eta }) +\left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^{\!\!2} {\mathcal {L}}_\mathrm {nl}^\prime (\varvec{\eta })\right] , \end{aligned}$$

where g(k) is given by (1.13). We decompose it into two coupled equations by defining $\varvec{\eta }_2 \in (H^2({\mathbb {R}}))^2$ by the formula

$$\begin{aligned} \varvec{\eta }_2 = {\mathcal {F}}^{-1}\!\!\left[ (1-\chi _S(k)) g(k)^{-1} {\mathcal {F}}\left[ {\mathcal {J}}_\mu ^\prime (\varvec{\eta }) - {\mathcal {K}}_\mathrm {nl}^\prime (\varvec{\eta }) + \left( \left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^2- \nu _0^2\right) {\mathcal {L}}_2^\prime (\varvec{\eta }) +\left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^{\!\!2} {\mathcal {L}}_\mathrm {nl}^\prime (\varvec{\eta })\right] \!\right] \end{aligned}$$

and $\varvec{\eta }_1 \in (H^2({\mathbb {R}}))^2$ by $\varvec{\eta }_1=\varvec{\eta }-\varvec{\eta }_2$, so that $\hat{\varvec{\eta }}_1$ has support in $S:=[-k_0-\delta _0,-k_0+\delta _0] \cup [k_0-\delta _0,k_0+\delta _0]$, where $\delta _0\in (0,k_0/3)$. Here we have used the fact that

$$\begin{aligned} \varvec{f} \mapsto {\mathcal {F}}^{-1}\left[ (1-\chi _S(k)) g(k)^{-1} \hat{\varvec{f}}(k)\right] \end{aligned}$$

is a bounded linear operator $(L^2({\mathbb {R}}))^2 \rightarrow (H^2({\mathbb {R}}))^2$.

It will also be useful to express vectors $\varvec{w}=({\underline{w}}, {{\overline{w}}})$ in the basis $\{\varvec{v}_0, \varvec{v}_0^\sharp \}$, where $\varvec{v}_0$ is the zero eigenvector of the matrix $g(k_0)$ (see Sect. 1.2) and $\varvec{v}_0^\sharp \not \parallel \varvec{v}$. The exact choice of the complementary vector $\varvec{v}_0^\sharp$ is unimportant, but in order to simplify the notation later on we choose $\varvec{v}_0^\sharp =(0,1)$. This implies that

$$\begin{aligned} \varvec{w}=c_1 \varvec{v}_0+c_2 \varvec{v}_0^\sharp :=\varvec{w}^{\varvec{v}_0}+\varvec{w}^{\varvec{v}_0^\sharp }, \end{aligned}$$

where $c_1={\underline{w}}$ and $c_2={{\overline{w}}}+a{\underline{w}}$.

The following propositions are used to estimate the special minimising sequence. The proofs follow Groves and Wahlén (2015, Sect. 4.1) and are omitted.

Proposition 2.7

• (i) The estimates $\Vert \varvec{\eta }\Vert _{1,\infty } \le c \mu ^\frac{\alpha }{2}|{}|{}|\varvec{\eta }|{}|{}|_\alpha$, $\Vert {\underline{K}}^0{{\underline{\eta }}}\Vert _\infty \le c \mu ^\frac{\alpha }{2}|{}|{}|\varvec{\eta }|{}|{}|_\alpha$, $\Vert {\overline{K}}^0_{ij}\varvec{\eta }\Vert _\infty \le c \mu ^\frac{\alpha }{2}|{}|{}|\varvec{\eta }|{}|{}|_\alpha$ hold for each $\varvec{\eta }\in (H^2({\mathbb {R}}))^2$.

• (ii) The estimates

  $$\begin{aligned} \Vert \varvec{\eta }^{\prime \prime }+k_0^2\varvec{\eta }\Vert _0 \le c \mu ^{\alpha }|{}|{}|\varvec{\eta }|{}|{}|_\alpha , \end{aligned}$$

  and

  $$\begin{aligned} \Vert ({\underline{K}}^0{\underline{\eta }})^{(n)}\Vert _\infty , \Vert ({\overline{K}}^0\varvec{\eta })^{(n)}\Vert _\infty \le \mu ^\frac{\alpha }{2}|{}|{}|\varvec{\eta }|{}|{}|_\alpha , \quad n=0,1,2,\ldots , \end{aligned}$$

  hold for each $\varvec{\eta }\in (H^2({\mathbb {R}}))^2$ with $\mathrm {supp}\,\hat{\varvec{\eta }} \subseteq S$.

Proposition 2.8

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies the inequalities

$$\begin{aligned} {\mathcal {R}}_1(\tilde{\varvec{\eta }}) \le \frac{\mu }{{\mathcal {L}}(\tilde{\varvec{\eta }})} -\nu _0 \le {\mathcal {R}}_2(\tilde{\varvec{\eta }}), \end{aligned}$$

and

$$\begin{aligned} {\mathcal {R}}_1(\tilde{\varvec{\eta }}) -{\tilde{{\mathcal {M}}}}_\mu (\tilde{\varvec{\eta }}) \le \frac{\mu }{{\mathcal {L}}_2(\tilde{\varvec{\eta }})} -\nu _0 \le {\mathcal {R}}_2(\tilde{\varvec{\eta }}) -{\tilde{{\mathcal {M}}}}_\mu (\tilde{\varvec{\eta }}) \end{aligned}$$

where

$$\begin{aligned} {\mathcal {R}}_1(\tilde{\varvec{\eta }})&= -\frac{\langle {\mathcal {J}}_\mu ^\prime (\tilde{\varvec{\eta }}),\tilde{\varvec{\eta }}\rangle }{4\mu } + \frac{1}{4\mu }\big (\langle {\mathcal {M}}_\mu ^\prime (\tilde{\varvec{\eta }}),\tilde{\varvec{\eta }}\rangle +4\mu {\tilde{{\mathcal {M}}}}_\mu (\tilde{\varvec{\eta }})\big ), \\ {\mathcal {R}}_2(\tilde{\varvec{\eta }})&= -\frac{\langle {\mathcal {J}}_\mu ^\prime (\tilde{\varvec{\eta }}),\tilde{\varvec{\eta }}\rangle }{4\mu } + \frac{1}{4\mu }\big (\langle {\mathcal {M}}_\mu ^\prime (\tilde{\varvec{\eta }}),\tilde{\varvec{\eta }}\rangle +4\mu {\tilde{{\mathcal {M}}}}_\mu (\tilde{\varvec{\eta }})\big ) -\frac{{\mathcal {M}}_\mu (\tilde{\varvec{\eta }})}{2\mu }, \end{aligned}$$

and

$$\begin{aligned} {\tilde{{\mathcal {M}}}}_\mu (\tilde{\varvec{\eta }}) = \frac{\mu }{{\mathcal {L}}(\tilde{\varvec{\eta }})}-\frac{\mu }{{\mathcal {L}}_2(\tilde{\varvec{\eta }})}. \end{aligned}$$

Proposition 2.9

The estimates

$$\begin{aligned} |{\mathcal {L}}_3(\varvec{\eta })|&\le c\Vert \varvec{\eta }\Vert _2^2 (\Vert \varvec{\eta }\Vert _{1,\infty } + \Vert \varvec{\eta }^{\prime \prime }+k_0^2\varvec{\eta }\Vert _0), \\ \begin{Bmatrix} |{\mathcal {K}}_4(\varvec{\eta })| \\ |{\mathcal {L}}_4(\varvec{\eta })| \end{Bmatrix}&\le c \Vert \varvec{\eta }\Vert _2^2 (\Vert \varvec{\eta }\Vert _{1,\infty } + \Vert \varvec{\eta }^{\prime \prime }+k_0^2\varvec{\eta }\Vert _0)^2, \\ \begin{Bmatrix} |{\mathcal {K}}_\mathrm {r}(\varvec{\eta })| \\ |{\mathcal {L}}_\mathrm {r}(\varvec{\eta })| \end{Bmatrix}&\le c\Vert \varvec{\eta }\Vert _2^3 (\Vert \varvec{\eta }\Vert _{1,\infty } + \Vert \varvec{\eta }^{\prime \prime }+k_0^2\varvec{\eta }\Vert _0)^2 \end{aligned}$$

hold for each $\varvec{\eta }\in U$.

Proposition 2.10

The estimates

$$\begin{aligned} \Vert {\mathcal {L}}_3^\prime (\varvec{\eta })\Vert _0&\le c\Vert \varvec{\eta }\Vert _2 (\Vert \varvec{\eta }\Vert _{1,\infty } + \Vert \varvec{\eta }^{\prime \prime }+k_0^2\varvec{\eta }\Vert _0 + \Vert {\underline{K}}^0 {\underline{\eta }}\Vert _{\infty }+\Vert {\overline{K}}^0\varvec{\eta }\Vert _{\infty }), \\ \begin{Bmatrix} \Vert {\mathcal {K}}_4^\prime (\varvec{\eta })\Vert _0 \\ \Vert {\mathcal {L}}_4^\prime (\varvec{\eta })\Vert _0 \end{Bmatrix}&\le c\Vert \varvec{\eta }\Vert _2 (\Vert \varvec{\eta }\Vert _{1,\infty } + \Vert \varvec{\eta }^{\prime \prime }+k_0^2\varvec{\eta }\Vert _0 +\Vert {\underline{K}}^0 {\underline{\eta }}\Vert _{\infty }+\Vert {\overline{K}}^0\varvec{\eta }\Vert _{\infty })^2, \\ \begin{Bmatrix} \Vert {\mathcal {K}}_\mathrm {r}^\prime (\varvec{\eta })\Vert _0 \\ \Vert {\mathcal {L}}_\mathrm {r}^\prime (\varvec{\eta })\Vert _0 \end{Bmatrix}&\le c\Vert \varvec{\eta }\Vert _2^2 (\Vert \varvec{\eta }\Vert _{1,\infty } + \Vert \varvec{\eta }^{\prime \prime }+k_0^2\varvec{\eta }\Vert _0)^2 \end{aligned}$$

hold for each $\varvec{\eta }\in U$.

It is also helpful to write

$$\begin{aligned} {\underline{{\mathcal {L}}}}_3^\prime ({\underline{\eta }}) = {\underline{m}}({\underline{\eta }},{\underline{\eta }}), \quad {\overline{{\mathcal {L}}}}_3^\prime (\varvec{\eta }) = {\overline{m}}(\varvec{\eta },\varvec{\eta }),\quad {\mathcal {L}}_3'(\varvec{\eta })=m(\varvec{\eta },\varvec{\eta })=\begin{pmatrix} {\underline{m}}({\underline{\eta }},{\underline{\eta }})\\ 0\end{pmatrix}+\rho {\overline{m}}(\varvec{\eta },\varvec{\eta }), \end{aligned}$$

where ${\underline{m}}\in {{\mathcal {L}}}_\mathrm {s}^2(H^2({\mathbb {R}}), L^2({\mathbb {R}}))$ and ${\overline{m}}\in {{\mathcal {L}}}_\mathrm {s}^2((H^2({\mathbb {R}}))^2, (L^2({\mathbb {R}}))^2)$ are defined by

$$\begin{aligned} {\underline{m}}({\underline{u}}_1,{\underline{u}}_2)&= -\frac{1}{2}{\underline{K}}^0({\underline{u}}_1 {\underline{K}}^0 {\underline{u}}_2) - \frac{1}{2}{\underline{K}}^0({\underline{u}}_2 {\underline{K}}^0 {\underline{u}}_1) \\&\qquad - \frac{1}{2}{\underline{K}}^0 {\underline{u}}_1 {\underline{K}}^0 {\underline{u}}_2 -\frac{1}{2}{\underline{u}}_{1x}{\underline{u}}_{2x} - \frac{1}{2}{\underline{u}}_{1xx}{\underline{u}}_2 - \frac{1}{2}{\underline{u}}_1{\underline{u}}_{2xx},\\ {\overline{m}}(\varvec{u}_1,\varvec{u}_2)&= \begin{pmatrix} \frac{1}{2}{\underline{u}}_{1x} {\underline{u}}_{2x}+\frac{1}{2}{\underline{u}}_{1xx}{\underline{u}}_2 +\frac{1}{2}{\underline{u}}_{2xx}{\underline{u}}_1 +\frac{1}{2}({\overline{K}}_{11}^0{\underline{u}}_1+{\overline{K}}_{12}^0 {\overline{u}}_1) ({\overline{K}}_{11}^0{\underline{u}}_2+{\overline{K}}_{12}^0 {\overline{u}}_2)\\ -\frac{1}{2}{\overline{u}}_{1x}{\overline{u}}_{2x} -\frac{1}{2}{\overline{u}}_{1xx}{\overline{u}}_2 -\frac{1}{2}{\overline{u}}_{2xx}{\overline{u}}_1 -\frac{1}{2}({\overline{K}}_{21}^0{\underline{u}}_1+{\overline{K}}_{22}^0 {\overline{u}}_1) ({\overline{K}}_{21}^0{\underline{u}}_2+{\overline{K}}_{22}^0 {\overline{u}}_2) \end{pmatrix}\\&\qquad + \frac{1}{2} \begin{pmatrix} {\overline{K}}_{11}^0 ({\underline{u}}_1 ({\overline{K}}_{11}^0{\underline{u}}_2+{\overline{K}}_{12}^0 {\overline{u}}_2)) +{\overline{K}}_{11}^0 ({\underline{u}}_2 ({\overline{K}}_{11}^0{\underline{u}}_1+{\overline{K}}_{12}^0 {\overline{u}}_1)) \\ -{\overline{K}}_{22}^0 ({\overline{u}}_1 ({\overline{K}}_{21}^0{\underline{u}}_2+{\overline{K}}_{22}^0 {\overline{u}}_2)) -{\overline{K}}_{22}^0 ({\overline{u}}_2 ({\overline{K}}_{21}^0{\underline{u}}_1+{\overline{K}}_{22}^0 {\overline{u}}_1)) \end{pmatrix}\\&\qquad + \frac{1}{2}\begin{pmatrix} -{\overline{K}}_{21}^0 ({\overline{u}}_1 ({\overline{K}}_{21}^0{\underline{u}}_2+{\overline{K}}_{22}^0 {\overline{u}}_2)) -{\overline{K}}_{21}^0 ({\overline{u}}_2 ({\overline{K}}_{21}^0{\underline{u}}_1+{\overline{K}}_{22}^0 {\overline{u}}_1)) \\ {\overline{K}}_{12}^0 ({\underline{u}}_1 ({\overline{K}}_{11}^0{\underline{u}}_2+{\overline{K}}_{12}^0 {\overline{u}}_2)) +{\overline{K}}_{12}^0 ({\underline{u}}_2 ({\overline{K}}_{11}^0{\underline{u}}_1+{\overline{K}}_{12}^0 {\overline{u}}_1))\end{pmatrix}, \end{aligned}$$

and similarly

$$\begin{aligned} {\underline{{\mathcal {L}}}}_3({\underline{\eta }})= & {} {\underline{n}}({\underline{\eta }},{\underline{\eta }},{\underline{\eta }}), \quad {\overline{{\mathcal {L}}}}_3(\varvec{\eta }) = {\overline{n}}(\varvec{\eta },\varvec{\eta },\varvec{\eta }),\quad {\mathcal {L}}_3(\varvec{\eta })=n(\varvec{\eta },\varvec{\eta },\varvec{\eta })={\underline{n}}({\underline{\eta }},{\underline{\eta }},{\underline{\eta }})\\&+\rho {\overline{n}}(\varvec{\eta },\varvec{\eta },\varvec{\eta }), \end{aligned}$$

where $n_j \in {{\mathcal {L}}}_\mathrm {s}^3(H^2({\mathbb {R}}), {\mathbb {R}})$, $j=1,2,3$, are defined by

$$\begin{aligned} {\underline{n}}({\underline{u}}_1,{\underline{u}}_2,{\underline{u}}_3)&= \frac{1}{6}\int _{{\mathbb {R}}}{\mathcal {P}}[{\underline{u}}_1^\prime {\underline{u}}_2^\prime {\underline{u}}_3] \, \mathrm{d}x- \frac{1}{6}\int _{{\mathbb {R}}}{\mathcal {P}}[({\underline{K}}^0{\underline{u}}_1)({\underline{K}}^0{\underline{u}}_2){\underline{u}}_3] \, \mathrm{d}x\\ {\overline{n}}(\varvec{u}_1,\varvec{u}_2,\varvec{u}_3)&= \frac{1}{6} \int _{{\mathbb {R}}} {\mathcal {P}}[{\overline{u}}_1'{\overline{u}}_2'{\overline{u}}-{\underline{u}}_1'{\underline{u}}_2'{\underline{u}}_3]\, \mathrm{d}x\\&\quad +\frac{1}{6}\int _{{\mathbb {R}}} {\mathcal {P}}\left[ ({\overline{K}}_{11}^0{\underline{u}}_1+{\overline{K}}_{12}^0 {\overline{u}}_1) ({\overline{K}}_{11}^0{\underline{u}}_2+{\overline{K}}_{12}^0 {\overline{u}}_2){\underline{u}}_3\right] \, \mathrm{d}x\\&\quad -\frac{1}{6}\int _{{\mathbb {R}}} {\mathcal {P}}\left[ ({\overline{K}}_{21}^0{\underline{u}}_1+{\overline{K}}_{22}^0 {\overline{u}}_1) ({\overline{K}}_{21}^0{\underline{u}}_2+{\overline{K}}_{22}^0 {\overline{u}}_2) {\overline{u}}_3 \right] \, \mathrm{d}x. \end{aligned}$$

The symbol ${\mathcal {P}}[\cdot ]$ denotes the sum of all distinct expressions resulting from permutations of the variables appearing in its argument.

Similarly to Groves and Wahlén (2015, Proposition 4.6) we obtain the following estimates by direct calculations.

Proposition 2.11

The estimates

$$\begin{aligned} \Vert {\underline{m}}({\underline{\eta }}_1,{\underline{u}}_2)\Vert _0&\le c(\Vert {\underline{\eta }}_1\Vert _{1,\infty } + \Vert {\underline{\eta }}_1^{\prime \prime }+k_0^2{\underline{\eta }}_1\Vert _0 + \Vert {\underline{K}}^0 {\underline{\eta }}_1\Vert _{1,\infty }) \Vert {\underline{u}}_2\Vert _2,\\ \Vert {\overline{m}}(\varvec{\eta }_1,\varvec{u}_2)\Vert _0&\le c(\Vert \varvec{\eta }_1\Vert _{1,\infty } + \Vert \varvec{\eta }_1^{\prime \prime }+k_0^2\varvec{\eta }_1\Vert _0 + \Vert {\underline{K}}^0 {\underline{\eta }}_1\Vert _{1,\infty }+\Vert {\overline{K}}^0\varvec{\eta }_1\Vert _{1,\infty }) \Vert \varvec{u}_2\Vert _2,\\ |n(\varvec{\eta }_1,\varvec{u}_2,\varvec{u}_3)|&\le c(\Vert \varvec{\eta }_1\Vert _{1,\infty } + \Vert \varvec{\eta }_1^{\prime \prime }+k_0^2\varvec{\eta }_1\Vert _0 + \Vert {\underline{K}}^0 {\underline{\eta }}_1\Vert _{1,\infty }\\&\quad +\Vert {\overline{K}}^0\varvec{\eta }_1\Vert _{1,\infty }) \Vert \varvec{u}_2\Vert _2 \Vert \varvec{u}_3\Vert _2 \end{aligned}$$

hold for each $\varvec{\eta }\in U$ and $\varvec{u}_2$, $\varvec{u}_3 \in (H^2({\mathbb {R}}))^2$.

Using Proposition 2.9 and arguing as in Groves and Wahlén (2015, Proposition 4.6 and Lemma 4.7) we obtain the following estimates.

Lemma 2.12

The estimates

$$\begin{aligned} {\mathcal {M}}_\mu (\varvec{\eta })&= - \nu _0^2 {\mathcal {L}}_3(\varvec{\eta }) +{\mathcal {K}}_4(\varvec{\eta }) - \nu _0^2 {\mathcal {L}}_4(\varvec{\eta }) \\&\quad -\left( \frac{\mu }{{\mathcal {L}}_2(\varvec{\eta })}-\nu _0\right) \!\!\left( \frac{\mu }{{\mathcal {L}}_2(\varvec{\eta })}+\nu _0\right) ({\mathcal {L}}_3(\varvec{\eta })+{\mathcal {L}}_4(\varvec{\eta })) \\&\quad +\frac{\mu ^2}{({\mathcal {L}}_2(\varvec{\eta }))^3}({\mathcal {L}}_3(\varvec{\eta }))^{2} + O(\mu ^\frac{3}{2}(\Vert \varvec{\eta }\Vert _{1,\infty } {+} \Vert \varvec{\eta }^{\prime \prime }+k_0^2 \varvec{\eta }\Vert _0)^2),\\ \langle {\mathcal {M}}_\mu '(\varvec{\eta }),\varvec{\eta }\rangle +4 \mu {\tilde{{\mathcal {M}}}}_\mu (\varvec{\eta })&= - 3\nu _0^2 {\mathcal {L}}_3(\varvec{\eta }) +4({\mathcal {K}}_4(\varvec{\eta })-\nu _0^2 {\mathcal {L}}_4(\varvec{\eta })) \\&\quad -\left( \frac{\mu }{{\mathcal {L}}_2(\varvec{\eta })}-\nu _0\right) \!\!\left( \frac{\mu }{{\mathcal {L}}_2(\varvec{\eta })}+\nu _0\right) (3{\mathcal {L}}_3(\varvec{\eta })+4{\mathcal {L}}_4(\varvec{\eta })) \\&\quad +\frac{4\mu ^2}{({\mathcal {L}}_2(\varvec{\eta }))^3} ({\mathcal {L}}_3(\varvec{\eta }))^{2} + O(\mu ^\frac{3}{2}(\Vert \varvec{\eta }\Vert _{1,\infty } {+} \Vert \varvec{\eta }^{\prime \prime }+k_0^2 \varvec{\eta }\Vert _0)^2) \end{aligned}$$

and

$$\begin{aligned} {\tilde{{\mathcal {M}}}}_\mu (\varvec{\eta }) = -\mu ^{-1}\left( \frac{\mu }{{\mathcal {L}}_2(\varvec{\eta })}\right) ^2 \!({\mathcal {L}}_3(\varvec{\eta })+{\mathcal {L}}_4(\varvec{\eta })) + O(\mu ^\frac{1}{2}(\Vert \varvec{\eta }\Vert _{1,\infty } + \Vert \varvec{\eta }^{\prime \prime }+k_0^2\varvec{\eta }\Vert _0)^2) \end{aligned}$$

hold for each $\varvec{\eta }\in U$ with $\Vert \varvec{\eta }\Vert _2 \le c\mu ^\frac{1}{2}$ and ${\mathcal {L}}_2(\varvec{\eta })>c\mu$.

The following proposition is an immediate consequence of the definition of $\varvec{\eta }_1$.

Proposition 2.13

The identity

$$\begin{aligned} \chi _S {\mathcal {F}}\left[ \begin{Bmatrix}{\mathcal {L}}_3^\prime (\varvec{\eta }_1) \end{Bmatrix} \right] =0 \end{aligned}$$

holds for each $\varvec{\eta }\in U$.

As a consequence, $\varvec{\eta }_1$ satisfies the equation

$$\begin{aligned} g(k)\hat{\varvec{\eta }}_1 = \chi _S(k) {\mathcal {F}}[ {\mathcal {S}}(\varvec{\eta })], \end{aligned}$$

(2.2)

where

$$\begin{aligned} {\mathcal {S}}(\varvec{\eta }) = {\mathcal {J}}_\mu ^\prime (\varvec{\eta }) - {\mathcal {K}}_\mathrm {nl}^\prime (\varvec{\eta }) +\left( \left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^2 -\nu _0^2\right) {\mathcal {L}}_2^\prime (\varvec{\eta })+\left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^{\!\!2} ({\mathcal {L}}_\mathrm {nl}^\prime (\varvec{\eta })-{\mathcal {L}}_3^\prime (\varvec{\eta }_1)). \end{aligned}$$

In keeping with Eq. (2.2) we write the equation for $\varvec{\eta }_2$ in the form

$$\begin{aligned} \underbrace{\varvec{\eta }_2+H(\varvec{\eta })}_{\displaystyle :=\varvec{\eta }_3} = {\mathcal {F}}^{-1}\left[ (1-\chi _S(k))g(k)^{-1} {\mathcal {F}}[{\mathcal {S}}(\varvec{\eta })]\right] , \end{aligned}$$

(2.3)

where

$$\begin{aligned} H(\varvec{\eta }) = -{\mathcal {F}}^{-1} \left[ g(k)^{-1} {\mathcal {F}}\left[ \left( \frac{\mu }{{\mathcal {L}}(\varvec{\eta })}\right) ^{\!\!2} {\mathcal {L}}_3^\prime (\varvec{\eta }_1)\right] \right] ; \end{aligned}$$

(2.4)

the decomposition $\varvec{\eta }=\varvec{\eta }_1-H(\varvec{\eta })+\varvec{\eta }_3$ forms the basis of the calculations presented below. An estimate on the size of $H(\varvec{\eta })$ is obtained from Eq. (2.4) and Proposition 2.11.

Proposition 2.14

The estimate

$$\begin{aligned} \Vert H(\varvec{\eta })\Vert _2 \le c (\Vert \varvec{\eta }_1\Vert _{1,\infty } + \Vert \varvec{\eta }_1^{\prime \prime }+k_0^2\varvec{\eta }_1\Vert _0 + \Vert {\underline{K}}^0 {\underline{\eta }}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \varvec{\eta }_1\Vert _{1,\infty } + \Vert \varvec{\eta }_3\Vert _2) \Vert \varvec{\eta }_1\Vert _2 \end{aligned}$$

holds for each $\varvec{\eta }\in U$.

The above results may be used to derive estimates for the gradients of the cubic parts of the functionals which are used in the analysis below.

Proposition 2.15

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies the estimates

$$\begin{aligned} \Vert {\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }})-{\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }}_1)\Vert _0\le & {} c \mu ^\frac{1}{2}((\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0 \\&+ \Vert {\underline{K}}^0 \underline{{\tilde{\eta }}}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty } )^2 +\Vert \tilde{\varvec{\eta }}_3\Vert _2). \end{aligned}$$

Proof

Observe that

$$\begin{aligned} {\mathcal {L}}_3^\prime (\varvec{\eta })-{\mathcal {L}}_3^\prime (\varvec{\eta }_1)= & {} m(H(\varvec{\eta }),H(\varvec{\eta }))+m(\varvec{\eta }_3,\varvec{\eta }_3) - 2m(\varvec{\eta }_1,H(\varvec{\eta }))\\&-2m(\varvec{\eta }_3,H(\varvec{\eta }))+2m(\varvec{\eta }_1,\varvec{\eta }_3) \end{aligned}$$

and estimate the right-hand side of this equation using Propositions 2.11 and 2.14. $\square$

An estimate for ${\mathcal {L}}_3(\tilde{\varvec{\eta }})$ is obtained in a similar fashion using Propositions 2.11, 2.13, and 2.14.

Proposition 2.16

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies the estimates

$$\begin{aligned} |{\mathcal {L}}_3(\tilde{\varvec{\eta }})| \le c\big (\mu (\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0 +\Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty }+ \Vert {{\overline{K}}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty })^2 + \mu \Vert \tilde{\varvec{\eta }}_3\Vert _2\big ) . \end{aligned}$$

Estimating the right-hand sides of the inequalities

$$\begin{aligned} \Vert {\mathcal {L}}_\mathrm {nl}^\prime (\tilde{\varvec{\eta }})-{\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }}_1)\Vert _0&\le \Vert {\mathcal {L}}_\mathrm {r}^\prime (\tilde{\varvec{\eta }})\Vert _0 + \Vert {\mathcal {L}}_4^\prime (\tilde{\varvec{\eta }})\Vert _0 + \Vert {\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }})-{\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }}_1)\Vert _0, \\ |{\mathcal {L}}_\mathrm {nl}(\tilde{\varvec{\eta }})|&\le |{\mathcal {L}}_\mathrm {r}(\tilde{\varvec{\eta }})|+|{\mathcal {L}}_4(\tilde{\varvec{\eta }})| + |{\mathcal {L}}_3(\tilde{\varvec{\eta }})| \end{aligned}$$

(together with the corresponding inequalities for ${\mathcal {K}}$ and ${\mathcal {L}}$). Using Propositions 2.9 and 2.10, the calculation

$$\begin{aligned}&\Vert \varvec{\eta }\Vert _{1,\infty } + \Vert \varvec{\eta }^{\prime \prime }+k_0^2\varvec{\eta }\Vert _0 + \Vert {\underline{K}}^0 {\underline{\eta }}\Vert _{\infty } + \Vert {\overline{K}}^0 \varvec{\eta }\Vert _{\infty } \quad \nonumber \\&\quad \le c(\Vert \varvec{\eta }_1\Vert _{1,\infty } + \Vert \varvec{\eta }_1^{\prime \prime }+k_0^2\varvec{\eta }_1\Vert _0 + \Vert {\underline{K}}^0 {\underline{\eta }}_1\Vert _{\infty } + \Vert {\overline{K}}^0 \varvec{\eta }_1\Vert _{\infty } + \Vert H(\varvec{\eta })\Vert _2 + \Vert \varvec{\eta }_3\Vert _2) \nonumber \\&\quad \le c(\Vert \varvec{\eta }_1\Vert _{1,\infty } + \Vert \varvec{\eta }_1^{\prime \prime }+k_0^2\varvec{\eta }_1\Vert _0 + \Vert {\underline{K}}^0 {\underline{\eta }}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \varvec{\eta }_1\Vert _{1,\infty } + \Vert \varvec{\eta }_3\Vert _2) \end{aligned}$$

(2.5)

and Propositions 2.15 and 2.16 yield the following estimates for the ‘nonlinear’ parts of the functionals.

Lemma 2.17

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies the estimates

$$\begin{aligned} \begin{Bmatrix} \Vert {\mathcal {K}}_\mathrm {nl}^\prime (\tilde{\varvec{\eta }})\Vert _0 \\ \Vert {\mathcal {L}}_\mathrm {nl}^\prime (\tilde{\varvec{\eta }})-{\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }}_1)\Vert _0 \end{Bmatrix}&\le c\big (\mu ^\frac{1}{2}(\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0 + \Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty } \\&\quad + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty })^2 + \mu ^\frac{1}{2}\Vert \tilde{\varvec{\eta }}_3\Vert _2\big ), \\ \begin{Bmatrix} |{\mathcal {K}}_\mathrm {nl}(\tilde{\varvec{\eta }})| \\ |{\mathcal {L}}_\mathrm {nl}(\tilde{\varvec{\eta }})| \end{Bmatrix}&\le c\big (\mu (\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0 + \Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty } \\&\quad + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty })^2+ \mu \Vert \tilde{\varvec{\eta }}_3\Vert _2\big ). \end{aligned}$$

We now have all the ingredients necessary to estimate the wave speed and the quantity $|{}|{}|\tilde{\varvec{\eta }}_1 |{}|{}|_\alpha$.

Proposition 2.18

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies the estimates

$$\begin{aligned} \begin{Bmatrix} \displaystyle \left| \frac{\mu }{{\mathcal {L}}(\tilde{\varvec{\eta }})} - \nu _0\right| \\ \displaystyle \left| \frac{\mu }{{\mathcal {L}}_2(\tilde{\varvec{\eta }})} - \nu _0\right| \end{Bmatrix}\le & {} c\big ((\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0\\&+ \Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty } )^2+ \Vert \tilde{\varvec{\eta }}_3\Vert _2 + \mu ^{N-\frac{1}{2}}\big ). \end{aligned}$$

Proof

Combining Lemma 2.12, inequality (2.5) and Lemma 2.17, one finds that

$$\begin{aligned}&|{\mathcal {M}}_\mu (\tilde{\varvec{\eta }})|,\ |\langle {\mathcal {M}}_\mu ^\prime (\tilde{\varvec{\eta }}),\tilde{\varvec{\eta }}\rangle +4\mu {\tilde{{\mathcal {M}}}}_\mu (\tilde{\varvec{\eta }})|\\&\quad \le c\big (\mu (\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0 + \Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty } )^2+ \mu \Vert \tilde{\varvec{\eta }}_3\Vert _2\big ),\\&|{\tilde{{\mathcal {M}}}}_\mu (\tilde{\varvec{\eta }})| \le c\big ((\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0) +\Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty }\\&\qquad \qquad \qquad + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty } )^2 + \Vert \tilde{\varvec{\eta }}_3\Vert _2\big ), \end{aligned}$$

from which the given estimates follow by Proposition 2.8. $\square$

Lemma 2.19

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies $|{}|{}|\tilde{\varvec{\eta }}_{1} |{}|{}|_\alpha ^2 \le c\mu$, $\Vert \tilde{\varvec{\eta }}_{1}^{\varvec{v}_0^\sharp } \Vert _0^2\le c\mu ^{3+2\alpha }$, $\Vert \tilde{\varvec{\eta }}_3\Vert _2^2 \le c\mu ^{3+2\alpha }$ and $\Vert H(\tilde{\varvec{\eta }})\Vert _2^2 \le c\mu ^{2+\alpha }$ for $\alpha <1$.

Proof

Lemma 2.17 and Proposition 2.18 assert that

$$\begin{aligned}&\left[ \Vert {\mathcal {S}}(\tilde{\varvec{\eta }})\Vert _0 \le c\big ( \mu ^\frac{1}{2} (\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0 +\Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty } )^2+ \mu ^\frac{1}{2}\Vert \tilde{\varvec{\eta }}_3\Vert _2 + \mu ^N\big )\right] , \end{aligned}$$

which shows that

$$\begin{aligned}&\left[ \Vert \tilde{\varvec{\eta }}_3\Vert _2 \le c\big ( \mu ^\frac{1}{2} (\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0 +\Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty } )^2+ \mu ^\frac{1}{2}\Vert \tilde{\varvec{\eta }}_3\Vert _2 + \mu ^N\big )\right] \end{aligned}$$

and therefore

$$\begin{aligned} \Vert \tilde{\varvec{\eta }}_3\Vert _2 \le c\big ( \mu ^\frac{1}{2} (\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0 +\Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty })^2 + \mu ^N\big ),\nonumber \\ \end{aligned}$$

(2.6)

and

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}} |g(k){\mathcal {F}}[\tilde{\varvec{\eta }}_1]|^2 \, \mathrm{d}k\\&\quad \le c\big ( \mu (\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0\\&\qquad +\Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty })^4+ \mu \Vert \tilde{\varvec{\eta }}_3\Vert _2^2 + \mu ^{2N}\big ) \\&\quad \le c\big ( \mu (\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0 +\Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty })^4 + \mu ^{2N}\big ). \end{aligned} \end{aligned}$$

(2.7)

Multiplying the above inequality by $\mu ^{-4\alpha }$ and adding $\Vert \tilde{\varvec{\eta }}_1\Vert _0^2 \le \Vert \tilde{\varvec{\eta }}\Vert _0^2 \le c \mu$, one finds that

$$\begin{aligned} |{}|{}|\tilde{\varvec{\eta }}_1 |{}|{}|_\alpha ^2&\le c\big ( \mu ^{1-4\alpha }(\Vert \tilde{\varvec{\eta }}_1\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}_1^{\prime \prime }+k_0^2\tilde{\varvec{\eta }}_1\Vert _0 + \Vert {\underline{K}}^0 \tilde{{\underline{\eta }}}_1\Vert _{1,\infty } + \Vert {\overline{K}}^0 \tilde{\varvec{\eta }}_1\Vert _{1,\infty } )^4 + \mu \big ) \nonumber \\&\le c(\mu ^{1-2\alpha }|{}|{}|\tilde{\varvec{\eta }}_1 |{}|{}|_\alpha ^4 +\mu ) \end{aligned}$$

(2.8)

where Proposition 2.7 and the inequality

$$\begin{aligned} |g(k) \varvec{w}|^2\ge c(||k|-k_0|^4 |\varvec{w}^{\varvec{v}_0}|^2 + |\varvec{w}^{\varvec{v}_0^\sharp }|^2)\ge c||k|-k_0|^4|\varvec{w}|^2 \end{aligned}$$

(2.9)

for $k \in S$ have also been used. The latter follows from (1.14) and the fact that $g(k) \varvec{v}_0^\sharp \ne 0$ for $k\in S$.

The estimate for $\tilde{\varvec{\eta }}_1$ follows from the previous inequality using the argument given by Groves and Wahlén (2010, Theorem 2.5), while those for $\tilde{\varvec{\eta }}_3$ and $H(\tilde{\varvec{\eta }})$ are derived by estimating $|{}|{}|\tilde{\varvec{\eta }}_1 |{}|{}|_\alpha ^2 \le c\mu$ in Eq. (2.6) and Proposition 2.14. Finally, as a consequence of (2.7)–(2.9) we obtain the inequality

$$\begin{aligned} \Vert \tilde{\varvec{\eta }}_{1}^{\varvec{v}_0^\sharp }\Vert _0^2\le \,c\,\int _{{\mathbb {R}}} |g(k){\mathcal {F}}[\tilde{\varvec{\eta }}_1]|^2 \, \mathrm{d}k\le \,c(\mu ^{1+2\alpha }|{}|{}|\tilde{\varvec{\eta }}_1 |{}|{}|_\alpha ^4 +\mu ^{2N})\le \,c\,\mu ^{3+2\alpha } \end{aligned}$$

using that $|{}|{}|\tilde{\varvec{\eta }}_1|{}|{}|^2_\alpha \le c\,\mu$. $\square$

The next step is to identify the dominant terms in the formulas for ${\mathcal {M}}_\mu (\tilde{\varvec{\eta }})$ and$\langle {\mathcal {M}}_\mu ^\prime (\tilde{\varvec{\eta }}), \tilde{\varvec{\eta }} \rangle + 4\mu {\tilde{{\mathcal {M}}}}_\mu (\tilde{\varvec{\eta }})$ given in Lemma 2.12. We begin by examining the quantities ${\mathcal {K}}_4(\tilde{\varvec{\eta }})$ and ${\mathcal {L}}_4(\tilde{\varvec{\eta }})$ using a lemma which allows us to replace Fourier multiplier operators acting on functions with spectrum localised around certain wavenumbers by multiplication by constants. The result is a straightforward modification of Groves and Wahlén (2011, Proposition 4.13; 2015, Lemma 4.23), and the proof is therefore omitted.

Lemma 2.20

Assume that $u, v \in H^2({\mathbb {R}})$ with $\mathrm {supp}\,{\hat{u}}, \mathrm {supp}\,{\hat{v}}\subseteq S$ and $|{}|{}|u|{}|{}|_\alpha , |{}|{}|v|{}|{}|_\alpha \le c\mu ^\frac{1}{2}$ for some $\alpha <1$ and let $u^+:={\mathcal {F}}^{-1}[\chi _{[0,\infty )}{\hat{u}}]$, $v^+:={\mathcal {F}}^{-1}[\chi _{[0,\infty )}{\hat{v}}]$ and $u^-:={\mathcal {F}}^{-1}[\chi _{(-\infty ,0]}{\hat{u}}]$, $v^-:={\mathcal {F}}^{-1}[\chi _{(-\infty ,0]}{\hat{v}}]$ (so that $u^-=\overline{u^+}$ and $v^-=\overline{v^+}$). Then u and v satisfy the estimates

• (i) $L(u^{\pm }) = m(k_0)u^\pm + {\underline{O}}(\mu ^{\frac{1}{2}+\alpha })$,

• (ii) $L(u^+ v^+)= m(2k_0) u^+ v^+ + {\underline{O}}(\mu ^{1+\frac{3\alpha }{2}})$,

• (iii) $L(u^- v^-)= m(-2k_0) u^- v^- + {\underline{O}}(\mu ^{1+\frac{3\alpha }{2}})$,

• (iv) $L(u^+ v^-) =m(0)u^+v^-+ {\underline{O}}(\mu ^{1+\frac{3\alpha }{2}})$,

where $L={\mathcal {F}}^{-1}[m(k) \cdot ]$ is a Fourier multiplier operator whose symbol m is locally Lipschitz continuous, and ${\underline{O}}(\mu ^p)$ denotes a quantity whose Fourier transform has compact support and whose $L^2({\mathbb {R}})$-norm (and hence $H^s({\mathbb {R}})$-norm for $s \ge 0$) is $O(\mu ^p)$.

Remark 2.21

Note in particular that we can take $L\in \{\partial _x, {\underline{K}}_0, {\overline{K}}^0_{ij}\}$ in estimates (i)–(iv) in Lemma 2.20 and that we can take $m(k)=(g(k)^{-1})_{ij}$ in (ii)–(iv) since $(g(k)^{-1})_{ij}$ is locally Lipschitz on ${\mathbb {R}}{\setminus } S$.

Using formulas (A.16), (A.20), (A.21), Lemmas 2.19 and 2.20 (with $\alpha$ sufficiently close to 1), and the identity $\tilde{\varvec{\eta }}_1^{\varvec{v}_0}= \tilde{{\underline{\eta }}}_1 (1,-a)$ we now obtain the following estimates.

Proposition 2.22

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies the estimates

$$\begin{aligned} \begin{Bmatrix} {\mathcal {K}}_4(\tilde{\varvec{\eta }}) \\ {\mathcal {L}}_4(\tilde{\varvec{\eta }}) \end{Bmatrix} = \begin{Bmatrix} {\mathcal {K}}_4(\tilde{\varvec{\eta }}_{1}^{\varvec{v}_0}) \\ {\mathcal {L}}_4(\tilde{\varvec{\eta }}_{1}^{\varvec{v}_0}) \end{Bmatrix} +o(\mu ^3). \end{aligned}$$

Proposition 2.23

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies the estimates

$$\begin{aligned} {\mathcal {K}}_4(\tilde{\varvec{\eta }}_{1}^{\varvec{v}_0})&= A_4^1 \int _{{\mathbb {R}}}\tilde{{\underline{\eta }}}_1^4 \, \mathrm{d}x+ o(\mu ^3), \qquad A_4^1= -\frac{1}{8}({\underline{\beta }} +\rho {\overline{\beta }}a^4)k_0^4,\\ {\mathcal {L}}_4(\tilde{\varvec{\eta }}_{1}^{\varvec{v}_0})&= A_4^2 \int _{{\mathbb {R}}}\tilde{{\underline{\eta }}}_1^4 \, \mathrm{d}x+ o(\mu ^3), \qquad A_4^2 = {\underline{A}}_4^2+\rho {{\overline{A}}}_4^2,\\ {\underline{A}}_4^{2}&=-\frac{1}{6}k_0^3 ,\\ {{\overline{A}}}_4^2&= -\frac{1}{2}\bigg ( ( {\overline{F}}_{11}(k_0)-a{\overline{F}}_{12}(k_0))-a^3 ( {\overline{F}}_{21}(k_0)-a{\overline{F}}_{22}(k_0)) \bigg )k_0^2,\\&\quad + \frac{1}{6} \Big ( {\overline{F}}_{11}(k_0)-a{\overline{F}}_{12}(k_0)\Big )^2 \Big (2{\overline{F}}_{11}(0)+{\overline{F}}_{11}(2k_0)\Big ) \\&\quad + \frac{1}{6} a^2\Big ( {\overline{F}}_{21}(k_0)-a{\overline{F}}_{22}(k_0)\Big )^2 \Big (2{\overline{F}}_{22}(0)+{\overline{F}}_{22}(2k_0)\Big )\\&\quad -\frac{1}{3} a\Big ( {\overline{F}}_{11}(k_0)-a{\overline{F}}_{12}(k_0)\Big )\Big ( {\overline{F}}_{21}(k_0)-a{\overline{F}}_{22}(k_0)\Big ) \Big (2{\overline{F}}_{21}(0)+{\overline{F}}_{21}(2k_0)\Big ). \end{aligned}$$

Corollary 2.24

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies the estimate

$$\begin{aligned} {\mathcal {K}}_4(\tilde{\varvec{\eta }}) - \nu _0^2 {\mathcal {L}}_4(\tilde{\varvec{\eta }}) = A_4 \int _{{\mathbb {R}}}\tilde{{\underline{\eta }}}_1^4 \, \mathrm{d}x+ o(\mu ^3), \end{aligned}$$

where

$$\begin{aligned} A_4=A_4^1-\nu _0^2A_4^2. \end{aligned}$$

We now turn to the corresponding result for ${\mathcal {L}}_3(\tilde{\varvec{\eta }})$. The following result is obtained by writing

$$\begin{aligned} {\mathcal {L}}_3(\tilde{\varvec{\eta }}) {=}n(\tilde{\varvec{\eta }}_1^{\varvec{v}_0}+\tilde{\varvec{\eta }}_1^{\varvec{v}_0^\sharp }-H(\tilde{\varvec{\eta }}) +\tilde{\varvec{\eta }}_3,\tilde{\varvec{\eta }}_1^{\varvec{v}_0}{+}\tilde{\varvec{\eta }}_1^{\varvec{v}_0^\sharp }-H(\tilde{\varvec{\eta }}) {+}\tilde{\varvec{\eta }}_3, \tilde{\varvec{\eta }}_1^{\varvec{v}_0}+\tilde{\varvec{\eta }}_1^{\varvec{v}_0^\sharp }-H(\tilde{\varvec{\eta }}) +\tilde{\varvec{\eta }}_3), \end{aligned}$$

expanding the right-hand side and estimating the terms using Propositions 2.7 and 2.11, Lemma 2.19 and the identity $n(\tilde{\varvec{\eta }}_1, \tilde{\varvec{\eta }}_1, \tilde{\varvec{\eta }}_1)=0$.

Proposition 2.25

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies the estimate

$$\begin{aligned} {\mathcal {L}}_3(\tilde{\varvec{\eta }}) = - \int _{{\mathbb {R}}} {\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }}_{1}^{\varvec{v}_0}) \cdot H(\tilde{\varvec{\eta }}) \, \mathrm{d}x+ o(\mu ^3). \end{aligned}$$

Proposition 2.26

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies the estimate

$$\begin{aligned} H(\tilde{\varvec{\eta }}) = - \nu _0^2{\mathcal {F}}^{-1} \left[ g(k)^{-1} {\mathcal {F}}[ {\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }}_1^{\varvec{v}_0})]\right] +{\underline{o}}(\mu ^3). \end{aligned}$$

Proof

Noting that

$$\begin{aligned}&\left| \frac{\mu }{{\mathcal {L}}(\tilde{\varvec{\eta }})} - \nu _0 \right| \ \le \ c(\mu ^\alpha |{}|{}|\tilde{\varvec{\eta }}_1 |{}|{}|_\alpha ^2 + \Vert \tilde{\varvec{\eta }}_3\Vert _2 + \mu ^{N-\frac{1}{2}})\ =\ O(\mu ^{1+\alpha }),\\&\Vert {\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }}_1)\Vert _0 \le \ c\mu ^\frac{\alpha }{2}|{}|{}|\tilde{\varvec{\eta }}_1 |{}|{}|_\alpha \Vert \tilde{\varvec{\eta }}_1\Vert _2\ =\ O(\mu ^{1+\frac{\alpha }{2}}) \end{aligned}$$

(see Propositions 2.7 and 2.10, Corollary 2.18 and Lemma 2.19) one finds that

$$\begin{aligned} H(\tilde{\varvec{\eta }})&= - \nu _0^2{\mathcal {F}}^{-1} \left[ g(k)^{-1} {\mathcal {F}}[ {\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }}_1)]\right] +O(\mu ^{1+\alpha }){\underline{O}}(\mu ^{1+\frac{\alpha }{2}})\\&=- \nu _0^2{\mathcal {F}}^{-1} \left[ g(k)^{-1} {\mathcal {F}}[ {\mathcal {L}}_3^\prime (\tilde{\varvec{\eta }}_1)]\right] + {\underline{o}}(\mu ^3) \end{aligned}$$

recalling the definition of H in (2.4). The proof is concluded by estimating

$$\begin{aligned} {\mathcal {L}}_3(\tilde{\varvec{\eta }}_1)-{\mathcal {L}}_3(\tilde{\varvec{\eta }}_1^{\varvec{v}_0})={\underline{o}}(\mu ^3) \end{aligned}$$

(cf. Propositions 2.7 and 2.11, and Lemma 2.19). $\square$

Combining Propositions 2.25 and 2.26, one finds that

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_3(\tilde{\varvec{\eta }})&= \nu _0^2\int _{{\mathbb {R}}} g(k)^{-1} {\mathcal {F}}[{\mathcal {L}}_3'(\tilde{\varvec{\eta }}_1^{\varvec{v}_0})] \cdot \overline{{\mathcal {F}}[{\mathcal {L}}_3'(\tilde{\varvec{\eta }}_1^{\varvec{v}_0})] } \, \mathrm{d}k+o(\mu ^3). \end{aligned} \end{aligned}$$

(2.10)

Expanding the right-hand side using Lemma 2.20 we then obtain the following result.

Proposition 2.27

Any near minimiser $\tilde{\varvec{\eta }}$ satisfies

$$\begin{aligned} - \nu _0^2{\mathcal {L}}_3(\tilde{\varvec{\eta }}) = A_3 \int _{{\mathbb {R}}}\tilde{{\underline{\eta }}}_1^4 \, \mathrm{d}x+ o(\mu ^3), \end{aligned}$$

where

$$\begin{aligned} A_3&= -\frac{1}{3}g(2k_0)^{-1} \varvec{A}_3^1\cdot \varvec{A}_3^1-\frac{2}{3}g(0)^{-1} \varvec{A}_3^2\cdot \varvec{A}_3^2,\\ \varvec{A}_3^1&=\rho \nu _0^2\begin{pmatrix} \frac{3}{2} k_0^2 - \frac{1}{2}( {\overline{F}}_{11}(k_0)-a{\overline{F}}_{12}(k_0))^2 -{\overline{F}}_{11}(2k_0) ( {\overline{F}}_{11}(k_0)-a{\overline{F}}_{12}(k_0))\\ -\frac{3}{2} k_0^2a^2 +\frac{1}{2}( {\overline{F}}_{21}(k_0)-a{\overline{F}}_{22}(k_0))^2 -a {\overline{F}}_{22}(2k_0) ( {\overline{F}}_{21}(k_0)-a{\overline{F}}_{22} (k_0)) \end{pmatrix}\\&\quad +\rho \nu _0^2 \begin{pmatrix} -a {\overline{F}}_{21}(2k_0)( {\overline{F}}_{21}(k_0)-a{\overline{F}}_{22}(k_0))\\ -{\overline{F}}_{12}(2k_0) ( {\overline{F}}_{11}(k_0)-a{\overline{F}}_{12}(k_0))\end{pmatrix}+\begin{pmatrix} \nu _0^2 k_0^2 \\ 0 \end{pmatrix},\\ \varvec{A}_3^2&=\rho \nu _0^2 \begin{pmatrix} \frac{1}{2} k_0^2 - \frac{1}{2}( {\overline{F}}_{11}(k_0)-a{\overline{F}}_{12}(k_0))^2-{\overline{F}}_{11}(0)( {\overline{F}}_{11}(k_0)-a {\overline{F}}_{12}(k_0))\\ -\frac{1}{2} k_0^2a^2+\frac{1}{2}( {\overline{F}}_{21}(k_0)-a{\overline{F}}_{22}(k_0))^2 -a {\overline{F}}_{22}(0)( {\overline{F}}_{21}(k_0)-a{\overline{F}}_{22}(k_0)) \end{pmatrix} \\&\quad +\rho \nu _0^2 \begin{pmatrix} -a {\overline{F}}_{21}(0)( {\overline{F}}_{21}(k_0)-a {\overline{F}}_{22}(k_0)) \\ -{\overline{F}}_{12}(0) ( {\overline{F}}_{11}(k_0)-a {\overline{F}}_{12}(k_0)) \end{pmatrix}. \end{aligned}$$

The following estimates for ${\mathcal {M}}_\mu (\tilde{\varvec{\eta }})$ and $\langle {\mathcal {M}}_\mu ^\prime (\tilde{\varvec{\eta }}), \tilde{\varvec{\eta }} \rangle + 4\mu {\tilde{{\mathcal {M}}}}_\mu (\tilde{\varvec{\eta }})$ may now be derived from Corollary 2.24 and Proposition 2.27.

Lemma 2.28

The estimates

$$\begin{aligned}&{\mathcal {M}}_{s^2\mu }(s\tilde{\varvec{\eta }}) = -s^3 \nu _0^2 {\mathcal {L}}_3(\tilde{\varvec{\eta }}) +s^4\big ({\mathcal {K}}_4(\tilde{\varvec{\eta }}) - \nu _0^2 {\mathcal {L}}_4(\tilde{\varvec{\eta }})\big ) + s^3 o(\mu ^3),\\&\langle {\mathcal {M}}_{s^2\mu }^\prime (s\tilde{\varvec{\eta }}), s\tilde{\varvec{\eta }} \rangle + 4s^2\mu {\tilde{{\mathcal {M}}}}_{s^2\mu }(s\tilde{\varvec{\eta }})\\&\quad =-3s^3\nu _0^2 {\mathcal {L}}_3(\tilde{\varvec{\eta }})+4s^4\big ({\mathcal {K}}_4(\tilde{\varvec{\eta }}) - \nu _0^2 {\mathcal {L}}_4(\tilde{\varvec{\eta }}) \big ) + s^3o(\mu ^3) \end{aligned}$$

hold uniformly over $s \in [1,2]$.

Proof

Lemma 2.12 asserts that

$$\begin{aligned} {\mathcal {M}}_{s^2\mu }(s\tilde{\varvec{\eta }})&= -s^3 \nu _0^2 {\mathcal {L}}_3(\tilde{\varvec{\eta }}) +s^4\big ({\mathcal {K}}_4(\tilde{\varvec{\eta }}) - \nu _0^2 {\mathcal {L}}_4(\tilde{\varvec{\eta }})\big ) \\&\quad -\left( \left( \frac{\mu }{{\mathcal {L}}_2(\tilde{\varvec{\eta }})}\right) ^2-\nu _0^2\right) (s^3{\mathcal {L}}_3(\tilde{\varvec{\eta }})+s^4{\mathcal {L}}_4(\tilde{\varvec{\eta }}))\\&\quad +\frac{s^4\mu ^2}{({\mathcal {L}}_2(\tilde{\varvec{\eta }}))^3}({\mathcal {L}}_3(\tilde{\varvec{\eta }}))^2 + O(s^5\mu ^\frac{3}{2}(\Vert \tilde{\varvec{\eta }}\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}^{\prime \prime }+k_0^2 \tilde{\varvec{\eta }}\Vert _0)^2) \end{aligned}$$

uniformly over $s \in [1,2]$. The first result follows by estimating

$$\begin{aligned} \Vert \tilde{\varvec{\eta }}\Vert _{1,\infty } + \Vert \tilde{\varvec{\eta }}^{\prime \prime }+k_0^2 \tilde{\varvec{\eta }}\Vert _0 \ \le \ c(\mu ^\frac{\alpha }{2}|{}|{}|\tilde{\varvec{\eta }} |{}|{}|_\alpha +\Vert \tilde{\varvec{\eta }}_3\Vert _2) \ \le \ c\mu ^{\frac{1}{2}+\frac{\alpha }{2}} \end{aligned}$$

(see Eq. (2.5)),

$$\begin{aligned} {\mathcal {L}}_3(\tilde{\varvec{\eta }}) = O(\mu ^{2+\alpha }), \quad {\mathcal {L}}_4(\tilde{\varvec{\eta }}) = O(\mu ^{2+\alpha }) \end{aligned}$$

(by Propositions 2.22, 2.23 and 2.27) and

$$\begin{aligned} \left| \frac{\mu }{{\mathcal {L}}_2(\tilde{\varvec{\eta }})} - \nu _0\right| \le c( \mu ^\alpha |{}|{}|\tilde{\varvec{\eta }}_1 |{}|{}|_\alpha ^2 + \Vert \varvec{\eta }_3\Vert _2 + \mu ^{N-\frac{1}{2}}) \le c \mu ^{1+\alpha }. \end{aligned}$$

The second result is derived in a similar fashion. $\square$

Lemma 2.29

Any near minimiser satisfies the inequality

$$\begin{aligned} {\mathcal {M}}_\mu (\varvec{{{\tilde{\eta }}}})\le -c\mu ^3. \end{aligned}$$

Proof

Note first that an arbitrary function $\varvec{\eta }\in U{\setminus }\{0\}$ satisfies the inequality

$$\begin{aligned} \frac{\mu ^2}{{\mathcal {L}}_2(\varvec{\eta })}+{\mathcal {K}}_2(\varvec{\eta })\ge 2\mu \sqrt{\frac{{\mathcal {K}}_2(\varvec{\eta })}{{\mathcal {L}}_2(\varvec{\eta })}}\ge 2\mu \nu _0 \end{aligned}$$

where we have used that

$$\begin{aligned} {\mathcal {K}}_2(\varvec{\eta })- \nu _0^2 {\mathcal {L}}_2(\varvec{\eta })=\frac{1}{2} \int _{{\mathbb {R}}} g(k) \hat{\varvec{\eta }}\cdot \hat{\varvec{\eta }}\, \mathrm{d}k\ge 0 \end{aligned}$$

(cf. (1.14)). The result now follows from the calculation

$$\begin{aligned} {\mathcal {M}}_\mu (\tilde{\varvec{\eta }})={\mathcal {J}}_\mu (\tilde{\varvec{\eta }})-\frac{\mu ^2}{{\mathcal {L}}_2(\tilde{\varvec{\eta }})}-{\mathcal {K}}_2(\tilde{\varvec{\eta }}) <2\nu _0 \mu -c \mu ^3 -2\nu _0 \mu =-c\mu ^3 \end{aligned}$$

$\square$

Corollary 2.30

The estimates

$$\begin{aligned}&{\mathcal {M}}_{s^2\mu }(s\tilde{\varvec{\eta }}) = (s^3A_3+s^4A_4)\int _{{\mathbb {R}}}\tilde{{\underline{\eta }}}_1^4 \, \mathrm{d}x+ s^3 o(\mu ^3),\\&\langle {\mathcal {M}}_{s^2\mu }^\prime (s\tilde{\varvec{\eta }}), s\tilde{\varvec{\eta }} \rangle + 4s^2\mu {\tilde{{\mathcal {M}}}}_{s^2\mu }(s\tilde{\varvec{\eta }}) =(3s^3A_3+4s^4A_4)\int _{{\mathbb {R}}}\tilde{{\underline{\eta }}}_1^4 \, \mathrm{d}x+ s^3 o(\mu ^3), \end{aligned}$$

hold uniformly over $s \in [1,2]$ and

$$\begin{aligned} \int _{{\mathbb {R}}}\tilde{{\underline{\eta }}}_1^4 \, \mathrm{d}x\ge c\mu ^3. \end{aligned}$$

Proof

The estimates follow by combining Corollary 2.24, Proposition 2.27 and Lemma 2.28, while the inequality for $\underline{{\tilde{\eta }}}_1$ is a consequence of the first estimate (with $s=1$) and Lemma 2.29. $\square$

Proposition 2.31

There exist $s_0\in (1,2]$ and $q>2$ with the property that the function

$$\begin{aligned} s\mapsto s^{-q}{\mathcal {M}}_{s^2\mu }(s\tilde{\varvec{\eta }}),\quad s\in [1,s_0 ] \end{aligned}$$

is decreasing and strictly negative.

Proof

This result follows from the calculation

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}s}\left( s^{-q}{\mathcal {M}}_{s^2\mu }(s\tilde{\varvec{\eta }})\right) \\&\quad = s^{-(q+1)}\left( -q{\mathcal {M}}_{s^2\mu }(s\tilde{\varvec{\eta }})+\langle {\mathcal {M}}^\prime _{s^2\mu }(s\tilde{\varvec{\eta }}),s\tilde{\varvec{\eta }}\rangle _0 + 4s^2\mu {\tilde{{\mathcal {M}}}}_{s^2\mu }(s\tilde{\varvec{\eta }})\right) \\&\quad = s^{-(q+1)}\left( \big (-q(s^3A_3+s^4A_4)+3s^3A_3+4s^4A_4\big )\int _{{\mathbb {R}}}\tilde{{\underline{\eta }}}_1^4 \, \mathrm{d}x+ s^3 o(\mu ^3)\right) \\&\quad = S^{2-q}\left( \big ((3-q)A_3+s(4-q)A_4\big )\int _{{\mathbb {R}}}\tilde{{\underline{\eta }}}_1^4 \, \mathrm{d}x+ o(\mu ^3)\right) \\&\quad \le -c\mu ^3 \\&\quad < 0, \end{aligned}$$

for $s \in (1,s_0)$ and $q \in (2,q_0)$, where we have used Corollary 2.30 and chosen $s_0>1$ and $q_0>2$ so that $(3-q)A_3+s(4-q)A_4$, which is negative for $s=1$ and $q=2$ (by Assumption 1.3), is also negative for $s \in (1,s_0]$ and $q \in (2,q_0]$. $\square$

The sub-homogeneity of $I_\mu$ now follows using a simplified form of the argument in the proof of Groves and Wahlén (2015, Corollary 4.32), which is repeated here for the reader’s convenience.

Corollary 2.32

There exists $\mu _0>0$ such that the map $(0, \mu _0)\ni \mu \mapsto I_\mu$ is strictly sub-homogeneous, that is

$$\begin{aligned} I_{s\mu }<s I_\mu \end{aligned}$$

(2.11)

whenever $0<\mu<s\mu <\mu _0$.

Proof

It follows from the previous lemma that there exists $q>2$ such that

$$\begin{aligned} {\mathcal {M}}_{s\mu }(s^{\frac{1}{2}} \tilde{\varvec{\eta }}) \le s^{\frac{q}{2}} {\mathcal {M}}_{\mu }(\tilde{\varvec{\eta }}), \quad s\in [1, s_0^2]. \end{aligned}$$

Combining this with Lemma 2.29 and letting $\{\tilde{\varvec{\eta }}_n\}$ be the special minimising sequence in Theorem 2.2, we find that

$$\begin{aligned} I_{s\mu }&\le {\mathcal {J}}_{s\mu } (s^{\frac{1}{2}} \tilde{\varvec{\eta }}_n)\\&={\mathcal {K}}_2(s^{\frac{1}{2}} \tilde{\varvec{\eta }}_n)+\frac{s^2 \mu ^2}{{\mathcal {L}}_2(s^{\frac{1}{2}} \tilde{\varvec{\eta }}_n)}+ {\mathcal {M}}_{s\mu }(s^{\frac{1}{2}} \tilde{\varvec{\eta }}_n)\\&=s \left( {\mathcal {K}}_2( \tilde{\varvec{\eta }}_n)+\frac{\mu ^2}{{\mathcal {L}}_2( \tilde{\varvec{\eta }}_n)}+{\mathcal {M}}_{\mu } (\tilde{\varvec{\eta }}_n)\right) +{\mathcal {M}}_{s\mu }(s^{\frac{1}{2}} \tilde{\varvec{\eta }}_n)-s{\mathcal {M}}_{\mu } (\tilde{\varvec{\eta }}_n)\\&\le s {\mathcal {J}}_{\mu }(\tilde{\varvec{\eta }}_n) +(s^\frac{q}{2}-s){\mathcal {M}}_\mu (\tilde{\varvec{\eta }}_n)\\&\le s{\mathcal {J}}_{\mu }(\tilde{\varvec{\eta }}_n) -c(s^\frac{q}{2}-s)\mu ^3, \qquad s\in [1, s_0^2]. \end{aligned}$$

As $n\rightarrow \infty$ this inequality yields

$$\begin{aligned} I_{s\mu } \le s I_\mu -c(s^\frac{q}{2}-s) \mu ^3 < sI_\mu , \quad s\in (1, s_0^2]. \end{aligned}$$

For $s>s_0^2$ choose $p\ge 2$ such that $s\in (1,s_0^{2p}]$ and note that

$$\begin{aligned} I_{s\mu }< s^{\frac{1}{p}} I_{s^{\frac{p-1}{p}} \mu }< s^{\frac{2}{p}} I_{s^{\frac{p-2}{p}} \mu }< \cdots < s I_\mu . \end{aligned}$$

$\square$

Theorem 2.3 follows from Corollary 2.32 using a classical argument. Indeed, if $0<\mu _2 \le \mu _1$ with $\mu _1+\mu _2 <\mu _0$, then

$$\begin{aligned} I_{\mu _1+\mu _2} <\frac{\mu _1+\mu _2}{\mu _1} I_{\mu _1}=I_{\mu _1} +\frac{\mu _2}{\mu _1} I_{\mu _1} \le I_{\mu _1}+I_{\mu _2}. \end{aligned}$$

Appendices

The Functional-Analytic Setting

The goal of this section is to introduce rigorous definitions of the Dirichlet–Neumann operators ${\underline{G}}({{\underline{\eta }}})$ and ${\overline{G}}(\varvec{\eta })$ and their inverses ${\underline{N}}({{\underline{\eta }}})$ and ${\overline{N}}(\varvec{\eta })$, as well as the operators $G(\varvec{\eta })$ and $K(\varvec{\eta })$.

1.1 Definition of Operators

1.1.1 Lower Fluid

In order to define ${\underline{G}}({{\underline{\eta }}})$ and ${\underline{N}}({{\underline{\eta }}})$, we first introduce suitable function spaces on which these operators are well defined. We begin by recalling the definition of the Schwartz class ${\mathcal {S}}({\overline{\Omega }})$ for an open set $\Omega \subset {\mathbb {R}}^n$:

$$\begin{aligned} {\mathcal {S}}({{\overline{\Omega }}}):=\left\{ u\in C^\infty ({{\overline{\Omega }}}):\sup _{\varvec{x} \in {{\overline{\Omega }}}} |\varvec{x}|^m|\partial ^\alpha u(\varvec{x})| <\infty \text { for all } m,\alpha \in {{\mathbb {N}}}_0^{n}\right\} . \end{aligned}$$

Definition A.1

• (i) Let $\dot{H}^{\frac{1}{2}}({\mathbb {R}})$ be the completion of ${\mathcal {S}}({\mathbb {R}})$ with respect to the norm

  $$\begin{aligned} \Vert u\Vert _{\dot{H}^{\frac{1}{2}}({\mathbb {R}})}:=\left( \int _{\mathbb {R}}|k| |{\hat{u}}(k)|^2 \, \mathrm{d}k\right) ^{\frac{1}{2}}. \end{aligned}$$

• (ii) Let ${\dot{H}}^{-\frac{1}{2}}({\mathbb {R}})$ be the completion of ${\overline{{\mathcal {S}}}}({\mathbb {R}})=\{u\in {\mathcal {S}}({\mathbb {R}}):{\hat{u}}(0)=0\}$ with respect to the norm

  $$\begin{aligned} \Vert u\Vert _{\dot{H}^{-\frac{1}{2}}({\mathbb {R}})}:=\left( \int _{\mathbb {R}}|k|^{-1} |{\hat{u}}(k)|^2\, \mathrm{d}k\right) ^{\frac{1}{2}}. \end{aligned}$$

• (iii) Let $\dot{H}^1(\Omega )$ be the completion of ${\mathcal {S}}({\overline{\Omega }})$ with respect to the norm

  $$\begin{aligned} \Vert u\Vert _{\dot{H}^1(\Omega )}:=\left( \int _{\Omega }|\nabla u|^2\, \mathrm{d}x\, \mathrm{d}y\right) ^{\frac{1}{2}}. \end{aligned}$$

The following result is classical, and the proof is therefore omitted. (We do, however, present a proof of a similar result for the upper domain later; see Proposition A.7.)

Proposition A.2

• (i) The trace map $u \mapsto u|_{y={\underline{\eta }}}$ defines a continuous map $\dot{H}^1({\underline{\Sigma }}({\underline{\eta }})) \rightarrow \dot{H}^{\frac{1}{2}}({\mathbb {R}})$ and has a continuous right inverse $\dot{H}^{\frac{1}{2}}({\mathbb {R}})\rightarrow \dot{H}^1({\underline{\Sigma }}({\underline{\eta }}))$.

• (ii) The space ${\dot{H}}^{-\frac{1}{2}}({\mathbb {R}})$ can be identified with $({\dot{H}}^{\frac{1}{2}}({\mathbb {R}}))^\prime$.

Definition A.3

For $\eta \in W^{1,\infty }({\mathbb {R}})$, the bounded linear operator ${\underline{G}}(\eta ):\dot{H}^{\frac{1}{2}}({\mathbb {R}})\rightarrow \dot{H}^{-\frac{1}{2}}({\mathbb {R}})$ is defined by

$$\begin{aligned} \langle {\underline{G}}({\underline{\eta }}){\underline{\Phi }}_1, {\underline{\Phi }}_2\rangle =\int _{{\underline{\Sigma }}({\underline{\eta }})} \nabla {\underline{\phi }}_1 \cdot \nabla {\underline{\phi }}_2 \,\mathrm{d}x\, \mathrm{d}y, \qquad {\underline{\Phi }}_1, {\underline{\Phi }}_2 \in \dot{H}^{\frac{1}{2}}({\mathbb {R}}), \end{aligned}$$

where $\langle \cdot \,, \cdot \rangle$ denotes the $\dot{H}^{-\frac{1}{2}}({\mathbb {R}}) \times \dot{H}^{\frac{1}{2}}({\mathbb {R}})$ pairing and ${\underline{\phi }}_j$, $j=1,2$, is the unique function in $\dot{H}^1({\underline{\Sigma }}({\underline{\eta }}))$ such that ${\underline{\phi }}_j|_{y={\underline{\eta }}}={\underline{\Phi }}_j$ and

$$\begin{aligned} \int _{{\underline{\Sigma }}({\underline{\eta }})} \nabla {\underline{\phi }}_j\cdot \nabla {\underline{\psi }}\, \mathrm{d}x\, \mathrm{d}y =0 \end{aligned}$$

for all ${\underline{\psi }} \in \dot{H}^1({\underline{\Sigma }}({\underline{\eta }}))$ with ${\underline{\psi }}|_{y={\underline{\eta }}}=0$.

Using Proposition A.2 and the definition of ${\underline{G}}({\underline{\eta }})$, we find that

$$\begin{aligned} \langle {\underline{G}}({\underline{\eta }}) {\underline{\Phi }}, {\underline{\Phi }}\rangle =\int _{{\underline{\Sigma }}({\underline{\eta }})} |\nabla {\underline{\phi }}|^2 \,\mathrm{d}x\, \mathrm{d}y \ge c\Vert {\underline{\Phi }}\Vert _{\dot{H}^{\frac{1}{2}}({\mathbb {R}})}^2 \end{aligned}$$

(A.1)

for some constant $c>0$ which depends on $\Vert {\underline{\eta }}\Vert _{W^{1, \infty }({\mathbb {R}})}$. From this we immediately obtain the following result.

Lemma A.4

The Dirichlet–Neumann operator ${\underline{G}}({\underline{\eta }}):\dot{H}^{\frac{1}{2}}({\mathbb {R}}) \rightarrow \dot{H}^{-\frac{1}{2}}({\mathbb {R}})$ is an isomorphism for each ${\underline{\eta }}\in W^{1,\infty }({\mathbb {R}})$.

Definition A.5

For ${\underline{\eta }}\in W^{1,\infty }({\mathbb {R}})$, the Neumann–Dirichlet operator ${\underline{N}}({\underline{\eta }}) :\dot{H}^{-\frac{1}{2}}({\mathbb {R}})\rightarrow \dot{H}^{\frac{1}{2}}({\mathbb {R}})$ is defined as the inverse of ${\underline{G}}({\underline{\eta }})$.

1.1.2 Upper Fluid

We next discuss the same questions for the upper fluid. Here we have the additional difficulty that both boundaries are free. Choose $h_0 \in (0,1)$. In order to prevent the boundaries from intersecting, we consider the class

$$\begin{aligned} W:=\{\varvec{\eta }=({\underline{\eta }}, {\overline{\eta }}) \in W^{1,\infty }({\mathbb {R}}):1+\inf ({\overline{\eta }}-{\underline{\eta }})>h_0\} \end{aligned}$$

of surface and interface profiles.

Definition A.6

• (i) Let $H_\star ^{\frac{1}{2}}({\mathbb {R}})$ be the completion of ${\mathcal {S}}({\mathbb {R}})$ with respect to the norm

  $$\begin{aligned} \Vert u\Vert _{H_\star ^{\frac{1}{2}}({\mathbb {R}})}:=\left( \int _{{\mathbb {R}}} (1+k^2)^{-\frac{1}{2}}k^2|\hat{u}|^2\, \mathrm{d}k\right) ^{\frac{1}{2}}, \end{aligned}$$

• (ii) Let $H_\star ^{-\frac{1}{2}}({\mathbb {R}})$ be the completion of ${\overline{{\mathcal {S}}}}({\mathbb {R}})$ with respect to the norm

  $$\begin{aligned} \Vert u\Vert _{H_\star ^{-\frac{1}{2}}({\mathbb {R}})}:=\left( \int _{{\mathbb {R}}} (1+k^2)^{\frac{1}{2}}k^{-2}|\hat{u}|^2\, \mathrm{d}k\right) ^{\frac{1}{2}}. \end{aligned}$$

• (iii) Let X be the Hilbert space

  $$\begin{aligned} \{ \overline{\varvec{\Phi }}=({\overline{\Phi }}_i, {\overline{\Phi }}_s)\in (H_\star ^{\frac{1}{2}}({\mathbb {R}}))^2 :{\overline{\Phi }}_s-{\overline{\Phi }}_i \in H^{\frac{1}{2}}({\mathbb {R}})\} \end{aligned}$$

  equipped with the inner product

  $$\begin{aligned} \langle \overline{\varvec{\Phi }}_1,\overline{\varvec{\Phi }}_2\rangle _X= \langle \overline{\varvec{\Phi }}_1,\overline{\varvec{\Phi }}_2\rangle _{(H_\star ^{\frac{1}{2}}({\mathbb {R}}))^2}+\langle {\overline{\Phi }}_{1,s}-{\overline{\Phi }}_{1,i},{\overline{\Phi }}_{2,s}-{\overline{\Phi }}_{2,i}\rangle _{H^{\frac{1}{2}}({\mathbb {R}})}. \end{aligned}$$

• (iv) Let Y be the Hilbert space

  $$\begin{aligned} \{\overline{\varvec{\Psi }}=({\overline{\Psi }}_i, {\overline{\Psi }}_s) \in (H^{-\frac{1}{2}}({{\mathbb {R}}}))^2:{\overline{\Psi }}_s+ {\overline{\Psi }}_i \in H_\star ^{-\frac{1}{2}}({\mathbb {R}})\} \end{aligned}$$

  equipped with the inner product

  $$\begin{aligned} \langle \overline{\varvec{\Psi }}_1,\overline{\varvec{\Psi }}_2\rangle _Y=\langle \overline{\varvec{\Psi }}_1,\overline{\varvec{\Psi }}_2\rangle _{(H^{-\frac{1}{2}}({\mathbb {R}}))^2}+\langle {\overline{\Psi }}_{1,s}+{\overline{\Psi }}_{1,i},{\overline{\Psi }}_{2,s}+{\overline{\Psi }}_{2,i}\rangle _{H_\star ^{-\frac{1}{2}}({\mathbb {R}})}. \end{aligned}$$

Note that we have the inclusions

$$\begin{aligned} H^{\frac{1}{2}}({\mathbb {R}}) \subset \dot{H}^{\frac{1}{2}}({\mathbb {R}})\subset H_\star ^{\frac{1}{2}}({\mathbb {R}}) \quad \text {and} \quad H_\star ^{-\frac{1}{2}}({\mathbb {R}}) \subset \dot{H}^{-\frac{1}{2}}({\mathbb {R}})\subset H^{-\frac{1}{2}}({\mathbb {R}}). \end{aligned}$$

The reason for introducing the space X is that it is the natural trace space associated with $\dot{H}^1({\overline{\Sigma }}(\varvec{\eta }))$. Since this is not completely standard, we include a proof.

Proposition A.7

Fix $\varvec{\eta }\in W$. The trace map $u \mapsto (u|_{y={\underline{\eta }}}, u|_{y=1+{\overline{\eta }}})$ defines a continuous map $\dot{H}^1({\overline{\Sigma }}(\varvec{\eta }))\rightarrow X$ with a continuous right inverse $X\rightarrow \dot{H}^1({\overline{\Sigma }}(\varvec{\eta }))$.

Proof

We flatten the domain using the transformation $(x,y)\mapsto (x, y^\prime (x,y))$, where

$$\begin{aligned} y^\prime (x,y) =\frac{y-{\underline{\eta }}(x)}{1+{\overline{\eta }}(x)-{\underline{\eta }}(x)}. \end{aligned}$$

This maps the domain ${\overline{\Sigma }}(\varvec{\eta })$ onto the strip ${{\overline{\Sigma }}}_0=\{(x,y)\in {\mathbb {R}}^2 :0<y<1\}$, and $\dot{H}^1({\overline{\Sigma }}(\varvec{\eta }))$ to $\dot{H}^1({\overline{\Sigma }}_0)$. Letting $\chi \in C_0^\infty ({\mathbb {R}})$ be a cut-off function with $\chi (0)=1$ and support in $[-1/2,1/2]$, we find that

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}y}(\chi (y) |{\hat{\phi }}(k, y)|^2)= \chi '(y)|{\hat{\phi }}(k, y)|^2 + 2\chi (y){{\,\mathrm{Re}\,}}({\hat{\phi }}(k, y)\overline{{\hat{\phi }}_y(k,y)}), \qquad \phi \in {\mathcal {S}}(\overline{{\overline{\Sigma }}_0}) \end{aligned}$$

and hence

$$\begin{aligned} \int _{{\mathbb {R}}} \langle k\rangle ^{-1}|k|^2 |{\hat{\phi }}(k, 0)|^2\, \mathrm{d}k&\le \int _{{\overline{\Sigma }}_0} (|k|^2 |{\hat{\phi }}(k, y)|^2+2|k| |{\hat{\phi }}(k,y)| |{\hat{\phi }}_y(k,y)|)\, \mathrm{d}k\, \mathrm{d}y\\&\le 2\int _{{\overline{\Sigma }}_0} (|k|^2 |{\hat{\phi }}(k, y)|^2+|{\hat{\phi }}_y(k,y)|^2)\, \mathrm{d}k\, \mathrm{d}y\\&=2\Vert \phi \Vert _{\dot{H}^1({\overline{\Sigma }}_0)}^2. \end{aligned}$$

Moreover,

$$\begin{aligned} \int _{{\mathbb {R}}} (\phi (x,1)-\phi (x,0))^2\, \mathrm{d}x= \int _{{\mathbb {R}}} \left( \int _{0}^{1} \phi _y\, \mathrm{d}y\right) ^2 \, \mathrm{d}x\le \Vert \phi \Vert _{\dot{H}^1({\overline{\Sigma }}_0)}^2. \end{aligned}$$

It follows that $\Vert \phi (\cdot , 1)-\phi (\cdot , 0)\Vert _{H^{\frac{1}{2}}({\mathbb {R}})}\le c\Vert \phi \Vert _{\dot{H}^1({\overline{\Sigma }}_0)}$, and hence that $\Vert (\phi |_{y=0}, \phi |_{y=1})\Vert _X\le c\Vert \phi \Vert _{\dot{H}^1({\overline{\Sigma }}_0)}$. The continuity of the trace map now follows by a density argument.

Conversely, given $({\overline{\Phi }}_i,{\overline{\Phi }}_s)$ we formally define $u\in \dot{H}^1({\overline{\Sigma }}_0)$ by

$$\begin{aligned} {\widehat{u}}=\frac{\sinh (k(1-y))}{\sinh (k)}\widehat{{\overline{\Phi }}_i} +\frac{\sinh (ky)}{\sinh (k)}\widehat{{\overline{\Phi }}_s}. \end{aligned}$$

This means that u is the element of $\dot{H}^1({\overline{\Sigma }}_0)$ whose partial derivatives have Fourier transforms

$$\begin{aligned} {\mathcal {F}}[u_x](k,y)&={i}k\frac{\sinh (k(1-y))}{\sinh (k)}\widehat{{\overline{\Phi }}_i} +{i}k\frac{\sinh (ky)}{\sinh (k)}\widehat{{\overline{\Phi }}_s},\\ {\mathcal {F}}[u_y](k,y)&=-k\frac{\cosh (k(1-y))}{\sinh (k)}\widehat{{\overline{\Phi }}_i} +k\frac{\cosh (ky)}{\sinh (k)}\widehat{{\overline{\Phi }}_s}. \end{aligned}$$

It is clear from these formulas that the map $X\ni ({\overline{\Phi }}_i, {\overline{\Phi }}_s) \mapsto u\in \dot{H}^1({\overline{\Sigma }}_0)$ is continuous. $\square$

Note that $(H_\star ^{\frac{1}{2}}({\mathbb {R}}))'$ can be identified with $H_\star ^{-\frac{1}{2}}({\mathbb {R}})$. A straightforward argument shows that the dual space of X is Y.

Proposition A.8

The space Y can be identified with the dual of X using the duality pairing

$$\begin{aligned} \langle \overline{\varvec{\Psi }}, \overline{\varvec{\Phi }}\rangle _{Y\times X}= \langle {\overline{\Psi }}_s, {\overline{\Phi }}_s-{\overline{\Phi }}_i \rangle _{H^{-\frac{1}{2}}({\mathbb {R}})\times H^{\frac{1}{2}}({\mathbb {R}})} + \langle {\overline{\Psi }}_s+ {\overline{\Psi }}_i, {\overline{\Phi }}_i \rangle _{H_\star ^{-\frac{1}{2}}({\mathbb {R}})\times H_\star ^{\frac{1}{2}}({\mathbb {R}})}. \end{aligned}$$

Definition A.9

For $\varvec{\eta }\in W$, the bounded linear operator ${\overline{G}}(\varvec{\eta }):X\rightarrow Y$ is defined by

$$\begin{aligned} \langle {\overline{G}}(\varvec{\eta })\overline{\varvec{\Phi }}_1, \overline{\varvec{\Phi }}_2 \rangle =\int _{{\overline{\Sigma }}(\varvec{\eta })} \nabla {\overline{\phi }}_1\cdot \nabla {\overline{\phi }}_2 \, \mathrm{d}x\, \mathrm{d}y, \qquad \overline{\varvec{\Phi }}_1, \overline{\varvec{\Phi }}_2 \in X, \end{aligned}$$

where $\langle \cdot , \cdot \rangle$ denotes the $Y\times X$ pairing and ${\overline{\phi }}_j$, $j=1,2$, is the unique function in $\dot{H}^1({\overline{\Sigma }}(\varvec{\eta }))$ such that ${\overline{\phi }}_j|_{y=1+{\overline{\eta }}}={\overline{\Phi }}_{j,s}$, ${\overline{\phi }}_j|_{y={\underline{\eta }}}={\overline{\Phi }}_{j,i}$ and

$$\begin{aligned} \int _{{\overline{\Sigma }}(\varvec{\eta })} \nabla {\overline{\phi }}_j \cdot \nabla {\overline{\psi }} \, \mathrm{d}x\, \mathrm{d}y=0 \end{aligned}$$

for all ${\overline{\psi }} \in \dot{H}^1({\overline{\Sigma }}(\varvec{\eta }))$ with ${\overline{\psi }}|_{y={\underline{\eta }}}=0$ and ${\overline{\psi }}|_{y=1+{\overline{\eta }}}=0$

As in the case of the lower fluid, we obtain that

$$\begin{aligned} \langle {\overline{G}}(\varvec{\eta }) \overline{\varvec{\Phi }}, \overline{\varvec{\Phi }}\rangle \ge c\Vert \overline{\varvec{\Phi }}\Vert _{X}^2, \end{aligned}$$

(A.2)

for some constant $c>0$ which depends on $h_0$ and $\Vert \varvec{\eta }\Vert _{W^{1,\infty }({\mathbb {R}})}$, and the following consequence.

Lemma A.10

The operator ${\overline{G}}(\varvec{\eta }):X \rightarrow Y$ is an isomorphism for each $\varvec{\eta }\in W$.

Definition A.11

For $\varvec{\eta }\in W$, the Neumann–Dirichlet operator ${\overline{N}}(\varvec{\eta }) :Y \rightarrow X$ is defined as the inverse of ${\overline{G}}(\varvec{\eta })$.

1.1.3 Further Operators

We now proceed with the rigorous definition of the operators $G(\varvec{\eta })$, $N(\varvec{\eta })$ and $K(\varvec{\eta })$. Recall that the definition of ${\overline{G}}(\varvec{\eta })$ involves various combinations of the components of ${\overline{G}}(\varvec{\eta })$ (cf. (1.23)). We can formally write

$$\begin{aligned} {\overline{G}}(\varvec{\eta })\overline{\varvec{\Phi }}= \begin{pmatrix} {\overline{G}}_{11}(\varvec{\eta }) &{} {\overline{G}}_{12}(\varvec{\eta })\\ {\overline{G}}_{21}(\varvec{\eta }) &{} {\overline{G}}_{22}(\varvec{\eta }) \end{pmatrix} \begin{pmatrix} {\overline{\Phi }}_i\\ {\overline{\Phi }}_s \end{pmatrix}, \end{aligned}$$

but since the definition of the function space X involves the condition ${\overline{\Phi }}_s-{\overline{\Phi }}_i \in H^{\frac{1}{2}}({\mathbb {R}})$ which couples the components ${\overline{\Phi }}_s$ and ${\overline{\Phi }}_i$, the definition of the components ${\overline{G}}_{ij}$ requires some care. Note, however, that $(H^{\frac{1}{2}}({\mathbb {R}}))^2 \subset X$, so that the components ${\overline{G}}_{ij}(\varvec{\eta })$ define bounded operators $H^{\frac{1}{2}}({\mathbb {R}})\rightarrow H^{-\frac{1}{2}}({\mathbb {R}})$. The components ${\overline{N}}_{ij}(\varvec{\eta })$ can similarly be defined by considering the subspace $(H_\star ^{-\frac{1}{2}}({\mathbb {R}}))^2\subset Y$.

Proposition A.12

The operators ${\overline{G}}_{ij}(\varvec{\eta }):H^{\frac{1}{2}}({\mathbb {R}})\rightarrow H^{-\frac{1}{2}}({\mathbb {R}})$ and ${\overline{N}}_{ij}(\varvec{\eta }):H_\star ^{-\frac{1}{2}}({\mathbb {R}})\rightarrow H_\star ^{\frac{1}{2}}({\mathbb {R}})$ are continuous.

Lemma A.13

For each $\varvec{\eta }\in W$, the operator $B(\varvec{\eta }):={\overline{G}}_{11}(\varvec{\eta })+ \rho {\underline{G}}({\underline{\eta }})$ is an isomorphism $H^{\frac{1}{2}}({\mathbb {R}})\rightarrow H^{-\frac{1}{2}}({\mathbb {R}})$.

Proof

Recall that ${\underline{G}}({\underline{\eta }}):\dot{H}^{\frac{1}{2}}({\mathbb {R}})\rightarrow \dot{H}^{-\frac{1}{2}}({\mathbb {R}})$ is an isomorphism, with

$$\begin{aligned} \langle {\underline{G}}({\underline{\eta }}){\underline{\Phi }}, {\underline{\Phi }}\rangle _{\dot{H}^{-\frac{1}{2}}({\mathbb {R}}) \times \dot{H}^{\frac{1}{2}}({\mathbb {R}})} \ge c\Vert {\underline{\Phi }}\Vert _{\dot{H}^{\frac{1}{2}}({\mathbb {R}})}^2 \end{aligned}$$

(cf. (A.1) and Lemma A.4) for some $c>0$. On the other hand,

$$\begin{aligned} \langle {\overline{G}}_{11}(\varvec{\eta }){\overline{\Phi }}_i, {\overline{\Phi }}_i\rangle _{H^{-\frac{1}{2}}({\mathbb {R}}) \times H^{\frac{1}{2}}({\mathbb {R}})} \ge c\Vert {\overline{\Phi }}_i\Vert _{H^{\frac{1}{2}}({\mathbb {R}})}^2, \end{aligned}$$

by Definition A.6 and (A.2) with ${\overline{\Phi }}_s=0$. It follows that

$$\begin{aligned} \langle B(\varvec{\eta }) \Phi , \Phi \rangle _{H^{-\frac{1}{2}}({\mathbb {R}})\times H^{\frac{1}{2}}({\mathbb {R}})} \ge c \Vert \Phi \Vert _{H^{\frac{1}{2}}({\mathbb {R}})}^2 \end{aligned}$$

and hence $B(\varvec{\eta }) :H^{\frac{1}{2}}({\mathbb {R}})\rightarrow H^{-\frac{1}{2}}({\mathbb {R}})$ is an isomorphism. $\square$

Recall that we formally defined the operator $G(\varvec{\eta })$ by

$$\begin{aligned} G(\varvec{\eta }):=\begin{pmatrix}{\underline{G}}({\underline{\eta }}) B(\varvec{\eta })^{-1}{\overline{G}}_{11}(\varvec{\eta }) &{}-{\underline{G}}({\underline{\eta }})B(\varvec{\eta })^{-1}{\overline{G}}_{12}(\varvec{\eta })\\ -{\overline{G}}_{21}(\varvec{\eta })B(\varvec{\eta })^{-1}{\underline{G}}({\underline{\eta }})&{}\tfrac{1}{\rho }{\overline{G}}_{22}(\varvec{\eta })-\tfrac{1}{\rho }{\overline{G}}_{21}(\varvec{\eta })B(\varvec{\eta })^{-1}{\overline{G}}_{12}(\varvec{\eta })\end{pmatrix}. \end{aligned}$$

It is not difficult to see that $G(\varvec{\eta })$ is bounded $(H^{\frac{1}{2}}({\mathbb {R}}))^2 \rightarrow (H^{-\frac{1}{2}}({\mathbb {R}}))^2$. However, we need to extend it to a larger space in order to define $K(\varvec{\eta })$. We record some lemmas which enable us to do this.

Lemma A.14

The operators ${\overline{G}}_{11}(\varvec{\eta }) B^{-1}(\varvec{\eta })$ and ${\overline{G}}_{21}(\varvec{\eta }) B^{-1}(\varvec{\eta })$ are bounded on $\dot{H}^{-\frac{1}{2}}({\mathbb {R}})$.

Proof

The first part follows from the facts that ${\overline{G}}_{11}(\varvec{\eta })B^{-1}(\varvec{\eta })=I-\rho {\underline{G}}({\underline{\eta }})B^{-1}(\varvec{\eta })$ as well as ${\underline{G}}({\underline{\eta }})B^{-1}(\varvec{\eta }) \in {\mathcal {L}}(H^{-\frac{1}{2}}({\mathbb {R}}), \dot{H}^{-\frac{1}{2}}({\mathbb {R}}))$. The second part now follows from the fact that ${\overline{G}}_{11}(\varvec{\eta })+{\overline{G}}_{21}(\varvec{\eta })\in {\mathcal {L}}(H^{\frac{1}{2}}({\mathbb {R}}), H_\star ^{-\frac{1}{2}}({\mathbb {R}}))$. $\square$

Corollary A.15

The maps $B^{-1}(\varvec{\eta }) {\overline{G}}_{11}(\varvec{\eta })$ and $B^{-1}(\varvec{\eta }) {\overline{G}}_{12}(\varvec{\eta })$ extend to bounded mappings on $\dot{H}^{\frac{1}{2}}({\mathbb {R}})$ by duality.

Recall that $\varvec{\xi }$ is defined in terms of ${\underline{\Phi }}$ and $\overline{\varvec{\Phi }}$ through (1.17). Conversely, we can formally recover ${\underline{\Phi }}$ and $\overline{\varvec{\Phi }}$ from $\varvec{\xi }$ through (1.20) under assumption (1.18). We now investigate these relations in more detail. We begin defining appropriate function spaces for $\varvec{\xi }$ and $G(\varvec{\eta }) \varvec{\xi }$.

Definition A.16

• (i) Let ${{\tilde{X}}}$ be the Hilbert space

  $$\begin{aligned} \{\varvec{\xi }=({\underline{\xi }}, {\overline{\xi }})\in (H_\star ^{\frac{1}{2}}({\mathbb {R}}))^2 :{\underline{\xi }}+{\overline{\xi }} \in \dot{H}^{\frac{1}{2}}({\mathbb {R}})\} \end{aligned}$$

  equipped with the inner product

  $$\begin{aligned} \langle \varvec{\xi }_1,\varvec{\xi }_2\rangle _{{{\tilde{X}}}}=\langle \varvec{\xi }_1, \varvec{\xi }_2\rangle _{(H_\star ^{\frac{1}{2}}({\mathbb {R}}))^2}+\langle {\overline{\xi }}_{1}+{\underline{\xi }}_{1},{\overline{\xi }}_{2}+{\underline{\xi }}_{2}\rangle _{\dot{H}^{\frac{1}{2}}({\mathbb {R}})}. \end{aligned}$$

• (ii) Let ${{\tilde{Y}}}$ be the Hilbert space

  $$\begin{aligned} \{\varvec{\zeta }=({\underline{\zeta }}, {\overline{\zeta }}) \in (\dot{H}^{-\frac{1}{2}}({\mathbb {R}}))^2 :{\overline{\zeta }}-{\underline{\zeta }}\in H_\star ^{-\frac{1}{2}}({\mathbb {R}})\} \end{aligned}$$

  equipped with the inner product

  $$\begin{aligned} \langle \varvec{\zeta }_1, \varvec{\zeta }_2\rangle _{{{\tilde{Y}}}}=\langle \varvec{\zeta }_1,\varvec{\zeta }_2 \rangle _{(\dot{H}^{-\frac{1}{2}}({\mathbb {R}}))^2}+\langle {\overline{\zeta }}_{1}-{\underline{\zeta }}_{1},{\overline{\zeta }}_{2}-{\underline{\zeta }}_{2}\rangle _{H_\star ^{-\frac{1}{2}}({\mathbb {R}})}. \end{aligned}$$

An argument similar to Proposition A.8 shows that ${{\tilde{Y}}}$ is dual to ${{\tilde{X}}}$.

Lemma A.17

Equation (1.20) defines bounded linear operators

$$\begin{aligned} \varvec{\xi }\mapsto {\underline{\Phi }}:{{\tilde{X}}} \rightarrow \dot{H}^{\frac{1}{2}}({\mathbb {R}}) \end{aligned}$$

and

$$\begin{aligned} \varvec{\xi }\mapsto \overline{\varvec{\Phi }}:{{\tilde{X}}} \rightarrow X \end{aligned}$$

with

$$\begin{aligned} {\underline{G}}({\underline{\eta }}) {\underline{\Phi }}=-({\overline{G}}_{11}(\varvec{\eta }){\overline{\Phi }}_i+ {\overline{G}}_{12}(\varvec{\eta }){\overline{\Phi }}_s). \end{aligned}$$

Proof

By definition, we have that

$$\begin{aligned} {\underline{\Phi }}&=B^{-1}(\varvec{\eta }){\overline{G}}_{11}(\varvec{\eta }){\underline{\xi }}-B^{-1}(\varvec{\eta }){\overline{G}}_{12}(\varvec{\eta }){\overline{\xi }}\\&=B^{-1}(\varvec{\eta }){\overline{G}}_{11}(\varvec{\eta })({\underline{\xi }}+{\overline{\xi }}) -B^{-1}(\varvec{\eta })({\overline{G}}_{11}(\varvec{\eta })+{\overline{G}}_{12}(\varvec{\eta })){\overline{\xi }}. \end{aligned}$$

This defines an element of $\dot{H}^{\frac{1}{2}}({\mathbb {R}})$ by Corollary A.15 and the continuity of

$$\begin{aligned} ({\overline{G}}_{11}(\varvec{\eta })+{\overline{G}}_{12}(\varvec{\eta })) :H_\star ^{\frac{1}{2}}({\mathbb {R}}) \rightarrow H^{-\frac{1}{2}}({\mathbb {R}}). \end{aligned}$$

Similarly,

$$\begin{aligned} {\overline{\Phi }}_i&=-B^{-1}(\varvec{\eta }){\underline{G}}({\underline{\eta }}){\underline{\xi }}-\frac{1}{\rho } B^{-1}(\varvec{\eta }){\overline{G}}_{12}(\varvec{\eta }){\overline{\xi }}\\&=-B^{-1}(\varvec{\eta }){\underline{G}}({\underline{\eta }})({\underline{\xi }}+{\overline{\xi }})\\&\quad + \frac{1}{\rho } B^{-1}(\varvec{\eta })(\rho {\underline{G}}({\underline{\eta }})+{\overline{G}}_{11}(\varvec{\eta })){\overline{\xi }}-\frac{1}{\rho } B^{-1}(\varvec{\eta })({\overline{G}}_{11}(\varvec{\eta })+{\overline{G}}_{12}(\varvec{\eta })){\overline{\xi }}\\&= -B^{-1}(\varvec{\eta }){\underline{G}}({\underline{\eta }})({\underline{\xi }}+{\overline{\xi }})+ \frac{1}{\rho } {\overline{\xi }}-\frac{1}{\rho } B^{-1}(\varvec{\eta })({\overline{G}}_{11}(\varvec{\eta })+{\overline{G}}_{12}(\varvec{\eta })){\overline{\xi }} \in H_\star ^{\frac{1}{2}}({\mathbb {R}}). \end{aligned}$$

It is obvious that ${\overline{\Phi }}_s=\frac{1}{\rho } {\overline{\xi }} \in H_\star ^{\frac{1}{2}}({\mathbb {R}})$. To see that $\overline{\varvec{\Phi }}\in X$, we note that

$$\begin{aligned} {\overline{\Phi }}_s-{\overline{\Phi }}_i =B^{-1}(\varvec{\eta }){\underline{G}}({\underline{\eta }})({\underline{\xi }}+{\overline{\xi }}) +\frac{1}{\rho } B^{-1}(\varvec{\eta })({\overline{G}}_{11}(\varvec{\eta })+{\overline{G}}_{12}(\varvec{\eta })){\overline{\xi }}\in H^{\frac{1}{2}}({\mathbb {R}}). \end{aligned}$$

It is easily seen that all of the involved operators are bounded. The final formula follows by straightforward algebraic manipulations. $\square$

Proposition A.18

The operator $G(\varvec{\eta })$ is bounded ${{\tilde{X}}} \rightarrow {{\tilde{Y}}}$.

Proof

Assume that $\varvec{\xi }\in {{\tilde{X}}}$. A direct computation then shows that

$$\begin{aligned}&{\underline{G}}({\underline{\eta }})B(\varvec{\eta })^{-1}{\overline{G}}_{11}(\varvec{\eta }){\underline{\xi }}-{\underline{G}}({\underline{\eta }})B(\varvec{\eta })^{-1}{\overline{G}}_{12}(\varvec{\eta }){\overline{\xi }} \\&\quad = {\underline{G}}({\underline{\eta }})(B(\varvec{\eta })^{-1} {\overline{G}}_{11}(\varvec{\eta }){\underline{\xi }} -B(\varvec{\eta })^{-1}{\overline{G}}_{12}(\varvec{\eta }){\overline{\xi }})\\&\quad ={\underline{G}}({\underline{\eta }}){\underline{\Phi }}\in \dot{H}^{-\frac{1}{2}}({\mathbb {R}}), \end{aligned}$$

where we have used Lemma A.17. Similarly,

$$\begin{aligned}&-{\overline{G}}_{21}(\varvec{\eta })B(\varvec{\eta })^{-1}{\underline{G}}({\underline{\eta }}){\underline{\xi }} + (\tfrac{1}{\rho }{\overline{G}}_{22}(\varvec{\eta })-\tfrac{1}{\rho }{\overline{G}}_{21}(\varvec{\eta })B(\varvec{\eta })^{-1}{\overline{G}}_{12}(\varvec{\eta })){\overline{\xi }}\\&\qquad ={\overline{G}}_{21}(\varvec{\eta })(-B(\varvec{\eta })^{-1}{\underline{G}}({\underline{\eta }}){\underline{\xi }} -\tfrac{1}{\rho } B(\varvec{\eta })^{-1}{\overline{G}}_{12}(\varvec{\eta }){\overline{\xi }}) +{\overline{G}}_{22}(\varvec{\eta }){\overline{\Phi }}_s\\&\qquad ={\overline{G}}_{21}(\varvec{\eta }){\overline{\Phi }}_i+{\overline{G}}_{22}(\varvec{\eta }){\overline{\Phi }}_s \in H^{-\frac{1}{2}}({\mathbb {R}}). \end{aligned}$$

We have to show that the last expression is actually an element of $\dot{H}^{-\frac{1}{2}}({\mathbb {R}})$. To see this, we note that

$$\begin{aligned} {\overline{G}}_{11}(\varvec{\eta }){\overline{\Phi }}_i+{\overline{G}}_{12}(\varvec{\eta }){\overline{\Phi }}_s+ {\overline{G}}_{21}(\varvec{\eta }){\overline{\Phi }}_i+{\overline{G}}_{22}(\varvec{\eta }){\overline{\Phi }}_s \in H_\star ^{-\frac{1}{2}}({\mathbb {R}}), \end{aligned}$$

(A.3)

by the definition of Y and Definition A.9. On the other hand,

$$\begin{aligned} {\overline{G}}_{11}(\varvec{\eta }){\overline{\Phi }}_i+{\overline{G}}_{12}(\varvec{\eta }){\overline{\Phi }}_s =-{\underline{G}}({\underline{\eta }}){\underline{\Phi }} \in \dot{H}^{-\frac{1}{2}}({\mathbb {R}}). \end{aligned}$$

This shows that ${\overline{G}}_{21}(\varvec{\eta }){\overline{\Phi }}_i+{\overline{G}}_{22}(\varvec{\eta }){\overline{\Phi }}_s\in \dot{H}^{-\frac{1}{2}}({\mathbb {R}})$. The fact that $(G(\varvec{\eta })\varvec{\xi })_2-(G(\varvec{\eta })\varvec{\xi })_1\in H_\star ^{-\frac{1}{2}}({\mathbb {R}})$ follows from (A.3). The boundedness of $G(\varvec{\eta })$ follows from the above formulas and Lemma A.17. $\square$

Define

$$\begin{aligned} N(\varvec{\eta }):=\begin{pmatrix} \rho {\overline{N}}_{11}(\varvec{\eta }) +{\underline{N}}({\underline{\eta }}) &{}\quad -\rho {\overline{N}}_{12}(\varvec{\eta })\\ -\rho {\overline{N}}_{21}(\varvec{\eta }) &{} \quad \rho {\overline{N}}_{22}(\varvec{\eta }) \end{pmatrix}. \end{aligned}$$

Proposition A.19

$G(\varvec{\eta }):{{\tilde{X}}} \rightarrow {{\tilde{Y}}}$ is invertible with

$$\begin{aligned} G(\varvec{\eta })^{-1}= N(\varvec{\eta }). \end{aligned}$$

Proof

We begin by showing that $N(\varvec{\eta })$ defines an operator ${{\tilde{Y}}}\rightarrow {{\tilde{X}}}$. Indeed, if $\varvec{\zeta }=({\underline{\zeta }}, {\overline{\zeta }})\in {{\tilde{Y}}}$, then $({\underline{\zeta }}, -{\overline{\zeta }})\in Y$ whence

$$\begin{aligned}&{\overline{N}}_{11}(\varvec{\eta }){\underline{\zeta }} -{\overline{N}}_{12}(\varvec{\eta }){\overline{\zeta }} =({\overline{N}}(\eta ) ({\underline{\zeta }}, -{\overline{\zeta }}))_1\in H_\star ^{\frac{1}{2}}({\mathbb {R}}),\\&\quad -{\overline{N}}_{21}(\varvec{\eta }){\underline{\zeta }} +{\overline{N}}_{12}(\varvec{\eta }){\overline{\zeta }} =-({\overline{N}}(\eta ) ({\underline{\zeta }}, -{\overline{\zeta }}))_2\in H_\star ^{\frac{1}{2}}({\mathbb {R}}), \end{aligned}$$

and

$$\begin{aligned} {\underline{N}}({\underline{\eta }}){\underline{\zeta }} \in \dot{H}^{\frac{1}{2}}({\mathbb {R}}). \end{aligned}$$

Finally,

$$\begin{aligned}&({\overline{N}}_{11}(\varvec{\eta }){\underline{\zeta }}-{\overline{N}}_{12}(\varvec{\eta }){\overline{\zeta }}) +(-{\overline{N}}_{21}(\varvec{\eta }){\underline{\zeta }} +{\overline{N}}_{12}(\varvec{\eta }){\overline{\zeta }})) \\&\quad = ({\overline{N}}_{11}(\varvec{\eta }){\underline{\zeta }} -{\overline{N}}_{12}(\varvec{\eta }){\overline{\zeta }}) -({\overline{N}}_{21}(\varvec{\eta }){\underline{\zeta }} -{\overline{N}}_{12}(\varvec{\eta }){\overline{\zeta }})) \in H^{\frac{1}{2}}({\mathbb {R}}), \end{aligned}$$

which implies that

$$\begin{aligned} \rho (({\overline{N}}_{11}(\varvec{\eta }){\underline{\zeta }}-{\overline{N}}_{12}(\varvec{\eta }){\overline{\zeta }}) +(-{\overline{N}}_{21}(\varvec{\eta }){\underline{\zeta }} +{\overline{N}}_{12}(\varvec{\eta }){\overline{\zeta }})) +{\underline{N}}({\underline{\eta }}){\overline{\zeta }} \in \dot{H}^{\frac{1}{2}}({\mathbb {R}}). \end{aligned}$$

The equation $G(\varvec{\eta }) \varvec{\xi }=\varvec{\zeta }\in {{\tilde{Y}}}$ can equivalently be written

$$\begin{aligned} {\overline{G}}_{11}(\varvec{\eta }){\overline{\Phi }}_i+{\overline{G}}_{12}(\varvec{\eta }){\overline{\Phi }}_s&=-{\underline{\zeta }},\\ {\overline{G}}_{21}(\varvec{\eta }){\overline{\Phi }}_i+{\overline{G}}_{22}(\varvec{\eta }){\overline{\Phi }}_s&={\overline{\zeta }}, \end{aligned}$$

with the unique solution

$$\begin{aligned} \overline{\varvec{\Phi }}={\overline{N}}(\varvec{\eta })(-{\underline{\zeta }}, {\overline{\zeta }}). \end{aligned}$$

On the other hand, we also have ${\underline{G}}({\underline{\eta }}){\underline{\Phi }} ={\underline{\zeta }}$, so that ${\underline{\Phi }}={\underline{N}}({\underline{\eta }}) {\underline{\zeta }}$. It follows that $G(\varvec{\eta }) \varvec{\xi }=\varvec{\zeta }$ if and only if

$$\begin{aligned} {\underline{\xi }}={\underline{\Phi }}-\rho {\overline{\Phi }}_i =(\rho {\overline{N}}_{11}(\varvec{\eta }) +{\underline{N}}({\underline{\eta }})){\underline{\zeta }} -\rho {\overline{N}}_{12}(\varvec{\eta }){\overline{\zeta }} \end{aligned}$$

and

$$\begin{aligned} {\overline{\xi }}=\rho {\overline{\Phi }}_s =-\rho {\overline{N}}_{21}(\varvec{\eta }){\underline{\zeta }} +\rho {\overline{N}}_{22}(\varvec{\eta }){\overline{\zeta }}. \end{aligned}$$

Hence, $N(\varvec{\eta })$ is the inverse of $G(\varvec{\eta })$. $\square$

We are now finally ready to discuss the operator $K(\varvec{\eta })$.

Definition A.20

• (i) Let $\breve{X}$ be the Hilbert space

  $$\begin{aligned} \{\varvec{\xi }=({\underline{\xi }}, {\overline{\xi }})\in (\dot{H}^{\frac{1}{2}}({\mathbb {R}}))^2 :{\underline{\xi }}-{\overline{\xi }} \in H^{\frac{1}{2}}({\mathbb {R}})\} \end{aligned}$$

  equipped with the inner product

  $$\begin{aligned} \langle \varvec{\xi }_1,\varvec{\xi }_2\rangle _{\check{X}}=\langle \varvec{\xi }_1, \varvec{\xi }_2\rangle _{(\dot{H}^{\frac{1}{2}}({\mathbb {R}}))^2}+\langle {\overline{\xi }}_{1}-{\underline{\xi }}_{1},{\overline{\xi }}_{2}-{\underline{\xi }}_{2}\rangle _{H^{\frac{1}{2}}({\mathbb {R}})}. \end{aligned}$$

• (ii) Let $\breve{Y}$ be the Hilbert space

  $$\begin{aligned} \{\varvec{\zeta }=({\underline{\zeta }}, {\overline{\zeta }}) \in (H^{-\frac{1}{2}}({\mathbb {R}}))^2 :{\overline{\zeta }}+{\underline{\zeta }}\in \dot{H}^{-\frac{1}{2}}({\mathbb {R}})\} \end{aligned}$$

  equipped with the inner product

  $$\begin{aligned} \langle \varvec{\zeta }_1,\varvec{\zeta }_2\rangle _{\check{X}}=\langle \varvec{\zeta }_1, \varvec{\zeta }_2\rangle _{(H^{-\frac{1}{2}}({\mathbb {R}}))^2}+\langle {\overline{\zeta }}_{1}+{\underline{\zeta }}_{1},{\overline{\zeta }}_{2}+{\underline{\zeta }}_{2}\rangle _{\dot{H}^{-\frac{1}{2}}({\mathbb {R}})}. \end{aligned}$$

Note $\breve{X}$ and $\breve{Y}$ are each other’s duals and that $(H^{\frac{1}{2}}({\mathbb {R}}))^2 \hookrightarrow \breve{X}$, $\breve{Y}\hookrightarrow (H^{-\frac{1}{2}}({\mathbb {R}}))^2$.

Proposition A.21

The formula $K(\varvec{\eta })=-\partial _x N(\varvec{\eta }) \partial _x$ defines an isomorphism $\breve{X}\rightarrow \breve{Y}$ with

$$\begin{aligned} \langle K(\varvec{\eta })\varvec{\xi }, \varvec{\xi }\rangle _{\breve{Y}\times \breve{X}} \ge c\Vert \varvec{\xi }\Vert _{\breve{X}}^2. \end{aligned}$$

Proof

The fact that $K(\varvec{\eta })$ is a bounded operator from $\breve{Y}$ to $\breve{X}$ follows by noting that $\partial _x$ is an isomorphism from $\breve{X}$ to ${{\tilde{Y}}}$ and from ${{\tilde{X}}}$ to $\breve{Y}$. The lower bound follows by setting $\tilde{\varvec{\xi }}=({\underline{\xi }}, -{\overline{\xi }})$ and noting that

$$\begin{aligned}&\langle K(\varvec{\eta })\varvec{\xi }, \varvec{\xi }\rangle _{\breve{Y} \times \breve{X}} \\&\qquad =\rho \langle {\overline{N}}(\varvec{\eta })\partial _x \tilde{\varvec{\xi }}, \partial _x\tilde{\varvec{\xi }}\rangle _{(H_\star ^{\frac{1}{2}}({\mathbb {R}}))^2 \times (H_\star ^{-\frac{1}{2}}({\mathbb {R}}))^2}+ \langle {\underline{N}}({\underline{\eta }}) \partial _x {\underline{\xi }}, \partial _x {\underline{\xi }} \rangle _{\dot{H}^{\frac{1}{2}}({\mathbb {R}})\times \dot{H}^{-\frac{1}{2}}({\mathbb {R}})}\\&\qquad \ge c(\Vert \partial _x \tilde{\varvec{\xi }}\Vert _Y^2+\Vert \partial _x {\underline{\xi }}\Vert _{\dot{H}^{-\frac{1}{2}}({\mathbb {R}})}^2)\\&\qquad \ge c(\Vert \varvec{\xi }\Vert _{(\dot{H}^{\frac{1}{2}}({\mathbb {R}}))^2}^2 +\Vert {\underline{\xi }}-{\overline{\xi }}\Vert _{H^{\frac{1}{2}}({\mathbb {R}})}^2). \end{aligned}$$

This also shows that $K(\varvec{\eta })$ is an isomorphism. $\square$

It will be useful to write $K(\varvec{\eta })$ in the form

$$\begin{aligned} K(\varvec{\eta }) = \begin{pmatrix} {\underline{K}}({\underline{\eta }}) &{}\quad 0 \\ 0 &{}\quad 0 \end{pmatrix} + \rho {\overline{K}}(\varvec{\eta }), \end{aligned}$$

(A.4)

where ${\underline{K}}({\underline{\eta }}):=-\partial _x {\underline{N}}({\underline{\eta }})\partial _x$ and

$$\begin{aligned} {\overline{K}}(\varvec{\eta }):=- \partial _x\begin{pmatrix} {\overline{N}}_{11}(\varvec{\eta }) &{}\quad - {\overline{N}}_{12}(\varvec{\eta }) \\ - {\overline{N}}_{21}(\varvec{\eta }) &{}\quad {\overline{N}}_{22}(\varvec{\eta }) \end{pmatrix}\partial _x. \end{aligned}$$

1.2 Analyticity and Higher Regularity

In this section we discuss the analyticity of the operators ${\overline{K}}(\varvec{\eta })$ and ${\underline{K}}({{\underline{\eta }}})$ as functions of $\varvec{\eta }$ and ${{\underline{\eta }}}$, respectively. We also discuss how they act on higher-order Sobolev spaces, assuming that $\varvec{\eta }$ is sufficiently regular. We begin by considering the second operator using the method explained by Groves and Wahlén (2015). First, note that ${\underline{N}}({\underline{\eta }})$ is given by

$$\begin{aligned} {\underline{N}}({\underline{\eta }}){\underline{\Psi }}={\underline{\phi }}|_{y={\underline{\eta }}}, \end{aligned}$$

where ${\underline{\phi }} \in \dot{H}^1({\underline{\Sigma }}({\underline{\eta }}))$ is a weak solution of the boundary value problem

$$\begin{aligned} \begin{aligned}&\Delta {\underline{\phi }}=0,&y<{\underline{\eta }},\\&{\underline{\phi }}_y - {\underline{\eta }}^\prime {\underline{\phi }}_x = {\underline{\Psi }},&y={\underline{\eta }}, \end{aligned} \end{aligned}$$

(A.5)

that is,

$$\begin{aligned} \int _{{\underline{\Sigma }}(\underline{\eta )}} \nabla {\underline{\phi }} \cdot \nabla {\underline{\psi }} \, \mathrm{d}x\, \mathrm{d}y=\int _{{\mathbb {R}}} {\underline{\Psi }} \psi |_{y={\underline{\eta }}} \, \mathrm{d}x\end{aligned}$$

for all $\psi \in \dot{H}^1({\underline{\Sigma }}({\underline{\eta }}))$.

We study the dependence of ${\underline{N}}({\underline{\eta }})$ by transforming this boundary value problem into an equivalent one in the fixed domain ${\underline{\Sigma }}_0 :={\underline{\Sigma }}(0)$. For this purpose we make the change of variables

$$\begin{aligned} y'=y-{\underline{\eta }} \end{aligned}$$

and define

$$\begin{aligned} {\underline{F}}(x,y^\prime )=(x, y^\prime +{\underline{\eta }}(x)) \end{aligned}$$

and

$$\begin{aligned} {\underline{u}}(x,y')={\underline{\phi }}({\underline{F}}(x,y')) \end{aligned}$$

This change of variable transforms the boundary value problem (A.5) into

$$\begin{aligned}&\nabla \cdot ((I+{\underline{Q}})\nabla {\underline{u}})=0&y <0,\\&(I+{\underline{Q}})\nabla {\underline{u}} \cdot (0, 1) = {\underline{\Psi }},&y=0, \end{aligned}$$

where

$$\begin{aligned} {\underline{Q}}= \begin{pmatrix} 0 &{} \quad - {\underline{\eta }}_x \\ - {\underline{\eta }}_x &{}\quad {\underline{\eta }}_x^2 \end{pmatrix} \end{aligned}$$

and the primes have been dropped for notational simplicity. The weak form of this problem is

$$\begin{aligned} \int _{{\underline{\Sigma }}} (1+{\underline{Q}})\nabla {\underline{u}} \cdot \nabla w \, \mathrm{d}x\, \mathrm{d}y=\int _{{\mathbb {R}}} {\underline{\Psi }}\,w|_{y=0} \, \mathrm{d}x\end{aligned}$$

for all $w\in \dot{H}^1({\underline{\Sigma }}_0)$. Fix ${\underline{\eta }}_0$ and write $\tilde{{\underline{\eta }}}={\underline{\eta }}-{\underline{\eta }}_0$ and

$$\begin{aligned} {\underline{Q}}(x,y)=\sum _{n=0}^\infty {\underline{Q}}^n(x,y), \qquad {\underline{Q}}^n ={{\tilde{m}}}^n({{\tilde{\eta }}}^{(n)}), \end{aligned}$$

where ${{\tilde{m}}}^n \in {\mathcal {L}}_\mathrm {s}^n(W^{1, \infty }({\mathbb {R}}), (L^\infty ({\mathbb {R}}^2))^{2\times 2})$ (in which ${\mathcal {L}}_\mathrm {s}^n$ denotes the set of bounded, symmetric, n-linear operators). We seek a solution of the above boundary value problem of the form

$$\begin{aligned} {\underline{u}}(x,y)=\sum _{n=0}^\infty {\underline{u}}^n(x,y), \qquad {\underline{u}}^n=m^n(\{\tilde{{\underline{\eta }}}\}^{(n)}), \end{aligned}$$

where $m^n \in {\mathcal {L}}_\mathrm {s}^n(W^{1, \infty }({\mathbb {R}}), \dot{H}^1({\underline{\Sigma }}_0))$ is linear in ${\underline{\Psi }}$. Substituting this ansatz into the equations, one finds that

$$\begin{aligned}&\nabla \cdot ((I+{\underline{Q}}^0)\nabla {\underline{u}}^0)=0\quad&y<0, \\&(I+{\underline{Q}}^0)\nabla {\underline{u}}^0 \cdot (0, 1) ={\underline{\Psi }},\quad&y=0, \\ \end{aligned}$$

and

$$\begin{aligned}&{\nabla \cdot ((I+{\underline{Q}}^0)\nabla {\underline{u}}^n)=\nabla \cdot {\underline{F}}^n}\quad&y <0, \\&{(I+{\underline{Q}}^0)\nabla {\underline{u}}^n \cdot (0, 1) = {\underline{F}}^n\cdot (0,1),}\quad&y=0, \\ \end{aligned}$$

where

$$\begin{aligned} {\underline{F}}^n=-\sum _{k=1}^n {\underline{Q}}^k\nabla {\underline{u}}^{n-k}. \end{aligned}$$

These equations can be solved recursively. Estimating the solutions we obtain the following result.

Lemma A.22

The Dirichlet–Neumann operator ${\underline{G}}(\cdot ) :W^{1,\infty }({\mathbb {R}}) \rightarrow {\mathcal {L}}(\dot{H}^{\frac{1}{2}}({\mathbb {R}}),\dot{H}^{-\frac{1}{2}}({\mathbb {R}}))$ and the Neumann–Dirichlet operator ${\underline{N}}(\cdot ) :W^{1,\infty }({\mathbb {R}}) \rightarrow {\mathcal {L}}(\dot{H}^{-\frac{1}{2}}({\mathbb {R}}),\dot{H}^{\frac{1}{2}}({\mathbb {R}}))$ are analytic.

The upper domain can be treated in a similar way. Set

$$\begin{aligned} y'=\frac{y-{\underline{\eta }}}{1+{\overline{\eta }}-{\underline{\eta }}}, \end{aligned}$$

so that

$$\begin{aligned} y=y'+f(x,y'), \qquad f(x,y')={\underline{\eta }}+({\overline{\eta }}-{\underline{\eta }})y', \end{aligned}$$

(A.6)

and let ${\overline{F}}(x,y')=(x, y'+f(x,y'))$. The function ${\overline{u}}(x,y)={\overline{\phi }}(F(x,y))$ then solves the boundary value problem

$$\begin{aligned}&{\nabla \cdot ((I+{\overline{Q}})\nabla {\overline{u}})=0},0 \quad&< y <1, \end{aligned}$$

(A.7)

$$\begin{aligned}&{(I+{\overline{Q}})\nabla {\overline{u}} \cdot (0, 1) = {\overline{\Phi }}_s,}\quad&y=1, \end{aligned}$$

(A.8)

$$\begin{aligned}&{(I+{\overline{Q}})\nabla {\overline{u}} \cdot (0,-1)={\overline{\Phi }}_i,}\quad&y=0, \end{aligned}$$

(A.9)

where

$$\begin{aligned} {\overline{Q}}= \begin{pmatrix} f_y&{}\quad -f_x\\ -f_x &{}\quad \frac{-f_y+f_x^2}{1+f_y} \end{pmatrix}. \end{aligned}$$

Proceeding as before, we obtain the following result.

Lemma A.23

The Dirichlet–Neumann operator ${\overline{G}}(\cdot ) :W \rightarrow {\mathcal {L}}(X, Y)$ and the Neumann–Dirichlet operator ${\overline{N}}(\cdot ) :W \rightarrow {\mathcal {L}}(Y,X)$ are analytic.

The next theorem follows from the above lemmas and the definitions of the involved operators.

Theorem A.24

The operators $K(\cdot ), {\overline{K}}(\cdot ):W \rightarrow {\mathcal {L}}((H^{\frac{1}{2}}({\mathbb {R}}))^2, (H^{-\frac{1}{2}}({\mathbb {R}}))^2)$ and ${\underline{K}}(\cdot ) :W^{1,\infty }({\mathbb {R}})\rightarrow {\mathcal {L}}(H^{\frac{1}{2}}({\mathbb {R}}), H^{-\frac{1}{2}}({\mathbb {R}}))$ are analytic.

It is also possible to study these operators in spaces with more regularity. A straightforward modification of the techniques in Groves and Wahlén (2015), Lannes (2013) results in the following theorem. The key is to study higher regularity properties of solutions to the involved boundary value problems defining the corresponding operators.

Theorem A.25

The operators $K(\cdot ), {\overline{K}}(\cdot ) :(H^{s+\frac{3}{2}}({\mathbb {R}}))^2\cap W \rightarrow {\mathcal {L}}((H^{s+\frac{3}{2}}({\mathbb {R}}))^2, (H^{s+\frac{1}{2}}({\mathbb {R}}))^2)$ and ${\underline{K}}(\cdot ) :H^{s+\frac{3}{2}}({\mathbb {R}}) \rightarrow {\mathcal {L}}((H^{s+\frac{3}{2}}({\mathbb {R}})), (H^{s+\frac{1}{2}}({\mathbb {R}})))$ are analytic for each $s>0$.

1.3 Variational Functionals

In this section we study the functionals

$$\begin{aligned} {\underline{{\mathcal {L}}}}({\underline{\eta }})=\frac{1}{2} \int _{{\mathbb {R}}} {\underline{\eta }} {\underline{K}}(\eta ){\underline{\eta }} \, \mathrm{d}x, \end{aligned}$$

(A.10)

$$\begin{aligned} {\overline{{\mathcal {L}}}}(\varvec{\eta })=\frac{1}{2} \int _{{\mathbb {R}}} \varvec{\eta }{\overline{K}}(\varvec{\eta })\varvec{\eta }\, \mathrm{d}x, \end{aligned}$$

(A.11)

and

$$\begin{aligned} {\mathcal {K}}(\varvec{\eta })&= \int _{{\mathbb {R}}} \left\{ \frac{(1-\rho )}{2}{\underline{\eta }}^2 +\frac{\rho }{2}{\overline{\eta }}^2+ {\underline{\beta }}\sqrt{1+{\underline{\eta }}_x^2}-{\underline{\beta }}+ \rho {\overline{\beta }}\sqrt{1+{\overline{\eta }}_x^2}-\rho {\overline{\beta }} \right\} \, \mathrm{d}x. \end{aligned}$$

(A.12)

Note that

$$\begin{aligned} {\mathcal {L}}(\varvec{\eta })={\underline{{\mathcal {L}}}}({{\underline{\eta }}})+\rho {\overline{{\mathcal {L}}}}(\varvec{\eta }) \end{aligned}$$

(A.13)

by equations (1.24) and (A.4).

As a direct consequence of the above formulas and Theorem A.25 we obtain the following result.

Lemma A.26

Equations (A.10), (A.11) and (A.12) define analytic functionals $\underline{{\mathcal {L}}} : H^{s+\frac{3}{2}}({\mathbb {R}})\rightarrow {\mathbb {R}}$, $\overline{{\mathcal {L}}} :(H^{s+\frac{3}{2}}({\mathbb {R}}))^2\cap W \rightarrow {\mathbb {R}}$ and ${\mathcal {K}}:(H^{s+\frac{3}{2}}({\mathbb {R}}))^2\rightarrow {\mathbb {R}}$ for each $s>0$.

In particular, this lemma implies that ${\mathcal {J}}_\mu \in C^\infty (U{\setminus }\{0\}, {\mathbb {R}})$, where $U=B_M(0)\subset H^2({\mathbb {R}})$ with M sufficiently small.

We turn now to the construction of the gradients $\underline{{\mathcal {L}}}'({\underline{\eta }})$ and $\overline{{\mathcal {L}}}'(\varvec{\eta })$ in $L^2({\mathbb {R}})$ and $(L^2({\mathbb {R}}))^2$, respectively. The following result can be proved by a direct computation similar to Groves and Wahlén (2015, Sect. 2.2.1).

Lemma A.27

The gradient $\underline{{\mathcal {L}}}'({\underline{\eta }})$ in $L^2({\mathbb {R}})$ exists for each ${\underline{\eta }}\in H^{s+\frac{3}{2}}({\mathbb {R}})$ and is given by the formula

$$\begin{aligned} \underline{{\mathcal {L}}}'({\underline{\eta }})=\frac{1}{2}\Big ( (1+{\underline{\eta }}_x^2)u_y^2-u_x^2\Big )-u_x\Big |_{y=0}. \end{aligned}$$

This formula defines an analytic function $\underline{{\mathcal {L}}}':H^{s+\frac{3}{2}}({\mathbb {R}})\rightarrow H^{s+\frac{1}{2}}({\mathbb {R}})$.

We also find that

$$\begin{aligned} {\underline{{\mathcal {L}}}}_2'({\underline{\eta }})&={\underline{K}}^0{\underline{\eta }}:={\mathcal {F}}^{-1}(|k|\widehat{{\underline{\eta }}}),\\ {\underline{{\mathcal {L}}}}'_3({\underline{\eta }})&=-\frac{1}{2}({\underline{K}}^0{\underline{\eta }})^2-\frac{1}{2}{\underline{\eta }}_x^2-{\underline{\eta }} {\underline{\eta }}_{xx}-{\underline{K}}^0({\underline{\eta }} {\underline{K}}^0{\underline{\eta }}),\\ {\underline{{\mathcal {L}}}}'_4({\underline{\eta }})&={\underline{\eta }}{\underline{\eta }}_{xx}{\underline{K}}^0{\underline{\eta }}+{\underline{K}}^0{\underline{\eta }}\, {\underline{K}}^0({\underline{\eta }} {\underline{K}}^0{\underline{\eta }})+{\underline{K}}^2({\underline{\eta }}){\underline{\eta }}, \end{aligned}$$

and

$$\begin{aligned} {\underline{{\mathcal {L}}}}_2({\underline{\eta }})&=\frac{1}{2} \int _{{\mathbb {R}}} {\underline{\eta }} {\underline{K}}^0 {\underline{\eta }} \, \mathrm{d}x, \end{aligned}$$

(A.14)

$$\begin{aligned} {\underline{{\mathcal {L}}}}_3({\underline{\eta }})&=\frac{1}{2}\int _{{\mathbb {R}}} \Big (({\underline{\eta }}_x)^2-({\underline{K}}^0{\underline{\eta }})^2\Big )\,{\underline{\eta }} \, \mathrm{d}x, \end{aligned}$$

(A.15)

$$\begin{aligned} {\underline{{\mathcal {L}}}}_4({\underline{\eta }})&=\frac{1}{2}\int _{{\mathbb {R}}} \Big ({\underline{\eta }}^2 {\underline{\eta }}_{xx}K^ 0{\underline{\eta }}+{\underline{\eta }} K^ 0{\underline{\eta }} \, {\underline{K}}^0({\underline{\eta }} {\underline{K}}^0 {\underline{\eta }})\Big ) \, \mathrm{d}x \end{aligned}$$

(A.16)

where ${\underline{{\mathcal {L}}}}_k({\underline{\eta }})$, $k=2, 3, \ldots$, are the terms in the power series expansion of ${\underline{{\mathcal {L}}}}({\underline{\eta }})$ at the origin.

Lemma A.28

The gradient $\overline{{\mathcal {L}}}'(\varvec{\eta })$ in $(L^2({\mathbb {R}}))^2$ exists for each $\varvec{\eta }\in (H^{s+\frac{3}{2}}({\mathbb {R}}))^2\cap W$ and is given by the formula

$$\begin{aligned}&\overline{{\mathcal {L}}}'(\varvec{\eta })=\left( \frac{1}{2}\Big (u_x^2-\frac{1+{\overline{\eta }}_x^2}{(1+{\overline{\eta }}-{\underline{\eta }})^2} u_y^2\Big )\Big |_{y=0}+u_x|_{y=0},\right. \\&\quad \left. -\frac{1}{2}\Big (u_x^2-\frac{1+{\underline{\eta }}_x^2}{(1+{\overline{\eta }}-{\underline{\eta }})^2} u_y^2\Big )\Big |_{y=1}-u_x|_{y=1}\right) . \end{aligned}$$

This formula defines an analytic function $\overline{{\mathcal {L}}}':(H^{s+\frac{3}{2}}({\mathbb {R}}))^2\cap W \rightarrow (H^{s+\frac{1}{2}}({\mathbb {R}}))^2$.

The first few terms in the power series expansion of ${\overline{{\mathcal {L}}}}'$ are given by

$$\begin{aligned}&{\overline{{\mathcal {L}}}}_2'(\varvec{\eta })={\overline{K}}^0\varvec{\eta }:={\mathcal {F}}^{-1}[{{\overline{F}}}(k)\hat{\varvec{\eta }}],\\&{\overline{{\mathcal {L}}}}_3'(\varvec{\eta })\\&\quad = \begin{pmatrix} \frac{1}{2} {\underline{\eta }}_x^2+{\underline{\eta }}_{xx}{\underline{\eta }} +\frac{1}{2}({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }})^2 +{\overline{K}}_{11}^0 ({\underline{\eta }} ({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }})) -{\overline{K}}_{21}^0 ({\overline{\eta }} ({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }})) \\ -\frac{1}{2} {\overline{\eta }}_x^2-{\overline{\eta }}_{xx}{\overline{\eta }} -\frac{1}{2}({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }})^2 -{\overline{K}}_{22}^0 ({\overline{\eta }} ({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }})) +{\overline{K}}_{12}^0 ({\underline{\eta }} ({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }})) \end{pmatrix},\\&{\overline{{\mathcal {L}}}}'_4(\varvec{\eta })\\&\quad = \begin{pmatrix} ({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }}) ({\underline{\eta }}_{xx}{\underline{\eta }} +{\overline{K}}_{11}^0 ({\underline{\eta }} ({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }})) -{\overline{K}}_{21}^0 ({\overline{\eta }} ({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }}))) \\ ({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }}) ({\overline{\eta }}_{xx}{\overline{\eta }} +{\overline{K}}_{22}^0 ({\overline{\eta }} ({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }})) -{\overline{K}}_{12}^0 ({\underline{\eta }} ({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }}))) \end{pmatrix} + {\overline{K}}^2(\varvec{\eta }) \varvec{\eta }, \end{aligned}$$

where

$$\begin{aligned} {{\overline{F}}}(k)= \begin{pmatrix} |k| \coth |k|&{} -\frac{|k|}{\sinh |k|}\\ -\frac{|k|}{\sinh |k|}&{} |k| \coth |k| \end{pmatrix}. \end{aligned}$$

(A.17)

and

$$\begin{aligned} {\overline{{\mathcal {L}}}}_2(\varvec{\eta })&=\frac{1}{2}\int _{{\mathbb {R}}} \varvec{\eta }{\overline{K}}^0 \varvec{\eta }\, \mathrm{d}x, \end{aligned}$$

(A.18)

$$\begin{aligned} {\overline{{\mathcal {L}}}}_3(\varvec{\eta })&= \frac{1}{2} \int _{{\mathbb {R}}} \left\{ - \Big (({\underline{\eta }}_x)^2- ({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }})^2\Big ){\underline{\eta }} +\Big (({\overline{\eta }}_x)^2- ({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }})^2\Big ){\overline{\eta }}\right\} \, \mathrm{d}x, \end{aligned}$$

(A.19)

$$\begin{aligned} {\overline{{\mathcal {L}}}}_4(\varvec{\eta })&= \frac{1}{2} \int _{{\mathbb {R}}} \left\{ ({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }}){\underline{\eta }}_{xx}{\underline{\eta }}^2 +({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }}){\overline{\eta }}_{xx}{\overline{\eta }}^2 \right. \nonumber \\&\qquad \qquad +{\underline{\eta }} ({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }}) {\overline{K}}_{11}^0 ({\underline{\eta }} ({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }})) \nonumber \\&\qquad \qquad -2 {\underline{\eta }}({\overline{K}}_{11}^0{\underline{\eta }}+{\overline{K}}_{12}^0 {\overline{\eta }}) {\overline{K}}_{21}^0 ({\overline{\eta }} ({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }}))\nonumber \\&\qquad \qquad \left. + {\overline{\eta }}({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }}) {\overline{K}}_{22}^0 ({\overline{\eta }} ({\overline{K}}_{21}^0{\underline{\eta }}+{\overline{K}}_{22}^0 {\overline{\eta }})) \right\} \, \mathrm{d}x. \end{aligned}$$

(A.20)

Note that the previous results together with (A.13) immediately imply that ${\mathcal {L}}:(H^{s+\frac{3}{2}}({\mathbb {R}}))^2\cap W \rightarrow {\mathbb {R}}$ is analytic for each $s>0$ and has a gradient in $(L^2({\mathbb {R}}))^2$ given by ${\mathcal {L}}'(\varvec{\eta })={\underline{{\mathcal {L}}}}'({\underline{\eta }})+\rho {\overline{{\mathcal {L}}}}'(\varvec{\eta })$.

The first terms in the power series expansion of ${\mathcal {K}}(\varvec{\eta })$ will also be needed later (the corresponding gradients are readily obtained from these expressions):

$$\begin{aligned} \begin{aligned} {\mathcal {K}}_2(\varvec{\eta })&=\frac{1}{2} \int _{{\mathbb {R}}} \left\{ (1-\rho ){\underline{\eta }}^2 +\rho {\overline{\eta }}^2 + \rho {\overline{\beta }} {\overline{\eta }}_x^2 + {\underline{\beta }} {\underline{\eta }}_x^2 \right\} \, \mathrm{d}x,\\ {\mathcal {K}}_4(\varvec{\eta })&=-\frac{1}{8} \int _{{\mathbb {R}}} \left\{ \rho {\overline{\beta }} {\overline{\eta }}_x^4 +{\underline{\beta }}{\underline{\eta }}_x^4\right\} \, \mathrm{d}x. \end{aligned} \end{aligned}$$

(A.21)

Note in particular that

$$\begin{aligned} {\mathcal {K}}_2(\varvec{\eta })=\frac{1}{2} \int _{{\mathbb {R}}} P(k) \hat{\varvec{\eta }}\cdot \hat{\varvec{\eta }} \, \mathrm{d}k \quad \text {and} \quad {\mathcal {L}}_2(\varvec{\eta })=\frac{1}{2} \int _{{\mathbb {R}}} F(k) \hat{\varvec{\eta }} \cdot \hat{\varvec{\eta }} \, \mathrm{d}k, \end{aligned}$$

(A.22)

where P(k) and F(k) are given by Eq. (1.9).

We end this section by recording some useful inequalities.

Proposition A.29

The estimates

$$\begin{aligned} {\mathcal {K}}(\varvec{\eta }) \ge c\Vert \varvec{\eta }\Vert _1^2, \qquad c\Vert \varvec{\eta }\Vert _{\breve{X}}^2 \le \, {\mathcal {L}}_2(\varvec{\eta }), {\mathcal {L}}(\varvec{\eta })\, \le c\Vert \varvec{\eta }\Vert _{\breve{X}}^2 \end{aligned}$$

hold for each $\varvec{\eta }\in U$.

Proof

The first estimate is immediate from the form of ${\mathcal {K}}(\varvec{\eta })$. The estimates for ${\mathcal {L}}(\varvec{\eta })$ follow directly from Proposition A.21, while those for ${\mathcal {L}}_2(\varvec{\eta })$ follow from (A.22). $\square$

Test Function

In order to show that $C_\mu$ is non-empty we have to construct a special test function. Here the eigenvector $\varvec{v}_0=(1,-a)$ to the eigenvalue $\lambda _-(k_0)$ of the matrix $F(k_0)^{-1} P(k_0)$ plays an important role (see Sect. 1.2).

Lemma B.1

Suppose that Assumptions 1.1 and 1.3 hold. There exists a continuous invertible mapping $\mu \mapsto \varepsilon (\mu )$ such that

$$\begin{aligned} {\mathcal {J}}_\mu (\varvec{\eta }_\star )=2\nu _0\mu +I_\mathrm {NLS} \mu ^3 +o(\mu ^3), \end{aligned}$$

where

$$\begin{aligned} \varvec{\eta }_\star (x)&=\varepsilon \varvec{\phi }(\varepsilon x)\cos (k_0 x)+ \varepsilon ^2 \varvec{\psi }(\varepsilon x)\cos (2k_0x)+\varepsilon ^2\varvec{\zeta }(\varepsilon x),\\ \varvec{\phi }&=\phi _\mathrm {NLS}\varvec{v}_0,\quad \varvec{\psi }=-\frac{1}{2} \phi _\mathrm {NLS}^2 g(2k_0)^{-1}\varvec{A}_3^1 \quad \text {and} \quad \varvec{\zeta }=-\frac{1}{2} \phi _\mathrm {NLS}^2 g(0)^{-1} \varvec{A}_3^2. \end{aligned}$$

Proof

We expand the functional ${\mathcal {K}}(\varvec{\eta })-\nu _0^2{\mathcal {L}}(\varvec{\eta })$ evaluated at $\varvec{\eta }_\star$ in powers of $\varepsilon$. We begin by computing the contribution from ${\mathcal {K}}(\varvec{\eta }_\star )$. We have

$$\begin{aligned} {\mathcal {K}}(\varvec{\eta })&={\mathcal {K}}_2(\varvec{\eta })+{\mathcal {K}}_4(\varvec{\eta })+{\mathcal {K}}_\mathrm {r}(\varvec{\eta }), \end{aligned}$$

where ${\mathcal {K}}_2$ and ${\mathcal {K}}_4$ are given by (A.21). Using the formulas

$$\begin{aligned} \varvec{\eta }_\star ^\prime (x)&=\varepsilon ^2\varvec{\phi }^\prime (\varepsilon x)\cos (k_0 x)-\varepsilon k_0 \varvec{\phi }(\varepsilon x)\sin (k_0 x)\\&\quad +\varepsilon ^3\varvec{\psi }^\prime (\varepsilon x)\cos (2k_0 x)-2k_0 \varepsilon ^2\varvec{\psi }(\varepsilon x)\sin (2k_0 x) +\varepsilon ^3\varvec{\zeta }^\prime (\varepsilon x),\\ \varvec{\eta }_\star ''(x)&= \varepsilon ^3 \varvec{\phi }''(\varepsilon x)\cos (k_0 x) -2\varepsilon ^2 k_0 \varvec{\phi }'(\varepsilon x)\sin (k_0 x)-\varepsilon k_0^2\varvec{\phi }(\varepsilon x)\cos (k_0 x) \\&\quad +\varepsilon ^4 \varvec{\psi }''(\varepsilon x)\cos (2k_0x)-4\varepsilon ^3k_0 \varvec{\psi }'(\varepsilon x)\sin (2k_0x)\\&\qquad -4\varepsilon ^2k_0^2 \varvec{\psi }(\varepsilon x)\cos (2k_0x)+\varepsilon ^4\varvec{\zeta }''(\varepsilon x), \end{aligned}$$

we find that

$$\begin{aligned} {\mathcal {K}}_2(\varvec{\eta }_\star )&= \frac{\varepsilon }{4}(1-\rho +{\underline{\beta }}k_0^2+a^2\rho (1+{\overline{\beta }}k_0^2)) \int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2\, \mathrm{d}x\\&\quad + \frac{\varepsilon ^3}{4}({\underline{\beta }}+\rho a^2{\overline{\beta }}) \int _{{\mathbb {R}}} (\phi _\mathrm {NLS}')^2 \, \mathrm{d}x\\&\quad + \frac{\varepsilon ^3}{4}((1-\rho +4{\underline{\beta }}k_0^2)\int _{{\mathbb {R}}}{\underline{\psi }}^2\, \mathrm{d}x+\rho (1+4{\overline{\beta }}k_0^2)\int _{{\mathbb {R}}}{\overline{\psi }}^2\, \mathrm{d}x)\\&\quad +\frac{\varepsilon ^3}{2}\left( \int _{{\mathbb {R}}}(1-\rho ){\underline{\zeta }}^2\, \mathrm{d}x+\int _{{\mathbb {R}}} \rho {\overline{\zeta }}^2\, \mathrm{d}x\right) +O(\varepsilon ^4) \end{aligned}$$

and

$$\begin{aligned} {\mathcal {K}}_4(\varvec{\eta }_\star )= -\frac{\varepsilon ^3}{64}(3{\underline{\beta }}k_0^4 +3\rho a^4{\overline{\beta }}k_0^4) \int _{{\mathbb {R}}} \phi _\mathrm {NLS}^4 \, \mathrm{d}x+O(\varepsilon ^4). \end{aligned}$$

Finally, the remainder term satisfies ${\mathcal {K}}_\mathrm {r}(\varvec{\eta }_\star ) = \ O(\varepsilon ^{\frac{7}{2}})$ in view of Proposition 2.9.

We next compute the contribution from ${\mathcal {L}}(\varvec{\eta })={\underline{{\mathcal {L}}}}({\underline{\eta }})+\rho {\overline{{\mathcal {L}}}}(\varvec{\eta })$, beginning with the first term. Recall that

$$\begin{aligned} {\underline{{\mathcal {L}}}}({\underline{\eta }})={\underline{{\mathcal {L}}}}_2({\underline{\eta }})+{\underline{{\mathcal {L}}}}_3({\underline{\eta }})+{\underline{{\mathcal {L}}}}_4({\underline{\eta }})+{\underline{{\mathcal {L}}}}_{\mathrm {r}}({\underline{\eta }}), \end{aligned}$$

where ${\underline{{\mathcal {L}}}}_2$, ${\underline{{\mathcal {L}}}}_3$ and ${\underline{{\mathcal {L}}}}_4$ are given in (A.14)–(A.16). In particular, ${\underline{{\mathcal {L}}}}_2({\underline{\eta }})= \frac{1}{2} \int _{{\mathbb {R}}} {\underline{\eta }} \underline{K^0} {\underline{\eta }}\, \mathrm{d}x$, where ${\underline{K}}^0$ is the Fourier multiplier operator with symbol |k|. Straightforward calculations yield the formulas

$$\begin{aligned} {\underline{K}}^0(\varepsilon ^2\varvec{\zeta }(\varepsilon x))&= \varepsilon ^3({\underline{K}}^0\varvec{\zeta })(\varepsilon x),\\ {\underline{K}}^0(\varepsilon \varvec{\phi }(\varepsilon x)\cos (k_0 x))&= \varepsilon ^2 \varvec{\phi }^\prime (\varepsilon x)\sin (k_0 x) + \varepsilon k_0 \varvec{\phi }(\varepsilon x)\cos (k_0 x) + O(\varepsilon ^n),\\ {\underline{K}}^0(\varepsilon ^2\varvec{\psi }(\varepsilon x)\cos (2k_0 x))&= \varepsilon ^3 \varvec{\psi }^\prime (\varepsilon x)\sin (2k_0 x) + 2k_0\varepsilon ^2 \varvec{\psi }(\varepsilon x)\cos (2k_0 x) + O(\varepsilon ^n), \end{aligned}$$

for each $n \in {{\mathbb {N}}}$ uniformly over $x \in {\mathbb {R}}$ (because $\hat{\phi } \in {\mathcal {S}}({\mathbb {R}})$). Using the formulas (A.14)–(A.16) we therefore find that

$$\begin{aligned} {\underline{{\mathcal {L}}}}_2({{\underline{\eta }}}_\star )&= \frac{\varepsilon k_0}{4}\int _{\mathbb {R}}\phi _\mathrm {NLS}^2\, \mathrm{d}x+ \frac{\varepsilon ^3 k_0}{2} \int _{\mathbb {R}}{\underline{\psi }}^2\, \mathrm{d}x+ O(\varepsilon ^4),\\ {\underline{{\mathcal {L}}}}_3({{\underline{\eta }}}_\star )&= -\frac{\varepsilon ^3 k_0^2}{4} \int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2 {\underline{\psi }}\, \mathrm{d}x+O(\varepsilon ^4),\\ {\underline{{\mathcal {L}}}}_4({{\underline{\eta }}}_\star )&= -\frac{\varepsilon ^3 k_0^3}{16}\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^4\, \mathrm{d}x+O(\varepsilon ^4). \end{aligned}$$

Again, the remainder term satisfies ${\underline{{\mathcal {L}}}}_\mathrm {r}({\underline{\eta }}_\star )= O(\varepsilon ^{\frac{7}{2}})$ by Proposition 2.9.

Similarly,

$$\begin{aligned} {\overline{{\mathcal {L}}}}(\varvec{\eta })={\overline{{\mathcal {L}}}}_2(\varvec{\eta })+{\overline{{\mathcal {L}}}}_3(\varvec{\eta })+{\overline{{\mathcal {L}}}}_4(\varvec{\eta })+{\overline{{\mathcal {L}}}}_{\mathrm {r}}(\varvec{\eta }), \end{aligned}$$

with ${\overline{{\mathcal {L}}}}_2(\varvec{\eta })$, ${\overline{{\mathcal {L}}}}_3(\varvec{\eta })$ and ${\overline{{\mathcal {L}}}}_4(\varvec{\eta })$ given by (A.18)–(A.20). In particular, ${\overline{{\mathcal {L}}}}_2(\varvec{\eta })= \frac{1}{2} \int _{{\mathbb {R}}} \varvec{\eta }{\overline{K}}^0\varvec{\eta }\, \mathrm{d}x$, where ${\overline{K}}^0(\varvec{\eta })={\mathcal {F}}^{-1}[{{\overline{F}}}(k)\widehat{\varvec{\eta }}]$ and ${{\overline{F}}}(k)$ is given in (A.17). Writing

$$\begin{aligned} {\mathcal {F}}[\varepsilon \varvec{\phi }(\varepsilon x)\cos (k_0 x)]&=\frac{1}{2}\widehat{\phi }_\mathrm {NLS}\Big (\frac{k-k_0}{\varepsilon }\Big )\varvec{v}_0+\frac{1}{2}\widehat{\phi }_\mathrm {NLS}\Big (\frac{k+k_0}{\varepsilon }\Big )\varvec{v}_0, \end{aligned}$$

we find that

$$\begin{aligned}&{{\overline{F}}}(k){\mathcal {F}}[\varepsilon \varvec{\phi }(\varepsilon x)\cos (k_0 x)]\\&\quad = \frac{1}{2}\Big [{{\overline{F}}}(k_0)+{{\overline{F}}}'(k_0)(k-k_0)+\frac{1}{2}{{\overline{F}}}''(k_0)(k-k_0)^2\Big ]\widehat{\phi }_\mathrm {NLS}\Big (\frac{k-k_0}{\varepsilon }\Big ) \varvec{v}_0\\&\qquad +\frac{1}{2}\Big [{{\overline{F}}}(k_0)-{{\overline{F}}}'(k_0)(k+k_0)+\frac{1}{2}{{\overline{F}}}''(k_0)(k+k_0)^2\Big ]\widehat{\phi }_\mathrm {NLS}\Big (\frac{k+k_0}{\varepsilon }\Big ) \varvec{v}_0\\&\qquad +{\hat{S}}_1(k), \end{aligned}$$

and hence

$$\begin{aligned} {\overline{K}}^0(\varepsilon \varvec{\phi }(\varepsilon x)\cos (k_0 x))&=\varepsilon \phi _\mathrm {NLS}(\varepsilon x) \cos (k_0 x){{\overline{F}}}(k_0)\varvec{v}_0\\&\quad +\varepsilon ^2 \phi _\mathrm {NLS}'(\varepsilon x)\sin (k_0 x){{\overline{F}}}'(k_0)\varvec{v}_0\\&\quad -\frac{1}{2} \varepsilon ^3 \phi _\mathrm {NLS}''(\varepsilon x)\cos (k_0 x){{\overline{F}}}''(k_0) \varvec{v}_0+S_1(x), \end{aligned}$$

where $S_1$ satisfies the estimates $\Vert S_1\Vert _\infty =O(\varepsilon ^3)$, $\Vert S_1\Vert _1=O(\varepsilon ^{\frac{7}{2}})$. Similarly, we find that

$$\begin{aligned} {\overline{K}}^0(\varepsilon ^2 \varvec{\psi }(\varepsilon x)\cos (2k_0x))&= \varepsilon ^2 \cos (2k_0 x) {{\overline{F}}}(2k_0)\varvec{\psi }(\varepsilon x)\\&\quad + \varepsilon ^3 \sin (2k_0 x){{\overline{F}}}'(2k_0)\varvec{\psi }'(\varepsilon x)+S_2(x),\\ {\overline{K}}^0(\varepsilon ^2\varvec{\zeta }(\varepsilon x))&= \varepsilon ^2 {{\overline{F}}}(0) \varvec{\zeta }(\varepsilon x)+S_0(x), \end{aligned}$$

where $S_2$ satisfies the same estimates as $S_1$ and $\Vert S_2^{(m)}\Vert _0=O(\varepsilon ^{m+3/2})$. Note also that

$$\begin{aligned} \int _{{\mathbb {R}}}\varphi (\varepsilon x) \left\{ \begin{array}{c}\ \sin \\ \cos \end{array}\right\} (m_1 x) \cdots \left\{ \begin{array}{c}\ \sin \\ \cos \end{array}\right\} (m_\ell x) \, \mathrm{d}x= O(\varepsilon ^n) \end{aligned}$$

for all $\varphi \in {\mathcal {S}}({\mathbb {R}})$, $n\in {{\mathbb {N}}}$ and $m_1,\ldots ,m_\ell \in {{\mathbb {N}}}$ with $m_1 \pm \cdots \pm m_\ell \ne 0$. (Write the product of the trigonometric functions as a linear combination of sine and cosine functions and integrate by parts.) Using the above rules and formulas (A.18)–(A.20) we find that

$$\begin{aligned} {\overline{{\mathcal {L}}}}_2(\varvec{\eta }_\star )&= \frac{\varepsilon }{4} \int _{{\mathbb {R}}}\phi _\mathrm {NLS}^2 {{\overline{F}}}(k_0)\varvec{v}_0\cdot \varvec{v}_0\, \mathrm{d}x+ \frac{\varepsilon ^3}{8} \int _{{\mathbb {R}}} (\phi _\mathrm {NLS}')^2 {{\overline{F}}}''(k_0)\varvec{v}_0 \cdot \varvec{v}_0 \, \mathrm{d}x\\&\quad +\frac{\varepsilon ^3}{4} \int _{{\mathbb {R}}}{{\overline{F}}}(2k_0)\varvec{\psi }\cdot \varvec{\psi }\, \mathrm{d}x+\frac{\varepsilon ^3}{2}\int _{{\mathbb {R}}} {{\overline{F}}}(0)\varvec{\zeta }\cdot \varvec{\zeta }\, \mathrm{d}x+ O(\varepsilon ^4),\\ {\overline{{\mathcal {L}}}}_3(\varvec{\eta }_\star )&=-\frac{3\varepsilon ^3k_0^2}{8}\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2 {\underline{\psi }}\, \mathrm{d}x-\frac{\varepsilon ^3k_0^2}{4}\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2 {\underline{\zeta }}\, \mathrm{d}x\\&\quad + \frac{\varepsilon ^3}{4}\big ({{\overline{F}}}_{11}(k_0)-a\,{{\overline{F}}}_{12}(k_0)\big )\left( {{\overline{F}}}_{11}(2k_0) \int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\underline{\psi }}\, \mathrm{d}x+\,{{\overline{F}}}_{12}(2k_0)\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\overline{\psi }}\, \mathrm{d}x\right) \\&\quad +\frac{\varepsilon ^3}{8}({{\overline{F}}}_{11}(k_0)-a\,{{\overline{F}}}_{12}(k_0))^2\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\underline{\psi }}\, \mathrm{d}x+\frac{\varepsilon ^3}{4}\big ({{\overline{F}}}_{11}(k_0)-a\,{{\overline{F}}}_{12}(k_0))^2\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\underline{\zeta }}\, \mathrm{d}x\\&\quad +\frac{\varepsilon ^3}{2}\big ({{\overline{F}}}_{11}(k_0)-a\,{{\overline{F}}}_{12}(k_0)\big )\left( {{\overline{F}}}_{11}(0)\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\underline{\zeta }}\, \mathrm{d}x+{{\overline{F}}}_{12}(0)\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\overline{\zeta }}\, \mathrm{d}x\right) \\&\quad + \frac{3\varepsilon ^3k_0^2a^2}{8}\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2 {\overline{\psi }}\, \mathrm{d}x+\frac{\varepsilon ^3k_0^2a^2}{4}\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2 {\overline{\zeta }}\, \mathrm{d}x\\&\quad +\frac{\varepsilon ^3a}{4}\big ({{\overline{F}}}_{21}(k_0)-a\,{{\overline{F}}}_{22}(k_0)\big )\left( {{\overline{F}}}_{21}(2k_0)\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\underline{\psi }}\, \mathrm{d}x+\,{{\overline{F}}}_{22}(2k_0)\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\overline{\psi }}\, \mathrm{d}x\right) \\&\quad -\frac{\varepsilon ^3}{8}\big ({{\overline{F}}}_{21}(k_0)-a\,{{\overline{F}}}_{22}(k_0)\big )^2\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\overline{\psi }}\, \mathrm{d}x-\frac{\varepsilon ^3}{4}\big ({{\overline{F}}}_{21}(k_0)-a\,{{\overline{F}}}_{22}(k_0)\big )^2\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\overline{\zeta }}\, \mathrm{d}x\\&\quad +\frac{\varepsilon ^3a}{2}\big ({{\overline{F}}}_{21}(k_0)-a\,{{\overline{F}}}_{22}(k_0)\big )\left( {{\overline{F}}}_{21}(0)\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\underline{\zeta }}\, \mathrm{d}x+{{\overline{F}}}_{22}(0)\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2{\overline{\zeta }}\, \mathrm{d}x\right) +O(\varepsilon ^4), \end{aligned}$$

and

$$\begin{aligned} {\overline{{\mathcal {L}}}}_4(\varvec{\eta }_\star )&=\varepsilon ^3\left[ -\frac{3k_0^2}{16}({{\overline{F}}}_{11}(k_0)-a\,{{\overline{F}}}_{12}(k_0)) +\frac{3a^3k_0^2}{16}({{\overline{F}}}_{21}(k_0)-a\,{{\overline{F}}}_{22}(k_0)) \right. \\&\qquad \quad + \frac{1}{16}({{\overline{F}}}_{11}(k_0)-a\,{{\overline{F}}}_{12}(k_0) )^2({{\overline{F}}}_{11}(2k_0)+2{{\overline{F}}}_{11}(0)) \\&\qquad \quad +\frac{a}{8}({{\overline{F}}}_{11}(k_0)-a\,{{\overline{F}}}_{12}(k_0) )({{\overline{F}}}_{21}(2k_0)+2{{\overline{F}}}_{21}(0)) ({{\overline{F}}}_{21}(k_0)-a\,{{\overline{F}}}_{22}(k_0) ) \\&\left. \qquad \quad +\frac{a^2}{16}({{\overline{F}}}_{21}(k_0)-a\,{{\overline{F}}}_{22}(k_0) )^2({{\overline{F}}}_{22}(2k_0)+2{{\overline{F}}}_{22}(0)) \right] \int _{{\mathbb {R}}} \phi _\mathrm {NLS}^4\, \mathrm{d}x+O(\varepsilon ^4). \end{aligned}$$

Again, ${\overline{{\mathcal {L}}}}_\mathrm {r}(\varvec{\eta }_\star ) = \ O(\varepsilon ^{\frac{7}{2}})$.

Combining the above expansions, we find that

$$\begin{aligned}&\varepsilon ^{-3}({\mathcal {K}}(\varvec{\eta }_\star )-\nu _0^2 {\mathcal {L}}(\varvec{\eta }_\star )) =\frac{1}{8} g''(k_0)\varvec{v}_0\cdot \varvec{v}_0 \int _{{\mathbb {R}}} (\phi _\mathrm {NLS}')^2\, \mathrm{d}x\\&\qquad +\left( \frac{3}{8}A_4-\frac{1}{16} g(2k_0)^{-1}\varvec{A}_3^1 \cdot \varvec{A}_3^1- \frac{1}{8} g(0)^{-1}\varvec{A}_3^2 \cdot \varvec{A}_3^2\right) \int _{{\mathbb {R}}}\phi _\mathrm {NLS}^4 \, \mathrm{d}x\\&\qquad +\int _{{\mathbb {R}}} \frac{1}{4} g(2k_0)(\varvec{\psi }+\tfrac{1}{2} \phi _\mathrm {NLS}^2 g(2k_0)^{-1} \varvec{A}_3^1)\cdot (\varvec{\psi }+\tfrac{1}{2} \phi _\mathrm {NLS}^2 g(2k_0)^{-1}\varvec{A}_3^1)\, \mathrm{d}x\\&\qquad +\int _{{\mathbb {R}}} \frac{1}{2} g(0)(\varvec{\zeta }+\tfrac{1}{2} \phi _\mathrm {NLS}^2 g(0)^{-1}\varvec{A}_3^2)\cdot (\varvec{\zeta }+\tfrac{1}{2} \phi _\mathrm {NLS}^2 g(0)^{-1}\varvec{A}_3^2)\, \mathrm{d}x\\&\qquad +O(\varepsilon ^{\frac{1}{2}}). \end{aligned}$$

Our choice of $\varvec{\psi }$ and $\varvec{\zeta }$ minimises the above expression up to $O(\varepsilon ^{\frac{7}{2}})$, and we obtain that

$$\begin{aligned} {\mathcal {K}}(\varvec{\eta }_\star )-\nu _0^2 {\mathcal {L}}(\varvec{\eta }_\star )&=\varepsilon ^3\left( A_2\int _{{\mathbb {R}}} (\phi _\mathrm {NLS}')^2\, \mathrm{d}x+A_3\int _{{\mathbb {R}}}\phi _\mathrm {NLS}^4 \, \mathrm{d}x\right) +O(\varepsilon ^{\frac{7}{2}})\\&=\varepsilon ^3 E_\mathrm {NLS}(\phi _\mathrm {NLS})+O(\varepsilon ^{\frac{7}{2}})\\&= \varepsilon ^3 I_\mathrm {NLS}+O(\varepsilon ^{\frac{7}{2}}). \end{aligned}$$

The mapping

$$\begin{aligned} \varepsilon \mapsto \nu _0 {\mathcal {L}}(\varvec{\eta }_\star )=\varepsilon \frac{\nu _0F(k_0)\varvec{v}_0\cdot \varvec{v}_0}{4}\int _{{\mathbb {R}}} \phi _\mathrm {NLS}^2 \, \mathrm{d}x+O(\varepsilon ^3) \end{aligned}$$

is continuous and strictly increasing and therefore has a continuous inverse $\mu \mapsto \varepsilon (\mu )$, such that $\varepsilon (\mu )=\mu +o(\mu )$. Furthermore,

$$\begin{aligned} {\mathcal {J}}_\mu (\varvec{\eta }_\star )-2\nu _0\mu = {\mathcal {K}}(\varvec{\eta }_\star )-\nu _0^2 {\mathcal {L}}(\varvec{\eta }_\star )= I_\mathrm {NLS} \mu ^3+o(\mu ^3), \end{aligned}$$

which concludes the proof. $\square$