1 Introduction

Water waves constitute a very classical problem in hydrodynamics [7]. This problem is traditionally formulated in terms of the velocity potential to achieve some simplifications. In other words, there has always been an implicit assumption of zero vorticity in the flow region. In numerous recent studies, this assumption started to be dropped and the assumption of constant vorticity in the flow region used. One of the pioneering studies was made by Burns [6], and later, Da Silva and Peregrine [8] studied steep and steady waves on finite depth with constant vorticity. More recently, this problem was analyzed mathematically in some two-component systems [12]. The effect of the vorticity on travelling wave solutions (solitary and cnoidal) was investigated in the purely hydrodynamic context in [11] using the qualitative phase space analysis methods. and a Hamiltonian formulation has been reported in [20]. This problem in electrohydrodynamics seems to be still open to the best of our knowledge and the present study should be considered as a further attempt to fill in this gap in the literature.

The current approach to examining flows with constant vorticity in two dimensions is via the use of a stream function, \(\psi \), and its harmonic conjugate, the velocity potential, and \(\varphi \), so \(\mathbf {u}=\nabla \varphi +\nabla ^{\perp }\psi \). This approach introduces two unnecessary functions which complicates the problem and has the limiting effect in being restricted to fully nonlinear and linear computations. There has been no attempt to undertake a weakly nonlinear analysis which is the purpose of this manuscript. Previous work on constant vorticity models typically has been fully nonlinear; for example, see [19].

The present manuscript is organized as follows. The problem is formulated in Sect. 2. The linear analysis of this problem is performed in Sect. 3, while the weakly nonlinear analysis is presented in Sect. 4. Some numerical predictions of the weakly nonlinear theory are presented in Sect. 5. Finally, the main conclusions and perspectives of this study are outlined in Sect. 6.

2 Formulation

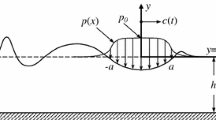
A two-dimensional fluid in region 1 is considered which is incompressible and inviscid. The vorticity, \(\omega \), is constant as is the surface tension \(\sigma \). Cartesian co-ordinates are introduced, as shown in Fig. 1. Region 1 is defined as \(-h<y<\eta (t,x)\) \(\forall x\in \mathbb {R}\). The moving pressure distribution \(\mathcal {P}(t,x)\) is chosen to act along the interface \(y=\eta (t,x)\) and \(\mathcal {P}\rightarrow 0\) as \(|x|\rightarrow 0\).

Fig. 1
figure 1

Physical problem schematic representation

Full size image

In region 2 defined by \(\left\{ (x,y)|x\in \mathbb {R},y>\eta (t,x)\right\} \), there is an electric field, \(\mathbf {E}\) which has no charges and is, therefore, obtained by a potential \(\mathbf {E}=-\nabla V\). The potential is chosen as \(V(x,-h)=0\) and as the fluid is perfectly conducting this also means that \(V(x,\eta (t,x))=0\). A vertical electric field is set up by imposing:

$$\begin{aligned} V\sim -E_{0}y,\quad y\rightarrow \infty . \end{aligned}$$
(2.1)

The equation for the electric potential is, therefore, given by:

$$\begin{aligned} \frac{\partial ^{2}V}{\partial x^{2}}+\frac{\partial ^{2}V}{\partial y^{2}}=0, \end{aligned}$$
(2.2)

with the condition:

$$\begin{aligned} \left[ \mathbf {E}\cdot \hat{\mathbf {t}}\right] _{1}^{2}=0 \end{aligned}$$
(2.3)

which is one of the general boundary conditions derivable from Maxwell’s equations. In region 1, the Navier–Stokes equations are used with the stress tensor:

$$\begin{aligned} T_{ij}=-P\delta _{ij}+\Sigma _{ij}, \end{aligned}$$
(2.4)

where:

$$\begin{aligned} \Sigma _{ij}=\epsilon _{p}\left( \frac{\partial V}{\partial x_{i}}\frac{\partial V}{\partial x_{j}} -\frac{1}{2}\delta _{ij}\sum _{k=1}^{2}\frac{\partial V}{\partial x_{k}}\frac{\partial V}{\partial x_{k}}\right) . \end{aligned}$$
(2.5)

Here, \(\epsilon _{p}\) is called the electric permittivity. The tensor \(\Sigma _{ij}\) has various names, in the fluids literature, it is known as the Maxwell-stress tensor. It can be shown that:

$$\begin{aligned} \sum _{i=1}^{2}\frac{\partial \Sigma _{ij}}{\partial x_{i}}=0. \end{aligned}$$
(2.6)

Therefore, the Navier–Stokes equations reduce to the Euler equations:

$$\begin{aligned} \frac{\partial \mathbf {u}}{\partial t}+(\mathbf {u}\cdot \nabla )\mathbf {u}=-\frac{1}{\rho }\nabla P -g\mathbf {j}, \end{aligned}$$
(2.7)

where \(\mathbf {u}=(u,v)\) is the velocity and P is the pressure in the fluid. The boundary \(y=-h\) is taken as impenetrable, so \(v(x,-h)=0\). The fluid is incompressible and has constant vorticity, \(\omega \), and so:

$$\begin{aligned} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,\quad \frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}=\omega . \end{aligned}$$
(2.8)

These equations can be cross differentiated to obtain a single equation for v:

$$\begin{aligned} \frac{\partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}v}{\partial y^{2}}=0. \end{aligned}$$
(2.9)

The function v will take the place of the velocity potential when the KdV equation is derived for irrotational fluids. The free surface equation is given by:

$$\begin{aligned} \frac{\partial \eta }{\partial t}+u\frac{\partial \eta }{\partial x}=v, \quad y=\eta (t,x). \end{aligned}$$
(2.10)

This gives a boundary condition for v on \(y=\eta (t,x)\). The lower boundary for v is given by:

$$\begin{aligned} v(t,x,-h)=0. \end{aligned}$$
(2.11)

Equations (2.9)–(2.11) are the core of the technique in deriving the free surface profiles. The other boundary condition used is the Young–Laplace equation given by:

$$\begin{aligned} \left[ \hat{\mathbf {n}}\cdot \mathbf {T}\cdot \hat{\mathbf {n}}\right] _{1}^{2} =\sigma \frac{\partial _{x}^{2}\eta }{(1+(\partial _{x}\eta )^{2})^{\frac{3}{2}}}. \end{aligned}$$
(2.12)

The Euler equations may be simplified using electrostatic equilibrium. The equilibrium condition is:

$$\begin{aligned} -\frac{1}{\rho }\frac{\partial p}{\partial y}-g=0. \end{aligned}$$
(2.13)

Integrating this equation shows that \(p=-\rho gy+C\) To compute the value of C, use the Young–Laplace equation to see \(C=P_{a}-\epsilon _{d}E_{0}^{2}/2\), where \(P_{a}\) is the atmospheric pressure. Therefore, now, write:

$$\begin{aligned} P=P_{a}-\frac{\epsilon _{p}E_{0}^{2}}{2}-\rho gy+p. \end{aligned}$$
(2.14)

The Euler equations now become:

$$\begin{aligned} \frac{\partial \mathbf {u}}{\partial t}+(\mathbf {u}\cdot \nabla )\mathbf {u}=-\frac{1}{\rho }\nabla p. \end{aligned}$$
(2.15)

The Young–Laplace equation becomes:

$$\begin{aligned} p-\rho g\eta -\frac{\epsilon _{p}E_{0}^{2}}{2}=\mathcal {P}-\frac{1}{1+(\partial _{x}\eta )^{2}}\left[ (\partial _{x}\eta )^{2}\Sigma _{11}-2\partial _{x}\eta \Sigma _{12} +\Sigma _{22}\right] -\sigma \frac{\partial _{x}^{2}\eta }{(1+(\partial _{x}\eta )^{2})^{\frac{3}{2}}}.\nonumber \\ \end{aligned}$$
(2.16)

3 Linear Theory

The scaling for the linear theory is:

$$\begin{aligned} (x,y,\eta )= & {} h(\hat{x},\hat{y},\hat{\eta }),\quad t=\sqrt{\frac{\rho h^{3}}{\sigma }}\hat{t},\quad (p,\mathcal {P}) =\frac{\sigma }{h}(\hat{p},\hat{\mathcal {P}}), \quad \mathbf {u}=\sqrt{\frac{\sigma }{\rho h}}\hat{\mathbf {u}} \end{aligned}$$
(3.1)
$$\begin{aligned} \mathcal {P}= & {} \rho gh\hat{\mathcal {P}}\quad V=hE_{0}\hat{V}. \end{aligned}$$
(3.2)

The equations become:

$$\begin{aligned}&\frac{\partial ^{2}\hat{V}}{\partial \hat{x}^{2}}+\frac{\partial ^{2}\hat{V}}{\partial \hat{y}^{2}}=0,\quad \hat{y}>\hat{\eta } \end{aligned}$$
(3.3)
$$\begin{aligned}&\frac{\partial \hat{V}}{\partial \hat{x}}+\frac{\partial \hat{\eta }}{\partial \hat{x}}\frac{\partial \hat{V}}{\partial \hat{y}}=0,\quad \hat{y}=\hat{\eta } \end{aligned}$$
(3.4)
$$\begin{aligned}&\frac{\partial \hat{\mathbf {u}}}{\partial \hat{t}}+(\hat{\mathbf {u}}\cdot \hat{\nabla })\hat{\mathbf {u}}=-\hat{\nabla }\hat{p},\quad -1<\hat{y}<\hat{\eta } \end{aligned}$$
(3.5)
$$\begin{aligned}&\frac{\partial \hat{u}}{\partial \hat{x}}+\frac{\partial \hat{v}}{\partial \hat{y}}=0,\quad \frac{\partial \hat{v}}{\partial \hat{x}}-\frac{\partial \hat{u}}{\partial \hat{y}}=\Omega ,\quad -1<\hat{y}<\hat{\eta } \end{aligned}$$
(3.6)
$$\begin{aligned}&\frac{\partial \hat{\eta }}{\partial \hat{t}}+\hat{u}\frac{\partial \hat{\eta }}{\partial \hat{x}}=\hat{v},\quad \hat{y}=\hat{\eta } \end{aligned}$$
(3.7)
$$\begin{aligned}&\frac{\partial ^{2}\hat{v}}{\partial \hat{x}^{2}}+\frac{\partial ^{2}\hat{v}}{\partial \hat{y}^{2}}=0 \end{aligned}$$
(3.8)
$$\begin{aligned}&\hat{p}-B\hat{\eta }-\frac{E_{b}}{2}=\hat{\mathcal {P}}-\frac{E_{b}}{1+(\partial _{\hat{x}}\hat{\eta })^{2}}\left[ (\partial _{\hat{x}}\hat{\eta })^{2}\hat{\Sigma }_{11}-2\partial _{\hat{x}}\hat{\eta }\hat{\Sigma }_{12}+\hat{\Sigma }_{22}\right] \nonumber \\&\quad -\frac{\partial _{\hat{x}}^{2}\hat{\eta }}{(1+(\partial _{\hat{x}}\hat{\eta })^{2})^{\frac{3}{2}}}, \quad \hat{y}=\hat{\eta }. \end{aligned}$$
(3.9)

Here:

$$\begin{aligned} \Omega =\omega \sqrt{\frac{\rho h^{3}}{\sigma }},\quad B=\frac{\rho gh^{2}}{\sigma },\quad E_{b}=\frac{\epsilon _{p}E_{0}^{2}}{\sigma }. \end{aligned}$$
(3.10)

Expand according to:

$$\begin{aligned} \hat{u}= & {} -\Omega \hat{y}+\varepsilon u_{1}+o(\varepsilon ) \end{aligned}$$
(3.11)
$$\begin{aligned} \hat{v}= & {} \varepsilon v_{1}+o(\varepsilon ) \end{aligned}$$
(3.12)
$$\begin{aligned} \hat{p}= & {} \varepsilon p_{1}+o(\varepsilon ) \end{aligned}$$
(3.13)
$$\begin{aligned} \hat{\mathcal {P}}= & {} \varepsilon \mathcal {P}_{1}+o(\varepsilon ) \end{aligned}$$
(3.14)
$$\begin{aligned} \hat{\eta }= & {} \varepsilon \eta _{1}+o(\varepsilon ) \end{aligned}$$
(3.15)
$$\begin{aligned} \hat{V}= & {} -\hat{y}+\varepsilon V_{1}+o(\varepsilon ). \end{aligned}$$
(3.16)

The set of linear equations now becomes:

$$\begin{aligned} \frac{\partial ^{2}V_{1}}{\partial \hat{x}^{2}}+\frac{\partial ^{2}V_{1}}{\partial \hat{y}^{2}}= & {} 0,\quad \hat{y}>0, \end{aligned}$$
(3.17)
$$\begin{aligned} \frac{\partial V_{1}}{\partial \hat{x}}-\frac{\partial \eta _{1}}{\partial \hat{x}}= & {} 0, \quad \hat{y}=0, \end{aligned}$$
(3.18)
$$\begin{aligned} \frac{\partial u_{1}}{\partial \hat{t}}-\Omega y\frac{\partial u_{1}}{\partial \hat{x}}-\Omega v_{1}= & {} -\frac{\partial p_{1}}{\partial \hat{x}} ,\quad -1<\hat{y}<0 \end{aligned}$$
(3.19)
$$\begin{aligned} \frac{\partial v_{1}}{\partial \hat{t}}-\Omega y\frac{\partial v_{1}}{\partial \hat{x}}= & {} -\frac{\partial p_{1}}{\partial y},\quad -1<\hat{y}<0 \end{aligned}$$
(3.20)
$$\begin{aligned} \frac{\partial ^{2}v_{1}}{\partial \hat{x}^{2}}+\frac{\partial ^{2}v_{1}}{\partial \hat{y}^{2}}= & {} 0,\quad -1<\hat{y}<0 \end{aligned}$$
(3.21)
$$\begin{aligned} \frac{\partial \eta _{1}}{\partial \hat{t}}= & {} v_{1},\quad \hat{y}=0, \end{aligned}$$
(3.22)
$$\begin{aligned} p_{1}-B\eta _{1}= & {} \mathcal {P}_{1}+E_{b}\frac{\partial V_{1}}{\partial \hat{y}}-\frac{\partial ^{2}\eta _{1}}{\partial \hat{x}^{2}}. \end{aligned}$$
(3.23)

3.1 General Dispersion Relation

To obtain a dispersion relation set \(\mathcal {P}_{1}=0\) and write all perturbations in the form:

$$\begin{aligned} f(t,x,y)=\frac{1}{2\pi }\int _{\mathbb {R}}\hat{f}(\xi (k),k,y)e^{i(kx-\xi t)}\mathrm{{d}}k. \end{aligned}$$
(3.24)

Solving the equation for \(v_{1}\) and \(V_{1}\) shows that:

$$\begin{aligned} v_{1}=\alpha \sinh k(y+1),\quad V_{1}=\beta e^{-|k|y}. \end{aligned}$$
(3.25)

Using Eqs. (3.18) and (3.22) yields \(\beta \) in terms of \(\alpha \):

$$\begin{aligned} \beta =-\frac{i}{\xi }\alpha \sinh k. \end{aligned}$$
(3.26)

Only \(p_{1}\) at the surface is required, so it is possible to set \(y=0\) in Eq. (3.19) to find:

$$\begin{aligned} \hat{p}_{1}=\frac{\alpha i}{k}(\xi \cosh k -\Omega \sinh k). \end{aligned}$$
(3.27)

Inserting everything into the linearised Young–Laplace equations shows:

$$\begin{aligned} \xi ^{2}-\xi \Omega \tanh k-Bk\tanh k+E_{b}k|k|\tanh k-k^{3}\tanh k=0. \end{aligned}$$
(3.28)

The phase velocity, c, is given by \(c=\xi /k\) and solving for the phase velocity shows that:

$$\begin{aligned} c=\frac{\Omega \tanh k}{2k}\pm \frac{1}{2k}\sqrt{\Omega ^{2}\tanh ^{2}k+4(Bk-E_{b}k|k|+k^{3})\tanh k}. \end{aligned}$$
(3.29)

It can be seen that setting \(\Omega =0\) reduces to the dispersion relation in [14] and setting \(E_{b}=0\) results in the dispersion relation in [15]. It was noted in [14] that to have a linear wave profile the parameters had to satisfy the inequality \(4B\geqslant E_{b}^{2}\); however, with the inclusion of positive vorticity, this is no longer the case.

Fig. 2
figure 2

Linear dispersion relation with constant vorticity for three fixed values of parameter \(\Omega \)

Full size image

As can be seen in Fig. 2, there is a minimum which is positive. For various choices of B and \(E_{b}\), there is a positive minimum for a wide range of vorticity (Fig. 3). By differentiation of Eq. (3.29), one can show:

$$\begin{aligned} \left. \frac{{\mathrm {d}}c}{{\mathrm {d}}k}\right| _{k=0}=-\frac{E_{b}}{\sqrt{\Omega ^{2}+4B}}<0 \end{aligned}$$
(3.30)

on the branch for which \(c(0)>0\). One can also show that for large k, \(c(k)\sim \sqrt{k}\) as \(k\rightarrow \infty \) which shows the existence of a minimum in the dispersion relation. The beginning point at \(k=0\) can be seen to satisfy the equation:

$$\begin{aligned} c^{2}-\Omega c-4B=0\Rightarrow c=\frac{\Omega + \sqrt{\Omega ^{2}+4B}}{2}. \end{aligned}$$
(3.31)
Fig. 3
figure 3

Minimal value of the dispersion relation as a function of the vorticity parameter \(\Omega \), with \(B=0.1\) and \(E_{b}=\sqrt{0.2}\)

Full size image

3.2 Free Surface Profiles

Consider a moving pressure distribution moving with non-dimensional speed U. Then, a frame of reference moving with speed U is selected, so all time derivative terms may be dropped. The horizontal velocity component is expanded as:

$$\begin{aligned} \hat{u}=U-\Omega y+\varepsilon u_{1}+o(\varepsilon ). \end{aligned}$$
(3.32)

The equations which are changed are then:

$$\begin{aligned} (U-\Omega y)\frac{\partial u_{1}}{\partial x} -\Omega v_{1}= & {} -\frac{\partial p_{1}}{\partial x} \end{aligned}$$
(3.33)
$$\begin{aligned} (U-\Omega y)\frac{\partial v_{1}}{\partial x}= & {} -\frac{\partial p_{1}}{\partial y} \end{aligned}$$
(3.34)
$$\begin{aligned} U\frac{\partial \eta _{1}}{\partial x}= & {} \eta _{1} \end{aligned}$$
(3.35)

The method of derivation is very similar to that of the derivation of the dispersion relation will be omitted. The perturbations will be expressed at:

$$\begin{aligned} f(x,y)=\frac{1}{2\pi }\int _{\mathbb {R}}\hat{f}(k,y)e^{ikx}\mathrm{{d}}k. \end{aligned}$$
(3.36)

The free surface is given by:

$$\begin{aligned} \hat{\eta }=\frac{\hat{\mathcal {P}}_{1}\tanh k}{k\hat{U}^{2}+(-B+\Omega \hat{U}+E_{b}|k|-k^{2})\tanh k}. \end{aligned}$$
(3.37)

Choosing a U below the minimum of dispersion relation, one uses Eq. (3.37). To compute the waves for which U is above the minimum of the dispersion, one must include Rayleigh viscosity \(\mu \) in the following way:

$$\begin{aligned} \hat{\eta }=\frac{\hat{\mathcal {P}}_{1}\tanh k}{k\hat{U}^{2}+(-B+\Omega \hat{U}+E_{b}|k|-k^{2})\tanh k+\mu i}. \end{aligned}$$
(3.38)

For \(0<\mu <1\), it gives waves of the form (Fig. 4a). Figure 4a, b show the free surface profiles under a moving pressure distribution for \(B\ =\ E_{b}\ =\ 2\) and \(\Omega \ =\ 1\,\).

Fig. 4
figure 4

Free surface profiles under a moving pressure distribution

Full size image

4 The Weakly Nonlinear Free Surface

To obtain a weakly nonlinear model of the phenomena, scale according to:

$$\begin{aligned} x= & {} \lambda \hat{x},\quad y^{(1)}=h\hat{y},\quad y^{(2)}=\lambda \hat{y},\quad t=\frac{\lambda }{c_{0}}\hat{t},\quad u=c_{0}\hat{u},\quad v=\frac{hc_{0}}{\lambda }\hat{v} \end{aligned}$$
(4.1)
$$\begin{aligned} \eta= & {} a\hat{\eta },\quad V=\lambda E_{0}\hat{V},\quad P=P_{a}-\rho gy-\frac{\epsilon _{d}E_{0}^{2}}{2}+\rho gh\hat{p}, \end{aligned}$$
(4.2)

where \(c_{0}=\sqrt{gh}\). The scaled equations are then:

$$\begin{aligned} \frac{\partial ^{2}\hat{V}}{\partial \hat{x}^{2}}+\frac{\partial ^{2}\hat{V}}{\partial \hat{y}^{2}}= & {} 0 \\ \frac{\partial \hat{V}}{\partial x}+\alpha \sqrt{\beta }\frac{\partial \hat{\eta }}{\partial \hat{x}}\frac{\partial \hat{V}}{\partial \hat{y}}= & {} 0 \\ \frac{\partial \hat{u}}{\partial \hat{t}}+\hat{u}\frac{\partial \hat{u}}{\partial \hat{x}}+\hat{v}\frac{\partial \hat{u}}{\partial \hat{y}}= & {} -\frac{\partial \hat{p}}{\partial \hat{x}} \\ \beta \left( \frac{\partial \hat{v}}{\partial \hat{t}}+\hat{u}\frac{\partial \hat{v}}{\partial \hat{x}}+\hat{v}\frac{\partial \hat{v}}{\partial \hat{y}}\right)= & {} -\frac{\partial \hat{p}}{\partial \hat{y}} \\ \beta \frac{\partial \hat{v}}{\partial \hat{x}}-\frac{\partial \hat{u}}{\partial \hat{y}}= & {} \Omega \\ \frac{\partial \hat{u}}{\partial \hat{x}}+\frac{\partial \hat{v}}{\partial \hat{y}}= & {} 0 \\ \frac{\partial \hat{\eta }}{\partial \hat{t}}+\hat{u}\frac{\partial \hat{\eta }}{\partial \hat{x}}= & {} \frac{\hat{v}}{\varepsilon }, \end{aligned}$$

where \(\Omega =h\omega /c_{0}\). The Young–Laplace equation becomes:

$$\begin{aligned}&\hat{p}-\alpha \hat{\eta }-\frac{F_{E}^{2}}{2}=\alpha \hat{\mathcal {P}}-\frac{F_{E}^{2}}{1+\alpha ^{2}\beta (\partial _{\hat{x}}\hat{\eta })^{2}}(\alpha ^{2}\beta (\partial _{\hat{x}}\hat{\eta })^{2}\hat{T}_{11}-2\alpha \sqrt{\beta }\partial _{\hat{x}} \hat{\eta }\hat{T}_{12}+\hat{T}_{22}) \nonumber \\&\quad -B\alpha \beta \frac{\partial _{\hat{x}}^{2}\hat{\eta }}{(1+\alpha ^{2}\beta (\partial _{\hat{x}}\hat{\eta })^{2})^{\frac{3}{2}}}, \end{aligned}$$
(4.3)

where:

$$\begin{aligned} F_{E}^{2}=\frac{\epsilon _{d}E_{0}^{2}}{\rho gh},\quad B=\frac{\sigma }{\rho gh^{2}}. \end{aligned}$$
(4.4)

The term, \(F_{E}\), is the ratio of a velocity to \(c_{0}\), which shows that there is a natural velocity occurring which is given by, \(U=\sqrt{\epsilon _{d}E_{0}^{2}/\rho }\); for this reason, \(F_{E}\) should be referred to as the electric Froude number. The next step is to make the transformation:

$$\begin{aligned} (\hat{p},\hat{u},\hat{v})=(\alpha \bar{p},-\Omega y+\alpha \bar{u},\alpha \bar{v}). \end{aligned}$$
(4.5)

To obtain the required PDE for the free surface, the KdV scaling is required. This is \(\alpha =\beta =\varepsilon \ll 1\). The speed of propagation, c, of the (linear) waves is unknown at this point; the following co-ordinate transformation is used:

$$\begin{aligned} X=\hat{x}-c\hat{t},\quad T=\varepsilon \hat{t}. \end{aligned}$$
(4.6)

Dropping bars and hats, the equations then become:

$$\begin{aligned}&\frac{\partial ^{2}V}{\partial X^{2}}+\frac{\partial ^{2}V}{\partial y^{2}} = 0,\quad y>\varepsilon \eta \end{aligned}$$
(4.7)
$$\begin{aligned}&\frac{\partial V}{\partial X} +\varepsilon ^{\frac{3}{2}}\frac{\partial \eta }{\partial X}\frac{\partial V}{\partial y} = 0,\quad y=\varepsilon \eta \end{aligned}$$
(4.8)
$$\begin{aligned}&-c\frac{\partial u}{\partial X}+\varepsilon \frac{\partial u}{\partial T}+\varepsilon u\frac{\partial u}{\partial X}+\varepsilon v\frac{\partial u}{\partial y} = -\frac{\partial p}{\partial X},\quad -1<y<\varepsilon \eta \end{aligned}$$
(4.9)
$$\begin{aligned}&\varepsilon \left( -c\frac{\partial v}{\partial X}+\varepsilon \frac{\partial v}{\partial T}+\varepsilon u\frac{\partial v}{\partial X}+\varepsilon v\frac{\partial v}{\partial y}\right) = -\frac{\partial p}{\partial y},\quad -1<y<\varepsilon \eta \end{aligned}$$
(4.10)
$$\begin{aligned}&-c\frac{\partial \eta }{\partial X}+\varepsilon \frac{\partial \eta }{\partial T}+\varepsilon u\frac{\partial \eta }{\partial X} = v,\quad y=\varepsilon \eta \end{aligned}$$
(4.11)
$$\begin{aligned}&\varepsilon \frac{\partial v}{\partial X}-\frac{\partial u}{\partial y} = 0,\quad -1<y<\varepsilon \eta \end{aligned}$$
(4.12)
$$\begin{aligned}&\frac{\partial u}{\partial X}+\frac{\partial v}{\partial y} = 0,\quad -1<y<\varepsilon \eta \end{aligned}$$
(4.13)
$$\begin{aligned} p-\eta&-\frac{F_{E}^{2}}{2\varepsilon }=\mathcal {P}-\frac{1}{\varepsilon } \frac{F_{E}^{2}}{1+\varepsilon ^{3}(\partial _{X}\eta )^{2}}(\varepsilon ^{2}(\partial _{X}\eta )^{2}T_{11}-2\varepsilon ^{\frac{3}{2}}\partial _{X}\eta T_{12}-T_{22}) \nonumber \\&\quad -B\varepsilon \frac{\partial _{X}^{2}\eta }{(1+\varepsilon ^{3}(\partial _{X}\eta )^{2})^{\frac{3}{2}}},\quad y=\varepsilon \eta . \end{aligned}$$
(4.14)

It can be noted that the combination of Eqs. (4.12) and (4.13) can be combined into:

$$\begin{aligned} \varepsilon \frac{\partial ^{2}v}{\partial X^{2}}+\frac{\partial ^{2}v}{\partial y^{2}}=0,\quad -1<y<\varepsilon \eta . \end{aligned}$$
(4.15)

Expand according to:

$$\begin{aligned} u(T,X,y)= & {} -\frac{\Omega y}{\varepsilon }+u_{0}(T,X,y)+\varepsilon u_{1}(T,X,y)+o(\varepsilon )\quad y>\varepsilon \eta \end{aligned}$$
(4.16)
$$\begin{aligned} v(T,X,y)= & {} v_{0}(T,X,y)+\varepsilon v_{1}(T,X,y)+o(\varepsilon ) \end{aligned}$$
(4.17)
$$\begin{aligned} p= & {} p_{0}(T,X,y)+\varepsilon p_{1}(T,X,y)+o(\varepsilon ) \end{aligned}$$
(4.18)
$$\begin{aligned} \mathcal {P}= & {} \varepsilon \mathcal {P}_{1}+o(\varepsilon ) \end{aligned}$$
(4.19)
$$\begin{aligned} V(T,X,y)= & {} -y+\varepsilon ^{\frac{3}{2}} V_{1}(T,X,y)+o(\varepsilon ^{\frac{3}{2}}) \end{aligned}$$
(4.20)
$$\begin{aligned} \eta= & {} \eta _{0}(T,X)+\varepsilon \eta _{1}(T,X)+o(\varepsilon ). \end{aligned}$$
(4.21)

The O(1) equations are:

$$\begin{aligned} \partial _{y}p_{0}=0,\quad -(c+\Omega y)\partial _{X}u_{0}-\Omega v_{0} =-\partial _{X}p_{0},\quad \partial _{y}^{2}v_{0}=0,\quad \partial _{X}u_{0}+\partial _{y}v_{0} \end{aligned}$$
(4.22)

with boundary conditions:

$$\begin{aligned} p_{0}=\eta _{0},\quad -c\partial _{X}\eta _{0}=v_{0},\quad \text {on}\quad y=0. \end{aligned}$$
(4.23)

The equation \(\partial _{y}^{2}v_{0}=0\) has solution:

$$\begin{aligned} v_{0}=(y+1)A_{0}(T,X)\Rightarrow \partial _{X}u_{0}=-A_{0}(T,X). \end{aligned}$$
(4.24)

Setting \(y=0\) shows that \(A_{0}=-c\partial _{X}\eta _{0}\), and so, \(u_{0}=c\eta _{0}\). The equation \(\partial _{y}p_{0}=0\) shows that \(p_{0}=\eta _{0}\). The equation \(-(c+\Omega y)\partial _{X}u_{0}-\Omega v_{0} =-\partial _{X}p_{0}\) can be evaluated at \(y=0\). Using the previous solutions yields:

$$\begin{aligned} -c^{2}\partial _{X}\eta _{0}+\Omega c\partial _{X}\eta _{0}=-\partial _{X}\eta _{0}, \end{aligned}$$
(4.25)

which gives the following expression for c:

$$\begin{aligned} c^{2}-\Omega c-1=0\Rightarrow c=\frac{\Omega \pm \sqrt{\Omega ^{2} +4}}{2}. \end{aligned}$$
(4.26)

The usual way to obtain this expression is to evaluate the Burns condition, which, in this case, is evaluating the integral:

$$\begin{aligned} \int _{-1}^{0}\frac{dz}{(c+\Omega z)^{2}}=1. \end{aligned}$$
(4.27)

The method presented here bypasses the evaluation of increasingly complicated integrals with simple substitution. The next order equations are:

$$\begin{aligned} \frac{\partial ^{2}V_{1}}{\partial X^{2}}+\frac{\partial ^{2}V_{1}}{\partial y^{2}}= & {} 0 \end{aligned}$$
(4.28)
$$\begin{aligned} V_{1}-\eta _{0}= & {} 0 \end{aligned}$$
(4.29)
$$\begin{aligned} -c\frac{\partial u_{1}}{\partial X}-\frac{\partial u_{0}}{\partial T}+u_{0}\frac{\partial u_{0}}{\partial X}-\Omega y\frac{\partial u_{1}}{\partial X}-\Omega v_{1}= & {} -\frac{\partial p_{1}}{\partial X} \end{aligned}$$
(4.30)
$$\begin{aligned} (c+\Omega y)\frac{\partial v_{0}}{\partial X}= & {} -\frac{\partial p_{1}}{\partial y} \end{aligned}$$
(4.31)
$$\begin{aligned} \frac{\partial ^{2}v_{0}}{\partial X^{2}}+\frac{\partial ^{2}v_{1}}{\partial y^{2}}= & {} 0 \end{aligned}$$
(4.32)
$$\begin{aligned} -c\frac{\partial \eta _{1}}{\partial X}+\frac{\partial \eta _{0}}{\partial T}+(2c-\Omega )\eta _{0}\frac{\partial \eta _{0}}{\partial X}= & {} v_{1} \end{aligned}$$
(4.33)
$$\begin{aligned}&p_{1}-\eta _{1} = \mathcal {P}_{1}-\hat{F}_{E}^{2}\frac{\partial V_{1}}{\partial y}-B\frac{\partial ^{2}\eta _{0}}{\partial X^{2}}. \end{aligned}$$
(4.34)

To keep the electric term in the Young–Laplace equation, a scaling has to be made on \(F_{E}\) of the form, \(F_{E}=\hat{F}_{E}\varepsilon ^{1/4}\). To progress, one finds the expression for \(p_{1}\) by integrating (4.31) and using (4.34) to obtain:

$$\begin{aligned} p_{1}&=c\left( \frac{(c-\Omega )}{2}[(y+1)^{2}-1]-\frac{\Omega }{3} [(y+1)^{3}-1]\right) \frac{\partial ^{2}\eta _{0}}{\partial X^{2}}\nonumber \\&\quad +\eta _{1}+\mathcal {P}_{1}-\hat{F}_{E}^{2}\frac{\partial V_{1}}{\partial y}-B\frac{\partial ^{2}\eta _{0}}{\partial X^{2}}. \end{aligned}$$
(4.35)

To obtain the required equation for the free surface, the function \(v_{1}(T,X,0)\) is needed. Solving Eq. (4.32) for \(v_{1}\) shows that:

$$\begin{aligned} v_{1}=\frac{c}{6}(y+1)^{3}\frac{\partial ^{3}\eta _{0}}{\partial X^{3}}+A_{1}(T,X)(y+1). \end{aligned}$$
(4.36)

Setting \(y=0\) in Eq. (4.30) allows \(A_{1}(T,X)\) to be computed:

$$\begin{aligned} (c-\Omega )A_{1}(T,X)= & {} \left[ -B+\frac{\Omega c}{6}-\frac{c^{2}}{2}\right] \frac{\partial ^{3}\eta _{0}}{\partial X^{3}}+\frac{\partial u_{0}}{\partial T} \nonumber \\&-u_{0}\frac{\partial u_{0}}{\partial X}-\frac{\partial \eta _{1}}{\partial X}-\frac{\partial \mathcal {P}_{1}}{\partial X}+\hat{F}_{E}^{2}\frac{\partial ^{2}V_{1}}{\partial X\partial y}, \end{aligned}$$
(4.37)

showing that:

$$\begin{aligned} A_{1}(T,X)= & {} c\left[ B+\frac{\Omega c}{6}-\frac{c^{2}}{2}\right] \frac{\partial ^{3}\eta _{0}}{\partial X^{3}}+c\frac{\partial u_{0}}{\partial T} \nonumber \\&-cu_{0}\frac{\partial u_{0}}{\partial X}-c\frac{\partial \eta _{1}}{\partial X}-c\frac{\partial \mathcal {P}_{1}}{\partial X}+c\hat{F}_{E}^{2}\frac{\partial ^{2}V_{1}}{\partial X\partial y}. \end{aligned}$$
(4.38)

Therefore, this gives \(v_{1}(T,X,0)\) to be:

$$\begin{aligned} v_{1}(T,X,0)= & {} \frac{c}{6}\frac{\partial ^{3}\eta _{0}}{\partial X^{3}}+c\left[ B+\frac{\Omega c}{6}-\frac{c^{2}}{2}\right] \frac{\partial ^{3}\eta _{0}}{\partial X^{3}}-c\frac{\partial u_{0}}{\partial T} \nonumber \\&-cu_{0}\frac{\partial u_{0}}{\partial X}-c\frac{\partial \eta _{1}}{\partial X}- -c\frac{\partial \mathcal {P}_{1}}{\partial X}+c\hat{F}_{E}^{2}\frac{\partial ^{2}V_{1}}{\partial X\partial y} \end{aligned}$$
(4.39)

To compute \(V_{1}\), use the Fourier representation to obtain:

$$\begin{aligned} \frac{\partial ^{2}\hat{V}_{1}}{\partial y^{2}}-k^{2}\hat{V}_{1}=0,\quad \hat{V}_{1}(t,k,0)=\hat{\eta }_{0} \end{aligned}$$
(4.40)

and to obtain:

$$\begin{aligned} V_{1}=\frac{1}{2\pi }\int _{\mathbb {R}}\hat{\eta }_{0}e^{-|k|y}e^{ikX}\mathrm{{d}}k. \end{aligned}$$
(4.41)

Then:

$$\begin{aligned} \frac{\partial v_{1}}{\partial y}(T,X,0)= & {} \frac{1}{2\pi }\int _{\mathbb {R}}-|k|\hat{\eta }_{0}e^{ikX}\mathrm{{d}}k \\= & {} \frac{1}{2\pi }\int _{\mathbb {R}}(ik)(i\text {sgn}(k))\hat{\eta }_{0}e^{ikX}\mathrm{{d}}k \\= & {} \widehat{\mathscr {H}(\partial _{X}\eta _{0})}, \end{aligned}$$

where \(\mathscr {H}(\cdot )\) denotes the Hilbert transform. From the properties of Hilbert transforms:

$$\begin{aligned} \frac{\partial ^{2}V_{1}}{\partial X\partial y}=\mathscr {H}(\partial _{X}^{2}\eta _{0}). \end{aligned}$$
(4.42)

Inserting \(v_{1}\) into Eq. (4.33) yields the equation of interest:

$$\begin{aligned} (1+c^{2})\frac{\partial \eta _{0}}{\partial T}+(2c+c^{3}-\Omega )\eta _{0}\frac{\partial \eta _{0}}{\partial X}+c\left[ \frac{c^{2}}{3}-B\right] \frac{\partial ^{3}\eta _{0}}{\partial X^{3}}-c\hat{F}_{E}^{2}\mathscr {H}\left( \frac{\partial ^{2}\eta _{0}}{\partial X^{2}}\right) +c\frac{\partial \mathcal {P}}{\partial X}=0. \end{aligned}$$
(4.43)

A quick check by setting \(c=1\) and \(\Omega =0\) shows that it reduces to the dispersion relation for electrohydrodynamics for irrotational flows. Putting the dimensions back in shows that:

$$\begin{aligned}&(1+c^{2})\left( c\frac{\partial \eta }{\partial x}+\frac{1}{c_{0}}\frac{\partial \eta }{\partial t}\right) +\frac{2c+c^{3}-\Omega }{h}\eta \frac{\partial \eta }{\partial x}+h^{2}c\left[ \frac{c^{2}}{3}-B\right] \frac{\partial ^{3}\eta }{\partial x^{3}} \nonumber \\&\quad -chF_{E}^{2}\mathscr {H}\left( \frac{\partial ^{2}\eta }{\partial x^{2}}\right) +\frac{1}{\rho g}\frac{\partial p}{\partial x}=0. \end{aligned}$$
(4.44)

This is the celebrated Benjamin equation, first discovered in [4]. Travelling wave profiles are examined by \(\eta =\eta (x-Vt)\) to get the equation:

$$\begin{aligned} (1+c^{2})(c-F)\eta +\frac{2c+c^{3}-\Omega }{h}\eta ^{2}+h^{2}c\left[ \frac{c^{2}}{3}-B\right] \eta ''-hcF_{E}^{2}\mathscr {H}(\eta ')+\frac{p}{\rho g}=0, \end{aligned}$$
(4.45)

where \(F=V/c_{0}\). Setting \(\Omega =0\) which it follows that \(c=1\) reduces to the equation in [14]. In the paper [15], a weakly nonlinear equation for constant vorticity is derived comparable to the one with \(E_{b}=0\).

The derived equation (4.44) belongs to the family of the so-called Benjamin-type (integro-differential) equations [4]. Its localized travelling wave solutions are described by the ordinary differential equation (4.45) with one non-local term. The travelling wave solution to the classical Benjamin equation was first analyzed in [5]. The stability of its solitary waves was recently studied in [9].

5 Numerical Methods and Results

To numerically generate the solitary wave solutions to Eq. (4.45), the classical Fourier-type pseudo-spectral discretization is employed on a sufficiently large domain. The solution decays below the machine accuracy to annihilate the effect of implied periodic boundary conditions. In other words, formally, a periodic BVP is solved, but the repeated value is actually zero in agreement with the decaying properties of solitary waves. The discrete problem for spectral coefficients is solved using the classical Petviashvili iteration as it was described in [10] for the classical Benjamin equation.

To implement the Petviashvili scheme, Eq. (4.45) is written in the following form:

$$\begin{aligned} \mathcal {L}\eta \ =\ \mathcal {N}\,(\eta ), \end{aligned}$$
(5.1)

where the linear \(\mathcal {L}\) and nonlinear \(\mathcal {N}(\cdot )\) operators are defined as:

$$\begin{aligned} \mathcal {L}\eta \&:=\ (1+c^{2})(c-F)\eta \ +\ h^{2}c\left[ \frac{c^{2}}{3}-B\right] \eta ''\ -\ h\,c\,F_{\,E}^{2}\mathscr {H}(\eta '),\\ \mathcal {N}\,(\eta )\&:=\ \frac{\Omega \ -\ 2c\ -\ c^{3}}{h}\eta ^{2}\,. \end{aligned}$$

Then, the Petviashvili iteration for Eq. (5.1) reads:

$$\begin{aligned} \eta ^{(n+1)}\ =\ \gamma _n^{\,2}\,\mathcal {L}^{-1}\circ \mathcal {N}\,(\eta ^{(n)})\,, \end{aligned}$$

taking into account that the mapping \(\mathcal {N}(\cdot )\) is a homogeneous function of degree two of its argument. Finally, the stabilizing factor \(\gamma _n\) is defined as:

$$\begin{aligned} \gamma _n\ :=\ \frac{\int _{{\mathbb {R}}} \eta _n\cdot \mathcal {L}\eta _n\, {\mathrm {d}}x}{\int _{{\mathbb {R}}} \eta _n\cdot \mathcal {N}(\eta _n)\, {\mathrm {d}}x} \,. \end{aligned}$$

For more details on the Petviashvili iteration, refer [3, 10].

5.1 Numerical Results

Equation (4.45) was discretized in space using the standard Fourier-type pseudo-spectral method; \(N = 1024\) modes were used in the computations. Localized travelling waves are of interest to the study, and the computational domain was taken to be \(T = [-10,\, 10]\), assuming periodic boundary conditions ensured by the choice of basis functions. The Petviashvili iterations were stopped when the \(L_\infty \) norm of the difference of two successive iterations became smaller than \(\epsilon = 5\times 10^{-15}\). The initial guess was a localized bump of negative polarity. The convergence of the method was marginally dependent on the choice of initial guess, which only influenced the total number of iterations. In any case, from the end user perspective, the code ran virtually instantaneously. It was noticed that the number of iterations increased with the electric Froude number \(F_E\). The computation of an oscillating travelling wave for \(F_E = 1.27\) took 117 Petviashvili iterations, while, for \(F_E = 0.5\), the method needed only 59 iterations to converge. The dimensionless physical and numerical parameters used in this computation are reported in Table 1.

Table 1 Dimensional parameters used in numerical computations
Full size table

At this point, it is pertinent to mention that for some values of parameters, it was possible to compute the periodic travelling wave solutions, which was not the initial goal. One such solution is reported in Fig. 5. Even if this solution appears to be a single Fourier mode (such as a sine wave), the Fourier power spectrum shown in the bottom panel of Fig. 5 shows that it is actually a superposition of infinite number of modes with exponentially decaying amplitude. There are only a finite number of modes have an amplitude above the machine precision and those were captured by the numerical method. It was demonstrated that this solution is generic in some sense to Eq. (4.45). In the computations, this type of solutions arose in a majority of the tested parameters values leading to the convergence of the algorithm.

From now on, the focus is on localized (in space) travelling wave solutions, which are less generic, but they are, nevertheless, present. Several examples of such structures are shown in Fig. 6 (for \(\Omega \ =\ 1\)) and Fig. 7 (for \(\Omega \ =\ 2\)), where the electric Froude number, \(F_{E}\), was gradually increased by keeping all other values constant (see Table 1).

Fig. 5
figure 5

Fully converged travelling periodic wave solution to Eq. (4.45) with \(B = 0.1\) and \(F_E = 0.5\). All other parameters are reported in Table 1. The bottom panel shows the Fourier power spectrum of the computed solution

Full size image
Fig. 6
figure 6

Computed localized solitary waves to Eq. (4.45) for the constant vorticity \(\Omega \ =\ 1\) and different values of the electric Froude number \(F_E\). All other parameters are reported in Table 1

Full size image
Fig. 7
figure 7

Computed localized solitary waves to Eq. (4.45) for the constant vorticity \(\Omega \ =\ 2\) and different values of the electric Froude number \(F_E\). All other parameters are reported in Table 1

Full size image
Fig. 8
figure 8

The dependence of positive and negative travelling wave amplitudes on the vorticity parameter \(\Omega \) for several values of the electric Froude number \(F_E\). All other parameters (except \(F_E\) and \(\Omega \)) are reported in Table 1

Full size image
Fig. 9
figure 9

Examples of a travelling wave solutions (for \(F_E\ =\ 1.22\)) near the lowest positive value of the vorticity parameter \(\Omega \) (the left panel, here, we took \(\Omega \ =\ 0.6\)) and the highest value taken in this study (the right panel, \(\Omega \ =\ 5.0\)). All other parameters (except \(F_E\) and \(\Omega \)) are reported in Table 1

Full size image

The dependence of the localized travelling wave solutions (such as depicted in Figs. 6, 7) on the vorticity parameter \(\Omega \,\) is also studied. For this purpose, a series of computations were performed with varying parameter \(\Omega \) between its lowest positive value for which the travelling solution exists and the maximal value fixed here to be \(\Omega \ =\ 5.0\,\). The result is presented in Fig. 8. The dependence turns out to be non-monotonic. Though, for high values of the vorticity parameter, the positive amplitude seems to decrease and the negative amplitude seems to increase monotonically. To illustrate the shape of solutions at two extremes on Fig. 8c, a typical solution near the lowest positive vorticity value is depicted in Fig. 9a, while the solution corresponding to the highest value is depicted in Fig. 9b.

5.1.1 Moving Pressure Effect

In the previous section, the moving pressure effect was set to zero to concentrate on the free wave propagation. In this section, the effect of the moving pressure distribution is studied. To fix the ideas, consider the following localized pressure distribution:

$$\begin{aligned} p\,(x)\ =\ a\,\exp \left( -\frac{1}{4}\;x^{\,2}\right) \,. \end{aligned}$$

This additional ingredient poses a slight technical problem, however: the nonlinearity \(\mathcal {N}(\eta )\) ceases to be a homogeneous function in \(\eta \), since the pressure term has the degree zero, while the rest of terms has the degree two. Consequently, this addition forces the algorithm to switched to the extended Petviashvili method [2]. The convergence of the extended Petviashvili method is slower than in its classical counterpart. Indeed, for zero vorticity case (i.e., \(\Omega \ =\ 0\)) the iterative procedure converges up to machine accuracy with about \(\sim \ 200\) iterations (cf. \(\sim \ 60\) iterations above). When the vorticity effects are included, the extended method takes more than 2500 iterations to converge to the same accuracy. In the same time, the classical method diverges. All parameters used in this study are reported in Table 2. The fully converged results of the numerical computations are shown in Fig. 10, where profiles were obtained for two different values of the vorticity parameter \(\Omega \,\). It was not possible find the localized solutions in this regime. Thus, the periodic profiles to which the extended Petviashvili method converged. These solutions appeared already in the free wave propagation regime, cf. Fig. 5. In particular, it may seen on Fig. 5 that the negative vorticity seems to reduce the effect of the moving pressure. To check this preliminary conclusion, a series of additional experiments was performed for several values of the vorticity parameter \(\Omega \) and moving pressure amplitude \(a\,\). The result of these computations is shown in Fig. 11. In particular, it can see that the trough amplitude is essentially a linear function of a (except at small values of this parameter). This conclusion is intuitively clear.

Table 2 Dimensional parameters used in numerical computations involving moving pressure effects
Full size table
Fig. 10
figure 10

Nonlinear periodic travelling waves under the moving pressure effect for two different values of the constant vorticity parameter \(\Omega \). All other parameters are reported in Table 2

Full size image
Fig. 11
figure 11

Dependence of the deepest trough amplitude under the pressure action on the free surface. The horizontal axis shows the parameter a in Table 2

Full size image

6 Conclusions and Discussion

This paper has not been the first to study the properties of the Benjamin equation, and previous works such as [1, 16, 18] where the emphasis was usually been on irrotational flow. It has, to the authors knowledge, been the first to study it in reference to constant vorticity. The goal of the paper is to study the affect of vorticity on waves rather than a study of the properties of the Benjamin equation itself.

In the present manuscript, the propagation of free surface electrohydrodynamic waves in the presence of non-zero, but constant vorticity distribution was investigated. The problem was analyzed from the linear and weakly nonlinear points of view. The linear analysis allowed us to get rid of Burns’s condition. The weakly nonlinear approach allowed us to compute solitary wave solutions by solving numerically the non-local ODE which describes them. The non-local effects are described by a linear term involving the Hilbert transform of the free surface excursion derivative \(\eta ^{\,\prime }\). It turns out that the dynamics of weakly nonlinear electrohydrodynamic waves is described by a generalized Benjamin equation [4]. So far, it appeared as a model equation for internal capillary-gravity waves [4, 5]. In our study, it serves to predict the shape of coherent structures in electrohydrodynamic flows with constant vorticity. We notice that the authors studied earlier the effect of viscosity on the electrohydrodynamic waves in [13].

Concerning the perspectives, in future works, we would like to consider internal waves with differing constant vorticities and more general vorticity distributions. The equation:

$$\begin{aligned} \frac{\partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}v}{\partial y^{2}}=\frac{\partial \omega }{\partial x} \end{aligned}$$
(6.1)

allows the vorticity, \(\omega \), to be some a priori prescribed function of t, x, y. Finally, the unsteady simulations have to be performed to understand better the dynamics of solutions discussed hereinabove. We suspect also that the derived Benjamin-type Eq. (4.45) possesses also other types of travelling wave solutions such as multi-pulsed solitary waves which were computed in [10] in the context of internal waves.