1 Introduction

Despite decades of efforts to curb and eradicate the malaria pandemic, it still retains its status as one of the most dangerous and fatal infections in the tropical and subtropical endemic countries, having over 500 million reported cases with approximately one million deaths yearly [1]. The disease is caused by Plasmodium falciparum (P. falciparum), the most lethal of all the five Plasmodium species, others are; Plasmodium malariae (P. malariae), Plasmodium knowlesi (P. knowlesi), Plasmodium falciparum (P. falciparum), Plasmodium vivax (P. vivax), and Plasmodium ovale (P. ovale) [2,3,4]. The protozoan parasite Plasmodium falciparum produced in the red blood cell (RBCs) requires various hosts for its growth and survival. The host is unable to manufacture purine rings de novo, hence purine is reclaimed from the host by the parasite [5]. Within the digestive vacuole of the parasite, the hemoglobin releases heme molecules that are toxic to the parasite. The heme is crystallized into hemozoin to nullify its toxicity. A large amount of hemoglobin is accumulated in the digestive vacuole [6]. The rate of heme release must equal to that of hemozoin crystallization for the survival of the parasite otherwise toxic heme buildup in the parasite [7].

Several compounds including chloroquine, artemisinin, amodiaquine, and quinine have been reported to have antimalarial activity and are employed in the treatment of malaria [8]. The treatment of malaria is faced with great challenges which include the rapid resistance developed by Plasmodium parasites to the available antimalarial drugs as well as the lack of an effective antimalarial vaccine. This resistance ensures that the available antimalarial drugs become ineffective in the treatment of pandemic disease. Hence, the need to develop new and novel antimalarial agents through chemical modification of existing compounds becomes a necessity [9].

Triazolopyrimidines identified with either lack of potency or poor plasma exposure due to metabolic stability were found to have improved potency as a result of the substitution of arylamine moiety [10]. In light of this, aryl and aralkyl amine-based triazolopyrimidine compounds reported for their antimalarial activity against the multi-drug resistant Plasmodium falciparum strain, 3D7 [10] could provide an alternative application to the orthodox antimalarial drugs.

Quantitative structure–activity relationship (QSAR) is an essential tool in the drug design field by reducing the time as well as the cost of drug development [11]. QSAR relates the physicochemical properties of congeneric compounds with the structural features responsible for their activity [12].

Several QSAR studies related to the design of anti-malarial drugs were reported. In 2018, Hadanu and co. investigated the antimalarial activity of nitrobenzothiazole derivatives [13]. Beheshti and Co study the modeling of antimalarial activity of urea derivatives [14]. Prediction of anti‑malarial activity in a set of new imidazolopiperazines using artificial neural networks was reported [9], but no systematic QSAR studies were conducted on a series of aryl and aralkyl amine-based triazolopyrimidine compounds as an antimalarial. This research is aimed at establishing a virgin QSAR regression model for predicting the antimalarial activity of 32 derivatives of aryl and aralkyl amine-based triazolopyrimidine compounds through the application of a hybrid of GA–MLR approach. Thereafter, we performed in silico design of a template (a compound with the highest activity), into new derivatives with enhanced activity against P. falciparum with the aid of the most contributive molecular descriptor determined by the descriptors mean effect, which saves time and cost enquired in the drug development analysis.

2 Material and Methods

2.1 Sources of Data

The dataset of thirty-two aryl and aralkyl amine-based triazolopyrimidine derivatives consisting of their structures and activities (Table 1) were extracted from the literature [15]. Their biological activities were expressed as pEC50 (-Log10 drug concentration to cause a 50% reduction in cell proliferation) suitable for QSAR analysis (Tables 2 and 3).

Table 1 Molecular structures of substituted aryl amine-based triazolopyrimidine derivatives and their biological activities against P. falciparum strain 3D7
Full size table
Table 2 Molecular structures of alicyclic/aralkyl and alkyl amine-based triazolopyrimidine derivatives and their biological activities against P. falciparum strain 3D7
Full size table
Table 3 Molecular structures of pyrimidine ring-modified triazolopyrimidine derivatives and their biological activities against P. falciparum strain 3D7
Full size table

2.2 Geometry Optimization

The structures of the compounds were drawn with the help of ChemDraw software, while Spartan 14 software (Spartan 14v114) was utilized in the optimization of the molecular geometries [16] based on the density functional theory (DFT) level using Becke's three parameters Lee–Yang–Parr hybrid functional (B3LYP) in combination with the 6–31 + G* basis set. The optimized Spartan 14 structures are saved in SDF format.

2.3 Descriptors Calculation

The lowest energy-optimized geometries were imported into the PaDel-Descriptor version 2.20 for descriptors calculation. About 1500 varieties of molecular descriptors were calculated for each molecular geometry present in Table 1. The descriptors range from Atom Count, Autocorrelation, BaryszMatrix, BCUT, Burden Modified Eigenvalues, Carbon Types, Electrotopological State Atom Type, Extended Topochemical Atom, Autocorrelation3D, and RDF descriptors were calculated [17].

2.4 Dataset Division

The dataset was split in the ratio 78:22 with 25 training compounds (78% of the data set) and 7 test compounds (covering the remaining 22%) with the aid of the DatasetDivision1.2 program [18] by employing the Kennard-Stone’s algorithm method.

2.5 QSAR Model Development

The training set was utilized in the development of the QSAR model, where the activities (dependent variable) and the molecular descriptors (independent variables) were exposed to model development by the Genetic Function Approximation (GFA) method contained in the material studio software. The Genetic algorithms (GAs), a copycat of biological evolution, are currently the ultimately used variable selection method that addresses both the constrained and unconstrained optimization challenges based on an essential selection process [19, 20]. GA is a prying search method that looks for the correct or approximate solutions to any optimization challenges [21]. Its ability to produce more than one blend of descriptors useable in model construction is an added advantage. With GAs, users have the liberty of imposing the equation length and employs a lack of fit (LOF) function to check over-fitting in the models produced. The lack-of-fit (LOF) was calculated in the material studio to estimate the model fitness using Eq. 1.

$$ LOF = SSE/\left( {1 - ^{c + dp/M} } \right)^{2} $$
(1)

where SSE stands for the sum of squares of errors, c, number of terms other than the constant in the model, d stands for the user-defined smoothing parameter, p is the number of descriptors in the model, and M, represent the samples counts in the training set.

2.6 Multi-co-linearity analysis

The possibility of a huge degree of correlation among the model descriptors was evaluated using a variance inflation factor (VIF). For a descriptor, i, the VIFi was calculated from Eq. 2.

$$ VIF_{i} = \left( {1 - R_{ij}^{2} } \right)^{ - 1} $$
(2)

where R2ij represents the multiple regression’s correlation coefficients between the descriptor i and the remaining j model descriptors.

2.7 Model Validation

2.7.1 Internal Validation

The leave- one- out (LOO) cross-validation technique was deployed to internally validate the model. It involves the elimination of one compound from the data set at random in each cycle and the model is built with the remaining compounds. The constructed model is used for predicting the activity of the compound eliminated. This process is carried out again and again until the entire compounds are eliminated once. The cross-validated squared coefficient of correlation, R2cv (Q2) was calculated from the equation below.

$$ Q^{2} = 1 - \frac{{\sum \left( {Y_{obs } - Y_{pred} } \right)^{2} }}{{\sum \left( {Y_{obs } - \hat{Y} } \right)^{2} }} $$
(3)

where Yobs is the observed activity of the training set, Ypred represents the predicted activity of the training set and Ŷ is the mean observed activity of the training set.

2.7.2 External Validation

The developed model was externally validated to determine its predictive strength, through predicting the activity of some dataset (test set) separated from the training set. This is achieved using Eq. 4 below.

$$ R_{pred}^{2} = 1 - \frac{{\sum \left( {Y_{{obs \left( {test} \right)}} - Y_{{pred \left( {test} \right)}} } \right)^{2} }}{{\sum \left( {Y_{{obs \left( {test} \right)}} - \hat{Y}_{training} } \right)^{2} }} $$
(4)

where Yobs (test) and Y(test) indicates the test set predicted and observed activity values respectively, Ŷtraining, indicates training set means activity. R2pred is the predicted coefficient of correlation estimated from the predicted test set activity.

2.8 Y-Randomization

The possibility of the model occurring by chance was determined through the Y-randomization test, which also ascertains the robustness of the developed model. The Y-Randomization test involves constructing a model with a randomizing the activities of the training set. A detour in the square of the mean correlation coefficient of the randomized activity model (R2r) from that of the non-randomized activity model (R2) is reflected in the value of R2m parameter calculated with help of the Eq. 5 [22].

$$ R_{m}^{2} = R^{2} X \sqrt {\left( {R^{2} - R_{r}^{2} } \right)} $$
(5)

Normally, the average value of R2r for the randomized activity model is expected to be zero, implying equal values of R2m and R2r for the developed model, necessitate the use of cRp2 in place of R2m. A model is deemed not due to a chance when the coefficient of determination (cRp2) is found to be greater than 0.5 [23]. The value of cRp2 was calculated for each randomized activity model with the aid of Eq. 6 given below.

$$ cR_{p}^{2} = R X \sqrt {\left( {R^{2} - R_{r}^{2} } \right)} $$
(6)

2.9 Model Applicability Domain

The applicability domain (AD) provides an assessment of the model in terms of its ability to predict the activity of unknown compounds excellently in form of chemical space. Every model is only able to predict the activity of a certain number of compounds; such prediction is conditioned on the satisfaction of the assumptions applied in the construction of the model [24]. The chemical space of the AD is designed by plotting the values of leverage against the standardized residuals (Williams plot) of the entire data set. The leverages are obtained from the diagonals of a hat matrix obtainable from Eq. 7 [17].

$$ H_{i} = X_{i} \left( {X_{i}^{T} X_{i} } \right)^{ - 1} X_{i}^{T} $$
(7)

where, \({H}_{i}\), is the hat matrix of the training/test set, \({X}_{i}\) is the original matrix of training/test set, and \({X}_{i}^{T}\) is the transpose matrix of the training/test set.

Being a prediction tool, the AD has warning leverage (h*) defining the limit of normal values for X outliers and it’s defined as \({h}^{*}=3(z+1)/n\), where n is the number of the training set, and z is the number of descriptors in the model. Only compounds with leverages less than or equal to the warning (h*) are considered to be within the chemical space and their activities are reliably predicted by the model. In addition to the AD, a plot of the normalized mean distance of the model descriptors against the standardized residuals of the predicted activities of the data set (UZAIRU’S plot) was employed to detect outliers present in the data set [25].

2.10 Mean Effect (MF)

The model descriptor's relevance was analyzed by evaluating the descriptors mean effect (MF). The contribution by individual descriptor to the model are reflected by the size as well as the signs of their mean effect. The most contributive descriptor has the largest mean effect, while the small mean effect size is for the least contributive descriptor. The mean effect is evaluated from Eq. 7.

$$ Mean\;Effect = \frac{{\beta_{j} \sum\nolimits_{i}^{n} {D_{j} } }}{{\sum\nolimits_{j}^{m} {\left( {\beta_{j} \sum\nolimits_{i}^{n} {D_{j} } } \right)} }} $$
(8)

where \({\beta }_{j}\) is the coefficient of j, Dj is the value of each training set in the descriptor matrix and m is the tally of model descriptors and n is the tally of molecules used as the training set [26].

2.11 Molecular Design

The relevance of the model's descriptors cannot be overemphasized as such the interpretations of the most contributive descriptor could provide a guide to design several hypothetical derivatives of aryl and aralkyl amine-based triazolopyrimidine having enhanced antimalarial activities. This is made possible by selecting the compound with the highest activity as a design template. The structural feature of the most informative descriptor forms the basis of manipulating the design template by substituting group(s) based on the information from the size of the descriptors mean effect, to design some theoretical compound possessing higher antimalarial activity than the design template through replacing atom/group of atoms at different positions on the template. The design derivatives were then optimized and their descriptor calculated from which the antimalarial activity was obtained.

3 Results and Discussion

3.1 QSAR Studies

Two QSAR models developed through the genetic function algorithm analysis of the datasets were as presented in Table 4:

Table 4 Generated models with their statistical parameters
Full size table

3.2 QSAR Model Selection

The second tetra parametric equation (model II) was announced as the best QSAR model based on its statistical data obtained from multiple linear regression (MLR) of the material studio. The model was used in evaluating the theoretical activity of the aryl and aralkyl amine-based triazolopyrimidine derivatives used in the analysis. The model may not have the highest R2 (0.8884) compared to that of the model I (0.8931), but its higher square coefficient of correlation for the test set (R2ext = 0.7019) which is in line with the prerequisite for a dependable, foretelling and robust QSAR model [27] ensures model II emerges as the best model. The definition of the descriptors in the model as well as their class were reported in Table 5.

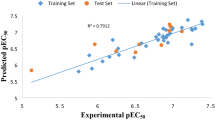
Table 5 List of the physiochemical descriptors that constitute the model
Full size table

The meager residual values of the data set (Tables 1, 2, and 3) calculated by the best model, is an indication of a good agreement between the observe and predicted activity as well as the reliability of the model, this was supported by the distribution of the data set around the legend, displayed in the plot of experimental pEC50 vs predicted pEC50 presented as Fig. 1.

Fig. 1
figure 1

The predicted pEC50 against the experimental values for the data set

Full size image

3.3 Model Validation

A significant QSAR model is one that can predict the activities of an external data set, (R2ext) not just in its ability to clone the training set (Q2 LOO). Hence, the training set prediction was affirmed by the leave-one-out (LOO) cross-validation method. The large Q2 LOO value, 0.8317 calculated is a good indication of an excellent internal validation. The results of the external validation, R2ext = 0.7019, show the predictive strength of the model and hence its robustness. Analysis of the correlation matrix shown in Table 6, shows a large value of correlation coefficients between the descriptors and the activity, an indication of a great interrelation between the two. Whereas the low correlation coefficients between the descriptors themselves indicate noncollinearity between the descriptors. The descriptor's multicollinearity is explained with variation inflation factors (VIF). The VIF values of the model's descriptors as reflected in Table 6, all fall within, 1 < VIF ≤ 5 range, which is a VIF criterion for model acceptance [28, 29]. The results of the VIF confers orthogonality and acceptability on the model. The outcome of the Y-randomization inquiry after scrambling the activity ten folds shows that the R2 and Q2 values for the scrambling activity model are significantly low, confirming the robustness of the model. Table 7, shows the Y-randomization parameters with \({cR}_{p}^{2}\) greater than 0.5 reaffirming the model’s quality. The standardized residuals plotted against the calculated leverage values (Williams plot) gives a graphical identification of both the outliers and the influential substances within a model. The applicability domain (Fig. 2), is entrenched within ± 3 standardized residual range and a leverage threshold (h* = 0.6). Figure 2, clearly shows no compound of the data set beyond the standard deviation, ± 3d, and a leverage value, h > 0.6. Hence, the entire data set contain neither an outlier nor an influential substance. Furthermore, the Uzairu’s plot (the normalized mean distance of the model descriptors versus the standardized residuals of the predicted activities of the data set) presented in Fig. 3, also confirms the absence of an outlier.

Table 6 The correlation matrix of the descriptors and their VIF
Full size table
Table 7 Y-randomization model parameters
Full size table
Fig. 2
figure 2

The plot of the standardized residuals versus the leverage values

Full size image
Fig. 3
figure 3

The Uzairu’s plot of the normalized mean distance versus the standardized residuals

Full size image

3.4 Interpretation of Descriptors

In this research, the four molecular descriptors chosen by GA play a significant role in the discovery of new drugs for the treatment of malaria. The contributions of each descriptor to the model were carried out in the MF analysis displaced in Fig. 4. The first two descriptors are MATS6i and GATS5e, which are both 2D-autocorrelated descriptors obtained from a molecular graph through the addition of the atomic weight of the terminal atoms of the considered path length. While MATS6i descriptor encodes the ionization potential of the substituted aryl amine-based triazolopyrimidine analogs, it expresses the tendency of an electron cloud or molecule to interact with a target [30], from the MF analysis, the descriptor has the least contribution (MF = 0.00298) to the antimalarial activity and its positive sign is an indication of a direct relationship with the activity. The GATS5e relates to the electronegativity of the compound which has an inverse relation with the activity as a result of the MF sign.

Fig. 4
figure 4

3-D clustered column descriptors mean effect

Full size image

The third descriptor, GATS6p is also a 2D descriptor [31] that reflects the topological structure of the molecules. The difference in the atomic polarizabilities of the molecule is explained by the descriptor [32]. This descriptor is the most relevant with MF = 1.66902, and its positive MF sign indicates increasing the value of the descriptor, increases the antimalarial activity.

The last descriptor, RDF30m indicates the existence of some linear dependence between the inhibitory activities of aryl amine-based triazolopyrimidine derivatives and the 3-dimensional molecular distribution of mass determined at a radius of 4.0 Å from the centers of all molecule. The descriptor's negative MF is a reflection of its indirect relation with the activity. A decrease in the value of the descriptor increases the antimalarial activity.

3.5 Molecular Design

The compound with the highest antimalarial activity, DSM191 (pEC50 = 7.1805) was exploited as the design template. The most contributive descriptor, GATS6p (MF = 1.6690) influences the antimalarial activity of the derivatives of aryl and aralkyl amine-based triazolopyrimidine greatly, and relate to the atomic polarizabilities of the molecule. With the positive mean effect, antimalarial activity increases with an increase in the descriptor value (atomic polarizabilities) of the molecule. Atomic polarizability increases with an increase in the number of electrons (leading to a reduction in the effective nuclear charge). Therefore, various electron-donating groups such as; -CH3, -CH2CH3, -COCH3, -OCH3, -OH, -NH2, and -N(CH3)2 were added to the design template at ortho/para positions to release electron density into the ring thereby creating derivatives of the template which increase the polarizability and by extension, increase the antimalarial activity of the designed derivatives. Sixteen (16) derivatives of the template were designed, out of which nine of the designed compounds (2D, 4D, 8D, 11D, 12D, 13D, 14D, 15D, and 16D) have improved hypothetical antimalarial activity than the design template as well as Chloroquine (pEC50 = 4.6352) and Pyrimethamine (pEC50 = 6.2593) standards as shown in Table 8. Compound D8, N7-(benzo[b]thiophen-5-yl)-N6,N6,5-trimethyl-[1,2,4]triazolo[1,5-a]pyrimidine-6,7-diamine was identified with the highest antimalarial activity (pEC50 = 8.9545) as reflected (Table 8), hence is the most active designed derivative (Fig. 5).

Table 8 The structures of the design template, designed derivatives of aryl and aralkyl amine-based triazolopyrimidine along with their respective theoretical activities
Full size table
Fig. 5
figure 5

Design Template, DSM191, N-(benzo[b]thiophen-5-yl)-5-methyl-[1,2,4]triazolo[1,5-a]pyrimidin-7-amine (pEC50 = 7.1805)

Full size image

4 Conclusions

This research is focused on designing antimalarial derivatives through the developed QSAR model used for predicting the activities of aryl and aralkyl amine-based triazolopyrimidine derivatives. The PaDel-Descriptor version 2.20 software was employed to calculate several descriptors used for the regression analysis carried conducted by the GA–MLR process and the developed model validated comprehensively. The selected model revealed descriptors; MATS6i, GATS5e, GATS6p, and RDF30m played a significant role in the antimalarial activity of the compounds. The mean effect analysis indicated GATS6p as the most contributive descriptor (MF = 1.6690) which estimates the polarizability of the molecule whose positive values increasing the activity of the compounds. Sixteen compounds were designed using DSM191 (a compound with the highest antimalarial activity) as the design template and various electron-donating groups used to increase the atomic polarizability were directed at the ortho/para positions of the aromatic rings of the template. Compound D8, N7-(benzo[b]thiophen-5-yl)-N6,N6,5-trimethyl-[1,2,4]triazolo[1,5-a]pyrimidine-6,7-diamine, was found to have the highest hypothetical activity (pEC50 = 8.9545) than the template (pEC50 = 7.1805) and the fellow designed compounds. These designed compounds when synthesized could be clinically validated for antimalarial treatment. Hence, the studies will reduce trial and error as well as minimize the time and cost involved in drug design. Furthermore, in the future, we could conduct the molecular docking studies of the design compounds against their target to observe the nature of interactions responsible for the antimalarial activity.