1 Introduction

The China Fusion Engineering Test Reactor (CFETR) represents a novel fusion reactor, bridging the technological gap between the International Thermonuclear Experimental Reactor (ITER) and the Demonstration Fusion Reactor (DEMO). Given the challenging radiation environment within CFETR, the maintenance procedures necessitate implementation through Remote Handling Technology [1]. A heavy-duty Bionic Caterpillar-like Robot (BCR) is engineered to facilitate the transfer of blankets of CFETR from the Vacuum Vessel to the Hot Cell. Two BCRs move along two toroidal tracker rails fixed to the inner board of the Vacuum Vessel, together facilitating the transportation of a heavy blanket to the desired position, as illustrated in Fig. 1a. The BCR comprises multiple motion modules, mimicking the characteristics of a caterpillar [2, 3]. These modules include the Jacking Unit (JU), the Driving Unit (DU), and the Locking Unit (LU), as illustrated in Fig. 1b [4, 5]. The motion system of the BCR primarily comprises various hydraulic cylinders powered by hydraulic mechanisms. The motion diagram of BCR is depicted in Fig. 2. A key distinction from a bionic caterpillar is that both locking module and the jacking module consistently slide on the tracker through roller bearings. Given the substantial weight of a single blanket—60 tons and a height of 7.6 m, transferring it presents a notable challenge for the BCR control system. Meeting the safety standards of the entire system necessitates stringent requirements for dynamic tracking and steady-state accuracy in the displacement of DU of BCR. Specifically, the dynamic tracking accuracy is mandated to be within ± 5 mm, while the steady-state accuracy should fall within ± 2 mm. How to accomplish blanket maintenance with high accuracy, stability and efficiency is a difficult problem that needs to be solved. The key design parameters of BCR are shown in Table 1.

Fig. 1
figure 1

Blanket transportation and BCR schematic diagram. a Blanket transportation schematic diagram. The upper BCR and lower BCR hold and transport blanket along toroidal rail synchronously; b BCR schematic diagram. JU, DU and LU are hydraulic system. JU consists of 4 hydraulic cylinders. DU consists of 1 hydraulic cylinder. LU consists of 2 main locking cylinders and 2 deputy locking cylinders. Jacking module takes the weight of the blanket

Full size image
Fig. 2
figure 2

BCR motion diagram. a The caterpillar can be segmented into two parts, with one connected to the ground (indicated by the red circle) and the other not connected (indicated by the green circle). The back parts of the caterpillar and BCR have a connection with the ground (Jacking module of BCR is fixed to the rail by LU). b Front parts move forward. c The front parts of the caterpillar and BCR have a connection with the ground (Locking module of BCR is fixed to the rail by LU). d Back parts move forward

Full size image
Table 1 BCR key design parameters
Full size table

The hydraulic driven unit of the BCR is characterized as a highly nonlinear system. In the domain of model establishment, two primary methods are commonly employed: physics-based methods and data-based methods. Physics-based methods rely on the fundamental principles and equations of the hydraulic system, offering a profound understanding of the underlying physics and establishing clear relationships among various components. These approaches are flexible and easily adaptable, allowing for modifications to accommodate changes in system parameters, component characteristics, or operating conditions [6,7,8,9].

Data-based methods prove valuable in capturing intricate relationships within the hydraulic system. These approaches excel at uncovering patterns and correlations that may not be immediately apparent through traditional physics-based modeling alone. Data-based methods are known for their flexibility, making them adept at adapting to changing conditions and uncertainties. By leveraging empirical data and employing techniques such as machine learning or statistical modeling, these methods enhance the system's modeling accuracy, especially when dealing with complex nonlinearities and real-world variability [10,11,12,13].

In the domain of automotive control systems, Model Predictive Control (MPC) has evolved since the 1970s [14]. Due to its model-based prediction and receding horizon optimization characteristics, MPC provides several advantages in the automotive control systems domain. These advantages include enhanced control performance, adaptability to changing system conditions, safe constraint handling, capability for multivariable control, and effectiveness in managing nonlinear systems. For example, a controller utilizing the MPC algorithm for pressure control in heavy-duty transmission shifting was introduced in reference [15]. The simulation validated the efficacy of pressure control. There are also similar applications discussed in the references [16, 17]. Reference [18] introduced an MPC-based controller to enhance the dynamic performance of an excavator boom, resulting in a substantial reduction in cost function and vibration. In [19], MPC was employed to enhance the energy efficiency of legged robots while maintaining commanded motion. MPC was proposed for hydraulic multi-chamber actuator force control in order to address challenges associated with mode switching [20]. In [21], an MPC feedback controller with steady-state feedforward was devised to control engine torque and pump displacement. To handle tracking control of all motion axes of a hydraulic mini excavator, an offset-free model predictive controller with extended Kalman filters was proposed in [22]. Nonlinear Model Predictive Control (NMPC) was introduced for anti-sway control of a hydraulic forestry crane, demonstrating significant sway reduction [23]. In [24], a model predictive controller was developed, embedding convex inequality constraints of foothold feasibility local approximations for dynamic locomotion control of robots. For new semi-active hydro-pneumatic inerter-based suspension systems, a two-stage hierarchical control scheme based on MPC was proposed in [25] to achieve optimal dynamic performance. Moreover, MPC found applications across various industries [26,27,28].

However, the control performance of MPC-type control algorithms can be susceptible to inaccuracies in the mathematical model, external disturbances, and controller parameters such as the prediction domain, control domain, control weights, etc. [29]. To enhance the control performance of MPC/NMPC, various methods have been employed recently, encompassing aspects such as model accuracy, parameter optimization, supplementation with other control methods, and more, across a range of system applications. For instance, one approach involves the utilization of an adaptive parameter estimator to estimate system parameters online within NMPC, thereby enhancing control performance [30]. In another study [31], a sophisticated neural network architecture was incorporated into MPC as dynamic models to achieve optimal control performance. The notion of addressing the increment of the unmodeled dynamics was proposed in [32], where a designed compensator was employed for its elimination. Robust methods and adaptive parameters were utilized in [33] to optimize the model and obtain an enhanced MPC controller [34] employed adaptive methods and backstepping technology to address model parametric uncertainties and disturbance compensation, respectively. In the context of parameter optimization and adjustment, numerous intelligent algorithms, such as fuzzy logic and genetic algorithms, prove to be valuable tools. These methods are frequently employed in optimizing controller parameters, showcasing robust performance, and contributing significantly to achieving superior control values in motion simulation platforms, aero-engine, and so on [35,36,37,38].

Nevertheless, in these studies, the optimized MPC/NMPC focus tends to be more on the control algorithm rather than the MPC/NMPC optimization process. Particularly within the hydraulic system control domain, the optimization of controller parameters during the MPC/NMPC optimization process is infrequently explored. Additionally, the incorporation of outer loop error and disturbance compensation methods is seldom employed. To achieve precise motion control of the BCR and ensure the stable and efficient transfer and maintenance of blankets, inspired by the preceding studies, the primary contributions of this paper can be summarized as follows:

(1) The nonlinear model of the DU of the BCR is formulated into the standard state space function type by using the physics-based method. Additionally, the nonlinear feedback term is incorporated to simplify the model form, providing a foundational model for subsequent controller design.

(2) A novel NMPC-FRDNNF controller is developed. Initially, an NMPC controller is constructed based on the nonlinear model outlined in (1). Subsequently, a fuzzy-based adaptive parameter regulator is introduced to adjust the control weight dynamically in real time, thereby enhancing the control receding horizon optimization process in the NMPC controller. Furthermore, to mitigate the effects of disturbances such as model uncertainty, etc. in MPC-type controllers for real-world applications, the concept of a disturbance compensator utilizing a system inverse model is proposed. Constructing a physics-based inverse model presents challenges. However, the data-based inverse model offers advantages such as robust learning capabilities for handling system nonlinearity, etc. Inspired by the aforementioned studies, a novel disturbance compensator leveraging the Deep Neural Network (DNN) inverse model is proposed to generate feedforward control values for effective disturbance compensation.

(3) Simulation and experimental validations are conducted to assess the control efficacy of the proposed hybrid controller. Comparative analyses with various controllers for the BCR demonstrate that both simulation and experimental results affirm the effectiveness of this control strategy. This provides valuable theoretical insights for the successful operation of fusion reactors in the future.

The subsequent sections of this paper are organized as follows: Sect.  2 details the modeling of the DU of BCR. Section 3 elaborates on the design of the hybrid controller. Section 4. Presents simulation and experimental results, comparing the proposed hybrid controller with alternative controllers. The conclusion is drawn in Sect. 5.

2 DU of BCR Nonlinear Model Establishment

The proportional servo valve has an internal closed-loop control between the input signal \(u\) and output valve spool displacement \({x}_{v}\), so the proportional servo valve module can be simplified as the following linear equation (hydraulic servo system close loop control diagram is shown in Fig. 3).

$${x}_{v}={K}_{1}u$$
(1)

where.

Fig. 3
figure 3

Asymmetric hydraulic servo system close loop control diagram

Full size image

\({X}_{v}\)–The spool displacement;

\({K}_{1}\)–The gain;

\(u\)–The input signal.

Because DU is an asymmetric hydraulic system, the system model must be established as forward (\({X}_{v}>0\)) and backward (\({X}_{v}<0\)). The definition details are shown in reference [39]. When the piston of the cylinder moves forward, the flow continuity equation is obtained as follows:

$${Q}_{L}={A}_{1}\dot{y}+{C}_{ief}{P}_{Lf}-{C}_{eef}{P}_{s}+\frac{{V}_{tf}}{{\beta }_{e}}\dot{{P}_{Lf}}$$
(2)

where.

\({Q}_{L}\)–Load flow;

\({A}_{1}\)–Piston effective area with rodless cavity;

\(y\)–Hydraulic cylinder piston displacement;

\({P}_{Lf}\)–Load pressure when piston moves forward;

\({P}_{s}\)–Pump pressure;

\({\beta }_{e}\)–The effective bulk modulus of elasticity;

\({V}_{tf}\)–Effective volume when piston moves forward;

\({C}_{ief}\)–Equivalent leakage coefficient when piston moves forward;

\({C}_{eef}\approx 0\)–Additional leakage coefficient when piston moves forward.

The nonlinear flow equation is obtained:

$${Q}_{L}=sign({P}_{s}-{P}_{Lf}){C}_{d}\omega {x}_{v}\sqrt{\frac{2\left|{P}_{s}-{P}_{Lf}\right|}{\rho (1+{n}^{3})}}$$
(3)

where.

\({C}_{d}\)–Valve flow coefficient;

\(\omega\)–Valve port gradient area;

\(\rho\)–Hydraulic oil density;

\(n\)–The ratio of a rod cavity to a rodless cavity;

$$sign\left( \cdot \right) = \left\{ {\begin{array}{*{20}c} { - 1, if \cdot < 0} \\ {0, if \cdot = 0} \\ {1, if \cdot \ge 0} \\ \end{array} } \right.$$

The force equilibrium equation is obtained:

$${A}_{1}{P}_{Lf}=M\ddot{\text{y}}+{B}_{p}\dot{y}+Ky-{F}_{l}$$
(4)

where.

\(M\)–Total piston and load mass;

\({B}_{p}\)–Viscous damping coefficient of piston and load;

\(K\)–Load elastic stiffness;

\({F}_{l}\)–The external force.

By combining eqs. (1–4), the following equations are obtained:

$$\dot{x} = A_{f} x + B_{f} \left( {x_{1} ,x_{2} ,x_{3} } \right)u + d_{f} \left( {x_{2} ,x_{3} } \right)$$
(5)
$$y={C}_{f}x$$
(6)

Where.

$$x = \left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} y \\ {\dot{y}} \\ {\ddot{y}} \\ \end{array} } \right];$$
$$A_{f} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ { - \frac{{\beta_{e} C_{ief} K}}{{V_{tf} M}}} & { - \left( {\frac{K}{M} + \frac{{\beta_{e} C_{ief} B_{p} }}{{V_{tf} M}} + \frac{{\beta_{e} A_{1}^{2} }}{{V_{tf} M}}} \right)} & { - \left( {\frac{{B_{p} }}{M} + \frac{{\beta_{e} C_{ief} }}{{V_{tf} }}} \right)} \\ \end{array} } \right];$$
$${\varvec{B}}_{{\varvec{f}}} \left( {x_{1} ,x_{2} ,x_{3} } \right) = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {B_{f1} B_{f2} } \\ \end{array} } \right];$$
$$B_{f1} = \frac{{\beta_{e} A_{1} C_{d} \omega K_{1} }}{{V_{tf} M}}\sqrt {\frac{{2P_{s} }}{{\rho \left( {1 + n^{3} } \right)}}}$$
$${B}_{f2}=sign\left({P}_{s}-{P}_{Lf}\right)\sqrt{\left|\frac{{P}_{s}-{P}_{Lf}}{{P}_{s}}\right|};$$
$${C}_{f}=\left[\begin{array}{ccc}1& 0& 0\end{array}\right];$$
$${d}_{f}({x}_{2},{x}_{3})=\left[\begin{array}{c}0\\ 0\\ \frac{{\beta }_{e}{C}_{ief}}{{V}_{tf}M}{F}_{l}+\frac{1}{M}\dot{{F}_{l}}\end{array}\right]$$

In the same way, when piston of cylinder moves backward, the following equations are obtained:

$$\dot{x}={A}_{b}x+{B}_{b}({x}_{1},{x}_{2},{x}_{3})u+{d}_{b}({x}_{2},{x}_{3})$$
(7)
$$y={{\varvec{C}}}_{{\varvec{b}}}{\varvec{x}}$$
(8)

where.

$${A}_{b}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -\frac{{\beta }_{e}{C}_{ieb}K}{{V}_{tb}M}& -(\frac{K}{M}+\frac{{\beta }_{e}{C}_{ieb}{B}_{p}}{{V}_{tb}M}+\frac{{\beta }_{e}{A}_{2}^{2}}{{V}_{tb}M})& -(\frac{{B}_{p}}{M}+\frac{{\beta }_{e}{C}_{ieb}}{{V}_{tb}})\end{array}\right];$$
$${B}_{b}\left({x}_{1},{x}_{2},{x}_{3}\right)=\left[\begin{array}{c}0\\ 0\\ {B}_{b1}{B}_{b2}\end{array}\right];$$
$${B}_{b1}=\frac{{\beta }_{e}{A}_{2}{C}_{d}\omega {K}_{1}}{{V}_{tb}M}\sqrt{\frac{2{n}^{3}{P}_{s}}{\rho (1+{n}^{3})};}$$
$${B}_{b2}=sign({P}_{s}-{P}_{Lb})\sqrt{\left|\frac{{P}_{s}-{P}_{Lb}}{{P}_{s}}\right|;}$$
$${C}_{b}=\left[\begin{array}{ccc}1& 0& 0\end{array}\right];$$
$${d}_{b}\left({x}_{2},{x}_{3}\right)=\left[\begin{array}{c}0\\ 0\\ \frac{{\beta }_{e}{C}_{ieb}}{{V}_{tb}M}{F}_{l}+\frac{1}{M}\dot{{F}_{l}})\end{array}\right];$$

\({C}_{ieb}\)–Equivalent leakage coefficient when piston moves backward;

\({V}_{tb}\)–Effective volume when piston moves backward;

\(A_{2}\)–Piston effective area with rod cavity.

Combing eqs. (5–8), the general state space model of asymmetric hydraulic cylinder is obtained.

$$\dot{x}=Ax+B({x}_{1},{x}_{2},{x}_{3})u+d({x}_{2},{x}_{3})$$
(9)
$$y=Cx$$
(10)

where.

$$A={g}_{f}\left(u\right){A}_{f}+{g}_{b}\left(u\right){A}_{b};$$
$$B\left({x}_{1},{x}_{2},{x}_{3}\right)={g}_{f}\left(u\right){B}_{f}\left({x}_{1},{x}_{2},{x}_{3}\right)+{g}_{b}\left(u\right){B}_{b}\left({x}_{1},{x}_{2},{x}_{3}\right);$$
$$C=\left[\begin{array}{ccc}1& 0& 0\end{array}\right];$$
$$d\left({x}_{2},{x}_{3}\right)={g}_{f}\left(u\right){d}_{f}\left({x}_{2},{x}_{3}\right)+{g}_{b}\left(u\right){d}_{b}\left({x}_{2},{x}_{3}\right);$$
$${g}_{f}\left(\bullet \right)=\frac{1+sign\left(\bullet \right)}{2};$$
$${g}_{b}(\bullet )=\frac{1-sign(\bullet )}{2}$$

This is the general mathematical model of the DU when the hydraulic cylinder moves forward and backward.

In order to increase controller stability and decrease the nonlinear model complexity, the nonlinear feedback linearization method is used.

Set:

$$V={B}_{k2}({x}_{1},{x}_{2},{x}_{3})u+\frac{{{\varvec{d}}({x}_{2},{x}_{3})}_{(\text{3,1})}}{{B}_{k1}}$$
(11)

where.

$${B}_{k1}={g}_{f}\left(u\right){B}_{f1}+{g}_{b}\left(u\right){B}_{b1};$$
$${B}_{k2}\left({x}_{1},{x}_{2},{x}_{3}\right)={g}_{f}\left(u\right){B}_{f2}+{g}_{b}\left(u\right){B}_{b2};$$

\((\text{3,1})\)–The element in the third row and first column of the matrix.

Then:

$$\dot{x}=Ax+{B}_{k}V$$
(12)
$$y=Cx$$
(13)

where.

$${B}_{k}={\left[\begin{array}{ccc}0& 0& {B}_{k1}\end{array}\right]}^{T}.$$

This is the general mathematical model of the DU with nonlinear feedback term.

3 NMPC-FRDNNF Controller Design

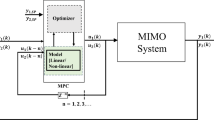
The hybrid controller primarily comprises three components: NMPC, FR, and DNNF, as illustrated in Fig. 4. Within NMPC, the nonlinear feedback term serves to streamline the model while encapsulating its nonlinear characteristics. FR plays a crucial role in adjusting parameters during the receding horizon optimization process. In the case of DNNF, the DNN is trained to approximate the inverse system using real-world data, encompassing disturbances and other factors.

Fig. 4
figure 4

Diagram of NMPC-FRDNNF controller

Full size image

3.1 NMPC Controller Design

According to eqs. (12–13), system states for the subsequent \({N}_{p}\) sample points are predicted as shown in the following equation:

$$\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {x\left( {k + 1|k} \right)} \\ {x\left( {k + 2|k} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {x\left( {k + N_{p} |k} \right)} \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{d}^{ } } \\ {A_{d}^{2} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {A_{d}^{{N_{p} }} } \\ \end{array} } \\ \end{array} } \right]x\left( k \right) + \left[ {\begin{array}{*{20}c} {B_{kd} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ {A_{d}^{{N_{p} - 1}} B_{kd} } & \cdots & {A_{d}^{{N_{p} - N_{c} }} B_{kd} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {V\left( k \right)} \\ {V\left( {k + 1} \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {V\left( {k + N_{c} - 1} \right)} \\ \end{array} } \\ \end{array} } \right]$$
(14)

where.

\({A}_{d}\), \({B}_{kd}\) are discrete forms of \(A\), \({B}_{k}\) respectively;

\({N}_{p}\)–Prediction horizon;

\({N}_{c}\)–Control horizon.

That is,

$$X=\Psi x\left(k\right)+\Phi V$$
(15)

Then, the control value can be obtained by solving the following optimization problem. The constraints in Eq. (16) are inequality constraints coming from the physical input constraint of system.

$$\genfrac{}{}{0pt}{}{\mathit{min}J={\left(\mathfrak{R}-X\right)}^{\text{T}}{Q}_{1}(\mathfrak{R}-X)+{\text{V}}^{\text{T}}{Q}_{2}\text{V}}{s.t. { S}_{1}V\le {S}_{2}}$$
(16)

where.

$$\Re = R\left[ {\begin{array}{*{20}c} 1 \\ \vdots \\ 1 \\ \end{array} } \right]_{{\left( {N_{p} \times 1} \right)}}$$

\(R\)–Reference signal;

\({Q}_{1}={\left[\begin{array}{ccc}{q}_{11}& \cdots & 0\\ \vdots & \ddots & \vdots \\ 0& \cdots & {q}_{1{N}_{p}}\end{array}\right]}_{({N}_{p}\times {N}_{p})}\)–Weight matrix of displacement, velocity and acceleration on the whole prediction horizon;

\({q}_{11}=\left[\begin{array}{ccc}{q}_{x}& 0& 0\\ 0& {q}_{v}& 0\\ 0& 0& {q}_{a}\end{array}\right]\)–Weight matrix on the first sample time, \({q}_{1{N}_{p}}\) is same as \({q}_{11}\);

\({q}_{x}\)–Displacement weight;

\({q}_{v}\)–Velocity weight;

\({q}_{a}\)–Acceleration weight;

\({Q}_{2}={\left[\begin{array}{ccc}{q}_{21}& \cdots & 0\\ \vdots & \ddots & \vdots \\ 0& \cdots & {q}_{2{N}_{c}}\end{array}\right]}_{({N}_{c}\times {N}_{c})}\)–Weight matrix of control value on the whole control horizon;

\({q}_{21}={q}_{u}\)–Control value weight on the first sample time, \({q}_{2{N}_{c}}\) is same as \({q}_{21}\);

$${S}_{1}={\left[\begin{array}{c}I\\ -I\end{array}\right]}_{({2N}_{c}\times {N}_{c})};$$
$${S}_{2}={\left[\begin{array}{c}{C}_{2}\\ -{C}_{1}\end{array}\right]}_{({2N}_{c}\times 1)};$$
$${C}_{1}=\left(-{B}_{k2}({x}_{1},{x}_{2},{x}_{3})+\frac{{d\left({x}_{2},{x}_{3}\right)}_{\left(\text{3,1}\right)}}{{B}_{k1}}\right){\left[\begin{array}{c}1\\ \vdots \\ 1\end{array}\right]}_{({N}_{c}\times 1)};$$
$${C}_{2}=\left({B}_{k2}({x}_{1},{x}_{2},{x}_{3})+\frac{{d\left({x}_{2},{x}_{3}\right)}_{\left(\text{3,1}\right)}}{{B}_{k1}}\right){\left[\begin{array}{c}1\\ \vdots \\ 1\end{array}\right]}_{({N}_{c}\times 1)}.$$

By the substitution of Eq. (15) into Eq. (16), the following optimization equation is obtained:

$$\genfrac{}{}{0pt}{}{\mathit{min}J={V}^{\text{T}}EV+2{V}^{\text{T}}F}{s.t. { S}_{1}V\le {S}_{2}}$$
(17)

Where.

$$E={\Phi }^{T}{Q}_{1}\Phi +{Q}_{2};$$
$$F={\Phi }^{T}{Q}_{1}\Psi x\left(k\right)-{\Phi }^{T}{Q}_{1}\mathfrak{R}.$$

After solving the Eq. (17), the input control signal is obtained as follows:

$$u=\frac{\left({V}_{\left(\text{1,1}\right)}-\frac{{d\left({x}_{2},{x}_{3}\right)}_{\left(\text{3,1}\right)}}{{B}_{k1}}\right)}{{B}_{k2}\left({x}_{1},{x}_{2},{x}_{3}\right)}$$
(18)

The approach can ascertain the stability of the closed-loop control system, and its stability can be substantiated through the application of the Lyapunov method [40].

3.2 FR Design

In Sect.  3.1, the parameters \({{\varvec{Q}}}_{1}\) and \({{\varvec{Q}}}_{2}\) significantly influence the optimization outcome of Eq. (17). A high value for \({{\varvec{Q}}}_{1}\) or a low value for \({{\varvec{Q}}}_{2}\) can result in oscillations around the reference signal. Conversely, a low \({{\varvec{Q}}}_{1}\) or a high \({{\varvec{Q}}}_{2}\) may lead to suboptimal control effects, requiring an extended duration to bring the system to the reference signal. In this study, a two-dimensional FR is employed to generate optimal weights, striking a balance between response speed and system oscillation. The input variables consist of the absolute value of the error and the differential of the absolute value of the error. The output variables are denoted as \(\Delta {q}_{x}\) and \(\Delta {q}_{u}\). The absolute value of error is classified as {Z, B} and the differential of absolute value of error is classified as {P}. Both \(\Delta {q}_{x}\) and \(\Delta {q}_{u}\) fall under the category of {Z, B}. The fuzzy field of absolute value of error is [0,0.01]; The fuzzy field of the differential of absolute value of error is [-0.01,0.01]; The range for \(\Delta {q}_{x}\) and \(\Delta {q}_{u}\) is [0,1]. The membership functions employed are Z and S types as shown in Fig. 5. The fuzzy diagram contains fuzzy rules is shown in Fig. 6. The centroid defuzzification method is used in FR as shown in Eq. (19). Finally, the \({q}_{x}\) and \({q}_{u}\) can be obtained by eqs. (20) and (21).

Fig. 5
figure 5

Membership functions

Full size image
Fig. 6
figure 6

Fuzzy diagram

Full size image
$$\Delta q=\sum \frac{\mu (X)\bullet X}{\mu (X)}$$
(19)
$${q}_{x}={q}_{xmin}+\Delta {q}_{x}({q}_{xmax}-{q}_{xmin})$$
(20)
$${q}_{u}={q}_{umax}-\Delta {q}_{u}({q}_{umax}-{q}_{umin})$$
(21)

3.3 System DNN Inverse Model

The DNN inverse model comprises a total of i layers, consisting of i-2 hidden layers in addition to one input layer and one output layer, as depicted in Fig. 7. The number of neurons in each layer is denoted as \({N}_{i}\) (\(i\in {\mathbb{N}}^{+}\)). The input variable represents the difference between the displacement at the (i + 1)-th sample time and the displacement at the i-th sample time, which corresponds to the network output representing the system control value at the i-th sample time. In the hidden layer, the activation function is set as the sigmoid function, while in the output layer, it is set as the linear function. Due to noise present in actual data, a technique is employed in which the input layer incorporates multiple displacement difference data to mitigate the effect of noise during the training process. The DNN is trained using Bayesian regularization backpropagation in MATLAB. In the DNNF process, displacement information, including disturbances such as modeling errors, is input to the DNN inverse model. Subsequently, the output control value derived from the DNN inverse model, which suppresses the corresponding disturbances, is added to the control value calculated by the controller as supplementary feedforward. This addition aims to alleviate the impact of disturbances on the control system and enhance overall control performance.

Fig. 7
figure 7

Diagram of DNN inverse model

Full size image

4 Case Study

4.1 Simulation

To assess the control effectiveness of the hybrid controller, simulations were conducted using MATLAB/Simulink. Key simulation parameters are presented in Table 2 based on the experimental platform as shown in Fig. 8. The simulations are categorized into two parts (FR simulation and DNNF simulation): the FR simulation involves the comparison between NMPC, NMPC-FR, and PD controllers, while the DNNF simulation includes the comparison between NMPC, NMPC-DNNF, and PD controllers. The simulation platform for the comparison of various controllers employing FR is depicted in Fig. 9, and for DNNF in Fig. 10.

Table 2 Experimental platform key parameters in simulation/experiment
Full size table
Fig. 8
figure 8

Hydraulic system experimental platform

Full size image
Fig. 9
figure 9

Diagram of FR simulation platform for various controller comparison. 1-NMPC-FR controller; 2-NMPC controller; 3-PD controller; 4-Parameter initialization; 5-Reference signal; 6-Solver [41]

Full size image
Fig. 10
figure 10

Diagram of DNNF simulation platform for various controller comparison. 1-NMPC-DNNF controller; 2-NMPC controller; 3-PD controller; 4-Parameter initialization; 5-Reference signal; 6-Disturbances

Full size image

4.1.1 FR Simulation

In the FR simulation, the displacement responses with various controllers are illustrated in Fig. 11. The corresponding errors are depicted in Fig. 12. Table 3 presents the Root Mean Square Error (RMSE) values for various controllers. The parameters of the PD controller were tuned using the Ziegler-Nichols method.

Fig. 11
figure 11

Displacement responses of various controllers

Full size image
Fig. 12
figure 12

Displacement errors of various controllers

Full size image
Table 3 RMSE of various controllers (FR simulation)
Full size table

In the detailed figure presented in Fig. 11, it is observed that the system response reaches the reference signal with NMPC-FR at approximately 5.14 s, whereas the corresponding times for NMPC and PD are approximately 5.35 s and 5.96 s, respectively. These findings suggest that the response of NMPC-FR outpaces that of NMPC, while NMPC demonstrates a significantly quicker response compared to PD.

Based on the data provided in Fig. 12, the error range for NMPC-FR is observed to be − 4.70–5.33 mm, with a maximum error of 10.03 mm. Comparatively, for NMPC, the error range is − 8.38–7.45 mm, with a maximum error of 15.83 mm, while for PD, it spans from − 18.93–16.47 mm, with a maximum error of 35.40 mm. Notably, the maximum error of NMPC-FR exhibits a reduction of 36.6% in comparison to that of NMPC, while the maximum error of NMPC demonstrates a 55.3% decrease when compared to PD.

According to the data provided in Table 3, the RMSE value for NMPC-FR exhibits a reduction of 45.7% when compared to the NMPC controller. Furthermore, the RMSE of NMPC demonstrates a decrease of 54.7% in comparison to the PD controller. These findings affirm the effectiveness of the FR within the NMPC optimization process, highlighting its pivotal role in enhancing control performance.

4.1.2 DNNF Simulation

In the DNNF simulation, the displacement responses with various controllers are presented in Fig. 13, while the corresponding errors are depicted in Fig. 14. Table 4 provides the RMSE values for the various controllers.

Fig. 13
figure 13

Displacement responses of various controllers

Full size image
Fig. 14
figure 14

Displacement errors of various controllers

Full size image
Table 4 RMSE of various controllers (DNNF simulation)
Full size table

In Fig. 14, the findings reveal that the controller incorporating DNNF yields superior results in mitigating the effects of disturbances. Specifically, the maximum error of NMPC-DNNF is approximately 4.54 mm, whereas for NMPC and PD, the respective maximum errors are around 8.61 mm and 7.40 mm. Notably, the maximum error of NMPC-DNNF showcases a reduction of 47.3% compared to that of NMPC.

According to Table 4, the RMSE of NMPC-DNNF demonstrates a decrease of 49.7% in comparison to the NMPC controller. This simulation result emphasizes the efficacy of DNNF in minimizing errors under disturbance conditions, thereby affirming its significance in improving control performance.

4.2 Experiment

4.2.1 FR Experiment

The experiment is conducted utilizing the hydraulic system experiment platform depicted in Fig. 8. The experimental key parameters remain consistent with those presented in the simulation, as detailed in Table 2. The experimental platform key components are shown in Table 5. In line with Sect. 4.1.1, the FR experiment showcases displacement responses with various controllers in Fig. 15. The corresponding errors are illustrated in Fig. 16, and the RMSE values for the various controllers are provided in Table 6.

Table 5 Experimental platform key components
Full size table
Fig. 15
figure 15

Displacement responses of various controllers

Full size image
Fig. 16
figure 16

Displacement errors of various controllers

Full size image
Table 6 RMSE of various controllers (FR experiment)
Full size table

Similar to the findings from the FR simulation, it is evident that MPC-type algorithms, owing to their ability to predict system output and conduct receding horizon optimization in real-time, exhibit superior performance compared to the PD controller. Furthermore, with the real-time adjustment of controller parameters facilitated by FR, NMPC-FR demonstrates enhanced performance when compared to NMPC. This underscores the effectiveness of incorporating FR in improving the performance of the NMPC controller.

In the detailed figure presented in Fig. 15, it is observed that the system response reaches the reference signal with NMPC-FR at approximately 5.07 s, whereas the corresponding times for NMPC and PD are approximately 5.38 s and 5.68 s, respectively. These findings indicate that both NMPC-FR and NMPC controllers exhibit faster responses compared to the PD controller, thereby affirming the effectiveness of MPC-type algorithms in control applications.

Based on the data provided in Fig. 16, the error range for NMPC-FR is observed to be − 5.25–3.92 mm, with a maximum error of 9.17 mm. In comparison, for NMPC, the error range is − 7.89–5.69 mm, with a maximum error of 13.58 mm, while for PD, it spans from − 18.16–12.00 mm, with a maximum error of 30.16 mm. Remarkably, the maximum error of NMPC-FR exhibits a reduction of 32.5% in comparison to that of NMPC, while the maximum error of NMPC demonstrates a 55.0% decrease when compared to PD.

Furthermore, since the FR can dynamically regulate optimization parameters in real-time, the RMSE values for NMPC-FR decrease by 33.2% compared to the NMPC controller, as indicated in Table 6. Moreover, the RMSE of NMPC decreases by 55.1% in comparison with the PD controller. These results provide further evidence of the efficacy of FR in the NMPC optimization process.

4.2.2 DNNF Experiment

In the DNNF experiment, displacement responses with various controllers are depicted in Fig. 17, while the corresponding errors are illustrated in Fig. 18. Table 7 provides the RMSE values for the various controllers.

Fig. 17
figure 17

Displacement responses of various controllers

Full size image
Fig. 18
figure 18

Displacement errors of various controllers

Full size image
Table 7 RMSE of various controllers (DNNF experiment)
Full size table

Consistent with the results from the DNNF simulation, the DNNF experiment demonstrates that the DNNF term is effective in reducing errors caused by disturbances.

In Fig. 18, the maximum error of NMPC-DNNF is approximately 4.56 mm, whereas for NMPC and PD, the respective maximum errors are around 8.95 mm and 7.94 mm. Notably, the maximum error of NMPC-DNNF showcases a reduction of 49.1% compared to that of NMPC.

From Table 7, the RMSE of NMPC-DNNF decreases by 48.9% compared to the NMPC controller, providing further confirmation of the effectiveness of DNNF in minimizing errors under disturbance conditions.

5 Conclusion

This study focuses on achieving the high accuracy, stability, and efficient transportation of blankets using BCR. Considering the strengths and limitations of existing research, a hybrid NMPC algorithm was explored, leading to the proposal of a novel NMPC-FRDNNF controller. Initially, the nonlinear model of the DU of BCR was established using the physics-based method. To simplify the model without sacrificing nonlinear information, nonlinear feedback linearization was applied to create a model foundation for controller design. Subsequently, FR was introduced to adjust the weight matrices of receding horizon optimization, enhancing the precision of control outcomes. To address disturbances, the concept of an inverse model was introduced. In comparison to physics-based inverse models, data-based models are easier to construct and adept at representing the intricate relationship between system input and output. The inverse model, constructed using a DNN architecture, contributed to the compensation of disturbances. Then, the hybrid NMPC controller was then designed based on the amalgamation of these algorithms. Additionally, simulations and experiments were conducted to validate the control effectiveness. The experiment results indicated that the RMSE of the controller with FR decreased by 33.2% compared to the controller without FR. The RMSE of the controller with DNNF decreased by 48.9% compared to the controller without DNNF, affirming the significant improvement in control performance. In the end, the outcomes of the study offer valuable insights into motion control in the BCR. The findings serve as a theoretical foundation for future application of the blanket high-accuracy synchronization transportation.