1 Introduction

The research and development of energy-absorbing structures, which dissipate energy during impact or intense dynamic loading, is receiving an increasing attention for a wide array of applications, such as transportation, aerospace, and infrastructure [1, 2]. For instance, in automotive industry, crashworthiness is still a challenge [3], since impacts may occur in various directions and collision protection often implies less streamlined designs. Another common application focuses on the protection of mountain constructions and their inhabitants from rockfall destruction and eventual damage [4]. Personal protective devices like bicycle helmets, and bullet-proof jackets are other examples requiring high energy absorption capacity [5]. Protection is a key factor also in good preservation, storage, and shipping, for which crashworthiness is an essential target to pursue.

The escalating demand for energy absorbent structures, paired with the need for more efficient use of materials, has led to a wide range of designs in the form of porous sandwiches [6,7,8], honeycomb [6, 9,10,11], and foams [12,13,14,15]. Thin-walled multi-cell columns exhibit excellent mechanical properties and optimal energy absorption when subjected to axial compressive load [16,17,18,19]. Concerning standard honeycomb patterns, despite the possibility to implement hierarchical configurations with tunable mechanical properties, limitations arise when dealing with their high production costs, structural preparation barriers, and limited feasibility in large-scale industrial applications [10]. These criticalities are partially overcome by sandwich structures, the multi-layer design of which allows to distribute contact pressure, increasing the efficiency while offering a low weight [7]. Foams, characterized by a typically randomized cellular structure, have been also found attractive due to their high specific strength and stiffness provided by the porous arrangement [12, 13]. Among cellular materials, lattice structures, formed by regular repeating of unit cells, appear to have a unique potential in addressing the energy absorbance issue, especially thanks to Additive Manufacturing (AM) techniques [20]. As an example, varying the relative density across the lattice structures is a clever strategy in cellular structures to enhance energy absorption-to-weight ratio under compression [21,22,23]. They offer the opportunity of designing single-phase lattice architectures that can combine lightweight and energy absorption properties by a rational variation of porosity within the cellular architecture.

Although the mentioned strategies and structures have made great advances in energy absorption capacity, these arrangements are still not optimized. To achieve an even better performance, an ingenious solution is to learn how biological structures adjust their configurations to absorb energy without catastrophic failure [1, 24]. Lessons from nature could be as inspiring as they are puzzling: indeed, plants and animals offer an enormous range of promising but hierarchically complex structures with low density, high strength, and high energy absorption capacities that could inspire the design of novel lattice structures with remarkable energy absorption capacity [25]. For example, the pomelo fruit has a spongy layer that can dissipate energy of 80 J from free fall without visible outer damage of the peel [26]. Nut shells are also known to exhibit excellent impact and puncture resistance [27]. Passing to the animal world, a beetle forewing can dissipate an impacting puncture force higher than its fighting force, and thus play a vital role in shielding its hindwing and thorax [28]. The extremely high precision of the AM process has paved the way for the design of bionic thin-walled structures based on the beetle's front wing structure showing excellent energy absorption capability [29].

Mimicking crystal structures of natural solids have also shown an increased energy absorption capability with the introduction of hierarchical order in the lattices [30]. An additional hint derives from [22, 31, 32], where the investigated trabecular bone-inspired lattice configurations demonstrated an optimal balance between energy absorption and mass. In that case, the final application is a bicycle helmet, thought as a prominent substitute of the expanded polystyrene foams commonly used for personal protective devices. The advancement of AM and the versatility it offers in realization of complex geometrical shapes [33,34,35], inaccessible by traditional manufacturing schemes, has opened the doors to manufacturing of lightweight and strong cellular lattice structures with tailored properties. At the same time, AM offers an efficient use of material, high customization, and design flexibility. This flexibility has provided the treat for the “design to drive the shape”, opposed to the strategy of “manufacturing drives the shape”, common for the traditional manufacturing approaches.

In this study, we have attempted to blend the freedom of shape, offered by AM, with the biomimetic approach, to propose new lattice structures for energy absorbent applications. To this aim, we have combined multiple bio-inspirational sources for the design of lattice configurations. Periodic lattice structures are fabricated based on the designed unit cell geometries and studied using experimental tests. A finite element model was also developed to analyze the deformation mechanisms in representative designs. The effect of individual bio-inspired features has been evaluated on compressive response and the energy absorbance performance of the designed structures.

2 Materials and Methods

Various bio-inspired structures were reviewed regarding the structures’ topological features, their resistance to different loads, and compatibilities with available manufacturing processes. Accordingly, as described in detail in this section, a series of promising morphological characteristics were selected and combined in structural design of lattice structures. Two base topologies of lattice structures with variation of their geometrical aspects were fabricated and tested under compressive loading. For each unit cell, three variations of the original version were considered: the height was halved, doubled and the fillet radiuses were changed, to evaluate the effects of these design parameters on the mechanical performance, and thus the functionality of the structures.

2.1 Design and Development of Unit Cells

2.1.1 Unit Cell Inspiration

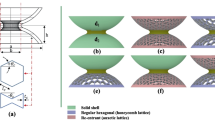
Among different biomimetic structures and natural principles, we exploit two elements that are the internal diaphragm of bamboo and honeycomb’s close-packing strategy as intelligent solutions to combine energy absorbance and lightweight design. This allows us to move from the nature to the engineering level, by isolating and adapting features of interest (transitional level) to reach the target goal (Fig. 1).

Fig. 1
figure 1

Transition from natue to engineering level, by isolating and adapting features of interest for anergy absorbance applications in the transitional level. a internal diaphragm of bamboo; b bee honeycomb representation; c non-convex multi corner tube with bulkheads; d closest packing arrangement; e 2D profile design based on honeycomb structure; f Burj Khalifa’s buttress core; g geometrical details of unit cell A and the corresponding variations of planar cross section; h geometrical details of unit cell B and the corresponding variations of planar cross sections

Full size image
2.1.1.1 Nodal Diaphragm of Bamboos

Bamboo is a giant woody grass composed of hollow culms, separated by nodes along its length; these are characterized by an internal diaphragm and an external ridge [36] (see Fig. 1a). The diaphragm is a fundamental feature as it enhances both the bending and compressive strength; it is reported to raise the transverse tensile strength of bamboo and prevent expanding and splitting. Experimental studies on the mechanical response of bamboo under dynamic loading indicated that its energy absorption ability is highly affected by the presence of nodal diaphragms [37]. That is why bamboo is able to effectively withstand severe environmental loads (gravity when considering its height, wind, and snow pressure), despite its remarkable slenderness ratio [38]. Multiple structures inspired by bamboo’s features are reported in the current research landscape; as an example, numerical analyses on a bionic thin-walled structure designed with a reinforcement rib inspired by bamboo plant (Fig. 1c) showed improved energy absorption capacity [37]. Another structure with bulkheads (Fig. 1c) inspired by the diaphragms in bamboo’s structure showed higher energy absorption compared to a similar column without the bulkhead feature. These studies suggest that the nodes themselves absorb a small amount of energy, but their presence mostly changes the expansion–contraction under compressive load to a progressive deformation [16].

2.1.1.2 Honeycomb’s Closest-Packing Principle

Another intelligent strategy of nature to enhance energy absorption capacity is the close-packing principle, that refers to the most tightly packed or space-efficient composition in several biological structures. Perhaps the most familiar and sublime example of closest packing in nature is the bee honeycomb (Fig. 1b); it is designed to contain the highest quantity of honey within the least amount of beeswax; in addition, the construction of this structure requires the least effort and energy for the bees [39]. Triangular structures (Fig. 1d) or eventual compositions of them (Fig. 1e) offer the most closely packed and geometrically stable configuration observed in the three-dimensional arrangement of polyhedral cells in biological systems; this packing style is also noted in the dense arrangement of atoms in the structure of certain metals. The principle of closest packing could be efficiently translated to engineered configurations and it is equivalent to that of triangulation, exploited regardless the scale or material, with the same energetically conservative effect. For instance, when stacking cylinders of equal diameter, their natural tendency is to arrange themselves in a triangular arrangement, as it is simply the one that requires the least effort to maintain stability, thus also called the minimum-energy configuration or the minimum-resource state. Inspired by this principle, the profile highlighted in Fig. 1f is exploited for the generation of unit cells suggested in this study.

2.1.2 Unit Cell Design

The two elements described in Sect. 2.1.1 are incorporated to design two functional unit cells (Fig. 1g and h). The shape and dimensions of the unit cells are defined considering practical limitations of Fused Deposition Modeling (FDM), the AM technique used in the present work. Mainly, a dimensional constraint is set to limit the minimum thickness of each element to 0.65 mm. The shape generated for the unit cell is modeled by means of the SolidWorks 2020 software.

2.1.2.1 Unit Cell A

This unit cell (Fig. 1g) is constructed by first defining its base 2D profile. In view of reproducing the packing arrangement, the geometrical construction of the profile is based on an equilateral triangle fit in a circle, where the medians of the angles meet in the center; these three segments are used to generate the 2D profile, as shown in Fig. 2b. The 3D shape is then constructed by considering two planes with a distance of 6 mm, set as the height of the unit cell. The profile designed on the base plane is rotated by 60° on the top plane. These two planes are connected through a loft transition inducing gradual variation of the planar cross section, as illustrated in Fig. 1g; for instance, when cutting the unit cell in half, the cross section exhibits the form of a solid hexagram (the third image from left in Fig. 1g); this section represents the nodal diaphragm of the unit cell that is planned to improve the load-bearing capacity by taking inspiration from the bamboo structure. As the last step, the corners are filleted to avoid critical contact sites and sharp corners that are not easily printable and could also constitute possible issues for numerical analysis and stress concentration in experimental tests; in addition, an extrusion of 1 mm with constant section is added on the top and bottom profiles to facilitate the generation of the honeycomb packing arrangement.

Fig. 2
figure 2

Lattice structure generation: the letter refers to the lattice structure type (A or B), the first number corresponds to the unit cell height and the second number to the fillet radius. a BLS A and its geometrical characteristics; b BLS B and its geometrical characteristics; c representative views of 3D printed specimens for both designs

Full size image
2.1.2.2 Unit Cell B

This unit cell (Fig. 1h) starts from a 2D generating profile inspired by Burj Khalifa skyscraper buttress core (Dubai, UAE), which, in turn, takes inspiration from the structure of Hymenocallis, a desert flower. Owing to the building significant height (~ 830 m), wind is one of the biggest structural design challenges. To address this, a triangular outline is introduced to enhance the skyscraper stability against winds; the buttress core consists in a strong central hub that plays an essential role in endowing torsional strength; the core is connected to three building wings that provide stiffness toward wind and earthquake’s horizontal actions. As each wing is supported by the other two via the six-sided central core, the stability of the structure is greatly enhanced (Fig. 1h). This system is effective to resist both lateral loads and gravity [38]. Also for this design, the profiles are connected through a loft transition to obtain the nodal diaphragm feature by inducing gradual variation of the planar cross section (Fig. 1h). The loft is applied twisting the structure similar to what observed in the DNA structure where the intertwined helices are decisive for the compression-twisting coupling deformation mode [40]. Compared to the unit cell A, which is planned to improve the compressive and bending strength, unit cell B may have the additional capacity to resist torsional load, although it is not the focus of the current study.

2.2 From the Unit Cell to the Lattice Structure

The final uniform Bio-inspired Lattice Structures (BLS), namely BLS A (Fig. 2a) and BLS B (Fig. 2b), were generated by assembling five unit cells in vertical and horizontal directions to create a cube of 30 mm per edge. To evaluate the effect of geometrical features on the mechanical response of the lattice structure, for each unit cell, three variations of the original version were considered. The geometrical variables were the height and the fillet radius. A comparable porosity was maintained among all designs, ranging from 46 to 48% for BLS A and from 55 to 57% for BLS B. Porosity is defined as the percentage of the void volume in solid material calculated according to Eq. 1:

$$\mathrm{Porosity}\left(\mathrm{\%}\right)=\frac{\mathrm{Vvoid}}{\mathrm{ Vtotal}}\times 100=\frac{\mathrm{Vtotal}-\mathrm{Vsolid}}{\mathrm{Vtotal}}\times 100$$
(1)

where Vtotal is the volume of the box enclosing the lattice structure, Vvoid is the void volume within the enclosing box and Vsolid is the volume of the solid in the lattice structure, obtained from CAD models. Detailed information on all suggested structures is presented in Fig. 2a, b.

2.3 Specimen Preparation and Experimental Tests

The specimens (shown in Fig. 2c) were printed by an Original Prusa i3 MK3 printer using 3D Net PLA black filament of 1.75 mm diameter. To obtain the printed PLA’s material properties, tensile tests were carried out on dog-bone specimens of 3 mm thickness following ASTM D638 standard. The tests were conducted on a MTS Criterion C42 electromechanical system at a displacement rate of 2 mm/min at room temperature. The detailed printing process parameters are listed in Table 1, while mechanical properties of the base material determined from the tensile tests are presented in Table 2.

Table 1 Process parameters used for fabricating the specimens
Full size table
Table 2 Mechanical properties calculated based on standard ASTM D638 specimen
Full size table

It is worth mentioning that standard dog-bone specimens were fabricated via a horizontal orientation with the broadest dimension against the building platform. The purpose of performing tensile tests is to obtain the mechanical properties such as elastic modulus and Poisson’s ratio that can be used for the numerical simulation of experimental compressive behavior. In addition, identical printing process parameters were used for both tensile and lattice samples during fabrication.

Lattice structures were tested under quasi-static compressive tests conducted on MTS Alliance RF150 System at room temperature, following the ISO 604 standard. Maximum displacement and crosshead velocity were set to 15 mm and 2 mm/min, respectively. An extensometer was used to measure the actual displacement on the specimens during the test. To guarantee the accuracy and reproducibility of the experimental results, three specimens were tested for each lattice geometry. The differences in the compressive response of the BLSs were also visually monitored during the experimental tests. Concerning the analysis of compressive response, stress values were determined by dividing the compression load by the nominal area of the contacting surface. Strain was computed according to the actual displacement under compression divided by the original height of the specimen. In addition, the Young’s modulus (E) was calculated as the slope of the stress–strain curve in the linear deformation region (strain range from 0–0.2). Yield stress σy was computed as the intersection between the compressive stress–strain curve and the 0.2% offset line parallel to the elastic region. The Initial Peak of Crushing Force (IPCF) was estimated as the compressive stress corresponding to the first local maximum in the stress–strain curve. Finally the Energy Absorption (EA) capacity during compression was calculated by integrating the area under the stress–strain curve from 0 to εd, where εd is the densification strain; i.e., when the strain reaches εd, the cellular material is completely compacted, causing a steep increase in the slope of the stress–strain curve.

2.4 Numerical Simulations

To reveal the deformation and failure mode and precisely locate stress concentration sites in the lattice structures, the compressive behavior of few representative designs was simulated in Abaqus CAE, 2017. To reduce the computational cost, time scaling method was considered implementing a constant vertical velocity of 2 m/s to the upper face of the lattice, while all the degrees of freedom were blocked on the bottom face. An elastic perfectly plastic material model was defined based on experimental tensile tests performed on dog-bone specimens (see Table 2). The maximum displacement that was imposed in the numerical model was 2% of the height of the structures.

For meshing, shrink wrap method was adopted in Hypermesh 2019 software; it is particularly suitable for complex geometries such as lattice structures, since this approach can recognize the three-dimensional topology and generates an adaptive mesh around it. After conducting a mesh convergence analysis, the mesh size was set as 0.25 mm using a second-order modified tetrahedral elements (C3D10M); the total average number of elements in the analyses was 5,150,034.

3 Results and Discussion

3.1 Experimental Results

The compressive stress–strain curve of the cellular structure can be effectively simplified into three regimes: the linear elastic regime, the plateau regime, and the densification regime. For many types of cellular structures, the plateau regime starts from the crushing strain, εy, or crush stress, σy, representing a change in the deformation mechanism of the cell wall or the cell wall failure, and ends at a critical strain, εcd, representing the onset of densification. After this point, upon further compression, more cell walls start to come into contact. Ultimately, the cellular material is completely compacted when the strain reaches a full densification strain, εd, when the cell walls jam together, causing a steep increase in the slope of the stress–strain curve [41].

3.1.1 Lattices from Design A and B Categories

Representative stress–strain curves obtained from the compression tests on BLS A and B are illustrated in Fig. 3, and the corresponding mechanical properties are reported in Table 3. The tests showed good repeatability per each geometry as shown by the shadowed area around the curves in Fig. 3 and listed values in Tables 5, 6, 7, 8, 9, 10, 11, and 12 in the Appendix. Snapshots of the deformation states of the lattice structures under compression in a strain range of 0 to 50% are presented in Fig. 4.

Fig. 3
figure 3

Stress–strain curves of quasi-static compression tests for a all the structures belonging to BLS A and b BLS B

Full size image
Table 3 Mechanical properties extracted from the compression tests for different geometries of BLS A and BLS B
Full size table
Fig. 4
figure 4

Snapshots of lattice structures under compressive loading at progressively increasing strain levels a A-6-0.5, b A-3-0.5, c A-12-0.5, d A-6-0.75, e B-6-2.5, f B-3-2.5, g B-12-2.5 and h B-6-5 (all loaded from 0 to 50% strain) (white arrows refer to local change of color from black to off-white as a sign of local degradation in the polymeric material)

Full size image

In Fig. 3, the connection regions (i.e., filleted corners) between the unit cells were identified as the critical sites where failure occurred for both BLS A and BLS B. This translates into critical elbow points visible in Fig. 3; an in-depth analysis is reported for each configuration. As it can be observed in Fig. 3a, the initial peak crushing force was reached with a strain around 0.1 for lattice BLS A-6-0.5. At this point, the lattice withstood the load without displaying visible cracks within the structure; however, signs of material degradation, represented by local color lightening, was detected around the boundaries of the unit cells (Fig. 4a), confirming the initiation of plastic deformation in these regions. By increasing the applied displacement up to 0.15 strain, cracks initiated from these areas and extended by the gradual increase of strain. The majority of the damage in specimen BLS A-6-0.5 occurred in the mid height of the specimen, away from the contact surfaces. Finally, at around strain of 0.25, the structure was considerably damaged and unit cells failed prior to densification. Similar compression behaviors were observed within other specimens of the BLS A category (BLS A-3-0.5, BLS A-12-0.5 and BLS A-6-0.75); however, at the peak load, visible damage, cracks, and densification occurred at slightly different strains, as design parameters were varied. When unit cell height was reduced (BLS A-3-0.5), the appearance of the cracks within the lattice structure was less noticeable and a general global plastic failure was perceived to be dominant. This structure represented a plateau of nearly constant stress (equal to the crush stress) until the strain of about 0.25. On the contrary, in BLS A-12-0.5 specimen with height aspect ratio of 4, the appearance and propagation of the cracks between the two layers with an opening angle (in the mid height) was the most dominant cause of failure. This resulted in a more local collapse in that specific layer with a limited plastic deformation in the rest of the structure. In this case, the higher crushing stress compared to the previous two designs was followed by a steep drop in the stress carried by the structure, showing an unstable failure mode.

As concerns the lattice structure BLS B-6-2.5 illustrated in Fig. 4e, the elastic stage of the structure ended approximately at a strain of 0.02 (Fig. 3a). The initial damage started at the strain of 0.1 followed by the splitting and fracturing of the second to fourth layers, while the first layer maintained its integrity. Similar compression behaviors were also observed with other structures of BLS B category.

The main parameter that was changed between the specimens within the same group was the unit cell height, and thus the aspect ratio. In general, regardless the base unit cell design, the experimental results revealed a high degree of association between the height of the unit cells and their mechanical properties. Lattice structures with higher unit cell heights exhibited higher Young’s modulus, yield stress, and IPCF under the same fillet radius. Furthermore, more variations between the peak and valley of the curves could be observed when the height of unit cells increased. A potential reason could be the fact that the lattice structures with smaller unit cell height experienced more global failure patterns under compression as illustrated in Fig. 4b, f, while the shorter unit cells experienced more local failure patterns such as buckling on the struts, as illustrated in Fig. 4c, g for both designs. In addition, in the case of BLS A, the specimens with the smallest unit cell height had the tendency to show improved resistance (without splitting) under compressive when compared with the same porosity for the same strain values of 0.3.

As for the energy absorption capacity, the experimental results indicated slightly higher EA for BLS A-6–0.5 compared to BLS A-3-0.5 (205.6 ± 21.8 J compared to 203.6 ± 7.09 J). However, a significantly lower energy absorption was obtained for BLS A-12-0.5 compared to BLS A-6-0.5 and BLSA-3-0.5, due to the fact that the stress dropped substantially in these specimens just after buckling occurred, as can be highlighted in Fig. 3.

As a core issue, it can be pointed out that the contact parts between unit cells were found to be the critical regions for compression resistance. Therefore, for future designs, it is recommended that the shape of the unit cell is tuned to increase the quantity of material in the connecting part to improve the compression resistance. More in depth, it is preferable to enhance the contact zone between the layers of unit cells when they are vertically packed.

In addition, by analyzing the unit cell shape (as illustrated in Fig. 5a), it is possible to see that on the top and bottom of the cell, there is a vertical extrusion that allows the unit cells to be in contact with the grips for loading. From that point, the extruded profile is lofted to generate the central part of the cell. We deduce that, the sudden change of cross section deriving from the extrusion to the loft, could have made the structure weaker at those points.

Fig. 5
figure 5

a Detail of the profile extrusion for the unit cell of Design A, b unit cell profile of (I) B-6-2.5 and (II) B-6–5

Full size image

Regarding energy absorption, the energy absorption capacity for BLS B-6-2.5 was almost the same as BLS B-3-2.5 (120 ± 4 J for BLS B-6-2.5 compared to 117.3 ± 8.3 J for BLS B-3-2.5). In addition, the value of energy absorption for BLS B-12-2.5 was even less than half that of BLS B-6-2.5 and BLS B-3-2.5 since stresses dropped significantly faster for B-12-2.5 after buckling.

Comparing two lattice structures with the same unit cell height but different fillet radius i.e., BLS A-6-0.5 and BLS A-6-0.75, interestingly both structures showed almost identical energy absorption capacities (205.6 ± 21.8 J for BLS A-6-0.5 and 205.6 ± 28.5 J for BLS A-6-0.75), while the initial peak force for BLS A-6–0.75 was slightly higher than that for BLS A-6-0.5. Furthermore, it was observed that fewer nodes were damaged for the structures with larger fillet radius at the same strain of 0.2 under compression, as illustrated in Fig. 4a, d, which indicated that BLS A-6-0.75 had a slightly higher compression resistance compared to BLS A-6-0.5.

On the contrary, BLS B category demonstrated different behaviors when comparing the geometries of BLS B-6-2.5 and BLS B-6-5 with different fillet radius. The experimental results revealed that more joints failed in the structure with larger fillet radius at the strain of 0.1, as observed in Fig. 4e and Fig. 4h, indicating that BLS B-6-2.5 had a slightly higher compression resistance than BLS B-6-5. In addition, unlike the lattice structures of BLS A-6-0.5 and BLS A-6-0.75, the BLSs with smaller fillet radius exhibited higher energy capacities (120 ± 4 J for BLS B-6-2.5 and 86.3 ± 18.5 for BLS B-6-5). BLS B-6-5 showed lower εd than BLS B-5-2.5 due to the fact that the core became larger by increasing the fillets when compared to the wings, as illustrated in Fig. 5b. The experimental results indicated that BLS B-6-5 was less suitable for compression. This could be partially attributed to the fact that local stress was more concentrated at the connecting points of the unit cells and the structure itself was not capable of adequately resisting axial compression.

3.1.2 Comparisons Between Design A and Design B

The main difference between the two designed configurations of BLS A and BLS B is the way the lofted profile was generated for each design; this results in different critical elbow points, as reported in Fig. 3. The profile in A category has a more ‘stable and balanced’ design while the unit cell B is composed of a larger core and three slenderer wings. This generates opposite effects on lattice structures when increasing the fillet radius. For the lattice structures of Design A, increasing the fillet radius slightly increased the compression resistance, although the critical site where failure occurred remained the connecting points between the unit cells. However, the trend was different in the case of Design B. The BLS B structure exhibited a lower compression resistance since its three wings were excessively narrow at the point where the unit cells were connected. The criticality of the connection points between the unit cell for BLS B design is illustrated in Fig. 6, showing BLS B-12-2.5 specimen as a representative case.

Fig. 6
figure 6

B-12-2.5 unit cell packing and collapse during the quasi-static compressive test

Full size image

Thus, the lofted profile from the Design B category is found less ideal for compression but may have the potential to be considered for a possible torsion application instead [42]. It was also noticed that all the BLS B specimens displayed relatively lower resistance to compression compared to the BLS A category. This can be partially attributed to the slightly higher porosity in this design (47.5% for BLS A vs. 56.5% for BLS B), which directly influences the load carrying capacity of the lattice structures [43]. Comparisons of mechanical properties for all specimens are presented in Fig. 7.

Fig. 7
figure 7

Comparing the mechanical properties of all studied lattice structure in terms of a yield stress, b young’s modulus, c energy absorption capacity and d IPCF

Full size image

The results confirm that the features of the nodes or diaphragms inspired by bamboo structures successfully increased the compression resistance of the structures, as clearly identified in lattice BLS A-12-0.5 or BLS B-12-2.5. As a matter of fact, it can be noticed in Fig. 4 that the bottom sides are characterized by the bamboo’s diaphragm feature, that effectively allowed the last layer of the unit cell to remain intact during the compression tests, limiting cell expansion and splitting. This is linked to the number of unit cells per height that influences the compactness of the configuration during compression tests.

3.2 Stress Analysis

With the purpose of localizing the regions characterized by stress intensification, a numerical campaign was conducted on few representative lattice configurations. BLS B-12-2.5 was specifically considered for model validation as among all the designed geometries it led to lower computational costs. Furthermore, the original structures without parameter variations BLS A-6-0.5 and BLS B-6-2.5 were selected as representative structures form BLS A and BLS B categories, respectively.

Figure 8 illustrates the von-Mises stress contours of the analyzed structures in the elastic deformation region under 2% strain. According to the numerical analyses, the highly stressed regions in the lattice structures were located at the joint sections between the unit cells with a maximum stress value of 53.41 MPa for all the analyzed designs; this value corresponds to the yield stress of the base material. Stress concentration in joints is showing an increasing trend by the increase of the unit cell height, representing a more critical stress state. Furthermore, the von-Mises stress distributions at different strains from 0 to 2% for BLS A-6-0.5, BLS B-5-2.5, and BLS B-12-2.5 models are presented in Fig. 9. The numerical results revealed higher values of elastic modulus, yield stress, and compressive strength for lattice BLS A-6-0.5 compared to BLS B-6-2.5, while plastic deformation for both lattice structures started at a strain of almost 0.2. The higher yield stress of BLS A could be correlated to its lower porosity, which would result in larger effective area that carried the applied load. Besides, the lower number of stress concentration sites (reaching the yielding) in this model as a result of smoother critical areas compared to BLS B, improved its performance under compressive load.

Fig. 8
figure 8

Stress distribution showing stress intensification sites at unit cell connection points of a A-6-0.5, b B-6-2.5 and c B-12-2.5

Full size image
Fig. 9
figure 9

Von-Mises stress distributions at different strains from 0 to 2% for a A-6-0.5, b B-6-2.5, and c B-12-2.5

Full size image

3.3 Comparison Between Experimental and Numerical Results

Figure 10 compares the numerical and experimental stress–strain curves for A-6-0.5 and B-6-2.5a and a comparison of the respective mechanical properties is presented in Table 4.

Fig. 10
figure 10

Comparison between the numerical and experimental results for a A-6-0.5, and b B-6-2.5

Full size image
Table 4 Mechanical properties extracted from the finite element analysis
Full size table

The yield strains computed from the numerical analyses are similar to the values obtained in the experiments (approximately 0.02), while the numerical yield stresses are higher than the experimentally measured values: 24 MPa for BLS A-6-0.5 compared to the experimental result of 19 ± 1 MPa, and 19 MPa for BLS B-6-2.5 compared to the experimental data of 15.6 ± 0.5 MPa. Moreover, the slope of the elastic stage is higher than the experimental results; for BLS A-6-0.5, the numerical analysis showed a Young’s modulus of 1280 MPa compared to 913 ± 113 MPa measured from the experiments and in the case of BLS B-6-2.5, the numerically estimated value was 1105 MPa compared to experimentally measured modulus of 775.6 ± 30 MPa. We have postulated three key reasons for this discrepancy: the material model definition, surface roughness and geometrical deviation, and the possible internal defects. The considered material model, indeed, neglects the anisotropy caused by the manufacturing process that can lead to anisotropic material response in the specimen [44].

Besides, structures fabricated by FDM technique commonly present several surface and internal defects, which can be related to the used filament, the 3D printing parameters, and the geometric details. These geometrical deviations, surface roughness, and internal defects may lead to reduced stiffness, especially in structures comprising relatively thin members; in this case, the adverse effect of geometrical irregularities in reducing the load-bearing cross section can be more critical. Since the numerical models are considering the ideal designed geometry, they overestimate the performance of the specimens compared to the experimental data. Despite this discrepancy, the numerical models have a notable potential to estimate stress distributions and localize intensifications in the designed lattice structure.

4 Conclusion

Two bio-inspired lattice structures were designed implementing specific elements to enhance their energy absorption properties. The mechanical performance of the specimens fabricated via fused deposition modeling process was tested under compressive loading. Different design features such as nodal diaphragm, height/width ratio of the unit cells, and the fillet radius were varied to evaluate their impact on the structure’s mechanical performance. Finite element models were developed to evaluate the stress distribution within the lattices and define critical locations with intensified stress under compressive loading. According to the obtained results, the bamboo inspired design represented effective resistance against compression confirming the initial hypothesis made on the morphological element that was inspired by the diaphragm in bamboo’s structure. The connection point between individual unit cells was found to be a critical site, highly affecting the overall performance of the structures. The results indicate that by varying the design parameters, a tuning between the strength and energy absorption can be obtained, paving the way for metamaterial transition within a wide range of real-life applications. Further studies are required to optimize the mechanical performance of the proposed lattices by systematically evaluating the effect of individual geometrical features also under other loading conditions.