1 Introduction

Flight gives an animal a very potent predator-escape route, and the privilege to reach remote or for non-flying animals inaccessible locations [1]. Through the evolution over millions of years, remarkable flight abilities have developed with complex modes of locomotion [2]. The evolution of aerial locomotion was accompanied by the acquisition of anatomical and physiological adaptations in flapping flying [3,4,5]. The adaptions in birds include the fusion of parts of the skeleton, the pneumaticity of bones, and equipment of wings with strong yet lightweight feathers [6].

Bird wings consist of arm and hand parts that can be easily stretched and folded [7]. Primary flight feathers are attached to the metacarpal and phalangeal bones [8]. The balance between the robustness, flexibility, and lightweight properties of the feathers is supposed to be the result of specific materials and the particular organization of their macro-, micro-, and nanostructures [9]. Feathers of recent birds have evolved from simple keratinous filaments to fascinating outer coverings and complex epidermal structures of varying lengths and diameters [10,11,12,13].

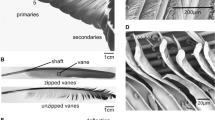
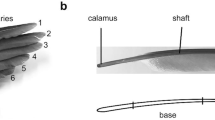
Typical flight feathers consist of a shaft and asymmetrical vanes on two sides. The shaft is composed of a rigid outer cortex and the inner foam-like medulla [14]. The vanes consist of numerous barbs oriented in parallel but at some angle to the shaft [15]. The architecture of the vanes is linked with advancements in aerial locomotion during evolution [16]. The microstructure of goose vanes was first observed by Hooke [17], and two types of barbules were described by Ennos et al. [18]. The barbules on the distal barb with hooks interlock with grooves situated on the proximal barbules of the next barb (Fig. 1). The mechanism of interlocking of the barbs, its ease of reestablishment after separation, and the separation forces of hooklets have been experimentally studied by Kovalev et al. [19] and finally summarized in a dynamical mathematical model. The robustness and flaw-tolerance of the interlocking barbs have been explained using an analytical model based on small- and large-beam deflections by Chen et al. [20].

Fig. 1
figure 1

Morphology of the primary flight feathers (PFF). a The wing of the pigeon, with spread (upper image) and folded (lower image) primaries. b The primary feather is composed of the main shaft and vanes (No. 1 PFF). c Barbs of the vane branch from the shaft, and barbules branch from barbs. d Hooklets at the tip of distal barbules interlock with the proximal barbules on the neighboring barbs

Full size image

During the flight, wings undergo continuous vibrations [21]. At a particular orientation, a feather becomes a driven oscillator when air velocity exceeds a threshold [22]. Unwanted vibrations can influence flight stability and make noise, as have been previously studied in other flying animals [23, 24]. Concerning the shaft, a damping ratio ranging from 0.015 to 0.035 has been revealed for the bending of swan feathers [25], while the damping ratio of shafts in pigeons has been estimated to be 0.448 ± 0.041 [26]. The loss factor of single pigeon primary feathers (0.1573, 0.093 vertically, and 0.0912, 0.0709 parallelly) and single barb (0.0790 vertically, and 0.1234 parallelly) [27]. The different shaft regions of the pigeon feathers under deflections were investigated, and graded damping properties from base to tip were found (from 0.268 to 0.034) [28].

The investigations of sound are also closely related to vibration. Sound classified as pressure waves is generated by vibrating structures that can induce the vibration [27]. In courtship display, peacock feathers perform the train-rattling using a range of vibration frequencies (22–28 Hz); higher damping of feathers broadens the resonant peaks and has the advantage of quickly damping out oscillations [29]. In addition to furnishing flight, the various acoustic communication functions are served by pressure waves when birds flap their wings [30]. The flag model was used to explain the fluttering and accompanying sound by the outermost tail feathers, that subtle changes in shape tune the produced sound frequency [31]. The distinctive flight sound is produced by wings in hummingbirds, enabled via morphological changes of primaries [32]. Male Club-winged Manakins produce tonal sound with specialized feathers, and the resonant properties were determined that the feathers exhibit unusually high Q-values [33]. The aeroacoustic behavior of hummingbird tail feathers that vary in shape over a range of air velocities in a wind tunnel was examined [12]. The communication sounds generated in the wing and tail are mainly attributable to three mechanisms: flutter, percussion, and wing whirring [22]. Aeroelastic flutter results from the dynamic coupling of aerodynamic forces with the feather’s geometry and stiffness to produce a limited cycle vibration of a feather [22]. Pigeons produce tonal sounds (700 ± 50 Hz) during the downstroke when a small region of long, curved barbs on the inner vane of the outermost primary flutters [34]. The modified feather P8 of crested pigeons produces a specific tonal sound that acts as an alarm sonation [35].

However, it remains unclear how different feather parts contribute to their damping properties. Despite the important aerodynamic function of the vanes, its damping significance in vibration lacks a systematic study. To support the feathers’ aerodynamic function, the vanes form an airfoil stabilized by the interlocked barbules, which may strongly contribute to the feather damping. We hypothesize that vanes help to enhance the damping of primary flight feathers. To examine the effects of vanes removal on feathers’ damping, in this study the underdamped vibrations (parallel and perpendicular to the vane plane) were studied on feathers with the vanes and bare shafts without the vanes. The role of the vanes in the damping behavior of feathers was quantified and analyzed in combination with their morphological characteristics.

2 Materials and methods

2.1 Morphological analysis

Outermost primary flight feathers (Nos. 1–5, Fig. 1) were taken from the wings of an adult male pigeon (Columba livia). They were imaged using an iPhone X camera (Apple, California, USA). A Scanning Electron Microscope (SEM) Hitachi S-4800 (Hitachi, Chiyoda, Japan) was used to examine the vanes microstructure. The middle section of the shaft and vanes were cut. The specimens were then mounted on a vertical SEM stub. SEM samples were coated with 8 nm gold–palladium using a sputter coater EM SCD500 (Leica, Wetzlar, Germany) before SEM observation and examined at an acceleration voltage of 3.0 kV.

2.2 Damping tests

In this study, damping tests were performed under room temperature of 18 °C–20 °C and humidity of 40–45%. The intact feather with the vanes was fixed horizontally at their calamus part in a micromanipulator. Feather vibrations were excited by vertical (perpendicular to the vanes) and horizontal (parallel to the vanes) step deflections (10 mm). Five flight feathers (Nos. 1–5) were tested under two deflection directions, repeated three times for each feather and each direction. Then the vanes were removed from the shaft of the feathers using a razor blade and the damping tests were repeated on the shafts without the vanes.

The feather vibrations were recorded using a digital high-speed video system (Olympus, I-Speed 3). The videos were recorded at a 1280 × 1024 pixels resolution, 3000 fps, and a shutter time of 0.667 µs. To facilitate tracking, the distal tips of feathers were marked with white markers point (compared to feather mass is low enough and can be ignored) before experiments. The video recordings were transformed into single-frame stacks in the JPG image format. The motion of the feather tip was analyzed using the image analysis software ImageJ (version 1.48; Wayne Rasband, National Institute of Health, USA.). The tracking positions of the tip (horizontal position, X and vertical position, Y) were determined using the MJTrack function (version 1.48; Wayne Rasband, National Institute of Health, USA), an ImageJ plugin for motion tracking in a single frame.

Fast Fourier Transformation (FFT) with the rectangular window was employed to obtain the natural frequencies of the feathers with the vanes and the shaft without the vanes using the software Origin (OriginLab, Massachusetts, USA). For visualization purposes, the first main fundamental frequency (vibration modes) of the feathers was separated using a bandpass filter.

The equation of under-damped vibrations was employed to define the vibrations of the first main frequency. The displacement (X) and the decay time (t) satisfy the under-damped condition with the following equation.

$$X=A{e}^{-\beta t}\mathrm{cos}\left(\omega t+\varphi \right),$$
(1)

where β is the damping coefficient, A is the initial amplitude, ω is the frequency, and φ is the phase angle. The damping coefficient β was obtained by the curve fitting with the frequency ω being gained earlier by FFT analysis. For statistics, two-way Analysis of Variance (ANOVA) was used for the damping data, including the Turkey test for multiple comparisons by the software SigmaPlot 12.0 (SPSS Inc, Chicago, USA). The damping ratios were normalized by rank cases using the software IBM SPSS Statistics 25 (SPSS Inc, Chicago, USA). To compare our results with those obtained in previous studies, the damping ratios ζ were calculated from the damping coefficient using the following equation

$$\zeta = \frac{\beta }{\omega }.$$
(2)

3 Results and discussion

3.1 Morphology

The arrangement of the primary feathers in the spread and the folded wing is shown in Fig. 1 a. In the primaries, the shaft is asymmetrically surrounded by the vanes on the two sides (Fig. 1b). In the vanes, barbs, barbules, and hooklets responsible for the integrity of the vanes are easily recognizable in the SEM images (Fig. 1c, d). The barbs are arranged at angles of approximately 30°–40°, decreasing from the base towards the tip. These branching angles are smaller at the leading edge in comparison to the trailing edge. Additionally, the barbs have asymmetrical and cambered cross-sections. The barbules can be divided into two types [18]: (i) the distal barbules, which branch out towards the tip and have hooklets on their underside, and (ii) the proximal barbules with rounded ridges on the upper side. The hooklets of the distal barbules overlap with the proximal barbules of adjacent barbs and keep them in parallel (Fig. 1d). Many of the outstanding properties of feathers are linked to this interlocking mechanism [16, 19, 26]. The uniformly overlapping barbules prevent an increase in the distance between the barbs and their separation. However, these overlapping structures allow for a decrease in the distance between the barbs during the compression in the vane plane. In vibrating feathers, this behavior of the overlapping barbs should potentially affect the damping behavior of the vanes in different deflection directions differently.

3.2 Damping behavior

Damping tests were conducted to investigate a possible difference in the damping behavior of the intact feathers with vanes and the shafts without vanes in two deflection directions, parallel, and perpendicular to the vanes. The shapes of the trajectories, excursion of amplitudes, and the directionality of the vibrations varied regarding with or without the feather vanes and deflection direction (Fig. 2). Compared to feathers with the vanes (Fig. 2a, b), the vibrations of the shafts without vanes have more complex trajectories (Fig. 2c, d).

Fig. 2
figure 2

Exemplary trajectories of the primary flight feather’s (no. 1) tip vibrations were observed perpendicular to the shaft. Feather with vane after a vertical and b horizontal excitation. Feather shaft without vane after c vertical and d horizontal excitation. The top-right icon indicates the feathers and the deflection direction

Full size image

The trajectories were further separated into the X and Y amplitudes by time (Fig. 3). Vibration amplitudes in the direction of their excitation continuously decreased from their maximum at the first oscillation. However, vibration amplitudes observed perpendicular to their excitation direction first increased. Compared to the intact feather, the vibrations of the shaft without vanes showed more harmonics and possible phase shifts. After removing the vanes, the varied vibrations may be due to the decreased mass, the changed stiffness distribution, and the asymmetric shape of the shaft.

Fig. 3
figure 3

Amplitudes of damped vibrations as a function of time. a, b X- and Y- vibrations of the feather with vane at vertical deflection; c, d X- and Y- vibrations of the feather with vane at horizontal deflection; e, f X- and Y- vibrations of the shaft without vane at vertical deflection; g, h X- and Y- vibrations of the shaft without vane at horizontal deflection

Full size image

The frequency spectra obtained by FFT of the X(t) and Y(t) curves are shown in Fig. 4. Although flat plates with a uniform cross-sectional area and constant elastic modulus have easily predicted orders of frequencies and mode shapes, it is difficult to apply these models that do not have uniform cross-section area or elastic moduli [36]. A related aspect of flutter in airflows was described that feathers may exhibit a dozen or more modes, and can abruptly switch from one mode to another [12]. To simplify the frequency analysis, the first main frequencies of the vibrations in horizontal (fx) and vertical (fy) directions (PFF1, Fig. 4) and summarized in Table 1. After trimming the vanes, the fundamental frequencies of the bare shaft increased by 51–70%.

Fig. 4
figure 4

Typical power spectra and natural frequencies of feather vibrations. a Frequencies of X- and Y- vibrations in the feather with vane at the vertical deflection; b Frequencies of X- and Y- in the feather with vane at the horizontal deflection; c Frequencies of X-, Y- in the shaft without vane at the vertical deflection; d Frequencies of X-, Y- in the shaft without vane at the horizontal deflection

Full size image
Table 1 First main frequencies of feathers at two deflection directions (n = 60)
Full size table

The feathers with vanes had significantly lower fundamental vibration frequencies f(x) and f(y) than the shafts without vanes (P < 0.001). Interestingly, the frequency f(x) of the vibrations in the shafts is significantly lower at vertical excitations than at horizontal excitation (P = 0.024). Reasons for this difference could be the influence of the zipped vanes plane. The excited vibrations perpendicular to the vanes will trigger the vibrations parallel to the vanes as driven vibrations or crosstalk because of the shaft twisting.

Summed up, the vibrations of the feathers with vanes decayed faster than those of the bare shafts. The loss of mass, different stiffness distribution and the increased air friction of the vanes may explain the increased frequencies of the shaft after trimming the vanes.

3.3 Damping ratio

Bird feathers are known to be coupled to vibration-sensitive nerves allowing birds to sense and respond to mechanical changes [37, 38]. Besides nerve and muscle control, the structure could also help. The developed serrations along the leading edges were investigated in different owl species [39]. And the specialized feather velvet in owls was confirmed to reduce the sound produced [40]. The damping significance of vanes was exhibited by damping ratios. The damping ratios were determined for the first natural vibration frequencies. In all preparations and excitation directions, the damping ratios of feathers with the vanes compared to those of shafts without the vanes were significantly higher (P < 0.001, n = 60) (Fig. 5). For feathers with vanes, the damping ratios for excitations parallel and perpendicular to the vanes also differed significantly (P = 0.010, n = 30). In the shafts without vanes, the damping ratios significantly differed only for vibrations perpendicular to the vane plane (P < 0.001, n = 30). Remarkably, in the feathers with vanes and the shafts without vanes, the damping ratio for vibrations perpendicular to the vane plane was the highest at vertical excitation. Compared to the intact feathers, the damping ratios are decreased by 38–60% after trimming the vanes. Possible damping mechanisms of the vanes are listed below.

Fig. 5
figure 5

Damping ratios of the feathers with vane (open bars) and the shafts without vane (hatched bars). ζx and ζy were calculated for vibrations in X (a parallel to the vane)- and Y (b perpendicular to the vane) directions. Here, the results are presented for two deflections. ‘NS’ means no significant difference

Full size image

I. Aerodynamic damping. During the flight, the feathers are practically air-impermeable by the pressure gradient in the overlapping inner and outer vanes [41]. Airflow may aerodynamically damp vibrations of an airfoil [42]. Wingbeat frequencies of the pigeon Columba livia were measured to be 6.5 ± 0.2 Hz in paired flight and 5.5 ± 0.2 Hz in solo flight [43]. In homing flights, the maximum airspeed of C. livia was 23.0 ms−1 with a mean value of 19.9 (± 2.6 s.d.) ms−1 [44]. At such high wingbeat frequencies and airspeeds, the air friction especially perpendicular to the vanes by beating wing will strongly affect the damping of feathers. In addition, the passive structure responses of flexible membranes with the flow could alter the aerodynamic characteristic of simple flat-plate wings confirmed [45], which makes the motion of zipped vanes surface result in an aerodynamic benefit.

II. Structural damping. At low speeds, structural damping is also a significant factor [46]. Under loading, the feather barbules and hooklets move, generating friction at these interfaces and bending, generating energy storage in structural deformations. At a certain load, the hooked anchoring separates, the energy stored in the structural deformation releases, and the vibration energy dissipates. The collective effect of neighboring barbs allows the accumulation of more elastic energy and, in this way, further enhances energy dissipation [19]. Vibrations excited perpendicular to the vanes can be effectively transferred to vibrations in the vane plane. Other mechanisms, which are not discussed in detail here, could be the vibrations transferred to the surrounding feathers and tissues (skin, bones).

III. Material damping. Material damping refers to inherent energy dissipation during material deformation [42]. The shaft and vanes elements of the feather are filled with a foam medulla, which was shown to effectively damp vibrations [28].

The interesting feature of the interlocking mechanism in the vanes not only increases the damping ratio but transfers the vibrations excited perpendicular to the vanes to vibrations in the vane plane. This transfer shortens decay time and quickly stabilizes the feather, due to the stronger energy dissipation caused by friction, deformations of hooks, and additional vibrations caused by neighboring barbs in the vanes.

This intricate design of multidirectional damping capability in the feather vanes also contributes to the efficiency of bird flight. During flapping, forces and stresses are higher on the dorsal and ventral sides, and the main vibrations of feathers are excited vertically, perpendicular to the vanes. The higher damping ratios of feathers under vertical deflection contribute to the stronger stability of the wing.

The vane features examined here may inspire more efficient lightweight aerospace materials with tailored damping properties and directional differences. The damping ratio of artificial wings or their parts could be potentially adjusted by layers of zipped structures in unmanned aerial vehicles.

4 Conclusions

Unwanted vibrations of bird wings and feathers may lead to instability during flight. To exclude specific functions related to alarm signal and courtship, high damping is desirable to attain low vibration and low noise. In this study, vanes have been confirmed to enhance the damping of feathers. The presence of vanes decreases the number of vibration modes and the first natural vibration frequency and increases damping ratios independent of the excitation direction (horizontal or vertical). Feathers with vanes are likely to be adapted to have the highest damping ratio perpendicular to the vanes at vertical deflections. The aerodynamic resistance of the vanes’ planar surface, the movement of the numerous hooklets and barbules, and the foam-filled shaft and barbs are likely to be the mechanisms responsible for the enhanced damping properties of the feathers.