1 Introduction

Over the past few decades, tactile sensors have become an emerging research field in academia and industry. Tactile sensors are designed for mimicking the complex function of human sense-of-touch, which have great application potential in the fields of intelligent robots, e-skins, artificial prosthetics, rehabilitation medicine, human health monitoring, etc. Similar to human skins, the sensing information collected by tactile sensors mainly includes pressure, temperature, hardness and humidity. Except for above parameters, comprehensive information from contact object, such as shape [1, 2], texture [3, 4], and slip [5,6,7], is also required. Based on the different sensing mechanisms, tactile sensors mainly include piezoresistive [8, 9], piezoelectric [10, 11], capacitive [12, 13] and optical [14] types, which are commonly used approaches for converting tactile information into electrical signals. However, one of the existing problems of the tactile sensor is that it is difficult to effectively improve the sensing accuracy.

Recently, biomimetics, i.e., the mimicry of biological structures and functions, has emerged as a burgeoning area in tactile sensors, which have opened new avenues to develop high-performance tactile sensors [15]. After hundreds of millions of years of evolution, typical creatures in nature have evolved excellent biological tactile receptors for the sake of survival and reproduction in the harsh natural environment. For example, some arthropods (e.g., spiders and scorpions) have ultra-sensitive sensory organs including slit sensilla and trichobothria sensilla, which has provided bionic inspirations for the design of crack-based and hair-like sensors [16]. Some plants also have high-performance sensory organs, and the pursuit to explore their sensing mechanism has also attracted much interest. The Venus flytrap (Dionaea muscipula), which lives in swamps, is a typical example of an insectivorous plant with an extraordinary tactile sense. Related studies have revealed that deflections of 2.9°, angular velocities of 3.4/s and forces of 29 µN could produce action potential (AP) in the trigger hair of Venus flytrap, and flytrap can detect much small torques (160 nN·m) [17]. At present, despite a good understanding of the Venus flytrap with respect to the physiology of the snap-trap triggering mechanism, the hunting cycle, and the related prey digestion [18,19,20], analyses of characteristics of the tactile receptor of the Venus flytrap, that is trigger hair, remain incomplete. Besides, there is also no bionic design of tactile sensors based on the tactile receptors of the Venus flytrap.

The main goal of this work is to reveal the characteristics of the trigger hair and provide a theoretical basis for the design of sensors based on it.

2 Materials and Experiments

2.1 Experimental Material

Plants used in the experiment were B52 Venus flytraps which were purchased from a commercial supplier (https://chinese-cp.jiyoujia.com). The length of fully developed traps is in the range of 1–3 cm. The plants were maintained in 250 mL plastic pots with a light and dark photoperiod cycle of about 12:12 h at room temperature (about 22 °C), and the cultivation medium was well-drained peat moss.

2.2 Plant Tissue Fixation

Firstly, the traps of Venus flytraps were immersed in the beaker with the fixed solution (50% alcohol: formaldehyde: glacial acetic acid = 46:1:1) at 4 ℃ for 24 h. Secondly, 50% ethanol was poured into the beaker after emptying the fixed solution, and traps were immersed in the beaker for 30 min at room temperature, then repeating and immersing traps in the beaker for 20 min at room temperature. Subsequently, replacing ethanol with 1% Safranin O solution, and traps were immersed in the beaker overnight at room temperature. Finally, the dehydration process was continued the next day. And the solution concentration gradient and immersion time were as follows: 80% ethanol for 1 h, 95% ethanol for 1 h, anhydrous ethanol for 1 h and 40 min respectively.

2.3 Freeze-Drying and Metal-Spraying of Plant Tissue

The Freeze-Dryer (FD-1-A50, Beijing Boyikang Experimental Instrument Co., Ltd, China) was pre-cooled for about 30 min until the temperature in its container reached – 50 ℃. Then, the traps that had been pre-frozen in liquid nitrogen were placed in the container of the freezer-dryer. The metal-spraying of the sample is carried out after the treatment of freeze-drying. The device used for metal spraying was an Ion Sputtering Apparatus (E-1010, HITACHI, Japan), and a layer of platinum was sprayed on the surface of the sample.

2.4 Morphological and Structural Analysis

The morphology of the traps was observed using Optical Microscope (OM, VHX-7000, KEYENCE, Japan). To study the structural characteristic of trigger hairs that grow on the inner surface of traps, the Environmental Scanning Electron Microscope (ESEM, QUANTA FEG 250, FEI, USA) were used. In addition, the 3D morphological structures of the trigger hairs were observed with the help of X-ray Computed Tomography (CT, Xradia 620 Versa, ZEISS, Germany) at 0.3 \({\upmu {\rm m}}\) voxel size. The 3D structures of trigger hairs were reconstructed using the Dragonfly software (Object Research Systems (ORS) Inc., Canada), and the post-processing of the reconstructed images, such as section cut and density distribution, were carried out by the software.

2.5 The Elemental Analysis

The element composition of the trigger hairs was measured by Energy Disperse Spectroscopy (EDS, X-Max, Oxford, UK), which is equipped with the Scanning Electron Microscope (SEM, EVO 18, ZEISS, Germany). Pre-prepared samples were fixed on the sample stage by conducting adhesive. The data of elemental analysis from EDS were imported into the Origin software (OriginLab, USA) and finally integrated into a single diagram.

2.6 The Mechanical Property of Plant Tissues

Atomic Force Microscope (AFM, Dimension Icon, Bruker, USA) combined with NanoScope Analysis software (Bruker Corporation, USA) were used to measure elastic coefficient and Young’s modulus of trigger hairs. Firstly, Young’s modulus of the trigger hair was analyzed by the experiment of AFM indentation, which is a widely used technique to measure the mechanical properties of deformable materials [21, 22]. In the indentation experiment, conical probes (HQ: XSC11/HARD/ALBS, MikroMasch, Estonia) whose force constant is 11.66 N·m−1 and half cone angle is 20° were used. Figure 1a displays the freshly cut trigger hair fixed on the glass substrate in a lying-down posture. The operation process of the indentation experiment was shown in Fig. 1b. The data from the above experiment were F–D curves, where F is the loading force and D is the distance between the probe and sample. Converting the F–D curve into F–Indentation curve, Young’s modulus of the sample can be fitted with the help of the rigidity model.

Fig. 1
figure 1

Experimental designs: a, b the procedure of measuring Young’s modulus of trigger hair. a Fixation of the sample; b diagram of AFM indentation. c–e The procedure of measuring the elastic coefficient of trigger hair. c Selection of sample; d fixation of the sample; e diagram of the experiment: 1, glue; 2, trigger hair; 3, glass substrate; 4, probe tip; 5, cantilever; 6, holder chip; 7, lobe

Full size image

For a conical probe, Sneddon’s model describes the relationship between force and indentation depth in the absence of adhesive interaction between the AFM probe and the experimental sample. Sneddon’s model is expressed by the following equation [23]:

$$F = \frac{2}{\uppi }\frac{E}{{1 - \upsilon^{2} }}\delta^{2} {\text{tan}}\theta$$
(1)

where F is the loading force, E is Young’s modulus, \(\upsilon\) is the Poisson ratio (0.3 for trigger hairs), \(\delta\) is the indentation depth, and \(\theta\) is the half cone angle of the probe.

When the probe-sample adhesion is not negligible, Eq. (1) need to be corrected, so Sirghi et al. [24] proposed a correction term to Sneddon’s model:

$$F = \frac{2}{\uppi }\frac{E}{{1 - \upsilon^{2} }}\delta^{2} {\text{tan}}\theta + F_{{{\text{ad}}}}$$
(2)
$$F_{{{\text{ad}}}} = \frac{{8\gamma {\text{tan}}\theta }}{{\uppi {\text{cos}}\theta }}\delta$$
(3)

with the same notations as in Eq. (1), \(F_{{{\text{ad}}}}\) is the adhesive force between the AFM probe and the experimental sample, and \(\gamma\) is the adhesion energy.

Second, the elastic coefficient of the trigger hair, which has a cantilever beam structure, was measured using an AFM probe (All-In-One-DD, BudgetSensors, Bulgaria). The force constant of the probe is 0.7 N·m−1. As shown in Fig. 1c, the fresh local plant tissue containing trigger hair was cut from the trap with a razor blade. Then, the trigger hair was extended out and suspended in the air (Fig. 1d). The trigger hair will generate a deflection after the AFM probe contacts it (Fig. 1e). Data got from the above AFM experiment were the F–Z curves, where F is loading force and Z is the displacement of the AFM scanner that includes the bending of probe cantilever (Z0) and the deflection of the trigger hair (Z1) after the AFM probe touches it. Furthermore, both the F–Z curve and F–D curve are types of force curves, and they can transform into each other. Thus, Z1 can be calculated using the following equation:

$$Z_{1} = Z - Z_{0} = Z - \frac{F}{{K_{0} }}$$
(4)

where K0 is the force constant of the probe used in the experiment.

Therefore, elasticity coefficient K of the trigger hair is

$$K = \frac{F}{{Z_{1} }}$$
(5)

3 Results and Discussions

3.1 External Morphology

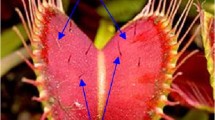
Venus flytrap shows a particular fascinating adaptation to carnivory and it can catch small animals through its trap, which is its specialized capture organ, to improve nutrient status. As shown in Fig. 2a, the trap is composed of a modified leaf with two lobes that can revolve around the central midrib. Each lobe has a red inner surface that is covered with glands and attractants for attracting prey. Besides, nearly three trigger hairs grow on the center of each lobe. The two lobes are all fringed with toothed tines which can interlock with each other when the trap closes [25]. The trigger hair, which is similar to that of a cantilever, acts as a mechanosensor to sense the external irritation. The trap will close in a fraction of a second when one or more trigger hairs are stimulated several times over several seconds, as shown in Fig. 2b. This rapid closure is mediated by the transmission of an intercellular electrical signal. Touching trigger hairs would activate mechano-sensitive ion channels and generate receptor potentials, inducing a propagating AP [26]. This signal, in turn, mediates changes in hydrostatic pressure and the release of elastic tension, resulting in a rapid transition of the trap from open to closed state [27].

Fig. 2
figure 2

a Images of the trap with open state and b close state. c ESEM images of lobe and d gland and e gland that loses water

Full size image

Surrounding the trigger hairs, there are many glands distributed across the inner surface of the lobe (Fig. 2c). Each gland is composed of 46 cells and its structural organization is constituted by three functional layers including an inner layer formed by 8 cells, an outer layer of 32 cells and an endodermoid layer [28,29,30]. All gland cells are connected by plasmodesmata, and both the cuticle and the cell wall of the glands are less developed and more permeable to solutes than the common epidermal cells [31]. More than five APs would lead to the trap becoming hermetically sealed while two APs trigger fast trap closure. Meanwhile, numerous glands covering the inner surface of the lobe start to express genes that encode enzymes involved in decomposing the prey into its nutrient building blocks, alongside the expression of transporters for the uptake of prey-derived nutrients [32]. Besides, glands covering the inner surface of the lobe that is cut from the Venus flytrap will lose water quickly and shrivel, as shown in Fig. 2d, e.

Figure 3a, b are ESEM images of external morphology of trigger hairs without any pre-treatments, and it can be found the trigger hair is composed of many elongated tissues. Tissues of the trigger hair would more tightly bound after being treated with fixed solution, which show better ESEM image (Fig. 3c, d). Meanwhile, the trigger hairs with freeze-drying and metal-spraying treatment display the best ESEM image and the measurement under high vacuum mode eliminated the influence of factors such as water and air, as shown in Fig. 3e, f. However, the whole structure of trigger hair would undergo torsion and shrinkage deformation due to the dehydration of its tissues. It can be found from Fig. 3g that trigger hairs are actually characterized by a slender hair lever and a basal podium [17], and there is a notch that concaves inward between the hair lever and basal podium. The hair lever has a large longitudinal diameter ratio up to about 10–50. Its length is generally 800–3000 \({\upmu {\rm m}}\) and the diameter at the bottom of it is almost 60–200 \({\upmu {\rm m}}\). The profile of the hair lever is similar to a slender cone whose diameter gradually decreases from the bottom to the top and tubular tissues that make up it are arranged in a more orderly manner. By contrast, the basal podium, which connects the hair lever and the lobe, has a smaller size, and the arrangement of tissues constituting it is not in good order. Furthermore, the basal podium functioning as a flexible constrained end can fix the trigger hair on the lobe. Under the action of external force, the trigger hair deflects rather than bends. After the external force disappears, the deflected trigger hair would quickly return to its original position under the elastic recovery of the basal podium. Interestingly, the trigger hairs do not deflect when there is airflow acting around the hair sensilla. Therefore, unlike the hair-based sensilla of Arachnids, triggers hairs are tactile sensilla which are not sensitive to airflow.

Fig. 3
figure 3

Comparison of ESEM image effects of the trigger hair: a, b fresh and untreated; c, d fixed fluid fixation; e, f freeze-drying and metal-spraying. g ESEM image of a whole trigger hair

Full size image

3.2 The Micro/Nanoscale Structure of Trigger Hair

The structural characteristic of mechano-sensilla has a great influence on the sensing performance of sensilla. Here, the micro/nanoscale structure of trigger hairs is researched by utilizing the ESEM. In this experiment, the sample is immediately frozen in liquid nitrogen after freshly cutting from the lobe to minimize structural deformation. It can be seen from Fig. 4a that the internal structure of trigger hair shows honeycomb, and many holes of varying sizes make up its section. The thickness of outer tissue walls is in the range of 3–6 \({\upmu {\rm m}}\), and the thickness of thin tissue between the adjacent pores is in the range of 0.5–1.6 \({\upmu {\rm m}}\) (Fig. 4b). However, the trigger hair would twist when subjected a severe external force, making its internal holes deform (Fig. 4c, d). The basal podium of trigger hairs (Fig. 4e) and its cross-section (Fig. 4f) are also shown. The results indicate that there are also many holes in the cross-section of the basal podium, but the tissue thickness between holes of the basal podium is thicker than the tissue in the hair lever. Meanwhile, compared with the hair lever, the inner tissues of the basal podium are not well organized. Besides, the cross-section of trigger hair is variable because its shape, size and pores covering it vary with the longitudinal position. According to the knowledge of material mechanics, the cross-section geometry has a great influence on its overall resistance to deformation. The hollow structure with thin walls between adjacent holes can greatly reduce the weight while ensuring its own flexural and torsional strength. Meanwhile, the thick walls surrounding the section can also avoid local creasing when the trigger hairs are subjected to an external load, thus avoiding reducing its bearing capacity.

Fig. 4
figure 4

ESEM images of internal structures of trigger hair: a–d cross-section of the hair lever with a, b minor deformation (h1, the thickness of outer tissue wall; h2, tissue wall thickness between adjacent pores) and c, d large deformation; e, f basal podium and its cross-section

Full size image

3.3 Elemental Composition

As we all know, plants need some essential elements for their growth. Besides, the elemental composition has a great impact on the properties of the sample, such as hardness, plasticity and so on. Figure 5a, b displays seven positions where data are recorded by EDS, and an elemental map of them is shown in Fig. 5c. Through the EDS test, elements such as C and O, which are the most abundant, are detected at all positions. Also, some other elements like Cu, Na, Mg, P, Cl, K and Ca are also detected. The main differences between the spectra at different positions are the elemental intensities detected by EDS. For example, greater intensity of Na and Cl are recorded on the lobe surface that is position 7, but the greater intensity of P and Ca are found on the trigger hair including position 1–5. Meanwhile, though on the same trigger hair, basal podium (position 1) had a low intensity of Ca compared to that of hair lever (position 2–5), indicating the differences in material properties.

Fig. 5
figure 5

Elemental analysis of seven positions by SEM–EDS. a SEM image of trigger hair; b SEM image of gland and lobe; c EDS spectra collected from all positions

Full size image

3.4 Model of the Trigger Hair

3D structure of the trigger hair is reconstructed through X-ray Computed Tomography as well as Dragonfly software. It can be found from Fig. 6a, b that there are quite differences between hair lever and basal podium on tissue density and the size of tubular tissues making up them. The density of tissue distributed in the basal podium is higher than that of hair lever, but the tubular tissues constituting the basal podium are slenderer than that of the hair lever. The high-density area in the cross-section of trigger hair is highlighted with red in Fig. 6c which indicates the outermost layer has the highest tissue density. The outer tissues with high-density and thicker walls can protect internal structure and tissues effectively. Based on the detailed structural observation, the model of trigger hair is established. As shown in Fig. 6d, trigger hair can be regarded as a cantilever structure with a special tactile sensing function. From top to bottom, there is a relatively straight hair lever with a large longitudinal diameter ratio, followed by a basal podium. Both the hair lever and the basal podium are composed of many tubular tissues. Besides, there is a notch that concaves inward between the hair lever and the basal podium. The basal podium is connected to the lobe through tubular tissues, and there are many glands, which can express genes encoding enzymes that decompose the prey into its nutrient building blocks, covering the inner surface of the lobe.

Fig. 6
figure 6

Morphology and structure of the trigger hair via CT: a, b 3D reconstructed images from orthogonal angles; c sectional shape; d structural model of the trigger hair

Full size image

3.5 Mechanical Property of Tissue

Studies on the biological sensilla have shown that the mechanical properties of the tissues that constitute the biological sensilla have a significant impact on the sensing function. Therefore, we have carried out an in-depth analysis of the mechanical properties of the tissues constituting the trigger hair. Firstly, given the potential differences in micro/nanoscale structure and material composition between hair lever and basal podium, Young’s modulus of them is researched in detail. Figure 7a is one of the force curves of the hair lever. The periodic diagram of the F–D curve is composed of the approach curve and retract curve, which corresponds to the probe loading and unloading process respectively. The force between the probe tip and the measured sample follows Hooke’s law, which represents the elastic force of the probe cantilever. It can be found from the approach curve that the force changes abruptly and generates a small downward peak as the AFM probe approaching the hair lever because the probe is attracted by the surface charge of tissue constituting the hair lever. With the gradually decreasing distance between the probe tip and the hair lever, the probe tip occurs a jump and then directly contacts the hair lever surface (k point) at the moment of the attractive force exceeding the elastic force of the probe cantilever. Besides, the retract curve shows the phenomenon of dragging hysteresis instead of completely coinciding with the approach curve because of the adhesive force between the hair lever and probe tip preventing the elastic recovery of the probe cantilever. With the gradually increasing distance between the probe tip and hair lever, the probe tip occurs a jump again and separates from the hair lever surface completely (h point) at the moment when the elastic force exceeds the adhesive force. The maximum adhesive force is about 10 nN, which is equal to the elastic force of the probe cantilever at the h point. Figure 7b shows the F–Indentation curve corresponding to the F–D curve in Fig. 7a. The result displays that the retract curve does not coincide with the approach curve. Due to the strong adhesive interaction between the probe and material during the probe unloading process, the approach curve is generally used to analyze the mechanical properties of the measured sample. Meanwhile, the retract curve is used to analyze the flexibility, viscoelasticity and other information of the measured sample.

Fig. 7
figure 7

a–d Steps for analyzing Young's modulus of the hair lever: a experimental curves; b force-indentation curve; c Sneddon fitting of indentation process. d Fitting results of Young's modulus. e, f Analysis results of AFM indentation on the basal podium: e indentation curves; f Sneddon fitting results

Full size image

The fitting process of the approach curve using Sneddon’s model is shown in Fig. 7c. The result indicates that the fitting curve is in good agreement with the experimental data extracted from force curves. The fitting results reveal that Young’s modulus of the hair lever is 3.26 GPa. Furthermore, the retract curve is also analyzed based on Sneddon’s model to calculate Young’s modulus (Fig. 7d). The fitting result of the retract curve predicts a larger Young’s modulus of 3.77 GPa than that of the approach curve, due to the strong adhesion in the unloading process of the probe. However, the fitting result using Sneddon’s model of the retract curve overestimates Young’s modulus, compared to the corrected model in Eq. (4) which has a calculated Young’s modulus of 3.68 GPa, due to the adhesive force on the probe. Besides, the indentation experiments are repeated at different positions of trigger hairs, and Sneddon's model is used to analyze the approach curves obtained from experiments. Given the difference in structure, material composition, etc., there are differences in Young’s modulus between different positions of different trigger hairs. Finally, Young’s modulus of the hair lever is obtained by statistical analysis, which is 2.21–20.46 GPa.

Similarly, to explore the difference of mechanical property between the basal podium and hair lever, Young’s modulus of the basal podium is also analyzed. Figure 7e is an F–indentation curve corresponding to one of the positions of the basal podium. The result shows that the loading force applied to the basal podium is smaller than that to the hair lever at a similar indentation depth, suggesting that the surface material of the basal podium is softer than that of the hair lever. The Young’s modulus is approximately 1.45 GPa by fitting all valid indentation points at the position (Fig. 7f). Finally, the obtained Young’s modulus of the basal podium is about 0.18–3.34 GPa by counting all fitting results at different positions of different samples.

Secondly, the elasticity coefficient of the cantilever structure of trigger hairs is characterized. The primary data obtained from the experiment are F–Z curves, and one of them is shown in Fig. 8a. It can be seen that the approach curve and retract curve are both straight lines, and the linear coincidence of them is quite high in the range made out by dotted lines in Fig. 8b. Hence, the deformation of trigger hair generated is almost perfect elastic deformation in the experiment. Besides, many results can be found after converting the F–Z curve to a correspondingly F–D curve. As shown in Fig. 8b, although the force applied by the probe is far less than that in the AFM indentation experiment, more severe adhesion effects occurred when the probe tip detached from the trigger hair surface for the suspended arrangement of the trigger hair in the experiment. By counting all the measured trigger hairs, the elasticity coefficient of trigger hair is in the range of 130–900 pN·(nm)−1. Hence, it can be preliminarily estimated that only a force of 130–900 nN is needed to produce a deflection of 1 μm on the tip of the trigger hair, which indicates that the trigger hair is highly sensitive to force.

Fig. 8
figure 8

Force curve diagram of the trigger hair: a F–Z curve. Dotted lines mark out the boundaries of the loading process of the probe; b F–D curve

Full size image

4 Conclusion

In summary, the morphology, structure, elemental composition and mechanical properties of the trigger hair of Venus flytrap are characterized in this paper. As the tactile receptor in the trap of Venus flytrap, trigger hair consists of a hair lever and a basal podium with a notch concaving inward between them, and it shows a cantilever beam structure. The hair lever looks like a circular cone with a large longitudinal diameter ratio, and the closer to the tip of the trigger hair, the smaller the cross-sectional size. Trigger hair is made up of many tubular tissues with slender exteriors and hollow interiors, resulting in a honeycombed internal structure. However, some differences are observed in the size and arrangement of tubular tissues of the hair lever and basal podium with the help of ESEM and CT. Tubular tissues in the basal podium are thinner than those in the hair lever but a more complex arrangement. From the elemental analysis of EDS, we found that there are abundant C and O in the trigger hair, as well as some other elements such as Cu, Na, Mg, P, Cl, K and Ca. Besides, AFM indentation experiments are carried out on the trigger hair, and the obtained F-indentation curves are processed through the Sneddon model and corrected Sneddon model. The latter model takes into account adhesion between the probe and sample. Results reveal that adhesive effect do exist in the experiment and the probe unloading process is greatly affected by the adhesive force, thus Young’s modulus of trigger hair is analyzed based on the approach process. Young’s modulus of hair lever is 2.21–20.46 GPa while that of the basal podium is 0.18–3.34 GPa, which indicates the hair lever has greater rigidity in comparison to that of the basal podium in the trigger hair. Finally, the force curve experiment showes that trigger hair has an elasticity coefficient of 130–900 pN·(nm)−1, which means only 130–900 nN applied on the tip of trigger hair can make it deflect 1 μm. In the future, this study could probably be an inspiration for the development of tactile sensors based on the cantilever structure.