Examinations of Biases by Model Misspecification and Parameter Reliability of Reinforcement Learning Models

Abstract

Reinforcement learning models have the potential to clarify meaningful individual differences in the decision-making process. This study focused on two aspects regarding the nature of a reinforcement learning model and its parameters: the problems of model misspecification and reliability. Online participants, N = 453, completed self-report measures and a probabilistic learning task twice 1.5 months apart, and data from the task were fitted using several reinforcement learning models. To address the problem of model misspecification, we compared the models with and without the influence of choice history, or perseveration. Results showed that the lack of a perseveration term in the model led to a decrease in learning rates for win and loss outcomes, with slightly different influences depending on outcome volatility, and increases in inverse temperature. We also conducted simulations to examine the mechanism of the observed biases and revealed that failure to incorporate perseveration directly affected the estimation bias in the learning rate and indirectly affected that in inverse temperature. Furthermore, in both model fittings and model simulations, the lack of perseveration caused win-stay probability underestimation and loss-shift probability overestimation. We also assessed the parameter reliability. Test–retest reliabilities were poor (learning rates) to moderate (inverse temperature and perseveration magnitude). A learning effect was noted in the inverse temperature and perseveration magnitude parameters, showing an increment of the estimates in the second session. We discuss possible misinterpretations of results and limitations considering the estimation biases and parameter reliability.

Introduction

Reinforcement learning (RL) models are simple but successfully applied frameworks of value-based learning in humans, animals, and artificial intelligence (Sutton & Barto, 1998). Researchers have leveraged RL to decompose the elements that influence decision-making. The basic traits of the processes are extracted as free model parameters such as the learning rate (which governs the updating of option values) and inverse temperature (which controls the exploration–exploitation trade-off). The estimates of the parameters revealed individual differences, group differences, developmental changes, and links to specific neural substrates (Decker et al., 2016; Gillan et al., 2016; Glascher & O'Doherty, 2010; Lee et al., 2012; Nussenbaum & Hartley, 2019). Importantly, these study findings are meaningful only when the assumptions related to the nature of the model parameters are satisfied. However, recent studies have revealed that our implicit assumptions regarding the validity, reliability, generalizability, and interpretability of model parameters are not always correct and may be overly optimistic (Eckstein et al., 2022; Moutoussis et al., 2018). Thus, demands to address these potential problems in the use of computational models and their parameters and to develop infrastructure regarding proper estimation, evaluation, and use are increasing (Browning et al., 2020; Eckstein et al., 2021, 2022; Katahira & Toyama, 2021; Palminteri et al., 2017b; Wilson & Collins, 2019).

Inappropriate use of model parameters sometimes results from the problem of modelling that the model does not sufficiently capture meaningful features of the data (hereafter, referred to as model misspecification). Under model misspecification, the feature not included in a model is absorbed by other existing parameters, which can cause undesirable estimation biases in parameters, resulting in misleading interpretations and conclusions (Toyama et al., 2019). However, even if modelling is proper or improved, the model parameters still do not work as reliable trait indicators if they are unstable, vary from one measurement to the next, or have low identifiability. At a minimum, we should know the reliability of parameters as a limitation in the use of models in studies. Thus, in this study we addressed the problem of model misspecification and also examined parameter reliability. In the following, we introduced these two topics sequentially.

The basic assumption of RL models is that behavior is controlled by experience gained from prior positive and negative events. This form of learning is referred to as the value-dependent learning system. On the other hand, behavior is also influenced by perseveration, the tendency to repeat recent actions (Akaishi et al., 2014; Sugawara & Katahira, 2022); this form of learning may be referred to as the value-independent learning system. Together, these systems constitute the basic elements that govern learning. However, the latter learning system (i.e., preservation) is not always included in RL models. Previous studies have reported that RL models without perseveration induce estimation bias regarding the difference in learning rates for positive and negative prediction errors (i.e., learning asymmetry) (Katahira, 2018; Sugawara & Katahira, 2021). Palminteri (2021) reported that including perseveration at least weakens the effect of learning asymmetry observed in a model without perseveration. However, it is not yet examined how the lack of perseveration in a model relates to learning asymmetry in a situation in which a person must simultaneously process positive and negative outcomes. Given that real-life experiences have both positive and negative aspects, it is also important to consider such situations. In addition, more importantly in the wider use of RL models, the influence of the lack of perseveration has not been examined in basic parameters, i.e., learning rates themselves (rather than their asymmetry) and inverse temperature. Furthermore, the behavioral aspects that the perseveration-including model can capture and the mechanism by which model misspecification introduces biases should be clarified. Thus, we systematically examine the influence of neglecting to include a perseveration component in RL models through experiments and simulations; additionally, with simulations, we examine the influence of task settings such as action-outcome contingencies and reversal frequency on the estimation biases.

Another topic we addressed in this study was parameter reliability. Understanding the nature of the estimated parameters is essential for interpreting the results. At a minimum, parameter reliability puts an upper bound on the ability to detect individual differences in cognitive function, abnormality, and developmental changes. Some studies have examined test–retest reliability and suggested that indices of behavioral tasks are not optimal for detecting individual differences compared with questionnaires (Enkavi et al., 2019; Hedge et al., 2018; Moutoussis et al., 2018). Although there is growing interest in the parameter reliability of computational models (Ballard & McClure, 2019; Brown et al., 2020; Browning et al., 2020; Scheibehenne & Pachur, 2015; Waltmann et al., 2022), information on the reliability of RL model parameters is still very limited. Previously reported results on reliability have varied from poor (Moutoussis et al., 2018; Pike et al., 2022; Schaaf et al., 2023) to good or excellent (Brown et al., 2020; Mkrtchian et al., 2023; Waltmann et al., 2022). Further reports are needed to obtain the whole picture of the reliability of RL model parameters. Additionally, parameter recoverability is important as it is a prerequisite of good test–retest reliability.

Therefore, we assessed the reliability of model parameters by administering the same task at two time points, separated by 1.5 months, to the same participants; these participants were recruited and conducted tasks online. As indicators of parameter stability, we examined the correlation between the same parameters over time as well as the mean change in the values of the parameters over time. Considering that the task used for RL model is a learning task, there is a possibility that the parameter values change systematically at the time of the second data acquisition reflecting some learning effects. In addition, the current study provides information on whether the parameter changes between different blocks of the same task.

The behavioral task used in the current study is a version of the information bias learning task developed by Pulcu and Browning (2017). This behavioral task has the following advantages for future research. First, it is an expansion of a reversal learning task, which is often used with the RL model, so our study will provide some insights into other RL paradigms. Second, this task has ecological validity in that it involves a volatile environment in which the associations of action and outcomes change during the task, thus mimicking a natural, dynamic environment that changes over time. Third, this task, in which win and loss feedback were both provided after actions in each trial, can detect affective bias in an environment where both types of information are available. In the real world, although we need to pay attention to useful information and ignore useless information, affective bias modulates this process. In addition, some psychiatric disorders have problems in flexibility of responses to volatile environments and/or emotional processing biases (Browning et al., 2015; Cella et al., 2010; Crews & Boettiger, 2009; Mathews & MacLeod, 2005; Pulcu & Browning, 2017; Pulcu et al., 2019), so assessing the modelling and model parameters for this task can provide basic information that can be used in the field of computational psychiatry, in which the issue of parameter stability has gained increasing attention (Browning et al., 2020).

Studies that employ information bias learning tasks have reported that the learning rate is adjusted depending on the context. In a volatile situation where option values change frequently, people tend to learn more from immediate feedback, exhibiting a higher learning rate. In contrast, if option values are stable, people place a higher weight on past feedback, leading to a lower learning rate (Behrens et al., 2007; Browning et al., 2015). In addition, volatility is separately evaluated for the win and loss domains and utilized to adjust the learning rates of win and loss outcomes, respectively (Pulcu & Browning, 2017). Therefore, as part of our examination specific to this task, we investigated the effect of model misspecification on the volatility-dependent adjustment of learning rates.

In summary, the current study focused on two topics that should be considered for proper use of RL models: one regarding the influence of model misspecification on model parameters (especially on learning rates and inverse temperature) and interpretations of behavioral trends and the other regarding the reliability of model parameters, including test–retest reliability, learning effect, and recovery.

Methods

Participants

Participants were recruited through a crowdsourcing service of CrowdWorks, Inc., Japan. These participants took the experiment twice, separated by approximately 1.5 months; however, some dropped out before the second time point. A total of 516 participants completed all tasks and questionnaires at both time points, and data from 453 (245 females, 208 males; mean age = 38.09 years, range = 19–73, SD = 9.50) retained after application of the exclusion criteria were analyzed. All participants provided informed consent online. The protocol was approved by the Ethics Committee of Nagoya University.

Exclusion Criteria

In the analyses, we first excluded participant data from uncompleted trials (i.e., those in which the participant did not make a choice within 3 s) and data from trials in which the response time was < 100 ms, as these responses were considered to be anticipatory responses that did not reflect the stimulus types. Second, we excluded 44 participants with omitted data on more than 10% of trials based on the above criteria. Third, we excluded 33 participants who chose the same stimulus in either block on more than 90% of the trials as well as 6 participants who chose the stimulus on the same side of the screen on more than 90% of trials in either block. Some participants failed to meet multiple criteria; thus, in total, 63 participants were excluded. Data from the remaining 453 participants was included in the final analyses.

Decision-making Task

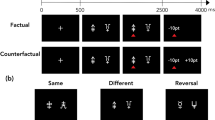
The task used in this study was based on the information bias learning task developed by Pulcu and Browning (2017). The version used in the current study consisted of win-volatile (WV) and loss-volatile (LV) blocks of 100 trials each. In each trial, participants were required to choose one of two stimuli (two monster images) within 3 s (Fig. 1, left). Each stimulus was presented randomly on the left or right side of the screen, and participants indicated their choice by pressing “F” or “J,” respectively, on a keyboard. Following a 500-ms yellow highlight, the loss outcome was displayed above either of the two stimuli. If the loss outcome was the chosen stimulus, the participant’s total points decreased by 15 points, accompanied by a “boo” sound; if the loss outcome was the unchosen stimulus, the participant’s total points remained the same. After 1 s, the win outcome was indicated by appearing under either of the stimuli. If the win outcome was the chosen stimulus, the participant’s total points increased by 15 points, accompanied by a “chink” sound; if the win outcome was the unchosen stimulus, the participant’s total points remained the same. The screen displayed both win and loss outcomes for 3 s. The order of loss and win outcomes was randomized over trials. One pair of stimuli was used in each block, and different pairs were used in different blocks (stimuli were downloaded from shutterstock.com).

Fig. 1

Structure of the information bias learning task. Left, example task sequence. Right, feedback regarding outcome, win (circle) or loss (cross), for each stimulus (Stimulus A and Stimulus B) in win- and loss-volatile blocks. The volatile outcomes are color-coded (red, win-volatile block; blue, loss-volatile block)

In the WV block, win outcomes were associated with one stimulus at a probability of 85% and the other stimulus at a probability of 15%, and loss outcomes were associated with both stimuli at a probability of 50%; in the LV block, this contingency was reversed for win and loss outcomes. Half of the participants first experienced the WV block, and the other half first experienced the LV block. The patterns of outcomes in each trial were the same in both blocks, only differing in win vs. loss (Fig. 1, right), and the same sequence was used for all participants. The reason we used the same trial sequences is that if the model parameter was intended to be used to detect individual differences (a potential purpose that is not examined in the current study), the sequence is needed to prevent the influence of different experiences in the task from overshadowing the individual differences. Using the same trial sequence has an advantage for this purpose. In addition, the reason that the WV and LV blocks were arranged to have symmetric feedback was to assure a fair comparison of the parameter values between the blocks.

Participants were instructed to maximize their total score by gaining as many as wins and avoiding as many losses as possible. They were also told that one stimulus was better than the other stimulus in a pair and that the better stimulus might switch over time, but they were not informed how a given stimulus was better.

In the series of computational simulations, the task settings were slightly varied in line with the various aims. Each aim and change are explained in the “Simulation Results” section.

Experimental Procedure

Participants accessed experiments through a web link and completed tasks via their web browser. Instructions and stimuli were presented using Inquisit 5 software (Millisecond Software, Seattle, Washington). After the behavioral task, participants were presented with several web-based questionnaires about mental illnesses at both time points; however, these data are not the focus of this paper and will be reported elsewhere.

Model-Neutral Regression Analysis

The candidate RL models in this study assumed that choice history and outcome history both influenced decision-making. To examine whether the data exhibited repeated selection of the same choice independent of outcome feedback (i.e., perseverance), we constructed a multi-trial regression model to quantify the effect of past outcomes and choices on future decisions (Katahira, 2015; Miller et al., 2016) separately for the WV and LV blocks. We defined vectors for the win-outcome history (${\mathrm{outW}}_{\mathrm{t}}$), loss-outcome history (${\mathrm{outL}}_{\mathrm{t}}$), and choice history (${\mathrm{c}}_{\mathrm{t}})$ for trial $\mathrm{t}$; these vectors were given the value of 1 if associated with option (stimulus) A and a value of − 1 if associated with option B. The mixed-effects logistic regression model, which includes a random effect of participant on the intercept, for the probability of choosing option A, $p(a(t) =\mathrm{ A})$, was constructed as:

$$\mathrm{logit}\left(p\left(a\left(t\right)=\mathrm{ A}\right)\right)={b}_{bias}+\sum_{m=1}^{10}{b}_{w}^{\left(m\right)}{\mathrm{outW}}_{\mathrm{t}-\mathrm{m}}+{b}_{L}^{\left(m\right)}{\mathrm{outL}}_{\mathrm{t}-\mathrm{m}}+{b}_{c}^{\left(m\right)}{\mathrm{c}}_{\mathrm{t}-\mathrm{m}}+(1|\mathrm{Participant})$$

where ${b}_{W}^{(m)}$, ${b}_{L}^{(m)}$, and ${b}_{c}^{(m)}$ are the regression coefficients $m$ trials ago (up to 10 trials ago). This model was fit using the R function “glmer” from the lme4 package (Bates et al., 2015). For this analysis, all data from each participant were used to obtain a sufficient number of trials for the analyses.

Computational Models

We used several RL models to analyze the choice data obtained in this task. Below, we introduce two models without a perseveration term (M0 and M0b) and two models with a perseveration term (M1s and M1m).

M0: Standard RL Model

For the standard model, we used a model with two learning rates and an inverse temperature (M0). This model was based on that used by Pulcu and Browning (2017). In each trial $t$, after the stimulus $i$ was chosen, the probabilities that this stimulus $i$ is connected to win and loss outcomes ($pwi{n}_{i}$ and $plos{s}_{i}$, respectively) were updated as follows:

$$pwi{n}_{i, t+1}= pwi{n}_{i, t}+{\alpha }_{W}\left(winou{t}_{i, t}-pwi{n}_{i, t}\right)$$

(1)

$$plos{s}_{i, t+1}= plos{s}_{i, t}+{\alpha }_{L}\left(lossou{t}_{i, t}-plos{s}_{i,t}\right)$$

(2)

In these equations, ${\alpha }_{W}\in [\mathrm{0,1}]$ and ${\alpha }_{L}\in [\mathrm{0,1}]$ express learning rates for $pwin$ and $ploss$, respectively; their initial values are 0.5, and they are updated based on the occurrence of win outcomes ($winou{t}_{i,t}$; 1 or 0) and loss outcomes ($lossou{t}_{i,t}$; 1 or 0) associated with this stimulus $i$ in trial t. The probabilities that the unchosen stimulus $j$ is connected to win and loss outcomes were defined as $pwi{n}_{j,t+1}=1-pwi{n}_{i,t+1}$ and $plos{s}_{j,t+1}= 1-plos{s}_{i, t+1}$.

The probability of choosing stimulus $A$ was calculated as follows:

$${choiceP}_{A,t}=\frac{1}{1+\mathrm{exp}\left(-\left(\beta pwi{n}_{A,t}-\beta plos{s}_{A, t}\right)\right)}$$

(3)

where the inverse temperature,$\beta \in (\mathrm{0,20}]$, adjusts the sharpness of the value difference between the options in the choice probability.

M0b: Standard RL Model with a Preference Bias for One Option

Next, we considered a model with a preference for one option over the other (M0b). This model was used in Pulcu et al. (2019). This model is identical to the standard RL model, with the addition of an action bias parameter $\kappa$, which expresses the increased likelihood of choosing one option over the other. In this model, Eq. (3) is replaced as follows:

$${choiceP}_{A,t}=\frac{1}{1+\mathrm{exp}\left(-\left(\beta pwi{n}_{A,t}-\beta plos{s}_{A, t}+\kappa \right)\right)}$$

(4)

where $\kappa$ represents the preference for stimulus $A$. When analysing this model parameter, it is better to use its absolute value.

M1s and M1m: Standard RL Models with a Perseveration Term

Finally, we introduce two kinds of models that include an action-perseveration component. These models have a new parameter $\phi$ that represents the perseveration magnitude and biases actions toward repeated selection of a previously chosen stimulus, independent of outcome history. We constructed two models including this perseveration term. One model assumed only a preference for the most recent option (that is, the choice on the single previous trial); hereafter, we refer to it as M1s. The other model assumed a preference for recently chosen options, with a stronger influence from recent trials (that is, it considers the choice history over multiple past trials); hereafter, we refer to it as M1m. In these models, Eq. (3) is replaced as follows:

$${choiceP}_{A,t}=\frac{1}{1+\mathrm{exp}\left(-\left(\beta pwi{n}_{A,t}-\beta plos{s}_{A, t}+\phi {C}_{A,t}-\phi {C}_{B,t}\right)\right)}$$

(5)

where $C$ represents the choice trace, or choice kernel, and the $C$ of the chosen stimulus ($i$) and unchosen stimulus ($j$) (i.e., ${C}_{i}$ and ${C}_{j}$) are defined as follows:

$$\left\{\begin{array}{l}C_{i,t+1}=\left(1-\tau\right)C_{i,t}+\tau\\C_{j,t+1}=\left(1-\tau\right)C_{j,t}\end{array}\right.$$

(6)

where initial value of $C$ for each of the two choices is set to zero, and $\tau$ is a choice-trace decay parameter, which determines the extent to which the effect of a new choice overrides that of older choices. In the M1s model, this parameter is set to 1. In the M1m model, it is a free parameter, $\tau \in [\mathrm{0,1}]$. Thus, M1s is a special case of M1m. A number of studies have introduced this or a similar perseveration term (Gershman, 2016; Katahira, 2018; Wilson & Collins, 2019).

Parameter Estimation and Model Comparison

We used the R function “solnp” from the Rsolnp package (Ghalanos & Theuss, 2015) to estimate the free parameters by optimizing the maximum a posteriori (MAP) objective function (R version 4.2.0, R Core Team, Vienna, Austria). Prior distributions and bounds were set as Beta (shape 1 = 1.1, shape 2 = 1.1), with bound [0,1] for parameters ${\alpha }_{W}$, ${\alpha }_{L}$, and $\tau$; Gamma (shape = 1.2, scale = 5), with bound [0,20] for $\beta$; Normal (mean = 0, SD = 3), with bound [− 5,5] for $\kappa$; and Normal (mean = 0, SD = 10), with bound [− 20,20] for $\phi$. To compare the candidate models, MAP estimates were used to approximate the marginal likelihood of each model by Laplace approximation (Bishop, 2006); these marginal likelihoods were then used to compute the protected exceedance probability of the models for model comparison (Stephan et al., 2009). This model comparison was performed with the Variational Bayesian Analysis (VBA) toolbox (Daunizeau et al., 2014), run in MATLAB R2020b.

Comparison of Models on Behavior Prediction and Generation

It has been pointed out that the ability to predict and the ability to generate behavioral traits are not necessarily related (Palminteri et al., 2017b). Thus, we compared models in predictive and generative performance on behavior. As behavioral measures, the choice accuracy and stay probability 12 trials before and 12 trials after reversal were analyzed. We also focused on the stay probabilities after each type of feedback and win-stay/loss-shift probabilities because these stay-probability-based measures may be sensitive to the presence or absence of a perseveration term in a model. Here, the stay probability was defined as whether the participants repeated the previous action or not regardless of the outcomes, and win-stay/loss-shift probabilities were defined as the stay-/shift- probability that if participants were rewarded/lost they would choose/avoid the same option for the next trial.

Predictive performance is the model’s ability to fit the observed choice patterns given the history of previous choices and outcomes. The prediction was calculated using the choice probability by the models. On the other hand, generative performance examines the model’s ability to generate the observed choice patterns using the simulation method. That is, choices were generated from the simulated value updates based on the simulated outcomes under the same win/loss probabilities as the experiment. In both examinations, the best-fit parameters estimated in the experiment at Time 1 were used.

Calculations of Parameter Reliability

Stability Assessments

In our study, participants performed the same task twice, separated by approximately 1.5 months. Thus, we could assess parameter stability over time. First, we examined test–retest reliability with Pearson correlation analyses. When we directly compared the stabilities, we used R’s package cocor (Diedenhofen & Musch, 2015), especially based on the method reported in Silver et al. (2004).

We also conducted a t test between blocks and between time points because there were possibly systematic changes in each parameter value over time caused by learning effects.

Recovery Assessments

To confirm whether the model parameters were identifiable, we carried out parameter recovery for the best-fit model. All parameters were independently sampled from uniform distributions which ranged from the minimum to maximum of estimates in the experiment ([0,1] for ${\alpha }_{W}$, ${\alpha }_{L}$, $\tau$ and [0, 17.7] for $\beta$, and [− 10.7,12.3] for $\phi$). Simulated data were generated by sampled 100 parameter sets, and they were re-fit to compare the true and estimated values and to compare the estimated values of different parameters. This simulation was repeated 100 times for each block and the average correlation results were reported. The true parameter value sets were the same between the blocks, and the WV and LV blocks were arranged to have symmetric feedback.

Statistical Analysis

The analyses were carried out using R. In the analysis of variance (ANOVA), the package “anovakun” version 4.8.7 (http://riseki.php.xdomain.jp/index.php) was used.

Simulation Settings

We conducted several simulations based on the results of the experiment. The detailed aim and settings of each simulation are presented in the “Simulation Results” section. In brief, we confirmed the estimation biases seen in the experimental results and examined the effects on the size of the estimation bias by varying the magnitude of intrinsic preservation in the generative model as well as several task settings. In addition, we clarified the direct and indirect estimation bias due to the lack of a perseveration term in the models.

Experimental Results

Evidence Supporting Perseveration

Model-Neutral Analysis

To roughly confirm the effect of outcome history (past wins and losses) and choice history (action perseveration) on participant decision-making in a model-neutral manner, we first conducted linear regression analysis to observe the influence of these histories (spanning up to 10 previous trials) on the current choice (see Supplementary Text 1 for the values of the variance inflation factor). Figure 2 presents the results of the multi-trial regression model. The impacts of outcome and choice histories on the current choice both gradually decayed over time in both blocks, roughly supporting the assumptions of the RL model regarding gradual value-learning and gradual perseveration processes.

Fig. 2

Results of the logistic regression analyses. Each point represents the median value of estimated regression coefficients for the choice history (red), loss-outcome history (green), and win-outcome history (blue). The panels show the results of the win-volatile (WV, left panel) and loss-volatile (LV, right panel) blocks

Model Comparison

We calculated the negative log marginal likelihood and compared this value among the four models (M0, M0b, M1s, and M1m) for each combination of time point and block. In all combinations, the negative log marginal likelihood of the model with gradual perseveration (M1m) was the most favored (i.e., had the lowest value, Table S1). Figure 3 presents the Bayesian model comparison, showing the exceedance probability (the posterior probability that a particular model is more frequent than all other models in the comparison set) for each model. Across any combination of time point and block, the M1m model was most favored.

Fig. 3

Bayesian exceedance probabilities of the M0, M0b, M1s, and M1m models in each combination of time point and block. M0 is the standard RL model without perseveration, and M0b is the same as M0 but includes a preference bias term. M1s and M1m incorporate a perseveration term, representing impulsive (only reliant on the immediately prior action) and gradual perseveration (reliant on multiple past actions), respectively. In all combinations of time point and block, the M1m model was most favored (with an exceedance probability of over 99%)

Model Fits and Simulations of Behavior

First, we checked the trial-by-trial choice accuracies of participants in the task. Figure 4A shows the observed and model-predicted choice probabilities for better options over trials. They are almost overlapped, showing good prediction by both the M0 and M1m models (orange and blue lines respectively) as an average. In the observation (black lines), after the reversals, the participants were temporarily unable to choose the better option, but they chose better ones at a rate of about 70% on average through the task (Time 1 WV: 0.72; Time 1 LV: 0.66; Time 2 WV: 0.76; Time 2 LV: 0.70).

Fig. 4

Observed behavior and model performance. A Trial-by-trial observed choice probabilities (black) and model-predicted choice probabilities (orange: M0, blue: M1m) of better options. Better options were defined at each trial as the option that had a higher probability of getting a win in the win-volatile (WV) block or of preventing losses in the loss-volatile (LV) block. The dashed lines represent the reversal points of the better option. The average among the participants for each block (LV or WV) at each time point (Time 1 or Time 2) are shown. B Predictive performance by the models. The left-most panel shows the mean choice probabilities of the better option around the reversal points, and the middle-left panel shows the mean stay probability around the reversal points. The middle-right panel shows stay probabilities per feedback condition, and the right-most panel shows win-stay/loss-shift probabilities. The observed data are shown as black lines or gray bars, and the model predictions are shown as colored lines or dots (orange: M0, blue: M1m). C Generative performance by the models. The observed data are the same with those shown in B. Behavior generated by the models appear smoother compared with the observed data because of the probability-based outcome schedule in the simulation. Error bars represent the standard errors

Next, we examined whether the behavioral traits in the task, which include elements that do not directly correspond to the likelihood-based model selection, can be predicted and/or generated by the M0 and M1m models. Here, we used the data from Time 1 as there were no noted differences between blocks and between time points, and focused on the four aspects of behaviors: choice accuracy before and after reversal, stay probability before and after reversal, stay probability per feedback condition, and win-stay/loss-shift probabilities. Figure 4B shows the predictive performance of the models. Regarding the choice accuracy (left-most panel), which is a summary of Fig. 4A around the reversal points, both models well predicted the observation. On the other hand, stay probability-based measures were better captured by the M1m model than the M0 model. The M0 model underestimated the stay probability overall (middle two panels). Especially, its prediction was worse after reversal (middle-left panel). Furthermore, underestimation of stay probability led to the overestimation of loss-shift and underestimation of win-stay probabilities (right-most panel). These tendencies were retained in the results of generative performance which were produced by simulations using different outcome sequences from those of the experiment (Fig. 4C). The model-generated behavior looks smoothed because the probabilistically generated outcomes were used in the simulations. Thus, both predictive and generative performance of the M1m model were better than the M0 model especially for the stay-probability based measures.

Parameter Estimates

The parameter estimates for M0 and M1m are listed in Table 1. Figure 5 also shows the estimated mean learning rates. The estimated learning rates were clearly lower in M0 (left panels) than M1 (right panels). We conducted a three-way analysis of variance (ANOVA) for each model that included the within-subject factors of time point (Time 1 or Time 2), block (WV block or LV block), and domain of the learning parameters (${\alpha }_{W} \mathrm{and} {\alpha }_{L}$) to examine whether we could replicate a previous finding that learning rates were higher for volatile conditions than for stable conditions (Pulcu & Browning, 2017).

Table 1 Estimated parameter values. The estimated parameter values for M0 and M1m in win-volatile (WV) and loss-volatile (LV) blocks, respectively, are shown as the median and 25th and 75th percentiles across participants. The negative log likelihood (nLL) and negative log marginal likelihood (nLML) are also shown. Median values are presented in bold

Fig. 5

Estimated learning rate. The parameters were estimated with the M0 model (left panels) or M1m model (right panels). The panels show the estimates according to block (LV: loss-volatile block, WV: win-volatile block) and time point (Time 1 or Time 2). Gray and white represent the estimated values of ${\alpha }_{L}$ and ${\alpha }_{W}$, respectively. Error bars display the standard errors

The interaction of block and domain of the learning parameters was significant in both models, with a higher effect size in M0 than in M1m [M0: F(1, 452) = 26.53, p < 0.001, ${\eta }^{2}= .055$; M1m: F(1, 452) = 4.66, p = 0.031, ${\eta }^{2}= .010$]. In the M0 model, post hoc analysis revealed that, regarding the effects of volatility on the learning parameters, the estimates were significantly higher in conditions with higher outcome volatility; specifically, ${\alpha }_{W}$ was higher in WV blocks than LV blocks (p = 0.004), and ${\alpha }_{L}$ was higher in LV blocks than WV blocks (p < 0.001). However, this pattern was not seen when the M1m model was used. Post hoc analysis revealed higher ${\alpha }_{W}$ in WV blocks than LV blocks (p = 0.026) but no significant difference in ${\alpha }_{L}$ between block types (p = 0.439). In other words, the previously reported influence of volatility on the learning rate was almost entirely erased by including a perseveration term. Furthermore, the estimates were higher for ${\alpha }_{W}$ than ${\alpha }_{L}$ in both blocks regardless of the models [M0: p < 0.001 in the WV block, p = 0.095 in the LV block; M1m: p < 0.001 in both the WV and LV blocks]. These results failed to show the effect of volatility on the learning parameter, and instead seemed to show positivity-bias-like phenomena (Lefebvre et al., 2017; Palminteri & Lebreton, 2022; Palminteri et al., 2017a).

Figure 6 shows the results regarding the inverse temperature ($\beta$). The estimated values were larger in the M0 model than in the M1m model. The model results were investigated with a two-way ANOVA that included the factors of time point (Time 1 and Time 2) and block (WV block and LV block). We found a main effect of block [M0: F(1, 452) = 40.02, p < 0.001, ${\eta }^{2}$= 0.081; M1m: F(1, 452) = 37.14, p < 0.001, ${\eta }^{2}$= 0.076] and time point [M0: F(1, 452) = 61.33, p < 0.001, ${\eta }^{2}$= 0.120; M1m: F(1, 452) = 79.98, p < 0.001, ${\eta }^{2}$= 0.150] in both models but no interaction effect.

Fig. 6

Estimated inverse temperature. The parameters were estimated with the M0 model (left panels) or the M1m model (right panels). The panels show the estimates for each block (LV: loss-volatile block, WV: win-volatile block) at each time point (Time 1 or Time 2). Error bars represent the standard errors

Thus, the experimental results can be summarized by the following three points. First, the model comparison favored the model with gradual perseveration (M1m) over the other models. Second, the exclusion of the perseveration term led to smaller learning rates (both ${\alpha }_{W}$ and ${\alpha }_{L}$) and a larger inverse temperature ($\beta$). Third, previous findings of increased learning rates under volatile conditions compared to stable conditions were replicated only when the model did not include a perseveration term.

Magnitude of the Estimation Bias

In the previous section, we confirmed that the model without a perseveration term (M0) had lower learning rates and a higher inverse temperature than the best-fit M1m model, which included a perseveration term. The magnitude of the observed bias is expected to correlate with the intrinsic perseveration of the data ($\phi$ in the M1m model). The data shown in Fig. 7 support this prediction. The larger the value of $\phi$ in the M1m model was, the smaller the values of the parameters ${\alpha }_{W}$ and ${\alpha }_{L}$ in the M0 model compared with those in the M1m model [r =  − 0.56 (p < 0.001) and r =  − 0.54 (p < 0.001), respectively, including all data]. On the other hand, the larger the value of $\phi$ in the M1m model was, the larger the value of the parameter $\beta$ in the M0 model compared with that in the M1m model [r = 0.59 (p < 0.001) including all data].

Fig. 7

Correlation between the magnitude of the estimation bias in the M0 model and the value of $\phi$ in the M1m model. “∆ Estimates” represents the magnitude of the estimation bias, which was calculated by subtracting the parameter estimates ($\alpha_L$, $\alpha_W$, and $\beta$) of the M1m model from those of the M0 model. The larger the value of $\phi$ in the M1m model was, the smaller the values of $\alpha_W$ and $\alpha_L$ estimated in the M0 model. The larger the value of $\phi$ in the M1m model was, the larger the value of $\beta$ estimated in the M0 model

Value Calculation Vs. Choice Perseveration

Do our choices rely more on the value-calculation process or the simple choice-perseveration process? This question has not been examined in detail, but Palminteri (2021) investigated past studies and summarized it as a comparison of $\beta$ and $\phi$; on the whole, people rely more on the value-calculation process than the simple choice-perseveration process. Our finding was consistent with this finding and was stable regardless of block condition or time point. Table 2 summarizes the mean values, the results of the t test, and Pearson’s r between the parameters $\beta$ and $\phi$. In the t test, the absolute values of $\phi$ were also used to compare the absolute strength of the two processes. $\beta$ exerted a stronger influence on choices than $\phi$ over all blocks and time points. In addition, these two parameters were positively correlated.

Table 2 Comparison between the parameters $\beta$ and $\phi$. Mean estimates of the parameters $\beta$ and $\phi$, the results of the t test and Pearson’s r between the parameters for each time point and block

Parameter Reliability

Stability of Parameter Values

First, we examined test–retest reliability. Table 3 shows the coefficients r for the parameter estimates between the blocks at each time point (“WV vs. LV at Time 1” and “WV vs. LV at Time 2” in the table) and between the two time points for each block type (“Time 1 vs. Time 2 for WV” and “Time 1 vs. Time 2 for LV” in the table). Among the parameters, $\beta$ and $\phi$ showed relatively high stability both between blocks and between times, while ${\alpha }_{W}$, ${\alpha }_{L}$, and $\tau$ did not. Regarding the two learning-rate parameters, we compared their stabilities over time (“Time 1 vs. Time 2” in Table 3) and found significantly better stability of ${\alpha }_{W}$ compared with that of ${\alpha }_{L}$ especially in the WV block (Supplementary text2 and Fig. S1).

Table 3 Stability of parameter values estimated by the best-fit model, M1m. Rows “Time 1 vs. Time 2” show the comparisons in the same block type between two time points; rows “WV vs. LV” show the comparisons between the two block types at the same time point

Table 3 also shows the results of the t test between blocks and between time points to determine the absolute change of each parameter. Regarding $\beta$ and $\phi$, the values increased at Time 2 compared with Time 1 (ps < 0.01). That is, the participants were more value-dependent and more likely to repeat recent actions at Time 2.

For comparison with these findings regarding model parameter reliability, we calculated the test–retest reliability of the questionnaires (Table S3). The Pearson’s correlation coefficients for the questionnaires between the two time points were most often more than 0.8; thus, they showed better stability than model parameters.

Parameter Recovery

Figure 8 shows the results of Pearson’s correlation analyses between the true parameter values of the synthetic data and the recovered parameter values (diagonals), and between recovered parameter values (off diagonals). The results of both blocks were similar as we used the same true parameter values set and symmetric feedback between WV and LV blocks.

Fig. 8

Parameter recovery analysis of the best-fit M1m model for the win-volatile block and loss-volatile block. The confusion matrices represent the mean of the Pearson’s correlations between parameters over 100 simulations. Each simulation includes 100 subjects whose true parameter values were randomly and independently sampled from uniform distributions and common among the win-volatile (WV) and loss-volatile (LV) blocks. The values on the diagonal represent correlations between simulated and estimated parameters. Off-diagonal values represent cross-correlations between estimated parameters

Regarding the recovery correlations shown in the diagonals, the parameters $\phi$ and $\beta$ showed the best recoveries with r = 0.93 and r = 0.76, respectively. The two learning rates (${\alpha }_{W}$ and ${\alpha }_{L}$), which are the main focus of researchers that use this task, showed parameter recoveries of r = 0.70.

Regarding the cross correlations shown in the off diagonals, most of them were small although there were weak negative correlations between $\phi$ and $\beta$ (WV: r =  − 0.17; LV: r =  − 0.19). Intriguingly, the correlation pattern between $\phi$ and $\beta$ was opposite in the estimates from experimental data showing moderate positive correlations (see Table 2, 0.48 < r < 0.69). This result tells us that humans may have meaningful positive correlations for behavior relating to value-dependency and perseveration in the current task, which cannot be attributed to artifacts in the estimation process.

The accuracy of parameter recovery is an upper limit of the test–retest reliability reported in the above section. However, parameter recovery alone does not determine the test–retest reliability, of course. For example, the difference in test–retest reliability between learning rates and inverse temperature (Table 3) appears to be larger than expected from their difference in the parameter recovery results (the diagonals of Fig. 8), suggesting that there are true differences in temporal stability between the parameters.

Simulation Results

Next, we conducted computational simulations to explore the following questions: How is the magnitude of the estimation bias in the parameters affected by the strength of preservation in the generative model? Is the magnitude of estimation bias influenced by the task settings? What is the underlying mechanism of the estimation bias? To address these questions, in the following simulations, we first generated synthetic data and then compared the estimated parameter values with the true parameter values. The first of these questions was examined using the same task settings as the experiment; the second and third were examined using a simplified task to clearly elucidate the phenomena.

Perseveration Strength and Estimation Biases

We simulated the effect of perseveration strength on parameter estimation bias (of ${\alpha }_{W}, {\alpha }_{L}, \mathrm{and} \beta$) when the perseveration term was not included in the fitting model. Here, the generative models included a perseveration term of various strengths. The true parameter values were fixed based on the estimates from the experimental data $({\alpha }_{W}=0.45,{\alpha }_{L}=0.35,\beta =4.0, \mathrm{and} \tau =0.6)$, while the perseveration strength ($\phi$) increased from 0 to 4 in steps of 0.5. We generated 1000 synthetic datasets using the M1m model for each parameter set. Figure 9A and B show the estimates from the M0 and M1m models for these generated data. Regarding the learning rate, the stronger the true perseveration was, the lower the estimated learning rate (left and middle panels of Fig. 9A). Given the estimates of $\phi$ in our experiment, the magnitude of the possible estimation bias in experimental studies was non-negligible. Indeed, in our experiment, the median value of $\phi$ was almost 2.0 (see Table 1). In the current simulation, this value was sufficient to halve the estimated values of $\alpha$ in the model that lacks a perseveration term. This finding implies that, for example, if two participants have different perseveration strengths and the same learning rate, a false difference in the learning rates will be detected if a model without perseveration is used.

Fig. 9

Parameter estimation bias in the model without and with perseveration. The three columns show the estimated parameters $\alpha_W$, $\alpha_L$, and $\beta$ when fitting the synthetic data with the model without a perseveration term (A; the M0 model) and with the model with gradual perseveration (B; the M1m model). The M0 model underestimates the learning rates and overestimates the inverse temperature. Error bars indicate the standard errors of the mean

In addition, the magnitude of this bias was weaker in WV blocks than in LV blocks for ${\alpha }_{W}$ (Fig. 9A, left panel), but the reverse was true for ${\alpha }_{L}$ (Fig. 9A, middle panel). In other words, the learning rates were estimated to be larger in volatile blocks than stable blocks even if the true learning rates were the same. These phenomena are intuitively consistent with the interaction observed in the M0 model in our experiment (Fig. 5, left panels).

We also explored the inverse temperature, $\beta$. For this parameter, estimates tended to be larger than the true value; this tendency was most obvious in the M0 model and less obvious in the M1m model. In the M0 model, the estimated values of $\beta$ were more than twice the true value when the true value of $\phi$ was more than 2.0. This result was again consistent with our estimation results from the experiment, showing larger values of $\beta$ from the M0 model than the M1m model (see Fig. 6). This result implies that parameter estimates from the model without perseveration may be misleading. For example, when comparing two groups, if one group had a stronger tendency to repeat their past choices regardless of the experienced outcomes, researchers are likely to conclude that this group relies more heavily on outcome history than the other group from the comparison of $\beta$ estimates. Thus, the group difference would be interpreted only as the difference in values of $\beta$ and not attributed to perseverance, which is the true origin of the group difference.

The possible mechanisms underlying these biases are discussed in the “Possible mechanism underlying estimation bias” section.

Influence of Task Setting on Estimation Bias

Simulations in this section used a simplified task where only win domain was used as feedback (i.e., this simplified task did not have loss domain outcomes); thus, the corresponding model included only a solo learning rate parameter, which facilitates interpretation of the influence of the missing perseveration term on the other model parameters. The number of trials was set at 200.

We first examined the influence of task settings (the reward probabilities and their reversal frequency) on estimation bias when the generative model includes a perseveration term (the M1m model) but the fitting model does not (the M0 model). We also varied the true perseveration strength while fixing the true values of the other parameters at $\alpha =0.4$, $\beta =4$, $\mathrm{and} \tau =0.5$. We generated 500 synthetic datasets using the M1m model for each combination of reward probability (50:50, 70:30, 80:20, and 90:10), reversal frequency (0, 1, and 3), and true perseveration strength (none: $\phi =0$, mild: $\phi =2$, and strong: $\phi =4$). Then, the generated data were fitted with the M0 model. Figure 10 shows the results of parameter estimates. Overall, the stronger the true perseveration strength was, the lower the estimated parameter $\alpha$ and the higher the estimated parameter $\beta$. These tendencies were robust regardless of task settings, while the estimation bias seemed to be slightly stronger in the condition with random reward probability.

Fig. 10

Influence of the task settings on parameter estimation bias. The results for parameters $\alpha$ (left) and $\beta$ (right). Simulated data were generated by tasks with different reward probabilities (50:50, 70:30, 80:20, and 90:10) and reversal frequency (0, 1, 3) for the two presented options. The generative model was the M1m model, and the fitting model was the M0 model. Error bars indicate the standard errors of the mean

Possible Mechanism of the Observed Biases

Model parameters can be more or less interdependent. Here, we clarified whether both the learning rate and inverse temperature exhibited direct estimation bias by excluding perseveration parameters or the parameter that exhibited indirect estimation bias, as it was influenced by the parameter that exhibited direct estimation bias. For this purpose, the synthetic datasets with mild perseveration ($\phi =2$) generated in the previous section were fit by the following four models.

• M0: a model with two free parameters, $\alpha$ and $\beta$

• M0_fixed $\alpha$: a model with a fixed parameter $\alpha$ and a free parameter $\beta$

• M0_fixed $\beta$: a model with a fixed parameter $\beta$ and a free parameter $\alpha$

• M1m: a model including a gradual perseveration component: $\alpha ,$ $\beta$, $\phi$, and $\tau$

The synthetic data were fit by the above four models by setting the fixed parameters to the true parameter values ($\alpha =0.4$, and $\beta =4$). Figure 11 shows the estimated values of $\alpha$ (left) and $\beta$ (right).

Fig. 11

Simulated estimation bias. The panels show the estimated values of $\alpha$ (right) and $\beta$ (left) from the four fitting models: M0, M0_fixed $\alpha$, M0_fixed $\beta$, and M1m. The reward probabilities were 50:50, 70:30, 80:20, or 90:10. The reversal frequency was set to 0, 1, or 3. Error bars indicate the standard errors of the mean

Comparing the results for $\alpha$ and $\beta$ provided important insight into the mechanism underlying bias due to the lack of a perseveration term. Regarding the parameter $\alpha ,$ a fixed $\beta$ value did not affect the magnitude of the estimation bias caused by the lack of perseveration term (see Fig. 11 left panel and compare $\alpha$ values between the M0 and M0_fixed $\beta$ models). That is, when a model lacks a perseveration component, the parameter $\alpha$ is directly negatively biased (i.e., to a lower value than the true value). On the other hand, regarding the parameter $\beta$, a fixed $\alpha$ value suppressed the estimation bias (see Fig. 11 right panel and compare the $\beta$ values between the M0 and M0_fixed $\alpha$ models). That is, the parameter $\beta$ is positively biased (i.e., produces higher values than the true value), especially when the parameter $\alpha$ is a free parameter. This result suggests that the lack of a perseveration term indirectly biases $\beta$; in other words, this absence first biases the estimation of $\alpha$, and then the change in $\alpha$ leads to bias in the value of $\beta$.

A possible explanation as to why the lack of a perseveration term first affects the $\alpha$ value is that lower values of $\alpha$ stabilize the option values, which can mimic the data characteristics caused by the perseveration (i.e., repeating the same choice). However, small $\alpha$ values simultaneously reduce the absolute difference in option values. Therefore, increased $\beta$ values may mitigate this reduction if $\beta$ is also a free parameter (i.e., if the M0 model is used). In contrast, changes to the $\beta$ value alone cannot mimic perseveration without the value stabilization provided by decreases in $\alpha$ values.

However, the parameter $\beta$ is also directly positively biased in situations in which there is a clear better option (e.g., 90:10 reward probabilities) and the reward probability is stable over the trials (e.g., no reversal condition). In such a situation, perseveration, i.e., repetition of the same action, can be expressed by value-dependent choices. Thus, the lack of a perseveration term is complemented by increases in the $\beta$ value. However, when the reward feedback is provided at random (e.g., 50:50 reward probability), the lack of a perseveration term is complemented by decreases in the $\beta$ value.

Discussion

Abundant research has shown that RL models contribute to an understanding of basic features or abnormalities in human information processing. These advances are based on interpretations of model parameters. However, studies often neglect the possibility of model misspecification and/or lack information on parameter reliability, which can mislead interpretations. Regarding the problem of model misspecification, this study focused on a perseveration term, which incorporates the effect of choice history on decision-making processes. Our experimental data showed that participant choices are well captured by including this term. Furthermore, if the RL model fitted to the data lacks a perseveration term, the value-calculation process results in undesirable estimation biases. Regarding reliability of RL model parameters, we conducted the same task twice with a 1.5-month interval and found poor (e.g., learning rates) to moderate (e.g., inverse temperature and perseveration strength) test–retest reliability and systematic changes reflecting the learning effect.

Parameter Estimation Bias in the RL Model Without a Perseveration Term

We showed that the lack of a perseveration term in an RL model leads to a decrease in the learning rate and increases in the inverse temperature. By examining models’ ability to predict and generate behavioral trends, we revealed that a model without a perseveration term underestimated win-stay probabilities and overestimated loss-shift probabilities. Furthermore, the bias magnitude correlated with the intrinsic perseveration, i.e., the tendency to repeat actions, in the data. Thus, the lack of a perseveration term can easily induce misinterpretations of parameters related to the value-calculation process. For example, consider a case where a group of depressed patients exhibits a lower perseveration tendency than a control group, although both exhibit equal value-based calculation. If researchers fit an RL model without a perseveration term, they will incorrectly find a lower inverse temperature in the patient group than the healthy group, which will lead to misinterpretations and may affect patient treatment. To prevent such misinterpretations, we recommend that analyses include a model with a perseveration term at least as a candidate for model comparison.

In addition, our simulations showed that the underestimates of learning rates due to use of a model without a perseveration term are slightly stronger in stable conditions than in volatile conditions. This bias can mimic the previous finding of a higher learning rate in volatile conditions than in stable conditions (Browning et al., 2015; Pulcu & Browning, 2017; Pulcu et al., 2019). Our experimental data replicated this finding when applying a model without a perseveration term but not when applying a model with a perseveration term. Therefore, part of the difference in learning rates attributed to volatility may actually be due to using a model without a perseveration term. This result occurred in our experimental data but does not immediately refute the possibility that volatility influences learning rates. For example, Gagne et al. (2020) used a model with a perseveration component (a choice kernel) and still reported volatility-based learning rate adjustment. Using RL models with a perseveration term in the future will help clarify the effect of volatility on learning rates.

Regarding the learning rates, it is also notable to mention that our result was in accordance with positivity biases reported as learning rate asymmetry (Lefebvre et al., 2017; Palminteri & Lebreton, 2022; Palminteri et al., 2017a). Although original positivity bias in the RL model was defined as the asymmetric learning rates depending on the prediction error (more weight on positive prediction errors than negative prediction errors), our finding is about asymmetric learning rates for win vs. loss domains. Despite these differences, our results supported a similar positivity bias in which positive outcomes are weighted more heavily. This was particularly evident in the model that included a perseveration term.

Using simulations, we also investigated the influence of task settings (such as reward probabilities and reversal frequency) on estimation biases. The estimation biases were consistently high across all task settings, and setting differences seemed to have negligible effects. However, these simulations had implications for appropriate task settings. For example, we found that estimation biases are slightly larger with random action-outcome contingencies but that when the action-outcome contingency is too extreme, even the model with a perseveration term showed estimation bias.

Possible Mechanism Underlying Estimation Bias

Our simulation results demonstrated that the lack of a perseveration term directly affects the learning rate estimations but indirectly affects the inverse temperature estimations (although some of the bias is still caused directly). The mechanism underlying this pattern may be explained as follows. A lower learning rate, $\alpha$, stabilizes the option values and their relative order. However, because the decrease in $\alpha$ reduced the differences among option values, the inverse temperature, $\beta$, was increased to enhance the impact of differences among option values on the choice probability, which resulted in repeated selection of the same option (i.e., perseveration-like choices). On the other hand, increased $\beta$ values alone cannot mimic action perseveration unless the value differences are stable (i.e., through decreases in $\alpha$).

We also found a nuanced interaction of bias regarding learning rates. That is, the underestimation of learning rates is slightly greater in stable conditions than in volatile conditions, leading to slightly larger learning rates in volatile conditions than in stable conditions (Fig. 9). The mechanism underlying the interaction between the learning rate and block volatility observed in the model without a perseveration term can be explained as follows. In the WV block, pursuing win outcomes rather than avoiding loss outcomes produces perseveration-like behavior. This is because the win outcomes are highly likely to accompany one option, while the loss outcomes are randomly distributed between two options. The opposite is true in the LV block. Thus, as this task’s volatility was linked with its predictability, the learning rate for wins, ${\alpha }_{W}$, was higher in the WV block compared to the LV block, and the learning rate for losses, ${\alpha }_{L}$, was higher in the LV block compared to the WV block, thus mimicking perseveration-like behavior. As mentioned in the “Parameter Estimation Bias in the RL Model Without a Perseveration Term” section, this interaction produces a phenomenon in which volatility appears to influence the learning rate.

Disentangling the interaction between the model parameters and clearly explaining the mechanism underlying estimation bias is not always straightforward. However, understanding both aspects is key to understanding the nature of bias; this knowledge could be applied to other bias problems that arise elsewhere. In addition, these findings provide hints toward the construction of appropriate models and appropriate task settings.

Relationship Between Value Calculation and Choice Perseveration

A model-neutral analysis and the model comparison showed that both value-calculation and choice-perseveration processes influence choices on the task. The effect of the former was significantly stronger than that of the latter. That is, there was a larger influence of inverse temperature, $\beta$, than the perseveration size, $\phi$, on decision-making. This finding is in accordance with that of Palminteri (2021), but as he also pointed out, the type of task used may influence which parameter has a larger impact on choices.

In addition, there was a strong positive correlation between $\beta$ and $\phi$ in our data. However, this correlation does not mean that the two parameters reflect the same data characteristics. As mentioned in the previous section, the overestimation of $\beta$ by a fitting model that lacked a perseveration component ($\phi$) was due to the indirect effect caused by the direct underestimation of $\alpha$. This finding implies that the two parameters, $\beta$ and $\phi$, capture different characteristics of the choice data.

Regarding the observed positive correlation between $\beta$ and $\phi$, there are two possibilities: a pseudo correlation occurred in the estimation process and a reflection of a meaningful feature of human behavior in this kind of task. The former possibility can be refuted based on the results of parameter recovery where we could not find a positive correlation between $\beta$ and $\phi$ (on the contrary, there was a weak negative correlation). Thus, the second possibility is likely the case. We think the positive correlation is caused by the task structure. The current task is a kind of reversal learning task; thus, both the outcome-based value calculation and a period of repetition of the same choice led to better outcomes. Then, those participants who understand well the structure of the task probably showed higher $\beta$ and $\phi$ values and these parameters showed a positive correlation. This possibility is supported by the fact that both parameters were higher in time 2 where a learning effect from time 1 might exist. The detailed analyses on this possibility are in the Supplementary text 3, Fig. S2, and Table S2.

Reliability Differences Between the Model Parameters

In our study, $\beta$ and $\phi$ showed better test–retest reliabilities and parameter recoveries than ${\alpha }_{W}$, ${\alpha }_{L}$, and $\tau$. These differences in parameter reliability possibly originate partly from the model structure. While $\beta$ and $\phi$ are the parameters that determine the weight of the specific information processes (value calculation and choice perseveration), ${\alpha }_{L}$, ${\alpha }_{W}$, and $\tau$ are the parameters that modify the contents of these processes. In an extreme example, if $\beta$ and $\phi$ were zero or very small, the values of the other parameters would not be meaningful. Thus, the estimates of ${\alpha }_{L}$, ${\alpha }_{W}$, and $\tau$ are inevitably noisier than those of $\beta$ and $\phi$. A previous study reported better parameter generalization for $\beta$ than $\alpha$ after comparing the parameters among different tasks (Eckstein et al., 2022). We speculate that these generalization differences may be partly caused by the differences in parameter reliability.

There are studies that have examined the parameter stability of RL models using tasks relating to the current study. A study using probabilistic learning tasks (a two-armed bandit and a reversal learning task) reported that the test–retest reliability of inverse temperature was better than those of the learning rates for gain and loss outcomes (Schaaf et al., 2023). Their study also parallels ours in its use of a large internet sample and a comparable interval between tests (5 weeks vs. 1.5 months). A study using a task to examine affective bias (the go/no-go task) also reported low test–retest reliability of a learning rate although it is not a main parameter of this task (Pike et al., 2022). On the other hand, Mkrtchian et al. (2023) reported generally good reliability including learning rates using a four-armed bandit task with win-and-loss outcomes in each trial as was used in the current task. The difference in the results of those studies and ours may be due to a different test–retest interval (2 weeks or 1.5 months) or trial length (200 or 100) as well as task, modelling, or parameter estimation methods. As a direction of future studies, it would be prudent to assess task-specific (additionally considering the difference in task settings, estimation methods, or interval lengths) reliability. Information on parameter reliabilities is important for discerning limitations in the interpretation of model parameters when models are applied to examine individual differences or used in the clinical field. It is also important to note differences in parameter stability, as stable parameters may facilitate the detection of group differences or correlations compared to noisy parameters in some contexts.

Overall Reliability of Model Parameters

In a comparison with self-report questionnaires, the reliability of the model parameters was not as excellent overall, consistent with a previous study (Enkavi et al., 2019; Moutoussis et al., 2018). It may reflect that variables from behavioral tasks have low between-subject variability and high within-subject variability, compared with variables of self-report questionnaires (Enkavi et al., 2019). High within-subject variability of parameters may be partly explained by one’s mood varying over time (Schaaf et al., 2023). In addition, low accuracy in parameter recovery cause within-subject variability and put an upper limit on test–retest reliability. In our study, parameter recovery, defined as correlations between true and simulated values, was around 0.7 (except for that of the perseveration strength, which was 0.9). There is a possibility that using a task with longer trials would improve parameter recovery. Shahar et al. (2019) reported fewer than 1000 trials were insufficient for recovery of their parameter of interest (as for our study, 100 trials were performed for model parameter estimations). Although task length depends on task difficulty and model complexity, it is often difficult to apply long tasks in experiments with human participants because participants may become bored and thus respond with random or fixed choices. In addition, if the task is intended to be used for clinical patients, shorter durations are desirable.

A solution that has received substantial attention in recent years is the use of other estimation methods, such as empirical priors (Gershman, 2016) or hierarchical Bayesian techniques (Brown et al., 2020; Katahira, 2016; Piray et al., 2019). Although the issue of shrinkage warrants caution when using these techniques (Scheibehenne & Pachur, 2015), they have been shown to increase estimation accuracy and improve test–retest reliability. However, differences in estimation methods cannot always compensate for parameter estimation when the task design is a main cause of inadequate parameter reliability (Spektor & Kellen, 2018). Alternatively, the use of other information, such as choice reaction time, in parameter estimation may improve estimation (Ballard & McClure, 2019; Shahar et al., 2019). The use of latent variables or factor scores from several tasks for examining the same cognitive function may also be a candidate solution to overcome the inherent inevitable noises in individual tasks (Friedman & Banich, 2019).

Learning Effect on Model Parameters

We found increments of the values of $\beta$ and $\phi$ at Time 2 reflecting a learning effect as discussed in the “Relationship Between Value Calculation and Choice Perseveration” section. The task used in the current study can be seen as a kind of reversal learning task. A reversal learning task is a typical task used with RL models but once the task is experienced, participants have a settled value-based strategy and random choices are reduced (reflected as larger $\beta$ values). Participants also learn the approximate number of trials until reversal and notice that repeating one option and neglecting rare bad outcomes for a while are beneficial (reflected as larger $\phi$ values).

It would be noted that such a learning effect should be a limitation of using the RL parameters as trait-like indices. These features of model parameter possibly occur in other learning tasks and are sometimes inevitable. They should be considered in assessments of parameter stability and in the use of model parameters to assess cognitive function.

Limitation

This study assessed the effect of model misspecification on model parameters and the reliability of model parameters. However, a proper computational model may change depending on the task and the same model parameters may show different levels of stability under different parameterization. For example, the current model formalized the processing of learning from dichotomic outcomes. This is an advantage of model simplification by neglecting flexible human valuation processing for various magnitudes of feedback. However, the results may change if a researcher is interested in another task that has various outcome magnitudes or another environment with different volatility.

It would be necessary to obtain information about what causes model reliability differences and to understand possible adverse effects of model misspecification for proper use of computational models as a tool to detect individual differences in cognitive function, track changes under development, and characterize mental illnesses.

Conclusion

In this study, we first clarified the estimation biases on learning rates and inverse temperature in a model without a perseveration term and its mechanism. Our findings showed that these biases were strong and could easily distort study conclusions. When the data are partly characterized by repetition of the same actions, independent of outcome history, we recommend using a model with a perseveration term. Second, we provided information about model parameter reliability. The test–retest reliability varied with model parameters, and that of the learning rates was worse than that of the inverse temperature. Also, some parameters showed a learning effect with an increment of the estimates in the second session. We recommend bearing in mind that parameter stability limits the study conclusions that can be drawn from the values of the parameters.

The simple truth is that a computational model is a hypothesis of information processing; thus, it inevitably possesses some level of estimation bias and noise. We believe that understanding possible estimation biases in parameters due to model misspecification as well as assessing and attempting to improve parameter reliability are necessary steps to deriving computational models that accurately describe individual differences and provide meaningful and profound insights.