Introduction

Decision-making has been a focus of psychological research for decades. In many decision-making contexts, time pressure is of critical importance. A well-studied decision outcome of time pressure is the speed-accuracy trade-off (SAT): a decision-maker can improve the accuracy of their decisions at the expense of taking longer to respond, or they can make very quick decisions that are more likely to be erroneous (Schouten and Bekker 1967; Wickelgren 1977). This pattern of results produces the trade-off between speed and accuracy, and it is the task of the decision-maker to balance the relationship between accuracy and speed to achieve their desired level of performance (cf. Bogacz et al. 2006).

A range of experimental manipulations have been used to elicit the SAT in previous research (see Heitz 2014 for an overview). Cue-based SAT is arguably the most frequently used speed-accuracy manipulation. The cues are typically verbal prompts instructing participants to focus on responding correctly or responding speedily (Hale 1969; Howell and Kreidler 1963). Another common SAT manipulation uses response deadlines (Ratcliff and Rouder 2000; Van Zandt et al. 2000). Response deadlines usually involve a visual or auditory message following each trial if the participant did not respond sufficiently fast. In most cases, the deadline is pre-specified by the experimenter. Recently, some authors have combined the two SAT manipulations into one design (e.g., Forstmann et al. 2008; Mulder et al. 2013; Wagenmakers et al. 2008). Although both manipulations produce a manifest SAT in behavioral data,Footnote 1 we hypothesize that the cognitive processes invoked by the two manipulations differ. In the current paper, we test this hypothesis in three experiments and show that choices and response times differ between cue-induced SAT conditions and deadline-induced SAT conditions. We also show that these differences can be attributed to different latent component processes of the popular diffusion decision model (DDM) of choice response time (Forstmann et al. 2016; Ratcliff 1978; Ratcliff and McKoon 2008; Ratcliff and Rouder 1998).

A standard practice in perceptual decision-making research has been the application of sequential sampling models, also known as evidence accumulation models, to draw inferences about the cognitive processing mechanisms underlying decision-making (Forstmann et al. 2016; Gold and Shadlen 2007; Mulder et al. 2014; Ratcliff and McKoon 2008; Ratcliff et al. 2016).Footnote 2 These models hypothesize that decisions involve accumulation of sensory information in favor or against certain choices at hand. Accumulation stops when enough information has been collected to support some specific choices. The stopping point represents the uncertainty that the decision-maker is willing to accept on the correctness for this particular choice: more lenient stopping points correspond to greater uncertainty.

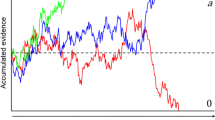
Within the class of sequential sampling models, the DDM (Ratcliff 1978; Ratcliff and McKoon 2008) is an important tool for isolating and understanding the cognitive processes that underlie decision behavior, because of its demonstrated ability to provide a quantitatively precise account of the response time (RT) distributions of correct/error responses in two-alternative forced choice tasks (Ratcliff and McKoon 2008; Ratcliff and Rouder 1998; Ratcliff and Smith 2004; Ratcliff et al. 2016). To account for time pressure in decision-making, the DDM assumes a set of two thresholds, one for each of the possible response options (Fig. 1, left panel). The decision-maker’s willingness to commit to decisions with greater uncertainty is translated into thresholds that are close to the starting point of the accumulation process (green lines). This response regime means that the accumulation process often reaches one of the two thresholds before much accumulation has even taken place; this leads to fast responses that are often erroneous. Conversely, thresholds that sit further from the starting point (blue lines) represent a more conservative decision strategy whereby the decision-maker accumulates a greater amount of evidence before committing to a decision; this leads to slower but more accurate responses. Such changes between low and high thresholds have provided a good explanation of SAT behavior across a range of contexts (Bogacz et al. 2010; Forstmann et al. 2008; Ratcliff and McKoon 2008; Ratcliff and Rouder 1998; Voss et al. 2004; Wagenmakers et al. 2008), although the link between the computational explanation of SAT and its low-level neural implementation is still a matter of active research (e.g., Heitz and Schall 2012; Reppert et al. 2018).

Fig. 1
figure 1

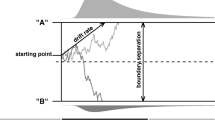
Different assumptions in diffusion models. Left panel: the standard diffusion decision model (DDM) assumes thresholds that are fixed throughout the course of a decision and only vary with respect to the distance between lower and upper threshold. Green thresholds indicate a speedy response regime; blue thresholds indicate a more accurate response regime. Right panel: DDM with collapsing thresholds where the slope indicates the amount of evidence required to make a decision as a function of elapsed decision time, and distance between the thresholds at time 0 indicates the initial response caution

Full size image

In contrast to the fixed-threshold adjustment explanation of the cue-used SAT, Frazier and Yu (2008), Cisek et al. (2009), and Thura et al. (2012) gave different but converging explanations about the cognitive processes involved when decision-makers are faced with deadlines (see also Malhotra et al. 2017). According to Frazier and Yu (2008), a stopping rule in the form of thresholds that dynamically move toward one another (decline) throughout the course of a decision provides a mechanism that ensures the decision-maker responds before a deadline, whether that deadline is internally or externally imposed, in the most efficient way (Fig. 1, right panel). Frazier and Yu (2008) argue that in the presence of response deadlines, thresholds that monotonically and nonlinearly collapse over time is the optimal decision-making strategy (i.e., the decision policy that maximizes reward over a series of trials). In a similar vein, Cisek et al. and Thura et al. proposed a decision-making model that incorporated an urgency signal that increases with elapsed decision time; this can be viewed as an internally imposed deadline, as the urgency signal monotonically increases the probability of committing to a choice as decision time increases.Footnote 3

Given that the collapsing thresholds and urgency signal models on the one hand, and DDMs with fixed thresholds on the other, make different quantitative behavioral predictions about choice and RT distributions (for a review see Hawkins et al. 2015b), the empirical validity of these contrasting theoretical accounts have been systematically studied by a variety of researchers (Evans et al. 2017; Ratcliff and Smith 2004; Van Zandt et al. 2000; Winkel et al. 2014). Although previous research has shed light on the way deadlines and cues affect core empirical measures of decision-making, such as the shape of RT distributions, and how these may be attributed to different psychological processes (Evans et al. in press), to our knowledge, the empirical effects of cue-based and deadline-based manipulations of the SAT have not been directly compared within the same experimental design. Such a direct comparison would make it possible to control for both SAT manipulations (cue, deadline) and to generalize their effects across different tasks. Furthermore, directly comparing these manipulations within the same design would allow us to propose a model-based account for the differential effects of the two SAT manipulations on the choice-RT distributions. This will contribute to the debate surrounding the nature of response thresholds (fixed vs. decreasing) in evidence accumulation models of decision-making under time pressure.

To that goal, we performed three behavioral experiments that each factorially crossed cue-based and deadline-based manipulations of the SAT in a within-subject design to determine whether they led to differential effects on observed choices and response times. Our central aim was to examine the cognitive processes that distinguish performance in cue-based and deadline-based SAT manipulations (Section 5). In particular, we accounted for decision processes in terms of evidence accumulation, where the threshold of the accumulation process was expected to discriminate between the two forms of SAT manipulation, by attributing the differential effects of cues and deadlines to distinct components of strategic adjustments to response caution. Our analyses included a systematic model comparison of DDMs with fixed and decreasing threshold parametrizations encoding different ways of adjusting response caution to establish which adjustment mechanisms better explain decision processes under different forms of time pressure.

Methods

Participants

Twenty-four participants affiliated with the University of Amsterdam participated in Experiments 1 and 2 (mean age = 23.45, SD age = 7.86, 58% female) in the same experimental session. A different sample of twenty-four participants affiliated with the University of Amsterdam participated in Experiment 3 (mean age = 22.75, SD age = 3.40, 62% female). All participants provided informed consent prior to participation and chose between a monetary or research credit reward at will.

Design and Procedure

Experiment 1

Participants made motion direction judgments about random-dot kinematograms (Ball and Sekuler 1982). In a random dot motion task, participants are presented with a cloud of dots, a subset of which move coherently in a particular direction, while the remaining dots move in random directions. The participant’s task is to determine the direction of the coherently moving dots. The experiment was implemented with the default version of the Random dot motion task in PsychoPy (Peirce 2007) for which the default random dot kinematic component was used (Scase et al. 1996). The settings were dot life-time of 5 frames, dot size of 4 pixels, cloud-size of 400 dots, and speed of dots of 0.5% of monitor dimensions per frame and the so-called position movement algorithm from PsychoPy. The experiment was conducted on a desktop computer with stimuli presented on a 21-in. monitor set at 60 Hz frame rate.

The task consisted of two phases: training and test. The aim of the training phase was to familiarize participants with the task and to establish settings for the test phase. Task instructions were provided on screen with participants briefly introduced to the structure of the task and given instructions to focus on the accuracy of their responses. Keyboard keys were used to make a response (“f” to indicate the dots move left, to the “j” to indicate dots move to the right). A trial finished with the participant’s response and feedback was given based on response accuracy.

In the training phase, participants made decisions across 6 difficulty levels where difficulty was manipulated by changing the percentage of coherently moving dots: 3%, 7%, 11%, 15%, 19%, and 23%. There were 40 trials for each difficulty level for a total of 240 trials. Following completion of the training phase, a single difficulty level was selected separately for each participant for use in their test phase. This value was selected as the lowest motion coherence at which a participant scored above 80% in the training session.

The test phase had a 2 × 2 within-subjects design. The first factor was whether participants were cued to respond fast or accurately. The second factor was whether there was a response deadline (i.e., an upper limit on the available decision time) or not. This produced four conditions in the experiment: speed cue with deadline, speed cue without deadline, accuracy cue with deadline, and accuracy cue without deadline. The four conditions were presented in separate blocks with block order counterbalanced across participants. Table 1 shows the task instructions given at the beginning of each block for the four conditions. There were 200 trials in each of the 4 conditions/blocks for a total of 800 trials in the test phase.

Table 1 Instructions and feedback given to participants in the test phase
Full size table

The cue-based SAT manipulation was operationalized by giving instructions prior to each block (Table 1). The deadline manipulation was operationalized as a trial cut-off at 1.35 s, which was selected based on pilot data. If a response had not been registered by the time of the deadline, then the stimulus was removed from the display, and responses were no longer accepted. No trial cutoff was present in blocks without deadlines.

The pre-stimulus period (fixation cross, 250 ms) directed focus to the center of the screen, after which the stimulus was presented. The stimulus duration then depended on the condition. In the no-deadline condition, the stimulus remained on the screen until the participant gave a response. In the deadline condition, the stimulus was presented at most for 1.35 s, which was the deadline cut-off. If participants missed the deadline, the trial was terminated immediately. Otherwise, by giving a response, the participant ended the trial.

To increase the likelihood that participants followed the block-based instructions, they received feedback following each trial tailored to the pair of conditions in the current block. The text that was given as feedback is shown in Table 1. In the deadline condition, feedback was based on whether the response was prior to the deadline or not. In the condition without a deadline, there was no feedback. In the accuracy cue condition, the feedback focused on whether the response was correct or not. In the speed cue condition, to ensure that participants did not associate feedback related to the cue with a specific cut-off value (i.e., as a deadline), we used a probabilistic feedback method. The feedback stated whether the response was fast or not fast. The probability of “not fast” feedback increased with the trial RT, according to a cumulative Gamma distribution fit to each participant’s RT data from the training phase. Thus, the slower a response, the more likely it was the participant would receive “not fast” feedback, but in an individualized fashion. Because feedback was probabilistic, there was no duration after which participants were guaranteed to receive “not fast” feedback, which would essentially implement a response deadline. For all conditions, the feedback duration varied with respect to being positive or negative; positive feedback was shown for 250 ms, and negative feedback was shown for 1 s.

Experiment 2

To generalize the results of Experiment 1 to a different decision environment, we used a rapid expanded judgment task where participants were presented with two flashing circles and they were asked which of the two circles has the higher flashing rate (cf. Brown et al. 2009; Hawkins et al. 2012; Smith and Vickers 1989); we refer to this as the flash task. The flash task that externalizes to the stimulus display a discrete and explicit evidence process, which we assume gives rise to a corresponding internal evidence accumulation process. This contrasts to the internalized evidence accumulation process that is assumed in most perceptual decision-making tasks, such as random dot motion in Experiment 1 (for a discussion of the differences, see Ratcliff et al. 2016). The flash and random dot motion tasks necessarily draw upon different perceptual processes, because the perceptual display qualitatively differs between tasks, yet this is not to say that the two tasks lead to different cognitive processes including (but not limited to) strategic adjustments to response caution.

All details of the flash task in Experiment 2 were the same as the random dot motion task in Experiment 1 with the exception of the manipulation of difficulty. There were 6 difficulty levels: 55%–45%, 60%–40%, 65%–35%, 70%–30%, 75%–25%, and 80%–20% frequency rate, where the percentage indicates the probability of a circle flashing on each frame rate of the task, and the first percentage represents the rate of one circle and the second of the other. The 6 difficulty levels and the circle with the faster flash rate (left or right) was randomized for each trial. As in Experiment 1, the difficulty level for the test phase was selected as the smallest difference in flash rate at which a participant scored above 80% in the training session.

Experiment 3

As we show below (see Results), the deadline used in Experiment 2 might have been too slow; few responses in the deadline condition cell received “you missed the deadline!” feedback, suggesting participants did not actually experience the time pressure of a response deadline. To address this concern, in Experiment 3, we modified the flash task to include an additional earlier deadline. The experiment had a 2 × 3 within-subjects design with two levels for cue-based SAT and 3 levels for deadline-based SAT (early, late, and no deadline). The late deadline was set equal to the deadline in Experiment 2, namely, 1.35 s, while the early deadline was set at 683 ms. The early deadline was selected as the 75% percentile of the aggregate RT distribution in the deadline conditions from Experiment 2. The additional deadline achieved two goals: to set a deadline that would be early enough to induce the experience of a response deadline in the flash task but not so early as to induce chance-level accuracy and to replicate and extend the findings of Experiment 2.

Most of the presentation settings were retained from Experiment 2, with the following exceptions. The number of training trials was reduced to 30. A lower difficulty level was selected during the training period to make the task easier since it had been found too difficult in Experiment 2. The level of difficulty selected for each participant was the hardest one at which they scored more than 90% during the training phase. The task was counterbalanced, and all participants saw all combinations of conditions. The combinatorial method used was Latin-Graeco square, because of the difficulty of presenting all possible permutations to all participants. To keep the duration of Experiment 3 similar to the duration of Experiments 1–2, the number of trials was initially set to 150 for each of the 6 blocks. After the first 5 participants had participated, it was clear that the experiment was too long. For that reason, the rest of the participants were tested for 130 trials per block (780 trials in total).

The instructions were as described in Experiment 1 and 2 with the exception of the new conditions. Unlike Experiment 1 and 2 which provided accuracy feedback only in accuracy conditions, we generalized accuracy feedback for every trial. This was done to ensure the increase of the overall level of performance. The RT comparison procedures and feedback text were as described in the previous two experiments.

Results and Discussion

We present the statistical results combined across experiments in text; E1–3 denotes Experiments 1–3. Descriptive statistics for mean RT and accuracy are shown in Table 2.

Table 2 Mean response time (RT) and accuracy in Experiments 1–3, including standard error of the mean (SE)
Full size table

Mean RT was significantly faster in trials with deadlines than trials without deadlines (E1–F(1,23) = 22.14, p < 0.001, \( {\eta}_G^2 \) = 0.09; E2–F(1,23) = 16.66, p < 0.001, \( {\eta}_G^2 \) = 0.12; E3–F(2,46) = 72.77, p < 0.001, \( {\eta}_G^2 \) = 0.43).5Footnote 4 Mean RT was also faster in speed-focused relative to accuracy-focused trials (E1–F(1,23) = 18.42, p < 0.001, \( {\eta}_G^2 \) = 0.08; E2–F(1,23) = 29.13, p < 0.001, \( {\eta}_G^2 \) = 0.19; E3–F(1,23) = 27.95, p < 0.001, \( {\eta}_G^2 \) = 0.13). There was a significant interaction between the cue-based and deadline-based manipulation on mean RT (E1–F(1,23) = 8.89, p = 0.006, \( {\eta}_G^2 \) = 0.02; E2–F(1,23) = 13.86, p < 0.001, \( {\eta}_G^2 \) = 0.09; E3–F(2,46) = 10.91, p < 0.001, \( {\eta}_G^2 \) = 0.09). In each experiment, the interaction was due to responses showing greater speeding from the no-deadline to the deadline conditions in the “accuracy” regime as opposed to the “speed” regime.

Accuracy was significantly greater in trials without deadlines compared to trials with deadlines (E1–F(1,23) = 14.87, p < 0.001, \( {\eta}_G^2 \) = 0.04; E2–F(1,23) = 14.36, p < 0.001, \( {\eta}_G^2 \) = 0.04; E3–F(2,46) = 58.93, p < 0.001, \( {\eta}_G^2 \) = 0.30). Accuracy was also significantly greater in accuracy-focused trials compared to speed-focused trials (E1–F(1,23) = 18.30, p < 0.001, \( {\eta}_G^2 \) = 0.16; E2–F(1,23) = 41.83, p < 0.001, \( {\eta}_G^2 \) = 0.20; E3–F(1,23) = 20.81, p < 0.001, \( {\eta}_G^2 \) = 0.08). There was a significant interaction between the cue-based and deadline-based manipulation on accuracy in Experiments 2 and 3 (E2–F(1,23) = 10.54, p < 0.003, \( {\eta}_G^2 \) = 0.04; E3–F(2,46) = 8.81, p < 0.001, \( {\eta}_G^2 \) = 0.04). The nature of the interaction on choice accuracy was similar to the interaction on RT: accuracy decreased to a larger degree between the no-deadline to the deadline conditions when given accuracy-emphasis cues compared to speed-emphasis cues. The interaction was not significant in Experiment 1 (F(1,23) = 0.17, p = 0.678, \( {\eta}_G^2 \) < 0.01; BF10 = 0.29), suggesting that the interaction between speed-accuracy trade-off manipulations on decision accuracy may be dependent on the decision task (random dot motion task vs flash task).

The analysis of mean RT and accuracy confirm that a SAT was induced in each experiment: participants were able to make faster decisions at the expense of more errors. These results were consistent across two types of perceptual decision-making task: one where evidence accumulated in discrete fashion (the flash task; Experiments 2 and 3) and another where evidence accumulated in a continuous fashion (the random-dot motion task; Experiment 1).

As expected, both deadline-based and cue-based manipulations of time-pressure induced a SAT, consistent with previous studies on time pressure. Stricter deadlines lowered choice accuracy and mean RT. Furthermore, the presence of response deadlines in the accuracy-focused conditions produced a larger SAT effect than those in speed-focused conditions, as indicated by the interaction between the two manipulations.Footnote 5

The stable interaction pattern between cue-based and deadline-based manipulations of the SAT suggests that different latent components of processing may have driven the effects observed in data. In the next section we argue that cue-based manipulations affect the overall level of cautiousness (initial threshold in Fig. 1) while deadlines influence moment-to-moment adjustments to response caution. We will use the popular Diffusion Decision Model (DDM) to test this hypothesis and contrast it to alternative hypotheses.

Cognitive Modeling of the Differential Effects of Deadline-Based and Cue-Based SAT Manipulations

In Experiments 1–3 we observed that the presence and the strictness of response deadlines during decision-making affect mean RT and accuracy. Though both cue-based and deadline-based manipulations led to a trade-off between speed and accuracy, in this section, we test whether the two manipulations invoked different cognitive processes. We interpret the behavioral results in terms of a latent process of evidence accumulation by fitting fixed and collapsing threshold DDMs to the data from Experiments 1–3. We make the simplifying assumption that the cognitive processes involved in performing the random dot motion task of Experiment 1 and the flash task of Experiments 2 and 3 is approximated by the evidence accumulation process assumed in the DDM. Thus, by comparing whether the fixed or collapsing threshold models provide a more parsimonious account of each experiment, we can identify the cognitive processes that were most likely to have generated the data, given the set of models under consideration.

Based on our earlier literature review, we hypothesize that cue-based manipulations of the SAT will affect the overall amount of evidence required by the decision-makers to commit to a decision, known as boundary separation (Forstmann et al. 2008; Ratcliff and McKoon 2008; Ratcliff et al. 2016; Wagenmakers et al. 2008). In contrast, we expect that deadline-based manipulations of the SAT will cause dynamic decreases to the threshold throughout the decision process to increase the likelihood of responding before the imposed deadline, known as a collapsing threshold (Cisek et al. 2009; Evans and Hawkins 2019; Miletić and van Maanen 2019; Thura et al. 2012). This will allow us to answer the question of whether cue-based and deadline-based manipulations of the SAT are best explained by different parameters of the DDM, within the same participants in the same task.

Models

We fitted the data of each experiment with a set of models that differed in terms of which model parameters were freely estimated across conditions of the experiment and which were constrained to common values (see Table 3). To simplify the model comparison, we note that the mean start point bias was always set to 0, making the assumption that on average evidence accumulation always begins equidistantly between the boundaries for the two response options (e.g., see Fig. 1 where the accumulation process starts from 0 evidence). It was not estimated since there was no explicit bias manipulation; however we do allow for random start point biases across trials (Sz, see below).

Table 3 Description of the models fitted to Experiments 1–3
Full size table

Table 3 shows the parameterization of all models we studied. We describe the set of models with a naming system that loosely follows Chandrasekaran and Hawkins (2019). The principle of the naming system is that a model is augmented with a character for each additional parameter freely estimated across conditions; the characters for each parameter are shown in the notes to Table 3. Parameters that are freely estimated from data though constrained to the same value across conditions are not referred to in the model name. For illustration, the model in the upper row of Table 3 is named f-DDM-vat-SvStSz because it is a fixed thresholds DDM (f-DDM) that freely estimates the base parameters of drift rate (v), threshold (a) and non-decision time (t), and across-trial variability parameters for drift rate (Sv), non-decision time (St), and starting point (Sz). By comparison, the model in the final row of Table 3 is named c-DDM-a because it is a collapsing threshold DDM (c-DDM) that freely estimates the threshold (a) and the slope of the collapsing threshold (which is encapsulated in the “c” of “c-DDM”).

The number of freely estimated parameters in each model for each participant is determined by multiplying the number of parameters listed in the “free parameters” column of Table 3 by the number of conditions in the experiment (4 in Experiments 1 and 2, 6 in Experiment 3) plus the number of parameters listed in the “constrained parameters” column. For example, in model f-DDM-vat-Sv, there are 4 (parameters) × 4 (E1/E2) or 6 (E3) + 0 = 16 (E1/E2) or 24 (E3) parameters per participant. For c-DDM-vat-Sv, the collapsing thresholds equivalent, there are 20 (E1/2) or 30 (E3) parameters per participant.

Some model parameters were of particular relevance to our hypotheses. In the collapsing threshold DDMs, the threshold parameter indicates the initial level of response caution (boundary separation at time 0), and the slope indicates how quickly this caution changes as the time since stimulus onset increases (rate of decline). We expect that the cue-based manipulation but not deadline-based manipulation will influence the initial threshold, and we expect that the deadline-based manipulation but not the cue-based manipulation will influence the slope. Therefore, if both hypotheses are supported, we expect evidence for a model with collapsing thresholds (any of the c-DDM models). For simplicity, we assume all collapsing thresholds decrease linearly as a function of elapsed decision time, which is a form of collapsing thresholds that is well-identified in data (Evans et al. 2019). For the fixed threshold DDMs, the threshold parameter indicates the general response caution of the participant, which is independent of elapsed decision time. Therefore, if there is support for our hypothesis about cue-based manipulations but not deadline-based manipulations, we expect evidence for a model with fixed thresholds (any of the f-DDM models).

We also considered the across-trial variability parameters of the DDM. Across-trial variability in drift rate was of particular importance as it plays an important role in allowing a fixed-threshold DDM to capture slow errors (Ratcliff 1978) which are also predicted by collapsing thresholds without across-trial variability in the drift rate (Hawkins et al. 2015b). As a result, by estimating drift rate variability, we create a level playing field in terms of the capacity for collapsing and fixed threshold DDMs to account for slow errors, which were present in the data. If across-trial variability in drift rate is the cause of slow errors, then we expect evidence for any of the f-DDM models with Sv, though if slow errors are instead due to collapsing thresholds, we expect support for any of the c-DDM models, which may also have an additional contribution from variability in drift rate. We also tested whether the additional flexibility of across-trial variability in starting point and/or non-decision time accounted for unique variance in the data not already explained by fixed or collapsing thresholds with or without drift rate variability. If this additional flexibility is required to account for the data, then we expect to support models with St and/or St.Footnote 6 We also tested much more constrained models by enforcing the same drift rate and non-decision time across conditions (f-DDM-a-Sv, c-DDM-a-Sv). Comparison of f-DDM-a-Sv with c-DDM-a (without drift rate variability) allowed us to test the unique contribution of the drift rate variability parameter and its potential substitutability with the collapsing threshold parameter.

Fitting Procedure

We followed the parameter estimation routines of Hawkins et al. (2015a). We used Monte Carlo simulation with 10,000 samples per experimental condition during parameter estimation, which was conducted by quantile maximum probability estimation. To ensure the comparison between the models was fair, we used the same simulation-based method for parameter fitting of the DDM with fixed thresholds. We set the diffusion coefficient (s = .1) as a scaling parameter and fitted the DDM to RT in seconds. In addition, we verified that the fixed and collapsing threshold models recovered almost all of the estimated parameters well (yet, the drift rate variability parameter recovered less well than other parameters). For details of the parameter recovery, see Supplementary Materials, and for a more complete treatment of parameter recovery in collapsing threshold models, see Evans et al. (2019).

The best-fitting parameters for all models listed in Table 3 were independently estimated for each participant in each experiment, which makes the model application consistent with the within-subject design of the three experiments. Parameters were estimated through the Differential Evolution optimization algorithm (Ardia et al., 2011) with a maximum of 1000 iterations.

Model Comparison and Model Fit

To assess which models provided the most parsimonious account of the data – that is, the best balance between goodness-of-fit to data and model flexibility – we used the Akaike Information Criterion (AIC), along with its correction for small samples (AICc), and the Bayesian Information Criterion (BIC). These three metrics are used as a standard practice in model comparison (Akaike 1974; Schwarz 1978; see also Heathcote et al. 2015). The three measures are based on the quantile maximum log-likelihood of the fitted models and reward goodness-of-fit but penalize for extra free parameters, with different complexity penalties across the three metrics. Lower values indicate more parsimonious accounts of data than higher values.Footnote 7

Table 4 shows the model comparison outcomes. All three experiments provided the most support for the same model: collapsing thresholds with across-trial variability in drift rate (c-DDM-vat-Sv). For models that did not include across-trial variability in starting point and non-decision time, the collapsing thresholds version of each model tended to provide the best explanation of the data, though not in all cases. However, for models that did include those sources of additional variability, the fixed thresholds models tended to outperform the collapsing thresholds models, though again not in all cases. Nevertheless, there was no combination of the variability parameters in the fixed thresholds model that provided a better explanation of the data than the best collapsing thresholds model. Generally, the models that allowed drift rates and non-decision times to vary across conditions showed a much better performance than those in which these parameters were constrained to the same value across conditions, in spite of the increased number of free parameters. Interestingly, omitting drift rate variability in c-DDM-a substantially worsened performance of the collapsing model, which underscores the fact that drift rate variability makes a unique contribution to the model and cannot be substituted by the slope parameter.Footnote 8 For the remainder of the results, we explore the performance of the best performing collapsing threshold model (c-DDM-vat-Sv) and best performing fixed threshold model (f-DDM-vat-Sv). For simplicity, we refer to these models simply as the collapsing and fixed threshold models rather than repeatedly naming their precise parameterizations.

Table 4 Model comparison between fixed and collapsing threshold DDMs
Full size table

To provide absolute model fit diagnostics, the fit of the preferred collapsing threshold model is shown in Figs. 2 and 3, taking Experiment 2 as an example. The model provides a very good account of the data, with correlations between observed and predicted data (RT quantiles and accuracy) greater than 0.97. The fit of the same model to Experiments 1 and 3 was equally good (see Supplementary Materials: Figs. 3–6). In Experiment 1, the model fit strongly correlated with observed data in correct responses (above 0.97), but error responses exhibited higher variability, especially in the conditions without a deadline (correlations above 0.70). Higher variability in fitting error responses is expected because of the fewer errors made in no-deadline conditions; a phenomenon observed in model fits of other tasks as well (Palminteri et al. 2017). In Experiment 3, the collapsing threshold model slightly underestimated accuracy in the early deadline condition though all correlations between observed and predicted values were above 0.95 for both error and correct responses.

Fig. 2
figure 2

Fit of model c-DDM-vat-Sv to the correct responses of Experiment 2. Observed vs. predicted accuracy and quantile RTs per participant and condition are shown. RTs are given for the 0.1, 0.3, 0.5, 0.7, and 0.9 quantiles. Lines represent the identity function

Full size image
Fig. 3
figure 3

Fit of model c-DDM-vat-Sv to the error responses of Experiment 2. Observed vs. predicted quantile RTs per participant and condition are shown. RTs are given for the 0.1, 0.3, 0.5, 0.7, and 0.9 quantiles. Lines represent the identity function

Full size image

To understand why the collapsing threshold model was preferred over its nearest fixed thresholds competitor (f-DDM-vat-Sv), we explored which quantitative patterns in data the fixed thresholds model missed. The goodness of fit to data of the fixed threshold model had some similar strengths and weaknesses to the collapsing threshold model: higher variability in error responses and underestimation of the observed accuracy in the early deadline condition of Experiment 3 (see Figs. 7–12 of Supplementary Materials). However, the fixed threshold model also tended to underestimate the RT distributions in all quantiles, especially in Experiments 1 and 3. This result is shown more completely in Fig. 4. The fixed threshold model underestimates the central body of the RT distributions (0.3 and 0.5 quantiles) but heavily overestimates the tails (0.9 quantile 0.9). This happens because the fixed threshold model predicts heavier-tailed distributions than what was observed in data. To predict shorter-tailed distributions, the fixed thresholds model underpredicts the main body of the RT distributions. The collapsing threshold model appears to fit the data better. Similar patterns were observed in the other two experiments; see Supplementary Materials Figs. 13–14.

Fig. 4
figure 4

Deviation between observed and predicted RTs for the 0.1, 0.3, 0.5, 0.7, and 0.9 quantiles of the RT distribution separately for each condition in Experiment 2, averaged across participants. Continuous lines indicate the fixed threshold model, and dashed lines indicate the collapsing threshold model. Bars represent standard errors

Full size image

Model Parameters

We now evaluate how the parameters of the best model of the data (i.e., the collapsing threshold model) changed across the conditions of the three Experiments. Figures 5 and 6 provide a graphical presentation of the model parameters. Figure 5 presents the model parameters of greatest interest to our hypotheses: the initial value of the response threshold and the rate of decline in that threshold as the time from stimulus onset increases. Figure 6 presents the rest of the parameters: drift rate, drift rate variability, and non-decision time.

Fig. 5
figure 5

Mean slope and threshold parameters of the collapsing thresholds model. Top row: Experiment 1. Middle row: Experiment 2. Bottom row: Experiment 3. Means are given with standard errors. “AC” and “SP” stands for “accuracy” and “speed” respectively. The right-hand column provides a mean representation of the threshold and slope parameters

Full size image
Fig. 6
figure 6

Mean non-decision time, drift rate, and drift rate variability parameters of the collapsing thresholds model along with the log drift rate – log drift rate variability (denoted as “signal-to-noise ratio”). Top row: Experiment 1. Middle row: Experiment 2. Bottom row: Experiment 3. Means are given with standard errors. “AC” and “SP” stands for “accuracy” and “speed” respectively

Full size image

Across all experiments, the response thresholds declined to a significantly greater extent in trials with deadlines than trials without deadlines (E1–F(1,23) = 9.97, p = 0.004, \( {\eta}_G^2 \) = 0.05; E2–F(1,23) = 5.20, p = 0.032, \( {\eta}_G^2 \) = 0.04; E3–F(1,46) = 58.75, p < 0.001, \( {\eta}_G^2 \) = 0.45). In contrast, the thresholds declined at different rates for speed-focused relative to accuracy-focused trials only in Experiment 2 (F(1,23) = 5.75, p = 0.024, \( {\eta}_G^2 \) = 0.04), not Experiments 1 or 3 (E1–F(1,23) = 1.33, p = 0.260, \( {\eta}_G^2 \) = 0.01; BF10 = 0.43; E3–F(1,23) = 0.13, p = 0.718, \( {\eta}_G^2 \) < 0.01; BF10 = 0.18). There was also no interaction between the cue-based and deadline-based manipulation on the slope parameter in Experiments 1 and 3 (E1–F(1,23) = 3.97, p = 0.058, \( {\eta}_G^2 \) = 0.02; BF10 = 0.99; E3–F(1,46) = 1.10, p = 0.339, \( {\eta}_G^2 \) = 0.01; BF10 = 0.24), though there was a significant interaction in Experiment 2 (F(1,23) = 6.19, p = 0.020, \( {\eta}_G^2 \) = 0.03). As seen in Fig. 5, this interaction was driven by the shallow decline in the threshold in the accuracy – no-deadline condition compared to the steeper decline in the remaining three conditions. It is worth noting that a similar trend was present in Experiment 1 though the pattern was not statistically significant.

In contrast, the initial value of the threshold – an indicator of the overall level of response caution – was significantly greater in accuracy-focused compared to speed-focused trials across all three experiments (E1–F(1,23) = 5.63, p = 0.026, \( {\eta}_G^2 \) = 0.01; E2–F(1,23) = 12.16, p = 0.001, \( {\eta}_G^2 \) = 0.10; E3–F(1,23) = 12.65, p = 0.001, \( {\eta}_G^2 \) = 0.07). The initial threshold was also greater in trials without a deadline compared to with a deadline in Experiments 1 and 2 (E1–F(1,23) = 7.27, p = 0.012, \( {\eta}_G^2 \) = 0.02; E2–F(1,23) = 6.60, p = 0.017, \( {\eta}_G^2 \) = 0.05), but not Experiment 3 (F(1.46) = 2.61, p = 0.084, \( {\eta}_G^2 \) = 0.03; BF10 = 0.65). The interaction followed a similar pattern; not significant in Experiments 1 and 2 (E1–(1,23) = 0.34, p = 0.563, \( {\eta}_G^2 \) < 0.01; BF10 = 0.30; E2–F(1,23) = 3.38, p = 0.078, \( {\eta}_G^2 \) = 0.02; BF10 = 0.92) though significant in Experiment 3 (F(1,46) = 5.78, p = 0.005, \( {\eta}_G^2 \) = 0.06). The interaction was driven by the early deadline – speed condition, which showed higher levels of threshold than expected. This was likely because this condition had a very large slope relative to the other deadline conditions, so to compensate the initial threshold was set to a higher value.

For the rest of the model parameters (Fig. 6), we observed that the parameter of non-decision time was slower in the accuracy-focused trials than in speed-focused ones in Experiments 1 and 2 but not in Experiment 3 (F(1,23) = 11.41, p = 0.002, \( {\eta}_G^2 \) = 0.07; E2–F(1,23) = 10.05, p = 0.004, \( {\eta}_G^2 \) = 0.07; E3–F(1,23) = 2.66, p = 0.116, \( {\eta}_G^2 \) = 0.02; BF10 = 0.60). In addition, non-decision time was faster in deadline conditions but only in Experiment 3 while the rest of the Experiments did not show significant differences (E1–F(1,23) = 2.14, p = 0.156, \( {\eta}_G^2 \) < 0.01; BF10 = 0.25; E2–F(1,23) = 0.46, p = 0.502, \( {\eta}_G^2 \) < 0.01; E3–F(1,46) = 25.85, p < 0.001, \( {\eta}_G^2 \) = 0.16). No interaction was observed (E1–F(1,23) = 0.13, p = 0.719, \( {\eta}_G^2 \) < 0.01; BF10 = 0.30; E2–F(1,23) = 1.25, p = 0.274, \( {\eta}_G^2 \) < 0.01; BF10 = 0.31; E3–F(1,46) = 0.38, p = 0.680, \( {\eta}_G^2 \) < 0.01; BF10 = 0.14).

The drift rate parameter – the rate perceptual information is accumulated by the decision-maker – showed a clear pattern according to which it was higher in across accuracy-focused than speed-focused trials (E1–F(1,23) = 20.85, p < 0.001, \( {\eta}_G^2 \)=0.12; E2–F(1,23) = 14.34, p < 0.001, \( {\eta}_G^2 \) = 0.07; E3–F(1,23) = 4.28, p = 0.049, \( {\eta}_G^2 \) = 0.01) as well as in trials without deadlines than in trials with deadlines in two out of the three Experiments (E1–F(1,23) = 10.67, p = 0.003, \( {\eta}_G^2 \) = 0.03; E2–F(1,23) = 0.02, p = 0.870, \( {\eta}_G^2 \) < 0.01; BF10 = 0.21; E3–F(1,46) = 15.53, p < 0.001, \( {\eta}_G^2 \) = 0.12). Additionally, no interaction was observed between these two factors (E1–F(1,23) = 0.15, p = 0.700, \( {\eta}_G^2 \) < 0.01; BF10 = 0.29; E2–F(1,23) < 0.001, p = 0.992, \( {\eta}_G^2 \) < 0.01; BF10 = 0.29; E3–F(1, 46) = 0.37, p = 0.691, \( {\eta}_G^2 \) < 0.01; BF10 = 0.13).

On the other hand, the drift rate variability parameter showed mixed results (for a relationship between the drift rate and drift rate variability see Fig. 6: last right column); it was higher in conditions without deadlines in Experiment 1, but it was lower for deadline conditions in Experiment 2, while no significant difference was found for Experiment 3 (E1–F(1,23) = 5.27, p = 0.031, \( {\eta}_G^2 \) = 0.13; E2–F(1, 23) = 5.35, p = 0.029, \( {\eta}_G^2 \) < 0.02; E3–F(1,46) = 0.16, p = 0.850, \( {\eta}_G^2 \) < 0.01; BF10 = 0.13). Furthermore, that model parameter did not significantly change across speed-focused vs. accuracy-focused trials (E1–F(1,23) = 0.03, p = 0.866, \( {\eta}_G^2 \) < 0.01; BF10 = 0.21; E2–F(1,23) = 2.17, p = 0.154, \( {\eta}_G^2 \) < 0.01; BF10 = 0.49; E3–F(1,23) = 1.94, p = 0.176, \( {\eta}_G^2 \) = 0.01; BF10 = 0.51). No interaction between the two factors was observed in the drift rate variability parameter (E1–F(1,23) = 0.03, p = 0.856, \( {\eta}_G^2 \) < 0.01; BF10 = 0.29; E2–F(1,23) = 0.11, p = 0.734, \( {\eta}_G^2 \) < 0.01; BF10 = 0.30; E3–F(1,46) = 1.94, p = 0.176, \( {\eta}_G^2 \) = 0.01; BF10 = 0.26).

Taken together, the deadline-based manipulations were most consistently associated with the slope parameter of the collapsing threshold model such that response deadlines induced steeper slopes than no-deadline conditions in Experiments 1 and 2, with the same pattern observed across the three deadline levels in Experiment 3. The threshold parameter, on the other hand, was most consistently associated with the cue-based manipulation such that speed-focused trials reduced the response threshold relative to accuracy-focused trials. This result aligns with a large body of literature (Evans et al. in press; Forstmann et al. 2008; Frazier and Yu 2007; Hawkins et al. 2015b; Rae et al. 2014; Ratcliff and McKoon 2008; Van Maanen et al. 2011; Wagenmakers et al. 2008). In addition, trials with deadlines and with speed-focused instructions produced lower drift rates than trials without deadlines or with accuracy-focused instructions. However, we found mixed results for the association of the non-decision time parameter with deadline conditions (the non-decision time parameter was faster in conditions with deadlines only in Experiment 3 in line with previous studies, e.g., Murphy et al. 2016) or the association of the drift rate variability with deadline conditions (drift rate variability was higher for trials with deadlines only in Experiment 2).

General Discussion

We have provided evidence that deadline-based and cue-based manipulations of the speed-accuracy trade-off have different psychological effects on latent decision-making processes. Our results indicate that cue-based manipulations affect the general level of response caution with which people make perceptual decisions. Throughout the course of a decision, this overall level is subject to dynamic changes due to a potential pressure to respond. Such time pressure can be experimentally induced through deadlines but is less sensitive to pre-stimulus cues. These results are in line with previous empirical investigations of deadline and instruction effects on human RT and accuracy data (Forstmann et al. 2010, 2008; Frazier and Yu 2007; Karşılar et al. 2014; Miletić and van Maanen 2019; Pike 1968; Pike and Dalgleish 1982; Van Maanen et al. 2011; Van Zandt et al. 2000).

The differences between the overall level of caution and how it changes throughout the course of a decision are well-explained within the theoretical framework of evidence accumulation models (such as the DDM) that incorporate collapsing thresholds. We found that the best explanation of the data assigned the effect of a cue-based manipulation of the SAT to the overall level of the decision threshold and the effect of a deadline-based manipulation of the SAT to dynamically collapsing thresholds. The model also assumed that mean drift rate, drift rate variability, and non-decision time changed across conditions. This model is preferable for three reasons. First, it provides a coherent conceptual account of the cognitive mechanisms triggered by time pressure manipulations during perceptual decision-making. Second, it is consistent with the differential effects of cue-based and deadline-based manipulations observed in the behavioral data. Third, it is able to better capture the choice and RT patterns in the behavioral data.

An alternative to a collapsing threshold model that is sometimes tested is the so-called fast guess model by Ollmann (Falmagne 1968; Ollman 1966; van Maanen et al. 2016; van Maanen et al. 2014). This model proposes that participants might switch to a guessing strategy to make faster responses. Such a strategy would indeed speed up behavior at the expense of accuracy, thus explaining the SAT. If participants guessed on a higher proportion of trials when they are cued for speed than when they are cued for accuracy, the response time distributions should show signatures of mixture distributions. In previous work, we found no evidence for the fast guess model in cue-based SAT data (van Maanen 2016). Reanalyzing the data of Experiment 3 of the current paper confirms this result for deadline-based SAT (see Supplementary mMterials). A change in the proportion of guess responses due to a deadline therefore does not seem likely. For this reason, we did not explore this class of models further. Nevertheless, for future research, it may be worth investigating the issue of mixtures of decision-making processes in the context of the DDM (cf. Ratcliff, 2006).

There are a number of practical and theoretical implications of our results. First, we showed that deadline-based and cue-based manipulations do not induce a speed-accuracy trade-off in the same way. Because the two manipulations target qualitatively different cognitive processes, the experimenter’s choice between the two methods should be carefully considered in studies aimed at experimentally inducing a speed-accuracy trade-off. Second, we provided evidence in favor of the use of accumulation models with collapsing bounds for the study of time pressure effects in perceptual decision-making. Collapsing threshold models may provide a more complete representation of how humans respond when faced with particular types of time pressure. Third, we found mixed support for the necessity of incorporating variability parameters in the DDM to explain behavior under time pressure: models without non-decision time and starting point variability parameters explained our data better (in contrast to the findings of Rae et al. 2014), but variability in the drift rate was necessary (in line with Voskuilen et al. 2016). These results indicate the need for further research on the set of variability parameters that are necessary to explain the cognitive processes involved in decisions under time pressure. We note that while our results have implications for a range of tasks and evidence accumulation models of perceptual decision-making, future investigations should evaluate whether the same computational principles of the SAT described in this study generalize to more complex forms of decision-making (e.g., value-based choices).

Our results regarding decision-making under time pressure are in line with recent literature on the topic. First, we provide empirical evidence supporting Frazier and Yu’s (2008) thesis, which predicted that when humans are faced with deadlines, decision-makers require less evidence to commit to a decision as time passes. This is in line with previous work suggesting that decisions for which not enough evidence can be obtained in the allotted time are characterized by collapsing thresholds (Boehm et al. 2016; Evans et al. in press; Hawkins et al. 2015a; Hawkins et al. 2015b; Miletić and van Maanen 2019; Murphy et al. 2016). It is important to note, however, that our modeling analyses did not address the question of whether people followed an optimal or a suboptimal decision policy. This remains a matter of research to be established in the future, though the interested reader is referred to Karşılar et al. (2014) for an earlier comprehensive treatment of the topic.

In the evidence accumulation models we studied here, we accounted for deadline-based time pressure with linearly collapsing thresholds for reasons of simplicity. However, many different functional forms of this kind of urgency signal have been proposed, and the current study did not aim to differentiate between those. In particular, some researchers have argued for an additive (Cisek et al. 2009) or multiplicative temporal signal (Drugowitsch et al. 2012; Frazier and Yu 2008) on the accumulation process (i.e., the drift rate), while others have argued for a concave collapsing threshold (Ratcliff and Frank 2012). However, in terms of response time and accuracy distributions, these proposals are difficult to disentangle, and for that reason we chose the simplest possible functional form with the primary aim of differentiating between conditions without an urgency signal (i.e., a fixed threshold) and conditions with urgency in a model specification that is well-identified in data (Evans et al. 2019). Although a DDM with linearly collapsing thresholds was able to capture many of the empirical patterns elicited by deadline-based time pressure (yet not perfectly, see, e.g., Fig. 4), it may be that evidence accumulation models with more complex functional forms for the decreasing threshold will further improve the explanation of performance under these conditions. Therefore, further research is required to establish under which conditions more complex functional forms are necessary to explain the behavioral patterns, which might also include other SAT manipulations that do not explicitly use deadlines (e.g., Palestro et al. 2018).