Skip to main content
SpringerLink
Log in

Transformation Field Analysis and Clustering Discretization Method in Peridynamic Micromechanics of Composites

  • Research
  • Published:
Journal of Peridynamics and Nonlocal Modeling Aims and scope Submit manuscript

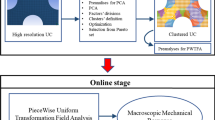
Abstract

In contrast to the classical local theories, the peridynamic equation of motion introduced by Silling (J Mech Phys Solids 48:175–209, 2000) is free of any spatial derivatives of the displacement field. A theory of thermoelastic composite materials (CMs) with nonlocal peridynamic properties of multiphase constituents of arbitrary geometry is analyzed for periodic structure CMs subjected to the volumetric periodic boundary conditions. At first, we consider a linear thermoelastic problem for perydynamics CMs. Effective properties of peridynamic CM are expressed through the introduced micro polarization tensor averaged over the extended inclusion phase. Decompositions of material and field parameters are performed for analysis of the fields produced by both mechanical loading and eigenfield loading. Transformation field analysis (TFA) and clustering discretization method (defining offline linear stage) adapted to the linear peridynamic micromechanics are proposed (the novelty of the approach proposed) by the use of formal similarity of suggested methods with corresponding approaches of local micromechanics (LM). Stress and displacement in each cluster are assumed to be constant and linear functions, respectively, even when a cluster is not a simply connected area in general. This fact greatly reduces the degree of freedom in the problem being considered and leads to a greatly improved computational efficiency with their wide potential applications (e.g., in machine learning). The clustering version of TFA for the homogenization of nonlinear elastic peridynamic micromechanics (PM, online nonlinear stage) is based on employing eigenstrains to account for inelastic displacements arising from material nonlinearity. The scheme of numerical solution of linear thermoelastic peridynamic problem and estimation of influence functions are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Availability of Data and Materials

No any datasets used.

References

  1. Silling S (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48:175–209

    Article  ADS  MathSciNet  Google Scholar 

  2. Madenci E, Oterkus E (2014) Peridynamic theory and its applications. Springer, NY

    Book  Google Scholar 

  3. Silling SA, Lehoucq RB (2008) Convergence of peridynamics to classical elasticity theory. J Elasticity 93:13–37

    Article  MathSciNet  Google Scholar 

  4. Silling SA, Lehoucq RB (2010) Peridynamic theory of solid mechanics. Adv Appl Mech 44:73–168

    Article  Google Scholar 

  5. Silling SA, Epton M, Weckner O, Xu J, Askari E (2007) Peridynamic states and constitutive modeling. J Elasticity 88:151–184

  6. Buryachenko VA (2014) Some general representations in thermoperistatics of random structure composites. Int J Multiscale Comput Eng 12:331–350

    Article  Google Scholar 

  7. Buryachenko VA (2017) Effective properties of thermoperistatic random structure composites: some background principles. Math Mech Solids 22:366–1386

    Article  MathSciNet  Google Scholar 

  8. Alali B, Lipton R (2012) Multiscale dynamics of heterogeneous media in the peridynamic formulation. J Elast 106:71–103

    Article  MathSciNet  Google Scholar 

  9. Diyaroglu C, Madenci E, Phan N (2019) Peridynamic homogenization of microstructures with orthotropic constituents in a finite element framework. Compos Struct 227:111334

    Article  Google Scholar 

  10. Diyaroglu C, Madenci E, Stewart RJ, Zobi SS (2019) Combined peridynamic and finite element analyses for failure prediction in periodic and partially periodic perforated structures. Compos Struct 227:111481

    Article  Google Scholar 

  11. Buryachenko VA (2024) Generalized Mori-Tanaka approach in peridynamic micromechanics of multilayered composites of random structure. J Peridyn Nonlocal Model. https://doi.org/10.1007/s42102-023-00114-8

  12. Silling SA (2014) Origin and effect of nonlocality in a composite. J Mech Mater Struct 9:245–258

    Article  Google Scholar 

  13. Xia W, Oterkus E, Oterkus S (2020) Peridynamic modeling of periodic microstructured materials Procedia Struct Integr 28:820–828

    Google Scholar 

  14. Buryachenko V (2019) Computational homogenization in linear elasticity of peristatic periodic structure composites. Math Mech Solids 24:2497–2525

    Article  MathSciNet  Google Scholar 

  15. Buryachenko VA (2022) Local and nonlocal micromechanics of heterogeneous materials. Springer, NY

    Book  Google Scholar 

  16. Diyaroglu C, Madenci E, Phan N (2019) Peridynamic homogenization of microstructures with orthotropic constituents in a finite element framework. Compos Struct 227:111334

  17. Dvorak G (1992) Transformation field analysis of inelastic composite materials. Proc R Soc Lond A 437:311–327

    Article  ADS  MathSciNet  CAS  Google Scholar 

  18. Dvorak GJ (2013) Micromechanics of composite materials. Springer, Dordrecht

    Book  Google Scholar 

  19. Dvorak G, Bahei-El-Din Y, Wafa A (1994) The modeling of inelastic composite materials with the transformation field analysis. Model Simul Mater Sci Eng 2:571–586

    Article  ADS  Google Scholar 

  20. Dvorak GJ, Benveniste Y (1992) On transformation strains and uniform fields in heterogeneous media. Proc R Soc Lond A 437:291–310

    Article  ADS  CAS  Google Scholar 

  21. Benaimeche MA, Yvonnet J, Bary B, He Q-C (2022) A k-means clustering machine learning-based multiscale method for inelastic heterogeneous structures with internal variables. Int J Numer Methods Eng 123:2012–2041

    Article  Google Scholar 

  22. Berkooz G, Holmes P, Lumley JL (1993) The proper orthogonal decomposition in the analysis of turbulent flows. Ann Rev Fluid Mech 25:539–575

    Article  ADS  MathSciNet  Google Scholar 

  23. Castrogiovanni A, Marfia S, Auricchio F, Sacco E (2021) TFA and HS based homogenization techniques for nonlinear composites. Int J Solids Struct 225:111050

    Article  Google Scholar 

  24. Covezzi F, Miranda S, Marfia S, Sacco E (2017) Homogenization of elastic-viscoplastic composites by the mixed TFA. Comput Meth Appl Mech Eng 318:701–723

    Article  MathSciNet  Google Scholar 

  25. Covezzi F, Miranda S, Fritzen F, Marfia S, Sacco E (2018) Comparison of reduced order homogenization techniques: pRBMOR, NUTFA and MxTFA. Meccanica 53:1291–1312

    Article  Google Scholar 

  26. Li H, Kafka OL, Gao J, Cheng Yu, Nie Y, Zhang L, Tajdari M, Shan Tang X, Guo GL et al (2019) Clustering discretization methods for generation of material performance databases in machine learning and design optimization. Comput Mech 64:281–305

    Article  MathSciNet  Google Scholar 

  27. Ri J-H, Hong H-S, Ri S-G (2021) Cluster-based nonuniform transformation field analysis: an efficient homogenization for inelastic heterogeneous materials. Int J Numer Methods Eng 122:4458–4485

    Article  MathSciNet  Google Scholar 

  28. Yvonnet J, He QC (2007) The reduced model multiscale method (R3M) for the non-linear homogenization of hyperelastic media at finite strains. J Comput Phys 223:341–368

    Article  ADS  MathSciNet  Google Scholar 

  29. Michel J, Suquet P (2003) Nonuniform transformation field analysis. Int J Solids Struct 40:6937–6955

    Article  MathSciNet  Google Scholar 

  30. Jain AK (2010) Data clustering: 50 years beyond K-means. Pattern Recognit Lett 31:651–666

    Article  ADS  Google Scholar 

  31. Liu Z, Bessa MA, Liu WK (2016) Self-consistent clustering analysis: an efficient multi-scale scheme for inelastic heterogeneous materials. Comput Methods Appl Mech Eng. 306:319–41

    Article  ADS  MathSciNet  Google Scholar 

  32. Tang S, Zhang L, Liu WK (2018) From virtual clustering analysis to self-consistent clustering analysis: a mathematical study. Comput Mech 62:1443–1460

    Article  MathSciNet  Google Scholar 

  33. Liu Z, Fleming M, Liu WK (2018) Microstructural material database for self-consistent clustering analysis of elastoplastic strain softening materials. Comput Methods Appl Mech Eng 330:547–577

    Article  ADS  MathSciNet  Google Scholar 

  34. Kafka OL, Yu C, Shakoor M, Liu Z, Wagner GJ, Liu WK (2018) Data-driven mechanistic modeling of influence of microstructure on high-cycle fatigue life of nickel titanium. JOM, pp 1-5

  35. Kilic B (2008) Peridynamic theory for progressive failure prediction in homogeneous and heterogeneous materials. Ph.D. Thesis, Dep Mechan Eng, The University of Arizona

  36. Han X, Gao J, Fleming M, Chenghai X, Xie W, Meng S, Liu WK (2020) Efficient multiscale modeling for woven composites based on self-consistent clustering analysis. Comput Methods Appl Mech Eng 364:112929

    Article  ADS  MathSciNet  Google Scholar 

  37. Li H, Kafka OL, Gao J, Cheng Yu, Nie Y, Zhang L, Tajdari M, Shan Tang X, Guo GL et al (2019) Clustering discretization methods for generation of material performance databases in machine learning and design optimization. Comput Mech 64:281–305

  38. Cheng G, Li X, Nie Y, Li H (2019) FEM-Cluster based reduction method for efficient numerical prediction of effective properties of heterogeneous material in nonlinear range. Comput Methods Appl Mech Eng 348:157–184

    Article  ADS  MathSciNet  Google Scholar 

  39. Liu Z, Fleming M, Liu WK (2018) Microstructural material database for self-consistent clustering analysis of elastoplastic strain softening materials. Comput Methods Appl Mech Eng 330:547–577

  40. Ferreira BP, Pires FM, Bessa MA (2022) Adaptive clustering-based reduced-order modeling framework: fast and accurate modeling of localized history-dependent phenomena. Comput Methods Appl Mech Eng 393

  41. Buryachenko V (2023) Transformation field analysis as a background of clustering discretization methods in micromechanics of composites. Math Mech Solids 28:2677–2703

    Article  MathSciNet  Google Scholar 

  42. Yu C, Kafka OL, Liu WK (2019) Self-consistent clustering analysis for multiscale modeling at finite strains Comput Meth Appl Mech Engng 349:339–359

    Google Scholar 

  43. Silling S (2011) A coarsening method for linear peridynamics. Int J Multiscale Comput Eng 9:609–622

    Article  Google Scholar 

  44. Galadima Y, Oterkus E, Oterkus S (2019) Two-dimensional implementation of the coarsening method for linear peridynamics. AIMS Mater Sci 6:252–275

    Article  Google Scholar 

  45. Bobaru F, Ha YD (2011) Adaptive refinement and multiscale modeling in 2D peridynamics. Int J Multiscale Comput Eng 9:635–659

    Article  Google Scholar 

  46. Lehoucq RB, Silling SA (2008) Force flux and the peridynamic stress tensor. J Mech Phys Solids 56:1566–1577

  47. Silling SA, Askari E (2005) A meshfree method based on the peridynamic model of solid mechanics. Comput Struct 83:1526–1535

    Article  Google Scholar 

  48. Jafarzadeh S, Mousavi M, Larios A, Bobaru F (2022) A general and fast convolution-based method for peridynamics: applications to elasticity and brittle fracture. Comput Meth Appl Mech Eng 392

  49. Bobaru F, Yang M, Alves LF, Silling SA, Askari A, Xu J (2009) Convergence, adaptive refinement, and scaling in 1d peridynamics. Int J Numer Methods Eng 77:852–877

    Article  Google Scholar 

  50. Silling SA, Zimmermann M, Abeyaratne R (2003) Deformation of a peridynamic bar. J Elasticity 73:173–190

  51. Weckner O, Abeyaratne R (2005) The effect of long-range forces on the dynamics of a bar. J Mech Phys Solids 53:705–728

    Article  ADS  MathSciNet  Google Scholar 

  52. Hu W, Ha YD, Bobaru F (2012) Peridynamic model for dynamic fracture in unidirectional fiber-reinforced composites. Comput Methods Appl Mech Eng 217–220:247–261

    Article  ADS  MathSciNet  Google Scholar 

  53. Emmrich E, Weckner O (2007) Analysis and numerical approximation of an integro-differential equation modeling non-local effects in linear elasticity. Math Mech Solids 12:363–384

    Article  MathSciNet  Google Scholar 

  54. Emmrich E, Weckner O (2007) On the well-posedness of the linear peridynamic model and its convergence towards the Navier equation of linear elasticity. Commun Math Sci 5:851–864

    Article  MathSciNet  Google Scholar 

  55. Silling SA, Lehoucq RB (2010) Peridynamic theory of solid mechanics. Adv Appl Mech 44:73–168

  56. Macek RW, Silling SA (2007) Peridynamics via finite element analysis. Finite Elem Anal Des 43:1169–1178

  57. Du Q, Gunzburger M, Lehoucq RB, Zhou K (2013) Analysis of the volume-constrained peridynamic Navier equation of linear elasticity. J Elast 113:193–217

    Article  MathSciNet  Google Scholar 

  58. Seleson P, Gunzburger M, Parks ML (2013) Interface problems in nonlocal diffusion and sharp transitions between local and nonlocal domains. Comput Methods Appl Mech Eng 266:185–204

    Article  ADS  MathSciNet  Google Scholar 

  59. Seleson P, Parks ML (2011) On the role of the influence function in the peridynamic theory. Int J Multiscale Comput Eng 9:689–706

    Article  Google Scholar 

  60. Schmidhuber J (2015) Deep learning in neural networks: an overview. Neural Netw 61:85–117

    Article  PubMed  Google Scholar 

  61. Simo JC, Taylor RL (1986) A return mapping algorithm for plane stress elastoplasticity. Int J Numer Methods Eng 22:649–670

    Article  MathSciNet  Google Scholar 

  62. Guo K, Yang Z, Yu C-H, Buehler MJ (2021) Artificial intelligence and machine learning in design of mechanical materials Mater Horiz 8:1153–1172

    CAS  PubMed  Google Scholar 

  63. Brunton SL, Kutz JN (2022) Data-driven science and engineering: machine learning, dynamical systems, and control. Cambridge University Press, Cambridge, UK

    Book  Google Scholar 

  64. Yang H, Guo X, Tang S, Liu WK (2019) Derivation of heterogeneous material laws via data-driven principal component expansions. Comput Mech 64:365–379

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The author acknowledges Dr. Stewart A. Silling for the fruitful personal discussions, encouragements, helpful comments, and suggestions. The author also acknowledges the reviewers for the encouraging comments that initiated a significant correction of the manuscript.

Author information

Authors and Affiliations

  1. Micromechanics & Composites LLC, Cincinnati, OH, 45202, USA

    Valeriy A. Buryachenko

Authors
  1. Valeriy A. Buryachenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

VB wrote the all manuscript text.

Corresponding author

Correspondence to Valeriy A. Buryachenko.

Ethics declarations

Ethical Approval

Applicable for both human and/ or animal studies. Ethical committees, Internal Review Boards, and guidelines followed must be named. When applicable, additional headings with statements on consent to participate and consent to publish are also required “not applicable”.

Competing Interests

The author declares no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Buryachenko, V.A. Transformation Field Analysis and Clustering Discretization Method in Peridynamic Micromechanics of Composites. J Peridyn Nonlocal Model (2024). https://doi.org/10.1007/s42102-023-00113-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42102-023-00113-9

Keywords

Search

Navigation