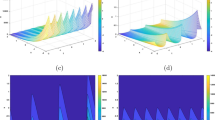
Abstract
Peridynamics (PD) is a new continuum mechanics formulation introduced to overcome limitations of classical continuum mechanics (CCM). This is mainly achieved by using integro-differential equations rather than partial differential equations. Another important difference of PD is its nonlocal nature with respect to local characteristic of CCM. Moreover, it has a length scale parameter, horizon, defining the range of nonlocal interactions between material points. This nonclassical behaviour also shows itself for dispersion relationships. As opposed to linear dispersion relationships for CCM, PD dispersion relationships are non-linear similar to the observed in experiments. In this study, closed-form dispersion relationships are provided for ordinary state-based peridynamics which is one of the most common PD formulations. Finally, derived closed-form solutions are used to demonstrate the dispersion relationships for various material systems including copper, gold, silver and platinum.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Continuum mechanics is a widely used approach for the analysis of materials and structures subjected to external loading conditions. Classical continuum mechanics (CCM) has been the most popular type of continuum mechanics formulations that was introduced by Cauchy almost 200 years ago. According to CCM, the motion of a material point is described by using a partial differential equation representing the Newton’s 2nd law of motion. The state of material points is monitored through several important parameters such as strain and stress. These parameters and associated criteria can provide useful information about when a structure could fail. However, despite all these positive aspects of CCM, CCM is limited predicting how cracks initiate and propagate since spatial derivatives are not defined along crack surfaces.
To overcome limitations of CCM, a new continuum mechanics formulation, peridynamics (PD), was introduced by Silling [1]. Compared to partial differential equation of CCM, peridynamics utilises integro-differential equation to describe the motion of a material point. Rather than using classical concepts such as strain and stress, interactions between material points are described by determining the stretch and force of peridynamic interactions (bonds). The range of interactions between material points is restricted to a domain of influence named the horizon. This nonlocal characteristic allows representation of material behaviours which cannot be captured by CCM. One such characteristic is wave dispersion. Wave dispersion relationships determined in the peridynamic framework are in non-linear form similar to the ones observed in experiments. CCM is not capable of capturing such behaviour since wave dispersion relationships of CCM are linear and only limited to waves with long wave lengths.
There has been significant progress on PD research especially during the last 10 years. Vazic et al. [2] investigated the important problem of how macrocrack is interacting with microcracks. Huang et al. [3] developed peridynamic formulation for visco-hyperelastic materials. Nguyen et al. [4] introduced a new energy-based peridynamic fatigue model suitable for different peridynamic formulations. De Meo et al. [5] examined how cracks can initiate and propagate from corrosion pits. Liu et al. [6] utilised peridynamics to investigate the fracture behaviour of graphene sheets. Zhu et al. [7] applied peridynamic fatigue model for polycrystalline materials. Karpenko et al. [8] investigated the effect of porosity on fatigue nucleation behaviour of additively manufactured titanium alloys. Lu et al. [9] used peridynamics for the fracture analysis of polycrystalline ice material. Various peridynamic beam [10] and plate [11] formulations are also available in the literature.
The determination of dispersion relationships in peridynamic framework has also been studied in various studies. Amongst these, Bazant et al. [12] examined the wave dispersion in linearized bond-based and state-based peridynamics and compared against classical nonlocal models. Butt et al. [13] investigated the dispersion properties of a state-based linear peridynamic model and the role of the horizon. Dayal [14] considered the approximation of peridynamics by strain-gradient models and used Taylor series to approximate peridynamic dispersion relationship. Chan and Chen [15] investigated wave dispersion by using peridynamic bond-associated material correspondence model. Mikata [16] analytically determined the dispersion relationships for one-dimensional problems. Zhang et al. [17] performed an in-depth investigation of wave dispersion in bond-based peridynamic framework. Alebrahim et al. [18] obtained dispersion properties of one-dimensional and two-dimensional bond-based peridynamic formulations. Li et al. [19] conducted an in-depth investigation of wave dispersion in bond-based peridynamics with different attenuation functions. Oterkus and Oterkus [20] provided a comparison of peridynamic wave dispersion relationships with the ones obtained from lattice models. Diyaroglu et al. [21] determined dispersion relationships for Timoshenko beam and Mindlin plate peridynamic formulations.
As mentioned by Hermann et al. [22] and Shojaei et al. [23, 24], dispersion relationships in PD are significantly affected by the employed numerical discretization scheme and can differ significantly from those of closed-forms. Therefore, in this study, closed-form relationships for wave dispersion and their derivations are given in the ordinary state-based peridynamic formulation presented by Madenci and Oterkus [25]. The derived expressions are demonstrated for various materials including copper, gold, silver and platinum. As expected, nonlinear wave dispersion relationships are obtained as opposed to linear characteristic obtained in CCM, which shows superior characteristic of peridynamics for representing the wave dispersion phenomenon.
2 Ordinary State-Based Peridynamics
The equation of motion in ordinary-state based peridynamics is given by [25]
where \({\mathbf{\underline {T} }}\left( {{\mathbf{x}},t} \right)\left\langle {{\mathbf{x^{\prime}}} - {\mathbf{x}}} \right\rangle\) and \({\mathbf{\underline {T} }}\left( {{\mathbf{x^{\prime}}},t} \right)\left\langle {{\mathbf{x}} - {\mathbf{x^{\prime}}}} \right\rangle\) represent the peridynamic forces that material points \({\mathbf{x^{\prime}}}\) and \({\mathbf{x}}\) are exerting on each other and can be written as
where \(a\),\(b\) and \(d\) are peridynamic parameters which can be related to the engineering material constants of shear modulus, \(\mu\), and bulk modulus, \(\kappa\). \(\delta\) represents the horizon size which is the range of a material point that can interact with its family material points. \(\Theta \left( {{\mathbf{x}},t} \right)\) is the dilation term representing the volumetric strain and defined as
The bond length, \(\xi\) is defined as
Substituting the peridynamic forces given in Eq. (2a, b) for material points \({\mathbf{x}}\) and \({\mathbf{x^{\prime}}}\) into the equation of motion given in Eq. (1) without considering the body force leads to
3 Dispersion Relationships in Ordinary State-Based Peridynamics
The solution of the equation of motion for the material point \({\mathbf{x}}\) can be obtained by considering the plane wave solution
where \({\mathbf{U}}_{{\mathbf{0}}}\) is the constant amplitude vector, \(k\) is the wavenumber, \(\omega\) is the angular frequency in rad/sec, and \({\mathbf{n}}\) is the direction of the wave propagation.
Similarly, for the material point \({\mathbf{x^{\prime}}}\), the plane wave solution can be written as
Next, the relative displacement between material points \({\mathbf{x}}\) and \({\mathbf{x^{\prime}}}\) can be determined as
or
By using the Euler formula
Equation (8b) can be rewritten as
Next, the stretch between material points \({\mathbf{x}}\) and \({\mathbf{x^{\prime}}}\),\(s\), can be derived for linearized version of ordinary state-based peridynamics as (see Fig. 1)
where \(u\),\(u^{\prime}\),\(v\) and \(v^{\prime}\) are displacement components represent the longitudinal (\(x\)-axis) and transverse (\(y\)-axis) displacements of material points \({\mathbf{x}}\) and \({\mathbf{x^{\prime}}}\), respectively, and \(\theta\) is the orientation of the peridynamic bond with respect to the horizontal axis.
3.1 Wave Dispersion in Longitudinal Direction
In the present study, wave is considered to propagate in the positive \(x\)-direction. For longitudinal waves, the particle displacement is parallel to the direction of wave propagation, whereas the transverse displacements of all material points are zero. Substituting the relative displacement between material points \({\mathbf{x}}\) and \({\mathbf{x^{\prime}}}\) given in Eq. (10) in stretch expression given in Eq. (11) leads to
According to ordinary state-based peridynamics, the dilatation of the material point \({\mathbf{x}}\),\(\Theta \left( {{\mathbf{x}},t} \right)\), for longitudinal waves becomes
where \({\text{BesselJ}}\left[ {m, \ldots } \right]\) is Bessel function of the \(m\) kind. Similarly, the dilatation of the material point \({\mathbf{x^{\prime}}}\), \(\Theta \left( {{\mathbf{x^{\prime}}},t} \right)\), can be calculated as
Adding dilation terms for material points \({\mathbf{x}}\) and \({\mathbf{x^{\prime}}}\) yields
Substituting Eq. (15) into the first term of the right hand side of the peridynamic equation of motion (Eq. 5) for a longitudinal wave yields
For two-dimensional structures, the peridynamic parameters \(a\) and \(d\) are given as [25]
and
Substituting Eqs. (17) and (18) into Eq. (16) leads to
Substituting the stretch term defined in Eq. (12) into the second term of the right hand side of the peridynamic equation of motion given in Eq. (5) for a longitudinal wave leads to
For two-dimensional structures, the peridynamic parameter \(b\) is given as [25]
Hence, Eq. (21) can be rewritten as
On the other hand, the left hand side of equation of motion can be written as
Finally, substituting Eq. (19), Eq. (22) and Eq. (23) into the equation of motion given in Eq. (5) yields
The dispersion relationship in the longitudinal direction can then be obtained from Eq. (24) as
3.2 Wave Dispersion in Transverse Direction
For a transverse wave propagating in the positive \(x\)-direction, the displacement of the particle oscillates upward and downward directions around equilibrium position as the wave travels which is perpendicular to the direction of wave propagation. On the other hand, longitudinal displacements of all material points vanish. The stretch of a bond for a transverse wave can be calculated as
Next, the dilation terms \(\Theta \left( {{\mathbf{x}},t} \right)\) and \(\Theta \left( {{\mathbf{x^{\prime}}},t} \right)\) can be obtained as
and
Hence,
This is expected since the oscillations of a transverse wave particles subjected to periodic shear are perpendicular to the direction of wave propagation and shear is related with change in shape without change of volume. Therefore, the dilation terms vanish for transverse waves propagating in the longitudinal direction. Hence, the first term on the right hand side of the peridynamic equation of motion given in Eq. (5) leads to
Next, substituting the stretch expression given in Eq. (26) into the second term on the right side of the peridynamic equation of motion yields
where \({\text{StruveH}}\left[ {m, \ldots } \right]\) is Struve function of the \(m\) kind. Recalling the peridynamic parameter \(b\) given in Eq. (21) for two-dimensional structures and substituting Eq. (21) into Eq. (31) leads to
On the other hand, the left hand side of the peridynamic equation of motion can be written as
Utilising Eqs. (30), (32) and (33), the peridynamic equation of motion given in Eq. (5) for a transverse wave propagating in the positive \(x\)-direction can be written as
Finally, the dispersion relationship in the transverse direction can then be obtained from Eq. (35) as
3.3 Comparison of Bond-Based and Ordinary State-Based Wave Dispersion Relationships
The bulk modulus, \(\kappa\), and shear modulus, \(\mu\) for two-dimensional structures can be written as
and
where \(E\) is the elastic modulus and \(\upsilon\) is Poisson’s ratio. For Poisson’s ratio of \(\upsilon = \frac{1}{3}\), ordinary state-based formulation reduces to bond-based formulation. Therefore, the following condition holds
Substituting Eq. (38) into Eq. (25) with \(\upsilon = \frac{1}{3}\) leads Eq. (25) to
Compared to the bond-based peridynamic dispersion relationship given in [26], the ordinary state-based longitudinal dispersion relationship reduces to same bond-based longitudinal peridynamic dispersion relationship for Poisson’s ratio value of \(\upsilon = \frac{1}{3}\).
Similarly, substituting Eq. (38) into Eq. (35) for \(\upsilon = \frac{1}{3}\) leads Eq. (35) to
This expression is also the same expression given in [26] for the bond-based transverse peridynamic dispersion relationship.
4 Numerical Results
In this section, nonlinear closed-form peridynamic dispersion relationships obtained for ordinary state-based peridynamics are shown for different materials including copper, gold, silver and platinum. For all cases, the horizon size is selected as \(\delta = 3 \times 10^{ - 10} {\text{m}}\).
4.1 Dispersion Relationships for Copper
First the closed-form peridynamic dispersion relationships given in Eqs. (25) and (35) for longitudinal and transverse waves, respectively, are obtained for copper. Density, Young’s modulus and Poisson’s ratio are specified as 8960 kg/m3, 130 GPa and 0.34, respectively. As shown in Fig. 2, peridynamics provides nonlinear dispersion relationships as opposed to linear dispersion relationships of CCM.
4.2 Dispersion Relationships for Gold
In the second example, gold material is considered. Density, Young’s modulus and Poisson’s ratio are specified as 19,320 kg/m3, 79 GPa and 0.42, respectively. By using the relationships given in Eqs. (25) and (35) for longitudinal and transverse waves, respectively, nonlinear dispersion relationships are obtained as shown in Fig. 3.
4.3 Dispersion Relationships for Silver
For the third case, silver material is considered. Density, Young’s modulus and Poisson’s ratio are specified as 10,490 kg/m3, 85 GPa and 0.37, respectively. Dispersion relationships for both longitudinal and transverse waves are shown in Fig. 4.
4.4 Dispersion Relationships for Platinum
Finally, platinum material is considered. Density, Young’s modulus and Poisson’s ratio are specified as 21,450 kg/m3, 171 GPa and 0.38, respectively. Nonlinear dispersion relationships for platinum are demonstrated in Fig. 5.
5 Conclusions
In this study, closed-form wave dispersion relationships were derived for linearized version of ordinary state-based peridynamics. For both longitudinal and transverse waves, dispersion characteristics were investigated for various materials including copper, gold, silver and platinum. For all materials, nonlinear wave dispersion behaviour was obtained similar to the ones observed in experiments which cannot be captured by classical continuum mechanics that has a linear wave dispersion relationship. This shows that peridynamics can be utilised for predicting material behaviour which cannot be represented by using classical models that are mostly seen at small scales.
Availability of Data and Materials
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48(1):175–209
Vazic B, Wang H, Diyaroglu C, Oterkus S, Oterkus E (2017) Dynamic propagation of a macrocrack interacting with parallel small cracks. AIMS Materials Science 4(1):118–136
Huang Y, Oterkus S, Hou H, Oterkus E, Wei Z, Zhang S (2019) Peridynamic model for visco-hyperelastic material deformation in different strain rates. Contin Mech Thermodynam 1–35
Nguyen CT, Oterkus S, Oterkus E (2021) An energy-based peridynamic model for fatigue cracking. Eng Fract Mech 241:107373
De Meo D, Russo L, Oterkus E (2017) Modeling of the onset, propagation, and interaction of multiple cracks generated from corrosion pits by using peridynamics. J Eng Mater Technol 139(4):041001
Liu X, He X, Wang J, Sun L, Oterkus E (2018) An ordinary state-based peridynamic model for the fracture of zigzag graphene sheets. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 474(2217):20180019
Zhu N, Kochan C, Oterkus E, Oterkus S (2021) Fatigue analysis of polycrystalline materials using peridynamic theory with a novel crack tip detection algorithm. Ocean Eng 222:108572
Karpenko O, Oterkus S, Oterkus E (2021) Peridynamic investigation of the effect of porosity on fatigue nucleation for additively manufactured titanium alloy Ti6Al4V. Theoret Appl Fract Mech 112:102925
Lu W, Li M, Vazic B, Oterkus S, Oterkus E, Wang Q (2020) Peridynamic modelling of fracture in polycrystalline ice. J Mech 36(2):223–234
Yang Z, Oterkus E, Oterkus S (2021) Peridynamic higher-order beam formulation. Journal of Peridynamics and Nonlocal Modeling 3:67–83
Yang Z, Oterkus E, Oterkus S (2021) Peridynamic formulation for higher-order plate theory. Journal of Peridynamics and Nonlocal Modeling 3:185–210
Bažant ZP, Luo W, Chau VT, Bessa MA (2016) Wave dispersion and basic concepts of peridynamics compared to classical nonlocal damage models. J Appl Mech 83(11)
Butt SN, Timothy JJ, Meschke G (2017) Wave dispersion and propagation in state-based peridynamics. Comput Mech 60:725–738
Dayal K (2017) Leading-order nonlocal kinetic energy in peridynamics for consistent energetics and wave dispersion. J Mech Phys Solids 105:235–253
Chan W, Chen H (2021) Peridynamic bond-associated correspondence model: wave dispersion property. Int J Numer Meth Eng 122(18):4848–4863
Mikata Y (2012) Analytical solutions of peristatic and peridynamic problems for a 1D infinite rod. Int J Solids Struct 49(21):2887–2897
Zhang X, Xu Z, Yang Q (2019) Wave dispersion and propagation in linear peridynamic media. Shock Vib 2019:1–9
Alebrahim R, Packo P, Zaccariotto M, Galvanetto U (2022) Improved wave dispersion properties in 1D and 2D bond-based peridynamic media. Computational Particle Mechanics 9(4):597–614
Li S, Jin Y, Lu H, Sun P, Huang X, Chen Z (2021) Wave dispersion and quantitative accuracy analysis of bond-based peridynamic models with different attenuation functions. Comput Mater Sci 197:110667
Oterkus S, Oterkus E (2022) Comparison of peridynamics and lattice dynamics wave dispersion relationships. J Peridynam Nonloc Mod 1–11
Diyaroglu C, Oterkus E, Oterkus S, Madenci E (2015) Peridynamics for bending of beams and plates with transverse shear deformation. Int J Solids Struct 69:152–168
Hermann A, Shojaei A, Seleson P, Cyron CJ, Silling SA (2023) Dirichlet‐type absorbing boundary conditions for peridynamic scalar waves in two‐dimensional viscous media. Intern J Num Meth Eng
Shojaei A, Hermann A, Seleson P, Silling SA, Rabczuk T, Cyron CJ (2023) Peridynamic elastic waves in two-dimensional unbounded domains: construction of nonlocal Dirichlet-type absorbing boundary conditions. Comput Methods Appl Mech Eng 407:115948
Shojaei A, Hermann A, Seleson P, Cyron CJ (2020) Dirichlet absorbing boundary conditions for classical and peridynamic diffusion-type models. Comput Mech 66:773–793
Madenci E, Oterkus E (2014) Peridynamic theory and its applications. New York, NY: Springer New York
Wang B, Oterkus S, Oterkus E (2020) Closed-form dispersion relationships in bond-based peridynamics. Procedia Structural Integrity 28:482–490
Funding
The first author (Bingquan Wang) would like to acknowledge the financial support of University of Strathclyde. This material is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-18–1-7004.
Author information
Authors and Affiliations
Contributions
Wang B: conceptualisation, methodology, model development, verification and validation, original manuscript draft, review and editing; Oterkus E: conceptualisation, methodology, original manuscript draft, review and editing, supervision; and Oterkus S: conceptualisation, methodology, original manuscript draft, review and editing, supervision.
Corresponding author
Ethics declarations
Ethical Approval
Not applicable.
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, B., Oterkus, S. & Oterkus, E. Closed-Form Wave Dispersion Relationships for Ordinary State-Based Peridynamics. J Peridyn Nonlocal Model (2023). https://doi.org/10.1007/s42102-023-00109-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42102-023-00109-5