1 Introduction

Continuum mechanics is widely used to analyse the response of materials and structures to external loading conditions. Without paying attention to atomistic details, continuum mechanics can provide us very accurate predictions as long as continuum approximation is valid. There are various continuum mechanics formulations available in the literature. The most common formulation was proposed by Cauchy 200 years ago and the equation of motion for a material point is described by using partial differential equations. Although these equations have been successfully utilised for the analysis of many different challenging problems of solid mechanics, they encounter difficulties when dealing with problems including discontinuities such as cracks. In such cases, a new continuum mechanics formulation, peridynamics [1], can be more suitable since the equations of motion in peridynamics are in integro-differential equation form and do not contain any spatial derivatives. As opposed to semi-analytical approaches [2] and finite element methodology, this brings a significant advantage to predict crack initiation and propagation since the displacement field is discontinuous if cracks exist in the structure and spatial derivatives are not defined along the crack surfaces.

There has been a significant progress on peridynamics. Amongst these, Alpay and Madenci [3] performed fully coupled thermomechanical peridynamic analysis to predict crack growth. Vazic et al. [4] studied the interaction of macro- and micro-crack under dynamic conditions. Basoglu et al. [5] investigated the potential of micro-cracks to deflect crack propagation. Karpenko et al. [6] investigated the effect of small defects such as holes and micro-cracks on crack propagation. Imachi et al. [7] investigated dynamic crack arrest in peridynamic framework. De Meo et al. [8] predicted how cracks initiate and propagate from corrosion pits by using peridynamics. Diyaroglu et al. [9] developed peridynamic wetness approach to determine moisture concentration in electronic packages. Guski et al. [10] performed peridynamic investigation of the microstructural behaviour of plasma-sprayed coatings. Ren et al. [11] developed dual horizon peridynamic formulation to use variable horizon in the solution domain. Huang et al. [12] developed a new peridynamic model for visco-hyperelastic materials. Kefal et al. [13] performed peridynamic topology optimisation study of structures with cracks. Liu et al. [14] studied fracture of graphene sheets by using peridynamics. Oterkus and Madenci [15] demonstrated peridynamic formulation to consider torsional and antiplane shear deformations. Vazic et al. [16] presented peridynamic Mindlin plate formulation by considering Winkler elastic foundation. In another study, Vazic et al. [17] compared different family member search algorithms that can be used in peridynamic simulations. Yang et al. [18, 19] demonstrated peridynamic Timoshenko beam and Kirchhoff plate formulation for isotropic and functionally graded materials, respectively. Peridynamic formulations for higher-order beams and plates are given in Yang et al. [20, 21], respectively. Zhu et al. [22] studied polycrystalline fracture by using peridynamics. During the recent years, several other new concepts such as peridynamic differential operator, peridynamic least squares minimisation and weak form of peridynamics were introduced by Madenci et al. [23,24,25]. An extensive review of peridynamics is given in Javili et al. [26].

In nano-materials, material properties close to the surfaces can be different than bulk properties. This variation causes surface stresses. Hamilton and Wolfer [27] considered different models that have been introduced for surface elasticity. Ru [28] provided simple geometrical explanation of Gurtin–Murdoch model of surface elasticity with clarification of its related versions. Attia [29] studied the mechanics of functionally graded nanobeams by taking into account the effect of surface elasticity. Ru [30] introduced a strain-consistent elastic plate model by incorporating surface elasticity. Eremeyev and Lebedev [31] presented their mathematical study of boundary value problems based on Steigmann-Ogden model of surface elasticity. Hu and Li [32] investigated a rigid line inclusion in an elastic film by considering surface elasticity. Ansari et al. [33] demonstrated postbuckling characteristics of nanobeams with the presence of surface elasticity. Chen et al. [34] studied the effect of surface elasticity on the wave propagation in anisotropic cylinders at nanoscale. Grekov and Yazovskaya [35] studied the influence of surface elasticity in an elastic body with an elliptic nanohole. Wang and Wang [36] presented the nonlinear free vibration of nanoscale plates by considering the effects of surface stress and surface elasticity. Soyarslan et al. [37] investigated the effect of surface elasticity on the elastic response of nanoporous gold. Xu and Fan [38] examined the torsional waves in nanowires with the presence of surface elasticity. On the other hand, in this study, modified core–shell model [39] is utilised to define the variation of material properties in the surface region by considering surface effects. Moreover, directional effective material properties are obtained by utilising analytical and peridynamic solutions.

2 Peridynamic Theory

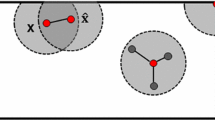
Peridynamics (PD) is a non-local continuum mechanics formulation since a material point can interact with other material points inside a region called horizon. The peridynamic equation of motion for a material point located at \(x\) can be written as:

$$\rho \ddot{\mathbf{u}}(\mathbf{x},t)=\underset{{H}_{x}}{\int }\mathbf{f}({\mathbf{u}}^{^{\prime}}-\mathbf{u},{\mathbf{x}}^{^{\prime}}-\mathbf{x})d{V}^{^{\prime}}+\mathbf{b}(\mathbf{x},t)$$
(1)

where \(\rho\) is mass density, \(t\) is time, \({\mathbf{u}}\) and \(\ddot{\mathbf{u}}\) represent the displacement and acceleration of the material point located at \(\mathbf{x}\), and \(\mathbf{b}\) is the body load acting on the material point at \(\mathbf{x}\). \({\mathbf{x}}^{^{\prime}}\) is the location of the material point inside the horizon of the material point located at \(\mathbf{x}\), \({H}_{x}\). Peridynamic force, \(\mathbf{f}\), between material points located at \(\mathbf{x}\) and \({\mathbf{x}}^{^{\prime}}\) can be expressed as:

$$\mathbf{f}=cs\frac{({\mathbf{x}}^{^{\prime}}+{\mathbf{u}}^{^{\prime}})-(\mathbf{x}+\mathbf{u})}{|({\mathbf{x}}^{^{\prime}}+{\mathbf{u}}^{^{\prime}})-(\mathbf{x}+\mathbf{u})|}$$
(2)

where \(c\) is the bond constant and the stretch, \(s\), can be defined as:

$$s=\frac{|({\mathbf{x}}^{^{\prime}}+{\mathbf{u}}^{^{\prime}})-(\mathbf{x}+\mathbf{u})|-|{\mathbf{x}}^{^{\prime}}-\mathbf{x}|}{|{\mathbf{x}}^{^{\prime}}-\mathbf{x}|}$$
(3)

The bond constant is \(c=9E/(\pi h{\delta }^{3})\) for 2-dimensional structures with \(E\) being Young’s modulus, \(h\) being plate thickness and \(\delta\) being horizon size. The simulations are conducted by using bond based peridynamics for plane stress conditions.

3 Obtaining Directional Effective Material Properties for Surface Elasticity

In nano-materials, material properties close to the surfaces can be different than bulk properties. This variation causes surface stresses. In this study, modified core–shell model (MC-S) [39] is utilised to define the variation of material properties in the surface. Based on the MC-S model developed by Yao et al. [39], an exponential increase of surface elasticity in the surface between the bulk region and the surface region is utilised by using the following expression:

$${E}_{s}(y)={E}_{bulk}{e}^{(\alpha (y-{W}_{b}))},\;{W}_{b}\le y\le {W}_{b}+{W}_{s}$$
(4)

with

$$\alpha =\tilde{\alpha }/{W}_{s}$$
(5)

where \({E}_{bulk}\) is the bulk elasticity of the nanomaterial and \(\alpha\) is the surface factor related to surface thickness \({W}_{s}\). The parameter \(\tilde{\alpha }\) is a dimensionless constant which represents the degree of inhomogeneity transitioning from the bulk region to the external surface layer and its sign (positive or negative) describes the stiffening or softening of the surface layer. For this study, \(\tilde{\alpha }\) value is chosen as \(\tilde{\alpha }=1.26\) [39]. In Fig. 1, x represents the longitudinal direction and y represents the transverse direction.

Fig. 1
figure 1

a Continuous model; b discrete model

Full size image

By using the surface material properties provided in Eqs. (4) and (5), directional properties can be obtained by applying arbitrary loadings in both directions by using static theory of elasticity for the continuous model (Fig. 1a).

The equivalent elastic modulus in the longitudinal direction with surface effects is found by assuming that the cross section is subjected to constant strain in the x direction:

$${E}_{eq}{A}_{eq}={E}_{bulk}{A}_{b}+2\underset{{W}_{b}}{\overset{{W}_{b}+{W}_{s}}{\int }}E(y)hdy$$
(6)
$${E}_{eq}{A}_{eq}={E}_{bulk}{A}_{b}+2\underset{{W}_{b}}{\overset{{W}_{b}+{W}_{s}}{\int }}{E}_{bulk}{e}^{(\alpha (y-{W}_{b}))}hdy$$
(7)
$${E}_{eq}{A}_{eq}={E}_{bulk}{A}_{b}+2\underset{0}{\overset{{W}_{s}}{\int }}{E}_{bulk}{e}^{(\alpha ({y}^{^{\prime}}))}hd{y}^{^{\prime}}$$
(8)
$${E}_{eq}2({W}_{s}+{W}_{b})h={E}_{bulk}2({W}_{b})h+2{E}_{bulk}h\frac{1}{\alpha }({e}^{(\alpha {W}_{s})}-1)$$
(9)
$${E}_{eq}2({W}_{s}+{W}_{b})h={E}_{bulk}2({W}_{b})h+2{E}_{bulk}h\frac{1}{\alpha }({e}^{(\alpha {W}_{s})}-1)$$
(10)

For numerical implementation, the continuous model in Eq. (10) can be approximated by considering a discrete model as shown in Fig. 1b. Therefore, the equivalent elastic modulus in the longitudinal direction with surface effects is found by using static theory of elasticity for the discrete model when the plate is subjected to constant strain in the x direction:

$${E}_{eq}{A}_{eq}={E}_{bulk}{A}_{b}+2\sum_{i=1}^{N}{E}_{i}h{W}_{i}$$
(11)
$${E}_{eq}2({W}_{s}+{W}_{b})h={E}_{bulk}2({W}_{b})h+2\sum_{i=1}^{N}{E}_{i}h{W}_{i}$$
(12)
$${E}_{eq}={E}_{bulk}\frac{({W}_{b})}{({W}_{s}+{W}_{b})}+\frac{\sum\limits_{i=1}^{N}{E}_{i}{W}_{i}}{({W}_{s}+{W}_{b})}$$
(13)

with

$${E}_{i}={E}_{bulk}{e}^{(\alpha ({y}_{i}-{W}_{b}))},\;{W}_{b}\le {y}_{i}\le {W}_{b}+{W}_{s}$$
(14)

The equivalent elastic modulus in the transverse direction with surface effects is found by assuming that the cross section is subjected to constant stress in the y direction:

$${\delta }_{T}={\delta }_{bulk}+{\delta }_{surface}$$
(15)
$${\varepsilon }_{eq}2({W}_{s}+{W}_{b})={\varepsilon }_{b}2({W}_{b})+2\underset{{W}_{b}}{\overset{{W}_{b}+{W}_{s}}{\int }}{\varepsilon }_{shell}dy$$
(16)
$$\frac{\sigma }{{E}_{eq}}2({W}_{s}+{W}_{b})=\frac{\sigma }{{E}_{bulk}}2({W}_{b})+2\underset{{W}_{b}}{\overset{{W}_{b}+{W}_{s}}{\int }}\frac{\sigma }{{E}_{shell}}dy$$
(17)
$$\frac{\sigma }{{E}_{eq}}2({W}_{s}+{W}_{b})=\frac{\sigma }{{E}_{bulk}}2({W}_{b})+2\underset{0}{\overset{{W}_{s}}{\int }}\frac{\sigma }{{E}_{bulk}{e}^{(\alpha ({y}^{^{\prime}}))}}d{y}^{^{\prime}}$$
(18)
$$\frac{1}{{E}_{eq}}=\frac{1}{{E}_{bulk}}\frac{({W}_{b})}{({W}_{s}+{W}_{b})}+\frac{1}{{E}_{bulk}}\frac{\underset{0}{\overset{{W}_{s}}{\int }}{e}^{-(\alpha ({y}^{^{\prime}}))}d{y}^{^{\prime}}}{({W}_{s}+{W}_{b})}$$
(19)
$$\frac{1}{{E}_{eq}}=\frac{1}{{E}_{bulk}}\frac{({W}_{b})}{({W}_{s}+{W}_{b})}-\frac{1}{{E}_{bulk}}\frac{({e}^{-(\alpha {W}_{s})}-1)}{\alpha ({W}_{s}+{W}_{b})}$$
(20)

Similarly, for numerical implementation, the continuous model in Eq. (20) can be approximated by considering a discrete model as shown in Fig. 1b. The equivalent elastic modulus in the transverse direction with surface effects can be found by using static theory of elasticity for the discrete model when the plate is subjected to constant stress in the y direction:

$${\delta }_{T}={\delta }_{bulk}+{\delta }_{surface}$$
(21)
$${\varepsilon }_{eq}2({W}_{s}+{W}_{b})={\varepsilon }_{b}2({W}_{b})+2\sum_{i=1}^{N}{\varepsilon }_{i}{W}_{i}$$
(22)
$$\frac{\sigma }{{E}_{eq}}2({W}_{s}+{W}_{b})=\frac{\sigma }{{E}_{bulk}}2({W}_{b})+2\sum_{i=1}^{N}\frac{\sigma }{{E}_{i}}{W}_{i}$$
(23)
$$\frac{1}{{E}_{eq}}=\frac{1}{{E}_{bulk}}\frac{({W}_{b})}{({W}_{s}+{W}_{b})}+\frac{\sum\limits_{i=1}^{N}\frac{1}{{E}_{i}}{W}_{i}}{({W}_{s}+{W}_{b})}$$
(24)

with

$${E}_{i}={E}_{bulk}{e}^{(\alpha ({y}_{i}-{W}_{b}))},{W}_{b}\le {y}_{i}\le {W}_{b}+{W}_{s}$$
(25)

4 Numerical Results

In this section, we investigated the size effect for a rectangular nanomaterial as shown in Fig. 1. The bulk elasticity of the rectangular nanomaterial is considered \({E}_{bulk}=140\text{ GPa}\) [39] and the surface layer is modelled with 4 surface materials with elastic modulus:

$${E}_{i}={E}_{bulk}{e}^{(\alpha ({y}_{i}-{W}_{b}))}$$
(26)

with \({y}_{i}={W}_{b}+\sum\limits_{k=1}^{i}{W}_{s,k}\) and \(\alpha =0.63\) \((\tilde{\alpha }=1.26)\). The height of the surface layers is taken as \({W}_{s,i}=0.5\text{ nm},i=\mathrm{1,2},\mathrm{3,4}\). The rectangular nanomaterial is subjected to a strain of 0.01 in the longitudinal and transverse directions, respectively. In our numerical peridynamic model, \(L=10\text{ nm}\) represents the width (Fig. 1). The height of the surface layer is \({W}_{s}=2\text{ nm}\) and the total height varied from 20 to 120 nm (20 < W < 120 nm). The boundary conditions are implemented by using fictitious layers as described in Madenci and Oterkus [40]. For peridynamic simulations, the discretisation size is specified as \(\Delta x=0.1\text{ nm}\). Therefore, in each layer of the surface region, there are 5 material points in the transverse direction. The horizon size is chosen as \(\delta =3.015\Delta x\) as suggested in Madenci and Oterkus [41]. For bonds between material points belonging to different layers, equivalent bond constant concept is utilised as described in [41]. The details of the numerical peridynamic implementation can also be found in Madenci and Oterkus [41].

Figure 2 presents the effective and normalised elastic moduli in the longitudinal direction. Normalised elastic modulus values are representing the ratio of the effective elastic modulus value and the bulk elasticity value. It has been observed that as the height of the material (W) increases, the effective elastic modulus in the longitudinal direction approaches to bulk properties. This behaviour is also similar to our discrete model in Eq. (13).

Figure 3 presents the effective and normalised elastic moduli in the transverse direction. Similar to the longitudinal direction, as the height of the material (W) increases, the effective elastic modulus in the transverse direction also approaches to bulk properties. This behaviour is also similar to our discrete model in Eq. (24).

Fig. 2
figure 2

The size effect of the normalised elastic modulus in the longitudinal direction, \({E}_{eq}/{E}_{bulk}\) for tension loading for [0001] oriented ZnO nanomaterial with \(\tilde{\alpha }=1.26\) [39], a normalised elastic modulus; b effective elastic modulus

Full size image

Please note that as we increase the number of layers, discrete equivalent material properties in longitudinal and transverse directions will approach to continuous equivalent material properties provided in Eqs. (10) and (19), respectively.

As mentioned earlier, there are five material points utilised in each layer for the peridynamic simulations. To investigate the effect of discretisation on the peridynamic results, different number of material points per layer is considered and normalised elastic modulus values in the transverse direction are evaluated as shown in Fig. 4. It can be seen that it is sufficient to use five material points per layer to achieve a convergent numerical solution.

Fig. 3
figure 3

The size effect of the normalised elastic modulus in the transverse direction, \({E}_{eq}/{E}_{bulk}\) for tension loading for [0001] oriented ZnO nanomaterial with \(\tilde{\alpha }=1.26\) [39], a normalised elastic modulus; b effective elastic modulus

Full size image

Finally, the effect of number of layers in the surface region on the normalised elastic modulus in the transverse direction is investigated as shown in Fig. 5. As can be seen in this figure, as the number of layers in the surface region increases, peridynamic solution converges to the analytical expression given in Eq. (20).

Fig. 4
figure 4

The effect of number of material points per layer in the surface region on the normalised elastic modulus in the transverse direction, \({E}_{eq}/{E}_{bulk}\) for tension loading for [0001] oriented ZnO nanomaterial with \(\tilde{\alpha }=1.26\) [39]  

Full size image
Fig. 5
figure 5

The effect of number of layers in the surface region on the normalised elastic modulus in the transverse direction, \({E}_{eq}/{E}_{bulk}\) for tension loading for [0001] oriented ZnO nanomaterial with \(\tilde{\alpha }=1.26\) [39] 

Full size image

5 Conclusion

In this study, modified core–shell model was utilised to define the variation of material properties in the surface region by considering surface effects. Moreover, directional effective material properties were obtained by utilising analytical and peridynamic solutions. Based on numerical results, it was shown that effective elastic modulus values for longitudinal and transverse directions obtained from peridynamics solutions and analytical expressions agree well with each other. It was observed that as the height of the material increases, the effective elastic moduli in the longitudinal and transverse directions approach to bulk properties. The effect of discretisation on peridynamic results was also investigated by considering different number of material points per layer in surface region and it was demonstrated that sufficient number of material points, i.e. five material points, were utilised in the transverse direction. Finally, the effect of number of layers in the surface region was examined. As the number of layers increases in the peridynamic simulations, the effective modulus values converge to the corresponding analytical solution. Based on the numerical results, it can be concluded that peridynamics can be a suitable tool for analysing surface elasticity problems.