1 Introduction

In many engineering applications including marine, civil and transport engineering, analysis of structures resting on an elastic foundation is an important problem of interest [1]. To represent the elastic foundation, Winkler and Pasternak formulations are widely utilised. In Winkler formulation, the elastic foundation is represented by the distribution of springs to resist the lateral deflection of the structure resting on the elastic foundation. On the other hand, Pasternak formulation can capture the shear interaction between springs [1].

Although there are numerous studies in the literature considering elastic foundation problem, only few of them investigated the behaviour of an existing crack inside a structure resting on an elastic foundation. Amongst these, Matysiak and Pauk [2] performed stress analysis near a crack tip in an elastic layer resting on a Winkler foundation by using the method of Fourier transforms and dual integral equations. Farjoo et al. [3] investigated rolling contact fatigue cracks in railway tracks and used a simplified finite element model (FEM) and extended finite element method (XFEM). They observed that the elastic foundation leads to an additional bending stress which increases the crack growth rate significantly. In another study, Attar et al. [1] investigated the free vibration of a shear deformable beam with multiple open edge cracks using lattice spring model. Finally, Nobili et al. [4] presented a full-field solution for the linear elastostatic problem of a homogeneous infinite Kirchhoff plate with a semi-infinite rectilinear crack resting on a two-parameter elastic foundation. They calculated stress intensity factors for both symmetric and skew-symmetric loading conditions.

In this study, an alternative approach, peridynamics [5], is used for the analysis of a Mindlin plate resting on a Winkler type elastic foundation. Peridynamics was originally introduced to overcome the limitations of classical continuum mechanics. The equations of motion in peridynamics are in the form of integro-differential equations, and they do not contain any spatial derivatives. Therefore, these equations are valid regardless of discontinuities. Peridynamics has been successfully used to analyse different material systems and geometrical configurations [6,7,8,9,10,11,12,13,14]. An extensive literature survey on peridynamics is given in Madenci and Oterkus [15] and Javili et al. [16]. Aforementioned benefits of peridynamics have attracted interest in solving solid mechanics problems particularly those involving damage and fracture. Majority of such attempts deal with full 3D models or 2D plane stress/plane strain models. There are relatively few peridynamic models considering structures resisting transverse deformation with one dimension (e.g. the thickness) significantly smaller than the other two (e.g. aircraft fuselage, ship hull, pressure vessel) including Silling and Bobaru [17] for 2D membranes, Taylor and Steigmann [18], O’Grady and Foster [19], Diyaroglu et al. [20] and Reddy et al. [21] for plates and flat shells, and Chowdhury et al. [22] for shells. This study is an extension of the Mindlin plate formulation developed by Diyaroglu et al. [20]. A similar approach was presented by Di Paola et al. [23] for non-local modelling of a beam on an elastic foundation. The current formulation is capable of analysing Mindlin plates resting on an elastic Winkler foundation with damage prediction capability. Moreover, the direct solution approach (Bobaru et al. [24], Breitenfeld et al. [25]) is presented to obtain the solution in static conditions rather than using widely adapted adaptive dynamic relaxation (ADR) scheme [26]. Finally, several verification and demonstration cases including a Mindlin plate with or without an initial crack subjected to transverse loading or pure bending loading conditions are presented to validate the current formulation and demonstrate its capabilities.

2 Peridynamic Theory

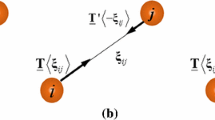
Peridynamic (PD) theory was introduced by Silling [5] as an alternative continuum mechanics formulation to classical continuum mechanics (CCM). As opposed to the localised concept of CCM, PD theory is based on non-local interactions between material points. Therefore, material points which are far from each other but within their interaction range, called horizon, can interact with each other (see Fig. 1). Material points, x′, inside the horizon, Hx, of the material point, x, can be considered as the family members of the material point, x. Moreover, PD theory uses displacements rather than derivatives of displacements. Therefore, the equation of motion of a material point is expressed as an integro-differential equation

$$ \rho \ddot{\mathbf{u}}\left(\mathbf{x},t\right)=\underset{H_{\mathbf{x}}}{\int}\mathbf{f}\left(\mathbf{u}\left({\mathbf{x}}^{\prime },t\right)-\mathbf{u}\left(\mathbf{x},t\right),{\mathbf{x}}^{\prime }-\mathbf{x}\right)d{V}_{{\mathbf{x}}^{\prime }}+\mathbf{b}\left(\mathbf{x},t\right) $$
(1)

and this equation is valid anywhere in the structure regardless of discontinuities such as cracks. In Eq. (1), u is the displacement vector, b is the body load, ρ is the mass density and \( d{V}_{{\mathbf{x}}^{\prime }} \) denotes the volume of the material point x′. ‘Dot’ symbol represents the time derivative, and f is the peridynamic force density vector representing the force that the material point x′ exerts on the material point x. The relative position and relative displacements of the material points x′ and x are defined, respectively, as

$$ \boldsymbol{\upxi} ={\mathbf{x}}^{\prime }-\mathbf{x} $$
(2)

and

$$ \boldsymbol{\upeta} =\mathbf{u}\left({\mathbf{x}}^{\prime },t\right)-\mathbf{u}\left(\mathbf{x},t\right) $$
(3)
Fig. 1
figure 1

The material point x interacts with other material points inside its horizon Hx

Full size image

In the original peridynamic formulation, i.e. bond based peridynamics, peridynamic force for an elastic and isotropic material can be expressed as

$$ \mathbf{f}\left(\boldsymbol{\upeta}, \boldsymbol{\upxi} \right)=\frac{\boldsymbol{\upxi} +\boldsymbol{\upeta}}{\mid \boldsymbol{\upxi} +\boldsymbol{\upeta} \mid }f\left(|\boldsymbol{\upxi} +\boldsymbol{\upeta} |,\boldsymbol{\upxi} \right) $$
(4)

where f(| ξ + η| , ξ) is a scalar-valued function which depends on the bond stretch, s, and the bond constant, c, as

$$ f\left(|\boldsymbol{\upxi} +\boldsymbol{\upeta} |,\boldsymbol{\upxi} \right)= cs $$
(5)

The bond stretch can be defined as

$$ s=\frac{\mid \boldsymbol{\upxi} +\boldsymbol{\upeta} \mid -\mid \boldsymbol{\upxi} \mid }{\mid \boldsymbol{\upxi} \mid } $$
(6)

The bond constant, c, can be specified in terms of elastic modulus, E, and horizon size δas

$$ c=\frac{2E}{A{\delta}^2}(1D);\frac{9E}{\pi h{\delta}^3}(2D);\frac{12E}{\pi {\delta}^4}(3D) $$
(7)

where h is the thickness and A is the cross-sectional area. In PD theory, the material damage is included as part of the constitutive relationship by introducing a failure parameter, so that if the stretch exceeds a critical stretch value, failure parameter reduces the peridynamic force value to zero. In other words, the peridynamic bond between two initially interacting material points is broken.

In order to solve the PD equation of motion given in Eq. (1), the meshless method is widely used. Therefore, Eq. (1) can be rewritten in a discrete form as

$$ \rho \ddot{\mathbf{u}}\left({\mathbf{x}}_{(k)},t\right)=\sum \limits_{i=1}^N\mathbf{f}\left(\mathbf{u}\left({\mathbf{x}}_{(j)},t\right)-\mathbf{u}\left({\mathbf{x}}_{(k)},t\right),{\mathbf{x}}_{(j)}-{\mathbf{x}}_{(k)}\right){V}_{(k)}+\mathbf{b}\left({\mathbf{x}}_{(k)},t\right) $$
(8)

where k is the main material point, j is the family member and N is the number of material points inside the horizon of the material point k.

3 Peridynamic Mindlin Plate Formulation

The peridynamic formulation presented in the previous section is for material points having translational degrees of freedom only. If rotational degrees of freedom are desired to be included to represent Mindlin plate formulation in peridynamics, appropriate changes to the original PD formulation should be made as explained in Diyaroglu et al. [20]. In Mindlin plate formulation, each material point has three degrees of freedom including transverse deflection, w and rotation of planes around x- axis, ϕy and y-axis, ϕx(see Fig. 2).

Fig. 2
figure 2

Initial and deformed configuration of a Mindlin plate [20]

Full size image

As presented in Diyaroglu et al. [20], the transverse shear angle and curvature can be respectively expressed in peridynamic form as

$$ {\varphi}_{(k)(j)}=\frac{w_{(j)}-{w}_{(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid }-\frac{\left({\phi}_{x(j)}\cos \theta +{\phi}_{y(j)}\sin \theta \right)+\left({\phi}_{x(k)}\cos \theta +{\phi}_{y(k)}\sin \theta \right)}{2} $$
(9)

and

$$ {\kappa}_{(k)(j)}=\left(\frac{\phi_{x(j)}-{\phi}_{x(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta +\left(\frac{\phi_{y(j)}-{\phi}_{y(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\sin \theta $$
(10)

where θ is the peridynamic bond orientation with respect to x-axis. Moreover, the peridynamic equations of motion for the material point k can be derived using the principle of virtual work as

$$ \rho h{\ddot{w}}_{(k)}={c}_s\sum \limits_{j=1}^N{\varphi}_{(k)(j)}{V}_{(j)}+{\hat{b}}_{(k)} $$
(11)
$$ \rho \frac{h^3}{12}{\ddot{\phi}}_{x(k)}={c}_b\sum \limits_{j=1}^N{\kappa}_{(k)(j)}\cos \theta\;{V}_{(j)}+\frac{1}{2}{c}_s\sum \limits_{j=1}^N\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid {\varphi}_{(k)(j)}\cos \theta\;{V}_{(j)}+{\tilde{b}}_{x(k)} $$
(12)
$$ \rho \frac{h^3}{12}{\ddot{\phi}}_{y(k)}={c}_b\sum \limits_{j=1}^N{\kappa}_{(k)(j)}\sin \theta\;{V}_{(j)}+\frac{1}{2}{c}_s\sum \limits_{j=1}^N\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid {\varphi}_{(k)(j)}\sin \theta\;{V}_{(j)}+{\tilde{b}}_{y(k)} $$
(13)

Using transverse shear angle and curvature equations given in Eqs. (9) and (10), Eqs. (11)–(13) can be rewritten as

$$ \rho h{\ddot{w}}_{(k)}={c}_s\sum \limits_{j=1}^N\left(\frac{w_{(j)}-{w}_{(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid }-\frac{\left({\phi}_{x(j)}+{\phi}_{x(k)}\right)}{2}\cos \theta -\frac{\left({\phi}_{y(j)}+{\phi}_{y(k)}\right)}{2}\sin \theta \right){V}_{(j)}+{\hat{b}}_{(k)} $$
(14)
$$ {\displaystyle \begin{array}{l}\rho \frac{h^3}{12}{\ddot{\phi}}_{x(k)}={c}_b\sum \limits_{j=1}^N\left(\left(\frac{\phi_{x(j)}-{\phi}_{x(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta +\left(\frac{\phi_{y(j)}-{\phi}_{y(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\sin \theta \right)\cos \theta\;{V}_{(j)}\\ {}+\frac{1}{2}{c}_s\sum \limits_{j=1}^N\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid \left(\frac{w_{(j)}-{w}_{(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid }-\frac{\left({\phi}_{x(j)}+{\phi}_{x(k)}\right)}{2}\cos \theta -\frac{\left({\phi}_{y(j)}+{\phi}_{y(k)}\right)}{2}\sin \theta \right)\cos \theta\;{V}_{(j)}+{\tilde{b}}_{x(k)}\end{array}} $$
(15)
$$ {\displaystyle \begin{array}{l}\rho \frac{h^3}{12}{\ddot{\phi}}_{y(k)}={c}_b\sum \limits_{j=1}^N\left(\left(\frac{\phi_{x(j)}-{\phi}_{x(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta +\left(\frac{\phi_{y(j)}-{\phi}_{y(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\sin \theta \right)\sin \theta\;{V}_{(j)}\\ {}+\frac{1}{2}{c}_s\sum \limits_{j=1}^N\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid \left(\frac{w_{(j)}-{w}_{(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid }-\frac{\left({\phi}_{x(j)}+{\phi}_{x(k)}\right)}{2}\cos \theta -\frac{\left({\phi}_{y(j)}+{\phi}_{y(k)}\right)}{2}\sin \theta \right)\sin \theta\;{V}_{(j)}+{\tilde{b}}_{y(k)}\end{array}} $$
(16)

where

$$ {c}_s=\frac{9E}{4\pi {\delta}^3}{k}_s^2 $$
(17)
$$ {c}_b=\frac{E}{\pi \delta}\left(\frac{3{h}^2}{4{\delta}^2}+\frac{27}{80}{k}_s^2\right) $$
(18)

and ks represents the shear correction factor. To describe mode-I and mode-III type fracture modes, Diyaroglu et al. [20] defined critical curvature and critical shear angle parameters, respectively, as

$$ {\kappa}_c=\sqrt{\frac{4{G}_{Ic}}{c_bh{\delta}^4}} $$
(19)
$$ {\varphi}_c=\sqrt{\frac{4{G}_{IIIc}}{c_sh{\delta}^4}} $$
(20)

where GIc and GIIIc represent mode-I and mode-III critical energy release rates, respectively.

4 Direct Solution of the Peridynamic Mindlin Plate Formulation

In peridynamics, the static solution can be obtained by using adaptive dynamic relaxation (ADR) [26] or direct approach [24]. In ADR, artificial damping is introduced to the system and the solution converges to the static solution after a certain number of iterations. In the direct approach, the inertia term is specified to zero and a matrix solution is required. Therefore, the PD force function can be expressed in terms of the second-order micromodulus tensor C as [5]

$$ \mathbf{f}=\mathbf{C}\left(\boldsymbol{\upxi} \right)\boldsymbol{\upeta} $$
(21)

where

$$ \mathbf{C}\left(\boldsymbol{\upxi} \right)=\frac{\partial \mathbf{f}}{\partial \boldsymbol{\upeta}}\left(0,\boldsymbol{\upxi} \right) $$
(22)

In the case of PD Mindlin plate formulation, micromodulus tensor, C can be defined as a Jacobian matrix which is a matrix of all first-order partial derivatives of a vector-valued function. Therefore, for the force vector function f which is a function of shear angle φ and curvature κ, the micromodulus tensor can be defined as:

$$ \mathbf{C}=\left[\begin{array}{cc}\frac{\partial {f}_z}{\partial \varphi }& \frac{\partial {f}_z}{\partial \kappa}\\ {}\frac{\partial {m}_{\phi_x}}{\partial \varphi }& \frac{\partial {m}_{\phi_x}}{\partial \kappa}\\ {}\frac{\partial {m}_{\phi_y}}{\partial \varphi }& \frac{\partial {m}_{\phi_y}}{\partial \kappa}\end{array}\right] $$
(23)

where fz, \( {m}_{\phi_x} \) and \( {m}_{\phi_y} \) represent force or moment functions between material points arising from transverse shear deformation and bending. Utilising peridynamic equations given in Eqs. (11)–(13), force and moment functions can be obtained as

$$ {f}_z={c}_s\varphi $$
(24)
$$ {m}_{\phi_x}={c}_b\kappa \cos \theta +\frac{c_s}{2}\mid \boldsymbol{\upxi} \mid \varphi \cos \theta $$
(25)
$$ {m}_{\phi_y}={c}_b\kappa \sin \theta +\frac{c_s}{2}\mid \boldsymbol{\upxi} \mid \varphi \sin \theta $$
(26)

Therefore, using Eq. (23) micromodulus tensor C takes the form of

$$ \mathbf{C}=\left[\begin{array}{cc}{c}_s& 0\\ {}\frac{c_s}{2}\mid \boldsymbol{\upxi} \mid \cos \theta & {c}_b\cos \theta \\ {}\frac{c_s}{2}\mid \boldsymbol{\upxi} \mid \sin \theta & {c}_b\sin \theta \end{array}\right] $$
(27)

Substituting Eq. (27) into Eq. (21) results in

$$ \left\{\begin{array}{c}{f}_z\\ {}{m}_{\phi_x}\\ {}{m}_{\phi_y}\end{array}\right\}=\left[\begin{array}{cc}{c}_s& 0\\ {}\frac{c_s}{2}\mid \boldsymbol{\upxi} \mid \cos \theta & {c}_b\cos \theta \\ {}\frac{c_s}{2}\mid \boldsymbol{\upxi} \mid \sin \theta & {c}_b\sin \theta \end{array}\right]\left\{\begin{array}{c}\varphi \\ {}\kappa \end{array}\right\} $$
(28)

The force and moment functions between material points j and k can be rewritten by substituting Eqs. (9) and (10) into Eq. (28) as

$$ \left\{\begin{array}{c}{f}_{z(k)(j)}\\ {}{m}_{\phi_x(k)(j)}\\ {}{m}_{\phi_y(k)(j)}\end{array}\right\}=\left[\begin{array}{cc}{c}_s& 0\\ {}\frac{c_s}{2}\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid \cos \theta & {c}_b\cos \theta \\ {}\frac{c_s}{2}\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid \sin \theta & {c}_b\sin \theta \end{array}\right]\left\{\begin{array}{c}\frac{w_{(j)}-{w}_{(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid }-\frac{\left({\phi}_{x(j)}\cos \theta +{\phi}_{y(j)}\sin \theta \right)+\left({\phi}_{x(k)}\cos \theta +{\phi}_{y(k)}\sin \theta \right)}{2}\\ {}\left(\frac{\phi_{x(j)}-{\phi}_{x(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta +\left(\frac{\phi_{y(j)}-{\phi}_{y(k)}}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\sin \theta \end{array}\right\} $$
(29)

After reorganising Eq. (29), the following matrix expression of force and moment functions can be obtained as

$$ \left\{\begin{array}{c}{f}_{z(k)(j)}\\ {}{m}_{\phi_x(k)(j)}\\ {}{m}_{\phi_y(k)(j)}\end{array}\right\}=\left[\begin{array}{cccccc}\frac{c_s}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid }& \frac{c_s}{2}\cos \theta & \frac{c_s}{2}\sin \theta & -\frac{c_s}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid }& \frac{c_s}{2}\cos \theta & \frac{c_s}{2}\sin \theta \\ {}\frac{c_s}{2}\cos \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|+\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right){\cos}^2\theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|+\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta \sin \theta & -\frac{c_s}{2}\cos \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|-\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right){\cos}^2\theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|-\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta \sin \theta \\ {}\frac{c_s}{2}\sin \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|+\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta \sin \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|+\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right){\sin}^2\theta & -\frac{c_s}{2}\sin \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|-\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta \sin \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|-\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right){\cos}^2\theta \end{array}\right]\left\{\begin{array}{c}{w}_{(k)}\\ {}{\phi}_{x(k)}\\ {}{\phi}_{y(k)}\\ {}{w}_{(j)}\\ {}{\phi}_{x(j)}\\ {}{\phi}_{y(j)}\end{array}\right\} $$
(30)

For static and quasi-static problems, the acceleration terms, \( \ddot{w} \), \( {\ddot{\phi}}_x \) and \( {\ddot{\phi}}_y \) can be omitted from the equation of motion as

$$ \sum \limits_{j=1}^N{\mathbf{f}}_{(k)(j)}{V}_{(j)}+{\mathbf{b}}_{(k)}=\mathbf{0} $$
(31)

where \( {\mathbf{f}}_{(k)(j)}={\left[{f}_{z(k)(j)}\kern0.5em {m}_{\phi_x(k)(j)}\kern0.5em {m}_{\phi_y(k)(j)}\right]}^T \) and \( {\mathbf{b}}_{(k)}={\left[{\hat{b}}_{(k)}\kern0.5em {\tilde{b}}_{x(k)}\kern0.5em {\tilde{b}}_{y(k)}\right]}^T \). Substituting force/moment functions given in Eq. (30) into Eq. (31) leads to

$$ {\displaystyle \begin{array}{l}\sum \limits_{j=1}^N\left[\begin{array}{cccccc}\frac{c_s}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid }& \frac{c_s}{2}\cos \theta & \frac{c_s}{2}\sin \theta & -\frac{c_s}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid }& \frac{c_s}{2}\cos \theta & \frac{c_s}{2}\sin \theta \\ {}\frac{c_s}{2}\cos \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|+\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right){\cos}^2\theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|+\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta \sin \theta & -\frac{c_s}{2}\cos \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|-\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right){\cos}^2\theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|-\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta \sin \theta \\ {}\frac{c_s}{2}\sin \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|+\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta \sin \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|+\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right){\sin}^2\theta & -\frac{c_s}{2}\sin \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|-\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right)\cos \theta \sin \theta & \left(\frac{c_s}{4}|{\boldsymbol{\upxi}}_{(j)(k)}|-\frac{c_b}{\mid {\boldsymbol{\upxi}}_{(j)(k)}\mid}\right){\cos}^2\theta \end{array}\right]\left\{\begin{array}{c}{w}_{(k)}\\ {}{\phi}_{x(k)}\\ {}{\phi}_{y(k)}\\ {}{w}_{(j)}\\ {}{\phi}_{x(j)}\\ {}{\phi}_{y(j)}\end{array}\right\}{V}_{(j)}+{\mathbf{b}}_{(k)}=\mathbf{0}\\ {}\end{array}} $$
(32)

5 Peridynamic Mindlin Plate Resting on an Elastic Foundation

In this study, the Winkler foundation is considered as the elastic foundation and coupled with PD Mindlin formulation presented in Section 4. Winkler foundation was originally introduced by Winkler [27] for modelling the soil-structure interactions. Winkler method assumes that vertical translation of the soil, w, at a point depends only upon the contact pressure, p, acting at that point in the idealised elastic foundation and a proportionality constant, k, as

$$ p= kw $$
(33)

The proportionality constant, k, is commonly referred to as the modulus of subgrade reaction or the coefficient of subgrade reaction. This model was first used to analyse the deflections and resultant stresses in railroad tracks. In the following years, it has been applied to many different soil/fluid-structure interaction problems, and it is known as die Winkler model (Fig. 3).

Fig. 3
figure 3

Mindlin plate on a Winkler foundation

Full size image

In order to combine the Winkler foundation with PD Mindlin plate matrix formulation, Winkler foundation formulation can be written in matrix form as

$$ \left[\begin{array}{cccccc}\frac{kh}{V_{(j)}}& 0& 0& -\frac{kh}{V_{(j)}}& 0& 0\\ {}0& 0& 0& 0& 0& 0\\ {}0& 0& 0& 0& 0& 0\end{array}\right]\left\{\begin{array}{c}{w}_{(k)}\\ {}{\phi}_{x(k)}\\ {}{\phi}_{y(k)}\\ {}{w}_{(j)}\\ {}{\phi}_{x(j)}\\ {}{\phi}_{y(j)}\end{array}\right\}+{\mathbf{b}}_{(k)}=\mathbf{0} $$
(34)

where k is the spring stiffness and h is the thickness of the plate. It is assumed that the Winkler foundation only affects transverse deflection.

6 Numerical Results

As part of the numerical results, simple static loading conditions are considered first to compare the PD predictions with the finite element analysis (FEA) results using ANSYS, a commercial FEA software. Next, a plate with a central crack under pure bending resting on a Winkler foundation with very small spring stiffness is considered as a validation case to compare against results obtained in Diyaroglu et al. [20]. Then, fracture behaviour of a pre-cracked ice sheet floating on water under transverse loading condition is investigated.

6.1 Mindlin Plate Rested on a Winkler Foundation Subjected to Transverse Loading

In the first example, a Mindlin plate rested on a Winkler foundation under half circular edge pressure is considered (see Figs. 4 and 5). This problem was first introduced by Lu et al. [28] to simulate displacement distribution for a finite size ice floe interacting with sloping structures.

Fig. 4
figure 4

Illustration of the model utilised to study displacement and rotation distributions [28]

Full size image
Fig. 5
figure 5

Peridynamic discretization of Mindlin plate subjected to the transverse loading (grey area)

Full size image

As it was stated by Lu et al. [28], there is no analytical closed-form solution to calculate the deflection and stress distribution of a finite plate with free edges under evenly distributed edge pressure within a half circular area. Therefore, a numerical solution is adopted in order to verify PD results. The length of the square plate is L = 0.43 m with a thickness of h = 0.01 m. The radius of the loading area is R = 0.2 L. The Young’s modulus of the plate is specified as E = 5.5 GPa. Only a single row of material points (collocation) in the thickness direction is necessary to discretize the domain. The distance between material points is ∆x = 0.00215 m. The loading is applied to a single row of material points at the half circular area as a resultant body load of \( \hat{b}=86.12\;\mathrm{N}/{\mathrm{m}}^2 \) for the transverse loading. The Winkler foundation modulus to represent the fluid base is k = ρwg = 1025 (kg/m3) ⋅ 9.81(m/s2) = 10055.25 Pa/m, with ρw and g being the fluid density and gravitational acceleration, respectively.

The peridynamic solutions for transverse displacement and rotations are compared with finite element solutions obtained by using ANSYS shell element, which is suitable for thick/thin shell structures. As depicted in Figs. 6 and 7, PD and FE solutions are in good agreement with each other and this verifies that the PD direct solution correctly captures the deformation behaviour of the Mindlin plate rested on an elastic foundation.

Fig. 6
figure 6

FEA results for displacement w (m) (a) and rotations ϕx (b) and ϕy (c)

Full size image
Fig. 7
figure 7

Peridynamic Mindlin plate results for displacement w (m) (a) and rotations ϕx (b) and ϕy (c)

Full size image

6.2 Pre-cracked Mindlin Plate Rested on a Winkler Foundation Subjected to Pure Bending Conditions

In the second example, a verification study is considered as in Diyaroglu et al. [20] to investigate the behaviour of a pre-existing crack in a Mindlin plate. A square plate with an initial central crack aligned with the y-axis is considered as shown in Fig. 8. The length and width of the square plate are L = W = 1 m with a thickness of h = 0.1 m. Plate thickness to crack length is h/2a = 0.5 where 2a is the initial crack length.

Fig. 8
figure 8

a Pre-cracked Mindlin plate under pure bending condition. b Peridynamic discretization of pre-cracked Mindlin plate resting on an elastic Winkler foundation

Full size image

The Young’s modulus of the plate is specified as E = 3.227 GPa, and the shear modulus is G = 1.21 GPa. The distance between material points is ∆x = 0.01 m. The horizon size is chosen as δ = 3.015∆x. The stiffness of the Winkler foundation is set to be a very small value, k = 10−9 N/m, in order to represent the original example of Diyaroglu et al. [20] which is free from the elastic foundation. The material is chosen as polymethyl methacrylate (PMMA), which shows brittle fracture behaviour. Mode-I fracture toughness of this material is given as 1.33 \( \mathrm{MPa}\sqrt{\mathrm{m}} \) [29]. In order to show simple mode-I crack growth, a bending moment loading is applied to a single row of points at horizontal boundary regions of the plate. Small increments of resultant body load of \( \varDelta {\tilde{b}}_x \) = 0.05 N/m are induced in order to obtain a stable crack growth. Crack starts to grow approximately at \( {\tilde{b}}_x \) = 284 N/m as shown in Fig. 9, and a similar crack pattern is obtained as in Diyaroglu et al. [20].

Fig. 9
figure 9

Crack propagation for PMMA pre-cracked plate resting on a Winkler foundation

Full size image

6.3 Pre-cracked Mindlin Plate Rested on a Winkler Foundation Subjected to Transverse Loading

This case represents a further development of the example presented in Section 6.1. Ice floe length is specified as L = 3.01 m. Load area radius representing the sloping structure load is set to R = 0.086 m. The thickness of the plate is h = 0.01 m (Fig. 4). Ice is modelled as an isotropic material with Young’s modulus of E = 5.5 GPa and shear modulus of G = 2.0625 GPa. The distance between material points is ∆x = 0.01935 m. The horizon size is chosen as δ = 3.015∆x. Winkler foundation stiffness k is set to k = 10055.25 Pa/m which roughly approximates water behaviour. Ice is a complex material and can exhibit either ductile or brittle fracture properties depending on the conditions [30]. For this example case, sea ice is considered a brittle material as considered in Lu et al. [28]. Mode-I fracture toughness of sea ice is given as 0.12 \( \mathrm{MPa}\sqrt{\mathrm{m}} \) [30]. To the authors’ knowledge, there is no available value for mode-III fracture toughness of sea ice in the current literature. We assumed mode-III toughness to be 7 times greater than mode-I by comparing the ratios to other brittle materials such as PMMA.

In order to generate initial damage, a small initial crack was introduced into the model. The size of the initial crack was set to 6∆x and crack orientation was perpendicular to the free edge. Initial load is set to 0, and then small increments of resultant body load, \( \varDelta {\hat{b}}_z \) = 0.1 N/m2, are induced in order to obtain a stable crack growth.

According to Lu et al. [28] and Nevel [31], the specified plate size in this problem case can be considered as a semi-infinite plate. According to observations in the field made by Kerr [32], the failure mechanism of a semi-infinite ice plate subjected to a force P at the free edge proceeds as follows. First, a radial crack forms, which starts under the load and propagates normal to the free boundary. This is followed by the formation of a circumferential crack that causes final failure. This behaviour is clearly captured by peridynamics and shown in Fig. 10 where Fig. 10 a shows initial crack before the plate is loaded, Fig. 10 b shows crack propagation at \( {\hat{b}}_z \) = 161 N/m2 and Fig. 10 c shows circumferential crack reaching the free surface at \( {\hat{b}}_z \) = 304 N/m2.

Fig. 10
figure 10

Ice failure for a pre-cracked Mindlin plate rested on a Winkler foundation subjected to transverse loading

Full size image

7 Final Remarks

In this study, a new peridynamic model is presented for a Mindlin plate resting on a Winkler type elastic foundation. The formulation is validated by comparing against FEA results for a transverse loading condition for a plate without a crack. For a pure bending loading condition applied to a plate with a central crack free from the elastic foundation provided a similar crack pattern that was obtained in an earlier study. Finally, a pre-cracked ice sheet floating on water under transverse loading conditions was investigated. As observed in field observations, peridynamic results showed that first a radial crack forms and propagates normal to the free boundary followed by a circumferential crack.