1 Introduction

The dynamics of wild animal populations is an important issue not only for ecological purposes, but also for agricultural and livestock production (Cumming et al., 2012). The wild boar (Sus scrofa) is considered to have one of largest geographical ranges of all terrestrial mammals (Lewis et al., 2017). It causes several types of losses related to the environment, agricultural activities, and animal production/trade by spreading diseases (Meng et al., 2009; Sánchez-Vizcaíno et al., 2019). With the re-emergence of African Swine Fever (ASF) as a threat to the global pig industry (Sánchez-Cordón et al., 2018), there is an ongoing need for better quantitative descriptions of the movement and land-occupation behaviors of wild boars (McClure et al., 2015; Morelle et al., 2014).

Animal dispersal occurs when individuals leave their social group or home range, redistributing the population (Breed & Moore, 2016). According to Casas-Díaz et al. (2013), dispersal is an important characteristic of the wild boar’s ecology and should be taken into account in the design of disease monitoring programs as these animals can affect the spread of diseases and the probability of new outbreaks. Several techniques are used to measure animal dispersal [e.g., radio telemetry, GPS, ground surveys, or hunting statistics (Morelle et al., 2014)], and datasets produced by recapture with hunting bags are important sources of information for veterinary epidemiology (Keuling et al., 2018; Scillitani et al., 2010; Vicente et al., 2018).

Animal dispersal data may have a complex structure: it may be right-skewed given the short-distance dispersal; have excessive zeros, because many animals do not disperse at all or they disperse distances that are inside the error margin of telemetry (Keuling et al., 2008). Also, censored observations may occur, when an animal’s track is lost (e.g., collars or ear tags are lost, or animals move away from the hunting perimeter) (Podgórski et al., 2014; Prévot & Licoppe, 2013; Truvé & Lemel, 2003). This data structure is challenging from an inferential perspective, creating issues for researchers attempting to formulate hypotheses or build models using dispersal distance information (Bowman et al., 2002). Thus, many authors discard the censored data and also avoid fitting generalized linear models. As a consequence, the datasets are not correctly used in making inferences and testing hypotheses about dispersal distances (Prévot & Licoppe, 2013; Truvé & Lemel, 2003). Evidently, improvements in quantitative analytical techniques on dispersal distance are still needed (Whitmee & Orme, 2013).

According to Lambert (1992), the zero values can have the following sources: they can come from a population where the value would always be zero, called “structural zeros”; alternatively, they can be “sampling zeros” from a population whose observations belong to some probability distribution. To analyze a zero-inflated non-negative outcome (semi-continuous outcome) data, Manning et al. (1981) proposed a two-part model (2PM), separating the zero and positive values explicitly in two submodels (parts). Liu et al. (2010) proposed an extension of the 2PM, assuming a generalized gamma distribution of the positive values. Lee et al. (2010) proposed a two-part multilevel modeling, in which the zero proportion is modeled by logistic regression and the continuous values by gamma regression. Gebregziabher et al. (2017) presented a family of models for zero-heavy continuous outcomes, with Weibull mixture regression as a special case, and with a marginal inference. Louzada et al. (2018) proposed a zero-inflated non-default rate regression, assuming that the positive values follow a Weibull distribution.

To consider the whole data structure of wild boar dispersal distances, we propose an extension of the zero-inflated gamma model (Lee et al., 2010), incorporating the right-censored observations in the continuous values through the gamma regression. Furthermore, we consider the zero-inflated, right-censored Weibull regression (Louzada et al., 2018), discarding the cure rate of the model. In the models proposed in this paper, both techniques allow the incorporation of the whole data (without excluding zeros and the right-censored observations) to make inferences. This includes covariates in the model, as the survival models can also be used to assess distances, as seen in Reader (2000) and Chatwin et al. (2013). The gamma is a flexible distribution; it describes a different type of survival pattern according to the hazard rate: increasing, decreasing, or constant; it fits a variety of lifetime data adequately and has the exponential distribution as a particular case (Lawless, 2011). The Weibull distribution is also flexible and has a monotonically increasing, decreasing, or constant hazard rate (Klein & Moeschberger, 2003); is probably the most used parametric lifetime model (Wienke, 2011); it has been widely used to model right-skewed data and has also motivated proposals of various types of generalizations (Liao et al., 2020; Ramos et al., 2018; Shinohara et al., 2020).

Given the lack of a dataset fully describing zeros, dispersal distances, and censored data, we apply both techniques to an artificial dataset that mimics the wild boar population’s dispersal. The simulated animal population includes three subpopulations: animals for which no dispersal was registered (zeros); animals that showed some measurable distance, and animals whose track has been lost (censored). Such data mimic situations of capture–recapture using hunting bags in which a proportion of animals moved away from the hunting perimeter. The manuscript is structured as follows.

First, we present the definitions and the construction of the zero-inflated-censored Weibull (ZIWeibull) and the zero-inflated-censored gamma (ZIGamma) models. Next, we show the properties of the models’ estimators and compare the two models. Finally, we demonstrate their application to the artificial wild boar dispersal dataset. An R function was created to enable users to run the models with their own data. Instructions regarding this function and package installation details are available in Appendix (instructions for installing the R functions and run the models).

2 Formulation of the models

Let T denote the random variable of interest, and it is the observable time to event, called lifetime or failure time. Finally, consider \(\pmb {\text {x}}_{1}, \pmb {\text {x}}_{2}, \pmb {\text {x}}_{3}\) three vectors of the covariates, where \(\pmb {\text {x}}_{1}\) relates to the zero-inflation probability, \(\pmb {\text {x}}_{2}\) relates to the scale, and \(\pmb {\text {x}}_{3}\) relates to the shape of the lifetime distribution.

We propose an alteration of the zero-inflated non-default regression model (Louzada et al., 2018), using the zero-inflated and regression parts while removing the cure rate part of the model. Thus, the probability density function (PDF) and the cumulative density function (CDF) of the observable lifetime time T of the zero-inflated model are, respectively, given by

$$\begin{aligned} \begin{aligned} f_0(t)&= \left\{ \begin{array}{ll} p_{0}, &{} \hbox { if}\ t = 0\\ (1-p_{0})f(t), &{} \hbox { if}\ t > 0 \end{array}\right. \\ \\&\qquad \text {and} \\ \\ \ F_0(t)&= p_{0} + (1-p_{0}) F(t), \,\,\,\, t \ge 0, \end{aligned} \end{aligned}$$
(1)

where \(p_{0} \in (0, 1)\) is the zero-inflation probability, f(t) is the probability density function, and F(t) is the cumulative density function of the observable lifetime time.

The observed data are denoted by \(D_\text {obs}=\{(t_i,\delta _i), i=1,\ldots ,n\}\), where \(\delta _i=1\) if the event of interest occurs and \(\delta _i=0\) if it is right-censored, \(i=1,\dots ,n\). Assuming independent and non-informative censoring, the likelihood function \(L(\pmb {\theta };D_\text {obs})\) is given by

$$\begin{aligned} L( \pmb {\theta };D_\text {obs})= \prod _{\begin{array}{c} i:t_i=0 \end{array}} p_{0i} \prod _{\begin{array}{c} i:t_i>0 \end{array}} \left\{ \left[ (1-p_{0i})f_i(t_i)\right] ^{\delta _i}\left[ (1-p_{0i})S_i(t_i)\right] ^{1-\delta _i}\right\} , \end{aligned}$$
(2)

where \(\pmb {\theta }=(p_{0i}, \pmb {\vartheta })\), \(\pmb {\vartheta }\) denotes the parameter vector associated to the probability density function f(t) and, consequently, to the survivor function S(t); \(p_{0i}\) is the zero-inflate probability of the ith subject.

Considering the relation \(f(t)=h(t)S(t)\) and \(S(t)=\exp \{-H(t)\}\) in (2), where h(t) is the hazard function and H(t) is the cumulative hazard function, we obtain the following likelihood function:

$$\begin{aligned} L( \pmb {\theta };D_\text {obs})= \prod _{\begin{array}{c} i:t_i=0 \end{array}} p_{0i} \prod _{\begin{array}{c} i:t_i>0 \end{array}} \left\{ \left[ h_i(t_i)\right] ^{\delta _i}\left[ (1-p_{0i})\exp \left[ -H_i(t_i)\right] \right] \right\} . \end{aligned}$$
(3)

Therefore, the log-likelihood function for \(\pmb {\theta }=(p_{0i},\pmb {\vartheta })\), corresponding to the observed data and the likelihood function as in (3), is given by

$$\begin{aligned} \begin{aligned} \log \{L( \pmb {\theta };D_\text {obs})\}&= \sum _{\begin{array}{c} i:t_i=0 \end{array}} \log (p_{0i})+ \sum _{\begin{array}{c} i:t_i>0 \end{array}}\delta _i \log \left[ h_i(t_i)\right] \\&\quad +\sum _{\begin{array}{c} i:t_i>0 \end{array}}\log \big \{(1-p_{0i})\exp \left[ -H_i(t_i)\right] \big \}\\&=\sum _{\begin{array}{c} i:t_i=0 \end{array}}\log (p_{0i})+\sum _{\begin{array}{c} i:t_i>0 \end{array}}\delta _i \log \left[ h_i(t_i)\right] \\&\quad +\sum _{\begin{array}{c} i:t_i>0 \end{array}}\log (1-p_{0i}) - \sum _{\begin{array}{c} i:t_i>0 \end{array}} H_i(t_i). \end{aligned} \end{aligned}$$
(4)

To obtain the maximum-likelihood estimates for the vector \(\pmb {\theta }=( p_{0i}, \pmb {\vartheta })\), we must find the score functions \(U(\pmb {\theta })=\frac{\partial \log \{L( \pmb {\theta };D_\text {obs})\}}{\partial \pmb {\theta }}\). To solve the non-linear system of equations \(U(\pmb {\theta })=\frac{\partial \log \{L( \pmb {\theta };D_\text {obs})\}}{\partial \pmb {\theta }}=0\), we chose the function “optim” in the R software (R Core Team, 2019) for numerical maximization, with the method “BFGS”, according to Louzada et al. (2018). Details on non-linear optimization can be found in Press et al. (2007).

The standard errors (SE) of the estimators are obtained through the diagonal of the inverted Fisher information matrix. The Fisher information matrix can be generically defined by

$$\begin{aligned} K(\pmb {\theta }) = \begin{matrix} \left( { \begin{array}{*{20}c} {K_{pp}} &{} 0 \\ 0 &{} {K_{ \pmb {\vartheta } \pmb {\vartheta }} } \\ \end{array} } \right) , \end{matrix} \end{aligned}$$
(5)

where \(K_{pp}\) denotes second-order partial derivatives of \(\pmb {\theta }\) with respect to the covariates vector associated with \(p_{0}\), \(K_{ \pmb {\vartheta } \pmb {\vartheta }}\) denotes second-order partial derivatives of \(\pmb {\theta }\) with respect to the vector \(\pmb {\vartheta }\).

According to Ospina and Ferrari (2012), the confidence intervals of the components of the vector \(\pmb {\theta }\) can be obtained through \(\pmb {{\hat{\theta }}} \pm z_{1-\alpha /2}[K(\pmb {{\hat{\theta }}})^{-1}]^{1/2}\), with asymptotic coverage \(100(1-\alpha )\%\), and \(z_{1-\alpha /2}\) is the \((1-\alpha /2)\)-th quantile of the standard normal distribution. For more details on the asymptotic theory, see Ospina and Ferrari (2012) and Louzada et al. (2018).

The approach presented thus far can be used for any choice of hazard function h(t) and, consequently, any cumulative hazard function H(t). In the following section, we present the equations when the Weibull and gamma distributions are chosen to adjust the survival times.

2.1 Zero-inflated-censored Weibull model

If we consider the Weibull distribution to model the non-negative random variable \(T|T>0\), in other words \(T|T>0\sim \text {Weibull}(\alpha _{\mathrm{w}},\lambda _{\mathrm{w}})\), which here denotes the observable survival time, we obtain the following probability density function:

$$\begin{aligned} f(t)=\frac{\alpha _{\mathrm{w}}}{\lambda _{\mathrm{w}}}\left( \frac{t}{\lambda _{\mathrm{w}}}\right) ^{\alpha _{\mathrm{w}}-1} \exp \bigg [-\left( \frac{t}{\lambda _{\mathrm{w}}}\right) ^{\alpha _{\mathrm{w}}}\bigg ], \, \, \, \, t \ge 0, \end{aligned}$$
(6)

where \(\alpha _{\mathrm{w}} > 0\) is the shape parameter and \(\lambda _{\mathrm{w}} > 0\) is the scale parameter of the distribution.

Replacing the hazard function h(t) and the cumulative hazard function H(t) from the log-likelihood function (4) with the hazard function and the cumulative hazard function from the Weibull distribution (6), we obtain the following log-likelihood function:

$$\begin{aligned} \begin{aligned} \log \{L( \pmb {\theta };D_\text {obs})\}&=\sum _{\begin{array}{c} i:t_i=0 \end{array}}\log (p_{0i}) +\sum _{\begin{array}{c} i:t_i>0 \end{array}}\delta _i\Bigg [\log \bigg (\frac{\alpha _{\mathrm{w}}}{\lambda _{\mathrm{w}}}\bigg ) + (\alpha _{\mathrm{w}}-1)\log \bigg (\frac{t_i}{\lambda _{\mathrm{w}}}\bigg )\Bigg ]\\& \quad +\sum _{\begin{array}{c} i:t_i>0 \end{array}}\log (1-p_{0i}) - \sum _{\begin{array}{c} i:t_i>0 \end{array}}\left( \frac{t_i}{\lambda _{\mathrm{w}}}\right) ^{\alpha _{\mathrm{w}}}. \end{aligned} \end{aligned}$$
(7)

The inclusion of covariates determines the effect of covariates on the observable survival time and the probability of zeros. The parameters \((p_{0i}, \alpha _{\mathrm{w}}, \lambda _{\mathrm{w}})\) are related to the proportion of zeros, the shape, and the scale parameters of the Weibull distribution, respectively. The systematic components of the regression version of the zero-inflated-censored Weibull model are given by

$$\begin{aligned} \left\{ \begin{array}{ll} G_1(p_{0i})&{} = \xi _{0i}\\ G_2(\lambda _{{\rm{w}}i})&{} =\eta _{1i}\\ G_3(\alpha _{{\rm{w}}i})&{} =\eta _{2i},\end{array} \right. \end{aligned}$$
(8)

where \(\xi _{0i}= \pmb {\text {x}}_{1i}^{\text {T}} \pmb {\beta }_1\) , \(\eta _{1i}= \pmb {\text {x}}_{2i}^{\text {T}} \pmb {\beta }_2\), and \(\eta _{2i}= \pmb {\text {x}}_{3i}^{\text {T}} \pmb {\beta }_3\) are the linear predictors and; \(\pmb {\beta }\)’s are the unknown regression coefficient vectors. The link functions \(G_1(.)\), \(G_2(.)\), and \(G_3(.)\) provide the connection between the linear predictor and the parameters of the probability density function. According to the fit by Louzada et al. (2018), \(G_1(.)\) is set as the logistic regression \(G_1(p_{0i})=\log \left( \frac{p_{0i}}{1-p_{0i}}\right)\), with \(p_{0i}=\frac{e^{ \pmb {\text {x}}_{1i}^{\text {T}} \pmb {\beta }_1}}{1+e^{ \pmb {\text {x}}_{1i}^{\text {T}} \pmb {\beta }_1}}\). Since the scale and shape parameters are defined on the positive real line, the \(G_2(.)\) and \(G_3(.)\) link functions are chosen as \(G_2(\lambda _{{\rm{w}}i})=\) log\((\lambda _{{\rm{w}}i})\) and \(G_3(\alpha _{{\rm{w}}i})=\log (\alpha _{{\rm{w}}i})\). Thus, \(\lambda _{{\rm{w}}i}=e^{ \pmb {\text {x}}_{2i}^{\text {T}} \pmb {\beta }_2}\) and \(\alpha _{{\rm{w}}i}=e^{ \pmb {\text {x}}_{3i}^{\text {T}} \pmb {\beta }_3}\).

Considering the observable time \(T|T>0\sim \text {Weibull}( \alpha _{\mathrm{w}}, \lambda _{\mathrm{w}})\) and the probability density function \(f_0(t)\) (see (1)), the expected value of T is defined by

$$\begin{aligned} \mathbb {E}(T) = (1-p_{0}) \lambda _{\mathrm{w}}\varGamma \left( 1+\frac{1}{\alpha _{\mathrm{w}}}\right) , \end{aligned}$$
(9)

where \(\varGamma (.)\) is the gamma function.

Replacing the parameters in (9) by the relations in (8), we have the following expected value given covariates:

$$\begin{aligned} \mathbb {E}(T| \pmb {\text {x}}_{1},\pmb {\text {x}}_{2},\pmb {\text {x}}_{3})=\left( 1-\frac{e^{\pmb {\text {x}}_{1}^{\text {T}}\pmb {\beta _{1}}}}{1+e^{ \pmb {\text {x}}_{1}^{\text {T}}\pmb {\beta _{1}}}}\right) e^{\pmb {\text {x}}_{2}^{\text {T}}\pmb {\beta _{2}}}\varGamma \left( 1+\frac{1}{e^{ \pmb {\text {x}}_{3}^{\text {T}}\pmb {\beta _{3}}}}\right) . \end{aligned}$$
(10)

2.2 Zero-inflated-censored gamma model

The zero-inflated-censored gamma model is an extension of Lee’s model (Lee et al., 2010). It is based on the concept of two-part or “hurdle” models, in which zeros and non-zeros are considered two independent processes (Mullahy, 1986; Nobre et al., 2017), and the right-censored data are considered in the continuous values. Here, the zeros will be modeled as “success events” using a logistic regression. The positive observable survival time is modeled by a gamma regression survival model.

Let Z be a binary variable, where \(Z=1\) when the observable time was zero in the database, and \(Z=0\) otherwise. Therefore, Z has Bernoulli distribution with \(p_{0}\) parameter, \(Z\sim \text {Ber}(p_{0})\). Since the zero probability, \(P(Z=1)=p_{0}\), is independent of the time distribution, the likelihood function (2) can be rewritten as follows:

$$\begin{aligned} L( \pmb {\theta };D_\text {obs})= \left\{ \prod _{\begin{array}{c} i:Z_i=1 \end{array}} p_{0i} \prod _{\begin{array}{c} i:Z_i=0 \end{array}} (1-p_{0i})\right\} \left\{ \prod _{\begin{array}{c} i:t_i>0 \end{array}} f_i(t_i)^{\delta _i}S_i(t_i)^{1-\delta _i}\right\} , \end{aligned}$$
(11)

where \(\pmb {\theta }=(p_{0i}, \pmb {\vartheta })\) and \(\pmb {\vartheta }\) denotes the parameter vector associated with the probability density function f(t). Factoring the likelihood allows for the estimation of \(p_{0i}\) to be made independently of the fit for the time distribution. To model the zero probability, \(p_{0i}\), we used a logistic regression with \(G_4(p_{0i})=\log \left( \frac{p_{0i}}{1-p_{0i}}\right)\).

Considering the observable time \(T|T>0\sim \text {Gamma}(\alpha _{\mathrm{g}},\lambda _{\mathrm{g}})\), with a shape parameter \(\alpha _{\mathrm{g}}\) and a scale parameter \(\lambda _{\mathrm{g}}\), we obtain the following probability density function:

$$\begin{aligned} f(t)=\frac{1}{\lambda _{\mathrm{g}}^{\alpha _{\mathrm{g}}}\;\varGamma (\alpha _{\mathrm{g}})}t^{\alpha _{\mathrm{g}}-1}\exp \left( -\frac{t}{\lambda _{\mathrm{g}}}\right) ,\, \, \, \, t > 0, \end{aligned}$$
(12)

where \(\alpha _{\mathrm{g}} > 0\) is the shape parameter and \(\lambda _{\mathrm{g}} > 0\) is the scale parameter of the distribution.

Considering the likelihood function (11), the relations \(f(t) = h(t)S(t)\) and \(S(t) = \exp \{-H(t)\}\), assuming gamma distribution to the observable survival time, produce the following log-likelihood function:

$$\begin{aligned} \begin{aligned} \log \{L( \pmb {\theta };D_\text {obs})\}&=\sum _{\begin{array}{c} i:Z_i=1 \end{array}}\log (p_{0i})+\sum _{\begin{array}{c} i:Z_i=0 \end{array}}\log (1-p_{0i})\\& \quad +\sum _{\begin{array}{c} i:t_i>0 \end{array}}\delta _i\Bigg [\alpha _{\mathrm{g}}\log \bigg (\frac{t_i}{\lambda _{\mathrm{g}}}\bigg ) - \log \left[ t_i\varGamma (\alpha _{\mathrm{g}})\right] - \left( \frac{t_i}{\lambda _{\mathrm{g}}}\right) \Bigg ]\\& \quad +\sum _{\begin{array}{c} i:t_i>0 \end{array}}(1-\delta _i)\left[ \log \left[ S(t_i)\right] \right] , \end{aligned} \end{aligned}$$
(13)

where \(S_i(t_i) = \int _{t_i}^{\infty }\frac{1}{\lambda _{\mathrm{g}}^{\alpha _{\mathrm{g}}}\;\varGamma (\alpha _{\mathrm{g}})}u^{\alpha _{\mathrm{g}}-1}\exp \left( -\frac{u}{\lambda _{\mathrm{g}}}\right) {\mathrm{d}}u.\)

We obtain the maximum-likelihood estimates for \(\pmb {\theta }=(p_{0i}, \alpha _{\mathrm{g}}, \lambda _{\mathrm{g}})\) using iterative techniques from the “glm” function for estimate \(p_{0i}\) and from the package “flexsurv” (Jackson, 2016) to estimate \(\alpha _{\mathrm{g}}\) and \(\lambda _{\mathrm{g}}\). Both functions are implemented in the software R (R Core Team, 2019).

The inclusion of the covariates associated with the observable time was achieved through the scale and shape parameters of the gamma distribution. The systematic component of the regression version of the zero-inflated-censored gamma model is given by

$$\begin{aligned} \left\{ \begin{array}{ll} G_4(p_{0i})&{} = \xi _{0i}\\ G_5(\lambda _{{\rm{g}}i})&{} =\eta _{1i}\\ G_6(\alpha _{{\rm{g}}i})&{} =\eta _{2i},\end{array} \right. \end{aligned}$$
(14)

where \(\xi _{0i}= \pmb {\text {x}}_{1i}^{\text {T}} \pmb {\beta }_1\) , \(\eta _{1i}= \pmb {\text {x}}_{2i}^{\text {T}} \pmb {\beta }_2\), and \(\eta _{2i}= \pmb {\text {x}}_{3i}^{\text {T}} \pmb {\beta }_3\) are the linear predictors, and \(\beta\)’s are the unknown regression coefficient vectors. The link functions \(G_4(.)\), \(G_5(.)\), and \(G_6(.)\) provide the connection between the linear predictor and the parameters of the probability density function. \(G_4(.)\) is a set of logistic regression \(G_4(p_{0i})=\log \left( \frac{p_{0i}}{1-p_{0i}}\right)\), with \(p_{0i}=\frac{e^{ \pmb {\text {x}}_{1i}^{\text {T}} \pmb {\beta }_1}}{1+e^{ \pmb {\text {x}}_{1i}^{\text {T}} \pmb {\beta }_1}}\). According to Jackson (2016) \(G_5(.)\) and \(G_6(.)\), link functions are \(G_5(\lambda _{{\rm{g}}i})=\) \(\hbox {log}(\lambda _{{\rm{g}}i})\) and \(G_6(\alpha _{{\rm{g}}i})=\log (\alpha _{{\rm{g}}i})\). Thus, \(\lambda _{{\rm{g}}i}=e^{ \pmb {\text {x}}_{2i}^{\text {T}} \pmb {\beta }_2}\) and \(\alpha _{{\rm{g}}i}=e^{ \pmb {\text {x}}_{3i}^{\text {T}} \pmb {\beta }_3}\).

Assuming the failure time \(T|T>0\sim \text {Gamma}( \alpha _{\mathrm{g}}, \lambda _{\mathrm{g}})\) and the probability density function (1), the expected value of T is defined by \(\mathbb {E}(T) = (1-p_0)\alpha _{\mathrm{g}}\lambda _{\mathrm{g}}\). Considering the inclusion of the covariates, we obtain the following expected value given covariates:

$$\begin{aligned} \mathbb {E}(T| \pmb {\text {x}}_{1},\pmb {\text {x}}_{2},\pmb {\text {x}}_{3})=\left( 1-\frac{e^{\pmb {\text {x}}_{1}^{\text {T}}\pmb {\beta _{1}}}}{1+e^{ \pmb {\text {x}}_{1}^{\text {T}}\pmb {\beta _{1}}}}\right) \exp (\pmb {\text {x}}_{2}^{\text {T}} \pmb {\beta _2}) \exp (\pmb {\text {x}}_{3}^{\text {T}} \pmb {\beta _3}). \end{aligned}$$
(15)

3 Simulation studies

In this section, we present a simulation study to evaluate the models proposed in the previous section. The ZIWeibull model was fitted in a dataset generated from a Weibull distribution, and the ZIGamma model was fitted in a dataset generated from a gamma distribution. The models’ parameters were estimated as described in Sect. 2. Computer codes are available online (see “Availability of data and codes” section for more information). To check the performance of the estimators, we examine the coverage probabilities of the 95% confidence intervals, the bias and root-mean-square errors, as well as the estimator’s asymptotic consistency. We consider five sample sizes \(n=(200,400,600,800,1000)\), and for each scenario, we generate 1000 datasets. In the process of generating each data set, we considered failure times to follow Weibull and gamma distributions with the following regression structure: \(\alpha _{i}=e^{\beta _{1}+\text {x}_{3i}\beta _{2}}\), \(\lambda _{i}=e^{\beta _{3}+\text {x}_{2i}\beta _{4}}\), and \(p_{0i}=\frac{e^{\beta _{5}+\text {x}_{1i}\beta _{6}}}{1+e^{\beta _{5}+\text {x}_{1i}\beta _{6}}}\), where the covariate vectors are specified by \(\text {x}_{i}\equiv \text {x}_{i1} = \text {x}_{i2} = \text {x}_{i3} \sim \text {Normal}(0,1)\) and the regression coefficients by \(\beta _{1}=0.5, \, \beta _{2}=0.5, \, \beta _{3}=1.5, \, \beta _{4}=2, \,\beta _{5}=-3, \, \beta _{6}=1\).

To simulate random samples of size n, we suppose that the time until the occurrence of the event of interest has the cumulative distribution function F(t) given by \(F_0(t) = p_{0i} + (1-p_{0i})F(t), \, t \ge 0\). The algorithmic steps to generate the random samples are as follows:

1. Generate \(\text {x}_{i} \sim \text {Normal}(0,1)\) and calculate \(p_{0i}, \alpha _{i}, \lambda _{i}\);

2. Generate \(u_{i}\) from a uniform distribution U(0, 1);

3. Generate \(v_{i}\) from a uniform distribution \(U(p_{0i},1)\);

4. If \(u_i \le p_{0i}\), set \(t_i = 0\);

5. If \(u_i > p_{0i}\), set \(t_i\) equals to the inverse function \(F_{0}^{-1}(v_{i})\);

6. Generate the censoring times \(c_i\) from a gamma distribution G(0.25, 128.2), specified to control the censoring percentage;

7. If \(t_i < c_i\), set \(\delta _i = 1\); otherwise, set \(\delta _i = 0\);

8. If \(t_i = 0\); set \(Z_i = 1\), otherwise, set \(Z_i = 0\).

For the zero-inflated-censored model, since failure times have a Weibull distribution, the average time until the event of interest is calculated by

$$\begin{aligned} \mathbb {E}(T|\text {x}_{1},\text {x}_{2},\text {x}_{3})=\left( 1-\frac{e^{\beta _{5}+\text {x}_{1}\beta _{6}}}{1+e^{ \beta _{5}+\text {x}_{1}\beta _{6}}}\right) e^{\beta _{3}+\text {x}_{2}\beta _{4}} \;\varGamma \left( 1+\frac{1}{e^{ \beta _{1}+\text {x}_{3}\beta _{2}}}\right) . \end{aligned}$$
(16)

For the zero-inflated-censored model, since failure times have a gamma distribution, the average time until the event of interest is calculated by

$$\begin{aligned} \begin{aligned} \mathbb {E}(T|\text {x}_{1},\text {x}_{2},\text {x}_{3})&= \left( 1-\frac{e^{\beta _{5}+\text {x}_{1}\beta _{6}}}{1+e^{ \beta _{5}+\text {x}_{1}\beta _{6}}}\right) e^{\beta _{1}+\text {x}_{3}\beta _{2}} \cdot e^{\beta _{3}+\text {x}_{2}\beta _{4}}. \end{aligned} \end{aligned}$$
(17)

For both models proposed, considering the 1000 replications of each scenario, Fig. 1 shows that as the sample size increases from 200 to 1000, the means of the six estimated parameters (\(\hat{\beta _1}, \ldots , \hat{\beta _6}\)) converge on the true values of the parameters \((0.5, 0.5, 1.5, 2, -3, 1)\).

Fig. 1
figure 1

Mean values of the \(\hat{\beta }\) estimated by the ZIWeibull model (when dataset were generated by the ZIWeibull model) and ZIGamma model (when datasets were generated by the ZIGamma model) using different sample sizes. The solid horizontal line is the true value

Full size image

Figure 2 shows that for both models, the increase of the sample size from 200 to 1000 reduces asymptotically the variance, pointing to the minimal variance of the parameters estimated in these models. In Appendix (parameter estimates in the simulation studies), several summary statistics for the parameters are provided, such as mean, standard deviation (SD), confidence interval, bias, mean squared error, and coverage probability. Notably, for all sample size scenarios, the means of the standard errors (SE) are similar to the SD, indicating the good performance of the models. The coverage probability is remarkably close to the nominal value of 95%.

Fig. 2
figure 2

Variance for the \(\hat{\beta }\) estimated by the ZIWeibull model (when dataset was generated by the ZIWeibull model) and ZIGamma model (when dataset was generated by the ZIGamma model) using different sample sizes

Full size image

For both ZIGamma and ZIWeibull models, the expected values of the proportion of zeros were similar, for all sample sizes, converging asymptotically to the true value (Table 1). The average times-to-event estimated by the ZIWeibull and ZIGamma models was close to the true value, regardless the scenario of gamma or Weibull distribution for both datasets generation (Table 1).

Table 1 The simulation results of estimating the probability of zero and for the expected time, given these two values for the covariates \(\text {x} = -1\) and \(\text {x} = 1\) and gamma and Weibull scenarios for data generation
Full size table

4 Wild boar dispersal application

In this section, we adjust the ZIWeibull and ZIGamma models to the wild boar natal dispersal study based on recapture by hunting bag (Truvé & Lemel, 2003). Dispersal occurs when wild boars leave their territory for new territories or home ranges (Breed & Moore, 2016). Dispersal accounts for three distinct subpopulations of animals: a segment that will not disperse, i.e., have zero distance; a segment that will disperse measurably (event), and animals whose dispersal is unknown (right-censored).

Examples of such a data structure in wild boar dispersal are available in Keuling et al. (2010), Prévot and Licoppe (2013), and Jerina et al. (2014). These authors report a dataset structure compatible with that of Koenig et al. (1996) and Paradis et al. (1998) who reported that recaptures often occur in the same location at which the animal was marked, creating zeros, or animals moving more than the limit set for recapture in generating right-censored data. Unfortunately, the full datasets for these papers are not publicly available. To address this limitation, we created a dataset that mimics a real situation. Details about the data generation are available in Appendix (Information used to generate the applied dataset). The computer code used to generate the data and the dataset spreadsheet are available as Electronic supplementary material.

Applied to wild boars, our interest is to adjust the dispersal distance, denoted by the random variable D, representing the observable distance. Therefore, the likelihood contribution of a dispersal distance \(D_i\) of an animal, or i, can assume two different values: \(p_{0i}\), if animal i has a dispersal equal to zero, and \((1 - p_{0i} ) f_0(d_i)\), if animal i has a dispersal larger than zero.

The models’ parameters were tested under null hypothesis of equality to zero using a Wald test. For both ZIWeibull and ZIGamma models, the regression coefficients \(\beta _2\) (age), \(\beta _3\) (sex) are accounting for the shape parameter (\(\alpha\)), and \(\beta _5\) (age), \(\beta _6\) (sex) are associated with the scale parameter (\(\lambda\)). The effects of the regression coefficients \(\beta _8\) (age) and \(\beta _9\) (sex) are associated with the proportion of zeros (\(p_0\)). Thus, regression coefficients have an indirect effect on the proportion of zeros estimated and on the expected dispersal distance, as we can see below for the ZIWeibull and ZIGamma models, respectively

$$\begin{aligned} \begin{aligned} \mathbb {E}(D| {\mathrm{age, sex}}) =&(1-p_{0})\times \alpha _{\mathrm{w}}\times \varGamma \left( 1+\frac{1}{\lambda _{\mathrm{w}}}\right) \\ \\&\text {and} \\ \\ \mathbb {E}(D| {\mathrm{age, sex}})=&(1-p_{0}) \times \alpha _{\mathrm{g}}\times \lambda _{\mathrm{g}}, \end{aligned} \end{aligned}$$
(18)

where \(\alpha _{\mathrm{w}}=e^{\beta _1+\beta _2{\mathrm{age}}+\beta _3{\mathrm{sex}}}\), \(\lambda _{\mathrm{w}}=e^{\beta _4+\beta _5{\mathrm{age}}+\beta _6{\mathrm{sex}}}\), and \(p_{0}=\frac{e^{\beta _7+\beta _8{\mathrm{age}}+\beta _9{\mathrm{sex}}}}{1+(e^{\beta 7+\beta _8{\mathrm{age}}+\beta _9{\mathrm{sex}}})}\) obtained through the ZIWeibull model adjust, and \(\alpha _{\mathrm{g}}=e^{\beta _1+\beta _2{\mathrm{age}}+\beta _3{\mathrm{sex}}}\), \(\lambda _{\mathrm{g}}=e^{\beta _4+\beta _5{\mathrm{age}}+\beta _6{\mathrm{sex}}}\), and \(p_{0}=\frac{e^{\beta _7+\beta _8{\mathrm{age}}+\beta _9{\mathrm{sex}}}}{1+(e^{\beta 7+\beta _8{\mathrm{age}}+\beta _9{\mathrm{sex}}})}\) obtained through the ZIGamma model.

In the ZIGamma model, the proportion of zeros in the simulated wild boar dataset is not significantly dependent on age \((\beta _8=-0.016\) P value = 0.163), or sex \((\beta _9=0.423\) P value = 0.135), as shown in Table 2. On the other hand, age \((\beta _5=0.04\ P {\mathrm{value}} < 0.001)\) and sex \((\beta _6=-0.64\) P value = 0.001) are associated with the scale parameter of the curve. For the shape of the curve, there is association of age \((\beta _2=-0.01\) P value = 0.028) but not sex \((\beta _3=0.027\) P value = 0.98). For the ZIWeibull model, the proportion of zeros in the simulated wild boar dataset is also not dependent on age (P value = 0.162) or on sex (P value = 0.134), see \(\beta _8\) (age) and \(\beta _9\) (sex) in Table 2. However, age and sex are associated with the scale of the curve \((\beta _5=0.032\ {\mathrm{and}}\ \beta _6=-0.644 \ P {\mathrm{value}} < 0.001\) for both); and age was associated with the shape \((\beta _2=-0.007\) P value = 0.042) (Table 2).

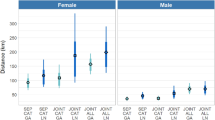
Table 2 Results of the ZIGamma and ZIWeibull models fitted for the simulated dataset of wild boar dispersal distance
Full size table

Because the generated dispersal distance is affected by sex and age, we have chosen to calculate the mean distance using the average age for both sexes. For males, the average age was 15 months, so the estimated mean distance was 13.9 km and 13.66 km with the ZIWeibull and ZIGamma models, respectively. For females, the mean age was 12 months, at which age the estimated mean distance was 6.1 km and 6.08 km with the ZIWeibull and ZIGamma models, respectively.

For the regression models proposed here, increase in the mean distance is associated with increased age and males dispersing more than females, as shown in Fig. 3. On average, males are known to disperse more than females. For both sexes, increased age increases the distances. These findings are expected, as we intentionally generated an applied dataset while attempting to account for the matrilineal, territorial societal structure (females and their offspring having very low dispersion), as well as for the solitary males that disperse more to seek territory and mating opportunities (Keuling et al., 2010).

Fig. 3
figure 3

Values for the mean dispersal distance (Km) estimated by the ZIWeibull and ZIGamma regression models

Full size image

To assess the models’ goodness-of-fit, we evaluated the following information criteria: Akaike and Bayes information criteria, (AIC and BIC). These were calculated according to \(qk-2\log ({\hat{L}})\), where k is the number of parameters, \({\hat{L}}\) is the likelihood, and \(q=2\) for AIC, or \(q=\ln (n)\), n = sample size for BIC (Brewer et al., 2016). As the ZIGamma model is a hurdle model, the full log-likelihood was calculated adding the log-likelihood of the logistic regression and the log-likelihood of the gamma regression (McDowell, 2003).

AIC are similar for both proposed models, but larger difference is observed in BIC which is smaller for the ZIGamma model (see Table 2). However, our aim here is not strictly to select the best model from between ZIGamma and ZIWeibull, but to present both as alternative methods in this applied context, allowing for the incorporation of all the information contained in the dataset to calculate the likelihood function.

5 Discussion

Although the lack of a real dataset hampers the attempt to draw a direct conclusion about an actual wild boar population, our aim was to highlight that both ZIWeibull and ZIGamma can be useful tools for statistical inferences in wild boar dispersal. According to Whitmee and Orme (2013), dispersal is one of the principal mechanisms underlying wild animals’ land occupation, and there is an urgent need to obtain quantitative empirical data and methods to analyze dispersal distance. The models presented here are designed to accommodate the proportions of individuals that will not disperse at all and zeros created by measurement error (accounting for the excess of zeros), the observable dispersal distance, and the cases in which the dispersal is greater than our capacity to follow it, or incomplete followings (right-censoring). In this sense, researchers could count with an inferential tool avoiding data exclusion using the full dataset in the same likelihood function. For instance, Truvé and Lemel (2003) excluded censored data and split the dataset to fit a non-parametric model to each covariate.

From an applied perspective, estimating the characteristics of wild boar populations [e.g., average dispersal across sexes and ages (Keuling et al., 2010)] is important in enabling animal health managers and decision-makers to make evidence-based decisions (EFSA, 2014; Morelle et al., 2014). For instance, risk assessment models for the introduction/spread of African Swine Fever are heavily dependent on parameters regarding the land occupation (De la Torre et al., 2015). Surveillance programs for commercial swine herds often consider the dynamics of the wild boar population in preventing diseases (Casas-Díaz et al., 2013). As such, the models proposed here are useful for generating inferences about dispersal distance and testing if covariates are associated with the distance, thus helping to overcome current gaps in our understanding of wild boar behavior (Guinat et al., 2016; EFSA, 2019).

For the zero-inflated-censored Weibull (ZIWeibull) model, the estimators were consistent and efficient, and both the standard deviation values and the estimated standard errors values are quite close, indicating a good adjustment. Likewise, for the ZIWeibull model, the coverage probabilities for the ZIGamma model were close to the nominal level, and both the standard deviation values and the standard error values are remarkably close. The large sample theory for the models proposed in this paper is still an open question. However, our simulation studies show that the asymptotic validity seems to be satisfied. Finally, we note that the zero-inflated gamma model proposed in this paper can be extended to include the cure rate in the model. Furthermore, the zero-inflated-censored Weibull and gamma regression models can be extended to interval-censored survival data.