Effective estimation algorithm for parameters of multivariate Farlie–Gumbel–Morgenstern copula

Abstract

This paper focuses on the parameter estimation for the d-variate Farlie–Gumbel–Morgenstern (FGM) copula ($d\ge 2$), which has $2^d-d-1$ dependence parameters to be estimated; therefore, maximum likelihood estimation is not practical for a large d from the viewpoint of computational complexity. Besides, the restriction for the FGM copula’s parameters becomes increasingly complex as d becomes large, which makes parameter estimation difficult. We propose an effective estimation algorithm for the d-variate FGM copula by using the method of inference functions for margins under the restriction of the parameters. We then discuss its asymptotic normality as well as its performance determined through simulation studies. The proposed method is also applied to real data analysis of bearing reliability.

1 Introduction

A copula is a function that joins several one-dimensional distribution functions to form a multivariate distribution function with dependency (Nelsen 2006). The copula works as a multivariate distribution function by itself.

In reliability engineering, the copula is used as a useful tool for reliability analysis of systems in which dependent failures sometimes occur. A dependent failure of systems and/or system components may occur due to sharing heat, vibration, and tasks (McCool 2012). We should consider the dependence of components to precisely assess the reliability of the system. For example, Eryilmaz and Tank (2012) showed that the positive dependence between two components improves the mean time to failure of a two-component series system by using an Farlie–Gumbel–Morgenstern (FGM) copula and Ali–Mikhail–Haq copula. Navarro et al. (2007) developed a reliability model for coherent systems with dependent components by using several types of copulas including the FGM copula.

There have been many studies on the FGM copula. Earlier studies (Farlie 1960; Gumbel 1960; Morgenstern 1956) discussed families of the bivariate FGM copula. Johnson and Kotz (1975) formulated the FGM copula as a multivariate distribution. The multivariate FGM copula is useful as an alternative to a multivariate normal distribution because it has a simple form and can express mutual dependencies among two or more variables (Jaworski et al. 2010). Therefore, the FGM copula has been applied to statistical modeling in various research fields such as economics (Patton 2006), educational engineering (Shih et al. 2019), finance (Cossette et al. 2013) and reliability engineering (Navarro et al. 2007; Navarro and Durante 2017).

However, there are no practical estimation methods of the parameters of the multivariate FGM copula. The reason mainly depends on the computational complexity of estimating a large number of the parameters. It is known that the d-variate FGM copula consists of $2^d-d-1$ constrained parameters for $d\ge 2$. In fact, the d-variate FGM copula has relatively many parameters compared with other multivariate copulas (e.g., a d-variate Gaussian copula has $d(d-1)/2 \,(\le 2^d-d-1)$ correlation parameters (Jaworski et al. 2010)). This implies that estimation for the multivariate FGM copula’s parameters is computationally more complicated than that for the other copulas’ parameters. Besides, maximum likelihood estimation (MLE) is infeasible over such a high dimensional space with the parameter constraint.

The method of inference functions for margins (IFM) is one acceptable estimation method for parameters of copulas. It was proposed by Joe and Xu (1996), and extensively reviewed by Xu (1996). This method first estimates the univariate parameters from separate univariate likelihood functions of a copula. It then estimates bivariate, trivariate and multivariate parameters step by step from respective bivariate, trivariate, and multivariate marginal likelihoods with lower order parameters fixed as the estimated values. The advantages of IFM are its computational efficiency and asymptotic normality that holds under several regularity conditions (Xu 1996; Joe 2005; Patton 2006). However, the following two problems exist when we apply IFM to the multivariate FGM copula: (1) it is not known how to consider the complex restriction for the FGM copula’s parameters, and (2) it has not been found whether the estimators of IFM for the multivariate FGM copula have asymptotic normality.

In this paper, we propose an effective estimation algorithm for the multivariate FGM copula by using IFM. The proposed algorithm requires linear optimization to consider the restriction of the multivariate FGM copula’s parameters. Besides, we analyze the asymptotic normality of the estimators given by the proposed algorithm.

The remainder of this paper is organized as follows. In Sect. 2, we introduce the definition and property of the multivariate FGM copula. In Sect. 3, we propose estimation algorithms for the multivariate FGM copula based on MLE and IFM. Their asymptotic properties are analytically investigated in Sect. 4. Section 5 consists of simulation results to compare MLE and IFM for the multivariate FGM copula from the viewpoint of estimation accuracy and computation time. In Sect. 6, our proposed method is applied to real data analysis of bearing reliability. Finally, we conclude our study with a summary in Sect. 7.

2 FGM copula

Let $\varvec{U}=(U_1,\ldots ,U_d)$ be a random vector that follows a d-variate FGM copula with d uniform marginal distributions in the interval [0, 1]. Let $\varvec{\theta }$ denote the parameter vector of the d-variate FGM copula. According to Johnson and Kotz (1975) and p. 108 of Nelsen (2006), the joint distribution function of the d-variate FGM copula, denoted by $C_d$, is defined as

$$\begin{aligned} C_d(u_1, \ldots ,u_d;\varvec{\theta }) & =\Pr [U_1\le u_1,\ldots ,U_d\le u_d]\\&=\prod _{j=1}^d u_i\Biggl ( 1+\sum _{k=2}^d \sum _{1\le j_1<\cdots <j_k\le d} \theta _{j_1\cdots j_k}(1-u_{j_1})\cdots (1-u_{j_k})\Biggr ), \end{aligned}$$

where $(u_1,\dots ,u_d)\in [0,1]^d$ and $\theta _{j_1\cdots j_k}\in \varvec{\theta }$ is a parameter. Since $\varvec{\theta }\ne \varvec{0}$ means that the random variables are obviously dependent, we call an element of $\varvec{\theta }$ a dependence parameter. For $d=2$ and 3, we obtain

$$\begin{aligned} C_2(u_1,u_2;\varvec{\theta })&=u_1u_2(1+\theta _{12}(1-u_1)(1-u_2)),\\ C_3(u_1,u_2,u_3;\varvec{\theta })&=u_1u_2u_3(1+\theta _{12}(1-u_1)(1-u_2)+\theta _{13}(1-u_1)(1-u_3)\\&\quad +\theta _{23}(1-u_2)(1-u_3)+\theta _{123}(1-u_1)(1-u_2)(1-u_3)).\nonumber \end{aligned}$$

The d-variate FGM copula consists of $\sum _{j=2}^{d} \left( {\begin{array}{c}d\\ j\end{array}}\right) =2^d-d-1$ dependence parameters. The correlation and regression properties for any pair of $\varvec{U}$ were studied by Johnson and Kotz (1977).

The joint density function of $\varvec{U}$, denoted by $c_d$, is given by

$$\begin{aligned} c_d(u_1,\ldots , u_d;\varvec{\theta })&=\frac{\partial ^d}{\partial u_1\cdots \partial u_d}C(u_1,\ldots ,u_d;\varvec{\theta })\\&=1+\sum _{k=2}^d \sum _{1\le j_1<\cdots <j_k\le d} \theta _{j_1\cdots j_k} (1-2u_{j_1})\cdots (1-2u_{j_k}). \end{aligned}$$

$\varvec{\theta }$ is a parameter vector such that the joint density function $c_d(u_1, \ldots ,u_d;\varvec{\theta })$ is non-negative for every $u_j \in [0,1]$. Thus, $\varvec{\theta }$ must satisfy the following restriction (Johnson and Kotz 1975; Jaworski et al. 2010).

$$\begin{aligned} 1+\sum _{k=2}^d \sum _{1\le j_1<\cdots <j_k\le d}\theta _{j_1\cdots j_k} (1-2u_{j_1})\cdots (1-2u_{j_k})\ge 0,\quad u_j\in [0,1], \end{aligned}$$

(1)

for $j=1,\dots ,d$. Since $c_d(u_1, \ldots ,u_d;\varvec{\theta })$ is a linear function of each $u_j$, the substitution of $u_j=0,1$ in every $2^d$ possible combinations will yield necessary and sufficient conditions of $\varvec{\theta }$ (Johnson and Kotz 1975). Thus, we can write Eq. (1) in a compact form as follows.

$$\begin{aligned} 1+\sum _{k=2}^d \sum _{1\le j_1<\cdots <j_k\le d} \theta _{j_1\cdots j_k} \varepsilon _{j_1}\cdots \varepsilon _{j_k}\ge 0, \quad\varepsilon _j=\pm 1, \end{aligned}$$

(2)

for $j=1,\dots ,d$. For example, when $d=2$, the parameter vector becomes $\varvec{\theta }=(\theta _{12})$, and we have $-1\le \theta _{12} \le 1$. When $d=3$, the parameters $\varvec{\theta }=(\theta _{12}$, $\theta _{13}$, $\theta _{23}$, $\theta _{123})$ are required to hold $2^3$ inequalities as follows (Johnson and Kotz 1975).

$$\begin{aligned} \left. \begin{array}{l} 1+\theta _{12}+\theta _{13}+\theta _{23}+\theta _{123}\ge 0\quad(\varepsilon _1=\varepsilon _2=\varepsilon _3=1)\\ 1+\theta _{12}-\theta _{13}-\theta _{23}-\theta _{123}\ge 0\quad(\varepsilon _1=\varepsilon _2=1,\varepsilon _3=-1)\\ 1-\theta _{12}+\theta _{13}-\theta _{23}-\theta _{123}\ge 0\quad(\varepsilon _1=\varepsilon _3=1,\varepsilon _2=-1)\\ 1-\theta _{12}-\theta _{13}+\theta _{23}-\theta _{123}\ge 0\quad(\varepsilon _2=\varepsilon _3=1,\varepsilon _1=-1)\\ 1-\theta _{12}-\theta _{13}+\theta _{23}+\theta _{123}\ge 0\quad(\varepsilon _1=1,\varepsilon _2=\varepsilon _3=-1)\\ 1-\theta _{12}+\theta _{13}-\theta _{23}+\theta _{123}\ge 0\quad(\varepsilon _2=1,\varepsilon _1=\varepsilon _3=-1)\\ 1+\theta _{12}-\theta _{13}-\theta _{23}+\theta _{123}\ge 0\quad(\varepsilon _3=1,\varepsilon _1=\varepsilon _2=-1)\\ 1+\theta _{12}+\theta _{13}+\theta _{23}-\theta _{123}\ge 0\quad(\varepsilon _1=\varepsilon _2=\varepsilon _3=-1)\\ \end{array} \right\} . \end{aligned}$$

(3)

The condition given by Eq. (2) becomes increasingly complex as d becomes large. When we estimate the dependence parameters, we need to consider this condition.

Multivariate FGM distributions can be constructed by the Sklar’s theorem (Nelsen 2006). Suppose $\varvec{X}=(X_1,\ldots ,X_d)$ is a random vector that follows the d-variate FGM distribution with arbitrary continuous marginal distributions. For $j=1,\ldots ,d$, let $F_j(x_j;\varvec{\delta }_j)$ and $f_j(x_j;\varvec{\delta }_j)$ be the jth marginal distribution function and the density function with a parameter vector $\varvec{\delta }_j$, respectively. Let us define $\varvec{\delta }$ as $\varvec{\delta }=(\varvec{\delta }_1,\dots ,\varvec{\delta }_d)$. Then, the cumulative distribution function of $\varvec{X}$, denoted by $H_d$, is represented as

$$\begin{aligned}&H_d(x_1,\dots ,x_d;\varvec{\delta },\varvec{\theta })=\Pr [X_1\le x_1,\dots ,X_d\le x_d] \\&=C_d(F_1(x_1;\varvec{\delta }_1),\dots , F_d(x_d;\varvec{\delta }_d);\varvec{\theta }) \\&=\prod _{j=1}^d F_j(x_j;\varvec{\delta }_j)\left( 1+\sum _{k=2}^d \sum _{1\le j_1<\cdots <j_k\le d}\theta _{j_1\cdots j_k} {\overline{F}}_{j_1}(x_{j_1};\varvec{\delta }_{j_1})\cdots {\overline{F}}_{j_k}(x_{j_k};\varvec{\delta }_{j_k})\right) , \end{aligned}$$

where ${\overline{F}}_j(x_j;\varvec{\delta }_j)\equiv 1-F_j(x_j;\varvec{\delta }_j)$.

The joint density function of $\varvec{X}$, denoted by $h_d$, is given by

$$\begin{aligned} h_d(x_1, \ldots ,x_d;\varvec{\delta },\varvec{\theta })&=\frac{\partial ^d}{\partial x_1\cdots \partial x_d}H_d(x_1,\ldots ,x_d;\varvec{\delta },\varvec{\theta })\\&=\prod _{j=1}^d f_j\left( 1+\sum _{k=2}^d \sum _{1\le j_1<\cdots <j_k\le d}\theta _{j_1\cdots j_k}(1-2F_{j_1})\cdots (1-2F_{j_k})\right) , \end{aligned}$$

where $f_{j}\equiv f_j(x_j;\varvec{\delta }_j)$ and $F_{j}\equiv F_j(x_j;\varvec{\delta }_j)$.

3 Estimation

In this section, we first introduce MLE and its limitation for the multivariate FGM distribution. To solve the limitation, we then propose an estimation algorithm for the multivariate FGM distribution by using IFM.

3.1 Maximum likelihood estimation

MLE is one of the natural choices to estimate parameters of probability distributions because its estimators satisfy asymptotic normality under several regularity conditions (Lehmann and Casella 1998; Joe 2014). With this method, we estimate all the parameters $\varvec{\delta }$ and $\varvec{\theta }$ simultaneously. For a sample size n, with observed independent random vectors $\varvec{x}_i=(x_{i1},\dots ,x_{id})$ for $i=1,\dots ,n$, the full-dimensional log-likelihood function of $\varvec{\delta }$ and $\varvec{\theta }$ can be written as

$$\begin{aligned} \ell&\equiv \ell (\varvec{\delta },\varvec{\theta };\varvec{x}_1,\ldots ,\varvec{x}_n)\\&\equiv \sum _{i=1}^n \log h_d(x_{i1},\ldots ,x_{id};\varvec{\delta },\varvec{\theta }) \\&=\sum _{i=1}^{n}\sum _{j=1}^{d}\log f_j+\sum _{i=1}^{n}\log \left( 1+\sum _{k=2}^d \sum _{1\le j_1<\cdots <j_k\le d}\theta _{j_1\cdots j_k}(1-2F_{j_1})\cdots (1-2F_{j_k})\right) . \end{aligned}$$

Thus, the estimators of MLE, denoted as $\widehat{\varvec{\delta }}$ and $\widehat{\varvec{\theta }}$, are given by

$$ ({\widehat{\varvec{\delta }}},{\widehat{\varvec{\theta }}}) = \mathop {{\text{arg }}\, {\text{max}}} \limits_{{{\varvec{\delta }},{\varvec{\theta }}}} \ell ({\varvec{\delta }},{\varvec{\theta }}; {\varvec{x}}_{1} , \ldots ,{\varvec{x}}_{n} ). $$

(4)

To find $(\widehat{\varvec{\delta }},\widehat{\varvec{\theta }})$, we need to use numerical optimization techniques because Eq. (4) does not have closed form expression. The problems of numerical optimization in Eq. (4) are high-dimensionality and the parameter constraints given by Eq. (2). Numerical optimization in a high-dimensional and constrained space requires a large amount of computational resources. This issue relates to computational feasibility.

Numerical optimization might take a large amount of computation time and fail as the dimension increases. Also, the estimation accuracy of MLE worsens because the numerical optimization technique may not find the global optimum but a local one. Even if all the marginal distributions are uni-parameter distributions (i.e., $\varvec{\delta }_j=\delta _j$), Eq. (4) consists of the $2^d-1$ unknown parameters $\varvec{\delta }$ and $\varvec{\theta }$. Moreover, the ignorance of parameter constraints is one of the most common reasons why the Newton-Raphson type algorithms diverge (MacDonald 2014). Therefore, other simple estimation methods have been required for the multivariate FGM distribution’s parameters.

3.2 The method of inference functions for margins

To reduce the computational difficulty of MLE, we introduce IFM for estimation of the multivariate FGM distribution. With this method, we estimate the dependence parameters one by one so that each estimation result satisfies the condition given by Eq. (2).

As the first step, let us define k-dimensional marginal likelihood functions for $k=1,2,\ldots ,d-1$. It is easy to see that the k-dimensional marginal distribution function is as follows.

$$\begin{aligned} H_k(x_1,\ldots ,x_k;\cdot )=\prod _{j=1}^k F_j\left( 1+\sum _{p=2}^k \sum _{1\le j_1<\cdots <j_p\le k}\theta _{j_1\cdots j_p} (1-F_{j_1})\cdots (1-F_{j_p})\right) . \end{aligned}$$

Thus, for example, we have

$$\begin{aligned}&H_1(x_{j_1};\varvec{\delta }_{j_1})=F_{j_1}, \\&H_2(x_{j_1},x_{j_2};\varvec{\delta }_{j_1},\varvec{\delta }_{j_2},\theta _{j_1j_2})= F_{j_1}F_{j_2}(1+\theta _{j_1j_2}(1-F_{j_1})(1-F_{j_2})),\\&H_3(x_{j_1},x_{j_2},x_{j_3};\varvec{\delta }_{j_1},\varvec{\delta }_{j_2},\varvec{\delta }_{j_3},\theta _{j_1j_2},\theta _{j_1j_3},\theta _{j_2j_3},\theta _{j_1j_2j_3})\\&\quad =F_{j_1}F_{j_2}F_{j_3}(1+\theta _{j_1j_2}(1-F_{j_1})(1-F_{j_2})+\theta _{j_1j_3}(1-F_{j_1})(1-F_{j_3})\nonumber \\&\qquad +\theta _{j_2j_3}(1-F_{j_2})(1-F_{j_3})+\theta _{j_1j_2j_3}(1-F_{j_1})(1-F_{j_2})(1-F_{j_3})). \end{aligned}$$

The key point of these functions is that their variables are controlled by only the parameters with the same subscripts of the marginal distribution functions. We then obtain the following log-likelihood functions of the k-dimensional marginal distribution for $k<d$ and $1\le j_1<\cdots <j_k\le d$.

$$\begin{aligned} \ell _{j_1}&\equiv \ell _{j_1}(\varvec{\delta }_{j_1};\varvec{x}_{1},\ldots ,\varvec{x}_{n})\equiv \sum _{i=1}^n\log f_{j_1}(x_{ij_1};\varvec{\delta }_{j_1}), \\ \ell _{j_1j_2}&\equiv \ell _{j_1j_2} (\varvec{\delta }_{j_1},\varvec{\delta }_{j_2},\theta _{j_1j_2};\varvec{x}_{1},\ldots ,\varvec{x}_{n}) \\&\equiv \sum _{i=1}^n \log h_2(x_{ij_1},x_{ij_2} ;\varvec{\delta }_{j_1},\varvec{\delta }_{j_2},\theta _{j_1j_2}),\\ \ell _{j_1j_2j_3}&\equiv \ell _{j_1j_2j_3} \left(\varvec{\delta }_{j_1},\varvec{\delta }_{j_2},\varvec{\delta }_{j_3},\theta _{j_1j_2},\theta _{j_1j_3},\theta _{j_2j_3},\theta _{j_1j_2j_3};\varvec{x}_{1},\ldots ,\varvec{x}_{n}\right) \\&\equiv \sum _{i=1}^n \log h_3 \left(x_{ij_1},x_{ij_2},x_{ij_3} ;\varvec{\delta }_{j_1},\varvec{\delta }_{j_2},\varvec{\delta }_{j_3},\theta _{j_1j_2},\theta _{j_1j_3},\theta _{j_2j_3},\theta _{j_1j_2j_3}\right),\\&\,\, \vdots \\ \ell _{j_1\cdots j_{d-1}}&\equiv \ell _{j_1\cdots j_{d-1}} (\varvec{\delta }_{j_1},\ldots ,\varvec{\delta }_{j_{d-1}},\theta _{j_1j_2},\ldots ,\theta _{j_1\cdots j_{d-1}};\varvec{x}_{1},\ldots ,\varvec{x}_{n}) \\&\equiv \sum _{i=1}^n \log h_{d-1}(x_{ij_1},\ldots ,x_{ij_{d-1}};\varvec{\delta }_{j_1},\ldots ,\varvec{\delta }_{j_{d-1}},\theta _{j_1j_2},\ldots ,\theta _{j_1\cdots j_{d-1}}). \end{aligned}$$

Now, we propose an estimation algorithm based on IFM for the d-variate FGM distribution. With IFM, we first estimate the parameters of marginal distributions as

$$ \varvec{\tilde{\delta }}_{{j_{1} }} = \mathop {{\text{arg}}{\mkern 1mu} {\text{max}}}\limits_{{\varvec{\delta }_{{j_{1} }} }} \ell _{{j_{1} }} (\varvec{\delta }_{{j_{1} }} ;\varvec{x}_{{j_{1} }} ), $$

for $j_1=1,2,\dots ,d$.

Next, we estimate bivariate, trivariate and d-variate dependence parameters step by step. For $1\le j_1<j_2\le d$, the bivariate dependence parameters $\theta _{j_1j_2}$ are estimated as follows.

$$ \tilde{\theta }_{{j_{1} j_{2} }} = \mathop {{\text{arg}}{\mkern 1mu} {\text{max}}}\limits_{{\theta _{{j_{1} j_{2} }} }} \ell _{{j_{1} j_{2} }} (\varvec{\tilde{\delta }}_{{j_{1} }} ,\varvec{\tilde{\delta }}_{{j_{2} }} ,\theta _{{j_{1} j_{2} }} ;\varvec{x}_{{j_{1} }} ,\varvec{x}_{{j_{2} }} ), $$

(5)

where $\theta _{j_1j_2}$ must satisfy Eq. (2) whose parameters already estimated are fixed by their estimated values, e.g., $\theta _{12}={\widetilde{\theta }}_{12},\theta _{13}={\widetilde{\theta }}_{13},\dots$, and so on.

After all the bivariate dependence parameters are estimated, the estimates of the trivariate dependence parameters $\theta _{j_1j_2j_3}$ are given by

$$ \tilde{\theta }_{{j_{1} j_{2} j_{3} }} = \mathop {{\text{arg}}{\mkern 1mu} {\text{max}}}\limits_{{\theta _{{j_{1} j_{2} j_{3} }} }} \ell _{{j_{1} j_{2} j_{3} }} (\varvec{\tilde{\delta }}_{{j_{1} }} ,\varvec{\tilde{\delta }}_{{j_{2} }} ,\varvec{\tilde{\delta }}_{{j_{3} }} ,\tilde{\theta }_{{j_{1} j_{2} }} ,\tilde{\theta }_{{j_{1} j_{3} }} ,\tilde{\theta }_{{j_{2} j_{3} }} ,\theta _{{j_{1} j_{2} j_{3} }} ;\varvec{x}_{{j_{1} }} ,\varvec{x}_{{j_{2} }} ,\varvec{x}_{{j_{3} }} ), $$

where $\theta _{j_1j_2j_3}$ must satisfy Eq. (2) whose parameters already estimated are fixed by their estimated values, e.g., $\theta _{12}={\widetilde{\theta }}_{12},\theta _{13}={\widetilde{\theta }}_{13}, \dots ,\theta _{123}={\widetilde{\theta }}_{123},\theta _{124}={\widetilde{\theta }}_{124},\dots$, and so on.

In the same manner, we estimate all dependence parameters of higher dimensions in order. Finally, $\theta _{12\cdots d}$ is estimated in a bottom-up fashion. Thus, we can estimate all dependence parameters by repeatedly maximizing functions with one unknown parameter (one equation per dependence parameter). Therefore, IFM can be used to estimate the dependence parameters of the d-variate FGM distribution no matter how large d is (even if MLE is infeasible).

If MLE is feasible, an estimator of IFM can be considered as a good starting point for the numerical maximization of the full log-likelihood function (Joe 2014). In Sec. 5.2, the detailed procedure of IFM for the d-variate FGM distribution is demonstrated in the case of $d=3$.

The proposed algorithm for the d-variate FGM distribution has the following characteristic remarks that are not seen when IFM is applied to other copulas.

Remark 1

For a given k, IFM for the d-variate FGM distribution requires linear optimization to determine the allowable range of a dependence parameter as $a_{j_1\cdots j_k}\le \theta _{j_1\cdots j_k} \le b_{j_1\cdots j_k}$ where $a_{j_1\cdots j_k}=\min \theta _{j_1\cdots j_k}$ and $b_{j_1\cdots j_k}=\max \theta _{j_1\cdots j_k}$ under the condition of Eq. (2), respectively.

For example, let us consider the case that $d=3$ and the dependence parameters are estimated in the order of $\theta _{12}\rightarrow \theta _{23}\rightarrow \theta _{13}\rightarrow \theta _{123}$. In this case, we have $a_{12}=\min \theta _{12}$ and $b_{12}=\max \theta _{12}$ s.t. Eq. (3), respectively. Then, $a_{12}=-1$ and $b_{12}=1$ hold as solutions of these two optimization problems. Eq. (50 can be represented as

$$ \tilde{\theta }_{{12}} = \mathop {{\text{arg}}{\mkern 1mu} {\text{max}}}\limits_{{ - 1 \le \theta _{{12}} \le 1}} \ell _{{12}} (\varvec{\tilde{\delta }}_{1} ,\varvec{\tilde{\delta }}_{2} ,\theta _{{12}} ;\varvec{x}_{1} ,\varvec{x}_{2} ). $$

After ${\widetilde{\theta }} _{12}$ is obtained, $a_{13}$ and $b_{13}$ are given by $\min \theta _{13}$ and $\max \theta _{13}$ s.t. Eq. (3) where $\theta _{12}={\widetilde{\theta }}_{12}$, respectively. The same discussion can be done for $a_{23},b_{23},a_{123}$, and $b_{123}$. In this way, the parameters of Eq. (2) are fixed by their estimated values one by one.

Remark 2

Since $\ell _{j_1\cdots j_k}$ is a single nonlinear equation, some numerical optimization is required to solve $\mathop {{\text{arg}}\,{\text{min}}}\limits_{{a_{{j_{1} \cdots j_{k} }} \le \theta _{{j_{1} \cdots j_{k} }} \le b_{{j_{1} \cdots j_{k} }} }} \ell _{{j_{1} \cdots j_{k} }}$ and $\mathop {{\text{arg}}\,{\text{max}}}\limits_{{a_{{j_{1} \cdots j_{k} }} \le \theta _{{j_{1} \cdots j_{k} }} \le b_{{j_{1} \cdots j_{k} }} }} \ell _{{j_{1} \cdots j_{k} }}$. A possible initial value of numerical optimization is $(a_{j_1\cdots j_k}+b_{j_1\cdots j_k})/2$.

One can use an interior point method as a numerical optimization method for such constrained nonlinear optimization problems (e.g., Mathematica supports an interior point method by the functions FindMinimum and FindMaximum).

Remark 3

For a given k, the order of estimating the $\left( {\begin{array}{c}d\\ k\end{array}}\right)$ dependence parameters (i.e., $\theta _{j_1\cdots j_k}$’s) is exchangeable. The number of possible ways to estimate $\theta _{j_1\cdots j_k}$’s is $\left( {\begin{array}{c}d\\ k\end{array}}\right) !$.

For example, when $d=3$ and $k=2$, we have $\theta _{12},\theta _{13}$, and $\theta _{23}$. The estimation order of these parameters is exchangeable because $\ell _{12},\ell _{13}$, and $\ell _{23}$ do not depend on $(\theta _{13},\theta _{23})$, $(\theta _{12},\theta _{23})$, and $(\theta _{12},\theta _{13})$, respectively. Thus, there are 6 ways to estimate these three parameters in the permutations of $(\theta _{12},\theta _{13},\theta _{23})$, $(\theta _{12},\theta _{23},\theta _{13})$, $(\theta _{13},\theta _{12},\theta _{23})$, $(\theta _{13},\theta _{23},\theta _{12})$, $(\theta _{23},\theta _{12},\theta _{13})$, and $(\theta _{23},\theta _{13},\theta _{12})$. In total, we have $\prod _{k=2}^{d}\left( {\begin{array}{c}d\\ k\end{array}}\right) !$ ways to estimate all $2^d-d-1$ dependence parameters.

The value of $\widetilde{\varvec{\theta }}$ may change depending on the estimation order of $\theta _{j_1\cdots j_k}$’s for a small sample. This is because $a_{j_1\cdots j_k}$ and $b_{j_1\cdots j_k}$ depend on the values of the dependence parameters already estimated. The estimation using a small sample may yield large estimation errors. As a result, large estimation errors of the dependence parameters obtained at the beginning of the algorithm (e.g., ${\widetilde{\theta }}_{12},{\widetilde{\theta }}_{13},\dots$) tend to shorten allowable ranges $[a_{j_1\cdots j_k},b_{j_1\cdots j_k}]$ of other dependence parameters to be estimated. Therefore, we should estimate $\varvec{\theta }$ by using various ways as long as the computation time is acceptable. If we obtain M different estimates $\widetilde{\varvec{\theta }}_1,\dots ,\widetilde{\varvec{\theta }}_M$ by M ways, we can select the best estimate so that the estimate yields the largest log-likelihood value as $\mathop {{\text{arg}}\,{\text{max}}}\limits_{{\varvec{\tilde{\theta }}_{m} }} \ell (\varvec{\tilde{\delta }},\varvec{\tilde{\theta }}_{m} ;\varvec{x}_{1} , \ldots ,\varvec{x}_{n} )$ for $m=1,\dots ,M$.

4 Asymptotic normality

An estimator of MLE satisfies asymptotic normality under regularity conditions (Cramer 1945). It is also known that an estimator of IFM supports asymptotic normality if the copula satisfies regularity conditions (Joe 2014). However, no studies found that the same property holds in the multivariate FGM distribution.

In this section, therefore, we argue that asymptotic normality of MLE and IFM hold for the FGM distribution. We then compare their asymptotic efficiencies for specific parameter cases.

Without loss of generality, let us consider asymptotic normality of each estimator of MLE and IFM for $d=3$ and $\varvec{\delta }_j=\delta _j$. Let $\varvec{\eta }$ be $(\varvec{\delta },\varvec{\theta })$ (i.e., $\varvec{\eta }=(\eta _1,\ldots ,\eta _7)=(\delta _1,\delta _2,\delta _3,\theta _{12},\theta _{13},\theta _{23},\theta _{123})$), and a parameter with the subscript 0 denotes the true value of the parameter (e.g., $\varvec{\theta }_0$ and $\varvec{\delta }_0$). Then, for a random vector of the FGM distribution $\varvec{X}=(X_1,X_2,X_3)$, the following theorems hold under suitable regularity conditions including interchange of differentiation and integration (see pp. 462-463 of Lehmann and Casella (1998) for the consistency and asymptotic normality of MLE and Joe (2014) for the reference of IFM).

Theorem 1

The estimator of MLE $\varvec{\widehat{\eta }}$ satisfies the following equation for $n\rightarrow \infty$.

$$\begin{aligned} \sqrt{n}(\varvec{\widehat{\eta }}-\varvec{\eta }_0)\overset{\mathcal {D}}{\rightarrow }N(\varvec{0},I^{-1}), \end{aligned}$$

where $\overset{\mathcal {D}}{\rightarrow }$ denotes the convergence in distribution, and I is the Fisher information matrix, which is given by

$$\begin{aligned} I=-E\left[ \left. \frac{\partial ^2\log h_3(X_1,X_2,X_3;\varvec{\eta } )}{\partial \varvec{\eta }\partial \varvec{\eta }^\mathrm{T}}\right| _{\varvec{\eta }=\varvec{\eta }_0}\right] , \end{aligned}$$

(6)

where $\mathrm{T}$ represents transpose of a vector or matrix, and

$$\begin{aligned} h_3(X_1,X_2,X_3;\varvec{\eta })&=\prod _{j=1}^3 f_j(X_j;\delta _j)\Biggl (1+\theta _{12}(1-2F_1(X_1;\delta _1))(1-2F_2(X_2;\delta _2))\\&\quad +\theta _{13}(1-2F_1(X_1;\delta _1))(1-2F_3(X_3;\delta _3))\\&\quad +\theta _{23}(1-2F_2(X_2;\delta _2))(1-2F_3(X_3;\delta _3))\\&\quad +\theta _{123}(1-2F_1(X_1;\delta _1))(1-2F_2(X_2;\delta _2))(1-2F_3(X_3;\delta _3))\Biggr ). \end{aligned}$$

Theorem 2

The estimator of IFM $\varvec{{\widetilde{\eta }}}$ satisfies the following equation for $n\rightarrow \infty$.

$$\begin{aligned} \sqrt{n}(\varvec{{\widetilde{\eta }}}-\varvec{\eta }_0)\overset{\mathcal {D}}{\rightarrow }N(\varvec{0},V), \end{aligned}$$

where

$$\begin{aligned} V&=D^{-1}M(D^{-1})^\mathrm{T},\nonumber \\ D&=E\left[ \left. \frac{\partial \varvec{s}(\varvec{X};\varvec{\eta })}{\partial \varvec{\eta }}\right| _{\varvec{\eta }=\varvec{\eta }_0}\right] , \end{aligned}$$

(7)

$$\begin{aligned} M&=E[\varvec{s}(\varvec{X};\varvec{\eta }_0)\varvec{s}(\varvec{X};\varvec{\eta }_0)^\mathrm{T}], \end{aligned}$$

(8)

$$\begin{aligned} \varvec{s}(\varvec{X};\varvec{\eta })&=\left[ \begin{array}{c} s_1 \\ s_2 \\ s_3 \\ s_4 \\ s_5 \\ s_6 \\ s_7 \end{array}\right] =\left[ \begin{array}{c} \frac{\partial }{\partial \delta _1}\log f_1(X_1;\delta _1) \\ \frac{\partial }{\partial \delta _2}\log f_2(X_2;\delta _2) \\ \frac{\partial }{\partial \delta _3}\log f_3(X_3;\delta _3) \\ \frac{\partial }{\partial \theta _{12}}\log h_{2}(X_1,X_2;\delta _1,\delta _2,\theta _{12}) \\ \frac{\partial }{\partial \theta _{13}}\log h_{2}(X_1,X_3;\delta _1,\delta _3,\theta _{13}) \\ \frac{\partial }{\partial \theta _{23}}\log h_{2}(X_2,X_3;\delta _2,\delta _3,\theta _{23}) \\ \frac{\partial }{\partial \theta _{123}}\log h_{3}(X_1,X_2,X_3;\varvec{\eta }) \end{array}\right] ,\nonumber \\ h_2(X_1,X_2;\delta _1,\delta _2,\theta _{12})&=f_1(X_1;\delta _1)f_2(X_2;\delta _2)(1\nonumber \\&\quad +\theta _{12}(1-2F_1(X_1;\delta _1))(1-2F_2(X_2;\delta _2)). \end{aligned}$$

(9)

Note that we cannot obtain the explicit forms of D and V but can compute them for a specific $\varvec{\eta }_0$. Proofs for Theorems 1 and 2 are given in Appendix.

A natural question arises: how much is $\widehat{\varvec{\eta }}$ relatively efficient compared with $\varvec{{\widetilde{\eta }}}$? To take into account this question, we investigate numerical examples. To simplify the asymptotic covariance matrices, let us consider the case in which $\varvec{\delta }$ is given. That is, the parameters of interest are only $\varvec{\theta }$. Suppose $(\theta _{12},\theta _{13},\theta _{23},\theta _{123})=(0.3,0.3,0.3,0.3)$. Then, each asymptotic covariance matrix is given by

$$\begin{aligned} I^{-1}&=\left( \begin{array}{cccc} 8.48 &{} 0.721 &{} 0.721 &{} -0.486\\ 0.721 &{} 8.48 &{} 0.721 &{} -0.486\\ 0.721 &{} 0.721 &{} 8.48 &{} -0.486\\ -0.486 &{} -0.486 &{} -0.486 &{} 24.32 \end{array} \right) , \end{aligned}$$

(10)

$$\begin{aligned} V&=\left( \begin{array}{cccc} 8.70 &{} 0.736 &{} 0.736 &{} -0.498\\ 0.736 &{} 8.70 &{} 0.736 &{} -0.498\\ 0.736 &{} 0.736 &{} 8.70 &{} -0.498\\ -0.498 &{} -0.498 &{} -0.498 &{} 24.32 \end{array} \right) . \end{aligned}$$

(11)

Note that we use the closed Newton-Cotes formula of degree 3 to numerically compute integrations for $I^{-1}$ and V. Since the ith diagonal element of Eq. (10) is less than that of Eq. (11) for $i=1,\ldots ,4$, we can find that MLE is more effective than IFM. For example, the variance of $\widehat{\theta }_{12}$ is around $97\%\,(=8.48/8.70)$ of the variance of ${\widetilde{\theta }}_{12}$.

As another example, let us consider the case of $(\theta _{12},\theta _{13},\theta _{23},\theta _{123})=(0,0,0,0)$ (i.e., the independent case). Then, each asymptotic covariance matrix is analytically obtained as

$$\begin{aligned} I^{-1}&=V=\left( \begin{array}{cccc} 9 &{} 0 &{} 0 &{} 0\\ 0 &{} 9 &{} 0 &{} 0\\ 0 &{} 0 &{} 9 &{} 0\\ 0 &{} 0 &{} 0 &{} 27 \end{array} \right) . \end{aligned}$$

Hence, the variances of $\widehat{\varvec{\theta }}$ are 100% of those of $\widetilde{\varvec{\theta }}$ if $(\theta _{12},\theta _{13},\theta _{23},\theta _{123})=(0,0,0,0)$.

5 Simulation study

In this section, we conduct simulation studies to evaluate the effectiveness of our proposed method in the estimation of the multivariate FGM distribution. We first explain how to generate simulation samples from the multivariate FGM distribution. Then, we compare MLE and IFM from the viewpoint of estimation accuracy and computation time and provide some discussion.

5.1 Generating the simulation samples

The conditional method (Xu 1996; Joe 2014) allows us to generate samples from the multivariate FGM distribution with arbitrary marginal distributions. Let $(X_1,\dots ,X_d)$ be a random vector of the d-variate FGM distribution. For $j=2,3,\ldots ,d$, we define the conditional distribution functions as follows.

$$\begin{aligned} C_{j|12\cdots j-1}(u_j|u_1,\ldots ,u_{j-1})=\mathrm{Pr}[U_j\le u_j|U_1=u_1,\ldots ,U_{j-1}=u_{j-1}]. \end{aligned}$$

Let $v_1,\ldots ,v_d$ be samples from the i.i.d. uniform distribution in the interval [0, 1]. We construct a random sequence through the following processes.

• Let $u_1=C^{-1}_1(v_1)$.

• Let $u_2=C^{-1}_{2|1}(v_2|u_1)$,...,

• Let $u_d=C^{-1}_{d|1\cdots d-1}(v_d|u_1,\ldots ,u_{d-1})$.

• Return $(x_1,x_2,\ldots ,x_d)=(F^{-1}_1(u_1;\varvec{\delta }_1),F^{-1}_2(u_2;\varvec{\delta }_2),\ldots ,F^{-1}_d(u_d;\varvec{\delta }_d))$.

Consequently, the random sequence $(x_1,x_2,\ldots ,x_d)$ follows the d-variate FGM distribution.

We need to know the closed form of $C^{-1}_{j|1\cdots j-1}(\cdot |\cdot )$ to use the conditional method for the d-variate FGM distribution. The conditional distribution function is generally given by

$$\begin{aligned} C_{j|1\cdots j-1}(u_j|u_1,\ldots ,u_{j-1})=\int _0^{u_j} \frac{c_j(u_1,\ldots ,u_{j-1},u)}{c_{j-1}(u_1,\ldots ,u_{j-1})} du. \end{aligned}$$

Since

$$\begin{aligned} c_j(u_1,\ldots ,u_j)=c_{j-1}(u_1,\ldots ,u_{j-1})+\sum _{p=2}^j \sum _{1\le j_1<\cdots <j_p=j}\theta _{j_1\cdots j_p}(1-2u_{j_1})\cdots (1-2u_{j_p}), \end{aligned}$$

it follows that

$$\begin{aligned} \frac{c_j(u_1,\ldots ,u_j)}{c_{j-1}(u_1,\ldots ,u_{j-1})}=1+\frac{\sum _{p=2}^j \sum _{1\le j_1<\cdots <j_p=j}\theta _{j_1\cdots j_p}(1-2u_{j_1})\cdots (1-2u_{j_p})}{c_{j-1}(u_1,\ldots ,u_{j-1})}. \end{aligned}$$

(12)

By integrating both sides of Eq. (12), we obtain

$$\begin{aligned} C_{j|1\cdots j-1}(u_j|u_1,\ldots ,u_{j-1})=(1+D)u_j-Du_j^2, \end{aligned}$$

where

$$\begin{aligned} D=\frac{\sum _{p=2}^j \sum _{1\le j_1<\cdots <j_p=j}\theta _{j_1\cdots j_p}(1-2u_{j_1})\cdots (1-2u_{j_{p-1}})}{c_{j-1}(u_1,\ldots ,u_{j-1})}. \end{aligned}$$

From $Du_j^2-(1+D)u_j-C_{j|1\cdots j-1}(u_j|u_1,\ldots ,u_{j-1})=0$, the inverse function $C^{-1}_{j|1\cdots j-1}(u_j|u_1,\ldots ,u_{j-1})$ takes one of the values of

$$\begin{aligned} \frac{1+D\pm \sqrt{(1+D)^2-4Du_j}}{2D}, \end{aligned}$$

(13)

for which it is positive and less than 1. For example, for $j=2$, we have

$$\begin{aligned} C^{-1}_{2|1}(v_2|u_1)=\frac{1+\theta _{12}(1-2u_1) +\sqrt{(1+\theta _{12}(1-2u_1))^2-4\theta _{12}(1-2u_1)v_2}}{2\theta _{12}(1-2u_1)}. \end{aligned}$$

As far as we have found, the signs of Eq. (13) for $j=2,3,4$ and 5 are $+,-,-$, and −, respectively. Consequently, we can generate samples of the multivariate FGM distribution by using the conditional method with Eq. (13).

5.2 Short example

By using simulation data, we demonstrate the procedure of IFM for the d-variate FGM distribution. The settings of this example are as follows.

• 1. The sample size is 1000.

• 2. All the marginal distributions are the i.i.d. uniform distribution in the interval [0, 1] (i.e., the target parameters are the only dependence parameters).

• 3. For $d=3$, $(\theta _{12},\theta _{13},\theta _{23},\theta _{123})=(0.3,0.3,0.3,0.3)$.

We generated random samples under the settings and estimate the parameters from the samples.

We estimated the dependence parameters through the following steps.

• Step 1: ${\widetilde{\theta }}_{12}=\mathop {\mathrm {arg \,max}}\limits _{\theta _{12}}\ell _{12}=\mathop {\mathrm {arg \,max}}\limits _{-1\le \theta _{12}\le 1}\ell _{12}=0.298$.

• Step 2: ${\widetilde{\theta }}_{13}=\mathop {\mathrm {arg \,max}}\limits _{\theta _{13},\theta _{12}=0.298}\ell _{13}=\mathop {\mathrm {arg \,max}}\limits _{-1\le \theta _{13}\le 1}\ell _{13}=0.272$.

• Step 3: ${\widetilde{\theta }}_{23}=\mathop {\mathrm {arg \,max}}\limits _{\theta _{23},\theta _{12}=0.298,\theta _{13}=0.272}\ell _{23}=\mathop {\mathrm {arg \,max}}\limits _{-0.431\le \theta _{23}\le 0.974}\ell _{23}=0.365$.

• Step 4: ${\widetilde{\theta }}_{123}=\mathop {\mathrm {arg \,max}}\limits _{\theta _{123},\theta _{12}=0.298,\theta _{13}=0.272,\theta _{23}=0.365}\ell =\mathop {\mathrm {arg \,max}}\limits _{-0.609\le \theta _{123}\le 0.609}\ell =0.222$.

Note that the allowable ranges of the dependence parameters are calculated based on Remark 1 in each step.

As mentioned in Remark 3, Step 1, 2, and 3 are exchangeable although we estimated the dependence parameters in the order of $\theta _{12},\theta _{13}$, and $\theta _{23}$ in this example. If the order is changed, the estimation result might be different from the above result. To illustrate this phenomenon, we conducted another experiment by changing the sample size from 1000 to 100. We estimated all dependence parameters by MLE and IFM with possible six estimation orders (see Table 1). Note that $(\alpha ,\beta )$ bellow each estimated value in Table 1 represents the allowable range of the corresponding dependence parameter (i.e., $\alpha =a_{j_1\cdots j_k}$ and $\beta =b_{j_1\cdots j_k}$). For example, $\theta _{12}$ was estimated in the interval $[-1,1]$ in the estimation order of $\theta _{12}\rightarrow \theta _{13}\rightarrow \theta _{23}\rightarrow \theta _{123}$.

Table 1 Comparison among simulation results of estimating $(\theta _{12},\theta _{13},\theta _{23},\theta _{123})=(0.3,0.3,0.3,0.3)$ by possible 6 IFM ways and MLE

As shown in Table 1, there were 3 different types of estimation results for IFM, and all ${\widetilde{\theta }}_{123}$ were 0 under the conditions of Eq. (2) and $(\theta _{12},\theta _{13},\theta _{23})=({\widetilde{\theta }}_{12}, {\widetilde{\theta }}_{13},{\widetilde{\theta }}_{23})$. The reason why we obtained such results due to the difference of the estimation order mainly depended on the accumulation of estimation errors in the process of IFM. For example, the estimated values ${\widetilde{\theta }}_{13}$ were different between the cases that the dependence parameters were estimated in the orders of $\theta _{12}\rightarrow \theta _{13}\rightarrow \theta _{23}\rightarrow \theta _{123}$ and $\theta _{12}\rightarrow \theta _{23}\rightarrow \theta _{13}\rightarrow \theta _{123}$ (i.e., 0.707 and 0.518). While the allowable range of $\theta _{13}$ thirdly estimated in the latter case was $[-0.156,0.518]$, that secondly estimated in the former case was $[-1,1]$. ${\widetilde{\theta }}_{13}$ could not be 0.707 in the latter case. Therefore, the value of $\widetilde{\varvec{\theta }}$ changed depending on the estimation order.

The result of MLE was also different from the results of IFM. Based on the log-likelihood values, the result of MLE should be chosen as the best estimate in this example.

5.3 Estimation accuracy

In this subsection, we investigated the estimation accuracy of the proposed algorithm through Monte Carlo simulation under the conditions that parameters of marginal distributions $\varvec{\delta }$ are known and unknown.

5.3.1 When $\varvec{\delta }$ is known

We again considered that all the marginal distributions were given, and $\varvec{\delta }$ was known. For $d=4$, we conducted the simulation under the following settings.

• 1. The sample sizes n were 100, 1000, and 10,000, and the number of iteration times m was 100.

• 2. All the marginal distributions were the i.i.d. uniform distribution in the interval [0, 1]. This means that the target parameters are only the dependence parameters.

• 3. We considered the following four situations of the dependence parameters.

  • (a) $(\theta _{12},\theta _{13},\theta _{14},\theta _{23},\theta _{24},\theta _{34},\theta _{123}, \theta _{124},\theta _{134},\theta _{234},\theta _{1234})$

    $=(0,0,0,0,0,0,0.2,0.2,0.2,0.2,0.2)$.

  • (b) $(\theta _{12},\theta _{13},\theta _{14},\theta _{23},\theta _{24},\theta _{34},\theta _{123},\theta _{124}, \theta _{134},\theta _{234},\theta _{1234})$

    $=(0,0,0,0,0,0,0.2,0.2,0.2,0.2,0.5)$.

  • (c) $(\theta _{12},\theta _{13},\theta _{14},\theta _{23},\theta _{24},\theta _{34},\theta _{123}, \theta _{124},\theta _{134},\theta _{234},\theta _{1234})$

    $=(0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2)$.

  • (d) $(\theta _{12},\theta _{13},\theta _{14},\theta _{23},\theta _{24},\theta _{34},\theta _{123}, \theta _{124},\theta _{134},\theta _{234},\theta _{1234})$

    $=(0,0,0,0,0,0,-0.2,-0.2,-0.2,-0.2,-0.2)$.

Under the settings, we calculated the following Bias and root-mean-squared error (RMSE) as indicators of estimation accuracy for each estimator of IFM.

$$\begin{aligned} Bias(\varvec{{\widetilde{\theta }}})&=\left[ \begin{array}{c} \frac{1}{m}\sum _{i=1}^m ({\widetilde{\theta }}_{12,i}-\theta _{12(0)}) \\ \vdots \\ \frac{1}{m}\sum _{i=1}^m ({\widetilde{\theta }}_{1234,i}-\theta _{1234(0)}) \end{array}\right] ,\\ RMSE(\varvec{{\widetilde{\theta }}})&= \left[ \begin{array}{c} \sqrt{\frac{1}{m}\sum _{i=1}^m ({\widetilde{\theta }}_{12,i}-\theta _{12(0)})^2} \\ \vdots \\ \sqrt{\frac{1}{m}\sum _{i=1}^m ({\widetilde{\theta }}_{1234,i}-\theta _{1234(0)})^2} \end{array}\right] , \end{aligned}$$

where ${\widetilde{\theta }}_{\cdot ,i}$ is ${\widetilde{\theta }}_{\cdot }$’s estimate obtained in the ith iteration step and ${\widetilde{\theta }}_{\cdot ,(0)}$ is the true value of ${\widetilde{\theta }}_{\cdot }$. Bias and RMSE represent the average and dispersion of the estimation errors, respectively.

The numerical results are presented in Tables 2, 3, 4, and 5. Note that MLE cannot work in the case of $n=10{,}000$ due to too much computation time for 100 iterations (represented as N/A). Besides, only one estimation order of $\varvec{{\widetilde{\theta }}}$ was considered to finish the experiments within reasonable computation time (e.g., there are 17280 estimation orders for $d=4$ as discussed in Remark 3).

The estimation accuracy improved with a power of 10 samples. To obtain estimates with Bias of less than 0.1, we require approximately 100, 1000, and 10,000 samples for $\theta _{j_1j_2},\theta _{j_1j_2j_3},$ and $\theta _{1234}$, respectively. As for RMSE, ratio values of the results of IFM to those of MLE for the corresponding dependence parameters are close to 1 in most of the cases.

Table 2 Simulation results of estimating $(\theta _{12},\theta _{13},\theta _{14},\theta _{23},\theta _{24},\theta _{34}, \theta _{123},\theta _{124},\theta _{134},\theta _{234},\theta _{1234})=(0,0,0,0,0,0,0.2,0.2,0.2,0.2,0.2)$ based on the average of 100 iterations

Table 3 Simulation results of estimating $(\theta _{12},\theta _{13},\theta _{14},\theta _{23},\theta _{24},\theta _{34},\theta _{123},\theta _{124},\theta _{134},\theta _{234},\theta _{1234})=(0,0,0,0,0,0,0.2,0.2,0.2,0.2,0.5)$ based on the average of 100 iterations

Table 4 Simulation results of estimating $(\theta _{12},\theta _{13},\theta _{14},\theta _{23},\theta _{24},\theta _{34}, \theta _{123},\theta _{124},\theta _{134},\theta _{234},\theta _{1234})=(0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2)$ based on the average of 100 iterations

Table 5 Simulation results of estimating $(\theta _{12},\theta _{13},\theta _{14},\theta _{23},\theta _{24},\theta _{34},\theta _{123}, \theta _{124},\theta _{134},\theta _{234},\theta _{1234}) =(0,0,0,0,0,0,-0.2,-0.2,-0.2,-0.2,-0.2)$ based on the average of 100 iterations

5.3.2 When $\varvec{\delta }$ is unknown

We next investigated the estimation accuracy when the marginal distributions were given, but $\varvec{\delta }$ was unknown. In this case, it is expected that the accuracy of IFM worsen because the estimation accuracy for the dependence parameters is affected by the error for the marginal parameters. To check how much the performance worsens, we conducted the simulation under the following settings for $d=4$.

• 1. The sample size n was 100, and the number of iteration times m was 100.

• 2. All the marginal distributions were an i.i.d. exponential distribution. We fixed the marginal parameters as $(\delta _1,\delta _2,\delta _3,\delta _4)=(1,1,1,1)$.

• 3. The dependence parameters were fixed as $(\theta _{12},\theta _{13},\theta _{14},\theta _{23},\theta _{24},\theta _{34},\theta _{123}, \theta _{124},\theta _{134},\theta _{234},\theta _{1234})$

  $=(0,0,0,0,0,0,0.2,0.2,0.2,0.2,0.2)$.

The estimation results of the marginal parameters and dependence parameters are summarized in Tables 6 and 7, respectively. In Table 6, since $n=100$ was enough to estimate the marginal parameters precisely, all biases are close to 0. Hence, the estimation accuracy for the dependence parameters did not significantly worsen even if the marginal parameters were unknown. Bias and RMSE for the dependence parameters in Table 7 were almost the same as those for the dependence parameters shown in the result of $n=100$ of Table 2. Therefore, we infer from these results that IFM and MLE for the parameter estimation of the FGM distribution work well under the condition that the sample size is enough to estimate $\varvec{\delta }$ at least.

Table 6 Simulation results of estimating $(\delta _{1},\delta _{2},\delta _{3},\delta _{4}) =(1,1,1,1)$ based on the average of 100 iterations

Table 7 Simulation results of estimating $(\theta _{12},\theta _{13},\theta _{14},\theta _{23},\theta _{24},\theta _{34},\theta _{123}, \theta _{124},\theta _{134},\theta _{234},\theta _{1234})=(0,0,0,0,0,0,0.2,0.2,0.2,0.2,0.2)$ if $\varvec{\delta }$ is unknown based on the average of 100 iterations

5.4 Computation time

In this subsection, we discuss the investigation of the computation times of MLE and IFM. We implemented IFM for the d-variate FGM distribution in Mathematica 11.3 and a PC equipped with Intel(R)Core(TM) i7-6700k 4.00-GHz, 32GB-RAM running on Windows 10 professional 64bit. We conducted the simulation under the following settings.

• 1. The dimensions d were 4 and 5.

• 2. The sample sizes n were 100, 1000, and 10,000.

• 3. All the marginal distributions were the i.i.d. uniform distribution in the interval [0, 1]. This means that the target parameters are only the dependence parameters.

• 4. For $d=4$, the values of the dependence parameters are as follows: $\theta _{j_1j_2}=0,\theta _{j_1j_2j_3}=0.2$, and $\theta _{1234}=0.2$ for $1\le j_1<j_2<j_3\le 4$.

• 5. For $d=5$, the values of the dependence parameters are as follows: $\theta _{j_1j_2}=0,\theta _{j_1j_2j_3}=0,\theta _{j_1j_2j_3j_4}=0.2$, and $\theta _{12345}=0.2$ for $1\le j_1<j_2<j_3<j_4\le 5$.

Fig. 1

Average computation times of estimating all dependence parameters of d-variate FGM distribution for $d=4,5$ (number of iterations: 5)

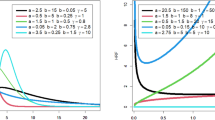
Figure 1 illustrates the computation times to estimate the dependence parameters under the above situation. We can find that IFM works faster than MLE in all cases, and both MLE and IFM require more computational time as d and n increase. If $d=5$ and $n=10{,}000$, MLE cannot work due to running out of memory (represented as N/A). Therefore, to estimate the parameters of the multivariate FGM distribution, we should not use MLE but IFM from the viewpoint of computational cost. A theoretical analysis of the computational complexity of IFM is required for future work.

6 Case study

In the previous section, we showed several aspects of the parameter estimation scheme proposed in this paper by utilizing simulation data. In this section, in turn, we depict another numerical example based on the actually collected data set. This is called Bearing data set, which is available in NASA Ames Prognostics Data Repository (Lee et al. 2007).

6.1 Bearing data set

This data set was collected for the purpose of the investigation of how four bearings with a coaxial rotating shaft degraded in time. For this case study, we employ “Set No. 1”  data set from the original data set. This “Set No.1”  contains 2156 files, and each file has 20480 data points of vibration signal yielded in one second from 4 working bearings with 2 data-collection channels of accelerometers on the test rig (see Fig. 2). Therefore one data file has 20480 lines, and each line has 8 numerical values (4 bearings $\times$ 2 channels). Also, one file was saved as a log file every 10 minutes (N.B., the first 43 files are logged every 5 minutes). Hence we obtain about 44.1 million ($\approx 2156 \times 20480$) lines of 8-dimension vibration signal values.

Fig. 2

Illustration of test rig [cited from Qiu et al. (2006)]. Each bearing has 2 channels for data collection. Bearing #1 has channels #1 and #2, bearing #2 has channels #3 and #4, bearing #3 has channels #5 and #6, and bearing #4 has channels #7 and #8, respectively

In order to reduce the size of the data set, we extracted the first line from every 2156 files. And from the structure of the test rig, we decided to use 4 channels of #1, #3, #5, and #7 from bearing #1, #2, #3, and #4, respectively. After such a data preparation, we finally obtain 2156 actual samples of 4-variate data set as follows ($i=1,2,\dots ,2156$).

$\cdot$:

$x_{i1}=$ the ith vibration signal (unit: arbitrary) of channel #1 in bearing #1.

$\cdot$:

$x_{i2}=$ the ith vibration signal (unit: arbitrary) of channel #3 in bearing #2.

$\cdot$:

$x_{i3}=$ the ith vibration signal (unit: arbitrary) of channel #5 in bearing #3.

$\cdot$:

$x_{i4}=$ the ith vibration signal (unit: arbitrary) of channel #7 in bearing #4.

Note that the unit of the vibration signal is not indicated in the original references of Bearing data set (Qiu et al. 2006; Lee et al. 2007). Since the vibration signal was collected from the accelerometers, we can guess that the unit is any of voltage (mV) [or (V)] and acceleration (m/s²) which is proportional to a voltage value. For this reason, we assume that the vibration signal has an arbitrary unit in this study.

In this paper, we use this data set to find some dependence property among four bearings via their vibration signal data. Since these four bearings are operated by a single rotating shaft, it is expected that some common factors may affect the degradation of the bearings. For this, we apply 4-variate FGM copula to the data set and estimate its 11 dependence parameters.

6.2 Finding marginal distribution

We separate the data set into three sets from the viewpoint of the size. We call them Data-A, Data-B, and Data-C, respectively. Data-C is the overall data (2156 lines). To make Data-A, we extracted the first 100 lines from Data-C. This means that this set was collected from the early stage of the operation time of four bearings. The second one, Data-B, consists of 1000 lines (i.e., Data-A plus successive 900 lines) to grasp the dependence property until the middle part of the data set. Data-C is used for the overall time domain analysis.

For each data set, we need to find the well-fitted marginal distribution firstly. Since the normal distribution was not fit these data sets, we chose the generalized t-distribution with the following probability density function:

$$\begin{aligned} f(x;\varvec{\delta })=\frac{{\bigr [ 1+(\frac{x-a}{b\sqrt{c}})^2\bigl ]}^{-\frac{c+1}{2}}}{b\sqrt{c}\, B[\frac{c}{2},\frac{1}{2}]}, \end{aligned}$$

(14)

where $\varvec{\delta }=(a,b,c)$ and $B[\alpha , \beta ]$ is the beta function defined by

$$\begin{aligned} \int ^1_0 t^{\alpha -1} (1-t)^{\beta -1} \mathrm{d}t. \end{aligned}$$

This distribution has a location parameter a and a scale parameter b. The parameter c denotes the degree of freedom. Therefore if $a=0$ and $b=1$, Eq. (14) describes the Student’s t-distribution.

Table 8 List of estimated parameters of marginal t-distribution. Normal distribution is not suitable because of the several small p values

Table 8 summarizes the estimation results of the marginal t-distribution and their p values by employing the Kolmogorov–Smirnov goodness-of-fit test. The right-most column also lists the p values if the normal distribution is applied. Therefore we choose t-distribution for the marginal, because all the cases are not rejected at the significance level of 0.05.

6.3 Parameter estimation and discussion

We estimated all the parameters included in the 4-variate FGM copula by the proposed method. Note that only one estimation order of $\varvec{{\widetilde{\theta }}}$ was considered to finish the experiment within acceptable computation time. Table 9 is a list of them for each data set. In the statistical sense, the results of Data-C are the most meaningful because the size of the data set is the largest (2156 data points) among the three. The values in each row vary by the combination of bearings. Actually, it is not easy to infer the actual dependence structure among the bearings on the test rig from such information seen in this table, but we dare to state the degree of dependence by categorizing the estimated values. That is, we set three categories of the dependence as positive, negative, and almost zero between two bearings. By following this categorization, ${{\widetilde{\theta }}}_{12}$, ${{\widetilde{\theta }}}_{34}$ are judged as positive, ${{\widetilde{\theta }}}_{13}$, ${{\widetilde{\theta }}}_{23}$, and ${{\widetilde{\theta }}}_{24}$ are negative, and ${{\widetilde{\theta }}}_{14}$ is almost zero.

Translating the subscript numbers 1, 2, 3, and 4 of $\theta$ into the channel numbers 1, 3, 5, and 7, respectively, we can infer that the bearings #1 and #4 are almost independent because ${{\widetilde{\theta }}}_{14}$ belongs to the category of almost zero. It is understandable that this result from the illustration of Fig. 2 is possible since the bearing #1 and #4 are placed at both ends on the test rig equipment. It is reasonable that they may yield mutually independent vibration signals.

On the other hand, the degree of the positive and negative dependence between two bearings seems to also suggest some structural dependence depicted in Fig. 2. In the case of positive, the pair of bearings #1 and #2 adjoin, and the direction of the radial load is opposite. The same relationship can be seen at the pair of bearings #3 and #4. Therefore we can presume that these pairs of bearings may fail dependently in the future. Regarding this matter, Qiu et al. (2006) reported that an inner race defect was discovered in the bearing #3 and a roller element defect and outer race defect were found in the bearing #4 at the end of the testing. This consequence results in supporting our inference stated above.

The last category, denoted as negative, contains three pairs of bearings as (#1, #3), (#2, #4), and (#2, #3). Among the three, the first two pairs of bearings suffer the opposite radial load direction, but have more distance than the case of positive. Whereas in the case of (#2, #3), these bearings take the same direction of the radial load and are equipped closely. It is not clear that how these factors affect that the estimated values tend to be negative. It may be needed to do more research from the viewpoint of mechanical engineering and other theoretical consideration to explain these interesting relationships between the estimated values and the physical layout of the equipment and other factors of the bearings.

Moreover, it becomes more complicated to explain the dependence structure and estimated values among three or more bearings (i.e., ${{\widetilde{\theta }}}_{123}$,..., ${{\widetilde{\theta }}}_{1234}$). It is desired that the reasons and implications for these phenomena are revealed in future studies. In any case, however, we have confirmed that the proposed algorithm for the parameter estimation of the FGM distribution worked well.

Table 9 List of estimated parameters by IFM. Subscript numbers 1, 2, 3, and 4 of the $\theta$ correspond to the channel numbers 1, 3, 5, and 7, respectively

7 Conclusion

We proposed an algorithm for estimating the parameters of the multivariate FGM distribution in practical computation time. The computational complexity of MLE was reduced by using IFM. Because of this, IFM can estimate all the dependence parameters of the multivariate FGM distribution no matter how high the dimension d is. We then revealed that the estimators of IFM satisfy asymptotic normality for the multivariate FGM distribution. Therefore, The proposed algorithm is useful for estimating the parameters of the FGM distribution.

From the viewpoint of reliability engineering, the proposed algorithm can be applied to a quantitative evaluation of the dependence among system components. If we have the lifetime data of system components, we can find the latent dependence structure among them by estimating the parameters of the multivariate FGM distribution with arbitrary marginal distributions.

Appendix: Proofs

Before we prove Theorems 1 and 2, we introduce a lemma and theorem as follows.

Lemma 1

Let $(X_1,X_2,X_3)$ be a random vector of the trivariate FGM distribution. Then, $E\left[ \varvec{s}(X_1,X_2,X_3;\varvec{\eta }_0)\right] =\varvec{0}$ and $E[\frac{\partial }{\partial \varvec{\eta }}\log h_{3}(X_1,X_2,X_3;\cdot )|_{\varvec{\eta }=\varvec{\eta }_0}]=\varvec{0}$ hold.

Proof of Lemma 1

(9), we prove that each element of $E\left[ \varvec{s}(\cdot ;\varvec{\eta }_0)\right]$ is 0, that is,

$$\begin{aligned}&E\left[ \frac{\partial }{\partial \delta _j}\log f_j(X_j;\cdot )\right] =0,\\&E\left[ \frac{\partial }{\partial \theta _{jk}}\log h_{2}(X_j,X_k;\cdot )\right] =0,\\&E\left[ \frac{\partial }{\partial \theta _{123}}\log h_{3}(X_1,X_2,X_3;\cdot )\right] =0, \end{aligned}$$

for $1\le j<k\le 3$. First, we have

$$\begin{aligned} E\left[ \frac{\partial }{\partial \delta _j}\log f_j(X_j;\cdot )\right]&=\int _{-\infty }^{\infty }f_j(x_j;\cdot )\frac{\partial }{\partial \delta _j}\log f_j(x_j;\cdot )dx_j \\&=\int _{-\infty }^{\infty }\frac{\partial }{\partial \delta _j} f_j(x_j;\cdot )dx_j\\&=\frac{\partial }{\partial \delta _j}\int _{-\infty }^{\infty } f_j(x_j;\cdot )dx_j=0, \end{aligned}$$

where we assume that the order of the differentiation and integration can be changed in the third step. In the same manner, we obtain

$$\begin{aligned} E\left[ \frac{\partial }{\partial \theta _{jk}}\log h_2(X_j,X_k;\cdot )\right]&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }h_{jk}(x_j,x_k;\cdot )\frac{\partial }{\partial \theta _{jk}}\log h_2(x_j,x_k;\cdot )dx_jdx_k \\&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{\partial }{\partial \theta _{jk}} h_2(x_j,x_k;\cdot )dx_jdx_k \\&=\frac{\partial }{\partial \theta _{jk}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty } h_2(x_j,x_k;\cdot )dx_jdx_k=0, \end{aligned}$$

and

$$\begin{aligned} E&\left[ \frac{\partial }{\partial \theta _{123}}\log h_3(X_1,X_2,X_3;\cdot )\right] \\&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }h_3(x_1,x_2,x_3;\cdot ) \frac{\partial }{\partial \theta _{123}}\log h_3(x_1,x_2,x_3;\cdot )dx_1dx_2dx_3 \\&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\frac{\partial }{\partial \theta _{123}} h_3(x_1,x_2,x_3;\cdot )dx_1dx_2dx_3 \\&=\frac{\partial }{\partial \theta _{123}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty } \int _{-\infty }^{\infty }h_3(x_1,x_2,x_3;\cdot )dx_1dx_2dx_3=0. \end{aligned}$$

Therefore, $E\left[ \varvec{s}(\cdot ;\varvec{\eta }_0)\right] =\varvec{0}$. Also, $E[\frac{\partial }{\partial \varvec{\eta }}\log h_{3}(X_1,X_2,X_3;\cdot )]=\varvec{0}$ holds in the same manner. Hence, the proof is complete. $\square$

Proof of Theorem 1

We provide a sketch of the proof of Theorem 1. Suppose $\varvec{Y},\varvec{Y}_1,\ldots ,\varvec{Y}_n$ are i.i.d. random vectors of the d-variate FGM distribution. By applying the mean value theorem for the maximum log likelihood function at $\varvec{\eta }_0$, we obtain

$$\begin{aligned} \varvec{0}&=\left. \frac{\partial \ell (\varvec{\eta };\varvec{Y}_1,\ldots ,\varvec{Y}_n)}{\partial \varvec{\eta }}\right| _{\varvec{\eta }=\varvec{\widehat{\eta }}}\nonumber \\&=\left. \frac{\partial \ell (\varvec{\eta };\varvec{Y}_1,\ldots ,\varvec{Y}_n)}{\partial \varvec{\eta }}\right| _{\varvec{\eta }=\varvec{\eta }_0}+K(\varvec{\overline{\eta }})(\varvec{\widehat{\eta }} -\varvec{\eta }_0), \end{aligned}$$

(15)

where a matrix $K(\varvec{\overline{\eta }})$ is given by

$$\begin{aligned} K(\varvec{\overline{\eta }})=\left. \frac{\partial ^2 \ell (\varvec{\eta };\varvec{Y}_1,\ldots ,\varvec{Y}_n)}{\partial \varvec{\eta }\partial \varvec{\eta }^\mathrm{T}}\right| _{\varvec{\eta }=\varvec{\overline{\eta }}}, \end{aligned}$$

and $\varvec{\overline{\eta }}\equiv diag(\alpha _1,\ldots ,\alpha _7) \varvec{\widehat{\eta }}+diag(1-\alpha _1,\ldots ,1-\alpha _7)\varvec{\eta }_0$ for $(\alpha _1,\ldots ,\alpha _7) \in [0,1]^7$ (N.B., $diag(a_1,\ldots ,a_7)$ is a diagonal matrix whose elements starting in the upper left corner are $a_1,\ldots ,a_7$). Let us assume the invertibility of I. From Eq. (15), we have

$$\begin{aligned}&\sqrt{n}(\varvec{\widehat{\eta }}-\varvec{\eta }_0)\nonumber \\&=-\left[ \frac{1}{n}K(\varvec{\overline{\eta }})\right] ^{-1}\frac{1}{\sqrt{n}} \left. \frac{\partial \ell (\varvec{\eta };\varvec{Y}_1,\ldots ,\varvec{Y}_n)}{\partial \varvec{\eta }} \right| _{\varvec{\eta }=\varvec{\eta }_0}\nonumber \\&=-\left[ \frac{1}{n}K(\varvec{\overline{\eta }})\right] ^{-1}\frac{1}{\sqrt{n}}\sum _{i=1}^{n}\left. \frac{\partial }{\partial \varvec{\eta }}\log h_3(\varvec{Y}_i;\varvec{\eta })\right| _{\varvec{\eta }=\varvec{\eta }_0} \end{aligned}$$

(16)

The first factor on the right-hand side of Eq. (16) can be applied to the law of large numbers because it is divided by the sample size n. By assuming $\varvec{\widehat{\eta }}\overset{p}{\rightarrow }\varvec{\eta }_0$ for $n\rightarrow \infty$, $\varvec{\overline{\eta }}\overset{p}{\rightarrow }\varvec{\eta }_0$ also holds for $n\rightarrow \infty$ . Recalling Eq. (6), we obtain

$$\begin{aligned} \frac{1}{n}K(\varvec{\overline{\eta }})\overset{p}{\rightarrow }-E\left[ \left. \frac{\partial ^2\log h_3(\varvec{Y};\cdot )}{\partial \varvec{\eta }\partial \varvec{\eta }^\mathrm{T}}\right| _{\varvec{\eta }=\varvec{\eta }_0}\right] =I. \end{aligned}$$

(17)

The second factor can be applied to the multivariate central limit theorem because it is divided by $\sqrt{n}$. From Lemma 1 and Eq. (17), we obtain

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{i=1}^{n}\left. \frac{\partial }{\partial \varvec{\eta }}\log h_3(\varvec{Y}_i;\varvec{\eta })\right| _{\varvec{\eta } =\varvec{\eta }_0}\overset{\mathcal {D}}{\rightarrow }N(\varvec{0},I). \end{aligned}$$

(18)

Therefore, by applying Slutsky’s theorem (see e.g., Cramer (1945), p. 254) to Eqs. (17) and (18), the following equation holds.

$$\begin{aligned} \sqrt{n}(\varvec{\widehat{\eta }}-\varvec{\eta }_0)\overset{\mathcal {D}}{\rightarrow }N(\varvec{0},I^{-1}). \end{aligned}$$

Hence, the proof is complete. $\square$

Proof of Theorem 2

By the same analogy with the proof of Theorem 1, we provide a sketch of the proof of Theorem 2. Suppose $\varvec{Y},\varvec{Y}_1,\ldots ,\varvec{Y}_n$ are i.i.d. random vectors of the d-variate FGM distribution. Let us define $\varvec{g}(\varvec{Y}_1,\ldots ,\varvec{Y}_n;\varvec{\eta })$ as follows.

$$\begin{aligned}&\varvec{g}(\varvec{Y}_1,\ldots ,\varvec{Y}_n;\varvec{\eta })\\&=(\frac{\partial \ell _1}{\partial \delta _1}, \frac{\partial \ell _2}{\partial \delta _2}, \frac{\partial \ell _3}{\partial \delta _3}, \frac{\partial \ell _{12}}{\partial \theta _{12}}, \frac{\partial \ell _{13}}{\partial \theta _{13}}, \frac{\partial \ell _{23}}{\partial \theta _{23}}, \frac{\partial \ell }{\partial \theta _{123}})^\mathrm{T}. \end{aligned}$$

Note that $\varvec{g}(\cdot ;\widetilde{\varvec{\eta }})=\varvec{0}$ holds because $\widetilde{\varvec{\eta }}$ is defined as the solution of $\varvec{g}(\cdot ;\varvec{\eta })=\varvec{0}$. By using the mean value theorem for $\varvec{g}(\cdot ;\varvec{{\widetilde{\eta }}})$ at $\varvec{\eta }_0$, we have

$$\begin{aligned} \varvec{0}&=\varvec{g}(\varvec{Y}_1,\ldots ,\varvec{Y}_n ;\widetilde{\varvec{\eta }})\nonumber \\&=\varvec{g}(\varvec{Y}_1,\ldots ,\varvec{Y}_n ;\varvec{\eta }_0)+J(\varvec{\overline{\eta }})(\varvec{{\widetilde{\eta }}}-\varvec{\eta }_0), \end{aligned}$$

(19)

where

$$\begin{aligned} J(\varvec{\overline{\eta }})=\left. \frac{\partial \varvec{g}(\varvec{Y}_1,\ldots ,\varvec{Y}_n;\varvec{\eta })}{\partial \varvec{\eta }}\right| _{\varvec{\eta }=\varvec{\overline{\eta }}}, \end{aligned}$$

and $\varvec{\overline{\eta }}\equiv diag(\alpha _1,\ldots ,\alpha _7) \varvec{{\widetilde{\eta }}}+diag(1-\alpha _1,\ldots ,1-\alpha _7)\varvec{\eta }_0$ for $(\alpha _1,\ldots ,\alpha _7) \in [0,1]^7$. From Eq. (19), we have $J(\varvec{\overline{\eta }})(\varvec{{\widetilde{\eta }}}-\varvec{\eta }_0)=-\varvec{g}(\varvec{Y}_1,\ldots ,\varvec{Y}_n ;\varvec{\eta }_0)$. Thus,

$$\begin{aligned} \sqrt{n}(\varvec{{\widetilde{\eta }}}-\varvec{\eta }_0) =-\left[ \frac{1}{n}J(\varvec{\overline{\eta }})\right] ^{-1}\frac{1}{\sqrt{n}}\varvec{g}(\cdot ;\varvec{\eta }_0). \end{aligned}$$

(20)

The first factor on the right-hand side of Eq. (20) can be applied to the law of large numbers because it is divided by the sample size n. By assuming $\varvec{{\widetilde{\eta }}}\overset{p}{\rightarrow }\varvec{\eta }_0$ for $n\rightarrow \infty$, $\varvec{\overline{\eta }}\overset{p}{\rightarrow }\varvec{\eta }_0$ also holds for $n\rightarrow \infty$ . Recalling Eq. (7), we obtain

$$\begin{aligned} \frac{1}{n}J(\varvec{\overline{\eta }})\overset{p}{\rightarrow }E\left[ \left. \frac{\partial \varvec{s}(\varvec{Y};\varvec{\eta })}{\partial \varvec{\eta }}\right| _{\varvec{\eta }=\varvec{\eta }_0}\right] =D. \end{aligned}$$

(21)

The second factor can be applied to the multivariate central limit theorem because it is divided by $\sqrt{n}$. From Lemma 1 and Eq. (8), we obtain

$$\begin{aligned} \frac{1}{\sqrt{n}}\varvec{g}(\varvec{Y}_1,\ldots ,\varvec{Y}_n ;\varvec{\eta }_0)\overset{\mathcal {D}}{\rightarrow }N(\varvec{0},M). \end{aligned}$$

(22)

Therefore, by applying Slutsky’s theorem to Eqs. (21) and (22), the following equation holds.

$$\begin{aligned} \sqrt{n}(\varvec{{\widetilde{\eta }}}-\varvec{\eta }_0)\overset{\mathcal {D}}{\rightarrow }N(\varvec{0},D^{-1}M(D^{-1})^\mathrm{T}). \end{aligned}$$

Hence, the proof is complete. $\square$