Introduction

Project-based processes are central in resolving major societal challenges [35], from accelerating economic growth through infrastructure development [25, 41] to fostering public resilience through mobilizing emergency resources [38], [47]. World Bank data (2009) indicate that more than 22% of the world’s gross domestic product—equivalent to approximately $48 trillion—relies almost entirely on project-based delivery mechanisms [57]. Despite the importance of delivering projects successfully, many fail to meet their targets [69]. Delays, cost overruns and quality problems are regularly observed across all project domains, from software development [48] and construction [43] to infrastructure [23] and defence [12]. An industry survey reviewed 10,624 projects from 200 companies in 30 countries and across a variety of industries and concluded that only 2.5% of the companies delivered all of their projects successfully [50]. More recently, a review of 1417 IT projects reveals that 236 of them experienced cost overruns of at least 200% and the delivery of these projects was delayed by almost 70% in time [22]. The implications of project failure are expected to increase even further in the future due to their projected 1.5–2.5% annual growth in project value [21].

Research into understanding project failure can be broadly classified into two distinct, yet complementary, strands [52]. This first strand relies on qualitative methods, focusing on mapping the relationships between sociological factors that contribute to project failure, e.g., importance of leadership [59, 65], team communication [45] and corporate culture [55]. This line of research is central in identifying potential relationships that can control project failure (e.g., that quality of the initial planning is correlated with the project performance, contextual task features (i.e., technical complexity, novelty) is correlated with project success [56]. Whilst important, this research strand is generally associated with a multitude of biases such as recollection bias (i.e., information bias in which recalled information is inaccurate) and self-report bias (i.e., behavioral bias in which participants over-report positive results). As a result, these biases challenge the integration of their findings towards more general mitigation strategies against project failure [52].

A second research strand relies on computational methods [4] that model the condition of project failure, from the mechanism by which delay propagates [17] to the propensity of wastefully repeating certain tasks [58]. Under this view, projects are typically modeled as directed acyclic graph, often called activity network. This activity network corresponds to a set of distinct, yet interdependent activities that need to be scheduled and sequenced under a given set of constraints [66].

Using tools from operations research, the first surge of work on project failure focused on simulating an intuitive failure scenario—project-wide delays that arise from delays in completing certain critical tasks [62]. The criticality of these tasks arises from their inclusion in the critical path, which is defined as the sequence of tasks that determines the project duration. As such, a delay of x days in completing a critical task—and assuming that task has zero buffer in relation to its immediate successor task(s)—the project will also be delayed by a maximum of x days [17, 30]. Note the linear nature of this failure scenario, i.e., the project delay can never be higher than the sum of the individual task delays. Prominent methods for evaluating the impact of delay propagation include critical path method [36], program evaluation and review technique [42], and their Monte-Carlo variants.

Subsequent work on project failure has focused on an alternative failure scenario in which changes in task specifications can trigger rework in subsequent, downstream tasks and similarly affect the timely delivery of the overall project. In this case, a relatively minor change in the specifications of a single task can propagate across an entire project, severely affecting the overall project performance. For example, Sosa [60] provides a case where a single, minor change in the specifications of a task impacted nearly a third of all tasks within a project. Similarly, Terwiesch and Loch [63] report a case where a similar change in task specifications resulted in a 20–40% increase in the overall project cost. Additional cases have also been reported by Mihm et al. [46]. In this case, a relatively minor change in the specifications of a single task can propagate across an entire project, severely affecting the overall project performance. This asymmetry between cause and effect suggests that nonlinear effects are in place [46], which is distinct from the linear effects of delay propagation as described in the previous paragraph.

Both failures scenarios—where a delay or a change in the task specification can be the cause of a failure propagating within the project—can be understood within the broader definition of an archetypal dynamical process called ‘cascading failure’. By ‘cascading failure’, we refer to iterative processes in which a single failure leads to subsequent failures, which can amplify the impact of the original failure, eventually leading to system-wide failure [9, 68]. Such cascade dynamics have been noted in a wide range of research domains, including epidemic spreading [49, 53], social contagion [2, 3], and traffic congestion in transportation systems [64], power grid blackouts [8] and financial systemic failure [28].

Work within the project space supports the relevance of this network-oriented view. For example, recent work has made links between project performance and the number of connections between tasks [5, 14, 34], the heterogeneity by which those connections are spread across tasks [33, 61], the necessity of these connections (i.e., “non-redundant” vs. “redundant”) [7] and the variety in the nature of these connections (e.g., functional dependency, information exchange) [5, 67].

Driven by the intersection of these lines of research (i.e., cascading failures and network-oriented project view) recent studies tackled long-lasting project management challenges using failure cascades as the central modeling framework. For example, Ellinas et al. [15] assessed the propensity of a project in promoting conflicts between subcontractors by assessing the different incentives generated by their respective involvement within different cascades of failures. Building on this work, Ellinas [13] and Guo et al. [26] developed broader modeling frameworks to identify certain project network features that influence the exposure of a project to cascading failures. However, this body of work does not provide any actionable mitigation strategies by which a decision maker can contain these failure cascades. They rather assessed the extent to which different project features could contribute to project’s robustness against failure cascades.

To fill this gap, we develop a simple failure cascade model and use it to evaluate the performance of six mitigation schemes. In terms of the cascade model, we build on a popular cascade model by integrating the buffering effect of float between pairs of tasks [24]. We do so by assuming that a large free float between two consecutive tasks lowers the probability that failure in a task impacts its immediate successors. We then use this model on an empirical activity network of 723 tasks and numerically evaluate the performance of six mitigation schemes. Each mitigation scheme relies on some properties of nodes, either structural or temporal. Our overall objective is to identify which node’s property can provide the most effective way for prioritizing which task(s) to be mitigated first. Our results suggest that in a majority of cases, and in contrast to current theoretical arguments, the temporal (i.e., start and end date of each task) rather than the structural properties of the activities (e.g., task connectivity) provides the most efficient way for mitigating failure cascades. This result has implications for decision makers on how to prioritize task mitigation for improving project performance.

Experimental design

Data

We use real-world project data to evaluate the performance of six mitigation strategies. The data are from a large-scale engineering project in the defence domain, were human generated by a team of professional project planners and were used throughout the lifecycle of the project to drive delivery. Specifically, the data set corresponds to a set of planned activities (\(N = 723\)), which we refer to as tasks, that need to be completed to deliver a commercial defence product. The overall duration of the project is 745 days. Each task has a scheduled start and end date and the resolution of time is a day. The dependency between a pair of tasks is represented by a directed edge. There are 1220 directed links in total. The directed edge from task i–j, denoted by \({{e}}_{ij} \in {E}\), indicates that the output of task i, such as information or a physical artifact (i.e., product), is an input to task j. A directed edge from task i to task j implies that task i must be completed before task j starts. Therefore, task j can start only after all tasks that send a directed edge to task j have been completed. Similarly, a failure in task i may directly impact task j, and potentially all following (and reachable) tasks (see Fig. 1). The free float between task i and j is defined as the time difference between the completion\(\tau_{ij}\) of task i and the start of task j [51]. The free float is equivalent to a widely used term, inter-event time [31, 32, 44]. We denote the free float between i and j as \(\tau_{ij}\).

Fig. 1
figure 1

Schematic of an activity network. A rounded rectangle represents a node (i.e., task). The gray rounded rectangles represent the tasks that may fail in response to a failure of the seed node shown in red

Full size image

The 723 activities (nodes) and the 1220 links define the activity network, which is a time-stamped directed acyclic graph. The number of immediate predecessors and successors of each task is equal to the task’s in-degree and out-degree, respectively. The mean in- and out-degrees of a task are equal to 1.69. The in-degree has standard deviation 4.45 and ranges from 0 to 90. A total of 111 nodes out of the 723 nodes have an in-degree of 0. Those tasks are located in the most upstream position in the network; and initiating any of these tasks does not need any other task to be completed beforehand. The out-degree has standard deviation 2.82 and ranges from 0 to 52. A total of 32 nodes have an out-degree of 0; these tasks are located in the most downstream position in the network, and failure of any of these tasks does not cause a cascading failure. The in- and out-degrees obey somewhat long-tailed distributions (Fig. 2a), as is evidenced by their relatively large standard deviations as compared to the mean. The inter-event time has the mean equal to 141.4 days, standard deviation 169.5 days, and ranges from 0 to 670 days. The distribution of inter-event times is shown in Fig. 2b. The duration of task has the mean equal to 62.1 days, standard deviation 112.5 days, and ranges from 1 to 647 days. The distribution of the duration of tasks is shown in Fig. 2c. As time progresses, tasks are completed; the fraction of completed tasks by day is shown in Fig. 2d. The data set of the temporal network of tasks, including the start time and end time of each task, is provided as supplementary information and is available online (see Data availability section).

Fig. 2
figure 2

Distributions of basic properties of the temporal network of tasks. a Survival probability (i.e., probability that the degree is larger than or equal to a specified value) of the in- and out-degrees of the node. b Survival probability of the inter-event time. c Survival probability of the task duration. d Fraction of tasks that have been completed by day t, plotted against t

Full size image

Modeling cascading failures of tasks

We introduce a discrete-time cascading failure model with binary states of the node, which is analogous to the Independent Cascade model [51] and other cascade-failure models [40, 52]. In our model, the probability that a failure propagates from an affected node i to a non-affected downstream neighbor node of node i, denoted by j, is a function of the free float between the two nodes and the values of the two parameters, as we explain in the following.

The final state of node j \(\left( {1 \le j \le N} \right)\) is denoted by \(s_{j} \in \left[ {0,1} \right]\), where ‘0’ and ‘1’ correspond to the non-affected and affected state, respectively. We start the cascade dynamics from an initial condition, where one seed node (which can be any node) is in state 1 and all the other \(N - 1\) nodes are in state 0. During the cascade dynamics, node j may irreversibly switch from state 0 to state 1 if node j has at least one upstream neighbour that is in state 1. Consequently, a node with no upstream neighbors can only be in a state of 1 if and only if it is a seed node.

We determine the final state of each node (and hence the final cascade size) by marking the nodes one by one as follows. Initially, the seed node is the only marked node (i.e., finalized to state 1) in the network. During the course of the following procedure, all nodes that are yet to be marked have state 0. Marked nodes have state either 0 or 1. In each round, we pick an unmarked node j whose all upstream neighbors have been marked. The first node to be marked after the seed node is a node that does not have any upstream neighbor (i.e., in-degree equal to 0) or a node that has the seed node as the only upstream neighbor. To determine the final state of node j (i.e., to mark node j), we assume that the failure of each upstream neighbor of node j, referred to as node i, independently causes node j to fail with probability \(p_{ij}\). Then, we set the final state of node j to 1 with probability

$$P_{j} = 1 - \prod\limits_{{{i; e}_{{ij}} \in E}} {\left[ {\left( {1 - s_{i} } \right) + s_{i} \left( {1 - p_{{ij}} } \right)} \right],}$$
(1)

where \(E\) is the set of links. Otherwise, we set the final state of node j to 0. In Eq. 1, the product term is the probability that node j does not fail, and each factor in the product is the probability that node i does not cause the failure of node j. If \(s_{i} = 0\), this probability is equal to 1. If \(s_{i} = 1\), this probability is equal to \(1 - p_{ij}\). Once the state of node j is determined in this manner, we mark node j and select a next unmarked node such that all its upstream neighbors have been marked. Note that the results do not depend on the order of marking the nodes.

To set the value of \(p_{ij}\), we consider the impact of time between the completion of task i and start of task j, which is called the free float in management literature and inter-event time in network science literature. We denote this quantity by \(\tau_{ij}\). We assume that the probability that the failure of node i causes the failure of node j decreases as \(\tau_{ij}\) increases because a larger \(\tau_{ij}\) indicates that more time is available for containing the effect of task i’s failure on its downstream neighbors [16, 39]. Reducing inter-event times has been suggested to reduce the risk of failure propagation as well [10, 29]. Therefore, we assume that

$$p_{ij} = q_{0} \exp \left( { - \frac{{\tau_{ij} }}{{\tilde{\tau }}}} \right),$$
(2)

where \(q_{0} \in \left[ {0,1} \right]\) and \(\tilde{\tau }\left( { > 0} \right)\) are parameters. Parameter \(q_{0}\) is the probability that task j fails if task i does and there is no spare time (i.e., no free float) between the two tasks, i.e., \(\tau_{ij} = 0\). Equation 2 indicates that if the two tasks are far apart in time, it is not likely that failure of one task triggers failure of a successor task. Parameter \(\tilde{\tau }\) controls the impact of the free float, \(\tau_{ij}\), on the probability that the failure of node i causes the failure of node j. By definition, a large \(\tilde{\tau }\) value yields a small probability that the failure of node i causes the failure of node j, and vice-versa.

Temporal mitigation of cascading failures

Robustness against cascading failures on networks can be engineered via structural or temporal mitigation schemes. Structural mitigation can be deployed when the structure of the network can be changed. For example, in power grids, one can modify the network structure to discourage the onset of large-scale cascades, e.g., by introducing network modules or purposefully fragmenting the network before a cascade happens [27]. However, some networks that are susceptible to cascading failures may not accommodate structural mitigation. In this situation, temporal mitigation, i.e., changing the timing of nodes or links without changing the static network structure, may be deployed without compromising the function of the system. In general, a temporal mitigation scheme can be implemented if nodes or links have timestamps that are relatively flexible. For example, in air traffic networks where nodes and time-stamped links are airports and flights, respectively, delaying flights is probably more feasible than changing the destination of the flights as a preventive measure against cascading failures [1, 20]. Similarly, in project management context, deploying structural mitigation in activity networks is not often practical because a directed edge from task i (e.g., designing a structural column for a building) to task j (e.g., manufacturing that column) indicates that task i’s output is necessary for starting task j, and therefore cannot be amended.

By the construction of our cascade model, increasing an inter-event time is a viable mechanism to reduce the probability that failure propagates from a task to another. Therefore, by postponing the start of a downstream task j, we reduce the probability of it being affected by a failure in its predecessor, task i. We utilize this mechanism to construct mitigation schemes, where we postpone some of the tasks located downstream to the seed node that has failed. Doing so increases some of the inter-event times in the nodes belonging to the out-component of the seed node (i.e., the nodes downstream to the seed node). Therefore, a mitigation scheme is expected to reduce the overall probability that the failure propagates.

A mitigation scheme has to respect the end date of the entire project; no task can be postponed beyond the delivery date of the entire project. Furthermore, any downstream neighbor of task j is only allowed to start after task j has been completed. Therefore, the extent of postponing task j is further constrained by the start date of its downstream neighbours. Note that we allow the end date of task j to coincide with the start date of its downstream neighbor, in which case the inter-event time is equal to zero.

Precisely, the fraction of the nodes in the out-component of the seed node for which we postpone the start time is denoted by \(\gamma \in \left[ {0,1} \right]\). For each mitigation scheme, we first consider the ranking of nodes in the out-component of the seed node. We then sequentially postpone a fraction \(\gamma\) of these nodes in descending order of the rank. When postponing each task i sequentially, we postpone it as much as possible under the following two conditions. First, adjacent tasks must not overlap [37]. In other words, the end date of task i must not exceed the start date of any task j that needs completion of task i. Second, the overall project duration must not be extended. In other words, the end date of task i must not exceed the original delivery date of the project.

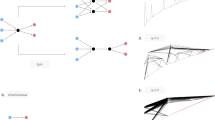
We test six mitigation schemes, in which nodes to be mitigated are ranked based on either the (i) out-degree, (ii) size of out-component (i.e., the number of nodes that are reachable from the node in question), (iii) duration of the task, (iv) start date of the task, (v) end date of the task or (vi) at random. For example, consider the network shown in the upper part of Fig. 3a and assume that node \(v_{1}\) fails. The subscript attached to the nodes in the figure represents the ranking in terms of the out-degree. The figure indicates that node \(v_{3}\) is the first node to be mitigated (i.e., postponed). The amount of maximum postponement that can be applied to node \(v_{3}\) is constrained by the start date of its immediate neighbor, node \(v_{4}\). Therefore, we postpone node \(v_{3}\) such that its new end date is equal to the start date of node \(v_{4}\) (the network shown in the lower part of Fig. 3a). Similarly, node \(v_{5}\) is postponed such that its new end date is equal to the start date of node \(v_{6}\). The same procedure is applied to node \(v_{2}\) and then to node \(v_{6}\). Note that postponing node \(v_{5}\) makes the inter-event time between node \(v_{5}\) and node \(v_{6}\) equal to zero. However, postponing node \(v_{6}\) subsequently increases the same inter-event time. We do not postpone the remaining two tasks with the lowest out-degrees, i.e., \(v_{4}\) and \(v_{7}\), because the fraction of the mitigated nodes, denoted by \(\gamma\), is set to 0.67 for illustration purposes, such that only four out of the six nodes downstream to node \(v_{1}\) can be mitigated. Implementation of three other mitigation schemes on the same network and the same \(\gamma\) value is schematically shown in Fig. 3b–d.

Fig. 3
figure 3

An example illustrating the four mitigation schemes: a out-degree, b start date, c end date and d random. For each mitigation scheme, the top and bottom panels correspond to before and after the mitigation, respectively. Every node is ranked (subscript index) and postponed in that order. The tie is broken uniformly randomly. In all examples, we set \(\gamma = 0.67\) such that four out of the six tasks are mitigated

Full size image

The mitigation scheme is implemented as follows. Once seed node i fails, all nodes reachable from node i along a directed path (i.e., nodes belonging to the out-component of node i), which can fail, are rank ordered based on the node’s score. The score of these nodes is equal to one of the following six quantities: out-degree, size of the out-component (i.e., the number of nodes that are reachable from the node to be scored), duration of the task, start date of the task, end date of the task, or an entirely randomly drawn value. When multiple nodes have identical scores, we break the tie by ranking the nodes having the same score in a uniformly random order.

We denote by \(\tilde{V}\) the rank-ordered set of the nodes downstream to node i. In the example shown in Fig. 3a, in which the rank is determined according to the out-degree of the task, we obtain \(\tilde{V}\) \(= \left\{ {v_{3} ,v_{5} ,v_{2} ,v_{6} ,v_{4} ,v_{7} } \right\}\). Parameter \(\gamma \in \left[ {0,1} \right]\) specifies the fraction of nodes in \(\tilde{V}\) that are to be mitigated. In Fig. 3a, we set \(\gamma = 0.67\). Therefore, the four highest-ranked nodes out of the six nodes, i.e., \(v_{3} ,v_{5} ,v_{2}\) and \({ }v_{6}\), are mitigated. Node \(v_{3}\) is first postponed until its end date coincides with the start date of its downstream neighbor \(v_{4}\). Next, the same postponement process is applied to node \(v_{5}\), node \(v_{2}\) and then node \(v_{6}\). The temporal network after the mitigation is shown in the lower part of Fig. 3a.

Performance measures for mitigation schemes, R 1 and R 2

We evaluate the performance of the six mitigation schemes in terms of their ability of containing cascading failures. These mitigation schemes attempt to increase \(\tau_{ij}\) for some i and j to reduce the probability that a failure cascade progresses. Our focus is on the impact of the parameters that control the cascading dynamics \(\left( {q_{0} {\text{ and }} { }\tilde{ \tau }} \right)\) and the fraction of the tasks to be postponed \(\left( \gamma \right)\).

We measure the performance of each mitigation scheme in terms of two quantities. The first quantity, denoted by R1, is defined as the cascade size that stems from a seed node when the mitigation scheme is implemented, divided by the cascade size when there is no mitigation, averaged over all seed nodes. Quantity R1 captures the relative impact of mitigation in the sense that the contribution of mitigating a large cascade is equivalent to that of mitigating a small cascade. The second quantity, denoted by R2, is defined as the cascade size averaged over all seed nodes when the mitigation is applied, which is then divided by the cascade size averaged over all seed nodes when no mitigation is applied. Quantity R2 captures the absolute impact of mitigation in the sense that mitigating a large cascade is considered to be more valuable than mitigating a small cascade. A small R1 or R2 value indicates that the mitigation scheme is efficient.

For the given values of \(q_{0}\), \(\tilde{\tau }\), \(\gamma\), and the given seed node, we ran the cascading dynamics 100 times (except for Supplementary Fig. 1, for which we ran the simulation 300 times). In the figures, we show the average values of the observables over all runs.

Results

We first focus on the unmitigated failure cascades to understand the effect of the free parameters of our model \(q_{0}\) and \(\tilde{\tau }\) on the impact of failure. By definition, higher values of \(q_{0}\) and \(\tilde{\tau }\) increase the probability of a single activity failing, resulting in a larger average cascade size (Fig. 4a). In addition, a higher value of \(\tilde{\tau }\) increases both the average cascade size and the probability of encountering a cascade of a given size (Fig. 4b). Activity networks are prone to large failure cascades, where the failure of a single activity can impact a disproportionately large number of subsequent activities. The heavy-tailed distribution of all cascade sizes highlights the disproportionate nature of these cascades, with a majority of failure cascades impacting a small number of tasks and a small number of failure cascades impacting many tasks. For example, when the probability that task j fails if task i does and there is no spare time between them (i.e., \(q_{0} = 1\)) and time dependence is low (i.e., \(\tilde{\tau } = 10^{3}\)), the average cascade size is ~ 7 (Fig. 4a), whilst the largest cascade size is over 100 (Fig. 4b).

Fig. 4
figure 4

a Average cascade size as a function of \(q_{0}\) for four values of \(\tilde{\tau }\). b Survival probability of observing a cascade of size \(x\), where we set \(q_{0} = 1\) (i.e., worst case scenario)

Full size image

In the case where we mitigate all downstream tasks (i.e., \(\gamma = 1\)), the mitigation scheme based on the end date of the task outperforms the other five mitigation schemes. This is the case in terms of both performance measures R1 (Fig. 5) and R2 (Fig. 6). Quantities R1 and R2 measure the relative and absolute reduction in the cascade size by a mitigation scheme. These figures also show that apart from the mitigation scheme based on the end date of the task, the random mitigation scheme outperforms the other four mitigation schemes. The relative ranking of the six mitigation schemes is consistent in the whole range of \(q_{0}\) and \(\tilde{\tau } \in \left\{ {1, 10, 10^{2} ,10^{3} } \right\}\), except for \(\tilde{\tau } = 10^{3}\), where there are some rank changes presumably due to random fluctuations. Note that as \(\tilde{\tau }\) tends large (\(\tilde{\tau } \ge 10^{3}\)), \(p_{ij}\) is approximately equal to \(q_{0}\) regardless of the size of \(\tau_{ij}\) and regardless of the mitigation scheme. Therefore, R1 and R2 converge to 1 for any \(q_{0}\) as \(\tilde{\tau }\) increases (see Supplementary Fig. 1 for numerical results with \(\tilde{\tau } = 10^{4}\) and \(\tilde{\tau } = 10^{5}\)).

Fig. 5
figure 5

Performance of the six mitigation schemes in terms of R1, as a function of \(q_{0}\). a \(\tilde{\tau } = 1\). b \(\tilde{\tau } = 10\). c \(\tilde{\tau } = 10^{2}\). d \(\tilde{\tau } = 10^{3}\). We set \(\gamma = 1\)

Full size image
Fig. 6
figure 6

Performance of the six mitigation schemes in terms of R2, as a function of \(q_{0}\). a \(\tilde{\tau } = 1\). b \(\tilde{\tau } = 10\). c \(\tilde{\tau } = 10^{2}\). d \(\tilde{\tau } = 10^{3}\). We set \(\gamma = 1\)

Full size image

To investigate the entire parameter space, we identified the mitigation scheme that was the most efficient, i.e., yielding the smallest value of R1 and R2, when we varied \(q_{0}\), \(\tilde{\tau }\) and \(\gamma\). The results in terms of R1 are shown in Fig. 7. When there is little variation between the best and worst performing schemes (<1%; arbitrarily chosen; white regions labeled ‘Unspecified’ in Fig. 7), we argue that no best mitigation scheme exists. Figure 7 reveals two parameter regimes. First, when \(\gamma \ge 0.8\), the mitigation scheme based on either the out-degree, duration, end date or at random performs the best, depending on the specific combination of \(\gamma\) and \(q_{0}\) values. As \(\tilde{\tau }\) increases from 1 to \(10^{3}\), the mitigation scheme based on the end date tends to be consistently the best in this parameter regime (Fig. 7d). Second, when \(\gamma < 0.8\), the mitigation scheme based on the start date tends to be the best performing mitigation scheme across the entire range of \(q_{0}\) and \(\tilde{\tau }\). The results in terms of R2 (Supplementary Fig. 2) are similar to those in terms of R1 (Fig. 7).

Fig. 7
figure 7

Best performing mitigation scheme in terms of R1 in the parameter space spanned by \(q_{0}\) and \(\gamma\). a \(\tilde{\tau } = 1\). b \(\tilde{\tau } = 10\). c \(\tilde{\tau } = 10^{2}\). d \(\tilde{\tau } = 10^{3}\)

Full size image

Discussion

We modeled project failures as cascading failures on networks composed of tasks constituting the project. The model incorporates both structural and temporal features of activity networks of projects. We implemented six mitigation schemes by postponing a fraction \(\gamma\) of tasks downstream to the task that has failed. When one was allowed to postpone all the tasks downstream to the task that has failed, our numerical results indicated that it was more efficient to prioritize task mitigation according to the end date of each task than the other five mitigation schemes. When one was allowed to postpone a relatively small fraction of tasks, it was generally more efficient to postpone tasks based on their start date. Some additional cases existed where the mitigation scheme based on the out-degree or duration of the task was the most efficient. Specifically, when \(\gamma\) is large, either the mitigation scheme based on the out-degree, that based on the duration, or that based on the end date was the best. These numerical results suggest that, in a majority of the parameter region that we have explored, temporal features of the tasks, such as the duration, start and end date of the task, may be more important than structural features, such as the out-degree of the task, for preventing large-scale cascading failures of projects.

The present results suggest that the importance of tasks should not only be ranked based on the impact (i.e., the size of the cascade failure) that the failure of a single task can cause (e.g., project delay) but also based on the extent to which the impact can be mitigated. We provided proxies for identifying important tasks in the sense of mitigation using a task’s start and end date. Using these proxies, decision makers can focus on proactively managing these tasks. One way for incorporating this in practice is to relax the typically strict constraints in terms of start (and end) date for some tasks by, for example, removing monetary penalties for such delays [19]. Relaxing such penalties can introduce planning flexibility for decision makers to purposefully postpone certain tasks, reducing the overall exposure of the project to cascading failures.

This work is aligned with other, domain-specific research strands that focus on the broader objective of improving project performance. For example, Eppinger et al. [18] focused on modular and decomposable projects, where links between activities can be modified to some extent [18]. By doing so, the authors were able to re-sequence certain activities to reduce risk and improve overall project performance [18]. Based on this idea, Baldwin and Clark [6] deployed task re-sequencing for optimizing project modularity, which was argued to be able to reduce project risk [6]. In these scenarios, structural mitigation is deployed because there are no hard constraints assumed on the links between activities, so that the links can be rewired. In our case, we assumed temporal mitigation due to the constraint that the network structure, which represents precise inter-dependency among the tasks, is not allowed to be changed. Despite the contextual differences, their work and ours have the common thread of utilizing network structure and complex systems thinking for improving project performance, which we believe is a promising research direction.

Our modeling framework has some limitations. First, our analysis has focused only on the benefits of deploying mitigation in the form of postponing the start date of tasks. However, postponing tasks may increase the number of active tasks on particular days, which is generally associated with poor project performance due to an increased cost or decreased quality [11, 37, 58]. In addition, postponing tasks is impossible when a sequence of tasks has no float between any consecutive pair of tasks, which is a type of critical path [54]. Future work should consider this drawback in conjunction with the benefits potentially gained through the mitigation mechanisms proposed in the present study. Second, from a methodological standpoint, our approach is limited by the single pass in which mitigation is applied to tasks. Consider the example shown in Fig. 3a, in which node \(v_{5}\) was postponed before node \(v_{6}\) was. In this case, the amount of postponement is constrained by the start date of node \(v_{6}\). Postponing node \(v_{6}\) at a later stage opens up the opportunity for node \(v_{5}\) to be further postponed, which is currently not exploited. One can exploit this opportunity to explore further improvements in mitigation efficiency. Third, a mitigation scheme can be classified into passive and active. In a passive mitigation scheme, one modifies the structure or time stamps of the activity network before a cascade is possibly seeded. In contrast, in an active mitigation scheme, one modifies the activity network while a cascade is progressing. In the present study, we focused on active mitigation schemes. Carefully planning the start time of each task, given, for example, the network structure and the possibility of different tasks to fail with different probabilities, may consist in a plausible passive mitigation scheme on the activity network. This topic also warrants future work. Fourth, we do know have mechanistic understanding of why one mitigation scheme works better than another. To clarity this requires a more systematic investigation, possibly involving multiple data sets, which is beyond the scope of the present study.

In addition, our methodology hints to the possibility of mitigation having unintended negative effects. In the example shown in Fig. 3a, the probability that the failure of node \(v_{1}\) propagates to node \(v_{2}\) has been reduced because \(\tau_{{v_{1} v_{2} }}\) has been increased. This is a positive effect of mitigation that we have intended. However, in the same example, the probability that the failure of node \(v_{2}\) propagates to node \(v_{3}\) has been increased compared to the case of the unmitigated activity network, because the mitigation has decreased \(\tau_{{v_{2} v_{3} }}\). This is a negative effect of mitigation that we have not intended.

Despite these and other possible limitations, the present modeling framework serves as a stepping stone for future work. It opens new pathways of exploring whether causal relationships exist between structural and/or temporal features of temporal networks of tasks and mitigation effectives and efficiency.