Introduction

Over the last two decades, microreactors have been deployed for a large number of applications, from organic reactions [1] to material synthesis [2, 3]. Microreactors present high heat and mass transfer rates associated to their high surface to volume ratio and small diameters in the range of hundreds of micrometres [4, 5]. It is also due to these properties that they normally operate at low Reynolds numbers under laminar flow. Mass transfer under laminar flow is dominated by diffusion, which even with short mixing distances associated to small diameters, is normally slow compared to convection [6]. Most of the chemical processes require the initial mixture of two or more streams and the efficiency of such mixture and the mixing time can affect the selectivity [1] and product quality [7, 8].

Due to the importance of mass transfer, the fluid dynamics inside batch [9] and flow reactors [10] are normally carefully considered in order to understand the mixing mechanisms and efficiency. In flow reactors, the mixers (point where different streams are mixed together) are normally overlooked due to the short residence time within them (normally within ms). However, different patterns of concentration distribution induced by mixers greatly affect the mixing efficiency in downstream reactors. Experimental research methods to investigate mass transfer efficiency such as the Villermaux-Dushman reaction [11] and the experimental determination of concentration distribution using tracers [12, 13] are difficult to deploy in such short times and small length scale. In this context, computational fluid dynamic calculations based on the Lagrangian scalar transport equations [14] can provide key information of the mixing efficiency. To date, mainly T-mixers with rectangular cross sections and jet flow have been studied systematically. As the Reynolds number increases from 1 to 240, the flow field varies from strict laminar flow to vortex and engulfment flow. Higher Reynolds numbers lead to unstable flow field [15]. However, T-mixers and Y-mixers with circular channel are commercially available but rarely studied.

Different studies have modified the inlet configuration of mixers to enhance mixing efficiency. For example, in contrast to a normal rectangular T-mixer with two opposite inlets (called jet flow), a T mixer with non-aligned tangential inlets displays higher mixing efficiency within a wide range of Reynolds number, by creating a vortex where both streams intertwine with each other [16, 17]. In addition, cyclone mixers, with multi tangential inlets, have the shortest published mixing time of 160 ns by far [18, 19]. Parametric studies of the mixing efficiency of cyclone mixers have been carried out experimentally, by monitoring the concentration distribution of fluorescence dye [18]. Concentration profiles captured by fluorescence microscope indicates high mixing efficiency at a low Reynolds number of 3.2 inside a cyclone mixer with 8 inlets [20]. Similarly, a cyclone mixer with 16 small area inlets exhibits high mixing efficiency [21]. Kolbl et al. concluded that the cyclone mixer with two inlets has better mixing effect than the one with four inlets [22]. Despite the numerous studies on cyclone mixers [21,22,23], the systematic study is hindered by the difficulties of experiments and the lack of accurate simulation technique.

In this work, we present a systematic evaluation and comparison of the different widely adopted mixers, T- and Y- mixers with different flow patterns as well as the advanced fluid dynamic guided design of cyclone mixers for enhanced mixing efficiency with mixing potentials one order of magnitude higher than the commercial configurations. Herein, we demonstrate that inlet cross section area and thus, resulting velocity is a key design parameter to predict mixing efficiency.

Methods

Model development and validation

In order to quantify the mixing efficiency in mixers under steady state, a number of simulations were set-up evaluating the mixing of streams with equal volumetric flowrate. Solutions of 1 mM aqueous Rhodamine B solution and pure water were considered. Three steps were needed to accurately simulate the concentration profiles of Rhodamine B in micromixers [14].

Velocity field-mathematic model

The first step was to calculate the velocity field by solving Navier-Stokes equation (Eqs. 1–2) with Ansys Fluent 2019 R3, where ρ represents density, \( \overrightarrow{u} \) is the velocity vector, t is time, and μ denotes viscosity. In all simulations, all inlets of a mixer had an equal volumetric flowrate. The fully developed parabolic velocity profile for a circular inlet channel was defined by user defined functions, while the velocity profile for a rectangular inlet was depicted by Eq. 3, where h and w denote the height and width of a rectangular inlet channel, l1 and l2 represent the distance between a point and the height or width edge, Uinlet was the average velocity of the inlet channel. Outlet pressure was set as 0 gauge pressure. In this paper, the Reynolds number is defined in the outlet channel as Eq. 4, where U is the average velocity in the main channel.

$$ \nabla \cdotp \overrightarrow{u}=0 $$
(1)
$$ \rho \frac{D\overrightarrow{u}}{Dt}=-\nabla p+\mu {\nabla}^2\overrightarrow{u} $$
(2)
$$ {u}_{inlet}=36\frac{l_1{l}_2\left(h-{l}_1\right)\left(w-{l}_2\right)}{h^2{w}^2}{U}_{inlet} $$
(3)
$$ \mathit{\operatorname{Re}}=\frac{\rho dU}{\mu } $$
(4)

Velocity field-discretization schemes and algorithm

High quality mesh was drawn by the O-grid tool of ICEM software for circular channel. More than 5 million cells were used for all simulations. Second order and second order upwind schemes were used for pressure and momentum discretization, respectively. Least squares cell-based method was employed to evaluate the gradient. The Coupled scheme provided by Fluent was used to solve the Navier-Stokes equation, which iterates the pressure field and velocity field simultaneously. The convergence tolerance was set as 10−5.

Convection

Then backward particle tracking was adopted to simulate the convection contributed concentration profile. The method was based on Lagrangian scalar transport equation (Eq. 5), rather than Eulerian scalar transport equation (Eq. 6). An array of sampling points were set on the interested cross section of the channel as shown in Fig. S1b. The reversed pathlines were traced (tolerance 10−4) starting from the sampling points to the nearest plane with a known tracer concentration, i.e. the planes in both inlet channels with 1 mm distance from the centre of the mixer. Then the traveling time, T, of the sampling particle along the reversed pathline and initial concentration CA0 of each sampling particle were obtained. Typically, 200*200 sampling points were set in the array.

Diffusion

In the last step, diffusion was estimated by solving Lagrangian scalar transport equations. However, the diffusion rate along the pathline is unknown, which was estimated by the diffusion rate on the cross sectional plane as Eq. 7 and Eq. 8, neglecting the axial diffusion. Thus, the concentration of internal sampling points are functions of concentrations of their neighbouring sampling points as Eq. 8.

$$ \frac{D{C}_A}{Dt}=D{\nabla}^2{C}_A $$
(5)
$$ \frac{\partial {C}_A}{\partial t}+\overrightarrow{u}\cdotp \nabla {c}_A=D{\nabla}^2{C}_A $$
(6)
$$ {C}_A={C}_A^0+D\int {\nabla}^2{C}_A dt\approx {C}_A^0+ DT\left(\frac{\partial^2{C}_A}{\partial {\mathrm{x}}^2}+\frac{\partial^2{C}_A}{\partial {\mathrm{y}}^2}\right) $$
(7)
$$ \frac{\partial^2{C}_A}{\partial {\mathrm{x}}^2}+\frac{\partial^2{C}_A}{\partial {\mathrm{y}}^2}=\frac{C_{i+1,j}+{C}_{i-1,j}+{C}_{i,j+1}+{C}_{i,j-1}-4{C}_{i,j}}{dl^2} $$
(8)
$$ {C}_{p,q}=0.5\left(\ {C}_{p,q-1}+{C}_{p+1,q}\right) $$
(9)
$$ {C}_{m,n}={C}_{m,n-1} $$
(10)

where CA is the concentration of the tracer, dl is the distance between two sampling points. Cp,q in Eq. 9 denotes the sampling points on the corner (Fig. S1b), which was estimated by the average of two neighbouring sampling points. Cm,n in Eq. 10 represents the sampling point on the edge, whose concentration was estimated by its neighbouring sampling point (Fig. S1b).

A linear equation group, describing the concentrations of each sampling points, was formed which was solved in Matlab to obtain the concentration distribution on the cross section (Fig. S1c).

The method is validated by the experimentally characterised concentration distributions inside a T-mixer by planar laser induced fluorescence [13] and a cyclone mixer [18] as shown in Fig. S1 and Fig. S2. For comparison purposes, the concentration profile was also calculated by default Eulerian scalar transport equation and third order Monotonic Upstream-centered Scheme for Conservation Laws (MUSCL) method was used for the discretization. The convergence tolerance was set as 10−6.

Fig. S1d, e and f clearly show that the novel method based on backward particle tracking has much higher accuracy than the commercial software. The commercial software uses Eulearian species transport equation to calculate the concentration field. However, the numerical error, also known as numerical diffusion, arising from the discretization of the flow field, causes overestimated mixing efficiency [14, 24]. Thus, the novel method is adopted to study the mixing efficiency in mixers.

Quantification of mixing efficiency and mesh independency test

Mixing index and mixing potential are adopted to quantify mixing efficiency. Mixing index is defined on a cross sectional plane as Eq. 11 [14, 15]. σ2 represents the concentration variance on the cross section, and σ2max is the maximum concentration variance. \( \dot{V_1} \) denotes the volumetric flowrate of the stream with the tracer, while \( \dot{V_2} \) represents the volumetric flowrate of the stream without the tracer. CA denotes the concentration of tracer, and \( \overline{C_A} \) represents the average concentration after perfect mixing. CA,max represents the maximum concentration of the tracer in the system, i.e. at the inlet. up is the velocity component perpendicular to the cross section, and A is the area. Mixing index has a range of 0 to 1, where 0 implies totally segregated while 1 means perfectly mixed.

Mixing potential is used to quantify the specific contact area between two streams as Eq. 12 [24]. f is the normalized concentration of tracer, and ∇ f is normalized concentration gradient. \( \dot{V} \) denotes the total volumetric flowrate. It is important to note that mixing potential is an important parameter to quantify the efficiency of mixing. Mixing potential is a measurement of the interface between two steams thus, it has a null value before the two streams meet, and reaches 0 again when mixing completes since there is no interface by then. The key to achieve high mixing efficiency is to reach high mixing potential as soon as possible to create a high contact area to enhance diffusion between two streams.

$$ {\displaystyle \begin{array}{c} MI=1-\sqrt{\frac{\sigma^2}{\sigma_{max}^2}}\\ {}\mathrm{with}\kern0.3em {\sigma}^2=\frac{\int_A{\left({C}_A-{\overline{C}}_A\right)}^2{u}_p dA}{\int_A{u}_p dA}\\ {}{\sigma}_{max}^2=\frac{\int_{\dot{{\mathrm{v}}_1}}{\left({C}_{A,\mathit{\max}}-{\overline{C}}_A\right)}^2d{\dot{\mathrm{V}}}_1+{\int}_{\dot{{\mathrm{v}}_2}}{\left(0-{\overline{C}}_A\right)}^2d{\dot{\mathrm{V}}}_2}{{\dot{V}}_1+{\dot{V}}_2}\end{array}} $$
(11)
$$ MP=\frac{\int_{\dot{V}}\left\Vert \nabla f\right\Vert d\dot{V}}{\dot{V}}=\frac{\int_A\left\Vert \nabla f\right\Vert {u}_p dA}{\int_A{u}_p dA}\kern0.5em \mathrm{with}\ f=\frac{C_A}{c_{A,\mathit{\max}}} $$
(12)

Mesh independency test was carried out to prove that 5 million cells are enough for the simulation as shown in Fig. S3 for a T-mixer and Fig. S4 for a cyclone mixer. The number of sampling points is related to the resolution of concentration profile. Fig. S3 and Fig. S4 indicate that 200*200 sampling points are enough for the T mixer and cyclone mixer. Thus, 200*200 sampling points are adopted for T- and Y-mixers. However, due to the complex concentration distribution pattern in cyclone mixers, 300*300 sampling points are conservatively adopted for cyclone mixers.

Results and discussion

A systematic analysis and comparison of the mass transfer mechanism and efficiency of a range of widely available mixers was carried out including Y-mixers and T-mixers. Both, square and circular cross sections were considered as both are commercially available. For the T-mixers, two different flow patterns were also considered, namely jet flow, where the inlet streams are opposite to each other, and cross flow, where the inlet streams are perpendicular to each other.

The fluid dynamics and mass transfer of each configuration was evaluated using the Navier-Stokes equation available on ANSYS Fluent combined with a backward particle tracking approach as described in the experimental section [14], to avoid the overestimation of the diffusion component by the Eulerian approach in what is called numerical diffusion. Figure 1 shows the geometry and the concentration profile of the different mixers at a given distance of 5 mm from the inlet as a function of Reynolds number. In Y-mixers, mass transfer is dominated by diffusion with negligible convection, independent of the geometry of the cross section (circular or square) and the Reynold number within the studied range (Fig. 1a and b respectively). At the position of 5 mm, the mixing potential is ~1700 m2/m3 and ~ 1400 m2/m3 in the circular and square Y-mixers, respectively. T-mixers with circular and square cross section with jet flow (Fig. 1c and d) present a similar low mass transfer efficiency than the Y-mixers at all Reynolds numbers, except for the square cross section T-mixer at Re 300 where engulfment of the two inlet streams takes places promoting mixing by convection in addition to diffusion (Fig. 1d). Interestingly, the mixing index in this case is one order of magnitude higher in the square cross section than the circular one. In this case at Re 300, the mixing potential is 1600 m2/m3 and 13,020 m2/m3 for the circular and square T-mixers respectively with jet flow. Such engulfment is however present at Re above 100 in T-mixers with cross flow, both with square and circular cross sections (Fig. 1e and f). As a consequence, the mixing potential in the circular T-mixer with jet flow increases from 1700 m2/m3 to 6200 m2/m3 as the Re increases from 10 to 300. Similarly, the mixing potential in the square T-mixer grows from 1400 m2/m3 to 5300 m2/m3 in the same Re range.

Fig. 1
figure 1

Geometries and concentration profiles at 5 mm of different conventional mixers a. Y-mixer with circular cross section, b. Y-mixer with square cross section, c. T-mixer with circular cross section and jet flow, d. T-mixer with square cross section and jet flow, e. T-mixer with circular cross section and cross flow, d. T-mixer with square cross section and cross flow. All mixers have 1 mm of diameter or equivalent, 3 mm inlet branched channel and 10 mm of total length. Conditions: each inlet has equal flowrate with developed velocity profile, diffusion coefficient 2.8*10−10 m2/s

Full size image

It is important to notice that in all cases, diffusion dominated mass transfer increases at low Reynolds numbers due to the increase in residence time at the given position of 5 mm. In these simulations, both inlets have an equal flowrate. However, the concentration profiles can also be affected by the ratio between the flowrates in each inlet [8].

To better understand the formation of stream engulfment, Fig. 2a (and Fig. S1) shows the evolution of the concentration profiles in the T-mixer with square cross section and jet flow. One can observe that stream engulfment is generated as soon as both inlet streams meet each other promoted by the mixer’s geometry driven by a phenomenon called Kelvin-Helmholtz instability [13, 25]. More interestingly, the concentration profile does not change any further after 6.5 mm under the studied conditions. From that point forward, mass transfer is dominated by diffusion only, limiting the maximum mixing efficiency that this conventional mixer can offer. As such, Dreher et al. stressed the importance of careful designs of downstream channel to further enhance mixing [15]. Figure 2b shows the corresponding evolution of the mixing index and mixing potential. The mixing potential plateaus after 6.5 mm due to the stagnation of convection. On the other hand, mixing index further increases with position due to diffusion. It is important to highlight that the increase of mixing index is higher as higher the value of mixing potential (i.e. higher contact area of both streams per unit of volume).

Fig. 2
figure 2

a. Evolution of the concentration distribution profile in a T-mixer with square cross section and jet flow 1 mm of equivalent diameter, 3 mm inlet branched channel and 10 mm of total length, b. Corresponding mixing index and mixing potential as a function of length. c. Evolution of the concentration profile in a cyclone mixer with four inlets. d. Corresponding mixing index and mixing potential as a function of length. Conditions: each inlet of the T mixer has equal flowrate of 1.50*10−7 m3/s with developed velocity profile, each inlet of the cyclone mixer has equal flowrate of 5.89*10−8 m3/s with developed velocity profile, outlet Re 300, diffusion coefficient 2.8*10−10 m2/s

Full size image

Modifying the inlet configuration by shifting the relative position of the inlet streams enhances the engulfment of the streams. Instead of introducing the streams perpendicular to the mixer (T-mixer), streams can be introduced tangentially in what is normally called cyclone mixers due to their resemblance to the inlet stream of conventional cyclones used for separation of fine particles [26]. Figure 2c shows the corresponding evolution of the concentration distribution profile in a cyclone mixer with four inlet streams. In comparison to the T-mixer counterpart, the convection continues to contribute to mass transfer for longer distances. Mixing efficiency is considerably higher than in the square T-mixer, with mixing index being 34% higher and mixing potential being 80% higher at 9.5 mm position (Fig. 2d). More interestingly, both parameters continue increasing from the entrance to up to 9.5 mm in comparison to the 6.5 mm of the T-mixer with square channel.

In order to pursue higher mixing efficiency and better understanding, a parametric study of cyclone mixer is carried out, including the effect of Re, inlet area and inlet shape. Figure 3 shows the concentration profiles at a position of 5 mm of a circular cyclone mixer with 4 inlet streams as a function of Reynolds number. One can observe the onset of the rotation of the fluid even a very low Reynolds number of 20 (Fig. 3a). This engulfment phenomenon is clearly visible at Reynolds of 100 (Fig. 3b) and further enhanced as Reynolds increases (despite the consequently lower residence time) (Fig. 3c-d). At Reynolds of 300, the mixing potential is ~22,500 m2 m−3 compared to the ~13,020 m2 m−3 achieved in the square T-mixer with jet flow under the same conditions (Fig. 3f). Although the mixing index is relatively similar (0.0744 and 0.0683 respectively), as mentioned above, the magnitude of diffusion increases proportional to the mixing potential, making the mixing more efficient.

Fig. 3
figure 3

Concentration profiles at 5 mm of a cyclone mixer with circular cross section and 4 square cross section inlets (0.98 mm * 0.50 mm, Fig. 2c) as a function of Reynolds number a. 20, b. 100, c. 180, d. 300 and e. normalised axial (Vz) and tangential (Vy) velocities by the axial velocity at the line z = 5 mm and y = 0 mm. F. Corresponding mixing index ( ) and mixing potential ( ) as a function of Reynolds number. Conditions: each inlet has equal flowrate with developed velocity profile, diffusion coefficient 2.8*10−10 m2/s

Full size image

Similarly to above, the rotation of the fluid is created by the inlet configuration of the mixer as evidenced by the normalised velocity profile (Fig. 3e). While the axial velocity plateaus from its characteristic parabolic profile as the Reynold number increases, the tangential velocity increases with Reynolds in a bimodal form, taking the centre of the channel as the rotation centre. Increasing Reynolds number leads to higher rotation angles, similar effect to the one observed in the cyclone separations created by the angular velocity of the inlet stream [27].

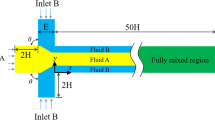
To investigate the effect of the angular velocity on the mixing efficiency, the configuration of the cyclone mixer can be further optimised by varying the cross section area of the inlet streams, in other words, varying inlet average velocity while keeping the total volumetric flowrate constant. Figure 4a shows the geometry of the considered 4 inlet cyclone mixer for the study, depicting the height and width of the rectangular inlet cross section. For a given flowrate, decreasing the cross section area of the inlet increases the average velocity which is translated into a sharp increase of the mixing index and mixing potential (Fig. 4c). It is important to note that the secondary x-axis representing the inlet velocity is not linear. This decrease in mixing efficiency associated to lower inlet velocity is related to the velocity profiles created by the cyclone configuration as mentioned above. As the average inlet velocity increases, the axial velocity plateaus, developing a bimodal shape at very high velocity values of 0.2863 m s−1. The origin of the bimodal distribution is believe to be related to the tangential velocity component which substantially increases with the average inlet velocity (Fig. 4d). As a result, the concentration distribution profiles shown in Fig. 4e demonstrate the higher mixing efficiency achieved by promotion of convection by fluid rotation as the average velocity increases.

Fig. 4
figure 4

a. Typical configuration of a circular cyclone mixer (1 mm diameter) with four inlet streams with rectangular cross sections (0.98 mm * 0.50 mm), b. A cyclone mixer with two inlets (0.98 mm * 0.50 mm), c. Corresponding mixing index ( ) and mixing potential ( ) at 5 mm as a function of cross section inlet area/inlet average velocity d. Normalised radial (Vx), axial (Vz) and tangential (Vy) velocities as a function of cross section inlet area/inlet average velocity, e. Concentration profiles at 5 mm as a function of cross section inlet area/inlet average velocity and f. The concentration profile at 5 mm in the cyclone mixer with two inlets. Conditions: each inlet has equal flowrate of 3.50*10−8 m3/s with developed velocity profile Re 180, diffusion coefficient 2.8*10−10 m2/s

Full size image

For further comparison, a cyclone mixer with two inlets (Fig. 4b) was also simulated with a total inlet area of 0.49 mm2 (0.98 mm*0.5 mm*2 inlets). Two different types of comparison can be done with respect to cyclones of four inlets. Keeping constant the inlet area (0.49 mm2, Fig. 4e and f), the average velocity is therefore double in the cyclone with two inlets than that with four. Interestingly, mixing index and mixing potentials in the same order of magnitude are achieved. The reason behind this is due to the considerably higher tangential velocity of the former one compared with the latter one as shown in Fig. 4d, but lower initial contact area due to smaller stream number of two. Keeping constant the average inlet velocity (0.1431 m s−1) shows a similar axial and tangential velocity components in both cases however, the mixing index and mixing potential are almost double in the four inlet system than in that with two inlets. The reason behind this is due to the decrease of the contact area between the streams when the number is decreased.

To further demonstrate the determining effect of the average velocity on the rotation of the fluid in cyclone mixers and consequently in the mixing efficiency, the height/width ratio of the inlet cross section was varied by keeping the cross section area constant. Figure 5a shows the concentration profiles for different height/width ratios. Despite of presenting similar mixing efficiency in terms of mixing index and mixing potential (Fig. 5b), the concentration profiles show that the rotation of the fluid is also affected by the inlet configuration geometry. For example, using a square inlet cross section (i.e. equal height and width) leads to a spiral type rotation while increasing the height to width ratio concentrates the rotation to the centre of the channel.

Fig. 5
figure 5

a. Concentration profiles at 5 mm of 4 inlet cyclone mixers and b. Corresponding mixing index and mixing potential as a function of the height/width ratio of the rectangular inlet cross section. Conditions: each inlet has equal flowrate of 3.50*10−9 m3/s with developed velocity profile, total cross section inlet area 0.49 mm2, inlet velocity 0.0716 m/s, Re 180, diffusion coefficient 2.8*10−10 m2/s

Full size image

To identify the key design parameter affecting mixing efficiency, all the studies presented above with varying Reynolds numbers, inlet areas and average inlet velocities for the cyclone mixers with four inlets were compared simultaneously. A clear direct relationship is presented between both mixing index and mixing potential with respect to average inlet velocity as shown in Fig. 6a and b. These results show, for the first time to the best of our knowledge, that inlet velocity is the key design parameter and it should be increased to increase the mixing efficiency. Such increase can be achieved by increasing Reynolds number or decreasing cross sectional inlet area indistinguishably.

Fig. 6
figure 6

Relationship between inlet average velocity and mixing efficiency expressed as a. mixing index (by changing Inlet shape, Inlet area, Re) and b. mixing potential (by changing Inlet shape, Inlet area, Re) at 5 mm for 4 inlet cyclone mixers. Conditions: each inlet has equal flowrate developed velocity profile, diffusion coefficient 2.8*10−10 m2/s

Full size image

These results provide the foundation for the extrapolation of the trends to other mixers with different dimensions. To demonstrate this, the cyclone mixer in Fig. 2c is shrink and expanded 10 times respectively. The Reynolds number of 180 is kept constant in the outlet channels of each mixer by increasing or decreasing the average inlet velocity by the same factor respectively. As Fig. 7 indicates, similar concentration distribution profiles are obtained at counterpart positions (middle of the outlet channel) at the same Re and almost equal mixing indices are observed, implying similar mixing efficiency. However, it is important to note that the time to reach the same mixing index increases 100 times from 0.0281 s to 2.81 s when the geometry expands 10 times and diameter increases from 1 mm to 10 mm. The longer time to reach the same mixing index is caused by one tenth of the original mixing potential (from 14,324 m2m−3 to 1432.3 m2m−3) as the diameters expands ten times from 1 mm to 10 mm. Despite longer time to reach the same mixedness at longer length scale of the mixer, larger mixer provide higher throughput and lower pressure drop. As the geometry expands 10 times, the cross section area increases 100 times, and the volume of the mixer increases 1000 times. The average velocity drops 10 times to keep the same Re, leading to 10 times volumetric flowrate.

Fig. 7
figure 7

Normalised concentration distribution profiles of cyclone mixers with four inlet streams with square cross sections a) cross section at 500 μm, mixer diameter of 100 μm, b) cross section at 5 mm, mixer diameter of 1 mm, and c) cross section at 50 mm, mixer diameter of 10 mm. Conditions: Re 180, 20 °C aqueous solution, developed inlet velocity profile, diffusion coefficient of Rhodamine B 2.8*10−10 m2/s

Full size image

Conclusions

The mixing efficiency in T-, Y- and cyclone mixers is systematically investigated by a novel method based on backward particle tracking, which eliminates numerical diffusion. The method is firstly validated by published experimentally characterized concentration profiles, showing higher accuracy than the default method in commercial software. The cross section shape of T-mixers with a jet flow is a key design parameter to enhance mixing in the inlet section of flow systems. Square channels lead to flow engulfment at high Reynolds number of 300 while circular channels do not. T-mixers with a cross flow always lead to flow engulfment event at relatively low Re of ~100. Y-mixers do not promote convection and the inlet section is solely dominated by diffusion in the investigated range. Relative position of the inlet streams is a key design parameter to promote mixing. Having the inlet streams tangential (cyclone mixers) instead of opposite (T-mixers) to each other, promotes the rotation of the fluid and thus, convection. We also demonstrate that the inlet average velocity is the main design parameter determining mixing efficiency in cyclone mixers. The higher the inlet average velocity, the more pronounced the rotation of the fluid and thus, higher the mixing efficiency. The cyclone mixer with the smallest inlet area presents the highest mixing efficiency among all investigated mixers. The geometry of the inlet configuration, mainly cross section inlet area, has a mild effect on the homogeneity of the fluid rotation.