The geometry of recombination

Abstract

With the tools of information geometry, we can express relations between marginals of a joint distribution in geometric terms. We develop this framework in the context of population genetics and use this to interpret the famous Ohta–Kimura formula (cf. Ohta and Kimura in Genet Res 13(01):47–55, 1969) and discuss its generalizations for linkage equilibria in Wright–Fisher models with recombination with several loci. The state space associated with the Ohta–Kimura model is simply a Riemannian manifold of constant positive curvature. Furthermore, the equilibria states for recombination can be interpreted geometrically as a product of spheres. In the case of only 2 loci, we also derive the behavior of the mutual information between these two loci.

1 Introduction

In mathematical terms, the most basic model of mathematical population genetics, the Wright–Fisher model [11, 20], is about iterated sampling with replacement. We shall explain the biological meaning in a moment, but first describe the mathematical structure, beginning with a simplified version and adding more details subsequently. In the discrete model, in each generation, we have M entities, called gametes (later, we shall let $M\rightarrow \infty$). They need not all be different, but they may fall into K different classes or types. For the next generation, we sample from that pool of M gametes with replacement, to create a new pool of M such gametes. For biological reasons, there might be sampling biases, but we ignore those here, and sample uniformly. Mathematically, this leads to the multinomial distribution. The question is how the class composition will evolve asymptotically, that is, how the relative frequencies of the different types will change when the number of generations goes to $\infty$, but we shall return to that later.

We are interested in another fundamental biological effect, recombination. To set this up, we first need a slight modification. We consider a population of N individuals that are diploid, i.e., carry two gametes each. That is, we have $M=2N$ gametes. As before, the gametes are sampled with replacement in each generation from the previous generation, and new individuals are randomly formed as pairs of gametes. Now recombination becomes possible, that is, two gametes can be fused into a single one. Biologically, that means that for each member of the next generation, we choose two individuals as parents and combine their altogether 4 gametes into 2 new ones. Of course, we could simply take one randomly from each parent, and then the sampling process, although now formulated in a more complicated manner, would not be different from the one described earlier. But now our gametes possess some internal structure that can get mixed or recombined during the sampling process. The gametes are strings with positions $A,B,\ldots$, the so-called loci and at each locus, different values are possible. These different values are called alleles. For instance, in the simplest nontrivial case of two loci, A and B, at A, the possible alleles might be $A^0,\ldots , A^m$, and at B, $B^0,\ldots ,B^n$. In the simplest case, each of these two loci can carry only two possible alleles. Let us denote those at the first locus by $A^0,A^1$, and those at the second locus as $B^0,B^1$. Thus, the possible gamete types are $(A^0,B^0)$, $(A^0,B^1)$, $(A^1,B^0)$, and $(A^1,B^1)$. When, for instance, a gamete of type $(A^0,B^0)$ is recombined with one of type $(A^1,B^1)$, and recombination gives the first allele of the first and the second allele of the second gamete to the offspring, that offspring then is of type $(A^0,B^1)$, hence different from either parent. Of course, when the gametes have more loci, more complicated recombination schemes are possible, but the preceding example already captures the essence.

Things become simpler when one passes to a continuum limit where the population size and the number of generation go to $\infty$ in an appropriate ratio. The process is then mathematically described by partial differential equations of Fokker-Planck or Kolmogorov type. Again, one is interested in the asymptotic limit states. Without recombination, the result is simple. Eventually, one gamete type will sweep through the population, and all others disappear. With recombination, other questions emerge. We may ask whether the frequency of a particular allele combination $(A^i,B^j)$ is equal to the product of the individual frequencies of $A^i$ and $B^j$ in the population. If that is so, one speaks of linkage equilibrium. Now, the famous Ohta–Kimura¹ formula [16] (see (3.13) below) describes the evolution of the coefficient of linkage disequilibrium that, as the name indicates, measures the deviation from equilibrium, in the continuum limit, for the simplest case of two loci with two alleles each. The formula looks complicated, and it does not appear clear how to systematically extend it to arbitrarily many loci with arbitrarily many alleles at each of them. But this is what we achieve in this paper. And we succeed in that by transforming the problem into a geometric one. Akin [1] had already developed a geometric interpretation of population genetics, but here we make the crucial observation that the underlying metric, called the Shashahani metric in mathematical biology, is nothing but the Fisher metric² of information geometry. And this enables us to draw systematically on information geometry, as developed for instance in Amari’s books [2,3,4] (see also [6]) to achieve a natural and clear geometric picture of linkage and recombination. This makes the Ohta–Kimura formula easy to derive and conceptually clear. As our approach is general, it naturally works for arbitrary numbers of loci and alleles, and it yields a natural geometric hierarchy within which allele distinctions can be refined. In the end, linkage equilibrium simply corresponds to a product of lower dimensional (positive sectors of) spheres sitting in a larger one.

Before developing that geometric structure, however, let us reformulate the preceding in the language of population genetics. As described, in the most basic model of mathematical population genetics, the Wright–Fisher model [11, 20], one considers a population of N individuals that are diploid, i.e., carry two gametes each. The population is resampled with replacement in each generation from the previous generation.³ More precisely, the 2N gametes are sampled to yield those of the new generation. (A mathematically equivalent model results from considering a population of 2N haploid individuals that carry one gamete each. The essential step of the model will consist in the recombination of gametes, and it is thus the population of gametes that counts.) Those gametes can carry different alleles, and because of the random sampling, the allele composition of the next generation in general will not be identical to that of the previous one. This is the phenomenon of random genetic drift. Additional effects, like mutation or selection, yield sampling biases. Here, we are concerned with recombination. That means that the gametes have several loci, at each of which they can carry different alleles. Before forming the next generation, gametes to be paired in a new individual are broken into two complementary pieces, and the first piece of the first gamete is combined with the second piece of the second one to form a new gamete. An alternative biological mechanisms consists of the formation of zygotes, that is, pairs of gametes, in an individual that are then recombined before being passed to the next generation.⁴ It turns out, however, that for the diffusion approximation of the Wright–Fisher model, with which we shall work in the present paper, it does not make a difference whether we randomly pair gametes or zygotes, and so, we shall ignore that distinction here.

Since, as described, the sampling from a generation of gametes is a stochastic process, we need to work with probability distributions for the population of gametes. A basic question is whether the allele probabilities at the different loci are independent of each other. The term linkage between certain loci (or sets of loci) means that the allelic configuration at one locus or loci set affects the allelic configuration at the other loci. In the two-loci 2-allelic model, each allele at one locus can be linked with both other alleles at the other locus. The question is, whether in hopefully obvious notation,

$$\begin{aligned} p(A^i,B^j)=p(A^i) p(B^j) \text { for all }i,j. \end{aligned}$$

(1.1)

If this is the case, the alleles at the two loci are not linked, and one speaks of a linkage equilibrium. This may be violated because of selective effects, because for instance a gamete of type $(A^0,B^0)$ is fitter than $(A^0,B^1)$, while $(A^1,B^1)$ in turn might be fitter than $(A^1,B^0)$. In that case, we would expect $p(A^0,B^0)>p(A^0) p(B^0)$, as well as other inequalities violating (1.1). Here, however, we shall not be concerned with effects of selection. A more basic question is when the first generation with which the process starts is not in linkage equilibrium, that is, does not satisfy (1.1) (where we now interpret the probabilities as relative frequencies), whether we may still expect that (1.1) will asymptotically hold when the number of generations goes to infinity.

In this paper, we shall develop a mathematical framework to study this question, taking the formula of Ohta and Kimura [16] as our reference point. As already mentioned, our geometric approach is based on the Fisher metric⁵ of information geometry, that makes the Ohta–Kimura formula easy to derive and conceptually clear. As our approach is general, it naturally works for arbitrary numbers of loci and alleles, and it yields a natural geometric hierarchy within which allele distinctions can be refined.

The mathematical perspective that we shall develop is that of information geometry. To put it simply, the family of linkage equilibrium states is simply an exponential subfamily of the family of all probability distributions of the alleles. In fact, the projection of a given distribution onto that family yields a maximum entropy distribution with the same marginals, see [4, 6].

In the sequel, we shall speak of genotypes rather than pairs of gametes. Each individual in the population is thus represented by its genotype $\xi$. $p_t(\xi )$ is the probability that an individual in generation $t$ carries the genotype $\xi$, and the aim of the model is to investigate the dynamics of the probability distribution $p_t$ in time $t$. (For the purposes of the present paper, we do not need to distinguish between probabilities in future and relative frequencies in past populations.) We assume that the genetic loci of the different members of the population are in one-to-one correspondence with each other. Thus, we have loci $\alpha =1,\ldots , k$. As we are looking at pairs of gametes, at each locus, there are two alleles, which could be the same or different. As explained above, each individual has two parents, and its genotype is assembled from the genotypes of its parents through sexual recombination. We are interested in how the distribution of genotypes changes over time through the combined effects random drift and recombination. Here, for simplicity, we ignore other evolutionary forces, like selection and mutation. We refer to [12] for the general theory.

Recombination is a binary operation, that is, an operation that takes two parent genotypes $\eta , \zeta$ as arguments to produce one offspring genotype $\xi$. Here, we assume that, like a chromosome, a genotype consists of a linear string⁶ of $k$ sites occupied by particular alleles. An offspring genotype is then formed through recombination by choosing at each locus of each of the two gametes the allele that one of the parents carries there. The selection rule for deciding which of the two possibly different alleles to choose is given by a mask$\mu$, a binary string of length $k$. An entry 1 at position $\alpha$ means that the allele is taken from the first parent, say $\eta$, and when there is a 0 the allele is taken from the second parent, say $\zeta$. For instance, for $k=5$, the mask 10010 produces from the parents $\eta =\eta _1 \ldots \eta _5$ and $\zeta =\zeta _1 \ldots \zeta _5$ the offspring $\xi =\eta _1\zeta _2\zeta _3\eta _4\zeta _5$. The recombination schemes $C_{\xi \eta \zeta }(\mu )$ for the masks $\mu$ and their probabilities $p_r(\mu )$ then yield the recombination operator

$$\begin{aligned} R_{\xi \eta \zeta }=\sum _\mu p_r(\mu )C_{\xi \eta \zeta }(\mu ). \end{aligned}$$

(1.2)

When all the possible $2^k$ masks are equally probable, then, at each locus, the offspring acquires an allele from either parent with probability 1 / 2, independently of the choices at the other loci. In particular, the linear arrangement of the loci plays no role in this case, and the loci are independent of each other.

In contrast, dependencies between sites arise in the cross-over models (see for example [7]). Such models permit only masks of the form $\mu _c=11\ldots 100 \ldots 0$. For such a mask, at the first $a(\mu _c)$ sites, the allele from the first parent is chosen, and at the remaining $k-a(\mu _c)$ sites, the one from the second parent. As a can range from 0 to k, we then have $k+1$ possible such masks $\mu _c$, and we may wish to assume again that each of those is equally probable. In such cross-over models, obviously, the linear arrangement of the sites is important.

Recombination cannot prevent the basic effect of random genetic drift in the Wright–Fisher model that some alleles may disappear from the population, and in fact, with probability 1, in the long term, only one allele will survive at each site. Because of the random selection, in each generation, it may happen that no carrier of a particular allele is chosen or that none of the chosen recombination masks preserves that allele when the mating partner carries a different allele at the locus under consideration. That would then lead to the irreversible extinction of that allele.

In this paper, we want to study the dynamics of probability distributions. For that purpose, we shall first analyze the geometry of the space of probability distributions. That will provide us with a geometric description and interpretation of the dynamics. In fact, we shall study the continuum limit of the dynamics, as is the custom in mathematical investigations of the Wright–Fisher model. That means that rescale population size N and generation time $\delta t$ in such a way that $N\rightarrow \infty$, but $N \delta t=1$. As is well-known since the work of Wright and Kimura, in the limit, the probability density $f(p,s,x,t)\mathrel {\mathop :}=\frac{\partial ^n}{\partial x^1 \ldots \partial x^n} P(X(t) \le x|X(s)=p)$ with $s<t$ satisfies the Kolmogorov forward or Fokker–Planck equation

$$\begin{aligned} \frac{\partial }{\partial t}f(p,s,x,t)&=\frac{1}{2}\sum _{i,j=1}^{n}\frac{\partial ^2}{\partial {x^i}\partial {x^j}}\left( x^i(\delta ^i_{j}-x^j)f(p,s,x,t)\right) \nonumber \\&\quad -\sum _{i=1}^{n}\frac{\partial }{\partial x^i}\left( b^i(x,t)f(p,s,x,t)\right) , \end{aligned}$$

(1.3)

and the Kolmogorov backward equation

$$\begin{aligned} -\frac{\partial }{\partial s}f(p,s,x,t)&=\frac{1}{2}\sum _{i,j=1}^{n} p^i(\delta ^i_{j}-p^j)\frac{\partial ^2}{\partial {p^i}\partial {p^j}}f(p,s,x,t) \nonumber \\&\quad + \sum _{i=1}^{n}b^i(p,s)\frac{\partial }{\partial p^i}f(p,s,x,t) . \end{aligned}$$

(1.4)

The second order terms arise from random genetic drift, whereas the first order terms with their coefficients $b^i$ may incorporate the effects of recombination.

We shall develop a geometric framework that will interpret the coefficients of the second order terms as the inverse of the Fisher metric of mathematical statistics. In particular, this will enable us to find a handy and insightful description of the state space and, importantly, the geometric effect of recombination and linkage on it. This will lead us to the following general result for the geometry of linkage equilibria:

Theorem3.5 (cf. p. 25) In linkage equilibrium, for all$n+1\ge 2$and$k\ge 2$the corresponding restriction of the state space$\Delta _{(n+1)^k-1}$of the diffusion approximation of ak-loci$(n+1)$-allelic recombinational Wright–Fisher model equipped with the Fisher metric of the multinomial distribution is akn-dimensional manifold and carries the geometric structure of

$$\begin{aligned} \underbrace{S^{n}_+\times \cdots \times S^{n}_+}_{{k}}\subset S_+^{k(n+1)-1}, \end{aligned}$$

(1.5)

where $S^{n}_+$ is the positive sector of the n-dimensional unit sphere.

And this is the geometry underlying the Ohta–Kimura formula and its generalization to arbitrarily many loci and alleles.

For simplicity, we have formulated this result under the assumption that the number of alleles at each locus is the same. Of course, that assumption is not necessary. We refer to Corollary 3.6 for the precise statement in the general case. This generalizes the corresponding results in [12].

Since the literature on the Wright–Fisher model is immense, we do not provide a literature review, but rather refer to [10].

We conclude this introduction with some remarks on the notations.

Random variables are denoted by capital Latin letters, like X or Y, their values by the corresponding minuscules, like x or y. Expectation of a random variable X is denoted by E(X). Time, be integer time $m\in \mathbb {N}$ or real time $t\in \mathbb {R}^+$, is represented by a subscript. So, $Z_m$ or $Z_t$ is the value of the random process Z at time m or t.

The random variable Y denotes absolute and X relative frequencies. When we have alleles $A^{0},\ldots ,A^{n}$ at a single locus, their relative frequencies are given by $X=(X^0,\ldots ,X^{n})$, and analogously for Y. Thus, $\sum _{i=0}^{{n}}Y^i=N$ and $\sum _{i=0}^{{n}}X^i=1$, and likewise their realizations satisfy $\sum _{i=0}^{{n}}x^i=1$. We usually write $p(x^0,\ldots ,x^n)=P(X^0=x^0,\ldots ,X^n=x^n)$ for the probability that the components of the random variable X take the values $x^i$. We shall employ the same notation for different random variables. Thus, p or P do not denote specific functions, but stand for the generic assignment of probabilities. Which random variable is meant will be clear from the variable names and the context.

When we have several loci $\mu =1,\ldots ,k$ and possible alleles $A^{i_\mu }_\mu$ at locus $\mu$, we denote the relative frequencies by $X^{i_1 \ldots i_k}$. Then $\sum _{i_1,\ldots , i_k}X^{i_1 \ldots i_k}=1$, and likewise for their realizations

$$\begin{aligned} \sum _{i_1,\ldots , i_k}x^{i_1 \ldots i_k}=1. \end{aligned}$$

(1.6)

2 Geometric structures and information geometry

2.1 The basic setting

As we are working with probability distributions, our underlying space is the probability simplex

$$\begin{aligned} \overline{\Sigma }^{n}:=\Bigg \{ (x^0,\dots ,x^{n}): \sum _{i=0}^{n} x^i=1\Bigg \}, \end{aligned}$$

(2.1)

where the $x^i$ stand for relative allele frequencies or probabilities of the alleles $i=0,\ldots ,n$. In the infinite population size limit, the $x^i$ can take any values between 0 and 1. The normalisation

$$\begin{aligned} \sum _{i=0}^{n} x^i=1 \end{aligned}$$

(2.2)

induces correlations between the $x^i$ that will be captured by the Fisher metric introduced below. On this space of relative frequencies or probabilities, we shall consider probability distributions p(x). As probability distributions, they need to satisfy the normalisation

$$\begin{aligned} \int _{\overline{\Sigma }^{n}} p(x)dx=1. \end{aligned}$$

(2.3)

In the sequel, we shall equip the probability simplex $\overline{\Sigma }^{n}$ with various geometric structures. Of course, it already possesses a geometric structures as an affine linear subset of $\mathbb {R}^{n+1}$. Another geometric structure is obtained by projecting it to the positive sector of the unit sphere in $\mathbb {R}^{n+1}$. The resulting, surprisingly rich, geometry is the content of information geometry, see [2, 4, 6]. For information geometry, we need to recall some basic concepts from Riemannian geometry, using [13] as a reference.

2.2 The Fisher metric

The results in this section are well known and described here only for completeness and ease of reference. The Fisher information metric of a smooth family of probability distributions on some domain $\Omega$ parametrised by $s=(s_1,\ldots ,s_n)\in S\subset \mathbb {R}^n$ with probability density functions $p(\omega |s)=p(s)$ (for short) is given by (cf. [3], p. 27)

$$\begin{aligned} g_{ij}(s)\mathrel {\mathop :}=&{{\,\mathrm{E}\,}}_{p(s)}\Big (\frac{\partial }{\partial s_i}\log p(s)\frac{\partial }{\partial s_j} \log p(s)\Big )&\quad \text {for }i,j\in \lbrace 1,\ldots ,n\rbrace , s\in S \end{aligned}$$

(2.4)

$$\begin{aligned} =&\sum _{\omega \in \Omega }\frac{\partial }{\partial s_i}\log p(\omega ;s) \frac{\partial }{\partial s_j}\log p(\omega ;s)\; p(\omega ;s)&\end{aligned}$$

(2.5)

$$\begin{aligned} =&\sum _{\omega \in \Omega }\frac{1}{p(\omega ;s)}\frac{\partial }{\partial s_i} p(\omega ;s) \frac{\partial }{\partial s_j}p(\omega ;s)&\end{aligned}$$

(2.6)

where ${{\,\mathrm{E}\,}}_{p(s)}$ is the expectation with respect to p(s).

For the basic Wright–Fisher model, we have $n+1$ alleles which are assigned probabilities $p^0,\ldots ,p^n$. The metric tensor $g_{ij}$ in the coordinates $p^1,\ldots , p^{{n}}$ on the $n$-dimensional simplex

$$\begin{aligned} \Delta _n=\Bigg \{ (p^1,\ldots , p^{n}): p^i > 0, \sum _{i=1}^{n} p^i <1\Bigg \}. \end{aligned}$$

(2.7)

(we have eliminated $p^0=1-\sum _{i=1}^np^i$ to make the coordinates independent) is the Fisher metric⁷ tensor

$$\begin{aligned} (g_{ij}({{p}}))_{i,j=1}^{{n}}= \left( \begin{array}{cccc} \frac{1}{p^1} +\frac{1}{p^0} &{} \frac{1}{p^0} &{} \ldots &{} \frac{1}{p^0}\\ \frac{1}{p^0}&{} \frac{1}{p^2} +\frac{1}{p^0} &{} \ldots &{} \frac{1}{p^0}\\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ \frac{1}{p^0}&{} \frac{1}{p^0} &{}\ldots &{} \frac{1}{p^{n}} +\frac{1}{p^0} \end{array} \right) \end{aligned}$$

(2.8)

and the inverse metric tensor $g^{ij}$ is

$$\begin{aligned} (g^{ij}({{p}}))_{i,j=1}^{n}= \left( \begin{array}{cccc} p^1(1-p^1)&{} -p^1p^2&{} \ldots &{}-p^1p^{n}\\ -p^1p^2&{} p^2(1-p^2)&{} \ldots &{} -p^2p^{n}\\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ -p^1p^{n}&{}-p^2p^{n}&{} \ldots &{}p^{n}(1-p^{n}) \end{array} \right) , \end{aligned}$$

(2.9)

that is, the covariance matrix of the probability distribution p.

For the multinomial distribution $\mathcal {M}(2N;p^0,\ldots ,p^n)$, the metric has to be scaled by the factor ${2N}$,

$$\begin{aligned} {g}_{kl}(p)={2N} \Big (\frac{\delta _{kl}}{p^k}+\frac{1}{p^0}\Big )\quad \text {for } k,l=1,\ldots ,n, p\in \Delta _n. \end{aligned}$$

(2.10)

The Fisher metric is nothing but the standard metric on the sphere, written in simplex coordinates $p^0,\ldots ,p^{n}$. We can also compute the Christoffel symbols (see [13], p.22)

$$\begin{aligned} \Gamma ^i_{jk}=\frac{1}{2}\sum _\ell g^{i\ell }\left( \frac{\partial g_{k\ell }}{\partial p^j}+\frac{\partial g_{j\ell }}{\partial p^k}-\frac{\partial g_{jk}}{\partial p^\ell }\right) \end{aligned}$$

(2.11)

of this metric as

$$\begin{aligned} \Gamma ^i_{ii}= & {} \frac{1}{2}\left( \frac{p^i}{p^n}-\frac{1-p^i}{p^i}\right) \nonumber \\ \Gamma ^i_{jj}= & {} \frac{1}{2}\left( \frac{p^i}{p^n}-\frac{p^i}{p^j}\right) \text { for }i\ne j\nonumber \\ \Gamma ^i_{j\ell }= & {} \frac{1}{2}\frac{p^i}{p^n} \text { for }j\ne \ell . \end{aligned}$$

(2.12)

We can also rewrite the metric in spherical coordinates, by simply putting

$$\begin{aligned} q^i:=\sqrt{p^i}, \quad \text {for } i=1,\ldots ,{n}. \end{aligned}$$

(2.13)

Applying the transformation rule for Riemannian metrics, $g_{ij}(y)=\gamma _{\alpha \beta }(x)\frac{\partial x^\alpha }{\partial y^i}\frac{\partial x^\beta }{\partial y^j}$ with $\frac{\partial p^\alpha }{\partial q^j}=2\delta ^\alpha _j q^j$ for $j,\alpha =1,\ldots ,{n}$, we obtain (noting that the normalization constraint now is $q^{0}=\sqrt{1-\sum _{j=1}^{{n}} {(q^j)}^2}$) the metric tensor $(h_{ij})$ in the coordinates $q^1,\ldots ,q^n$

$$\begin{aligned} \Big (h_{ij}({{q}})\Big )_{i,j=1}^{n}= \frac{4}{{(q^{0})}^2}\left( \begin{array}{cccc} {(q^1)}^2 + {(q^0)}^2&{} q^1q^2&{} \ldots &{}q^1q^{n}\\ q^1q^2&{} {(q^2)}^2 + {(q^0)}^2&{} \ldots &{} q^2q^{n}\\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ q^1q^{n}&{}q^2q^{n}&{} \ldots &{}{(q^{n})}^2 + {(q^{0})}^2 \end{array} \right) \nonumber \\ \end{aligned}$$

(2.14)

and

$$\begin{aligned} \Big (h^{ij}({{q}})\Big )_{i,j=1}^{n}= \frac{1}{4}\left( \begin{array}{cccc} 1-{(q^1)}^2&{} -q^1q^2&{} \ldots &{}-q^1q^{n}\\ -q^1q^2&{} 1-{(q^2)}^2&{} \ldots &{} -q^2q^{n}\\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ -q^1q^{n}&{}-q^2q^{n}&{} \ldots &{}1-{(q^{n})}^2 \end{array} \right) . \end{aligned}$$

(2.15)

Since this has been obtained as the restriction of the Euclidean metric to the unit sphere, this must simply be the standard metric on the unit sphere $S^{{n}}$ (up to the factor 4 that results from the normalization of the Fisher metric (2.4)). Since the standard metric on the sphere has sectional curvature $\equiv 1$, and since the sectional curvature of a Riemannian metric scales with the inverse of a scaling factor, our factor 4 leads to

Proposition 2.1

The Fisher metric on the standard simplex $\overline{\Sigma }^{{n}}$ is 4 times the standard metric on the unit sphere $S^{{n}}$, and its sectional curvature is $\frac{1}{4}$.

Remark 2.2

Compare this with the state space of recombination (Proposition 3.2), where the Fisher metric has been multiplied by four implying that the sectional curvature will be divided by four.

2.3 The transformation rule for geometric differential operators

Below, we shall encounter linear second order differential operators of the form

$$\begin{aligned} Mu(x)=\sum _{i,j} a^{ij}(x) \frac{\partial ^2}{\partial {x^i}\partial {x^j}}u(x)+\sum _{i} b^i(x)\frac{\partial }{\partial x^i}u(x) \end{aligned}$$

(2.16)

with coefficients $a^{ij}$ and $b^i$. In fact, the coefficients $a^{ij}$ of the leading second order term $M_0u(x):=\sum _{i,j} a^{ij}(x) \frac{\partial ^2}{\partial {x^i}\partial {x^j}}u(x)$ will arise as the inverse $g^{ij}$ of the metric tensor of the Fisher metric.

In order to understand this operator, we recall some constructions from geometric analysis (see [13]). For those, $g=(g_{ij})$ can be any Riemannian metric, not necessarily the Fisher one. The basic geometric second order operator is the Laplace–Beltrami operator

$$\begin{aligned} \Delta _g u(x)= & {} \frac{1}{\sqrt{\mathrm {det} g}}\sum _{i,j} \frac{\partial }{\partial x^i}\left( \sqrt{\mathrm {det} g} g^{ij} \frac{\partial u(x)}{\partial x^j}\right) \end{aligned}$$

(2.17)

$$\begin{aligned}= & {} \sum _{i,j}\left( g^{ij} \frac{\partial ^2 u(x)}{\partial x^i \partial x^j}- g^{ij}\sum _k \Gamma ^k_{ij}(x)\frac{\partial u(x)}{\partial x^k}\right) \end{aligned}$$

(2.18)

with the Christoffel symbols of (2.11). Thus

$$\begin{aligned} M_0u(x) - \Delta _gu(x) = \sum _{i,j,k}g^{ij}(x) \Gamma ^k_{ij}(x)\frac{\partial }{\partial x^k}u(x) = \sum _k 2 \, ch^k_g(x) \frac{\partial }{\partial x^k}u(x) \end{aligned}$$

(2.19)

with the Christoffel force $ch_g^k(x):= \frac{1}{2}\sum _{i,j}g^{ij}(x) \Gamma ^k_{ij}(x)$ defined in [5, Eq. (31)].

Remark 2.3

We can put this into a more general context, although this will not be explored more deeply in the present article. The Christoffel symbols as defined in (2.11), that is, in the notation of this section $\Gamma ^i_{jk}=\frac{1}{2}\sum _\ell g^{i\ell }(\frac{\partial g_{k\ell }}{\partial x^j}+\frac{\partial g_{j\ell }}{\partial x^k}-\frac{\partial g_{jk}}{\partial x^\ell })$, are the Christoffel symbols for the Levi–Civita connection for the metric g. More generally, we can consider the Christoffel symbols $\Gamma ^i_{jk}$ for any affine connection and define a corresponding operator $\Delta _\Gamma$ as in (2.18). This operator, however, in general will no longer be in divergence form as in (2.17). Such an operator arises, for example, in [9] in a statistical application. For the Wright–Fisher model which we have formulated on the simplex $\Delta _n$ as a Riemannian manifold with the Fisher information metric $g_{ij}(p)$ in (2.8), one considers (see [4, 6]) the general affine connection $\Gamma ^{(\alpha )}$ (with $\alpha \in [-1,1])$ with the symbols $\Gamma _{ij,k}:=\sum _\ell g_{k\ell }\Gamma ^\ell _{ij}$ given by

$$\begin{aligned} \Gamma ^{(\alpha )}_{ij,k}(p) := \frac{\alpha -1}{2} \Big (-\frac{\delta _{ijk}}{(p^i)^2} + \frac{1}{(p^0)^2}\Big ). \end{aligned}$$

(2.20)

For $\alpha =0$, this is (2.11). In fact, in that case, the symbols in (2.20) yield the Levi–Civita connection. The Christoffel force for this case is readily computed from (2.11) to be $ch^k_g(p) = -\frac{1}{4} \Big (1-(n+1)p^k\Big )$, and

$$\begin{aligned} \Delta _{\Gamma ^{(\alpha )}}u(p) = \sum _{i,j} g^{ij}(p) \frac{\partial }{\partial p^i}\frac{\partial }{\partial p^j}u(p) + \frac{\alpha +1}{2} \sum _{r} \Big (1-(n+1)p^r\Big )\frac{\partial }{\partial p^r} u(p). \end{aligned}$$

(2.19) then becomes

$$\begin{aligned} M_0u(p) - \Delta _{\Gamma ^{(\alpha )}}u(p) = 2 (\alpha +1) \sum _r \, ch^r_g(p) \frac{\partial }{\partial p^r}u(p) \end{aligned}$$

(2.21)

which reduces to (2.19) when $\alpha =0$, because for that case, we have the Levi–Civita connection of the Fisher metric. In information geometry (see [4, 6]), the cases $\alpha =\pm 1$ are particularly important. In fact, for $\alpha =1$, the symbols (2.20) vanish (meaning that the connection is flat). For $\alpha =-1$, the right hand side of (2.21) vanishes, that is, $M_0$ coincides with the corresponding Laplacian. In fact, the case $\alpha =-1$ is dual to $\alpha =1$ and hence also flat (meaning that we can find appropriate coordinates in which the corresponding symbols vanish).

We return to (2.19). The Laplace–Beltrami operator does not change its shape under coordinate transformations. The Christoffel symbols, however, do not transform as tensors. Therefore, when changing coordinates, we obtain additional first order terms in $M_0$ from the transformation of the metric. The precise formula is

Lemma 2.4

When changing coordinates ${(x_i)}_i\mapsto {({\tilde{x}}_i)_i}$, the partial differential operator (2.16) transforms into

$$\begin{aligned} M{\tilde{u}}({\tilde{x}})=\sum _{k,l} {\tilde{a}}^{kl}({\tilde{x}}) \frac{\partial ^2}{\partial {{\tilde{x}}^k}\partial {{\tilde{x}}^l}}{\tilde{u}}({\tilde{x}})+\sum _{k} {\tilde{b}}^k({\tilde{x}})\frac{\partial }{\partial {\tilde{x}}^k}{\tilde{u}}({\tilde{x}}) \end{aligned}$$

(2.22)

with ${\tilde{u}}({\tilde{x}}(x))=u(x)$ and

$$\begin{aligned} {\tilde{a}}^{kl}({\tilde{x}})= \sum _{i,j}a^{ij}(x)\frac{\partial {\tilde{x}}^k}{\partial x^i} \frac{\partial {\tilde{x}}^l}{\partial x^j}, \quad {\tilde{b}}^{k}({\tilde{x}})= \sum _{i}b^{i}(x)\frac{\partial {\tilde{x}}^k}{\partial x^i}+\sum _{i,j}a^{ij}(x)\frac{\partial ^2{\tilde{x}}^k}{\partial {x^i}\partial {x^j}}. \end{aligned}$$

(2.23)

Proof

Let ${\tilde{x}}$ be a coordinate change and $u(x)={\tilde{u}}({\tilde{x}}(x))$. The chain rule yields

$$\begin{aligned} \sum _{i,j}a^{ij} \frac{\partial ^2}{\partial {x^i}\partial {x^j}}u&=\sum _{i,j}\sum _{k} a^{ij}\frac{\partial }{\partial x^i}\Big (\frac{\partial {\tilde{x}}^k}{\partial x^j}\frac{\partial }{\partial {\tilde{x}}^k}{\tilde{u}}\Big )\\&=\sum _{i,j}\Big (\sum _{l,k} a^{ij}\frac{\partial {\tilde{x}}^l}{\partial x^i} \frac{\partial {\tilde{x}}^k}{\partial x^j}\frac{\partial ^2}{\partial {{\tilde{x}}^l}\partial {{\tilde{x}}^k}}{\tilde{u}} +\sum _k a^{ij}\frac{\partial ^2{\tilde{x}}^k}{\partial {x^i}\partial {x^j}}\frac{\partial }{\partial {\tilde{x}}^k}{\tilde{u}}\Big )\\&=\sum _{l,k}\sum _{i,j} a^{ij}\frac{\partial {\tilde{x}}^l}{\partial x^i} \frac{\partial {\tilde{x}}^k}{\partial x^j}\frac{\partial ^2}{\partial {{\tilde{x}}^l}\partial {{\tilde{x}}^k}}{\tilde{u}} +\sum _k \sum _{i,j}a^{ij}\frac{\partial ^2{\tilde{x}}^k}{\partial {x^i}\partial {x^j}}\frac{\partial }{\partial {\tilde{x}}^k}{\tilde{u}} \end{aligned}$$

and

$$\begin{aligned} \sum _{i} b^i\frac{\partial }{\partial x^i}u&=\sum _{i}\sum _{k}b^i\frac{\partial {\tilde{x}}^k}{\partial x^i}\frac{\partial }{\partial {\tilde{x}}^k}{\tilde{u}} =\sum _{k}\sum _{i}b^i\frac{\partial {\tilde{x}}^k}{\partial x^i}\frac{\partial }{\partial {\tilde{x}}^k}{\tilde{u}}. \end{aligned}$$

(2.24)

This yields

$$\begin{aligned} \sum _{i,j}a^{ij} \frac{\partial ^2}{\partial {x^i}\partial {x^j}}u+\sum _{i} b^i\frac{\partial }{\partial x^i}u&=\sum _{l,k}{\tilde{a}}^{lk}\frac{\partial ^2}{\partial {{\tilde{x}}^l}\partial {{\tilde{x}}^k}}{\tilde{u}} +\sum _k{\tilde{b}}^k\frac{\partial }{\partial {\tilde{x}}^k}{\tilde{u}}. \end{aligned}$$

(2.25)

$\square$

This formula will be used in the following Theorem 3.1.

2.4 Exponential families

There is more structure in information geometry than the Fisher metric, see [2, 6]. In fact, the probability simplex carries two affine structures that are dual to each other. Their deeper geometry was discovered and explored by Amari and Chentsov. On one hand, we have the mixture structure which is simply the affine geometry of the simplex. Dually, we have the exponential structure. To explain that structure, consider a probability distribution $p(x^0,\ldots , x^n)$. For any $1\le k\le n$, we have the marginals

$$\begin{aligned} p_{0,\ldots ,k-1}(x^0,\ldots , x^{k-1})= & {} \sum _{y^k,\ldots ,y^n} p(x^0,\ldots ,x^{k-1},y^k,\ldots ,y^n)\nonumber \\ p_{k,\ldots ,n}(x^k,\ldots , x^{n})= & {} \sum _{y^0,\ldots ,y^{k-1}} p(y^0,\ldots ,y^{k-1},x^k,\ldots ,x^n). \end{aligned}$$

(2.26)

We then have the exponential family of all those probability distributions that satisfy

$$\begin{aligned} {\hat{p}}(x^0,\ldots , x^n)=p_{0,\ldots ,k-1}(x^0,\ldots , x^{k-1})p_{k,\ldots ,n}(x^k,\ldots , x^{n}), \end{aligned}$$

(2.27)

that is, where the probabilities are simply the products of the marginals. W.r.t. the exponential structure, this is a flat subfamily.

A general probability distribution p does not satisfy (2.27), of course, and we have the Kullback–Leibler divergence

$$\begin{aligned}&d_{KL}(p\Vert p_{0,\ldots ,k-1}p_{k,\ldots ,n} ) = \sum \limits _{x^0,\ldots ,x^n} p(x^0,\ldots ,x^n) \nonumber \\&\quad \log \frac{p(x^0,\ldots ,x^n)}{p_{0,\ldots ,k-1}(x^0,\ldots , x^{k-1})p_{k,\ldots ,n}(x^k,\ldots , x^{n})} \end{aligned}$$

(2.28)

This can also be rewritten as

$$\begin{aligned} d_{KL}(p\Vert p_{0,\ldots ,k-1}p_{k,\ldots ,n})= & {} H(p_{0,\ldots ,k-1}p_{k,\ldots ,n})-H(p) \end{aligned}$$

(2.29)

$$\begin{aligned}= & {} I(p_{0,\ldots ,k-1};p_{k,\ldots ,n}), \end{aligned}$$

(2.30)

that is, as the difference between the entropy of the product distribution ${\hat{p}}=p_{0,\ldots ,k-1}p_{k,\ldots ,n}$ with the same marginals as p, or as the mutual information between these two marginals. In fact, as can be seen from the fact that the Kullback–Leibler divergence is always nonnegative, the entropy of the product distribution ${\hat{p}}=p_{0,\ldots ,k-1}p_{k,\ldots ,n}$ is largest among all distributions with the same marginals. And $p\rightarrow {\hat{p}}$ can be seen as the projection onto the exponential family defined by (2.27).

Of course, the same also applies when we refine the decomposition and look at products of more than two marginals. The extreme case is realized by the products

$$\begin{aligned} p_0(x^0)\ldots p_n(x^n) \end{aligned}$$

(2.31)

which have the highest entropy among all probability distributions with the same marginals. Importantly, the projections can be composed. For instance, a given distribution p can first be projected onto the product $p_{0,\ldots ,k-1}p_{k,\ldots ,n}$ and then further onto the distribution (2.31) with the same marginals. The result is the same as when we directly project p onto such a distribution.

3 Recombination

Gametes are strings of loci that are occupied by an allele from a set of alleles that is specific for the locus in question. The different gametes in the population are assumed to be perfectly aligned. That means that the number of loci, as well as the set of possible alleles for each, are the same for all gametes within the population under consideration. Thus, we can identify a locus across all the gametes. The loci are assumed to be linearly ordered. Instead of a locus, we may also speak of a site, but this means the same.

When now two gametes are paired, an offspring gamete is formed. Since the new gamete has the same number of loci as each of its parents, for each locus an allele from one of the two parents needs to be chosen. This is recombination; the possibilities for the combinations may be restricted by a recombination scheme.

In order to illustrate the principle, we start with the special case of two loci with two alleles each. With the conventions of Sect. 1, at the first locus the possible alleles are $A^{0},A^{1}$, and for the second locus $B^{0},B^{1}$. When using $G^\ell$ as symbol for ‘gamete’, the possible gametes then are

$$\begin{aligned} G^{0}\mathrel {\mathop :}=(A^{0},B^{0}),\,G^{1}\mathrel {\mathop :}=(A^{0},B^{1}),\,G^{2}\mathrel {\mathop :}=(A^{1},B^{0}),\,G^{3}\mathrel {\mathop :}=(A^{1},B^{1}), \end{aligned}$$

(3.1)

with relative frequencies denoted by $X^\ell \mathrel {\mathop :}=X^{ij}$ (as random variables) and $x^\ell \mathrel {\mathop :}=x^{ij}$ (as realized values) when $G^{\ell }=(A^{i},B^{j})$.

We let $i'$ be the allele index opposite to i, that is, $i'=0 (1)$ if $i=1(0)$ and put

$$\begin{aligned} D^{ij}\mathrel {\mathop :}=x^{ij'}x^{i'j}-x^{ij}x^{i'j'}, \text { and }D^\ell \mathrel {\mathop :}=D^{ij}\text { when }G^{\ell }=(A^{i},B^{j}). \end{aligned}$$

(3.2)

Linkage equilibrium corresponds to $D^{ij}=0$, i.e., the relative frequency of $(A^{i},B^{j})$ equals the product of the relative frequencies of $A^{i}$ and $B^{j}$.

For the mathematics of the model to be discussed shortly, recombination, instead of simply passing parental gametes on to the next generation, should take place only at a certain rate that depends on the population size (see (3.6) below). To formalize this, we introduce the recombination rateR. When the gamete $(A^{i},B^{j})$ is mated with the gamete $(A^{\ell },B^{h})$, then the gametes $(A^{i},B^{j})$ and $(A^{\ell },B^{h})$ are produced with probability $\frac{1}{2}(1-R)$ each, whereas the combinations $(A^{i},B^{h})$ and $(A^{\ell },B^{j})$ are produced with probability $\frac{1}{2}R$ each. The factor $\frac{1}{2}$ appears here because we assume that the mating and recombination of two gametes produces a single offspring in place of two.

The recombination rate R has to be interpreted as a probability. $R=0$ means that no recombination occurs, whereas $R=\frac{1}{2}$ means that the two loci behave independently. Since R and $1-R$ lead to mathematically equivalent models, it suffices to consider $0\le R \le \frac{1}{2}$.

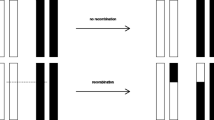
Let us look at some examples. When $(A^{0},B^{0})$ is paired with $(A^{0},B^{1})$, then $(A^{0},B^{0})$ is produced with probability $\frac{1}{2}$ independently of R. When $(A^{0},B^{0})$ is paired with $(A^{1},B^{1})$, then $(A^{0},B^{0})$ is only produced with probability $\frac{1}{2}(1-R)$. When $(A^{0},B^{1})$ is paired with $(A^{1},B^{0})$, then $(A^{0},B^{0})$ is produced with probability $\frac{1}{2}R$, even though neither parent was of this type. Thus, the effect of recombination on gamete frequencies can be neutral, negative or positive. Allele combination frequencies can stay invariant, get reduced or enhanced. In particular, recombination can create allele combinations that were not present in the parental population.

With recombination combined with random sampling, the relative frequency of $G^{\ell }$ changes between the generations $m\in \mathbb {Z}$ according to

$$\begin{aligned} {{\,\mathrm{E}\,}}(X^\ell _{m+1}|x_m)= x^\ell + R D^\ell . \end{aligned}$$

(3.3)

This may be calculated easily; as an example, for $\ell =0$,

$$\begin{aligned} {{\,\mathrm{E}\,}}\big (X^0_{m+1}|x_m\big )= & {} {(x^0)}^2 +2x^0x^1 \frac{1}{2}+2x^0x^2 \frac{1}{2}\nonumber \\&+2x^0x^3 \frac{1}{2}(1-R) +2x^1x^2 \frac{1}{2}R= x^0 +R D^0 \end{aligned}$$

(3.4)

since $x^0+x^1+x^2+x^3=1$; the factor 2 arises, because the order of the two gametes does not matter.

If there is no recombination, we have the martingale property in (3.3), but the presence of recombination introduces a bias. (This is the same with other evolutionary effects like selection or mutation, which, however, we do not study in this paper, but for recombination it may look more surprising than, say, for selection.)

In a population of N individuals, we have 2N gametes in each generation. We have two operations, sampling and recombination. Their order matters, but in the continuum limit case that we shall analyze below, this becomes irrelevant.

3.1 Diffusion approximation

We now turn to the diffusion approximation of the Wright–Fisher model with recombination. This is a very common technique, and its application is straightforward: We let the population size $N\rightarrow \infty$ and rescale time with $\delta t=\frac{1}{N}$. All expectation values then acquire a factor N. The coefficients of the drift term (i. e. coefficients $b^i$ in Eq. (1.4)) become

$$\begin{aligned} b^\ell (x)\mathrel {\mathop :}=\lim _{N\rightarrow \infty } N{{\,\mathrm{E}\,}}(\delta X^\ell _t)=\lim _{N\rightarrow \infty }(NRD^\ell ) \end{aligned}$$

(3.5)

with $\delta X^\ell _t\mathrel {\mathop :}=X^\ell _{t+\delta t} -X^\ell _t$. To keep them finite we have to assume

$$\begin{aligned} R=R(N)=O({N}^{-1}), \end{aligned}$$

(3.6)

i.e., the recombination rate has to go to 0 like $\frac{1}{N}$. The Eq. (3.6) in turn leads to

$$\begin{aligned}&a^{\ell h}(x)\mathrel {\mathop :}=\lim _{N\rightarrow \infty } N{{\,\mathrm{E}\,}}(\delta X^\ell _t \delta X^h_t)\nonumber \\&\quad =\lim _{N\rightarrow \infty }N\left( \frac{1}{N} x^\ell (\delta ^{\ell h} -x^h) +(RD^\ell )(RD^h)\right) \nonumber \\&\quad = x^\ell (\delta ^{\ell h} -x^h). \end{aligned}$$

(3.7)

Thus, the diffusion coefficients $a^{\ell h}$ are now independent of recombination. Since in this situation the third and higher moments behave like $o(\frac{1}{N})$, we can obtain the forward and backward Kolmogorov equations by passing to the diffusions limit (for a proof see [18], Proposition 3.5; cf. also the original derivation of Kolmogorov in [15] on $\mathbb {R}^n$ instead of on the simplex as here). The result is:

Theorem 3.1

The diffusion approximation of a 2 loci 2-allelic Wright–Fisher model with recombination is described by the Kolmogorov equations for its transition probability density $u:(\Delta _3)_\infty \longrightarrow \mathbb {R}^+$ of its gametic configuration $x=(x^{1},x^2,x^{3})\in \Delta _3$:

$$\begin{aligned} L^{\mathrm {rec}} u(x)=\frac{1}{4}\sum \limits _{\ell , h =1}^3 \frac{\partial ^2}{\partial {x^\ell }\partial {x^h}}(x^\ell (\delta _{\ell h}-x^h)u(x)) -\sum \limits _\ell \frac{\partial }{\partial x^\ell } (b^\ell (x) u(x)),\qquad \quad \end{aligned}$$

(3.8)

with $b^\ell (x)=\lim _{N\rightarrow \infty }(NRD^\ell )$ is the forward operator, and the Kolmogorov forward equation then is

$$\begin{aligned} \frac{\partial }{\partial t} u(x,t) = L^{\text {rec}} u(x,t) \quad \text { in } (\Delta _3)_\infty =\Delta _3\times (0,\infty ) \end{aligned}$$

(3.9)

for $u(\,\cdot \,,t)\in C^2(\Delta _3)$ for each fixed $t\in (0,\infty )$ and $u(x,\,\cdot \,)\in C^1((0,\infty ))$ for each fixed $x\in \Delta _3$.

Moreover, when we consider the dependency on the initial data $x_0,s$ of u, i. e. , consider a conditional probability density $u(x,t|x_0,s)$, then for any fixed $t\in (0,\infty )$, for any probability measure $\lambda _3$ on $\overline{\Delta }_n$, and for any Borel measurable subset B in $\overline{\Delta }_n$, the probability

$$\begin{aligned} v(s,x_0)=\int _{B} u(t,x|s,x_0) \lambda _3(dx) \end{aligned}$$

satisfies the Kolmogorov backward equation

$$\begin{aligned} \frac{\partial }{\partial s} v(x_0,s) = {L^{\text {rec}}}^*v(x_0,s) \quad \text { in } (\overline{\Delta }_n)_\infty =\overline{\Delta }_n\times (0,\infty ) \end{aligned}$$

(3.10)

for $v(\cdot ,s)\in C^2(\overline{\Delta }_3)$ for each fixed $s\in (0,\infty )$ and $v(x_0,\cdot )\in C^1((0,\infty ))$ for each fixed $x_0\in \overline{\Delta }_3$, where

$$\begin{aligned} {L^{\text {rec}}}^*u({p})=\frac{1}{4} \sum \limits _{\ell , h=1}^3 p^\ell (\delta _{\ell h}-p^h) \frac{\partial ^2}{\partial {p^\ell }\partial {p^h}} u({p})+ \sum \limits _\ell b^\ell ({p})\frac{\partial }{\partial p^\ell } u({p})\qquad \quad \end{aligned}$$

(3.11)

again with $b^\ell (x)=\lim _{N\rightarrow \infty }(NRD^\ell )$ is the backward operator.

When we change coordinates via

$$\begin{aligned} p=x^1+x^2,\quad q=x^1+x^3,\quad D=x^2x^3-x^1(1-x^1-x^2-x^3) \end{aligned}$$

(3.12)

(with $D\equiv D^0$ as in Eq. (3.2)), Eq. (3.10) and Lemma 2.4 directly yield the formula of Ohta and Kimura for the recombinational Wright–Fisher model (cf. [16]), i. e.

$$\begin{aligned} \frac{\partial f}{\partial t}&=\frac{1}{4}p(1-p)\frac{\partial ^2f}{{(\partial p)}^2}+\frac{1}{4}q(1-q)\frac{\partial ^2f}{{(\partial q)}^2}-\frac{1}{2}D\frac{\partial ^2f}{\partial {p}\partial {q}}+\frac{1}{2}D(1-2p)\frac{\partial ^2f}{\partial {p}\partial {D}}\nonumber \\&\quad +\frac{1}{2}D(1-2q)\frac{\partial ^2f}{\partial {q}\partial {D}}\nonumber \\&\quad +\frac{1}{4}\{pq(1-p)(1-q)-D(1-2p)(1-2q)-D^2\}\frac{\partial ^2f}{{(\partial D)}^2} \nonumber \\&\quad -\frac{1}{2}D(1+2NR)\frac{\partial f}{\partial D} \end{aligned}$$

(3.13)

for $f(\,\cdot \,,t)\in C^2(\Omega _{(p,q,D)})$ for every $t>0$ and $f(p,q,D,\,\cdot \,)\in C^1((0,\infty ))$ for $(p,q,D)\in \Omega _{(p,q,D)}$ and with

$$\begin{aligned}&\Omega _{(p,q,D)}\mathrel {\mathop :}=\nonumber \\&\quad \left\{ (p,q,D)\in \mathbb {R}^3\big \vert 0<p,q<1,\min (p,q)-pq<D<\max (p+q-1,0)-pq\right\} .\nonumber \\ \end{aligned}$$

(3.14)

Figure 1 illustrates the domain of new variables p, q, D.

Fig. 1

The transformed domain $\Omega _{(p,q,D)}$

3.2 Compositionality

There is an obvious hierarchy in the single locus case with alleles $A^0,\ldots ,A^k$. We could simply merge the alleles $A^{i_\ell }, \ldots , A^{i_{\ell -1}}$ into a single super-allele $S^\ell$, and then consider the dynamics of the $S^\ell$. In the multi-locus case, we also have a compositionality in the following sense. If, for instance in the two-locus case, one ignored the dynamics at the second locus and only considered the dynamics at the first locus, then the frequencies at the first locus would not be affected by those at the second locus. Recombination only affects the correlations between the probabilities at the two loci, but not the marginals.

Such hierarchies find a natural expression in our geometric model. For the frequencies of $A^{i}$, which are given as the sums of the frequencies of the pairs $(A^{i},B^{0})$ and $(A^{i},B^{1})$, we have a standard Wright–Fisher dynamics. When $X^i$ now denotes the frequency of $A^{i}$ and $X^{ij}$ that of the pair $(A^{i},B^{j})$, we have $X^i=\sum _j X^{ij}$. For instance, when we sum over the alleles at the second locus, the coefficients of the Kolmogorov operators satisfy, the index $\ell$ for an allele pair corresponding to the pair of indices (ij) in (3.5), (3.7),

$$\begin{aligned} \sum _{j,s =0}^1 a_{(ij)(rs)}= & {} \sum _{j,s =0}^1 \frac{1}{2}x^{(ij)}(\delta _{(ij)(rs)}-x^{(rs)})=\frac{1}{2}x^i(\delta _{ir}-x^r) \end{aligned}$$

(3.15)

$$\begin{aligned} \sum _{j=0}^1 b_{(ij)}= & {} 0, \end{aligned}$$

(3.16)

and analogously for summing over the first locus. Thus, by taking marginals, the frequency dynamics governed by the Kolmogorov operators (3.8), (3.11) lead to two frequency dynamics governed by the Kolmogorov operators on a one-dimensional state space. The dynamical process on the positive hyperoctant of the three-dimensional sphere projects to a process on the product of two one-dimensional spheres. The projected processes no longer see the recombination, because it has been summed over.

This compositionality simply expresses the fact described in Sect. 2.4 that the projections onto exponential families can be composed.

3.3 The geometry of recombination

In the following section, we will finally consider the geometrical properties of the state space of recombination. We shall find that the geometric perspective that we have developed in Sect. 2 can substantially clarify the underlying mathematical structure. Starting with the Ohta–Kimura formula (3.13), we have as the corresponding coefficient matrix of the 2nd order derivatives

$$\begin{aligned}&\big (a^{ij}(p,q,D)\big )\nonumber \\&\quad \mathrel {\mathop :}=\frac{1}{4} \begin{pmatrix} p(1-p)&{}-D&{}D(1-2p)\\ -D&{}q(1-q)&{}D(1-2q)\\ D(1-2p)&{}D(1-2q)&{} pq(1-p)(1-q)-D(1-2p)(1-2q)-D^2\\ \end{pmatrix}\!.\nonumber \\ \end{aligned}$$

(3.17)

We shall see that these coefficients coincide with those of the inverse of a Fisher metric on $\Omega _{(p,q,D)}$.

Instead of inverting those coefficients to get the Fisher metric directly, it is much simpler to switch back to the x-coordinates, i. e. , the simplex coordinates. In fact, we can work either with the simplex or the sphere coordinates.

We first change coordinates via

$$\begin{aligned}&(p,q,D)\longmapsto x=(x^1,x^2,x^3) \end{aligned}$$

(3.18)

$$\begin{aligned}&x^1\mathrel {\mathop :}=pq-D,\quad x^2\mathrel {\mathop :}=p(1-q)+D ,\quad x^3 \mathrel {\mathop :}=q(1-p)+D. \end{aligned}$$

(3.19)

The domain $\Omega _{(p,q,D)}$ then is mapped onto $\Delta _3$, and we have

$$\begin{aligned} \begin{pmatrix} \dfrac{\partial x^i}{\partial p},\dfrac{\partial x^i}{\partial q},\dfrac{\partial x^i}{\partial D} \end{pmatrix}_{i=1,2,3} =\begin{pmatrix} q&{}p&{}-1\\ 1-q&{}-p&{}1\\ -q&{}1-p&{}1 \end{pmatrix}\!. \end{aligned}$$

(3.20)

Applying the transformation formula of Lemma 2.4 transforms $a^{ij}$ into

$$\begin{aligned} (k^{ij}(x))=\frac{1}{4} \begin{pmatrix} x^1(1-x^1) &{}-x^1x^2 &{}-x^1x^3\\ -x^1x^2 &{}x^2(1-x^2) &{}-x^2x^3\\ -x^1x^3 &{}-x^2x^3 &{}x^3(1-x^3)\\ \end{pmatrix}\!, \quad x\in \Delta _3 \end{aligned}$$

(3.21)

whose inverse is

$$\begin{aligned} (k_{ij}(x))=4 \begin{pmatrix} {(x^1)}^{-1}+{(x^0)}^{-1} &{}{(x^0)}^{-1} &{}{(x^0)}^{-1}\\ {(x^0)}^{-1} &{}{(x^2)}^{-1}+{(x^0)}^{-1} &{}{(x^0)}^{-1}\\ {(x^0)}^{-1} &{}{(x^0)}^{-1} &{}{(x^3)}^{-1}+{(x^0)}^{-1}\\ \end{pmatrix}\!, \quad x\in \Delta _3 \end{aligned}$$

(3.22)

with $x^0\mathrel {\mathop :}=1-\sum _{i=1}^3 x^i$.

We then apply (2.13) to transform this via

$$\begin{aligned}&\Delta _3\longrightarrow S^3_+ \end{aligned}$$

(3.23)

$$\begin{aligned}&y^i\mathrel {\mathop :}=\sqrt{x^i} \text { for } i=1,2,3 \end{aligned}$$

(3.24)

from simplicial to spherical coordinates, which satisfies $\frac{\partial y^i}{\partial x^j}=\frac{1}{2\sqrt{x^j}} \delta ^i_j$. As a result, the coefficient matrix $(a^{ij}(p,q,D))$ of the 2nd order derivatives in Eq. (3.13) then as in (2.15), (2.14) turns from the tensor $(k^{ij})$ in coordinates x into the tensor $(l^{ij})$ in coordinates y

$$\begin{aligned} (\ell ^{ij}(y))=\frac{1}{16} \begin{pmatrix} 1-{(y^1)}^2 &{}-y^1y^2 &{}-y^1y^3\\ -y^1y^2 &{}1-{(y^2)}^2 &{}-y^2y^3\\ -y^1y^3 &{}-y^2y^3 &{}1-{(y^3)}^3\\ \end{pmatrix}\!, \quad y\in S^3_+ , \end{aligned}$$

(3.25)

and the inverse, that is the metric tensor itself, now is

$$\begin{aligned} (\ell _{ij}(y))=16 \begin{pmatrix} 1+\tfrac{{(y^1)}^{2}}{{(y^0)}^2} &{}\tfrac{y^1y^2}{{(y^0)}^2} &{}\tfrac{y^1y^3}{{(y^0)}^2}\\ \tfrac{y^1y^2}{{(y^0)}^2} &{}1+\tfrac{{(y^2)}^{2}}{{(y^0)}^2} &{}\tfrac{y^2y^3}{{(y^0)}^2}\\ \tfrac{y^1y^3}{{(y^0)}^2} &{}\tfrac{y^2y^3}{{(y^0)}^2} &{}1+\tfrac{{(y^3)}^{2}}{{(y^0)}^2}\\ \end{pmatrix}\!, \quad y\in S^3_+ \end{aligned}$$

(3.26)

with $y^0\mathrel {\mathop :}=\sqrt{1-\sum _{i=1}^3 {(y^i)}^2}$.

Thus, $(\ell _{ij})$ and $(k_{ij})$ coincide (up to the prefactor 16) with (the inverse of) the standard metric of the 3-sphere $S_+^3\subset \mathbb {R}^{4}$ in spherical or simplicial coordinates. Since scaling the Riemannian metric g with a factor $\lambda >0$, the corresponding sectional curvatures are scaled by $\frac{1}{\lambda }$, Proposition 2.1 therefore yields

Lemma 3.2

$\Omega _{(p,q,D)}$ equipped with the Fisher metric of the multinomial distribution carries the geometrical structure of a manifold of constant positive curvature $\equiv \frac{1}{16}$.

In particular, $k^{ij}(x)$ coincides (up to scaling and the missing prefactor N) with the covariance matrix of the multinomial distribution $\mathcal {M}(N;p^0,p^1,\ldots ,p^3)$ with parameters $p^i=x^i$, $i=1,2,3$; $p^0=1-\sum _{i=1}^3 x^i$. Therefore, it also coincides with the Fisher metric of the multinomial distribution on $\Delta _3$. We state this result as:

Proposition 3.3

The coefficients of the 2nd order derivatives of the Ohta–Kimura formula (3.13) are (up to a constant factor) the components of the inverse of the Fisher metric of the multinomial distribution on $\Omega _{(p,q,D)}$.

3.4 The geometry of linkage equilibrium

In order to investigate linkage equilibrium, we first consider the case of two loci. Linkage equilibrium then means that the product of the marginal frequencies of each pair of alleles $A^{i}$ and $B^{j}$ equals the frequency of the gamete $A^{i}B^{j}$. Figure 2 illustrates the set of linkage equilibrium states $W_2$ in the two-locus two-allele case. This corresponds to $D=0$. We shall now analyse the geometry of such linkage equilibrium states with the concepts of Sect. 2.

They will be represented by product metrics. Starting with the product metric on the product of two Riemannian manifolds, let $(M_1,g_1)$ and $(M_2,g_2)$ be Riemannian manifolds of dimensions n and m, and let $g_1\times g_2$ be the product metric on $M_1\times M_2$, given in local coordinates by

$$\begin{aligned} \big ((g_1\times g_2)_{rs}\big )_{r,s=1,\ldots ,n+m}= \begin{pmatrix} &{}&{}&{}\\ &{}({g_1}_{ij}(x_1))_{i,j=1,\ldots ,n} &{} 0^{n,m}&{}\\ &{}&{}&{}\\ &{} 0^{m,n} &{} ({g_2}_{kl}(x_2))_{k,l=n+1,\ldots ,n+m}&{}\\ &{}&{}&{}\\ \end{pmatrix} \end{aligned}$$

(3.27)

with $0^{n,m}$ being the $n\times m$ null matrix. The inverse metric is

$$\begin{aligned} \big ((g_1\times g_2)^{rs}\big )_{r,s=1,\ldots ,n+m}= \begin{pmatrix} &{}&{}&{}\\ &{}({g_1}^{ij}(x_1))_{i,j=1,\ldots ,n} &{} 0^{n,m}&{}\\ &{}&{}&{}\\ &{} 0^{m,n} &{} ({g_2}^{kl}(x_2))_{k,l=n+1,\ldots ,n+m}&{}\\ &{}&{}&{}\\ \end{pmatrix}. \end{aligned}$$

(3.28)

Similarly for product metrics with more than two factors.

Fig. 2

The set of linkage equilibrium states, the so-called Wright manifold, denoted by $W_2$, in two-locus two-allele case

We can now evaluate the Ohta–Kimura formula (3.13) for $D=0$. For $(p,q,0)\in \Omega _{(p,q,0)}=\left\{ (p,q,0)\in \mathbb {R}^2\times \lbrace 0\rbrace \big \vert 0<p,q<1\right\}$, (3.17) then becomes

$$\begin{aligned} (a^{ij}(p,q,0))=\frac{1}{4} \begin{pmatrix} p(1-p)&{}0&{}0\\ 0&{}q(1-q)&{}0\\ 0&{}0&{} p(p-1)q(q-1)\\ \end{pmatrix}. \end{aligned}$$

(3.29)

Its inverse is

$$\begin{aligned} (a_{ij}(p,q,0))=4 \begin{pmatrix} \frac{1}{p(1-p)}&{}0&{}0\\ 0&{}\frac{1}{q(1-q)}&{}0\\ 0&{}0&{}\frac{1}{ p(p-1)q(q-1)}\\ \end{pmatrix}. \end{aligned}$$

(3.30)

The $(a_{ij}(p,q,0))$ induces a product metric on $\Delta _1\times \Delta _1$, in which each factor $\Delta _1$ is equipped with the metric $g(x)=\frac{4}{ x(1-x)}$, that is, (up to the prefactor) the standard metric of the 1-dimensional sphere $S_{+}^1\subset \mathbb {R}_+^2$. Thus, the state space $\Omega _{(p,q,0)}$ resp. a corresponding restriction of $\Delta _3$ of the diffusion approximation of the two-loci two-allelic recombinational Wright–Fisher model in linkage equilibrium carries the geometrical structure of

$$\begin{aligned} S^1_+\times S^1_+\subset S_+^3, \end{aligned}$$

(3.31)

when equipped with the Fisher metric of the multinomial distribution (cf. Lemma 3.3). This is the positive part of the Clifford torus. We point out that the Clifford torus, while being a minimal surface with vanishing curvature, is not a totally geodesic submanifold of the 3-sphere. That means that geodesics connecting two points on the Clifford torus will in general not stay on this torus, but go through the ambient sphere. Upon reflection, this may not be so surprising in the present context, because the relevant geodesic structure is that of the unit simplex, rather than that of the sphere.

In fact, the natural interpretation is in terms of the exponential families of Sect. 2.4. The Clifford torus is nothing but the exponential family of product distributions, that is, at linkage equilibrium the distribution for the allele combinations equals the product of the marginals.

3.5 Linkage equilibria for two loci with several alleles

We now extend the notion of linkage equilibrium to models with more than two possible alleles at a locus, but for the moment still consider only two loci, say A and B. Thus, let the first locus A carry $m+1$ alleles $\{A^0,\ldots ,A^m\}$ and the second locus B carry $n+1$ alleles $\{B^0,\ldots ,B^n\}$. To simplify the notations, we put $J_A = \{0,\ldots , m\}$, $J_B = \{0,\ldots , n\}$, and $J = J_A \times J_B$. We have $(m+1)\cdot (n+1)$ linkage relations, but since the relative frequencies sum to 1, we only have mn independent linkage relations. Extending the previous definition (3.2), these are expressed by the mn coefficients of linkage disequilibrium

$$\begin{aligned} D^{ij}(x)\mathrel {\mathop :}=\sum _{\begin{array}{c} (k,l) \in J: k\ne i,l\ne j \end{array}}(x^{il}x^{kj}-x^{ij}x^{kl})\quad i=1,\ldots ,m,j=1,\ldots ,n,\quad \end{aligned}$$

(3.32)

If all $D^{ij}(x)$ vanish, the population is in linkage equilibrium.

Generalizing the scheme developed in Sect. 3.4, we want to make the $D^{ij}$ coordinates of the state space $\Delta _{(m+1)(n+1)-1}$. Again, we need additional coordinates, and so, we choose coordinates $(x^\bullet ,D)=(x^{i \bullet },x^{\bullet j},D^{ij})_{i=1,\ldots ,{m},j=1,\ldots ,{n}}$ consisting of m allele frequencies $x^{i\bullet }\mathrel {\mathop :}=\sum _{j=0}^n x^{ij}$ and n allele frequencies $x^{\bullet j}\mathrel {\mathop :}=\sum _{i=0}^m x^{ij}$ and the $D^{ij}$. Using this notation, the formula for the $D^{ij}$ simplifies, i. e.

$$\begin{aligned} D^{ij}(x)&=\sum \limits _{(k,l) \in J} (x^{il}x^{kj}-x^{ij}x^{kl})\nonumber \\&=\sum \limits _{l\in J_B} x^{il}\sum \limits _{k\in J_A} x^{kj} - x^{ij} \sum \limits _{(k,l)\in J} x^{kl} \nonumber \\&=x^{i\bullet } x^{\bullet j}- x^{ij}. \end{aligned}$$

(3.33)

Recalling (1.6), i.e., $\sum _{i,j}x^{ij}=1$, this implies that

$$\begin{aligned} D^{i\bullet }(x) = \sum \limits _{j\in J_B} (x^{i\bullet } x^{\bullet j}-x^{ij}) = x^{i\bullet } -x^{i\bullet } =0 \end{aligned}$$

(3.34)

and

$$\begin{aligned} D^{\bullet j}(x) = \sum \limits _{i\in J_A} (x^{i\bullet } x^{\bullet j}- x^{ij}) = x^{\bullet j} -x^{\bullet j} =0. \end{aligned}$$

(3.35)

Now, from (3.32)

$$\begin{aligned} \frac{\partial x^{i\bullet }}{\partial x^{kl}}= \delta ^i_k,\quad \frac{\partial x^{\bullet j}}{\partial x^{kl}}=\delta ^j_l,\quad \frac{\partial D^{ij}}{\partial x^{kl}}=-\delta ^i_k\delta ^i_l + \delta ^i_k x^{\bullet j}+x^{i\bullet }\delta ^j_l \end{aligned}$$

(3.36)

for $i,j\ne 0$ and $(k,l)\ne (0,0)$, and with (3.36), the transformation of the (inverse) metric $(a^{ij,kl}(x))=\big (x^{ij}(\delta ^{ij}_{kl}-x^{kl}) \big )$ leads to

$$\begin{aligned} a^{x^{i\bullet },x^{k\bullet }}(x^\bullet ,D)&=x^{i\bullet }(\delta ^i_k-x^{k\bullet })\nonumber \\ a^{x^{\bullet j},x^{\bullet l}}(x^\bullet ,D)&=x^{\bullet j}(\delta ^j_l-x^{\bullet l})\ a^{x^{i \bullet },x^{\bullet l}}(x^\bullet ,D)&=x^{il}-x^{i \bullet }x^{\bullet l}=D^{il} \end{aligned}$$

(3.37)

$$\begin{aligned}&\equiv a^{x^{\bullet l},x^{i \bullet }}(x^\bullet ,D) \text { by symmetry}. \end{aligned}$$

(3.38)

The coefficients $a^{x^{i \bullet },x^{\bullet l}}(x^\bullet ,D)$ vanish at linkage equilibrium. Next,

$$\begin{aligned} a^{x^{i\bullet },D^{k l}}(x^{\bullet },D)&=-\delta ^{i}_{k}D^{k l}+x^{i\bullet }D^{k l}+x^{k\bullet }D^{i l}\nonumber \\&\equiv a^{D^{k l},x^{i\bullet }}(x^\bullet ,D). \end{aligned}$$

(3.39)

Again, these entries vanish in linkage equilibrium. Finally,

$$\begin{aligned} a^{D^{i j },D^{k l }}(x^\bullet ,D) =(x^{i\bullet }-\delta ^{i}_{k})x^{k\bullet }(x^{\bullet j}-\delta ^{j}_{l})x^{\bullet l}. \end{aligned}$$

(3.40)

Again, the corresponding coordinate representation of the inverse metric in linkage equilibrium becomes a block matrix, i. e.

$$\begin{aligned} (a^{(x^\bullet ,D)})=\begin{pmatrix} &{}&{}&{}&{}\\ \,({a}^{x^{i\bullet },x^{k\bullet }}) &{} {0}^{m,n}&{}&{} {0}^{m,mn}\\ \,{0}^{n,m}&{}({a}^{x^{\bullet j},x^{\bullet l}})&{}&{} {0}^{n,mn}\\ \,{0}^{mn,m}&{} {0}^{mn,n} &{}&{}(a^{D^{ij},D^{kl}})\\ &{}&{}&{}&{}\\ \end{pmatrix}\!. \end{aligned}$$

(3.41)

Thus, we have generalized the representation of the metric corresponding to the Ohta–Kimura formula in linkage equilibrium (cf. Eq. (3.29)) to an arbitrary number of alleles. Since as before the inverse of a block matrix is a block matrix, we obtain the product structure of $(a_{(x^\bullet ,D)}(x^\bullet ,0))$, given as

Proposition 3.4

The states of linkage equilibrium of the Wright–Fisher model for two loci with $m+1$ and $n+1$, resp., alleles lie on the product manifold

$$\begin{aligned} S^{m}_+\times S^{n}_+\subset S_+^{m+n+1}. \end{aligned}$$

(3.42)

Note that here we have used a somewhat loose formulation. A more precise statement is given in Theorem 3.5 below.

3.6 General linkage equilibria

We now move on to an arbitrary number of loci and alleles. We shall again describe linkage equilibria as product metrics when equipped with their Fisher metric. However, when there are more than two loci, the situation gets significantly more complicated as now linkage, that is, deviation from independence of relative frequencies at different loci, can occur not only between pairs of loci, but also in higher order relations. That is, for instance, even in the absence of pairwise correlations, there could be triple correlations. In particular, we need to clarify the term ‘linkage equilibrium’ in this extended setting. This may be achieved by generalizing (3.32). A short reflection on the reasoning in Sect. 3.2 convinces us that we may assume for simplicity that the number of possible alleles at the different $k\ge 2$ loci is the same, say $n+1\ge 2$.

Extending the previous notation, we put $x^{\langle i_{j},\bullet \rangle }\mathrel {\mathop :}=x^{\bullet ,\ldots ,\bullet ,i_j\bullet ,\ldots ,\bullet }$ with index $i_j$ appearing at the j-th position while $\bullet$ again indicates that it is summed over the corresponding index. We then introduce the coefficients of generalisedl-linkage disequilibrium for $2\le l \le k$

$$\begin{aligned} D_l^{\langle i_{j_1},\ldots ,i_{j_l},\bullet \rangle }(x) \mathrel {\mathop :}=\prod _{m=1}^l x^{\langle i_{j_m},\bullet \rangle } - x^{\langle i_{j_1},\ldots ,i_{j_l},\bullet \rangle } \end{aligned}$$

(3.43)

for $i_{j_1},\ldots ,i_{j_l}=1,\ldots ,n$ and every subset $\lbrace j_1,\ldots ,j_l\rbrace \subset \lbrace 1,\ldots ,k\rbrace$ with $j_r\ne j_s$ for $r\ne s$. These coefficients express the linkages for sets of l loci.

The $\left( {\begin{array}{c}k\\ l\end{array}}\right) n^l$ coefficients of generalized l-linkage disequilibrium, $l=2,\ldots ,k$, together with the kn allele frequencies yield a set of as coordinates of the $\big ((n+1)^k-1\big )$-dimensional model. This follows from a counting argument, since

$$\begin{aligned} \sum _{l=1}^k\left( {\begin{array}{c}k\\ l\end{array}}\right) n^l=(n+1)^k-1. \end{aligned}$$

(3.44)

Instead of 1-linkage disequilibrium coefficients, which would provide no information, allele frequencies are used as non-interaction coordinates.

We then speak of a linkage equilibrium if for all l the coefficients of generalized l-linkage disequilibrium vanish. At linkage equilibrium, we again have a product structure for the state space $\Delta _{(n+1)^k-1}$ when equipped with the Fisher metric of the multinomial distribution,

$$\begin{aligned} \underbrace{S^{n}_+\times \cdots \times S^{n}_+}_{k}\subset S_+^{k(n+1)-1}. \end{aligned}$$

(3.45)

To see this, we start with the allele frequencies $x^{i_1\bullet \ldots \bullet }$, $i_1=1,\ldots ,n$. They parametrize the multinomial distribution $\mathcal {M}$. We consider the corresponding Fisher metric $g^{\cdot \bullet \ldots \bullet }$ on $\Delta _{n}$ (cf. also Sect. 2.2). Since $\sum _{i_1} x^{i_1\bullet \ldots \bullet }=1$, ${(x^{i_1\bullet \ldots \bullet })}_{i_1}$ may itself be interpreted as a discrete probability distribution in $\Delta _{n}$. The Fisher metric ${\tilde{g}}^{\cdot \bullet \ldots \bullet }$ on $\Delta _{n}$ is then given by

$$\begin{aligned} {\tilde{g}}^{\cdot \bullet \ldots \bullet }_{ij}(x^{\cdot \bullet \ldots \bullet })\mathrel {\mathop :}=\frac{1}{x^{i\bullet \ldots \bullet }}\delta ^i_j+\frac{1}{x^{0\bullet \ldots \bullet }} \end{aligned}$$

(3.46)

By (2.10), both metrics coincide, except for the factor N, which we shall simply ignore. The same works for $x^{\bullet i_2\bullet \ldots \bullet },\ldots ,x^{\bullet \ldots \bullet i_k}$, $i_j=1,\ldots ,n$.

We have the product

$$\begin{aligned} (\Delta _{n},{g}^{\cdot \bullet \ldots \bullet })\times (\Delta _{n},{g}^{\bullet \cdot \bullet \ldots \bullet })\times \cdots \times (\Delta _{n},{g}^{\bullet \ldots \bullet \cdot })&\longrightarrow (\Delta _{(n+1)^k-1},{g}) \end{aligned}$$

(3.47)

$$\begin{aligned} (x^{i_1\bullet \ldots \bullet },x^{\bullet i_2\bullet \ldots \bullet },\ldots ,x^{\bullet \ldots \bullet i_k})&\longmapsto x^{i_1i_2\ldots i_k} \end{aligned}$$

(3.48)

The image of the product, i. e. the corresponding restriction of the Fisher metric, has a product structure itself, if the following independence relations are satisfied:

$$\begin{aligned} x^{i_1\bullet \ldots \bullet }\cdot x^{\bullet i_2\bullet \ldots \bullet }\cdots x^{\bullet \ldots \bullet i_k}=x^{i_1i_2\ldots i_k},\quad i_1,i_2,\ldots ,i_k=1,\ldots , n \end{aligned}$$

(3.49)

Suppressing the respective n-th coordinate indices, this corresponds to the vanishing of all coefficients of linkage disequilibrium $D_l^{\langle i_{j_1},\ldots ,i_{j_l},\bullet \rangle }(x)$ for $i_{j_1},\ldots ,i_{j_l}=1,\ldots ,n$ and every subset $\lbrace j_1,\ldots ,j_l\rbrace \subset \lbrace 1\ldots ,k\rbrace$ with $j_r\ne j_s$ for $r\ne s$ and $l=2,\ldots ,k$. We thus have shown

Theorem 3.5

At linkage equilibrium, for $n+1\ge 2$ and $k\ge 2$ the restriction of the state space $\Delta _{(n+1)^k-1}$ of the diffusion approximation of a k-loci $(n+1)$-allelic recombinational Wright–Fisher model equipped with the Fisher metric of the multinomial distribution is the kn-dimensional product manifold

$$\begin{aligned} \underbrace{S^{n}_+\times \cdots \times S^{n}_+}_{{k}}\subset S_+^{k(n+1)-1}. \end{aligned}$$

(3.50)

Such a result of course also holds when the number of alleles at the different loci varies. Let the $j^{th}$ locus contain $n_j+1$ alleles ($j=1,\ldots ,k$). Putting ${\mathbf {n}} = (n_1,\ldots , n_k)$, $|{\mathbf {n}}| = n_1+\cdots +n_k$ and ${\mathbf {1}} = (1,\ldots ,1)$, we obtain for this k-loci $({\mathbf {n}}+{\mathbf {1}})$-allelic recombinational Wright–Fisher model:

Corollary 3.6

At linkage equilibrium, for $k\ge 2$ and $n_j+1 \ge 2$ for all $j=1,\ldots ,k$, the restriction of the state space $\Delta _{\prod _{j=1}^k (n_j+1)-1}$ of the diffusion approximation of a k-loci $({\mathbf {n}}+{\mathbf {1}})$-allelic recombinational Wright–Fisher model equipped with the Fisher metric of the multinomial distribution is the $|{\mathbf {n}}|$-dimensional product manifold

$$\begin{aligned} \underbrace{S^{n_1}_+\times \cdots \times S^{n_k}_+}_{{k}}\subset S_+^{|{\mathbf {n}}|+k-1}. \end{aligned}$$

(3.51)

The product manifolds appearing in these results are exponential families in the sense of Sect. 2.4.

We note that the preceding considerations do not depend on a particular recombination scheme. When no recombination takes place at all, however, the preceding becomes trivial insofar as in that case a k-loci $({\mathbf {n}}+{\mathbf {1}})$-allelic model is formally the same as a (1-locus) $(|{\mathbf {n}}|+k)$-allelic model.

4 Linkage disequilibrium and mutual information for two loci

In this section, we shall answer the question raised in the introduction, about the asymptotics of a process that starts outside of linkage equilibrium, in particular whether it will asymptotically reach equilibrium, and if so, at what rate. We study the asymptotic behavior of two quantities: linkage disequilibrium (local quantity) and mutual information (global quantity). We consider both the evolution of the Fokker–Planck or Kolmogorov forward equation and that of the corresponding Langevin equation. The former is a deterministic partial differential equation for the evolution of a probability density, and for simplicity, we call this the deterministic setting. The latter is a stochastic ordinary differential equation that describes the interaction of deterministic effects (coming from recombination, that is, the dynamics of linkage in the present setting) and stochastic effects (from random sampling). We call this the stochastic setting.

It turns out that in the deterministic setting, the linkage disequilibrium and mutual information exponentially decrease to zero when the number of generations goes to infinity. However, in the stochastic setting, only the expected linkage disequilibrium exponentially decreases to zero, the expected mutual information can increase or decrease, but eventually also converges to zero when the number of generations goes to infinity.

4.1 Deterministic setting

In this setting, we work with an infinite population each member of which has two loci A and B. Similar to the case of Sect. 3.5 for finite population size, the relative frequency of genotype $A_iB_j$, denoted by $x^{ij}$, evolves

$$\begin{aligned} x^{ij}(t+\delta t)= & {} \sum \limits _{(k,l)\in J: k\ne i, l\ne j} (1- r\delta t) x^{ij}(t) x^{kl}(t) + \sum \limits _{k\in J_A, k\ne i} x^{ij}(t)x^{kj}(t) \nonumber \\&+\sum \limits _{l\in J_B, l\ne j} x^{ij}(t)x^{il}(t) + (x^{ij}(t))^2 +\sum \limits _{(k,l)\in J: k\ne i, l\ne j} r\delta t x^{il}(t) x^{kj}(t) \nonumber \\= & {} x^{ij}(t) + r\delta t \sum \limits _{(k,l)\in J: k\ne i, l\ne j} (x^{il}(t) x^{kj}(t) - x^{ij}(t) x^{kl}(t)) \nonumber \\= & {} x^{ij}(t) + r \delta t D^{ij}(x(t)), \end{aligned}$$

(4.1)

where r is the deterministic recombination rate which can be considered as the limit of R(N)N when N goes to infinity in finite population. This implies the ODE

$$\begin{aligned} \frac{d}{dt} x^{ij}(t) = b_{ij}(x(t)), \quad \text { for all } (i,j) \in J, \end{aligned}$$

(4.2)

where

$$\begin{aligned} b_{ij}(x) = r D^{ij}(x) = r \Big (x^{i\bullet } x^{\bullet j} - x^{ij}\Big ), \end{aligned}$$

(4.3)

where $r=\lim _{N\rightarrow \infty }R(N) N$.

$D^{ij}(x)$ is the local linkage disequilibrium between $A_i$ and $B_j$ from (3.32). We let I(A; B) be the mutual information between the loci A and B, i.e.

$$\begin{aligned} \begin{aligned} I(A;B)(x)&= d_{KL}(p_{AB}\Vert p_A p_B) = \sum \limits _{(i,j)\in J} p_{A,B}(i,j) \log \frac{p_{A,B}(i,j)}{p_{A}(i)p_{B}(j)}\\&= \sum \limits _{(i,j)\in J} x^{ij} \log \frac{x^{ij}}{x^{i\bullet } x^{\bullet j}} \end{aligned} \end{aligned}$$

(4.4)

with the Kullback–Leibler divergence $d_{KL}$ of (2.28). We have the following result.

Theorem 4.1

In the deterministic setting, the local linkage disequilibrium coefficients $D^{ij}$ and the mutual information I(A; B) between two loci A and B exponentially decrease to zero when the number of generations goes to infinity.

Proof

From (4.2), (4.3), we obtain

$$\begin{aligned} \frac{d}{dt} D^{ij}(x(t)) = -r D^{ij}(x(t)) \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \frac{d}{dt} I(A;B)(x(t))&= -r \sum \limits _{(i,j)\in J} \sum \limits _{(k,l)\in J} (x^{il} x^{kj} -x^{ij} x^{kl})\Big (\log (x^{il} x^{kj}) - \log (x^{ij} x^{kl})\Big ) \\&= -r \sum \limits _{(i,j)\in J} (x^{ij} - x^{i\bullet } x^{\bullet j}) \log \frac{x^{ij}}{x^{i\bullet } x^{\bullet j}}\\&= -r \sum \limits _{(i,j)\in J} x^{ij} \log \frac{x^{ij}}{x^{i\bullet } x^{\bullet j}}-r \sum \limits _{(i,j)\in J} x^{i\bullet } x^{\bullet j} \log \frac{x^{i\bullet } x^{\bullet j}}{x^{ij}}\\&\le -r I(A;B)(x(t)) \end{aligned} \end{aligned}$$

because of $\sum _{(i,j)\in J} x^{i\bullet } x^{\bullet j} \log \frac{x^{i\bullet } x^{\bullet j}}{x^{i,j}} = d_{KL}(p_A p_B\Vert p_{AB})\ge 0.$ This implies the proof. $\square$

4.2 Stochastic setting

For an individual trajectory, rather than the ODE (4.2), we have the SDE

$$\begin{aligned} dX^{ij}(t) = b_{ij}(X(t)) dt + \sum \limits _{(k,l)\in J }\sigma _{ij,kl}(X(t)) dW_{kl}(t), \quad \text { for all } (i,j) \in J, \,t\ge 0,\nonumber \\ \end{aligned}$$

(4.5)

where

$$\begin{aligned} \sigma _{ij,kl}(X) = \sqrt{X^{ij}}(\delta _{ij,kl}-\sqrt{X^{ij} X^{kl}}). \end{aligned}$$

Summing over a locus yields, because the linkage terms sum to 0 (see (3.34) and (3.35))

$$\begin{aligned} dX^{i\bullet }(t) = \sum \limits _{(k,l)\in J }\sigma _{i\bullet ,kl}(X(t)) dW_{kl}(t), \quad \text { for all } i \in J_1, \,t\ge 0, \end{aligned}$$

(4.6)

and

$$\begin{aligned} dX^{\bullet j}(t) = \sum \limits _{(k,l)\in J }\sigma _{\bullet j,kl}(X(t)) dW_{kl}(t), \quad \text { for all } j \in J_2, \,t\ge 0, \end{aligned}$$

(4.7)

where $\sigma _{i\bullet ,kl}(X) = \sum _{j=0}^{n} \sigma _{ij,kl}(X)$ and $\sigma _{\bullet j,kl}(X) = \sum _{i=0}^{m} \sigma _{ij,kl}(X)$.

Although the trajectories of the SDE are subjected to noise, we can still derive the asymptotic decay of the expected local linkage disequilibria, similar to Theorem 4.1.

Theorem 4.2

The expected local linkage disequilibrium exponentially decrease to zero when the number of generations goes to infinity.

Proof

With the stochastic Leibniz rule (see also [16, Formula (28)] for another approach) we obtain

$$\begin{aligned} d D^{ij}(X(t)) = -(r+1) D^{ij}(X(t)) dt - \sum \limits _{(k,l)\in J} \alpha _{ij,kl}(X(t)) dW_{kl}(t), \end{aligned}$$

where

$$\begin{aligned} \alpha _{ij,kl}(X) = \sigma _{ij,kl}(X) - X^{i\bullet }\sigma _{\bullet j,kl}(X) -X^{\bullet j} \sigma _{i\bullet ,kl}(X). \end{aligned}$$

By taking the expectation, we obtain

$$\begin{aligned} d {{\,\mathrm{E}\,}}D^{ij}(X(t)) = -(r+1) {{\,\mathrm{E}\,}}D^{ij}(X(t)) dt, \end{aligned}$$

which implies ${{\,\mathrm{E}\,}}D^{ij}(X(t)) = e^{-(r+1)t}{{\,\mathrm{E}\,}}D^{ij}(0)$. This completes the proof. $\square$

However, this does not hold for the global quantity I(A; B). In fact, by applying Itô’s calculus, we obtain

$$\begin{aligned} dI(A;B)(X(t))= & {} \Bigg (\frac{mn}{2}-r \sum \limits _{(i,j)\in J} \Big (X^{ij}(t) - X^{i\bullet }(t)X^{\bullet j}(t)\Big ) \log \frac{X^{ij}(t)}{X^{i\bullet }(t)X^{\bullet j}(t)} \Bigg )dt \nonumber \\&+ \sum \limits _{(k,l)\in J} \beta _{kl}(X(t)) dW_{kl}(t) \end{aligned}$$

(4.8)

where

$$\begin{aligned} \beta _{kl}(X) = \sum \limits _{(i,j)\in J} \sigma _{ij,kl}(X) \log \frac{X^{ij}}{X^{i\bullet } X^{\bullet j}}. \end{aligned}$$

Therefore, when r is small enough, by taking expectations of both sides, we see that ${{\,\mathrm{E}\,}}I(A;B)$ can increase.

Since we do not allow for mutations, when one allele disappears, it will never come back. This is also contained in Eqs. (4.6) and (4.7). Indeed, when, for example, $A_i$ disappears at generation t, i.e. $X^{i\bullet }(t)=0$, then from Eq. (4.6) we obtain $dX^{i\bullet }(s) =0$ which implies that $X^{i\bullet }(s) = 0$ for all $s\ge t$. Then

$$\begin{aligned} X^{ij}(s) \log \frac{X^{ij}(s)}{X^{i\bullet } (s)X^{\bullet j}(s)} = 0 \quad \text { for all } j\in J_2. \end{aligned}$$

It implies that

$$\begin{aligned} I(A;B)(X) = \sum \limits _{(i',j)\in (J_1-\{i\})\times J_2} X^{i',j} \log \frac{X^{i',j}}{X^{i'\bullet } X^{\bullet j}}, \end{aligned}$$

redefining I(A; B) when allele $A_i$ disappears from the population.

This process will repeat until there is a fixation at some locus whence $I(A;B) =0$. Thus, I(A; B) will eventually reach 0, but as we have just seen, not necessarily monotonically.

Figure 3 shows a realization of $X^{ij}(t)$, $D(t):=D(X(t))$ and $I(t):=I(A;B)(X(t))$ for the two-locus two-allele model. We used a Mathematica code to simulate numerical solutions $X^{ij}(t)$ of SDE (4.5) for the two-locus two-allele model. The stepsize is $h=0.001$, the time is $T=3000$, the recombination rate $r=0.3$, the initial data is $X^{00}(0) = X^{01}(0)=X^{10}(0)=X^{11}(0) =0.25$. We then calculate the linkage disequilibrium $D(t)=X^{00}(t)X^{11}(t) - X^{01}(t)X^{10}(t)$ and the mutual information

$$\begin{aligned} \begin{aligned} I(t)&= X^{00}(t) \log \frac{X^{00}(t)}{X^{0\bullet }(t) X^{\bullet 0}(t)}+X^{01}(t) \log \frac{X^{01}(t)}{X^{0\bullet }(t) X^{\bullet 1}(t)}\\&\quad +X^{10}(t) \log \frac{X^{10}(t)}{X^{1\bullet }(t) X^{\bullet 0}(t)}+X^{11}(t) \log \frac{X^{11}(t)}{X^{1\bullet }(t) X^{\bullet 1}(t)}. \end{aligned} \end{aligned}$$

We note that in this realization, $X^{01}(t)$ (blue) goes to zero first (at time $t=508$). At this time D(508) and I(508) are still different from zero therefore we see that $X^{01}(t)$ becomes positive again after this time (e.g., at time $t=510$). However, at time $t=534$ when both $X^{01}(534)$ and $X^{11}(534)$ (cyan) are equal to zero (then $D(534) = I(534) = 0$) therefore they both remain zero and never become positive again. Now, only $X^{00}(t)$ (red) and $X^{10}(t)$ (green) are positive and varying. At time $t=2447$, $X^{00}(2447) = 0$ and $X^{10}(2447) = 1$ the process stops with the fixation of gamete $A^1B^0$ (see Fig. 3).

Fig. 3

A realization of $X^{00}(t), X^{01}(t), X^{10}(t), X^{11}(t), D(t), I(t)$ in the two-locus two-allele case with $r = 0.3$, $X^{00}(0) = X^{01}(0)=X^{10}(0)=X^{11}(0) =0.25$, h=0.001, T=3000. The stochastic process X(t) first touches the boundary $X^{01}=0$ but goes back inside the Wright manifold (see Fig. 2). It then touches the boundary part $[A_0B_0,A_1B_0]$ of the Wright manifold at (0.339, 0, 0.661, 0) and runs inside this segment until it stops at the vertex $A_1B_0$

4.3 A final remark

As explained in Sect. 2.4, among all distributions with the same marginals, the product distributions, that is, the linkage equilibria, are those of highest entropy, see (2.29). As explained in the preceding sections, the random dynamics of population genetics lead towards states of linkage equilibrium. Thus, we here see a tendency to increase the entropy. On the other hand, random genetic drift tends to eliminate alleles until only one remains at each site, and this is a state of vanishing entropy. Hence random genetic drift decreases the entropy.