1 Introduction

Gas journal bearings are extensively utilized in high-precision and high-speed machine tools owing to their low heat generation, high precision, and approximate zero friction. Bearing performance (the key component of equipment) is directly related to machining accuracy. Over the years, various experts have worked on parameter optimization and structural design to enhance the performance of gas journal bearings. Xiao et al. [1] concluded that the aerodynamic effect improves static performance of aerostatic journal micro-bearings at high speeds with large eccentricities. Yang et al. [2] conducted an investigation on how static and dynamic performance of the gas journal bearing is influenced by numbers and locations of orifice-type restrictors. Otsu et al. [3] conducted numerical and experimental verifications, which demonstrated that gas journal bearings equipped with circumferential shallow grooves between orifices had large stiffness and high threshold speeds. Chen et al. [4] discussed the length and depth effects of axial and circumferential grooves, orifice diameter, and misalignment angle on static performance of aerostatic journal bearings. Moreover, suggested values to achieve superior static performance were provided on the basis of simulations. Zhang et al. [5, 6] concluded that the horizontal deviation had a significant impact on static and dynamic performance of gas journal bearings. Load capacity and stiffness decreased as the degree of journal misalignment at stationary state increased, while they increased as misalignment at high speeds increased. Furthermore, the stability threshold of the inertial force increases with the growth of misalignment degree, whereas the stability threshold of the vortex ratio decreases with the increase of misalignment. Lu et al. [7] studied how structural deformation affects performance of aerostatic bearings based on a multi-physics coupling model.

Computational fluid dynamics (CFD) is frequently utilized in structural design and performance calculation of gas journal bearing to obtain detailed flow field in bearing clearances. Eleshaky [8] employed CFD to discuss phenomena of pressure depression in aerostatic bearings. The research showed that this phenomenon resulted from the transition of supersonic flow into subsonic flow through a pseudo-shock region. The CFD simulation was accompanied by numerous calculations. Therefore, finite difference method (FDM) and finite element method (FEM) were extensively utilized in performance analysis of gas journal bearings due to their high calculation efficiency. Lo et al. [9] adopted FDM for obtaining the gas pressure distributions in gas films, in which the rate cutting method was used to guarantee calculation convergence at a gas film thickness thinner than 8 μm. Furthermore, their discussion covered load capacities, mass flow rates, and stiffnesses, which were conducted using varying orifice diameters and supply pressures. Liu et al. [10] utilized FDM to calculate nonlinear Reynolds equation, taking into account shaft-rotating effects of the external pressure air journal bearing. Moreover, gas pressure distributions in bearing clearance at varied rotation speeds and eccentricity ratios were illustrated. Li et al. [11] utilized flow difference as the feedback in Gauss–Seidel iteration when calculating Reynolds equation through FDM and analyzed influences of bearing parameters on load capacity and stiffness. Their results verified that this method was insensitive to initial conditions and was helpful for reducing iteration times.

Compared with FDM, FEM was used to analyze the performance of gas journal bearings with complicated structures because of the flexibility of meshing grids and high precision. Gao et al. [12] employed FEM to research gas pressure distributions, mass flow rates, load capacities, attitude angles, and stiffnesses of gas journal bearings at rotation speeds higher than 100 krpm and varied eccentricity ratios. Du et al. [13] established the mathematical model for gas journal bearings with externally pressurized featuring circumferential or axial pressure-equalizing grooves (PEGs) and researched static performance by using FEM. They concluded that bearings with one or two axial PEGs situated close to the thinnest gas film thickness were advantageous in enhancing load capacities and stiffnesses. Cui et al. [14] researched effects of manufacturing error (surface waviness and non-flatness), bearing parameters, and journal misalignment on angular stiffness of aerostatic bearings by using FEM. Their results indicated that angular stiffness was significantly influenced by gas film thicknesses, orifice diameters, and eccentricity. Furthermore, misalignment angle and manufacturing errors exerted an enormous influence on distribution of gas pressure. Average gas film thicknesses according with the minimum angular stiffness increased as the orifice diameter enlarged.

The discharge coefficient is the correction factor between mass flow rate of the orifice and that of the ideal nozzle. This coefficient markedly influenced the calculation accuracy of FDM or FEM. Numerous scholars consider the discharge coefficient to be a constant of 0.8. Renn and Hsiao [15] compared the mass flow rate of aerostatic bearings obtained through CFD simulations with the results of experiments and verified that differences existed between orifice-type restrictors and ideal nozzles. Moreover, the discharge coefficient and the critical pressure ratio (the intersection of choked and subsonic flows) were recommended to be 0.8–0.85 and 0.35–0.4, respectively. Belforte et al. [16] experimentally given an empirical equation for calculating discharge coefficient of the bearing with the orifice-type restrictor. Furthermore, Song et al. [17] proposed a modified formula for discharge coefficient of gas journal bearing considering rotation speed and gas film thickness based on CFD results. Neves et al. [18] defined discharge coefficient as a function of pressure ratio (\(p_{\text{d}}\)/\(p_{0}\), \(p_{\text{d}}\) is gas pressure at orifice outlet, and \(p_{0}\) is supply pressure) at subsonic flow region and as a constant of 0.88 at the sonic flow region.

Attitude angle characterizes the relative positions of the rotor and sleeve centroids of gas journal bearings, which results from the aerodynamic effect and directly relates to the machining precision of high-speed and high-precision machine tools. However, introducing the rotation speed term into the stiffness matrix is difficult, and the impact of the speed term on the calculation results is rarely considered when FEM is employed to calculate Reynolds equation in existing literature. Some studies discussed performance of gas journal bearings with rotation speed using FEM, but the derivation process was incomplete. FEM is used in this paper to calculate Reynolds equation with speed terms and analyze performance of the gas journal bearing, in which the proportional division method is employed to enhance calculation accuracy and efficiency. The stiffness matrix calculation formula suitable for linear triangular element bodies with the rotation velocity term is also provided. The impact of speed changes on static performance of bearings is comprehensively analyzed, and the theoretical derivation process is complete. Furthermore, the influences of restriction parameters (average gas film thicknesses and orifice diameters) and operation parameters (supply pressure, rotation speed, and eccentricity ratio) on load capacity, stiffness, and attitude angle are discussed. The following sections in the article include as follows. Section 2 studies FEM for solving Reynolds equation with the rotation speed term. Section 3 analyzes influence of bearing parameters on the attitude angle, load capacity, and stiffness. This section also discusses the circumferential pressure distributions with varied restrictions and operation parameters. Finally, Sect. 4 summarizes the conclusions. The stiffness matrices in FEM are provided in Appendix A. Meanwhile, the derivation of the modified proportional factor in the proportional division method is presented in Appendix B.

2 Mathematical model

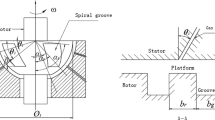
2.1 Structure of Gas Journal Bearings

Figure 1 shows the typical structure of the gas journal bearing, in which two rows of orifice-type restrictors are evenly distributed inside the sleeve in the circumference located at the L/4 bearing edges. The x, y, and z are the axial, radial, and circumferential coordinates of the gas journal bearings rotor, respectively. Pressurized gas flows into bearing clearances through orifices and discharges to the atmosphere at bearing edges. The rotor centroid is located at \(O^{\prime}_{\text{r}}\) in static conditions due to rotor gravity and external loads. However, pressurized gas is driven into the wedge-shaped film when the rotor rotates due to gas viscosity, which generates aerodynamic pressure and deviates the rotor centroid from \(O^{\prime}_{\text{r}}\) to \(O_{\text{r}}\). This attitude angle \(\varphi\) is a angle between \(\overline{{O_{\text{s}} O_{\text{r}} }}\) and \(\overline{{O_{\text{s}} O^{\prime}_{\text{r}} }}\). This angle changes the bearing clearance between the sleeve and rotor and markedly influences performance of the bearing. The gas film thickness in this bearing clearance is

$$h = h_{\text{m}} \left[ {1 - \varepsilon \cos \left( {\theta - \varphi } \right)} \right]$$
(1)

where eccentricity ratio \(\varepsilon = c/h_{\text{m}}\). The pressure difference in this bearing clearance caused by eccentricity ratio provides load capacity of this bearing.

Fig. 1
figure 1

Typical structure of gas journal bearing

Full size image

2.2 Governing Equation

The flow field is assumed to be isothermal and laminar for performance analysis of bearings. Moreover, the lubricant is regarded as an ideal gas, and its viscosity is constant. Therefore, the dimensionless steady-state Reynolds equation is

$$\frac{\partial }{{\partial \overline{x}}}\left( {\overline{h}^{3} \frac{{\partial \overline{p}^{2} }}{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{z}}}\left( {\overline{h}^{3} \frac{{\partial \overline{p}^{2} }}{{\partial \overline{z}}}} \right) + \overline{Q}\delta_{i} = \Lambda_{x} \frac{{\partial \overline{h}\overline{p}}}{{\partial \overline{x}}} + \Lambda_{z} \frac{{\partial \overline{h}\overline{p}}}{{\partial \overline{z}}}$$
(2)

where \(\delta_{i}\) is the Kronecker delta, \(\delta_{i} = 1\) at locations where an orifice exists, and \(\delta_{i} = 0\) at other locations.

The dimensionless parameters \(\overline{x}\), \(\overline{z}\), \(\overline{h}\), \(\overline{p}\), and \(\overline{Q}\) are defined as follows (ρ is the air density)

$$\overline{x} = \frac{x}{L},\overline{z} = \frac{z}{L},\overline{h} = \frac{h}{{h_{\text{m}} }},\overline{p} = \frac{p}{{p_{0} }},\overline{Q} = \frac{{24\eta L^{2} p_{\text{a}} }}{{h_{\text{m}}^{3} p_{0}^{2} \rho_{\text{a}} }}\rho \tilde{v}$$

\(\Lambda_{x}\) and \(\Lambda_{z}\) are dimensionless bearing numbers in the x and z directions, respectively.

$$\Lambda_{x} { = }\frac{12\eta uL}{{h_{\text{m}}^{2} p_{0} }},\Lambda_{z} { = }\frac{12\eta wL}{{h_{\text{m}}^{2} p_{0} }}$$

where u and w are gas velocities in the x and z directions, separately. The square of dimensionless gas pressure is

$$\overline{f} = \left( {\frac{p}{{p_{0} }}} \right)^{2} = \overline{p}^{2} (\overline{x},\overline{z}) = \overline{f}(\overline{x},\overline{z})$$
(3)

Substituting Eq. (3) into Eq. (2), the dimensionless Reynolds equation can be written as

$$\frac{\partial }{{\partial \overline{x}}}\left( {\overline{h}^{3} \frac{{\partial \overline{f}}}{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{z}}}\left( {\overline{h}^{3} \frac{{\partial \overline{f}}}{{\partial \overline{z}}}} \right) + \overline{Q}\delta_{i} - \lambda \left( {\overline{u}\frac{{\partial \overline{h}\overline{p}}}{{\partial \overline{x}}} + \overline{w}\frac{{\partial \overline{h}\overline{p}}}{{\partial \overline{z}}}} \right) = 0$$
(4)

where

$$\overline{u} = \frac{u}{V},\overline{w} = \frac{w}{V},\lambda { = }\frac{12\eta VL}{{h_{\text{m}}^{2} p_{0} }}$$

Boundary conditions are as follows:

  1. (1)

    Atmospheric boundary: \(\overline{f} = \frac{{p_{\text{a}}^{2} }}{{p_{0}^{2} }} = \overline{f}_{\text{a}}\).

  2. (2)

    Symmetric boundary: \(\frac{{\partial \overline{f}}}{{\partial \overline{n}_{\text{s}} }} = 0\) or \(\frac{{\partial \overline{p}}}{{\partial \overline{n}_{\text{s}} }} = 0\).

  3. (3)

    Orifice boundary: \(\overline{f} = \frac{{p_{\text{d}}^{2} }}{{p_{0}^{2} }} = \overline{f}_{\text{d}}\).

where \(\overline{n}_{\text{s}}\) is the dimensionless normal direction of the symmetric boundary. The weak solution of Eq. (4) is obtained through Galerkin weighted residual technique.

$$\begin{aligned} & & \int_{\Omega } {\left[ {\frac{\partial }{{\partial \overline{x}}}\left( {\overline{h}^{3} \frac{\partial f}{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{z}}}\left( {\overline{h}^{3} \frac{\partial f}{{\partial \overline{z}}}} \right) + \overline{Q}\delta_{i} } \right.} \\ & \quad \left. { - \lambda \left( {\overline{u}\frac{{\partial f^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \overline{h}}}{{\partial \overline{x}}} + \overline{w}\frac{{\partial f^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \overline{h}}}{{\partial \overline{z}}}} \right)} \right]\delta f{\text{d}}\overline{x}{\text{d}}\overline{z} \\ & \quad - \int_{{s_{\text{s}} }} {\overline{h}^{3} \frac{\partial f}{{\partial n_{\text{s}} }}\delta f{\text{d}}\overline{s} = 0} \\ \end{aligned}$$
(5)

where δf is the square variation of dimensionless gas pressure, \(s_{\text{s}}\) is the symmetric boundary, and \(\Omega\) is the computational domain.

The following equation can be obtained by integrating Eq. (5).

$$\begin{aligned} & \int_{\Omega } {\left[ {\overline{h}^{3} \left( {\frac{\partial f}{{\partial \overline{x}}}\frac{\partial \delta f}{{\partial \overline{x}}} + \frac{\partial f}{{\partial \overline{z}}}\frac{\partial \delta f}{{\partial \overline{z}}}} \right) - \overline{Q}\delta_{i} \delta f} \right.} \\ & \quad \left. { - \lambda f^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \overline{h}\left( {\overline{u}\frac{\partial \delta f}{{\partial \overline{x}}} + \overline{w}\frac{\partial \delta f}{{\partial \overline{z}}}} \right)} \right]{\text{d}}\overline{x}{\text{d}}\overline{z} = 0 \\ \end{aligned}$$
(6)

FEM is used to numerically solve Eq. (6). The rotor curvature is neglected because thicknesses of the gas film are significantly thinner than diameters of the bearing. Therefore, the gas film can be expanded to a plane, as illustrated in Fig. 2a. (n + 1) and (m + 1) nodes are distributed in the x and z directions, separately. The computational domain is divided into 2mn linear triangular elements, and Eq. (6) can be written as

$$\begin{aligned} & \sum\limits_{e = 1}^{2mn} {\int_{{\Delta_{\text{e}} }} {\left[ {\overline{h}^{3} \left( {\frac{\partial f}{{\partial \overline{x}}}\frac{\partial \delta f}{{\partial \overline{x}}} + \frac{\partial f}{{\partial \overline{z}}}\frac{\partial \delta f}{{\partial \overline{z}}}} \right) - \overline{Q}\delta_{i} \delta f} \right.} } \\ & \quad \left. { - \lambda f^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \overline{h}\left( {\overline{u}\frac{\partial \delta f}{{\partial \overline{x}}} + \overline{w}\frac{\partial \delta f}{{\partial \overline{z}}}} \right)} \right]{\text{d}}\overline{x}{\text{d}}\overline{z} = 0 \\ \end{aligned}$$
(7)

where e and \(\Delta_{\text{e}}\) denote linear triangular element and dimensionless area of the element, respectively. Thus, \(\Delta_{\text{e}} = {{\left( {\Delta \overline{x}\Delta \overline{z}} \right)} \mathord{\left/ {\vphantom {{\left( {\Delta \overline{x}\Delta \overline{z}} \right)} 2}} \right. \kern-0pt} 2}\).

Fig. 2
figure 2

Computational domain: a meshing grids; b elements related to nodes (i, j)

Full size image

Figure 2b shows six linear triangular elements related to node (i, j), (\(2 \le i \le n\), \(1 \le j \le m\)). Supposed node (i, j) as \(\sigma_{q}\) (q = 1, 2, …, m(n − 1)). The elements related to node \(\sigma_{q}\) are \(E_{qk}\) (k = 1, 2, …, 6). The nodes of \(E_{qk}\) are denoted as \(\sigma_{qk}\), \(\varsigma_{qk}\), and \(\tau_{qk}\) in the counterclockwise direction.

The interpolation functions are presented as follows:

$$\begin{aligned} & f = {\varvec{N}}^{\text{eT}} {\varvec{f}}^{\text{e}} ,\delta f = {\varvec{N}}^{\text{eT}} \delta {\varvec{f}}^{\text{e}} = \delta {\varvec{f}}^{\text{e}} {\varvec{N}}^{\text{e}} , \\ & f^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = {\varvec{N}}^{\text{eT}} \left( {{\varvec{f}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)^{\text{e}} ,\overline{h} = {\varvec{N}}^{\text{eT}} {\varvec{h}}^{\text{e}} \\ \end{aligned}$$

where

$$\begin{aligned} & {\varvec{N}}^{\text{e}} = \left[ {\begin{array}{*{20}c} {N_{{\sigma_{qk} }} } & {N_{{\varsigma_{qk} }} } & {N_{{\tau_{qk} }} } \\ \end{array} } \right]^{\text{T}} ,\quad {\varvec{f}}^{\text{e}} = \left[ {\begin{array}{*{20}c} {f_{{\sigma_{qk} }} } & {f_{{\varsigma_{qk} }} } & {f_{{\tau_{qk} }} } \\ \end{array} } \right]^{\text{T}} \\ & \left( {{\varvec{f}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)^{\text{e}} = \left[ {\begin{array}{*{20}c} {f_{{\sigma_{qk} }}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } & {f_{{\varsigma_{qk} }}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } & {f_{{\tau_{qk} }}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \\ \end{array} } \right]^{\text{T}} ,\quad {\varvec{h}}^{\text{e}} = \left[ {\begin{array}{*{20}c} {\overline{h}_{{\sigma_{qk} }} } & {\overline{h}_{{\varsigma_{qk} }} } & {\overline{h}_{{\tau_{qk} }} } \\ \end{array} } \right]^{\text{T}} . \\ \end{aligned}$$

Meanwhile, the shape functions are

$$\begin{aligned} & N_{{\sigma_{qk} }} = \frac{1}{{2\Delta_{\text{e}} }}\left( {a_{{\sigma_{qk} }} + b_{{\sigma_{qk} }} \overline{z} + c_{{\sigma_{qk} }} \overline{x}} \right),N_{{\varsigma_{qk} }} = \frac{1}{{2\Delta_{\text{e}} }}\left( {a_{{\varsigma_{qk} }} + b_{{\varsigma_{qk} }} \overline{z} + c_{{\varsigma_{qk} }} \overline{x}} \right) \\ & N_{{\tau_{qk} }} = \frac{1}{{2\Delta_{\text{e}} }}\left( {a_{{\tau_{qk} }} + b_{{\tau_{qk} }} \overline{z} + c_{{\tau_{qk} }} \overline{x}} \right), \\ \end{aligned}$$

where

$$\begin{aligned} & a_{{\sigma_{qk} }} = \overline{z}_{{\varsigma_{qk} }} \overline{x}_{{\tau_{qk} }} - \overline{z}_{{\tau_{qk} }} \overline{z}_{{\varsigma_{qk} }} ,b_{{\sigma_{qk} }} = \overline{x}_{{\varsigma_{qk} }} - \overline{x}_{{\tau_{qk} }} ,c_{{\sigma_{qk} }} = \overline{z}_{{\tau_{qk} }} - \overline{z}_{{\varsigma_{qk} }} , \\ & a_{{\varsigma_{qk} }} = \overline{z}_{{\tau_{qk} }} \overline{x}_{{\sigma_{qk} }} - \overline{z}_{{\sigma_{qk} }} \overline{z}_{{\tau_{qk} }} ,b_{{\varsigma_{qk} }} = \overline{x}_{{\tau_{qk} }} - \overline{x}_{{\sigma_{qk} }} ,c_{{\varsigma_{qk} }} = \overline{z}_{{\sigma_{qk} }} - \overline{z}_{{\tau_{qk} }} , \\ & a_{{\tau_{qk} }} = \overline{z}_{{\sigma_{qk} }} \overline{x}_{{\varsigma_{qk} }} - \overline{z}_{{\varsigma_{qk} }} \overline{z}_{{\sigma_{qk} }} ,b_{{\tau_{qk} }} = \overline{x}_{{\sigma_{qk} }} - \overline{x}_{{\varsigma_{qk} }} ,c_{{\tau_{qk} }} = \overline{z}_{{\varsigma_{qk} }} - \overline{z}_{{\sigma_{qk} }} . \\ \end{aligned}$$

Substituting the interpolation functions into Eq. (7):

$$\begin{array}{*{20}l} {\sum\limits_{{e \in \Delta_{i,j} }} {\int_{{\Delta_{\text{e}} }} {\left( {{\varvec{N}}^{\text{eT}} {\varvec{h}}^{\text{e}} } \right)^{3} } {\text{d}}\overline{x}\,{\text{d}}\overline{z}\left( {c_{{\sigma_{qk} }} {\varvec{c}}^{\text{eT}} + b_{{\sigma_{qk} }} {\varvec{b}}^{\text{eT}} } \right){\varvec{f}}^{\text{eT}} \frac{1}{{\left( {2\Delta_{\text{e}} } \right)^{2} }} - k_{\text{a}} \mu_{k} \dot{m}_{r} \delta_{i} } } \hfill \\ {\quad - \sum\limits_{{e \in \Delta_{i,j} }} {\lambda \left( {c_{{\sigma_{qk} }} \overline{u} + b_{{\sigma_{qk} }} \overline{w}} \right){\varvec{h}}^{\text{eT}} \int_{{\Delta_{\text{e}} }} {{\varvec{N}}^{\text{e}} {\varvec{N}}^{\text{eT}} } {\text{d}}\overline{x}\,{\text{d}}\overline{z}\frac{1}{{2\Delta_{\text{e}} }}\left( {{\varvec{f}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)^{\text{e}} } = 0} \hfill \\ \end{array}$$
(8)

\({\varvec{c}}^{\text{e}} = \left[ {\begin{array}{*{20}c} {c_{{\sigma_{qk} }} } & {c_{{\varsigma_{qk} }} } & {c_{{\tau_{qk} }} } \\ \end{array} } \right]^{\text{T}}\), \({\varvec{b}}^{\text{e}} = \left[ {\begin{array}{*{20}c} {b_{{\sigma_{qk} }} } & {b_{{\varsigma_{qk} }} } & {b_{{\tau_{qk} }} } \\ \end{array} } \right]^{\text{T}}\) and \(k_{\text{a}} { = }{{24\eta p_{\text{a}} } \mathord{\left/ {\vphantom {{24\eta p_{a} } {h_{{\text{m}}}^{3} p_{0}^{2} \rho_{0} }}} \right. \kern-0pt} ({h_{\text{m}}^{3} p_{0}^{2} \rho_{0} }})\).

where \(e \in \Delta_{i,j}\) are the elements including node (i, j). r is the orifice number in each row (r = 1, 2, …, R), and the mass flow rate of the rth orifice is represented as \(\dot{m}_{r}\). \(\mu_{k}\) denotes the ratio of orifice area located in the kth element to the orifice area.

The integral terms in Eq. (8) are calculated as follows:

$$\int_{{\Delta_{\text{e}} }} {\left( {{\varvec{N}}^{\text{eT}} {\varvec{h}}^{\text{e}} } \right)^{3} } {\text{d}}\overline{x}\,{\text{d}}\overline{z} = \frac{{\Delta_{\text{e}} }}{10}\left[ {\left( {\overline{h}_{{\sigma_{qk} }} + \overline{h}_{{\varsigma_{qk} }} + \overline{h}_{{\tau_{qk} }} } \right)\left( {\overline{h}^{2}_{{\sigma_{qk} }} + \overline{h}_{{\varsigma_{qk} }}^{2} + \overline{h}_{{\tau_{qk} }}^{2} } \right) + \overline{h}_{{\sigma_{qk} }} \overline{h}_{{\varsigma_{qk} }} \overline{h}_{{\tau_{qk} }} } \right]$$
(9)
$$\int_{{\Delta_{\text{e}} }} {\varvec{N}^{\text{e}} \varvec{N}^{\text{eT}} } {\text{d}}\overline{x}\,{\text{d}}\overline{z} = \frac{{\Delta_{\text{e}} }}{12}\left[ {\begin{array}{*{20}c} 2 & {\quad 1} & {\quad 1} \\ 1 & {\quad 2} & {\quad 1} \\ 1 & {\quad 1} & {\quad 2} \\ \end{array} } \right]$$
(10)

According to Eqs. (8)–(10), the functional of dimensionless Reynolds equation is expressed as follows:

$$\begin{array}{*{20}l} {\sum\limits_{{e \in \Delta_{i,j} }} {\frac{1}{{40\Delta_{\text{e}} }}\left[ {\left( {\overline{h}_{{\sigma_{qk} }} + \overline{h}_{{\varsigma_{qk} }} + \overline{h}_{{\tau_{qk} }} } \right)\left( {\overline{h}_{{\sigma_{qk} }}^{2} + \overline{h}_{{\varsigma_{qk} }}^{2} + \overline{h}_{{\tau_{qk} }}^{2} } \right) + \overline{h}_{{\sigma_{qk} }} \overline{h}_{{\varsigma_{qk} }} \overline{h}_{{\tau_{qk} }} } \right]\left( {c_{{\sigma_{qk} }} {\varvec{c}}^{\text{eT}} + b_{{\sigma_{qk} }} {\varvec{b}}^{\text{eT}} } \right){\varvec{f}}^{\text{eT}} } } \hfill \\ {\quad - k_{\text{a}} \mu_{k} \dot{m}_{r} \delta_{i} - \sum\limits_{{e \in \Delta_{i,j} }} {\frac{\lambda }{24}\left( {c_{{\sigma_{qk} }} \overline{u} + b_{{\sigma_{qk} }} \overline{w}} \right){\varvec{h}}^{\text{eT}} \left[ {\begin{array}{*{20}c} 2 & {\quad 1} & {\quad 1} \\ 1 & {\quad 2} & {\quad 1} \\ 1 & {\quad 1} & {\quad 2} \\ \end{array} } \right]\left( {{\varvec{f}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)^{\text{e}} } = 0} \hfill \\ \end{array}$$
(11)

Applying Eq. (11) to elements \(E_{qk}\) (k = 1, 2, …, 6), the square of dimensionless gas pressure of nodes (i, j) (\(2 \le i \le n\), \(1 \le j \le m\)) can be expressed as

$${\varvec{\alpha f}} - {\varvec{\beta f}}^{{{{{1}} \mathord{\left/ {\vphantom {{{1}} {{2}}}} \right. \kern-0pt} {{2}}}}} - k_{\text{a}} \dot{m}_{r} \delta_{i} = 0$$
(12)

For the nodes (i, j) (\(3 \le i \le n - 1\) and \(2 \le j \le m - 1\)),

$${{\varvec{\alpha}}} = \left[ {\begin{array}{*{20}l} {\alpha_{i,j - 1} } \hfill & {\alpha_{i + 1,j - 1} } \hfill & {\alpha_{i - 1,j} } \hfill & {\alpha_{i,j} } \hfill & {\alpha_{i + 1,j} } \hfill & {\alpha_{i - 1,j + 1} } \hfill & {\alpha_{i,j + 1} } \hfill \\ \end{array} } \right]$$
(13)
$${\varvec{f}} = \left[ {\begin{array}{*{20}l} {f_{i,j - 1} } \hfill & {f_{i + 1,j - 1} } \hfill & {f_{i - 1,j} } \hfill & {f_{i,j} } \hfill & {f_{i + 1,j} } \hfill & {f_{i - 1,j + 1} } \hfill & {f_{i,j + 1} } \hfill \\ \end{array} } \right]^{\text{T}}$$
(14)
$${{\varvec{\beta}}} = \left[ {\begin{array}{*{20}l} {\beta_{i,j - 1} } \hfill & {\beta_{i + 1,j - 1} } \hfill & {\beta_{i - 1,j} } \hfill & {\beta_{i,j} } \hfill & {\beta_{i + 1,j} } \hfill & {\beta_{i - 1,j + 1} } \hfill & {\beta_{i,j + 1} } \hfill \\ \end{array} } \right]$$
(15)

Vector f at the nodes adjacent to atmospheric boundaries (i = 2 and i = n, \(1 \le j \le m\)), symmetric boundaries (\(2 \le i \le n\), j = m), and symmetric boundaries (\(2 \le i \le n\), j = 1) are listed in Table 1.

Table 1 Vector at nodes adjacent to atmospheric and symmetric boundaries
Full size table

The elements in \({{\varvec{\alpha}}}\) and \({{\varvec{\beta}}}\) are calculated as follows

$$\alpha_{i,j} = \sum\limits_{{e \in \Delta_{i,j} }} {\frac{1}{{40\Delta_{\text{e}} }}\left[ {\left( {\overline{h}_{{\sigma_{qk} }} + \overline{h}_{{\varsigma_{qk} }} + \overline{h}_{{\tau_{qk} }} } \right)\left( {\overline{h}_{{\sigma_{qk} }}^{2} + \overline{h}_{{\varsigma_{qk} }}^{2} + \overline{h}_{{\tau_{qk} }}^{2} } \right) + \overline{h}_{{\sigma_{qk} }} \overline{h}_{{\varsigma_{qk} }} \overline{h}_{{\tau_{qk} }} } \right]\left( {c_{i,j}^{2} + b_{i,j}^{2} } \right)}$$
(16)
$$\alpha_{I,J} = \sum\limits_{{e \in \Delta_{i,j} \wedge \Delta_{I,J} }} {\frac{1}{{40\Delta_{\text{e}} }}\left[ {\left( {\overline{h}_{{\sigma_{qk} }} + \overline{h}_{{\varsigma_{qk} }} + \overline{h}_{{\tau_{qk} }} } \right)\left( {\overline{h}_{{\sigma_{qk} }}^{2} + \overline{h}_{{\varsigma_{qk} }}^{2} + \overline{h}_{{\tau_{qk} }}^{2} } \right) + \overline{h}_{{\sigma_{qk} }} \overline{h}_{{\varsigma_{qk} }} \overline{h}_{{\tau_{qk} }} } \right]\left( {c_{i,j} c_{I,J} + b_{i,j} b_{I,J} } \right)}$$
(17)
$$\beta_{i,j} = \sum\limits_{{e \in \Delta_{i,j} }} {\frac{\lambda }{24}\left( {c_{i,j} \overline{u} + b_{i,j} \overline{w}} \right)\left( {2h_{{\sigma_{qk} }} + h_{{\varsigma_{qk} }} + h_{{\tau_{qk} }} } \right)}$$
(18)
$$\beta_{I,J} = \sum\limits_{{e \in \Delta_{i,j} \wedge \Delta_{I,J} }} {\frac{\lambda }{24}\left( {c_{i,j} \overline{u} + b_{i,j} \overline{w}} \right)\left( {h_{{\sigma_{qk} }} + 2h_{I,J} + h_{{{{\varsigma_{qk} } \mathord{\left/ {\vphantom {{\varsigma_{qk} } {\tau_{qk} }}} \right. \kern-0pt} {\tau_{qk} }}}} } \right)}$$
(19)

where \(e \in \Delta_{i,j} \wedge \Delta_{I,J}\) is the element including nodes (i, j) and (I, J). (I, J) denotes (i, j − 1), (i + 1, j − 1), (i − 1, j), (i + 1, j), (i − 1, j + 1), or (i, j + 1).

The computation domain has (m + 1)(n + 1) nodes. The square of dimensionless gas pressure at the node (i, j) of atmospheric boundaries (i = 1 and i = n + 1, \(1 \le j \le m + 1\)) is \(\overline{f}_{a}\), while that at the node (i, j) of symmetric boundaries (\(1 \le i \le n + 1\), j = m + 1) is ignored. Therefore, m(n − 1) equations exist in accordance with Eq. (12) and can be written in matrix form.

$${\varvec{AF}} - {\varvec{BF}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} - {\varvec{T}} = 0$$
(20)

where \({\varvec{F}}{ = }\left[ {\begin{array}{*{20}c} {f_{1} } & {f_{2} } & \cdots & {f_{m(n - 1)} } \\ \end{array} } \right]^{\text{T}}\) is a vector of the square of dimensionless gas pressure, \({\varvec{T}}{ = }\left[ {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & \cdots & {t_{m(n - 1)} } \\ \end{array} } \right]^{\text{T}}\). A and B are stiffness matrices with \(m(n - 1) \times m(n - 1)\) dimensions. The elements of A and B can be calculated by Eqs. (16)–(19), and their detailed forms are provided in Appendix A. The difficulty in solving the Reynolds equation with the rotation speed term using FEM lies in the construction of the stiffness matrices. Equations (12)–(20) describe the theoretical derivation of solving the functional of Reynolds equation with rotation speed term.

The dimensionless load capacity of the linear triangular element is

$$\overline{W}_{\text{e}} = \frac{{8\Delta_{\text{e}} }}{15}\left[ {\frac{{f_{{\sigma_{qk} }}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} }}{{\left( {f_{{\sigma_{qk} }} - f_{{\varsigma_{qk} }} } \right)\left( {f_{{\sigma_{qk} }} - f_{{\tau_{qk} }} } \right)}} + \frac{{f_{{\varsigma_{qk} }}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} }}{{\left( {f_{{\varsigma_{qk} }} - f_{{\sigma_{qk} }} } \right)\left( {f_{{\varsigma_{qk} }} - f_{{\tau_{qk} }} } \right)}} + \frac{{f_{{\tau_{qk} }}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} }}{{\left( {f_{{\tau_{qk} }} - f_{{\sigma_{qk} }} } \right)\left( {f_{{\tau_{qk} }} - f_{{\varsigma_{qk} }} } \right)}}} \right]$$
(21)

For the elements related to atmospheric boundaries, nodes with the same gas pressures such as \(f_{{\varsigma_{qk} }} = f_{{\tau_{qk} }} = \overline{f}_{a}\) exist. Therefore, the dimensionless load capacity is

$$\overline{W}_{\text{e}} = \frac{{8\Delta_{\text{e}} }}{15}\frac{{\tfrac{3}{2}\overline{f}_{\text{a}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} - \tfrac{5}{2}f_{{\sigma_{qk} }} \overline{f}_{\text{a}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} + f_{{\sigma_{qk} }}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} }}{{\left( {\overline{f}_{\text{a}} - f_{{\sigma_{qk} }} } \right)^{2} }}$$
(22)

The dimensionless load capacities of the z and y directions are respectively presented as follows:

$$\overline{W}_{z} = \sum\limits_{e = 1}^{2mn} {\sin \left( {\left( {j - \frac{1}{2}} \right)\frac{2\uppi }{m}} \right)\overline{W}_{\text{e}} }$$
(23)
$$\overline{W}_{y} = \sum\limits_{e = 1}^{2mn} {\cos \left( {\left( {j - \frac{1}{2}} \right)\frac{2\uppi }{m}} \right)\overline{W}_{\text{e}} }$$
(24)

where j = 1, 2, …, m. The dimensionless load capacity of bearings can be concluded.

$$\overline{W} = \sqrt {\overline{W}_{z}^{2} + \overline{W}_{y}^{2} }$$
(25)

The load capacity, attitude angle, and stiffness of the bearings are as follows:

$$W = p_{0} L^{2} \overline{W}$$
(26)
$$\varphi = \arctan \left( {{{\overline{W}_{z} } \mathord{\left/ {\vphantom {{\overline{W}_{z} } {\overline{W}_{y} }}} \right. \kern-0pt} {\overline{W}_{y} }}} \right)$$
(27)
$$K_{\text{w}} = \frac{W(c + \Delta c) - W(c)}{{\Delta c}}$$
(28)

where Δc is the variation of eccentricity. The flow field in the calculations is adiabatic. Therefore, the mass flow rate is

$$\dot{m}_{r} = \Delta_{\text{a}} p_{0} \phi \sqrt {\frac{{2\rho_{0} }}{{p_{0} }}} \psi$$
(29)
$$\psi = \left\{ {\begin{array}{*{20}l} {\left[ {\frac{\kappa }{2}\left( {\frac{2}{\kappa + 1}} \right)^{{{{\left( {\kappa + 1} \right)} \mathord{\left/ {\vphantom {{\left( {\kappa + 1} \right)} {\left( {\kappa - 1} \right)}}} \right. \kern-0pt} {\left( {\kappa - 1} \right)}}}} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \hfill & {\frac{{p_{\text{d}} }}{{p_{0} }} \le \left( {\frac{2}{\kappa + 1}} \right)^{{{\kappa \mathord{\left/ {\vphantom {\kappa {\left( {\kappa - 1} \right)}}} \right. \kern-0pt} {\left( {\kappa - 1} \right)}}}} } \hfill \\ {\left\{ {\frac{\kappa }{\kappa - 1}\left[ {\left( {\frac{p}{{p_{0} }}} \right)^{{{2 \mathord{\left/ {\vphantom {2 \kappa }} \right. \kern-0pt} \kappa }}} - \left( {\frac{p}{{p_{0} }}} \right)^{{{{\left( {\kappa + 1} \right)} \mathord{\left/ {\vphantom {{\left( {\kappa + 1} \right)} \kappa }} \right. \kern-0pt} \kappa }}} } \right]} \right\}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \hfill & {\frac{{p_{\text{d}} }}{{p_{0} }} > \left( {\frac{2}{\kappa + 1}} \right)^{{{\kappa \mathord{\left/ {\vphantom {\kappa {\left( {\kappa - 1} \right)}}} \right. \kern-0pt} {\left( {\kappa - 1} \right)}}}} } \hfill \\ \end{array} } \right.$$
(30)

where \(\phi\) is a discharge coefficient, and \(\Delta_{\text{a}}\) is a sectional area of the orifice.

\(\kappa\) is an air specific heat ratio. Several researchers [15,16,17,18] verified that the discharge coefficient \(\phi\) is a function of a ratio of gas pressure of orifice outlet to supply pressure. Equation (31) presented in the research of Neves [18] is used in this paper.

$$\phi = \left\{ {\begin{array}{*{20}l} {0.88} \hfill & \quad {\frac{{p_{\text{d}} }}{{p_{0} }} \le \left( {\frac{2}{\kappa + 1}} \right)^{{{\kappa \mathord{\left/ {\vphantom {\kappa {\kappa - 1}}} \right. \kern-0pt} {\kappa - 1}}}} } \hfill \\ {0.9093 - 0.0751\frac{{p_{\text{d}} }}{{p_{0} }}} \hfill & \quad {\frac{{p_{\text{d}} }}{{p_{0} }} > \left( {\frac{2}{\kappa + 1}} \right)^{{{\kappa \mathord{\left/ {\vphantom {\kappa {\kappa - 1}}} \right. \kern-0pt} {\kappa - 1}}}} } \hfill \\ \end{array} } \right.$$
(31)

2.3 Calculation Procedure

In Fig. 3, the calculation procedure is shown. Successive Over-Relaxation method (SOR) is employed to solve Eq. (20), in which the proportional division method is introduced into the iteration to improve calculation efficiency. First, the attitude angle is set to zero, and the initial values of the square of dimensionless gas pressure \({\varvec{F}}^{(1)}\) are arbitrarily selected in the range of [0, 1]. The mass flow rate \(\dot{m}_{r}\) is calculated by solving Eqs. (29)–(31). The elements in matrix \({\varvec{T}}\) associated with the gas pressure of orifice outlet are calculated according to the initial values \(f_{{\text{d}}{r}}^{(1)}\) (\(f_{{\text{d}}{r}}\) is a square of dimensionless gas pressure of the rth orifice outlet). The elements in \({\varvec{T}}\) related to atmospheric boundaries are constant, and other elements are zeros. Second, Eq. (20) is solved by using SOR for obtaining \({\varvec{F}}^{{(1){*}}}\) and \(f_{{\text{d}}{r}}^{(1)*}\). The next square of dimensionless gas pressure \(f_{{\text{d}}{r}}^{(2)}\) is calculated by using the proportional division method.

$$f_{{\text{d}}{r}}^{(2)} = \frac{1}{aG}\left( {f_{{\text{d}}{r}}^{(1) * } - f_{{\text{d}}{r}}^{(1)} } \right) + f_{{\text{d}}{r}}^{(1)}$$
(32)
$$G = 1 + \frac{{T_{{\text{d}}{r}} }}{{\kappa \left( {2{A}_{{\text{d}}{r}} f_{{\text{d}}{r}} + {B}_{{\text{d}}{r}} f_{{\text{d}}{r}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)}}\left| {1 - \frac{{{{\left( {\kappa - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\kappa - 1} \right)} 2}} \right. \kern-0pt} 2}}}{{\left( {f_{{\text{d}}{r}} } \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 7}} \right. \kern-0pt} 7}}} - 1}}} \right|$$
(33)

where a is the relaxation factor (a = 1.3 in this paper). G is the modified proportional factor, which is related to the calculation speed. The rotation speed term is introduced into the proportional factor (derivation in Appendix B). \(T_{{\text{d}}{r}}\), \(A_{{\text{d}}{r}}\), and \(B_{{\text{d}}{r}}\) are the elements related to the rth orifice in matrices T, A, and B, respectively.

Fig. 3
figure 3

Calculation procedure by using FEM

Full size image

The calculation will be completed only if the following condition is satisfied.

$$\left| {\frac{{f_{{\text{d}}{r}}^{(i) * } - f_{{\text{d}}{r}}^{(i)} }}{{f_{{\text{d}}{r}}^{(i)} }}} \right| \le g$$
(34)

Finally, the attitude angle must satisfy the condition \(\left| {{{\overline{W}_{z} } \mathord{\left/ {\vphantom {{\overline{W}_{z} } {\overline{W}_{y} }}} \right. \kern-0pt} {\overline{W}_{y} }}} \right| \le g_{\varphi }\). Otherwise,

$$\varphi^{(i + 1)} = \varphi^{(i)} - \arctan \left( {{{\overline{W}_{z} } \mathord{\left/ {\vphantom {{\overline{W}_{z} } {\overline{W}_{y} }}} \right. \kern-0pt} {\overline{W}_{y} }}} \right)$$
(35)

The gas film thickness is modified in accordance with Eq. (1), and the calculation is repeated.

3 Results and Discussions

The gas journal bearing with the same geometric structure as in the research of Neves [18] is calculated. The geometric parameters and gas properties are listed as follows (Table 2):

Table 2 Gas journal bearing parameters and gas properties [18]
Full size table

The calculations have 21 and 65 evenly distributed nodes in x and z directions, separately. u is set to zero due to the negligible axial motion of the rotor. The convergence conditions of the square of dimensionless gas pressure and that of attitude angle are 1 × 10−6 and 1 × 10−4, respectively. Additional meshing nodes and high convergence conditions lead to a considerable amount of calculation time, while the improvement in calculation accuracy is negligible. Computed results are contrasted with those of Neves [18], as listed in Table 3 (\(h_{\text{m}}\) = 19.05 μm, w = 0 krpm, d = 0.15 mm, ε = 0.5, and \(p_{0}\) = 5 atm). The relative errors of mass flow rate and load capacity are 5.31% and 0.03%, respectively, and those on discharge coefficient are less than 1%.

Table 3 Calculation results compared with those of Neves [18]
Full size table

In Table 4, the comparison results for load capacity and attitude angle when the discharge coefficient is Eq. (31) and 0.8, respectively (\(h_{\text{m}}\) = 20 μm, d = 0.2 mm, ε = 0.2, and \(p_{0}\) = 5 atm), are listed. Those relative errors of load capacity are less than 3% and decrease with the growth of rotation speed. By contrast, the relative errors of attitude angle are larger than 9%. Therefore, the accuracy of the discharge coefficient makes a great difference to Computed results of the attitude angle.

Table 4 Calculation results of load capacity and attitude angle with different discharge coefficients
Full size table

Figure 4 illustrates the pressure distributions with different rotation speeds or eccentricity ratios. Figure 4a, b demonstrates that the pressure is symmetrically distributed around the circumference and along the axis at a rotation speed of 0 krpm. The smallest and largest gas film thicknesses are located at orifices 1 and 5, respectively. Moreover, when this eccentricity ratio changes from 0.05 to 0.2, load capacity raises from 36.82 to 143.11 N.

Fig. 4
figure 4

Pressure distributions with different rotation speeds or eccentricity ratios (hm = 20 μm, d = 0.2 mm, p0 = 5 atm): a w = 0 krpm, ε = 0.05; b w = 0 krpm, ε = 0.2; c w = 20 krpm, ε = 0.05; d w = 20 krpm, ε = 0.2

Full size image

This rotor centroid deviates from its original position due to aerodynamic pressure during rotor rotation, resulting in a lesser gas film thickness in Zone 1 than that in Zone 2, exhibited in Fig. 4c, d. Therefore, this gas pressure is asymmetrically distributed in a circumferential direction. Furthermore, the gas pressure in Zone 1 increases, while that in Zone 2 decreases. Load capacity increases from 38.46 to 150.84 N, and attitude angle changes from 6.42 to 7.27° when the eccentricity ratio grows from 0.05 to 0.2 at a rotation speed of 20 krpm. Compared with the bearing in static conditions, the load capacity increases to 1.64 and 7.73 N when eccentricity is 0.05 and 0.2, respectively.

The performance of bearings with various bearing parameters listed in Table 5 is calculated to research the effect of these parameters on attitude angle, load capacity, and stiffness. Cases 1, 2, and 3 analyze the influence of orifice diameter, eccentricity ratio, and supply pressure on the performance of bearings, respectively.

Table 5 Performance of bearings with different bearing parameters
Full size table

Figure 5a, b demonstrates the calculation results of case 1. Overall, a small orifice diameter leads to a small thickness of average gas film, which corresponds to both maximum load capacity and maximum stiffness. Furthermore, the maximum stiffness exhibits an upward trend as the orifice diameter decreases. When this orifice diameter is 0.1 mm, load capacities and stiffnesses continuously decrease as average gas film thickness. Calculation results of case 2 indicate that increasing the eccentricity ratio is advantageous in enhancing load capacity, as demonstrated in Fig. 5c and d. The influence of an increased eccentricity ratio on stiffness becomes apparent when considering a small average gas film thickness. But the negligible effect occurs when the average gas film thickness exceeds 25 μm. Figure 5e and f shows the calculation results of case 3. This finding indicates that a large supply pressure leads to a large load capacity and stiffness.

Fig. 5
figure 5

Influence of bearing parameters on load capacities and stiffnesses: a and b influence of orifices; c and d influence of eccentricity ratios; e and f influence of supply pressure

Full size image

Moreover, Fig. 5 shows that load capacities and stiffnesses exhibit a positive correlation with the enhancement in rotational speed. A small average gas film thickness leads to substantial influences of rotation speed on load capacity and stiffness. The average film thickness is 15 μm, the supply pressure is 4 atm, the orifice diameter is 0.2 mm, and the eccentricity ratio is 0.05. Therefore, the load capacity increases by 40.8% with the increase in rotation speed. Overall, gas journal bearings with small average gas film thicknesses and small orifice diameters have a large load capacity and high stiffness, and load capacities and stiffnesses of bearings are significantly enhanced at large operation parameters.

Figure 6 shows influence of bearing parameters on attitude angle of bearings. These rotation speeds are 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50 krpm.

Fig. 6
figure 6

Influence of bearing parameters on attitude angles: a and b influence of orifice diameters; c and d influence of eccentricity ratios; e and f influence of supply pressure

Full size image

The calculation results for case 1 indicate that a small orifice diameter leads to a small average gas film thickness, which corresponds to the minimum attitude angle, as mentioned in Fig. 6. When orifice diameter is 0.1 mm, attitude angle exhibits a consistent upward trend as average gas film thickness increases. Computed results of case 2 express that changing eccentricity ratios is slightly helpful for reducing attitude angle, as can be seen from Fig. 6. Attitude angles exhibit a slight increase as eccentricity ratios increase, provided that average gas film thicknesses fall within the range of 15–30 μm. However, if film thickness is greater than 30 μm, this angle decreases as eccentricity ratio increases. The results of case 3 are shown in Fig. 6e and f. The attitude angle exhibits a notable reduction as supply pressure increases within the investigated range of average gas film thicknesses and rotation speeds of bearings. The average film thickness is 20 μm, the rotation speed is 20 krpm, the orifice diameter is 0.2 mm, and the eccentricity ratio is 0.05. The attitude angle decreases by 40.8% as the supply pressure increases.

Furthermore, the attitude angle exhibits a positive correlation with the increase in rotation speed, while its growth rate slows down or even decreases at high rotation speeds. Therefore, gas journal bearings with a small average gas film thickness and a small orifice diameter are helpful for reducing attitude angle. Moreover, reducing the attitude angle by increasing the supply pressure is beneficial.

Figure 7 demonstrates the circumferential pressure distribution with rotation speeds of 0 and 40 krpm. The gas pressure is symmetrical about the central line between two orifices if the rotor is stationary (e.g., the pressure distribution between orifices 2 and 3). The gas velocity flowing from orifice 2 (\(v_{2}\)) is enlarged due to its similar direction to the rotor surface velocity (\(v_{0}\)) during rotor rotation. However, the gas velocity flowing from orifice 3 (\(v_{3}\)) is attenuated because of its contrary direction to \(v_{0}\). Therefore, rotor rotation influences the performance of gas journal bearings by changing the gas pressure distribution between orifices because of gas viscosity.

Fig. 7
figure 7

Circumferential pressure distribution of gas journal (hm = 15 μm, ε = 0.05, d = 0.2 mm, p0 = 5 atm)

Full size image

To analyze load capacity characteristics of bearings, the circumferential domain in Fig. 7 is partitioned into four equidistant parts. The dimensionless radial and circumferential load capacities (\(\overline{W}_{y}\) and \(\overline{W}_{z}\)) between orifices at rotation speeds of 0 and 40 krpm are showed in Table 6. The difference in dimensionless radial load capacity between parts I + IV and II + III increases during rotor rotation. The uneven distribution of gas pressure between orifices improves load capacity.

Table 6 Dimensionless radial and circumferential load capacity between orifices with different rotation speeds
Full size table

Moreover, the radial load capacity of this bearing is primarily attributed to radial load capacity difference between regions (1, 2), (8, 1) and regions (4, 5), (5, 6). The circumferential load capacity of this bearing is primarily because of circumferential load capacity difference between regions (2, 3), (3, 4) and regions (6, 7), (7, 8). Furthermore, the circumferential load capacity in part I is smaller than that in part IV, and that in part II is larger than that in part III. The difference in circumferential load capacity between parts I and IV is equal to that between parts II and III.

This variation of load capacity with different rotation speeds is in good agreement with that of the difference in dimensionless radial load capacity between regions (1, 2), (8, 1) and regions (4, 5), (5, 6), as can be seen from Fig. 8a. Figure 8b demonstrates that attitude angle synchronously changes with the difference in dimensionless circumferential load capacity between regions (2, 3), (3, 4) and regions (6, 7), (7, 8). Therefore, load capacity is substantially related to the difference in radial load capacity between regions (1, 2), (8, 1) and regions (4, 5), (5, 6). However, attitude angle is mainly influenced by the difference in circumferential load capacity between regions (2, 3), (3, 4) and regions (6, 7), (7, 8).

Fig. 8
figure 8

Relationship between load capacity, attitude angle, and differences in radial, circumferential load capacity (hm = 15 μm, ε = 0.05, d = 0.2 mm, p0 = 5 atm): a load capacity and difference in dimensionless radial load capacity; b attitude angle and difference in dimensionless circumferential load capacity

Full size image

Figure 9 illustrates the circumferential pressure distribution at a rotation speed of 40 krpm. Compared with the condition of d = 0.2 mm, \(h_{\text{m}}\) = 15 μm, ε = 0.05, \(p_{0}\) = 5 atm, and w = 40 krpm, gas pressure at orifice outlet decreases significantly if orifice diameters or supply pressure decreases or average gas film thickness increases. If this eccentricity ratio increases, gas pressure at orifice 1 increases while that at orifice 5 decreases. However, gas pressure near orifices 3 and 7 remains constant. Therefore, this influence of eccentricity ratio on load capacities and stiffnesses is evident, while that on attitude angle is ignorable. Overall, orifice diameter, eccentricity ratio, supply pressure, and average gas film thickness influence attitude angle by changing gas pressure at orifice outlets.

Fig. 9
figure 9

Circumferential pressure distributions (w = 40 krpm)

Full size image

4 Conclusions

FEM is employed to solve Reynolds equation for intensive analyzing the performance of gas journal bearings, in which the rotation speed term is introduced into the stiffness matrix. The effects of restrictions and operation parameters on load capacity, stiffness, and attitude angle are discussed. Furthermore, circumferential pressure distribution characteristics are analyzed. The conclusions are summarized as follows.

  1. (1)

    A small orifice diameter leads to small average gas film thicknesses, which corresponds to the maximum values of attitude angle, stiffness, and load capacity. Moreover, increasing the eccentricity ratio, supply pressure, and rotation speed at a small average gas film thickness can help improve load capacity and stiffness. In addition, a small average gas film thickness leads to considerable influences in rotation speed on load capacities and stiffnesses. The average film thickness is 15 μm, and the load capacity grows by 46.5% with the increase of rotation speed.

  2. (2)

    The most effective way of reducing the attitude angle is to increase supply pressure. The average film thickness is 20 μm, and the attitude angle reduces by 40.8% as the supply pressure increases. The attitude angle rises with the growth of rotation speed, and the growth rate slows down or even decreases at high speed. A gas journal bearing with small orifice diameters and small average gas film thicknesses has good static performance at high eccentricity ratios, large supply pressures, and high rotation speeds.

  3. (3)

    Eccentricity ratio, supply pressure, average gas film thickness, and orifice diameter influence attitude angle by changing gas pressure at the orifice outlet, while rotation speed influences attitude angle by changing gas pressure between orifices.