1 Introduction

MEMS accelerometers have been widely used in various consumable and industrial applications [1,2,3]; however, the thermal stability performance of most MEMS accelerometers cannot meet the requirements of applications such as long-term inertial navigation [4]. Further investigation of the characteristics of the temperature drift of the mechanical and electronic components and the development of drift compensation methodologies are required to improve the thermal stability of MEMS accelerometers. Online and offline compensation approaches have been proposed and found to effectively suppress the temperature drift of MEMS accelerometers [5,6,7,8,9,10,11,12,13,14,15,16].

Approaches based on temperature control and mechanical and circuit design optimization have been proposed to reduce the temperature effect on the mechanical sensitive structure and readout circuit. Li et al. [5] experimentally demonstrated that the temperature characteristic of the sensing element is the major cause of temperature bias drift in MEMS accelerometers. An adiabatic package integrated with a constant temperature system was designed for the sensing element and showed more power efficiency than an overall temperature control system. With the proposed temperature control, the TDC of the accelerometer output was reduced from 2.061 to 0.199 mg/°C when the environmental temperature changed from − 40 to 60 °C. He et al. [6] proposed a structural design of an accelerometer in which the temperature bias drift (TBD) and temperature drift of scale factor (TDSF) were reduced by deployed middle locating anchors for the moving and fixed electrodes. Experimental results showed that with the optimized structure, the TBD and TDSF were reduced from 1.85 to 0.52 mg/°C and from − 162.7 to − 50.8 ppm/°C, respectively. Ko and Cho [7] proposed a new readout circuit with low temperature sensitivity using a highly programmable capacitive sensing architecture and an on-chip EEPROM for calibrating the output bias and scale factor and successfully reduced the TDC of the accelerometer to 43 ppm/°C with the temperature varying between − 40 and 125 °C. Myers et al. [8] proposed a stress-enhanced resonant-type sensor structure with a device layer and substrate layer made from thermally mismatched materials. With the proposed structure, the thermal strains introduced by the mismatch canceled out the temperature effect of the elastic modulus, and TDC was reduced from 30 to 1.7 ppm/°C with the temperature ranging from 0 to 70 °C. Although these approaches are proven to effectively improve the temperature drift of MEMS accelerometers, the complexity of the accelerometer and the difficulty of fabrication may arise at the same time.

Another commonly used approach is to compensate for the temperature effect of MEMS accelerometers with the help of temperature-dependent variables, such as temperature-sensitive resistors, reference capacitors, and resonant frequency. Zhang et al. [9] used a temperature sensor for calibrating the TBD of MEMS accelerometers. The experimental results showed that TDC and TDSF were reduced from 9.00 mg/°C to 1.09 μg/°C and from 27.55 to 0.521 ppm/°C, respectively, with temperature varying from − 10 to 90 °C. Xiao et al. [10] proposed a compensation method using an integrated reference capacitor and a fully differential configuration of the sensing structure and successfully reduced TDC from 9.1 to 0.61 mg/°C with temperature varying from − 40 to 60 °C. Talha and Taufun [11] proposed a temperature compensation method for a capacitive MEMS accelerometer with an integrated double-ended-tuning-fork (DETF) resonator. The resonant frequency of the DETF resonator was used for temperature drift calibration, and TDC decreased from 1164 to 1.4 μg/°C for a temperature interval of − 20 °C to 60 °C. Jungshin and Jaewook [12] proposed a temperature compensation method for a resonant-type sensor. By controlling the electrostatic stiffness of DETF with a temperature-dependent DC voltage, they reduced the TDC of the resonant frequency from 2.13 to 0.02 Hz/°C with the temperature ranging from − 20 to 70 °C. Du et al. [13] proposed a phase-locked loop for calibrating the resonant frequency of a MEMS accelerometer and successfully reduced TDC from 3.54 to 0.05 mg/°C for a temperature interval of 0–60 °C.

Several approaches utilize the calibration of temperature drift based on an additional excitation of the accelerometer at an out-of-band frequency to avoid interference with the original sensing configuration of MEMS accelerometers. Liu and Ma [14] proposed a compensation method for an MEMS accelerometer based on the demodulated phase of a carrier signal. Only the temperature effect of the readout circuit was considered in their thermal drift model, and TDC was reduced from 1.319 to 0.601 mg/°C for a temperature interval of 0–60 °C. Ma et al. [15] used a sinusoidal excitation signal to drive the accelerometer along the orthogonal direction of the sensitive axis direction. The response phase was used for calibrating the temperature effect of the elastic modulus, and TDC was reduced from 4.68 to 0.1 mg/°C for a temperature range from 10 to 50 °C. We also proposed a similar compensation approach for a stiffness-tunable MEMS accelerometer with signal-sided parallel plate (SSPP) capacitors [16] by introducing an out-of-bandwidth sinusoidal excitation signal to the displacement closed-loop (DCL) control system. The amplitude of the excited response was used as a temperature reference to compensate for the temperature drift of the effective stiffness. The experimental results showed that TDC was reduced from 1.1717 to 0.0391 mg/°C in the temperature range from 5 to 35 °C. However, due to the introduced bias of SSPP capacitors, the proposed compensation was not fully automatic. In the current work, we extended the investigation of another different MEMS accelerometer with stiffness-tuning DSPP capacitors [17]. The phase of the out-of-band excitation response was used to calibrate the temperature-induced variation of the effective stiffness of the accelerometer with DSPP capacitors. A fully automatic compensation approach for the temperature drift of effective stiffness can be realized. The remainder of this paper was organized as follows. First, the MEMS accelerometer with stiffness-tuning DSPP capacitors was introduced. A TBD model was then established for the proposed accelerometer on the basis of the temperature effect on the mechanical structure and the electronic circuit. Finally, two different compensation methods based on the proposed phase-based calibration were realized and analyzed. In addition, the effects of pull-in instability and long-term bias drift were measured.

2 Methodology

2.1 Electrostatic Tuning Accelerometer

The MEMS accelerometer device in this study included a proof mass suspended by four flexible folded beams and a group of sensing/feedback/tuning capacitors. When external acceleration is applied, a set of capacitive electrodes attached to the proof mass displaces against to the opposite set of fixed capacitive electrodes, resulting in variable overlapping sizes for sensing and feedback capacitors and gap change for tuning capacitors of DSPP. The effective stiffness of the accelerometer can be tuned to even zero by utilizing the electrostatic softening effect of the DSPP capacitors. The working principle of the sensing/feedback/tuning capacitors of the accelerometer is detailed in a previous study [18]. The accelerometer was fabricated using a standard silicon-on-glass process, and the scanning electron microscope (SEM) image of the fabricated device is shown in Fig. 1.

Fig. 1
figure 1

Scanning electron microscope (SEM) image of the fabricated accelerometer device

Full size image

2.2 Readout Circuit and Control System

The readout, feedback, and tuning circuits and the corresponding digital signal processing algorithms are illustrated in Fig. 2. The definitions of the variables in Fig. 2 are listed in Table 1. The structure and working principle of the analog readout, feedback, and tuning circuits are detailed in our previous work [19, 20]. An AC stimulus signal of out-of-band acceleration was introduced in the force feedback loop, and the corresponding response in the displacement signal was obtained by demodulating the output of the C–V circuit twice with two quadrature demodulators. As a result, the corresponding amplitude and phase can be extracted from the response. Hereafter, we defined the amplitude and phase extracted from the excitation as stiffness-loop amplitude (SLA) and stiffness-loop phase (SLP, defined as θ2), respectively. SLA was used for calibrating the effective stiffness of a different accelerometer tuned with SSPP in our previous work [16]. In the current study, we proposed the use of SLP to calibrate the effective stiffness of an accelerometer tuned with DSPP, enabling the online compensation of the temperature drift. With the extracted SLP, a stiffness-loop phase closed loop (SLPCL) was further implemented by adjusting the electrostatic tuning voltage of DSPP with a proportional-integral (PI) controller, ensuring that SLP was locked to a preset value. The frequency of the AC stimulus was determined by considering the effect on the signal-to-noise ratio (SNR) of the response and the interference with the accelerometer output. If the AC stimulus frequency is set too large, then the interference with the acceleration output can be improved, and the SNR of the response from the AC stimulus would worsen, and vice versa. Thus, we determined the frequency at which the AC stimulus would respond with an SNR of 50 dB and the bias instability of the accelerometer output is slightly degraded. When the accelerometer was operated with SLPCL, switch E in Fig. 2 was initially turned on. DCL was also implemented for the force rebalance and the output of the accelerometer with the help of another PI controller. As explained in Sects. 3.2 and 3.3, SLP and displacement-loop-phase (DLP, defined as θ1) vary in response to the temperature change and can be used for calibrating the temperature drift of the acceleration output.

Fig. 2
figure 2

Control system of the proposed accelerometer

Full size image
Table 1 Variable definition in Fig. 2
Full size table

2.3 Temperature Drift Modeling

The dynamic model of the MEMS accelerometer system is shown in Fig. 3. For simplification, the displacement of the proof mass was defined relative to the center of the DSPP capacitor. The governing equation of motion of the accelerometer can be given by

$${F}_{m}\left(T\right)+{F}_{t}\left(T\right)+{F}_{\mathrm{fb}}\left(T\right)+m{a}_{\mathrm{ext}}-b\dot{x}-m\ddot{x}=0$$
(1)

where m is the mass, b is the damping coefficient, km is the mechanical stiffness, T is the temperature, Ft is the electrostatic force generated by the DSPP tuning capacitors, Fm is the elastic restoring force, Ffb is the force generated by the feedback capacitors, and aext is the applied external acceleration.

Fig. 3
figure 3

Dynamic model of the MEMS accelerometer system

Full size image

The elastic restoring force Fm can be given by

$${F}_{m}\left(T\right)=-{k}_{\mathrm{m}}\left(T\right)\left(x-{x}_{0}\right)$$
(2)

where x0 is the initial displacement without external acceleration and force rebalance.

The feedback force Ffb can be given by

$${F}_{\mathrm{fb}}\left(T\right)={k}_{\mathrm{fb}}\left(T\right){D}_{\mathrm{fb}}\left(T\right)$$
(3)

where kfb is the gain of the feedback circuit.

The electrostatic tuning force Ft can be given by

$${F}_{\mathrm{t}}\left(T\right)=-{k}_{e}\left(T\right)x+{F}_{\mathrm{nl}}(T)$$
(4)

where ke(T) is the electrostatic stiffness [17] and can be given by

$${k}_{\mathrm{e}}\left(T\right)=-\frac{{N}_{t}\varepsilon {L}_{t}{H}_{t}{{V}_{t}\left(T\right)}^{2}}{({d}_{0}-x{)}^{3}}-\frac{{N}_{t}\varepsilon {L}_{t}{H}_{t}{{V}_{t}\left(T\right)}^{2}}{({d}_{0}+x{)}^{3}}$$
(5)

where ε is the permittivity, d0, Lt and Ht are the initial gap, the overlapping length and width of plate pairs, and Nt is the number of plate pairs. Fnl (T) is the higher order term of Ft, which can be given by

$${F}_{\mathrm{nl}}\left(T\right)=\frac{-4x}{{{d}_{0}}^{2}/{x}^{2}+3}{k}_{\mathrm{e}}\left(T\right)$$
(6)

When operated with DCL, the displacement of the proof mass can be stably controlled to the reference position. By neglecting \(\dot{x}\) and \(\ddot{x}\), the displacement can be expressed by

$$x=\frac{{D}_{\mathrm{ref}}}{{k}_{\mathrm{re}}}+{x}_{1}$$
(7)

where x1 is the initial offset of the difference-sensing capacitor pairs due to fabrication imperfection, and kre is the amplification gain of the readout circuit.

The accelerometer output with DCL can be given by

$${D}_{\mathrm{fb}1}=\frac{{k}_{\mathrm{eff}}\left(T\right)}{{k}_{\mathrm{fb}} \left(T\right)}\left(\frac{{D}_{\mathrm{ref}}}{{k}_{\mathrm{re}}}+{x}_{1}\right)- \frac{{k}_{m}\left(T\right)}{{k}_{\mathrm{fb}}\left(T\right)}{x}_{0}- \frac{ma_{\mathrm{ext}}}{{k}_{\mathrm{fb}}\left(T\right)}-\frac{{F}_{nl}(T)}{{k}_{\mathrm{fb}}\left(T\right)}$$
(8)

where

$${k}_{\mathrm{eff}}\left(T\right)={k}_{\mathrm{m}}\left(T\right)+{k}_{\mathrm{e}}\left(T\right)$$
(9)

When the proof mass is driven by a sinusoidal excitation signal with amplitude gain Ae, the corresponding SLA and SLP can be given by

$$A=\frac{{{A}_{\mathrm{e}}k}_{\mathrm{re}}}{\sqrt{{\left({k}_{\mathrm{eff}}\left(T\right)-m{{\omega }_{d}}^{2}\right)}^{2}+{b}^{2}{{\omega }_{d}}^{2}}}$$
(10)
$${\theta }_{2}=-{\text{arctan}}\left(\frac{b{\omega }_{d}}{{k}_{\mathrm{eff}}\left(T\right)-m{\omega }_{d}^{2}}\right)+{\theta }_{c}\left(T\right)$$
(11)

where ωd is the angular frequency, and θc is the phase gain of the readout circuit.

With SLPCL, the electrostatic tuning voltage of DSPP capacitors can be adjusted to achieve a constant θ2. Equation (9) can be rewritten as

$${k}_{\mathrm{eff}2}=\frac{-b{w}_{d}}{\mathrm{tan}\left[{\theta }_{\mathrm{ref}}-{\theta }_{c}\left(T\right)\right]}+m{{w}_{d}}^{2}$$
(12)

The accelerometer output with DCL/SLPCL can be given by

$${D}_{\mathrm{fb}2}=\frac{{k}_{\mathrm{eff}2}}{{k}_{\mathrm{fb}}\left(T\right)}{(\frac{{D}_{\mathrm{ref}}}{{k}_{\mathrm{re}}}+x_{1}})-\frac{{k}_{m}\left(T\right)}{{k}_{\mathrm{fb}}\left(T\right)}{x}_{0}-\frac{m{a}_{\mathrm{ext}}}{{k}_{\mathrm{fb}}\left(T\right)}-\frac{{F}_{nl}(T)}{{k}_{\mathrm{fb}}\left(T\right)}$$
(13)

3 Results and Discussion

3.1 Temperature Drift Characterization

According to Eqs. (8,13), the temperature drift of the proposed accelerometer depends on its mechanical and electronic components. Thus, the temperature effects of the readout, feedback, and tuning circuits were experimentally investigated in a temperature-varied chamber to characterize the dominant factors. The contribution of each variable to the accelerometer drift was revealed by analyzing the experimental results. Equations (8,13) can be simplified by omitting the temperature drift from the negligible factors. As a result, a simplified temperature drift model was developed to verify the TBD characteristics of the proposed accelerometer implemented with DCL/SLPCL.

3.1.1 Temperature Drift of the Mechanical Sensor

A sweep-frequency experiment was conducted at different temperatures to reveal the temperature effect of the mechanical part of the accelerometer. The electrostatic tuning voltage of DSPP capacitors was set to zero during the experiment. The mechanical stiffness and damping coefficient at each tested temperature can be determined by analyzing the frequency responses. As shown in Fig. 4, an AC force was applied to the accelerometer through the feedback capacitors, and the measured frequency responses at different surrounding temperatures reflected the vibrational characteristics of the mechanical sensor. System parameters km and b can be derived by fitting the frequency responses using Eq. (10). The results of mechanical stiffness and damping coefficient are shown in Fig. 4b, c. Mechanical stiffness and damping coefficient varied linearly with the temperature. When the temperature increased from 20 to 50 °C, km dropped by 42.5% [17] and b increased by 7.87%. This finding indicated that the temperature drift of the mechanical part has a dominant effect on the accelerometer drift.

Fig. 4
figure 4

Measured frequency response of the accelerometer (a), mechanical stiffness (b), and damping coefficients (c) varying with the temperature

Full size image

3.1.2 Temperature Drift of the Readout Circuit

According to Eq. (7), the drift of the amplification gain of the readout circuit has an influence on the position of the force-rebalanced proof mass and thus affects the tuning and feedback force of the accelerometer. The temperature drift of the amplification gain of the readout circuit was measured during a cooling process with a 10 °C interval from 50 to 20 °C. The displacement of the proof mass was detected and maintained by a self-centering closed loop [21], which facilitated the measurements of the amplification gain of the readout circuit. In the absence of displacement change, the measured digital-form output of the readout circuit reducing with temperature is shown in Fig. 5. The readout amplification gain is derived using Eq. (7) and exhibited an increasing trend with the temperature. The variation of the readout amplification gain was about 2.1% under a temperature decrease from 50 to 20 °C, implying that the temperature effect of the readout amplification gain is another dominant factor of the accelerometer drift.

Fig. 5
figure 5

Measured outputs and amplification gains of the readout circuit at different temperatures

Full size image

The phase of the readout circuit shifted in response to the temperature change. As shown in Fig. 6, the measured phase of the readout circuit slightly increased with the surrounding temperature. This measurement was carried out by injecting a virtual single into the sense electrodes, which is the multiplication between the stimulus AC signal and the carrier signal. The readout circuit phase can be derived by demodulating the response signal of the readout circuit twice. According to Eq. (12), the effective stiffness of the proposed accelerometer can be maintained by SLPCL because the temperature drifts of the damping coefficient and the phase of the readout circuit are negligible.

Fig. 6
figure 6

Phase of the readout circuit at different temperatures (a) and its relation with temperature (b)

Full size image

3.1.3 Temperature Drift of the Tuning Circuit

The temperature drift of the tuning voltage was measured with a high-resolution source meter (2450, KEITHLEY) in a temperature cooling process from 50 to 0 °C. The TDC of Vt was about 0.12–0.21 mV/°C, as listed in Table 2. Given that the drift arose from the readout and tuning circuits, the electrostatic stiffness at different temperatures can be estimated using Eq. (5). When the tuning voltage was about 5.75 V, the variation of the electrostatic stiffness was about 0.47%, with the temperature ranging from 0 to 50 °C. This variation can be neglected relative to that of mechanical stiffness.

Table 2 Temperature drift of the tuning circuit at different Vt values
Full size table

3.1.4 Temperature Drift of the Feedback Circuit

The temperature drift of the feedback circuit can be measured using the same source meter. The feedback force was generated by a pull–pull differential feedback capacitor and is given by

$${F}_{\mathrm{fb}}\left(T\right)={k}_{vf}{V}_{\mathrm{fb}}\left(T\right){V}_{\mathrm{dc}}\left(T\right)$$
(14)

where kvf is the force gain of feedback capacitors.

By substituting Eq. (14) into (3), the feedback gain can be given by

$${k}_{\mathrm{fb}}\left(T\right)={{k}_{vf}k}_{\mathrm{DA}}{\left(T\right)V}_{\mathrm{dc}}\left(T\right)$$
(15)

where kDA is the amplification gain of the digital analog converter (DAC) in the feedback circuit.

Vfb and Vdc as a function of temperature were measured by the same source meter. DAC gain kDA was determined by fitting the slope of Vfb versus Dfb at different temperatures, as shown in Table 3. Force gain kvf was determined by calibration using an indexing table at a surrounding temperature of 20 °C. The temperature drift of the feedback gain is obtained using Eq. (15), as shown in Fig. 7. The variation of the feedback gain was about 0.062% with a temperature ranging from 20 to 50 °C, which is negligible relative to that of the readout amplification gain.

Table 3 Temperature drift of kDA and Vdc of the feedback circuit
Full size table
Fig. 7
figure 7

Feedback gain of the feedback circuit at different temperatures

Full size image

3.1.5 Comparison of Different Drift Contributions

The temperature drift of the accelerometer output was predicted while independently considering each factor to compare the temperature drift contributions from these factors. Figure 8 illustrates the predicted results of the accelerometer controlled with DCL or DCL/SLPCL when an initial tuning voltage of 5.75 V was applied. The predicted temperature drift was in good agreement with the measured results. The temperature drift arising from the mechanical stiffness and the readout amplification gain showed a dominant effect on the drift of the proposed accelerometer. The contribution of the drift of the mechanical stiffness was larger than that of the readout gain. The accelerometer with DCL and SLPCL exhibited a reduction in temperature drift compared with the accelerometer with only DCL. Therefore, the temperature drift model of the accelerometer with DCL is simplified by

Fig. 8
figure 8

Predicted and measured temperature drift when the accelerometer is controlled with DCL (a) or DCL/SLPCL (b)

Full size image
$${D}_{\mathrm{fb}1}\left(T\right)=\frac{{k}_{m}\left(T\right)+{k}_{\mathrm{e}}}{{k}_{\mathrm{fb}}}\left(\frac{{D}_{\mathrm{ref}}}{{k}_{\mathrm{re}}}+x_{1}-{x}_{0}\right)+\frac{{k}_{e}{x}_{0}}{{k}_{\mathrm{fb}}}-\frac{m{a}_{\mathrm{ext}}}{{k}_{\mathrm{fb}}}$$
(16)

The temperature drift model of the accelerometer with DCL and SLPCL is simplified by

$${D}_{\mathrm{fb}2}=\frac{{k}_{\mathrm{eff}}}{{k}_{\mathrm{fb}}}\left(\frac{{D}_{\mathrm{ref}}}{{k}_{\mathrm{re}}}+x_{1}\right)- \frac{{k}_{m}\left(T\right)}{{k}_{\mathrm{fb}}}{x}_{0}- \frac{m{a}_{\mathrm{ext}}}{{k}_{\mathrm{fb}}}$$
(17)

3.2 Offline Calibration-Based Compensation

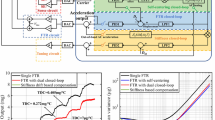
The simplified model revealed that the output bias drift of DCL and DCL/SLPCL had an approximately linear dependence on temperature and the temperature drift of the mechanical stiffness, indicating that the drift can be compensated with a temperature- or stiffness-dependent variable. According to Eq. (11), SLP was dependent on the temperature drift of the mechanical stiffness. As shown in Fig. 9, the SLP of the proposed accelerometer varied synchronously with the output bias in response to the temperature change. With the use of SLP variation for the offline calibration of the accelerometer drift, the temperature drift of the accelerometer can be compensated even in the absence of temperature sensors. Figure 10 shows the correlations between SLP and acceleration output drifts. Through the fitting of the measured correlations, the slope of SLP versus output drift can be obtained and used as the correction coefficients of offline calibration-based compensations. Figure 11 shows the uncompensated and compensated outputs of the proposed accelerometer with different electrostatic tuning voltages. The SLP-based offline compensations had about a one-order magnitude reduction for TDC. When the electrostatic tuning voltage Vt was 5.75 V, the TDC was reduced from 0.5403 mg/°C (without compensation) to 0.0925 mg/°C (with SLP-based compensation).

Fig. 9
figure 9

Output bias and stiffness-loop phase (SLP, defined as θ2) of the accelerometer with DCL at different temperatures

Full size image
Fig. 10
figure 10

Correlations between SLP and the temperature drift of the accelerometer with DCL

Full size image
Fig. 11
figure 11

Temperature drifts of the accelerometer before and after offline calibration-based compensation at different electrostatic tuning voltages: a Vt = 0; b Vt = 1.92 V, c Vt = 3.84 V; d Vt = 5.75 V

Full size image

3.3 Phase Closed-Loop-Based Compensation

Online compensation can also be achieved using the correlation between SLP and accelerometer output drifts. The effective stiffness of the proposed accelerometer can be tuned to keep SLP constant by adjusting the electrostatic tuning voltage of DSPP. As shown in Fig. 12, the effective stiffness and SLP can be altered by varying the electrostatic tuning voltages. The measured effective stiffness and SLP were in good agreement with those predicted by Eqs. (9) and (11), respectively.

Fig. 12
figure 12

Effective stiffness and SLP varying with electrostatic tuning voltage at 15 °C

Full size image

With SLPCL, the electrostatic stiffness is automatically adjusted during temperature changes. The temperature drift of the elastic restoring force is partially compensated by the electrostatic tuning force. However, due to the mismatch between the original position of the proof mass and the center position between the DSPP tuning capacitors, the compensation of accelerometer drift becomes incomplete, with a remaining output bias drift proportional to x0. Equations (16) and (17) were used to estimate the drift of the accelerometer with DCL or DCL/SLPCL, respectively. According to Eq. (16), the major bias drift of the proposed accelerometer with DCL was proportional to the reference displacement of the proof mass from the original position. Equation (17) revealed that the major remaining bias drift of the proposed accelerometer with DCL/SLPCL was proportional to the distance between the original position of the proof mass and the center point of the DSPP tuning capacitors.

As revealed in Figs. 13 and 14, DLP had an almost linear correlation with the remaining temperature drift of the accelerometer with DCL/SLPCL. Another offline phase-drift calibration based on DLP can be performed for further compensation of the output drift of the accelerometer with DCL/SLPCL. The compensated output of the proposed accelerometer is shown in Fig. 15, in which the electrostatic tuning voltage was 5.75 V. The TDC of the proposed accelerometer was first reduced from 0.5403 to 0.2905 mg/°C by an SLPCL online compensation and further reduced to 0.0403 mg/°C by an additional DLP-based compensation.

Fig. 13
figure 13

Measured temperature drift and displacement-loop-phase (DLP, defined as θ1) of the accelerometer with DCL/SLPCL

Full size image
Fig. 14
figure 14

Correlation between temperature drift and DLP of the accelerometer with DCL/SLPCL

Full size image
Fig. 15
figure 15

Temperature drift before and after DLP-based compensation of the accelerometer with DCL/SLPCL

Full size image

3.4 Pull-in and Bias Instability

With the increase in temperature, the effective stiffness of the proposed accelerometer might be reduced greatly, leading to electrostatic pull-in of DSPP capacitors. The temperature drift of the effective stiffness can be inhibited when the accelerometer is working with SLPCL; thus, the electrostatic pull-in instability can be prevented. Experimental results showed that the TDC of the effective stiffness can be improved by SLPCL from − 0.090 to 0.006 Nm−1 °C−1 when a stiffness-tuning voltage of 5.75 V was applied, as shown in Fig. 16.

Fig. 16
figure 16

Temperature drift of the effective stiffness of the accelerometer with and without SLPCL

Full size image

Acceleration outputs were recorded for the accelerometer with and without SLPCL for an hour to evaluate the effect of SLPCL on the bias instability of the accelerometer. As shown in Fig. 17, the Allan variance bias instability of the accelerometer with SLPCL was about 2.8 μg, indicating that the output stability is almost unaffected by SLPCL. The Allan variance also showed that the long-term drift of the accelerometer can be improved by SLPCL.

Fig. 17
figure 17

Allan variance bias instability of the accelerometer with and without SLPCL

Full size image

4 Conclusions

An in-operation phase-based compensation approach was proposed for the reduction in the TBD of a MEMS accelerometer with stiffness-tuning DSPP capacitors. An out-of-bandwidth AC stimulus signal is introduced to the feedback capacitors of the accelerometer, and the demodulated phase was used to calibrate the temperature drift of the effective stiffness. On the basis of the calibration results, an SLPCL was established by adjusting the electrostatic tuning voltage of the DSPP capacitors. A temperature drift model considering the original position mismatch between different capacitors was developed for the proposed accelerometer with DCL and SLPCL control. Characterizations of the temperature effect of the mechanical structure, the readout circuit, the tuning circuit, and the feedback circuit were carried out to obtain the temperature coefficients of each component. Results showed that the temperature effect of mechanical stiffness and readout amplification gain are dominant factors in the output bias drift. The predictions of the simplified model are in good agreement with the experimental results. Offline compensation approaches were first attempted based on the precalibration of SLP. An online compensation approach for the temperature drift of the proposed accelerometer based on SLPCL was alternatively implemented. The TDC of the proposed accelerometer was reduced by SLPCL from 0.5403 to 0.2905 mg/°C with temperature varying from 20 to 50 °C. The remaining output bias drift caused by the original mismatch can be further compensated by DLP-based calibration in a manual way, with TDC being further reduced to 0.0403 mg/°C. Meanwhile, the electrostatic pull-in of DSPP resulting from the temperature drift could be prevented by SLPCL without affecting the Allan bias instability of about 2.8 μg.