1 Introduction

Recent developments in nanotechnology-based devices have driven the research need to explore nanoscale fabrication processes. A range of fabrication methods exist to manufacture nanoscale features for applications in sensors and nanoelectromechanical systems for example [1]. Currently, adopted methods to produce nanoscale structures and patterned devices include deep and extreme ultraviolet nanolithography, nanoimprint lithography, focused ion beam machining, wet etching, electron beam cutting, and single-point nanoscale machining. In the context of prototype device development, most of these techniques can be limited by the choice of substrate materials or the cost of equipment and processing. Atomic force microscopy (AFM)-based nano-scratching may provide a cost-effective alternative to create features, such as nano-grooves with high levels of lateral and vertical resolutions [2,3,4]. Nanoindenter systems also fall into this category of enabling equipment, as they can be used to implement a similar mechanism to generate nanoscale grooves on various materials[5], with the added benefit of not being affected by the compliance of AFM cantilever probes [6, 7]. The development of different tool tip geometries, such as spherical tips [8], conical tips [9], and pyramidal tips [10], has enabled the production of various nanochannel shapes. A common characteristic of mechanical material removal at such a small scale is that the rake angle of a typical tool is often negative due to its inherent geometry and cutting edge radius. The resulting topography of nanoscale grooves is not only evidently influenced by the tool geometry but it also depends on the properties of the processed material and the specific removal mechanism at play, i.e., ploughing and/or cutting. For this reason, it is often desirable to model the nanoscale scratching process as a function of processing parameters, such as the rake angle of the tool. Such simulations can be useful not only to predict the scratched topography but also to understand how the process affects subsurface material properties, such as the extent of plastic strain underneath a groove.

The nanoscale scratching process is often modeled using molecular dynamics [11,12,13,14,15,16,17,18,19]. However, given that this approach is typically restricted to very small spatial and time scales, on the order of nanometers (nm) and nanoseconds (ns), its application can be limited when one needs to simulate more realistic length and time conditions. Based on continuum mechanics, smooth particle hydrodynamics (SPH) has recently emerged as a modeling technique to investigate the nanoscale scratching process. The SPH approach, initially developed by Gingold and Monaghan [20] and Lucy [21] for applications in astronomy, is a meshless numerical method that discretizes the problem domain with SPH particles and thus eliminates the issues related to mesh distortion experienced by traditional continuum mesh-based methodologies, such as finite element method, finite-volume method, and boundary element method [22]. With the successful development of the SPH method in handling large deformations in solid and fluid mechanics problems, its application has been extended to micro and nano machining in recent years [23]. For example, Leroch et al. [24] implemented a mesh-free total Lagrangian SPH algorithm using LAMMPS to simulate scratching on a viscoplastic material. While these authors found that the tangential forces observed in the simulations were lower than those measured in experimental trials, they found that the simulated scratch hardness still compared well with the experimental results. Guo et al. [25] performed SPH simulations using LS-DYNA of nanochannel scratching with two different indenter configurations, which included a spherical capped conical tip and a spherical capped regular three-side pyramid tip. These authors performed scratching along different directions on the workpiece, and their investigation showed that the magnitude of the normal forces, in the case of a pyramidal tip, vary significantly along different directions of scratching. Islam et al. [26] performed an SPH-based modeling study of nanoscale scratching with an elastoplastic material model. They also observed that the simulated normal forces were greater than the simulated cutting forces and that a higher negative rake angle led to a reduction in ploughing and an increase in the residual stress and strain.

A considerable amount of research has been published using modeling and experimental techniques to investigate the nanoscale scratching process. For atomic-scale modeling techniques, the length scale in simulations is not similar to that of experiments, and the mesh-based continuum-scale modeling techniques suffer from the mesh distortion problem. Moreover, it is very difficult to analyze subsurface deformation underneath grooves and underlying material removal, and deformation mechanisms with the available experimental characterization techniques. The particle-based SPH method is a robust modeling technique that eliminates the mesh distortion problem and can simulate the process in a similar length scale to experiments. In the research presented here, an in-house Lagrangian SPH code was developed to model the nanoscale scratching process and to investigate the effects of the scratching depth and tool rake angle on the resulting forces, groove topography, and the extent of the deformed layer under a groove as a function of the rake angle. The remainder of this paper is organized as follows: The nanoscale scratching model configuration and material properties of the tool and workpiece are described in Sect. 2. The computational procedure developed by detailing the governing equations, SPH discretization, and contact model adopted in the numerical simulations is explained in Sect. 3. The model validation and effect of scratching parameters on the groove formation, forces, and residual plastic deformed layer are discussed in detail in Sect. 4. Finally, concluding remarks are presented in Sect. 5.

2 Materials and Nanoscale Scratching Model

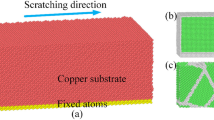
A 3D configuration of the nano-scratching process and its 2D schematic representation illustrating the tool and workpiece are shown in Fig. 1. The modeled tool was conical and had a spherical cap with a specified radius at the tip. As illustrated in Fig. 1b, for the purpose of the numerical simulation, the bottom and front ends of the workpiece were treated as fixed boundaries to provide a rigid base. The spherical capped conical tool had a radius (R0) and consisted of a rake angle (γ), as shown by the schematic diagram in Fig. 2. The tool tip was made of diamond, and its density, elastic modulus, and Poisson ratio were 3520 kg/m3, 1150 GPa, and 0.07, respectively. The tool was assumed to be rigid. The workpiece material was chosen as oxygen-free high-conductivity (OFHC) copper in the present work. The OFHC Cu has an elastic modulus of 124 GPa, a shear modulus of 46.3 GPa, a yield stress of 0.4 GPa, and a Poisson’s ratio of 0.34 [27]. As stated earlier, the workpiece material was described by an elastoplastic constitutive model.

Fig. 1
figure 1

a 3D model of nano-scratching and b 2D schematic view

Full size image
Fig. 2
figure 2

Schematic diagram of the spherical capped conical tip model

Full size image

The nanoscale scratching simulations were performed using a tool tip with a radius of 100 nm. Three different scratching depths, i.e., 100, 150, and 200 nm, were considered in this work to analyze the effect of the depth of cut on the deformation and scratched surface of the Cu workpiece material. Three different negative rake angles (i.e., 10°, 30°, and 60°) were also selected to determine the effect of various values of the negative rake angle on machined surfaces. In the presented simulations, the tool was initially indented into the copper workpiece up to a certain depth, and subsequently, it was moved parallel to the top surface at the same depth to produce a nanoscale scratch. For validating the developed code, experimental results available in the literature [26] for 100-, 150-, and 200-nm scratching depths with a 60° negative rake angle tool were compared with the outcome of the numerical simulations.

3 Computational Procedure

The computational approach used was based on the SPH method. SPH is a particle-based Lagrangian modeling technique where a continuum domain is represented by a set of particles. In a Lagrangian-based approach, field variables, such as density, pressure, and velocity can be traced at SPH particles, which follow the material deformation. A smoothing or kernel function is utilized in the SPH formulations to obtain the approximate field properties. For any particle, the approximated field variables or properties are determined by taking an average over neighboring particles using smoothing functions.

3.1 Governing Equations

In the Lagrangian approach, to solve governing conservation equations, the reference or undeformed configuration of the simulation domain remains fixed as the simulation progresses. The current or deformed configuration is computed with respect to the reference configuration. Therefore, the conservation and constitutive equations are expressed in terms of the coordinates of the reference configuration X. A mapping function ϕ relates the reference and current configuration and is used to define the body motion between two configurations at a given time t as

$$ {\varvec{x}} = \phi \left( {{\varvec{X}},t} \right) $$
(1)

where x represents the current configuration coordinates and X represents the corresponding reference configuration coordinates. Hence, displacement is given by

$$ {\varvec{u}} = {\varvec{x}} - {\varvec{X}} $$
(2)

The deformation gradient represents the gradient of the mapping function:

$$ {\varvec{F}} = \frac{{{\text{d}}{\varvec{x}}}}{{{\text{d}}{\varvec{X}}}} $$
(3)

The conservation equations for mass and momentum in the Lagrangian approach are represented by

$$ \frac{{{\text{d}}\rho }}{{{\text{d}}t}} = - \rho \nabla \cdot {\mathbf{v}} $$
(4)
$$ \frac{{{\text{d}}{\mathbf{v}}}}{{{\text{d}}t}} = \frac{1}{\rho }\nabla \cdot {\varvec{\sigma}} $$
(5)

where ρ is the mass density, σ is the stress tensor, v denotes the velocity, and ∇ is the gradient operator. For elastic solids, the stress tensor can be expressed as a composition of volumetric and deviatoric parts:

$$ {\varvec{\sigma}} = - pI + {\varvec{\sigma}}^{{\prime }} $$
(6)

where p is the mean stress or pressure and σ′ denotes deviatoric stress.

3.2 SPH Discretization

The nanoscale scratching model comprising of a tool and a workpiece was discretized with SPH particles [28], as shown in Fig. 3. SPH is a two-step approximation method: The first step is particle approximation, where a continuum is represented by clouds of particles. The second step is smoothing, which indicates that any property of the particle is approximated as the weighted average of values associated with surrounding particles. The SPH particles interact through a kernel function.

Fig. 3
figure 3

SPH particle discretization of the initial configuration

Full size image

Mathematically, a given function f(x) can be approximated, in a discretized form, by the values associated with neighboring particles and a kernel function W(x, h) [29] as follows:

$$ f\left( {\varvec{x}} \right) = \mathop \sum \limits_{b = 1}^{M} f_{b} W_{b} \left( {{\varvec{x}} - {\varvec{x}}_{{\varvec{b}}} ,h_{b} } \right) V_{b} $$
(7)

where h is the smoothing length and Vb is the volume associated with particle b. The kernel function should fulfill the following consistency conditions for accurately reproducing the given function f(x):

$$ \smallint W\left( {{\varvec{x}},h} \right){\text{d}}{\varvec{x}} = 1 $$
(8)
$$ \mathop {\lim }\limits_{h \to 0} W\left( {{\varvec{x}},h} \right) \to \delta \left( {\varvec{x}} \right) $$
(9)

where δ denotes the Dirac delta function. The SPH interpolation of the first derivative of the function f(x) in a discretized domain can be expressed as:

$$ \nabla f\left( {\varvec{x}} \right) = \mathop \sum \limits_{b = 1}^{M} V_{b} f_{b} \nabla W_{b} $$
(10)

The SPH method uses smoothing or the kernel function for interpolating the properties of a given particle from neighboring particles and is governed by a radius of influence, i.e., the smoothing length h. Various smoothing kernel functions exist for implementing numerical approximations. The quantic spline kernel is one of the most popular functions used, and it is defined as follows:

$$ W\left( q \right) = \alpha \left\{ {\begin{array}{*{20}l} {\left( {2 - q} \right)^{5} - 16\left( {1 - q} \right)^{5} ,} \hfill & {\quad q \le 1;} \hfill \\ {\left( {2 - q} \right)^{5} ,} \hfill & {\quad 1 < q \le 2;} \hfill \\ {0,} \hfill & {\quad q > 2,} \hfill \\ \end{array} } \right. $$
(11)

where \(q = \frac{{\left| {\varvec{x}} \right|}}{h}\) and α denotes the normalizing factor of the quintic spline kernel function. For the above kernel function, α is determined as

$$ \alpha = \left\{ {\begin{array}{*{20}l} {\frac{1}{{32\pi h^{2} }},} \hfill & {\quad {\text{for}}\quad 2 - D;} \hfill \\ {\frac{7}{{40\pi h^{3} }},} \hfill & {\quad {\text{for}}\quad 3 - D,} \hfill \\ \end{array} } \right. $$
(12)

The velocities and positions of the SPH particles are updated by the leapfrog time integration scheme, which can be expressed as

$$ {\mathbf{v}}_{{n + \frac{1}{2}}} = {\mathbf{v}}_{{n - \frac{1}{2}}} + {\varvec{a}}_{n} \Delta t $$
(13)
$$ {\varvec{x}}_{{n + \frac{1}{2}}} = {\varvec{x}}_{n} + {\mathbf{v}}_{{n + \frac{1}{2}}} \Delta t $$
(14)

where \({\mathbf{v}}_{{n + \frac{1}{2}}} ,{\mathbf{v}}_{{n - \frac{1}{2}}}\) are the velocities of SPH particles at the next and previous half steps, respectively. Similarly, \({\varvec{x}}_{{n + \frac{1}{2}}} ,{\varvec{x}}_{{n - \frac{1}{2}}}\) are the positions of SPH particles at the next and previous half steps, respectively. Δt in the above equations represents the time-step size associated with the time integration scheme. For any explicit time integration scheme, the time increment must satisfy the following stability condition:

$$ \Delta t < \frac{h}{c} $$
(15)

where c is the speed of sound in the material and is expressed as \(c = \sqrt {\frac{{\left( {K + 4G/3} \right)}}{\rho }}\), K denotes the bulk modulus, G is the shear modulus, and ρ is the material density.

3.3 Contact model

In the SPH modeling of nanoscale scratching, the particles representing the tool and workpiece come into contact and form an interface, as schematically shown by the tool–workpiece particle contact model in Fig. 4. The pressure distribution at the contact is semi-elliptical, and the interface between the two particles is circular with the peak pressure taking place at the center. The magnitude of the interaction force (F) between the tool and workpiece SPH particles is defined based on the Hertz contact model as

$$ F = \frac{4}{3}E^{*} R_{ij}^{0.5} d^{1.5} $$
(16)

where the contact modulus E* is expressed as

$$ \frac{1}{{E^{*} }} = \frac{{1 - \nu_{i}^{2} }}{{E_{i} }} + \frac{{1 - \nu_{j}^{2} }}{{E_{j} }} $$
(17)

In the above equation, Ei and Ej are the respective elastic modulus of the tool and workpiece. Similarly, νi and νj are the respective Poisson’s ratios for the tool and workpiece. d represents the penetration depth. Rij is the equivalent radius of two interacting smooth particles with radii Ri and Rj. The equivalent radius is expressed as

$$ \frac{1}{{R_{ij} }} = \frac{1}{{R_{i} }} + \frac{1}{{R_{j} }} $$
(18)

An algorithmic flow diagram describing computational modeling procedures adopted for the SPH simulation of nanoscale scratching is illustrated below.

figure a
Fig. 4
figure 4

Schematic diagram of the tool–workpiece particle contact model

Full size image

4 Results and Discussion

This section starts by reporting the validation of the obtained simulation results against available experimental results for various scratching depth values. Following the validation of the model, the scratched surface was further analyzed to understand the cutting and ploughing mechanisms for different scratching depths and rake angles. In the experimental investigation employed as a reference [26], the scratching speed was not mentioned. The speed used in the current simulation study was 100 m/s, which is higher than that employed in actual nano-scratching experiments. Initially, simulation trials were carried out with different scratching speeds. However, it was observed that the value of the scratching speed had little effect on the simulation outcomes, i.e., forces and produced topography. For this reason, the higher speed of 100 m/s was eventually used to save computational time. In the simulation study on nano-scratching carried out by Guo et al. [25], the magnitude of the scratching speed did not have a significant effect either on the normal and cutting forces.

4.1 Model Validation: Contact Forces

The normal and cutting forces obtained from the simulations were compared with the available experimental results from the work of Islam et al. [26]. For a fixed negative rake angle of 60°, the simulated and experimental results of normal and cutting forces for different scratching depth values of 100, 150, and 200 nm are presented in Figs. 5, 6, and 7, respectively. The overall evolution of the forces is similar for all scratching depths. In particular, when the scratching initiates, the normal force undergoes a drop in magnitude for all three cutting depths considered here. This is due to the fact that the tool is in contact with neighboring workpiece particles in all radial directions during the initial indentation process, and as the scratching process subsequently starts, the tool does not remain in contact with the particles behind the scratching direction. Thus, the normal force experienced by the tool is decreased as the number of particles in contact with the tool rapidly reduces. This drop in normal force is observed to be higher in the case of the simulation results. One of the reasons for such a large drop in the simulated normal force may be attributed to the fact that a high scratching speed used in simulations causes the tool and workpiece material behind the tool to lose contact rapidly as the effect of elastic recovery may not play a role in this case. Following the initial drop in magnitude, the normal force rapidly increases for a short period and subsequently fluctuates around a particular value. Moreover, the simulated values obtained for cutting and normal forces are consistently lower than the experimental ones for all scratching depths. This observation is summarized in Fig. 8 and is consistent with the observations reported by Leroch et al. [24]. In the case of the normal force, the difference between simulated results and experimental ones becomes more pronounced as the scratching depth decreases from 200 to 100 nm, whereas the opposite is observed for the cutting force. A likely explanation for this general discrepancy may be attributed to the fact that the material constitutive model used here does not take into account the well-known indentation size effect [30, 31], which was also shown to be existing when nanoscale scratching is considered [32, 33]. The other contributing factor to the difference between the simulation and experimental forces may also be the slight deviation in the tool geometry and workpiece surface used between the simulations and experiments. As suggested by Islam et al. [26], the tool and workpiece are usually not perfectly smooth in the experiments. In spite of these discrepancies, which will require further refinement of the material constitutive equations in future works, the model was subsequently used to gain some insights into the resulting groove topography, as presented in the following subsection.

Fig. 5
figure 5

Variation of forces for the 100-nm scratching depth with a 60° negative rake angle tool

Full size image
Fig. 6
figure 6

Variation of forces for the 150-nm scratching depth with a 60° negative rake angle tool

Full size image
Fig. 7
figure 7

Variation of forces for the 200-nm scratching depth with a 60° negative rake angle tool

Full size image
Fig. 8
figure 8

Variation of simulated average forces against the scratching depth for a 60° negative rake angle tool

Full size image

4.2 Groove Formation

Figure 9 presents contour plots illustrating the pile-up height and corresponding groove cross-sectional view at its mid-section obtained during the nanoscale scratching simulation of the Cu specimen for the three depths considered. As expected, with the increase in the depth, the pile-up height increases, and so does the width of the groove. It is known that when the depth of cut reaches the minimum chip thickness values for a given combination of material and cutting edge radius, then a transition between ploughing and cutting occurs, with material being removed essentially as a chip [34]. Consequently, if the given scratching depth is less than the minimum chip thickness, the material from the workpiece will not be removed as a chip, and the dominant mechanism could be ploughing or sliding. In the reported simulation, the material is mainly ploughed and accumulated on the sides of the groove along the scratching length which suggests that the scratching depth is below the minimum chip thickness.

Fig. 9
figure 9

Simulated groove topography and its cross-sectional view for a 60° negative rake angle tool with different scratching depth values: a 100 nm, b 150 nm, and c 200 nm

Full size image

Furthermore, in Fig. 9, the topography of the groove varies along the scratching direction on the workpiece. The experimental observations in [5] also reported the non-uniformity of the groove dimensions along the scratch. Therefore, to validate the simulated groove profile against the experimental results, the simulated groove profiles were extracted at five different cross sections along the scratch, as indicated in Fig. 10a. These cross sections were at distances of 500, 750, 1000, 1300, and 1600 nm from the point where the scratching was initiated. The extracted profiles from the five cross sections were used to produce an average cross-sectional profile for the 150 nm scratching depth, which was then compared against available experimental results from Islam and Ibrahim [35]. Figure 10b displays this comparison, where the height and depth of the simulated and experimental groove profiles agree well. The approximate width and height of the simulated groove profile were 946 and 192 nm, respectively, whereas the corresponding experimental groove profile values are 1.1 μm and 205 nm, respectively.

Fig. 10
figure 10

a Locations of the sampled groove profile and b comparison of the groove cross-sectional profiles

Full size image

4.3 Effect of the Tool Rake Angle on Contact Forces

Next, the influence of the rake angle value of the simulated forces was analyzed. In particular, Fig. 11a, b show the variation of the cutting and normal forces for a 30° negative rake angle tool. Contrary to the results obtained when scratching with a 60° negative rake angle tool, the cutting forces observed here were slightly higher than the simulated normal forces for the two scratching depths of 150 and 200 nm. For the 100 nm scratching depth, the normal force was still slightly higher than the cutting force. Figure 11c displays the difference between the average cutting and normal force at different scratching depths for the 30° negative rake angle tool. The comparison of Figs. 8 and 11c clearly noted that the rake angle has an influence on the cutting and normal forces. In the case of scratching with a 30° negative rake angle tool, the cutting force at higher scratching depths was comparable to or slightly higher than the normal forces. In general, the cutting force becomes comparable to the normal force when the scratching depth reaches the minimum chip thickness. This indicates that in the case of the 30° negative rake angle tool, the scratching depth is likely to have reached the minimum chip thickness at depths around 150 nm to 200 nm.

Fig. 11
figure 11

Simulated contact forces for the 30° negative rake angle tool: a cutting force; b normal force; c average forces

Full size image

To investigate further the influence of the tool rake angle on contact forces, simulations were also repeated for a tool with a 10° negative rake angle. Figure 12 illustrates the average cutting and normal forces obtained in this case. This figure shows a similar trend as in the case of nanoscale scratching with a 30° negative rake angle. However, the difference between the magnitudes of the cutting and normal forces is larger at increased scratching depths. This suggests that the transition from ploughing took place earlier with increasing scratching depth and that cutting likely becomes the dominant mechanism of material removal at larger depths. Based on these observations, it can be summarized that for a conical tool with 30° and 10° negative rake angles, the mechanism behind nanoscale scratching is either ploughing dominated or cutting dominated depending on the scratching depth and that when the rake angle becomes less negative, the transition from a ploughing-dominated to a cutting-dominated regime occurs at a reduced scratching depth.

Fig. 12
figure 12

Average cutting and normal forces from the nano-scratching simulation with the 10° negative rake angle tool

Full size image

4.4 Assessment of the Residual Strain Underneath a Scratched Groove

In this section, the effect of the scratching depth on the extent of the residual plastic strain is evaluated. Figure 13a–c display the equivalent plastic strain distribution at a mid-section of the scratch length obtained from the nanoscale scratching simulations for different depths of cut. According to Kermouche et al. [36], immediately underneath a single scratch, a small region of tensile stress should be present to a maximum depth of about 0.5 times the contact radius, followed by a larger region of compressive stress with a thickness of up to 2 to 3 times the contact radius. As a result, the surface of a groove is irregular, and the groove’s intended dimensions might vary. The deformed subsurface layers also influence the surface roughness, which in turn affects the mechanical characteristics of the workpiece. Thus, the depth of the subsurface deformed layer is an important parameter, which can be difficult to be assessed experimentally [37]. Following scratching, this layer can have an effect on the mechanical properties and life of the scratched component. In this study, the subsurface deformed layer was estimated using the equivalent plastic strain distribution below the scratched surface, as reported in Fig. 13. It is noticed that the subsurface deformed layer thickness increases with the increase in the scratching depth. In particular, the thickness of this layer for a 60° negative rake angle tool doubles from 190 nm at a 100 nm scratching depth to 375 nm at twice the scratching depth, i.e., 200 nm. Figure 14 summarizes the deformed layer thicknesses for a surface scratched on the nanoscale using 10°, 30°, and 60° negative rake angle tools. This bar chart shows that the more negative the rake angle, the larger the thickness of the deformed layer. This phenomenon was also observed in a conventional machining study based on different tool rake angles carried out by Dahlman et al. [38], where larger negative rake angle tools would lead to higher compressive stresses and a deeper deformed zone below the machined surface. Figure 14 also shows that for all rake angle values, the higher the scratching depth, the larger the deformed layer thickness.

Fig. 13
figure 13

Equivalent plastic strain distribution in the scratched workpiece for a 60° negative rake angle tool with different scratching depth values: a 100 nm, b 150 nm, and c 200 nm

Full size image
Fig. 14
figure 14

Deformed layer thickness at different depths of nano-scratching with 10°, 30°, and 60° negative rake angle tools

Full size image

The present study involving the SPH modeling of nanoscale scratching could be expanded to other nanoscale machining processes, such as single-point diamond turning, precision grinding, mechanical polishing, and lapping processes. These processes also make use of either a solid mechanical tool or loose abrasives to machine material from a workpiece. The underlying mechanisms of material removal and deformation in these processes bear some similarities to that of nanoscale scratching. For this reason, a model similar to that used in this study could be helpful in investigating such nanoscale machining processes.

5 Conclusions

In this study, the SPH method was employed for modeling the nanoscale scratching process on copper using negative rake angle tools. Three scratching depths, i.e., 100, 150, and 200 nm, and three different negative rake angle values, i.e., 10°, 30°, and 60°, were considered for the simulation. The output of the simulations focused on analyzing the tool–workpiece contact forces, scratched surface topography, and residual stresses underneath a scratched groove. The SPH simulation results were also compared with experimental data from the literature. The following conclusions can be drawn from the reported results:

  1. 1.

    The normal and cutting forces on the tool increase with an increase in the scratching depth. The tool rake angle also significantly influences the contact forces in the nanoscale scratching process. More negative rake angle values lead to higher cutting and normal forces for all scratching depths considered. For less negative rake angle values, the cutting forces eventually become larger than the normal force for increased scratching depths.

  2. 2.

    The averaged simulated groove profile is in close agreement with the experimental groove profile. In particular, the difference between the simulated and experimentally observed groove dimensions was less than 15%. However, this comparative study was possible only in the case of the 60° negative rake angle tool, as similar experimental results could not be found in the literature for other values.

  3. 3.

    Ploughing and cutting mechanisms were inferred based on the analysis of the simulated forces when scratching was performed with conical tools. The ploughing mechanism was more dominant during the nanoscale scratching process conducted with the 60° negative rake angle tool. In the case of the 10° and 30° negative rake angle tools, the ploughing mechanism was marginally dominant at lower scratching depths, whereas the cutting mechanism was more dominant at higher depths.

  4. 4.

    A layer of residual plastic strain could also be simulated beneath a groove following the scratching process. It was observed that the thickness of the plastically deformed region increased not only for higher scratching depths but also for more negative rake angle tools.