1 Introduction

In modern world, the task of process monitoring is very much crucial for product quality as well as safety [1]. The automation-based modern revolution has brought a major improvement in petrochemical industries since it is possible to convert raw materials into final products at improved quality. However, the modern revolution also carries few risks and accidents due to the added complexity in the processes and leads to many accidents that possess a major threat to the environment. Possible manual error, poor maintenance of the process plant, and malfunctioning sensors are some of the main causes of these mishaps. The above-mentioned accidents can be controlled if the process plants are monitored continuously. The last few decades have seen improved monitoring techniques for automated processes which are built around anomaly diagnosis, anomaly detection, and isolation. The anomaly detection suggests if any anomaly is present in the system, anomaly diagnosis suggests the type of anomaly that has occurred and anomaly isolation points out the particular sensor groups that were responsible for the anomaly. With improved data acquisition methods and inexpensive data management systems available, a large volume of sensor measurement data can be recorded very easily.

The availability of sensor data has ensured frequent utilization of data-driven anomaly detection methods over their counterparts, the model-driven methods, where the duty of model development is exigent due to the complexity in process plants [2, 3]. The data-driven methods depend on the availability of quality process data that contains information on the process and seizes intrinsic complexities within the process [4]. The uni-variate and multivariate techniques are the two sub-classes of data-driven anomaly detection methods. The multivariate strategies analyze high dimensional data to capture useful features through immeasurable variables (latent variables), thus having a clear advantage over uni-variate techniques that are restricted in analyzing single sensor measurement only [5]. Few regularly applied multivariate statistical methods include principal component analysis (PCA), partial least squares (PLS), and fisher discriminant analysis (FDA). The classic PCA technique reduces the dimension of data to retain information from the original data [6]. Though PCA has been widely applied in process monitoring problems, it represents input space without considering the features from output space.

Most chemical processes like continuous stirred tank heater and distillation column are represented using the relationship between input-output variables. Process monitoring can be enhanced if a technique can model input-output space and this is possible using partial least squares (PLS) strategy. The PLS method extracts latent factors from predictor (input) and response (output) variables to maximize the cross-correlation and generates a relationship between the two sets of variables. PLS method has also been used in soft-sensor applications to predict response variables using predictor variables [7, 8]. Recently, different variants of PLS strategy have been proposed in monitoring applications and this includes multi-block PLS [9], kernel PLS [10], dynamic PLS [11], modified PLS [12] and multi-scale PLS [13]. The anomalies occurring in the chemical process are monitored using \(T^{2}\) and squared prediction error (SPE) anomaly indicators. However, the \(T^{2}\) and SPE indicators are ineffective in monitoring since the decision regarding an anomaly is based only on previous observations. This makes the indicators insensitive to small magnitude faults which lead to missed detections and false alarms [14].

To overcome the shortcomings of \(T^{2}\) and SPE indicators, the PLS method has been integrated with the generalized likelihood ratio (GLR) test to improve the task of monitoring in recent years. The GLR is a hypothesis-testing technique used to compare the goodness of fit between two data distributions. The multi-scale PLS and kernel PLS strategies have been integrated with GLRT and the performance was found to be superior than \(T^{2}\) and SPE indicators [15, 16]. In recent years, the Kantorovich Distance (KD) based statistical index has been applied for the task of detecting anomalies. The KD index is defined as the minimum cost needed to shift a mass of data between two distributions [17]. The KD metric has been found to have better detection of small magnitude anomalies and has provided better results when data was corrupted with noise [18, 19]. Considering the benefits offered by the KD index, an improved anomaly detection scheme is proposed that uses PLS as a modeling framework and KD as an anomaly indicator. The residuals from the PLS model capture process information and aids in providing anomaly information. Hence, the proposed PLS-KD strategy evaluates the residuals of anomaly-free data and the anomaly data to detect possible anomalies.

The organization of the paper is as follows: Sect. 2 provides an overview of PLS modeling, \(T^{2}\), SPE, and GLR-based anomaly indicators. This is followed by the description of optimal mass transport and KD metric formulation in Sect. 3. Next, the proposed monitoring strategy that amalgamates PLS with KD metric, is discussed in Sect. 4. To assess the efficacy of the proposed PLS-KD strategy, two case studies are considered in Sect. 5. The performance of the PLS-KD scheme is contrasted against PLS-\(T^{2}\), PLS-SPE, and PLS-GLR based strategies. In Sect. 6, the concluding remarks about the work are provided.

2 Partial least squares

PLS is a useful multi-variate tool which provides dimension reduction and prediction performance [20, 21]. It finds the relationship between input X and output Y by transforming both X and Y into their latent variables which is then followed by relating the transformed latent variables. Consider a data \(\mathbf {X}\in \Re ^{\textit{n}\times \textit{m}}\) and \(\mathbf {Y}\in \Re ^{\textit{n}\times \textit{1}}\) where m and n represents the number of variables and observation samples respectively. After normalization, the model is developed which involves transforming X and Y into lower dimensional subspace and it can be represented as [22]:

$$\begin{aligned} \begin{aligned} \mathbf {X}={\varvec{\hat{X}}} + \mathbf {F} = \sum _{k=1}^{p}\mathbf {t}_{p}\mathbf {P}_{p}^{T} + \mathbf {F} = \mathbf {TP}^{T} + \mathbf {F} \\ \mathbf {Y}={\varvec{\hat{Y}}} + \mathbf {E} = \sum _{k=1}^{p}\mathbf {u}_{p}\mathbf {Q}_{p}^{T} + \mathbf {E} = \mathbf {UQ}^{T} + \mathbf {E} \end{aligned} \end{aligned}$$
(1)

The Eq. (1) is described as the outer model of PLS. While \(\mathbf {T}\in \Re ^{\textit{n}\times \textit{p}}\) and \(\mathbf {U}\in \Re ^{\textit{n}\times \textit{1}}\) represents the matrix of transformed latent variables, P and Q represent the loading matrices respectively. The number of transformed latent variables (LVs) are p where as \({\mathbf {F}}\) and \({\mathbf {E}}\) represent residual matrices. The latent variables \(t_{k}\) and \(u_{k}\) with k = 1,2,...p, are extracted iteratively through non-linear iterative partial least squares (NIPALS) algorithm. For each PLS dimension, the NIPALS algorithm calculates two LVs that are called as \(\mathbf {t}\) and \(\mathbf {u}\) and they are a linear combination of \(\mathbf {X}\) matrix and \(\mathbf {Y}\) matrix. These variables are chosen such that the co-variance between \(\mathbf {t}\) and \(\mathbf {u}\) is maximized.

It is important to retain few optimum LVs in the process model to have good prediction and the cross-validation approach is utilized. Next, a relationship between latent variables of input and output data is developed via the PLS inner model that is described in Eq. (2) as follows:

$$\begin{aligned} \mathbf {U} = \mathbf {TV} + \mathbf {W} \end{aligned}$$
(2)

where V is the regression matrix and W is the residual matrix. Once the PLS inner model is developed, the output Y can be expressed as:

$$\begin{aligned} \mathbf {Y} = \mathbf {TV}\mathbf {Q}^{T} + \mathbf {E}^{*} \end{aligned}$$
(3)

where \(\mathbf {E}^{*}\) is a residual matrix which presents unexplained variance in Eq. (3). The NIPALS algorithm used in this work is summarized as follows: [23]

  • Step-1: The \(\mathbf {u}\) is set equal to the column of \(\mathbf {Y}\).

  • Step-2: \(\mathbf {w}=\frac{\mathbf {u}^{T}\mathbf {X}}{\mathbf {u}^{T}\mathbf {u}}\).

  • Step-3: The \(\mathbf {u}\) is normalized to unit length.

  • Step-4: The scores are evaluated: \(\mathbf {t}=\frac{\mathbf {X}\mathbf {w}}{\mathbf {w}^{T}\mathbf {w}}\).

  • Step-5: The new \(\mathbf {u}\) vector is evaluated: \(\mathbf {u}=\frac{\mathbf {Y}\mathbf {q}}{\mathbf {q}^{T}\mathbf {q}}\).

  • Step-6: The convergence on \(\mathbf {u}\) is checked: if YES, proceed to Step-7, else return to Step-1.

  • Step-7: The \(\mathbf {X}\) loading \(\mathbf {p}=\frac{\mathbf {X}^{T}\mathbf {t}}{\mathbf {t}^{T}\mathbf {t}}\) is evaluated.

  • Step-8: The residual matrices \(\mathbf {E}= \mathbf {X}-\mathbf {t}\mathbf {p}^{T}\) and \(\mathbf {F}= \mathbf {Y}-\mathbf {t}\mathbf {q}^{T}\) are evaluated.

  • Step-9: If the additional PLS dimensions are required, \(\mathbf {X}\) and \(\mathbf {Y}\) get changed to \(\mathbf {E}\) and \(\mathbf {F}\) and then, step-1 to step-8 are repeated.

Once the reference PLS model is developed from data exhibiting normal operations, anomalies in online data can be captured using \(T^{2}\) and SPE based indicators. The \(T^{2}\) indicator monitors any changes in LV subspace of the model and for a new data, variations in the LVs at different time instances is represented as:

$$\begin{aligned} T^{2} = \sum _{i=1}^{p}\frac{t_{i}^{2}}{\sigma _{i}^{2}} \end{aligned}$$
(4)

For the LV \(t_{i}\), \(\sigma _{i}^{2}\) is the corresponding estimated variance. In contrast, the SPE index checks for any abnormal variations in the residual subspace not defined by the LVs and it may be computed in the following way for online data:

$$\begin{aligned} SPE=\mathbf {e}^{T}\mathbf {e} \end{aligned}$$
(5)

where \(\mathbf {e} = \mathbf {x} - \hat{\mathbf {x}}\) is difference between data x and predicted data \(\hat{\mathbf {x}}\). In other words, the SPE statistics defines the loss of fit from the developed PLS model. An anomaly is declared when the indicators described in Eqs. (4) and (5) exceed the threshold [24].

2.1 Generalized likelihood ratio test

In process monitoring problems, an anomaly is declared based on the decision taken by comparing present measurements with previous normally operating measurements. The simple and composite hypotheses have been usually employed in decision-making problems in literature. GLR is a statistical test that has been applied in solving problems related to the composite hypothesis. It solves the hypothesis problem by maximizing the likelihood ratio function over all possible anomalies. This test has been used as an anomaly indicator in many anomaly detection problems and has been found to detect faults better than conventional anomaly indicators of PLS and PCA-based strategies [16]. Consider an anomaly detection problem with \(\textit{Z}\in \textit{R}^{n}\) been generated by one of the distributions: \(\mathcal {N}(\mu ,\,\sigma ^{2})\) or \( \mathcal {N}(\mu \ne 0,\,\sigma ^{2})\). The Eq. (6) presents the hypothesis problem, which is defined as:

$$\begin{aligned} \begin{aligned} H_{A}= & {} {Z \sim \mathcal {N}(\mu =0,\,\sigma ^{2})} \\ H_{B}= & {} {Z \sim \mathcal {N}(\mu \ne 0,\theta ,\,\sigma ^{2})} \end{aligned} \end{aligned}$$
(6)

GLR test computes the ratio of anomaly-free data and the anomaly data while the unknown anomaly parameter \( \Omega \) is replaced by maximum likelihood estimate and this is possible by maximization of likelihood ratio function which is defined as in Eq. (7):

$$\begin{aligned} \begin{aligned} L(\alpha )= & {} 2log\dfrac{\sup _{\Omega \in \textit{R}^{\textit{n}}}f_{\Omega }(Z)}{f_{\Omega =0}(Z)} \\= & {} 2log\left\{ \dfrac{\sup _{\Omega }\exp \left( -\frac{Z-\Omega ^{2}_{2}}{2\sigma ^{2}}\right) }{\exp \left\{ -\frac{Z^{2}_{2}}{2\sigma ^{2}}\right\} }\right\} \end{aligned} \end{aligned}$$
(7)

where \(f_{\Omega }(Z)=\dfrac{1}{(2\pi )^{\frac{n}{2}}\sigma ^{n}}\exp \left\{ -\dfrac{Z-\Omega ^{2}_{2}}{2\sigma ^{2}}\right\} \) is probability density function of Z. Re-writing the above expression and solving yields [15] :

$$\begin{aligned} L(\alpha ) = \frac{1}{\sigma ^{2}}\bigl \{Z_{2}^{2}\bigr \} \end{aligned}$$
(8)

The GLR \(L(\alpha )\) in Eq. (8) adheres to chi-square \(\chi ^{2}\) distribution with l degrees of freedom since Z adheres to gaussianity. If \(L(\alpha )\) is less than \(v(\lambda )\), the null hypothesis is accepted suggesting no anomaly in the process. If \(L(\alpha )\) exceeds \(v(\lambda )\), the alternate hypothesis is accepted which suggests the presence of anomaly.

3 Kantorovich distance

The optimal mass transport has been an important topic of research in the field of economics, image processing, fluids mechanics, and process applications. Optimal mass transport deals with the relocation of data by minimizing the cost function. A convenient mode of transferring information from the first to second destination distribution concerning a cost function is referred to as optimal mass transport. The optimal mass transport theory has been applied in machine learning, medical, and image processing problems [17, 25]. It may be noted that the optimal transport problem was initially formulated by Monge who proposed a problem where a mass from source distribution can be moved to only one point in destination distribution [26]. Hence, in this formulation, there is no transport plan to rearrange one point to multiple points in the source distribution. The formulation problem was further improved by Kantorovich where it was proposed that multiple data from one distribution can be mapped to multiple data in a second and this method was named Kantorovich Distance.

Since anomaly detection problems detect anomalies by measuring the dissimilarity between data under normal operating conditions and the data with the anomaly, the KD statistic can be applied in anomaly detection problems. Moving a mass of data from the first destination to the second with respect to a cost function is termed Kantorovich distance (KD). For distributions G and H, minimum shifting distance needed for the data from G to H is the Kantorovich distance. The cost is minimal when distributions are similar and large when distributions are dissimilar [27]. The cost function is defined based on the norm in Eq. (9) :

$$\begin{aligned} c(g,h)=g-h^{r} \end{aligned}$$
(9)

When r=1, distance between the distributions relative to cost function is termed as 1-Wasserstein Distance and this is presented in Eq. (10):

$$\begin{aligned} W_{r}(G,H) = \bigg (\underset{\gamma \in \Gamma (G,H)}{inf} \int g-h^{r} d\gamma (g,h)\bigg )^{1/r} \end{aligned}$$
(10)

\(\Gamma (G,H)\) represents set of joint distributions. For r=2, Kantorovich Distance for two n-dimensional random variables g and h is expressed as:

$$\begin{aligned} W_{2}(G,H)&= \bigg (\mu _{g}-\mu _{h}{}^{2}_{2} + Tr\big (\Sigma _{g}\nonumber \\&+\Sigma _{h}-2(\Sigma _{g}^{\frac{1}{2}}\Sigma _{h}\Sigma _{g}^\frac{1}{2})^\frac{1}{2}\big )\bigg )^\frac{1}{2} \end{aligned}$$
(11)

where \(\mu _{g}\) and \(\mu _{h}\) indicate the means while \(\Sigma _{g}\) and \(\Sigma _{h}\) indicate the covariance matrices of variables g and h in Eq. (11). The computation of the KD metric is based purely on the available data and hence, it is not restricted to any particular distribution. This makes the KD metric flexible to be applied for data adhering to any statistical distribution. The KD index involves stacking data observations into segments and evaluating them, thus providing a smooth representation of the KD metric. The KD metric implementation is dependent on the number of segments in data sets and the moving window. A proper selection of both these parameters gives a smooth transition of the KD metric. In this paper, the number of segments in each distribution is represented by r and the moving window is represented by j. The computation of the KD metric between two distributions can be found in [18].

4 The PLS-KD anomaly detection strategy

In this work,a PLS model is constructed from normal operating data extracted from the process and the model is used for monitoring any abnormalities in new data through KD statistical index. The residuals from the PLS model can reveal useful process information and can be assessed to determine abnormalities in the process. When the process is operating customarily, residuals of the process are near zero. In the case of atypical process behavior, the process residuals deviate from zero thus, indicating that the process needs attention. The residuals from the PLS model are described mathematically in Eq. (12):

$$\begin{aligned} \mathbf {E} = \mathbf {Y} - \hat{\mathbf {Y}} \end{aligned}$$
(12)

Next, the KD metric is calculated between the residuals of training and the testing data. The KD metric then undergoes comparison with a threshold to decide the anomaly. The PLS-KD anomaly detection strategy can be mainly divided into two stages:

  1. 1.

    Computation of threshold using normal operating data.

  2. 2.

    Monitoring new data using KD metric.

The kernel density estimation (KDE) approach is used for determining reference threshold [19]. The probability density function \(\hat{f(y)}\) of a random variable is estimated by n samples \(y_{i}\), i = 1, 2, ...n:

$$\begin{aligned} \hat{f(y)}=\dfrac{1}{nh}\sum _{i=1}^{n}K\left\{ \dfrac{y-y_{i}}{h}\right\} \end{aligned}$$
(13)

where K represents uni-variate kernel estimator and h is smoothing parameter in Eq. (13). Initially, the training data are divided into Tr1 and Tr2 respectively. This is followed by developing a PLS model and generating the residuals Ra1 and Ra2. The KD statistic KD is calculated between the two residuals. Next, the density function of the KD index undergoes estimation through the use of a kernel estimator. The point that occupies 99% of the total area under the density function plot is considered as the reference.

Fig. 1
figure 1

Flow chart for PLS-KD anomaly detection strategy

Full size image

Once the reference threshold is computed, the next task is to monitor anomalies in new online data. The PLS-KD strategy is presented in Fig. 1. The off-line anomaly-free data undergoes normalization and progresses for PLS model development from which the residuals G are generated. When new data is available, it undergoes normalization, and residuals H are generated model parameters. Next, each segment of G undergoes comparison with each segment of H for computation of KD metric. The statistic KD is compared with the threshold h to take decision regarding anomaly \(\delta \) and this is presented in Eq. (14):

$$\begin{aligned} \delta = {\left\{ \begin{array}{ll} \text {No anomaly} &{} \text {if KD less than \textit{h}}; \\ \text {Anomaly} &{} \text {if KD greater than \textit{h}};\\ \end{array}\right. } \end{aligned}$$
(14)

5 Case studies

This section presents the monitoring results of PLS-KD strategy using two case studies. The PLS-KD strategy is compared with PLS-\(T^{2}\), PLS-SPE and PLS-GLR strategies using fault detection rate (FDR) and false alarm rate (FAR) indicators [18].

5.1 Tennessee Eastman process

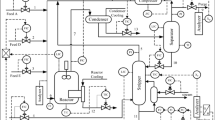
In the domain of process control, Tennessee Eastman (TE) benchmark is considered a standard for multi-variate control and anomaly detection tasks. Most researchers prefer validating the newly proposed anomaly detection strategy on this process [18]. The control structure of the TE process is presented in Fig. 2 and is made of a total 52 measurements that include 22 process measurements, 19 composition measurements, and 12 manipulated variables. The data has been downloaded from the following: http://depts.washington.edu/control/LARRY/TE/download.html [28]. In harsh environments having noise and disturbances, different real anomaly scenarios are proposed of which 15 are known anomalies while the remaining anomalies are defined as unknown. In this case study, the input matrix of the PLS model consists of 33 variables that include 22 process measurements and 11 manipulated variables while the composition variable 35 is treated as the output variable. The cross-validation technique is used to select 5 LVs for the PLS model while a moving window of 40 is employed for the PLS-KD formulation. The anomalies 3, 9, and 15 are not considered in this study since they give small detection rates [29].

Fig. 2
figure 2

TE process flowsheet [30]

Full size image
Fig. 3
figure 3

Monitoring of anomaly 14 by \(T^{2}\) and SPE anomaly indicators

Full size image
Fig. 4
figure 4

Monitoring of nomaly 14 by GLR and KD anomaly indicators

Full size image

The PLS-KD strategy is validated on different anomaly scenarios of the TE process. The monitoring performance of nomaly 14, which is a sticking anomaly in the cooling water valve, is presented. The Figs. 3 and 4 demonstrates the results of different methods in monitoring the nomaly. Though all strategies demonstrate good detection of this anomaly, the conventional anomaly detection schemes have few missed detections. However, the performance of the PLS-KD strategy is slightly better since it detects the anomaly with a higher detection rate and also has no false alarms. The FAR and FDR of the proposed PLS-KD, as well as PLS-\(T^{2}\), PLS-SPE and PLS-GLR methods, are presented in Table 1 and Table 2. It is observed that the PLS-KD and PLS-GLR strategies detect anomaly scenarios better in comparison with PLS-\(T^{2}\) and PLS-SPE based techniques. The PLS-KD strategy over-performs the PLS-GLR strategy as well as the conventional anomaly indicators with a better detection rate. However, it may be observed that for a few cases all the strategies have a high FAR value, but overall, the FAR of the KD index is less as compared to other methods. It can be inferred that the PLS-KD strategy provides better detection of anomalies, thus, over-performing other methods with a smooth detection profile.

Table 1 FAR (%) for TE process
Full size table
Table 2 FDR (%) for TE process
Full size table

5.2 Experimental DC process

The distillation column (DC) is a key unit operation in the oil and gas industry. The experimental DC process used in this study is housed in the Department of Chemical Engineering, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal, India. Figure 5 depicts the bubble cap distillation process used in this work. The construction details of the bubble cap DC process can be found in [31]. The sequential perturbation of reflux, as well as feed flow, aids in the generation of process data. Once the DC process is maintained at nominal operating condition, the feed flow undergoes perturbation for a magnitude of 50 and the reflux flow is maintained constant. Next, the DC process is maintained again to nominal condition and then, the reflux flow is perturbed for a magnitude of 40 while maintaining the flow rate constant. All the above actions result in a few modifications in the product quality (output) i.e xD which is recorded. Also, temperatures at five parts of the DC process are recorded to monitor the condition. Once the DC process data is generated, the next task is to develop a reference model. The input variables include flow rate, feed flow, and the temperatures in the DC process. The composition of light distillate (methanol) i.e., xD is considered as the output variable. Next, the input, as well as output matrices, are split equally to get training and testing data sets having 1000 observations each. The PLS model is developed on input training data while the cross-validation technique yields 2 LVs.

Fig. 5
figure 5

A schematic of distillation column set-up

Full size image

The proposed strategy is assessed by its ability to monitor bias, intermittent and drifts faults in the DC process. To begin with, a step signal is introduced in variable 5 between the observations 400 and the end of the testing data. The results of statistical indices in monitoring the anomaly is presented through Figs. 6 and 7. From Fig. 6, it is observed that both the conventional indicators fail in detecting this anomaly. Also, for PLS-\(T^{2}\) strategy, false alarms are visible between sampling instants 0 and 180. Figure 7 demonstrates improved detection by the PLS-GLR method but has few missed detections in the region of anomaly and few false alarms in anomaly free region. In contrast, the KD metric demonstrates precise detection without missed detections or false alarms, thus having a clear advantage over \(T^{2}\), SPE, and GLR-based anomaly indicators.

Fig. 6
figure 6

Monitoring of bias anomaly by \(T^{2}\) and SPE anomaly indicators

Full size image
Fig. 7
figure 7

Monitoring of bias anomaly by GLR and KD anomaly indicators

Full size image
Table 3 FAR (%) for experimental DC process
Full size table
Table 4 FDR (%) for experimental DC process
Full size table

Even in the case of monitoring intermittent and drift anomalies, the PLS-KD strategy carries a better advantage since it detects these anomalies much better than other methods. The FAR and FDR of the proposed PLS-KD, as well as PLS-\(T^{2}\), PLS-SPE, and PLS-GLR methods, are presented in Tables 3 and 4. In a summary, this case study demonstrates that PLS-\(T^{2}\), PLS-SPE, and PLS-GLR methods are not effective in handling anomalies of small magnitude whereas the PLS-KD strategy detects it reasonably well. Hence, it is safe to conclude that the proposed PLS-KD strategy over-performs other strategies in handling different anomalies in an experimental distillation column process with a good detection rate.

6 Conclusion

A novel statistical anomaly indicator based on Kantorovich Distance was proposed in this study. The detection performance of \(T^{2}\) and SPE anomaly indicators of PLS strategy was found to be abstemious. Hence, an alternative anomaly indicator based on the KD metric was integrated with the PLS modeling framework in this study. The KD metric was computed between the residuals of data under normal operating conditions and residuals of the testing data. The monitoring behavior of the integrated PLS-KD strategy was illustrated using the Tennessee Eastman process and distillation column process. The PLS-KD strategy was contrasted against PLS-\(T^{2}\), PLS-SPE, and PLS GLR-based anomaly detection schemes. The KD statistic was able to capture sensitive process information due to segment-by-segment comparison and this aided in improved anomaly detection. The results reveal that the KD index can be effectively integrated with the PLS strategy to enhance anomaly detection. As a part of future work, the PLS scheme is planned to be integrated with wavelet functions to have a novel multi-scale PLS strategy. The multi-scale PLS scheme will be used as a modeling framework and the KD metric will be used as a fault indicator. As the process data is embedded with heavy noise, the effect of noise can be reduced using wavelets and a multi-scale PLS-KD based strategy can enhance the detection of small magnitude faults.