1 Introduction

In recent decades, the increasing prevalence of infectious diseases has posed a serious threat to human health in the world, as well as for a complex set of social and economic outcomes. Microbial viruses and their environmental behavior in the atmosphere pose a significant threat to planet earth and human life (Anjani et al. 2021). In relation to coronavirus, several experimental studies have demonstrated that SARS-CoV-2 genetic material can remain airborne for at least three hours and potentially up to 16 h. In the case of no wind, strict recommendations from national governments were made for a person to keep a distance of at least 2 m from each other and avoid crowded places, which helps limit the spread of COVID-19 from one person to another (Cao et al. 2021; Pongpiachan et al. 2021). In addition, SARS-Cov-2 transmission arises through the inhalation of aerosol droplets by large droplets when in close contact between persons and dry outside the mouth. While facemasks Polypropylene (PPN)-based material have emerged as alternatives and to overcome the spread of potentially infectious respiratory particles. Thus, the importance of studying the phenomenon of transmission has emerged again. Understanding the mechanism underlying the airborne particle transmission is crucial for national governments, and partners are working urgently to coordinate the rapid development of medical countermeasures to know how to accelerate their diffusion by designing appropriate scenarios. Masks polymer-based Nano-composites reduce the amount of respiratory particles diffusing in the air and emitted by people infected with SARS-CoV-2 through coughing, speaking, and breathing by trapping them in the mask. Likewise, facial masks made of polypropylene materials are more effective against large virus-laden respiratory droplets and airborne transmission. To name just, ambient conditions indicate that transmission in antimicrobial is relevant to many areas of life and the physical sciences and there is a need for developing more efficient filtration masks (El-Atab et al. 2020). Serious consideration should be given to the choice of critical medical devices and the number of layers of material used and diffusion across the air to transport within individual cells (Fadare and Okoffo 2020; Zhou et al. 2015).

Mixing of two or more polymers plays a vital role in various applications that have been blended together to create new material or achieving commercially viable products, which can be done by mechanical or chemical methods. The study of Additive manufacturing has attracted the attention of many researchers in various industrial applications over the years. The use of Polypropylene (PPN) and its derivatives is a rather common strategy used in various fields of industry. Various blends such as copolymers and polymer Nano-composites have been developed to improve its functionality towards specific applications, which found applications in protective coatings (face masks), biofunctional materials (Schwach and Avérous 2004; Luzi et al. 2019; Moon et al. 2002; Ulbricht 2006; Malik et al. 2018; Zhu et al. 2017; Fard et al. 2018; Liu et al. 2019). Positively charged Polypropylene (PPN) have been proved to possess a resistance toward microbial and enveloped virus by creating an interaction between the virus and the facemasks, and by the use of three modified layers decreased particles flow. Generally, polypropylene, polyethylene and polystyrene could also be used to manufacture facial masks and using a polymer as the material treated with mechanical means, heat and chemical. The process of air filtration from viral particles can be done, whereas the polymeric facemask retains the particles on its surface due to its smaller pores.

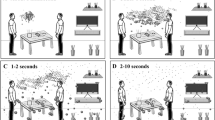
According to the National Academies Standing Committee on Emerging Infectious Diseases and twenty-first Century Health Threats, the SARS-CoV-2 virus could be spread through aerosolized droplets released via patients’ exhalations in conversation or sneeze/cough droplets. Furthermore, many researchers have shown that coughing could release potentially infectious saliva. Past research has shown that when we speak, breathe or sneeze, droplets are formed in the aerosols. Without taking into account coughing intensity, we investigate the transmission of droplets falling into the facial mask from the mouth and nose of the persons with virus cough. In other words, the transmission of droplets' of SARS-CoV-2 produced by an infected human from the mouth and nose to the face mask via sneezing, coughing and speaking. Our objective is to examine the fluid chemical of droplets that affects facemask performance. In this paper, we discuss the 2D transmission-induced mechanical changes occurring in the face masks medical of Non-woven Polypropylene (PPN) and its effect on sorption kinetic which may consequently exhibit a Navier–Stokes character. Moreover, the mathematical based on Navier–Stokes law was found better in the context of droplets in protective facemasks. The Navier–Stokes equations describe the motion of droplet substances (Baron and Willeke 2001; Anjani et al. 2021). In the present simulation, droplets are tracked by solving Newton's second law of motion, which equates inertia force on droplets with external forces. Among the obtained results, we present the profiles of the velocity, pressure and concentration and weight gain (Fig. 1).

Fig. 1
figure 1

A schematic of the diffusion process of aerosol and the droplet dispersion

Full size image

2 Mathematical Modeling

Generally, water is the main media of infectious diseases. Numerous studies have generally shown that some infections, e.g. COVID 19 may be transmitted via air and during sneezing by respiratory droplets consisting of water. In addition, in the mixture of air, the water droplet evaporation causes the reduction of the droplet size and the distribution of droplets in a not controlled environment. In physical modeling, the droplet motion is affected by external forces due to the effect of the motion of the surrounding fluid. Fluid mechanics is the study of how droplets move and it’s very complex. Therefore, we can apply Newton’s laws of motion in an attempt to predict how a droplet moves through space and time. The dynamics of the droplets are coupled to the falling dynamics of COVID-19 for which Newton’s and Stokes laws appeared to be applicable mostly to the respiratory water droplets (Hongping et al. 2020). In other words, we consider a saliva droplet as a pure water sphere with a diameter \(({D}_{\mathrm{v}})\), density and viscosity (inversely proportional according to Stokes’s equation) of an infected person, and that are transmitted through coughing, sneezing, and expectorating. Between the mouth and the mask, the droplet through the atmosphere is exposed to the gravitational force but without air resistance. And where, the volumetric fraction of the droplets is low, compared with the continuous phase (air), we derived the particle motion equation from Newton’s second law. This law (Newton’s second law of motion) applies mostly to big objects flying in the air at a certain height. Nevertheless, this law sufficiently reflect the motion of COVID-19 droplets in the air. And thus, in this study, the SARS-CoV-2 droplet was assumed as a Newtonian media of a spherical shape with an average diameter (\({D}_{\mathrm{v}}\)). Therefore, the water droplet is transported through the surrounding medium and modeled as a solvent and its transport is modeled using Newton's second law of motion (Mirikar et al. 2021). Generally, the fluid flow behavior of droplets has been modeled using two phases: discrete phase (large size) and continuous phase (small size) and is simulated by the Navier–Stokes equations. Moreover, The Navier–Stokes equations are derived from fundamental laws such as conservation of mass and momentum. The governing equations can be given by the continuity equation:

$$\nabla .\boldsymbol{ }\overrightarrow{u}\boldsymbol{ }=0,$$
(1)

where \({\varvec{u}}\) is the velocity vector (\({\mathrm{m s}}^{-1}\)) and in the absence of an applied overall flow:

$$u\boldsymbol{ }=0.$$
(2)

The differential form of the continuity equation is:

$$\frac{\partial \boldsymbol{ }\rho }{\partial \mathrm{t}}+\frac{\partial \boldsymbol{ }\left(\rho {u}_{{\varvec{i}}}\right)}{\partial {{\varvec{x}}}_{{\varvec{i}}}}=0.$$
(3)

The Momentum equation can be rewritten as:

$$\frac{\partial \boldsymbol{ }\left(\rho {u}_{{\varvec{i}}}\right)}{\partial {\varvec{t}}}+\frac{\partial \boldsymbol{ }\left(\rho {{u}_{{\varvec{j}}}u}_{{\varvec{i}}}\right)}{\partial {{\varvec{x}}}_{{\varvec{j}}}}-\left(\frac{\partial \boldsymbol{ }\left({\tau }_{ij}\right)}{\partial {{\varvec{x}}}_{{\varvec{j}}}}\right)-\left(\frac{\partial \boldsymbol{ }{\varvec{p}}}{\partial {{\varvec{x}}}_{{\varvec{j}}}}\right)=0,$$
(4)

where t, \(p\), \(\rho\) and \(\upupsilon\) denotes, the time, pressure (Pa), density (kg \({\mathrm{m}}^{-3}\)), and the kinematic viscosity. A mathematical model more broadly applicable and used to aid decision-making in flow regimes, is a dimensionless quantity which represents the ratio of inertial forces to viscous forces, where the particle Reynolds number is defined as the ratio of inertial forces to viscous forces and is a convenient parameter for predicting if a flow condition will be laminar or turbulent (Bale et al. 2021; Chia et al. 2021).

$${\mathcal{R}}_{{\varvec{e}}}=\frac{{D}_{\mathrm{v}}{\upsilon }_{\mathrm{v}}{\rho }_{\mathrm{air}}}{{\eta }_{\mathrm{air}}},$$
(5)

where \({D}_{\mathrm{v}}\) is the diameter of a respiratory particle, \({\upsilon }_{\mathrm{v}}\) is the virus velocity vector, \({\rho }_{\mathrm{air}}=1.2 \mathrm{kg}/{\mathrm{m}}^{3}\) is the air density at a temperature of (20 °C) (293 K) and \({\eta }_{\mathrm{air}}\) is the dynamic viscosity of air. One of the consequences of flow is a force called viscous drag \({F}_{\mathrm{v}}\) depends on the droplet’s speed. For laminar flow around a spherical particle, Stokes’ law describes the settling of respiratory droplets in a Newtonian mixture. However, the aerodynamic drag force is given by:

$${F}_{\mathrm{v}}=6\pi r\eta {\upsilon }_{\mathrm{v}},$$
(6)

where \(r\) is the radius of the spherical droplet in meters (m), \(\eta\) is the relative velocity of the respiratory droplets in kilograms-per-meter-per-second (\(\mathrm{kg}/\mathrm{m}/\mathrm{s})\) (Fig. 2).

Fig. 2
figure 2

Motion of respiratory droplet by laminar flow and the drag force

Full size image

When the air buoyancy force becomes negligible; the gravitational attraction over the air buoyancy force:

$${F}_{g}=g{M}_{\mathrm{d}},$$
(7)

where \({M}_{\mathrm{d}}\) respiratory droplet Mass. In addition, the deformation of a droplet in a shear flow is of fundamental relevance in many physical systems. More specifically, the study of the effect of droplet motion and deformation can provide valuable insights into porous polymers. As a consequence, a theoretical model has been proposed to predict the deformation, the droplet motion and breakup in shear stress, where the droplet maintains its nearly spherical shape:

$$\mathrm{Ca}=\frac{{{\upsilon }_{\mathrm{d}}\upsilon }_{\mathrm{a }}}{{\Gamma }_{\mathrm{c}}},$$
(8)

where \(\mathrm{Ca}\) is the dimensionless hydrodynamic capillary number; represents the ratio of the viscous force to the interfacial tension and \({\upsilon }_{\mathrm{d}}\) is the dynamic viscosity of the continuous phase. Respectively, the shear stress is caused by the flow and deformation of droplets across the facemask and is directly proportional to the velocity. Thus, the shear stress can be predicted using the droplet’s viscosity \({\upsilon }_{\mathrm{v}}\) and shear rate \(\frac{\partial u}{\partial \mathrm{r}}\):

$$\sigma ={\upsilon }_{\mathrm{v}}\frac{\partial u}{\partial \mathrm{r}}.$$
(9)

Moreover, mass transfer:

$$\frac{\partial \boldsymbol{ }c}{\partial \mathrm{t}}-{D}_{0}\Delta c+\overrightarrow{u}.\nabla {\varvec{c}}=0,$$
(10)

where \(c\) is the concentration and \({D}_{0}\) is the diffusion coefficient. In addition, the gas at the particle surface has zero velocity. However, is clear that masks can help prevent the spread of COVID-19. The present modelling work focuses on droplet dispersion in a facial mask as small droplets and as a cloud of spheroid particles. Moreover, we have studied the Newtonian incompressible fluid with no body forces of liquid droplets in protective facemasks made from polymer materials for respiratory protection.

During a human cough, this modeling of the transfer of liquid droplets from a nose and mouth to a mask is not governed by the considerations of as; size and shape depending on each individual’s morphology, the coalescence, breakup, the saliva droplet’s size distribution, intensity of the cough. In addition, environmental factors such as temperature, heat transfer, droplet evaporation, environmental wind, and humidity could influence the sneeze droplet’s transport. Transmission of COVID-19 via air during coughing and sneezing is phenomenologically described using the Navier–Stokes. Aerosol particles contain infectious pathogens and the epidemiology of COVID-19. The governing equation used to represent the physical scenario of diffusion can be described by the incompressible Navier–Stokes equations in two and three space dimensions. These Aerosol particles remain in the air for long enough for them to be inhaled and can be transferred from the mouth and nose to the facial mask by indoor airflow. Substituting this into the previous equation, the final form of Navier–Stokes equation in vector expression is;

$$\rho \left(\frac{D\overrightarrow{u}}{D\mathrm{t}}\right)=-\nabla {\varvec{p}}+\nabla \overrightarrow{T}+\overrightarrow{F}.$$
(11)

Therefore, \(\overrightarrow{T}=\mu {\nabla }^{2}\overrightarrow{u}\) is the deviatoric stress tensor and \(\mu\) is the dynamic viscosity of the solvent. During sneezing, most of the droplets of large size are expelled through the nose with high velocity. Moreover, the ratio between the particle inertia and the air viscous drag is presented by the Stokes number of the particles (Crawford et al. 2021).

$${n}_{\mathrm{s}}= \frac{{\rho }_{\mathrm{d}}{S}_{\mathrm{p}}^{2}{v}_{\mathrm{t}} }{{t}_{\mathrm{sc}}{\rho }_{\mathrm{air}}},$$
(12)

where; \({\rho }_{\mathrm{d}}\) is the particle density, \({S}_{\mathrm{p}}\) is the particle size, \({v}_{\mathrm{t}}\) is the typical velocity, and \({t}_{\mathrm{sc}}\) is the typical scale of the flow. In this modelling approach, saturation vapor pressure is dependent on the temperature of droplets. In the absence of other forces, the concentration of infectious viruses at time (t) is related to its initial concentration of infectious viruses \({(C}_{0})\), as described by Stokes’ law for small particles:

$$C={C}_{0}{e}^{-xt},$$
(13)

where \((x)\) is the inactivation rate constant. We suppose, that the droplet interaction such as breakup when coming in contact with surfaces is not considered. When coughing or sneezing, saliva droplets by the mucous coating of the lungs and vocal cords. But, these droplets do not travel independently on their trajectories and the smaller droplets are often invisible to the naked eye. In this paper, the transmission of the viral particles in the surrounding medium at standard conditions for temperature and pressure (T = 25 °C, \({P}_{\mathrm{atm}}\)=1 atm, mouth and nose temperature at 34 °C), as the temperature of the surrounding air does not undergo a drastic change. Transmission electron microscopy showed that the diameter of the droplets of 50–100 µm, droplets spread occurs with pathogens and pollutants found in exhaled droplets influenza < 5 μm in diameter (Ataei-Pirkooh et al. 2021; Vuorinen et al. 2020; Dbouk and Drikakis 2020; Chua et al. 2020). The thickness of the mask is taken as 2 mm, if a COVID-19 virus-laden droplet diameter is less than the critical diameter (60 μm), it can penetrate through the porous medium of the face mask (Mirikar et al. 2021). Moreover, reported physical properties of saliva are being 1.05 for men and 1.29 for women and the droplet radius \({R}_{0}={3.10}^{-5}\mathrm{m}\) (Dnyanesh et al. 2021). The viscosity is defined as close to that of water µ = 0.001 Pa s (Scharfman et al. 2016; Govindaraj et al. 2019). For particles 1.0 μm in size, the Brownian diffusion coefficient \({D}_{\mathrm{p}}={2.9\times 10}^{-11} {\mathrm{m}}^{2}/\mathrm{s}\) (Gao et al. 2008). In addition, the diffusion coefficient of the water vapor into ambient air; \({D}_{0}={\mathrm{2,42.10}}^{-5}{ \mathrm{m}}^{2}/\mathrm{s}\).

3 The Numerical Results and Discussion

Because it is difficult to examine the transmission of particles from the respiratory system by experiment, a physical modeling-dependent numerical method is adopted in this study. We study in particular the 2D transmission of the airborne virus transmission through coughed droplets and sneezed in cloth masks. Furthermore, these modeling have been used for the efficacy of facemasks and other respirators to prevent COVID-19 transmission.

The droplets dynamics have been predicted by solving a 2-D incompressible Navier Stokes equation. The governing equation cannot be easily solved by analytical methods. Hence, a numerical approach is necessary to solve the vorticity transport equation of droplets in the facemasks (Ghia et al. 1982; Tsega and Katiyar 2018; Harlow and Welch 1965; Shukla et al. 2011). And accordingly, a finite-difference method has been applied to the Poisson equation consisting of the droplets dynamics together with the time of the dispersion of cough droplets in facemasks. In addition to the Pressure P, we choose, as additional state variables, generalized droplets with a viscosity that depends on the strain rate \((u,v)\). The state variables are therefore as follows:

$$X=\left(u,v, P\right).$$
(14)

Therefore, we will show that the Navier–Stokes equations for incompressible droplets in non-dimensional form are:

Continuity equation

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0.$$
(15)

Momentum equation (x − dir)

$$\frac{\partial u}{\partial t}=-\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\frac{1}{\rho }\frac{\partial p}{\partial x}\right)+\frac{\mu }{\rho }\left({\nabla }^{2}u\right).$$
(16)

Momentum equation (y − dir)

$$\frac{\partial v}{\partial t}=-\left(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+\frac{1}{\rho }\frac{\partial p}{\partial x}\right)+\frac{\mu }{\rho }\left({\nabla }^{2}v\right).$$
(17)

Pressure equation

$$\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{{\partial }^{2}p}{\partial {y}^{2}}=-\left[\left(2\rho \frac{\partial u}{\partial x}\frac{\partial v}{\partial x}\right)+\rho \left(\frac{\partial }{\partial t}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial x}\right)+{\left(\frac{\partial u}{\partial x}\right)}^{2}+{\left(\frac{\partial v}{\partial y}\right)}^{2}\right)\right].$$
(18)

The reduction to simpler models requires us to use dimensionless analysis (Hairch and Afif 2020). We choose the direction of transmission to be along the Eulerian x-coordinate and we introduce the following dimensionless quantities for the state variables, the material coordinate x and time t. The dimensionless variables (reduced variables) and parameters are defined as \({(u}^{*},{v}^{*},{x}^{*},{y}^{*},{p}^{*})\):

$${u}^{*}=\left(\frac{u}{{V}_{0}}\right), {v}^{*}=\left(\frac{v}{{V}_{0}}\right), {x}^{*}=\left(\frac{x}{L}\right), {y}^{*}=\left(\frac{y}{L}\right), {t}^{*}=\left(\frac{{V}_{0}t}{L}\right), {p}^{*}=\left(\frac{p}{{\rho V}_{0}^{2}}\right),$$
(19)

where \((L)\) stands for the initial thickness of the facemask and \({V}_{0}\) is the reference speed. The dimensionless forms of the governing equations involve the Reynolds number defined as the ratio of the:

$${\mathcal{R}}_{{\varvec{e}}}=\frac{{V}_{0}L}{v}.$$
(20)

A dimensionless form of the two-dimensional unsteady filtered Navier–Stokes equations is written in the following form:

$$\frac{\partial \widetilde{u}}{\partial \widetilde{x}}+\frac{\partial \widetilde{u}}{\partial \widetilde{y}}=0,$$
(21)
$$\frac{\partial \widetilde{u}}{\partial \widetilde{t}}=-\left(\frac{\partial {\widetilde{u}}^{2}}{\partial \widetilde{x}}+\frac{\partial \left(\widetilde{u}\widetilde{v}\right)}{\partial \widetilde{y}}+\frac{\partial \widetilde{P}}{\partial \widetilde{x}}\right)+\frac{1}{{\mathcal{R}}_{{\varvec{e}}}}\Delta \widetilde{u},$$
(22)
$$\frac{\partial \widetilde{v}}{\partial \widetilde{t}}=-\left(\frac{\partial \left(\widetilde{u}\widetilde{v}\right)}{\partial \widetilde{x}}+\frac{\partial {\widetilde{v}}^{2}}{\partial \widetilde{y}}+\frac{\partial \widetilde{P}}{\partial \widetilde{y}}\right)+\frac{1}{{\mathcal{R}}_{{\varvec{e}}}}\Delta \widetilde{v}.$$
(23)

The boundary conditions on the top and bottom boundaries should be imposed by choosing the correct values. Thus, the boundary conditions are set as follows (Fig. 3):

Fig. 3
figure 3

Flow of droplets in square Cavity of surgical mask: Saliva droplet cloud kinematics resulting from a human cough

Full size image
$$x=0; \quad u=v=0,$$
(24)
$$x={L}_{x}; \quad u=v=0,$$
(25)
$$y=0; \quad u=v=0,$$
(26)
$$y={L}_{y}; \quad u=1; \quad v=0.$$
(27)

In practice, we discretize and solve the Navier–Stokes Equation using the explicit finite difference method which allows us to obtain profiles of speech-generated oral fluid droplets. In the following, we have solved numerically the Navier–Stokes equation for the transmission process of droplets dispersed in a continuous polymeric matrix of polypropylene. We study in particular the 2D transmission through a thin disposable face masks medical (PPN/PP). Generally, cloth masks and respirators made of materials with small pore sizes (range up to 5 µm in diameter) of polypropylene and water-resistant materials are the most important piece offering protection to persons and are able to effectively filter tiny virus-laden droplets.

In this section, we present some of the calculated profiles obtained by solving numerically the Eqs. (16–18) using the finite difference method. Modeling and the numerical resolution using dimensional analysis technique of these equations it possible to achieve profiles velocity components, the pressure and the droplets concentration in facemasks. We begin by reviewing the numerical data, and some new results are presented, including the physical properties of the saliva droplets. Figures 4, 5, 6 show a formal representation of a surface plot of velocity field X–Y component where the dimensionless velocity is plotted and pressure profiles.

Fig. 4
figure 4

a Illustration of the surface plot: velocity component, (u). b Velocity component (v)

Full size image
Fig. 5
figure 5

a Contours of the velocity component u in the streamwise direction for the steady turbulent flow. b Contour of velocity component, v

Full size image
Fig. 6
figure 6

The pressure fields for the steady turbulent flow over a backward-facing step

Full size image

For both symmetric and asymmetric wakes, the effect of streamwise development and turbulent velocity field are documented in detail. It is seen that the plots are identical in all three categories. The average velocities reported had a 1.5% deviation while the maximum velocities varied by 0.5%. Using the creeping flow equations, the force per droplet can easily be translated to permeability in the facemask, with the likelihood of survival of coronavirus in a respiratory droplet deposited on a facemask surface. Consequently, the internal force of saliva droplets is proportional to the change of the droplets velocity vector when the facemask moves away from the mouth in two directions. In addition, note however the presence of higher velocity regions of facemask at (x = y = 0).

This effect is also evident in Fig. 5 which shows a trend toward the development of a more symmetric mean velocity profile is also evident. Regarding the shape of the wake, a strong asymmetry can be noticed. In particular, profiles of flow velocity and turbulence quantities at x for several spanwise locations across the facemask exhibited perfect collapse. For the asymmetric wake, the local maximum velocity defect occurs at the centerline of the wake at the boundary (y = 0). This implies that mean velocity becomes more symmetric with streamwise distance in the facemask.

In addition, we document the streamwise pressure gradients exhibited by the asymmetric wake mean velocity and gradients in the droplets flow velocity. For Navier–Stokes flows, droplet flows are characterized by correlations between pressure and high velocity as an essential feature. The result suggests that pressure and velocity are mutually exclusive and we can use that as an explicit measure of the velocity–pressure correlation (Fig. 6). Nonetheless, the pressure moderation in the cavity of the facemask is unnecessary, where the velocity and pressure are mutually exclusive. It is well known in fluid mechanics, the droplets are accelerated when dynamic lower-pressure regions form in front of them in the facemask, without viscous resistance and that is consistent with the diagnostic equations of Navier–Stokes flows.

Therefore, an in vitro experimental model was created to test the effect of the face masks medical of (NPP) in preventing and filtering droplets emitted from one person for four hours (induced to cough) (Jayaweera et al. 2020). We use a surgical mask of (NPP) as a sheet flat and porous of polypropylene fibers bonded together: Duration of use: 4 h maximum, Package dimensions: 19.4 × 10.6 × 9.2 cm; 200 g. Moreover, the quantity \({\eta }_{\mathrm{b}}={10}^{-4}\mathrm{Pas}\) is the viscosity of virgin (PP) (Sleiman 2018). Furthermore, the elastic modulus is in essence the stiffness of a material, is a fundamental property of every material that cannot be changed and It is bounded between; \({G}_{\mathrm{p}}=(1.1-1.6 )\mathrm{GPa}\) (Fig. 7).

Fig. 7
figure 7

3-Ply surgical mask Type 2: Non-woven protective mask single use

Full size image

We study in particular the 2D transmission of the airborne virus transmission through coughed droplets and sneezed in cloth masks. Furthermore, these modeling have been used for the efficacy of facemasks and other respirators to prevent COVID-19 transmission. The droplet’s concentration has been predicted by solving Stokes’ law for small particles (Eq. 12). Hence, a numerical approach is necessary to solve the governing equation of droplets transmission in the facemasks. And accordingly, Stokes’ law has been applied to the differential equation consisting of droplets concentration together with the time of the dispersion of cough droplets in facemasks. Furthermore, Stokes’ law has been applied to the differential equation consisting of droplets concentration together with the time of the dispersion of cough droplets in facemasks.

The droplets concentration is assumed to be uniform among all droplets, and so the SARS-CoV-2 virus in a droplet is proportional to its volume and time of transmission. The droplets concentration is given a brief derivation of Stokes’ law for small particles using a Stokes flow as the drag force. Correspondingly, the drag force for the transmission of aerosol is the Stokes flow. Likewise and as described in Fig. 8a, b, Stokes’ law assumes fixed and accurate concentration changes with the time of droplets across the plane through which the flux of particles take place. And thus, the change of concentration versus thickness at any time is proportional to the flow of facemasks thickness. As in the equation for the transmission equation, the minus sign reflects that the saliva droplets flow from high to low concentrations of filtering droplets. Therefore, a linear correlation exists between saliva droplets concentration and cough flow rate when wearing the mask. Furthermore, the relationship between the mask, mass-uptake of droplets and cough flow rate with time was investigated.

Fig. 8
figure 8

a Profiles of droplets concentration (1D) against time. b Profiles of droplets concentration (2D) against thickness of the facemask

Full size image
Fig. 9
figure 9

a Professional precision balances with a maximum weighing capacity of up to 210 g and a display resolution between 1 mg (0001 g) and 1 g. b Oven set to a constant temperature of 60 °C. c Desiccator.

Full size image

4 Experimental

Several trials of disposable face masks (PPN (70%)/PP (30%)) have been conducted in a laboratory are designed to reduce the user’s exposure to airborne particles and biological aerosols generated from sneezing. To do so, first and in all the experiments, we have calculated the initial masks content (\({w}_{\mathrm{i}}\): Initial weight) with a precision balance (Fig. 9a). After 8 h of use by three persons, we have determined the final weight of the face masks (\({w}_{\mathrm{f}}\): Initial weight) at a fixed temperature. Thereafter, the masks are then placed in an oven set to a constant temperature of 60 °C for 2 h to achieve a drying of the facemask materials (Fig. 9b). Subsequently, the face masks are introduced inside a desiccator (sealable enclosure) containing desiccants used for preserving moisture-sensitive items (Fig. 9c).

Fig. 10
figure 10

Variation of coughed droplets uptake with time of (PPN 70%/PP 30%) facemask

Full size image

Three series of measurements are carried out, each consisting of twenty-four measuring points. We dry out the samples at 60 °C for a period of 2 h and then weigh them once again to determine the droplets-free dried-out mass. At every 250 s, we determined the weight loss percentage of the face masks by assessing the ratio of the weight of the respiratory droplets (respiratory droplets > 5 μm) water content present in the face masks. During drying, face masks will lose weight due to loss of moisture:

$$\%w=\frac{{w}_{\mathrm{i}-}{w}_{\mathrm{f}}}{{w}_{\mathrm{f}}}.$$
(27)

In return, we here present only the available experimental data of face masks (PPN 70%/PP 30%) versus the time (time in seconds). Therefore, the behaviour of droplets uptake transport is shown in (Fig. 10) and influenced by the internal structure of this type of mask. The continuous curves correspond to the experimental data of the sorption of droplets in a (PPN 70%/PP 30%) facemask at room temperature.

Likewise, a good agreement is found when comparing the experimental data of coughed droplets in face masks [PPN (70%)/PP (30%)]. We varied the three facemask, the results indicate that the mass-uptake is strongly influenced by the amount of cough drops per person as well as by the experimental condition. Although there was some leakage at the top of the face mask between the nose and the cloth polypropylene material, the mask reduced the spread of the droplets. Although the face masks tested in this study experienced varying results of flow leakage, they are to be effective in stopping respiratory droplets. Face masks combined with preventive measures, such as frequent physical distancing, can help slow the spread of COVID-19, also filters out particles in the air when the wearer breathes in. these results provide evidence of droplet transmission prevention by face masks and can't cause health problems.

5 Conclusion

Aerosol dispersion flows are often complex. Moreover, respiratory droplet motion is considered critical for the rapid diffusion of viruses by human expiratory droplets. In this paper, we have modeled physical processes related to viral particles in masks polymers and focused on diffusion by human cough in the context of COVID-19. The model mimics droplet transmission by modelling approach, which closely resembles cough experiments and supports the use of face masks to prevent COVID-19 transmission. The present study represents an effort to employ the finite-difference method in the solution of the Navier–Stokes equations for a model droplets dynamics problem with a goal of obtaining solutions for both velocity field and pressure. The integrated space–time finite-difference method for droplets dynamics, based on a unified discretization of space and time, has been developed. We have calculated numerically the profiles of the velocity and pressure. In practice, the diffusion equation is solved numerically using the finite difference method. This contribution investigates, through both scaling analysis and numerical resolution, the mass-uptake kinetics during the sorption process of measured droplets spread into face masks. Amongst the obtained results, the output of the model consists of profiles of the mass fraction and the mass uptake of respiratory droplets generated when a person coughs or sneezes. Finally, we believe that the results of our study will have interest and helps researchers realize the transmission mechanisms of COVID-19 and understand the effectiveness of the face masks. However, wearing the mask by covering the mouth and nose is not only to protect the person’s inhalation of the COVID-19 virus but also to prevent the spread of airborne SARS-CoV-2 viruses into the air and into the environment in respiratory droplets.