Quantitative linkage between global value chains’ backward participation and logistics performance in the host country: a structural gravity model analysis of emerging ASEAN economies

Abstract

This article addresses issues on the degree of participation in global value chains (GVCs) for emerging economies in the Association of Southeast Asian Nations (ASEAN). The main research question is whether there is a linkage between GVC backward participation, that is, vertical trade defined as the foreign value embedded in exports and logistics performance as a component of service links in the host country. The major contributions of this study are the usage of the UNCTAD-Eora Global Value Chain Database for describing vertical trade and the application of a “structural” gravity model setting for the specification of estimated equations. The statistical observations demonstrate that GVC backward participation in emerging ASEAN economies made substantial progress during the 1990s with per capita GDP growth, and a large gap occurred in the degree of GVC backward participation between forerunners and latecomers in the ASEAN economies. Empirical estimation can also identify a quantitative linkage between GVC backward participation and logistics performance in the host country.

1 Introduction

This article attempts to address issues on the degree of participation in global value chains (GVCs) of emerging economies in the Association of Southeast Asian Nations (ASEAN) and its linkage with host economies’ logistics performance.

GVCs have been a trend in global economic activities over the past two decades and have also been one of the prominent analytical targets for intensive theoretical and empirical studies in academic circles. The concept of GVCs was initially introduced by Koopman et al (2012) in their study of tracing value added by country in global production chains and measuring vertical specialization in international trade. Since Koopman et al (2012) provided a unified accounting framework for analyzing GVCs, empirical studies have been intensified. Among them, Gereffi (2018) presented a comprehensive study as the seminal work of GVCs and demonstrated the conceptual foundations of GVC analysis and the twin pillars of “governance” and “upgrading” along with detailed case studies of China, Mexico, and other emerging market economies. The economic effects of GVC participation were estimated by the World Bank (2020): a 1 percent increase in GVC participation would boost per capita income by more than 1 percent or cause a much more than 0.2 percent income gain from standard trade.

Regarding the forms of GVC participation characterized by “vertical specialization,” Hummels et al. (2001) originally suggested the following two modalities: (a) using imported intermediate inputs to produce exports (called “backward participation” in this study) and (b) exporting intermediate goods used as inputs by other countries to produce goods for export (called “forward participation” in this study). In the context of the analytical setting of the UNCTAD-Eora Global Value Chain Database¹ (UNCTAD-Eora database) that this study uses, the backward participation corresponds to the “foreign value embedded in a country’s exports” in the database, and the forward participation corresponds to the “domestic value added embedded in other countries’ exports.” This study focuses on the backward participation measured by the “foreign value embedded in a country’s exports,” because this study targets emerging ASEAN economies, which depend on foreign inputs for their exports and have less capacity to contribute to the third countries’ exports in their GVC participation process.

Vertical specialization has also been referred to by the seminal work of Kimura (2006) in the context of the “intra-industry trade” activated in the prevailing international production networks in East Asia. Kimura (2006) argued that the mechanics of the East Asian production networks are represented by the “vertical” division of labor in “intra-industries” among a number of countries with different income levels and that the mechanics are typically found in such sophisticated manufacturing industries as machinery, which involve many multi-layered vertical production processes.

As an analytical framework to illustrate the vertical intra-industry trade, Kimura (2006) applied “fragmentation theory.” The “fragmentation” was clearly defined by Deardorff (2001): the splitting of a production process into two or more steps that can be undertaken in different locations but that lead to the same final product. The theoretical rationale for “fragmentation” has been provided by Jones and Kierzkowski (1990, 2005). They argued that a firm’s decision on whether to fragment production processes depends on the differences in location advantages (e.g., the differences in factor prices such as wages) and the levels of the “service-link costs,” which are costs to link remotely located production blocks. The greater disparity in factor prices between countries could encourage the use of several international locations for production blocks, and the decline in the service-link costs could further facilitate the process of fragmentation at international levels. In this context, emerging ASEAN economies could be one of the major players in fragmentation mechanics, under such backgrounds as their large differences in factor prices with different development stages, and the reductions of service-link costs with the promotion of free trade and infrastructure development under the ASEAN Economic Community.

Thus, the service-link costs could be a key manageable factor to facilitate the vertical intra-industry fragmentation, because the policy efforts such as institutional improvements and infrastructure development could mitigate the service-link costs. The service links were defined byJones and Kierzkowski (1990) as the bundles of activities to connect fragmented production blocks, comprising coordination, administration, transportation, and financial services. Thus, the service-link costs contain not only bilateral trade costs such as transportation costs but also country-specific costs such as the costs for operating in a given country. This study focuses on the logistics performance on the host countryside in vertical trade as a component of the service links because the harmonization of logistics policies has been a crucial field for the trade facilitation in ASEAN economies (e.g., Nguyen et al. 2016). The index of logistics performance is presented by the World Bank,² measuring the performances of customs, infrastructure, international shipments, logistics quality and competence, tracking and tracing, and timeliness.

Given the aforementioned backgrounds, the research question in this study is as follows: is there a linkage between GVC backward participation (vertical trade defined as foreign value embedded in exports) and the logistics performance in the host country (as a component of the service links) in emerging ASEAN economies? The hypothesis behind this research question is that there would be a substantial difference in GVC backward participation between forerunners in ASEAN such as Malaysia and Thailand and latecomers such as Cambodia, Lao PDR, and Myanmar and that the difference would be from the gap in the logistics performance between them as host countries.

The contributions of this study to the literature are summarized as follows. First, this study expresses vertical trade by the foreign value added in exports, using the UNCTAD-Eora database. Studies such as Kimura et al. (2007) and Taguchi and Lar (2015, 2016) have analyzed vertical trade by using gross trade vales of manufactured parts and components, because it was useful to illustrate the “intra-industry” trade that has involved their back-and-forth international transactions. Gross trade values, however, do not necessarily gauge vertical trade precisely, because imported parts and components could, for instance, be used for domestic selling. However, the foreign value added in exports in this study measure vertical trade but are not confined to the “intra-industry” trade that characterizes the fragmentation, because the foreign value contains raw materials and services that manufacturing companies usually import. Thus, both indicators might have pros and cons and adding the value-added indicator might therefore contribute to enriching the evidence.

Second, this study applies a “structural” gravity model setting for the specification of estimated equations. Studies such as Kimura et al. (2007) and Taguchi and Lar (2015, 2016) have relied on a “traditional” gravity model setting for estimating vertical intra-industry trades in the manufacturing and machinery sectors. As Piermartini and Yotov (2016) argued, the traditional gravity model might lead to biased and even inconsistent estimates. Subsequently, Piermartini and Yotov (2016) presented a comprehensive and theoretically consistent econometric specification of a gravity model setting with the following six recommendations: (1) use panel data, (2) use interval data to allow for adjustment in trade flows, (3) include intra-national trade flows, (4) use directional time-varying fixed effects, (5) employ pair fixed effects, and (6) estimate gravity with the Poisson Pseudo Maximum Likelihood (PPML). This study adopts five recommendations out of the six, excluding recommendation (3), because this study concentrates on the comparison in vertical trade among the emerging ASEAN economies.

The remainder of the paper is structured as follows. Section 2 illustrates the degree of GVC backward participation for emerging ASEAN economies; Sect. 3 conducts an econometric analysis by estimating the structural gravity model, to verify a quantitative linkage between GVC backward participation (vertical trade) and logistics performance in the host country; and Sect. 4 summarizes and concludes.

2 GVC backward participation in emerging ASEAN economies

This section illustrates the degree of GVC backward participation in emerging ASEAN economies by using the UNCTAD-Eora Database. As mentioned in the introduction, GVC backward participation is defined as vertical trade measured by the foreign value embedded in a country’s exports in the database.

GVC participation has also been examined by international organizations such as UNCTAD (2013) and the World Bank (2016, 2020). The World Bank (2016), for instance, investigated differentiated buyer- and seller-related participations: the GVC participation on the buying side is indicated by the percentage of the foreign value added embodied in gross exports, and those on the selling side are shown by the percentage of the value of domestic inputs exported to third countries and used in their exports in gross exports. The GVC backward participation in this study corresponds to the buyer-related participation in the analytical framework of the World Bank (2016).

GVC backward participation is of significance in the industrial and economic development of emerging market economies because the participation could involve intermediate inputs containing foreign technology and thus boost the competitiveness of their exports by facilitating the combination of foreign technology with their own labor, capital, and technology. An economy’s ability to participate in GVCs is, therefore, linked with its capacity to import world-class inputs efficiently and to export competitive products.

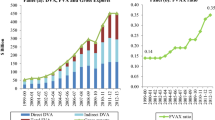
The UNCTAD-Eora database that this study uses offers global coverage (189 countries and a “Rest of World” region) and a time series from 1990 to 2019 of the key GVC indicators, i.e., foreign value added, domestic value added, and indirect value added. The methodological background was described by Casella et al. (2019). The value-added-based trade data originated from the work of the OECD and WTO as the “Trade in Value Added (TiVA)” dataset (see OECD and WTO 2012). Thus, Casella et al. (2019) also provided a comparison of the results of the UNCTAD-Eora database against the TiVA database.

The UNCTAD-Eora database also provides the country/sector by a country matrix of value-added decomposition in trade from 1990 to 2017 in addition to the key GVC indicators so that the gross exports of countries and their sectors could be decomposed into home countries’ value added and foreign countries’ value added with each country origin. By using this database, this section elucidates the GVC backward participation of emerging ASEAN economies by manufacturing industries,³ in terms of the foreign value added embodied in gross exports as the percentage of gross exports. This section also shows the foreign value added of emerging ASEAN economies by foreign country origins, in terms of the percentage of the total foreign value added. This study targets eight emerging ASEAN countries: Cambodia, Indonesia, Lao PDR, Malaysia, Myanmar, the Philippines, Thailand, and Vietnam. Brunei Darussalam and Singapore are excluded from this study’s sample because they belong to the high-income group according to the World Bank classification.⁴

Figure 1 displays, based on the UNCTAD-Eora database classification, the backward GVC participation of emerging ASEAN economies by total manufacturing and seven manufacturing sectors: food and beverages (food), textiles and wearing apparel (textile), wood and paper (wood), petroleum, chemical and non-metallic mineral products (chemical), metal products (metal), electrical and machinery (machinery), and transport equipment (transport).⁵ Figure 1 is described every 5 years from 1990 to 2015 and 2017, with the vertical axis being the foreign value-added share of gross exports (representing the degree of GVC backward participation), and with the horizontal axis being per capita GDP in real terms (showing the development stage of the economies). The data for per capita GDP in real terms is from UNCTAD Stat database and named “US dollars at constant prices (2010) per capita.”⁶

Fig. 1

Sources: UNCTAD-Eora Global Value Chain Database and UNCTAD Stat

GVC backward participation of emerging ASEAN by manufacturing industries for 1990–2017. The figure is plotted by seven points of years: 1990, 1995, 2000, 2005, 2010, 2015 and 2017

The main observations from Fig. 1 are summarized as follows. First, the foreign value-added share to exports is positively correlated with per capita GDP in total manufacturing and seven manufacturing sectors.⁷ This observation is consistent with the argument by World Bank (2020): a 1 percent increase in GVC participations would boost per capita income by more than 1 percent. There is also a large gap in GVC backward participation between the forerunners of ASEAN (e.g., Malaysia and Thailand) and the latecomers (e.g., Myanmar, Cambodia, and Lao PDR). Second, the gaps in GVC backward participation between the forerunners and the latecomers differ in manufacturing sectors: the gaps are moderate in traditional industries such as food and wood products, while the gaps are extreme in sophisticated industries such as metal products, machinery, and transport equipment.

Figure 2 shows the foreign value added of emerging ASEAN economies by country origin. The point observed commonly in eight sample economies is a clear contrast: the decreasing trends in the shares of Japan, the United States, and Taiwan and the increasing trend in China. Another point to be noted is that the intra-regional linkages among ASEAN economies have been strengthened in terms of the increasing trends in the shares of the foreign value added from ASEAN economies, such as Cambodia from Thailand, Indonesia from Malaysia, Lao PDR from Thailand, Malaysia from Indonesia, Thailand from Malaysia, and Vietnam from Malaysia.

Fig. 2

Sources: UNCTAD-Eora Global Value Chain Database

Foreign value added of emerging ASEAN by country origins for 1990–2017

In summary, the GVC backward participation in ASEAN economies has made substantial progresses during the 1990s, along with their per capita GDP growth. There has been, however, a large gap in the degree of GVC backward participation between the forerunners and the latecomers in ASEAN economies. Additionally, the country origins of foreign value added have changed from Japan, the United States, and Taiwan to China and the ASEAN countries themselves.

3 Empirical analysis

This section conducts an econometric analysis by estimating the structural gravity model to verify a quantitative linkage between GVC backward participation (vertical trade) and logistics performance on the host country in emerging ASEAN economies. The previous section identified the difference in GVC backward participation between the forerunners and latecomers in ASEAN. Thus, the analytical question is whether the difference would be from the gap in the logistics performance between them as host countries. This section first specifies the estimation models and the sample data and then presents estimation outcomes with discussions.

4 Specification of estimation models

This study equips the following three types of model specifications for examining the vertical trade in the manufacturing and machinery industries: (1) the traditional gravity setting (Eq. 1), (2) the structural gravity setting using the directional time-varying fixed effects (Eq. 2), and (3) the structural gravity setting using the logistics performance of host countries instead of the host country’s time-varying fixed effects. The models for the estimations are specified as follows:

$$\ln {\text{FVA}}_{ij,t} = \alpha_{0} + \, \alpha_{1} \ln {\text{DIS}}_{ij} + \alpha_{2} \ln {\text{GDP}}_{i,t} + \alpha_{3} \ln {\text{GDP}}_{j,t} + \alpha_{4} \ln {\text{GAP}}_{ij,t} + \varepsilon_{ij,t}$$

(1)

$${\text{FVA}}_{ij,t} = \, \exp \left[ { \, \beta_{0} + \, \mu_{ij} + \, \pi_{i,t} + \, \chi_{j,t} + \, \beta_{1} \ln {\text{GAP}}_{ij,t} } \right] + \varepsilon_{ij,t}$$

(2)

$${\text{FVA}}_{ij,t} = \exp \left[ { \, \gamma_{0} + \, \mu_{ij} + \gamma_{1} \ln \, LPI_{i,t} + \, \chi_{j,t} + \, \gamma_{2} \ln {\text{GAP}}_{ij,t} } \right] + \varepsilon_{ij,t}$$

(3)

where the subscripts i, j, and t denote host countries (receiving foreign value added in exports), origin countries (offering foreign value added in exports), and trading years, respectively; FVA is the vertical trade measured by foreign value added in exports; DIS is the geographical distance between host countries and origin countries; GDP is gross domestic product; GAP is the gap in per capita GDP between host countries i and origin countries j; μ_ij is the pair fixed effects between countries i and j; π_i,t and χ_j,t are the time-varying fixed effects of countries i and j, respectively; LPI is the logistics performance index; ε is an error term; α_i (i = 0,1, …, 4), β_i (i = 0,1), and γ_i (i = 0,1,2) are estimated coefficients of Eqs. (1), (2) and (3), respectively; and ln shows a logarithm form.

Equation (1), the traditional gravity setting, is based on Kimura et al. (2007). Kimura et al. (2007) modified the standard gravity equation to account for the elements that affect cross-border fragmentation, by incorporating location advantages and service-link costs in the equation, both factors that Jones and Kierzkowski (1990, 2005) identified as the determinants of fragmentation in their theory. The location advantages are reflected in the variable GAP as a proxy for the differential in the total level of factor prices in an economy, and the service-link costs are represented by the geographical distance between exporters and importers, DIS, due to the scarcity of their statistical information.⁸ For the estimation methodology, ordinary least squares (OLS) estimators are applied in this study, as in Kimura et al. (2007).

Equation (2), the structural gravity setting, conforms to the following recommendations of Piermartini and Yotov (2016), except for the existence of GAP representing location advantages. First, the time-varying fixed effects of countries i and j, π_i,t and χ_j,t are incorporated in the equation to control for the unobservable multilateral resistances initially addressed by Anderson and van Wincoop (2003). The time-varying fixed effects absorb both countries’ GDPs as well as all other observable and unobservable country-specific characteristics that influence bilateral trade (this study treats Indonesia as a benchmark country). Second, the pair fixed effects between countries i and j, μ_ij, are introduced to the equation to account for the effects of all time-invariant bilateral trade costs, as Agnosteva et al. (2014) demonstrated. The pair fixed effects absorb the geographical distance, DIS, as well as any other time-invariant bilateral elements such as the presences of contiguous borders, a common official language, and colonial ties. Third, the PPML is applied to the estimation to manage the possibility of zero trade flows and heteroscedasticity of trade data, as Santos Silva and Tenreyro (2006) suggested.⁹ Equation (2) also applies the OLS estimator as a robustness check for the PPML estimator, as Head and Mayer (2014) recommended.

The question is where the service-link costs are positioned in this equation. As mentioned in the introduction, the service-link costs contain not only bilateral trade costs such as transportation costs but also country-specific costs such as the costs for operating in a given country. Thus, the service-link costs occupy some portions of the time-varying fixed effects of host and origin countries (π_i,t, χ_j,t) and the pair fixed effects (μ_ij).¹⁰ This study focuses on the time-varying logistics performance of the host country side as one part of the service-links costs. Thus the major concern in Eq. (2) in this study is the volume of the time-varying fixed effects of host countries (π_i,t), and together with the estimation results of Eq. (3), this study demonstrates the contribution of the host country’s logistics performance to the country-specific fixed effects (Fig. 3).

Fig. 3

Source: Author’s description

Relationship between service-link costs and fixed effects. *: They are not incorporated in the estimation

Equation (3), in this context, replaces the time-varying fixed effects (π_i,t) with the logistics performance (LPI _i,t) of the host countries. The coefficient γ₁ is used to compute the contribution of the host country’s LPI _i,t to π_i,t. The PPML is applied to the estimation with Eq. (3).

5 Data

This subsection first describes the data of each variable in detail, and the descriptive statistics are presented in Table 1. Regarding the dependent variable FVA, foreign value added in exports, the data are from the UNCTAD-Eora database and expressed as thousand US dollar terms. The variable targets total manufacturing and the machinery industry (the sum of “machinery” and “transport” in Sect. 2). The machinery industry typically represents many multi-layered vertical production processes as the mode of fragmentation, as Kimura (2006) argued.

Table 1 Descriptive statistics

Regarding the DIS data in Eq. (1), the distance is measured by the Great Circle Distance between Cities on Map (Fromto).¹¹ The GDP data are retrieved from the World Economic Outlook (WEO) database (October 2019) of the International Monetary Fund by the series of “current prices US dollars.”¹² As for the GAP data, the GDP per capita is from the WEO, based on the series of “current prices US dollars.” The GAP is calculated by the GDP per capita of host countries divided by that of origin countries. The LPI index from the Logistics Performance Index of the World Bank takes the number ranging from 1 (very low in the performances) to 5 (very high).

Next, the sample economies and period are set as follows. The host countries are the eight countries from emerging ASEAN as in Sect. 2, and the origin countries/economies of foreign value added are selected as the eight ASEAN countries and their major seven trading partners: China, Germany, India, Japan, South Korea, Taiwan, and the United States. The foreign value added that the host countries receive from the sampled origin economies cover 60 to 80 percent of the total foreign value added they received from the world in 2017.¹³ As for the sample period, the study selects such discrete years as 2007, 2010, 2012, 2014, 2016, and 2017 because of the constraint of data availability of the LPI.¹⁴ The study then constructs panel data for six years with the combinations between host countries and origin economies (6 × 8 × 14 = 672) for the estimation.

5.1 Estimation outcomes and discussion

Tables 2, 3 report the estimation outcomes of Eqs. (1), (2), and (3) for the cases of total manufacturing and machinery industry. Both cases show similar results with the same directions of the coefficients’ signs, although their magnitudes differ between the two cases.

Table 2 Estimation outcomes on total manufacturing

Table 3 Estimation outcomes on machinery industry

Starting with the estimation results of Eq. (1) with the traditional gravity setting in column (1), the coefficients of the DIS and GDP of host and origin countries have expected signs with conventional significance. The coefficient of GAP representing the location advantages, however, has the sign opposite to what the fragmentation theory supposed in Eq. (1) and is of insignificance in the other equations. This result suggests that the location advantages do not necessarily constitute a major factor to explain the vertical trade in this study.

Columns (2) and (3) correspond to the OLS and PPML estimations of Eq. (2), with the structural gravity setting using the directional time-varying fixed effects. The major concern in this equation is the coefficients on the time-varying fixed effects in host countries (those in origin countries and the coefficients on the pair fixed effects are omitted for brevity). The coefficients show the wide range of the magnitudes with Indonesia in a middle position being a benchmark country, from the largest negative values in Myanmar to the largest positive values in Malaysia. The negative coefficients are displayed in the latecomers in ASEAN and the positive coefficients are in the forerunners, the contrast of which approximately corresponds to the gap in the degree of GVC backward participation between them. Comparing the coefficients between the OLS and PPML estimations in columns (ii) and (iii), their magnitudes in the OLS estimation are too large, for example, the negative maximum exp. (− 10.927) = 0.0000… in Myanmar (machinery industry). In the PPML estimation, by contrast, the negative maximum exp. (− 3.938) = 0.019 in Myanmar in 2010 (machinery industry) and the positive maximum exp. (0.212) = 1.236 in Malaysia in 2010 (machinery industry) are at reasonable levels. What is more important is that the RESET p values, at the bottom of Tables 2, 3, reveal that only PPML estimations pass the misspecification tests in the total manufacturing and machinery industry. This study thus identifies the PPML as a reasonable standard estimation and based on the PPML estimation in column (iii), Eq. (3) replaces the time-varying fixed effects with the LPI of host countries.

Column (iv) represents the PPML estimations of Eq. (3) with the structural gravity setting using the logistics performance of host countries. The RESET p values do not show, unfortunately, that the column (iv) estimations pass the misspecification tests, probably because the logistics performance itself does not necessarily cover all the time-varying country-specific characteristics. The coefficients of the LPI in both total manufacturing and machinery industry, however, have positive signs with conventional significance, as expected. This finding implies that the difference in logistics performance has some linkage with the gap in the degree of GVC backward participation among emerging ASEAN economies. This result leads to questioning the statistical degree of the logistics performance’s contribution to the time-varying fixed effects on host countries that reflect the degree of GVC backward participation.

Tables 4, 5 reveal the comparison between the host country’s fixed effect and logistics performance in 2017 for the total manufacturing and machinery industry: column (a) re-displays the coefficient of the host country’s fixed effect in 2017 in column (iii) of Tables 2, 3; the LPI deviation from the benchmark in column (c) is computed by subtracting Indonesia’s LPI from each country’s LPI in 2017 in column (b); the LPI effect in column (d) is then calculated by multiplying the LPI deviation with the estimated coefficient (0.512 in total manufacturing and 0.761 in machinery industry) in column (iv) of Tables 2, 3; and in column (e), the LPI effect in column (d) is divided by the coefficient of the host country’s fixed effect in column (a) for their comparisons.

Table 4 Host country’s fixed effect and logistics performance in 2017 on total manufacturing

Table 5 Host country’s fixed effect and logistics performance in 2017 on machinery industry

The result in column (e) suggests that the host country’s logistics performance accounts for the country-specific effect to a comparable extent, with the reasonable range of the LPI-fixed effect ratio from 0.186 in Malaysia (total manufacturing) to 1.230 in Thailand (machinery industry). This finding implies the existence of some linkage between the host country’s logistics performance and the degree of its GVC backward participation in ASEAN economies. This outcome is also consistent with the analyses by the World Bank (2016 and 2020) that GVC integrations are highly sensitive to logistics performances.

6 Concluding remarks

This article attempted to address the issue on the degree of GVC backward participation for emerging ASEAN economies, and the specific research question was whether there is a linkage between the GVC backward participation, namely, vertical trade defined as the foreign value embedded in exports, and the logistics performance as a component of the service links in the host country. This study’s major contributions were to represent vertical trade by the foreign value added in exports, using the UNCTAD-Eora Database, and to apply a “structural” gravity model setting for the specification of estimated equations.

The statistical observations demonstrated that the GVC backward participation in emerging ASEAN economies has made substantial progresses during the 1990s along with their per capita GDP growth and that there has been a large gap in the degree of GVC backward participation between the forerunners and the latecomers in ASEAN economies. The empirical estimation under the structural gravity model identified the quantitative linkage between GVC backward participation and the logistics performance of the host country.

Because the logistics performances are one of the manageable factors for countries’ strategies, there should still be the policy space for the ASEAN latecomers to catch up with the forerunners in GVC integrations. The latecomers, namely, Myanmar, Lao PDR, and Cambodia, are located in the Mekong region, where GVC activities have started to be activated in the border areas with Thailand in the form of so-called “Thailand-plus-one” (e.g., see Kuroiwa 2016). To fully utilize this momentum, the framework of special economic zones (SEZs) should be developed and upgraded in the border areas for the latecomers because it could provide a convenient avenue to facilitate “vertical” border trades with the high-end border logistics (e.g., single window, single stop) and with the privileges for foreign investors (e.g., custom-duty exemption, labor transferability, one stop services). However, Myanmar as a typical example of the lack of GVC backward participation has no active SEZ frameworks in the border areas with Thailand, although the areas could be the effective gateways for vertical border trades with Thailand (e.g., see Taguchi and Tripetch 2014). In this sense, there should be substantial room for the latecomers to facilitate their GVC participation in their development strategies.

Appendix

See Table 6.

Table 6 Conversion of manufacturing sector’s classifications