FormalPara Key Points for Decision Makers

We provide a framework to inform cure proportions given prior evidence.

We make our codes available to help the reader with model fitting.

We introduce a context to determine the plausibility of the existence of a cure proportion.

1 Introduction

Cancer imposes a significant clinical and economic burden on patients, healthcare systems, and societies around the world. While survival has improved for some cancers in recent years, it remains low for others, and the overall cancer burden is projected to increase further due to population growth and ageing [1,2,3,4]. As prevention has been shown to have little effect for a number of common cancers, healthcare providing access to highly effective pharmacologic treatments will be an important component of any cancer control strategy designed to reduce cancer burden and cost [1].

Several novel pharmacologic treatment options have become available over the past years. These include immunotherapy, which stimulates the host immune system to attack cancer cells [5, 6], and targeted therapies, which block specific molecular targets relevant for cancer growth and disease progression [7,8,9,10]. These therapies are associated with treatment response and survival patterns different from established treatments such as chemotherapy [6, 11]. In particular, these therapeutic approaches are often associated with the potential to lead to long-term survival in some patients, who are considered “statistically cured” and no longer susceptible to the disease [12, 13]. In other words, for those patients, background mortality is assumed to be equal to that of a population without cancer [6, 11, 14].

In a mixed population of statistically cured and non-cured patients, overall survival may no longer show a consistent decline to zero over the follow-up period of clinical studies. In combination with the delayed onset of effect and separation of survival curves, statistical cure reduces the power of traditional survival analysis methods and violates key assumptions of these methods, e.g., assumptions concerning proportional hazards and accelerated failure time [6, 14, 15].

While methods like flexible parametric models address these issues [16], these methods have the limitation of relying on several assumptions as far as extrapolating hazard is concerned. Notably, assumptions on the behavior of the hazard beyond the observed time need to be made.

The mixture cure model assumes that there are two groups, “cured” and “uncured,” at diagnosis (or time = 0), which may not be appropriate, especially in cases where cure can occur at any time during the follow-up, e.g., after a long disease stabilization phase. However, this assumption does not invalidate the use of the mixture cure model as you can still obtain useful summary statistics for those who will inevitably die (with or without the disease) [17].

Mixture cure models have been used to estimate the probability of survival of the cohort in order to provide accurate survival estimates in the presence of statistical cure [14, 15]. In particular, the long-term hazard is characterized by the one of the general population, thus requiring no extra assumption on its long-term behavior. It is worth mentioning that some disease areas suggest an increased propensity of dying for cancer survivors compared to the general population. For example, a recent evaluation of a health technology by the National Institute for Health and Care Excellence (NICE) suggests a background hazard for cancer survivors about 40% higher than that for the general population [18]. Mixture cure models assume that a proportion of the population is cured (the “cure fraction”) while the remainder is not [15, 19,20,21,22]. Different mortality rates are applied in each group to reflect the impact of statistical cure on the overall (average) survival curve assuming all patients belong to a cohort with the same age at the start of the trial.

Mixture cure models have been in use for some time in statistics and epidemiology but have only recently received attention in health economics and health technology assessment (HTA) [19, 23, 24]. These models may therefore be unfamiliar to some health economists and HTA analysts, especially as many of the currently available papers on mixture cure models have a technical focus and target statisticians and epidemiologists [15, 20]. This tutorial aims to provide a step-by-step introduction to mixture cure models and their implementation in the free statistical software R [25]. The tutorial is intended to complement earlier, more technical articles on cure models [20, 22].

2 Methods

The workflow for developing a mixture cure model is implemented in R, a free software environment for statistical analysis and computing [25,26,27,28]. The datasets and code used and/or analyzed during the current study are available under a CC BY-NC 4.0 license on GitHub [29].

2.1 Mixture Cure Models: Explanation and Notation

A standard mixture cure model estimates overall survival \({S}_{\mathrm{o}}(t+a)\) for a patient population at time \(t\) (since randomization, measured in years) and the mean age of the patient cohort, denoted \(a\). The crucial assumption underlying mixture cure models is that overall survival results from the survival experience of two subgroups: cured patients (with the cure fraction denoted as \(\pi\)) and uncured patients (\(1-\pi\)) [15, 20]. Note non-mixture cure models also exist, but are beyond the scope of this tutorial.

In cured patients, cancer no longer negatively affects survival, which is therefore at the “background” level of a cancer-free population of the same age, gender, and geographic origin. It is important to note that a specific patient cannot be identified as cured or uncured. Instead, the concept of cure applies to an entire patient population [19]. Background survival is written as \({S}_{\mathrm{b}}(t+a)\) and applied to the fraction \(\pi\) of cured patients, with time since randomization as the time scale of interest.

In uncured patients, cancer negatively affects survival, as patients, on average, die earlier than cancer-free individuals of the same age, sex, and geographic origin. The survival function for uncured patients is written as \({S}_{\mathrm{u}}(t)\). It may depend on covariates such as age or sex and can be estimated using parametric or flexible parametric survival models [20, 21].

In a mixture cure model, overall survival is then calculated as the product of background survival (for the cure fraction \(\pi\)) and cancer-specific survival (for the uncured fraction \(1-\pi\)):

$${S}_{\mathrm{o}}\left(t+a\right)={S}_{\mathrm{b}}\left(t+a\right)\times \left(\pi +\left(1-\pi \right){S}_{\mathrm{u}}\left(t\right)\right).$$
(1)

Mixture cure models can also be expressed in terms of mortality hazard functions [20, 30]. Again, the overall hazard rate \({h}_{\mathrm{o}}(t)\) has two components: the background mortality rate and the excess mortality rate due to cancer. While cured patients experience background mortality, uncured patients are affected by cancer-related excess mortality, yielding the following formula for the overall hazard rate:

$${h}_{\mathrm{o}}(t)={h}_{\mathrm{b}}(t+a)+\frac{(1-\pi )\times {f}_{u}(t)}{\pi +(1-\pi )\times {S}_{u}(t)},$$
(2)

where the term \({f}_{\mathrm{u}}(t)\) denotes the probability density function for \({S}_{\mathrm{u}}(t)\). Both the survival and hazard functions depend on the set of parameters characterizing the specific parametric form in use, e.g., a Weibull or Gompertz distribution (see “funs_hazard.R” and “funs_long_term_survival.R” in the GitHub repository).

Expressing the model in terms of hazard rates is useful to calculate the log likelihood \(L\), which is used to fit the model and is written as:

$${\text{log}}L=\sum_{i=1}^{N}{d}_{i}\times {\text{log}}{h}_{o}({t}_{i})+\sum_{i=1}^{N}{\text{log}}{S}_{o}({t}_{i}),$$
(3)

where \(i\) indicates the \(i\)th patient and \({d}_{i}\) indicates if patient \(i\) was censored (see the “funs_likelihood.R” file in the GitHub repository)

2.2 Building a Mixture Cure Model

Mixture cure models require data from different sources (Fig. 1). Initially, the countries of interest need to be defined. If the focus of the model is survival estimation within the trial, target countries are those from which trial participants were recruited. In contrast, if the focus is on extrapolation beyond the trial’s geographical and time scope (e.g., as part of an HTA assessment), the target country is the country for which the extrapolation is to be conducted. More specifically, the user can specify the country of interest in the hazard_time function available in the “functions/funs_hazard.R” file in the GitHub repository. The algorithm loops over the distribution of age and gender for the selected country and builds a general population background mortality curve that is the weighted average of the ones built for age groups, weighted according to their proportion.

Fig. 1
figure 1

Implementation workflow

Full size image

Next, background survival data need to be acquired for these countries. In addition, country-specific data on the distribution of patient age at disease onset and individual patient trial data are required. If an “informed” approach is chosen, information on the cure rate, which can be based either on real-world data or on expert opinion, is also needed [31].

All these data are passed into the model, which is estimated using maximum likelihood methods. For fitted models, goodness-of-fit can be assessed visually or using established criteria such as the Akaike information criterion (AIC) and Bayesian information criterion (BIC), for the observed period in the trial [32, 33].

2.3 Background Survival/Mortality Data

Life tables for the mortality in the general population are required to estimate background survival and mortality in cure patients, i.e., \({S}_{\mathrm{b}}(t+a)\) and \({h}_{\mathrm{b}}(t+a)\) in Eqs. 1 and 2. General population life tables reflect all causes of death, including cancer, so their use without subtracting the cancer of interest as a cause of death may introduce bias into the estimation of background mortality [34]. If cause-subtracted life tables are available, these can be used, and methods have been developed to correct for the inclusion of cancer as a cause of death [35]. However, even if cancer is not subtracted as a cause of death, bias is generally negligible because specific cancers (as opposed to all sites combined) account for only a small fraction of all deaths in a population [34,35,36]. Cause-subtracted and general background mortality usually differ little, with the possible exception of prostate cancer and cancer in older age groups [35, 36].

Mortality data for the general population are available from national statistical offices, the World Health Organization, and the Human Mortality Database (HMD). The HMD is a particularly useful source of mortality data, with abridged and single-year life tables by gender available for high-income and European countries over several decades [37]. HMD data are used in this tutorial to estimate background mortality (see, in the GitHub repository, the “funs_load_mort_table.R” file for downloading and the “mortality_table_wrap.R” file for combining and preparing HMD data for analysis).

Life tables follow a standardized format (see examples in [38]). Life table columns relevant to mixture cure models are mortality rates (column denoted \({m}_{x}\)) and the number of survivors (column denoted \({l}_{x}\)), which are used to obtain background mortality hazards and survival for each year of trial enrollment, age, and sex in the model. In the R code provided as part of this tutorial, life tables are automatically read into the model and matched to trial data by country, year of trial enrollment, age, and sex. Year of enrollment is relevant in real-world studies that recruit patients over a long-time period. The residual survival for patients enrolled later is notably larger than for patients recruited earlier, assuming they have the same age and gender.

2.4 Country-Specific Age at Cancer Onset

If survival is to be projected for a specific population not included in the trial, the age at cancer onset for this population is required. Country-specific data on mean ages at onset of cancer are available from the published literature, for example, national epidemiologic surveillance data such as the Surveillance, Epidemiology, and End Results Program (SEER) in the United States (US) [39], and research organizations such as Cancer Research UK in the United Kingdom (UK) [40]. In the absence of distributions on age, we can assume the population belongs to a cohort with the same age.

2.5 Clinical Trial Data

Patient demographic and survival data come from the clinical trial of interest. Relatively few data are required to build a mixture cure model, namely age at baseline, sex, and country for each patient, a censoring indicator, time under observation before censoring, and the year of trial enrollment.

For this tutorial, two datasets were simulated, based on the BRAF Inhibitor in Melanoma 3 (BRIM-3) and coBRIM trials [9, 10]. BRIM-3 was a phase 3, randomized controlled trial (RCT) that compared the efficacy of dacarbazine and vemurafenib for the treatment of melanoma. Vemurafenib selectively inhibits the kinase activity of BRAF molecules with the V600E mutation, thereby interrupting the mitogen-activated protein kinase/extracellular signal-regulated kinase pathway that may lead to uncontrolled cell growth [41]. In BRIM-3, overall survival was assessed in 675 adult patients with unresectable, previously untreated stage IIIC or stage IV melanoma (positive for the BRAF V600E mutation) [10, 42]. Survival patterns associated with treatments in metastatic melanoma showed a proportion of patients to be statistically cured, reflected in plateaus in overall survival Kaplan-Meier (KM) curves, so the BRIM-3 trial was considered an appropriate teaching example for this tutorial [11, 42]. The data used in this tutorial were taken from the BRIM-3 trial. To ensure patient anonymity, a random Gaussian noise with a mean of 0 and a variance of \(3\) years was added to patient ages, while a random Gaussian noise with a mean of 0 and a variance of 0.01 years was added to times to events. The clinical data required to build a mixture cure model are illustrated for BRIM-3 in Table 1 (see the “brim3_simulated.csv” file in the GitHub repository).

Table 1 Structure of required clinical data: example using simulated patients from the BRIM-3 trial
Full size table

The second dataset was based on the coBRIM trial, an RCT comparing vemurafenib plus placebo with vemurafenib plus cobimetinib [9, 43]. Cobimetinib is a mitogen-activated protein kinase inhibitor and is used in combination with vemurafenib for the treatment of metastatic melanoma [9, 44]. In coBRIM, progression-free and overall survival were assessed in 495 adult patients with unresectable, locally advanced stage IIIC or stage IV melanoma with BRAF V600 mutation in 19 countries. Data were obtained following the same procedures as those illustrated for the BRIM-3 cohort (Table 1) (see the “cobrim_simulated.csv” file in the GitHub repository).

Please note that both datasets are based on simulated data and are used only for illustrative purposes in this tutorial. None of the analyses and conclusions presented here should be used for real-world and/or clinical decision-making.

2.6 Estimate the Cure Fraction

The cure fraction can be treated as either an output from or an input to the mixture cure model, depending on the focus of the analysis and the availability of external data (Fig. 2). For example, if we have a plateau in the KM curves, and the follow-up time is long enough, we can estimate the cure from the trial [45]. Conversely, if we know that the long-term survival at—say—25 years is known to be above a certain value, we can use putative cure values as an input in determining the parameters of the survival functions representing uncured patients.

Fig. 2
figure 2

Different approaches on using and obtaining the cure fraction. The cure fraction can be obtained as an output or be used as an input to the model, based on real-world data, expert opinion or the literature

Full size image

Calculating the cure fraction as a model output based on the trial data is labeled as an “uninformed” approach. In this scenario, the cure fraction \(\pi\) is a parameter of the model and estimated alongside other parameters [31]. The resulting value for \(\pi\) can then be considered the best estimate of the cure fraction, based on the currently available, usually short-term, data. Estimating the cure fraction as an output of a mixture cure model is illustrated in this tutorial using the BRIM-3 dataset [10, 42].

The cure fraction may also be an input to a mixture cure model, e.g., in interim analyses of RCTs when follow-up is not yet long enough for statistical cure to be identifiable [31]. In this “informed” approach, the cure fraction in the model is informed by and set equal to the cure fraction from an external source. External sources that provide estimates of the cure fraction are expert opinion or real-world, long-term data for the same cancer and/or class of drugs (Fig. 2). If real-world evidence, e.g., from cancer registries and epidemiologic surveillance programs, is available as individual patient data, a “helper” mixture cure model may need to be estimated first, in which the cure fraction is the outcome of interest. This can come from, e.g., real-world data, as we showed here [31]. The cure fraction derived from this intermediate step can then be used as an input to the mixture cure model of interest. Sensitivity analyses around cure fractions should be performed and model fits compared across different cure fraction values. For example, there are approaches the plausibility of cure values via Bayesian model averaging [46], comprehensive work on elicitation methods for time-to-event and survival data have been presented Bojke et al. [47]. Their work does not specify the use of cure fractions explicitly. However, they provide a context for elicitation of the parameters of hazard functions in a Bayesian framework. In principle, the user can apply the implementation of our likelihoods within a Bayesian cure model framework [48] to build appropriate posteriors for the cure fraction and hazard parameters. Priors on cure proportions may, for example, be built from the SEER registry [39]. Using the cure fraction as an input to a mixture cure model is illustrated in this tutorial using the coBRIM dataset [9, 43] and cure fraction estimates obtained from the example demonstrating the uninformed approach based on simulated BRIM-3 data (see the “input_cure_cobrim.R” file in the GitHub repository) .

2.7 Model Estimation and Selection

Different parametric shapes can be chosen to model the survival and mortality hazard of uncured patients. Available options include exponential, Weibull, Gompertz, log-logistic, lognormal, gamma, and generalized gamma distributions, all of which are explored in this tutorial. For each model, the area under the curve is calculated to obtain estimated mean survival, which is typically an outcome of interest in decision analytical models. The model fit for different parametric shapes or cure fraction inputs can be assessed visually in plots of survival curves, e.g., by comparing the estimated curve to a KM curve and the value at which it plateaus [6]. In addition, a more formal statistical assessment of goodness-of-fit can be conducted using measures such as the AIC and BIC, which compare the fit of different models used on the same data, while penalizing models for the inclusion of additional parameters with little explanatory power [32, 33]. Of note, the flat tail in distributions like the lognormal and log-logistic distribution may affect the suitability of the AIC to choose the best fit in the context of cure fraction estimates (for more details, see [20]). This limitation needs to be considered when interpreting AIC values, but the AIC was still considered valuable to rule out distributions that fit the data poorly, e.g., the exponential and Gompertz distributions. In addition, visual assessment and BIC values were also used to assess model fit. When cure fractions were used as external input, potential problems regarding use of AIC values applied to a lesser extent. Cure fraction estimates that are too high or too low (see “Additional Files” in the electronic supplementary material) were associated with poor fits of the mixture extrapolations to the observed data. Extreme cure values could therefore be discarded. Maximum likelihood methods are generally used to fit mixture cure models [20].

3 Results

3.1 Cure Fraction as Output from Trial Data: BRIM-3

3.1.1 Background Mortality

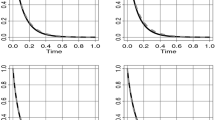
Life tables for the general population, indexed by age and sex, were sourced from the HMD [37] for the year of trial enrollment and all countries from which participants were included in the BRIM-3 trial. The importance of accounting for background mortality and survival differences by sex and country was confirmed in exploratory analyses of survival curves. The analyses, illustrated in Fig. 3 with the examples of Italy, Russia, and the US, may show differences in survival between countries and, within countries, between women and men, as for Russia in this example.

Fig. 3
figure 3

Different background survival by country and sex, illustrated for Italy, Russia, and the USA. Data from the Human Mortality Database [26]

Full size image

3.1.2 Age at Cancer Onset

As projections were only performed for the trial populations in this tutorial, age at onset data from countries were not required. Health economic analyses for a specific country would use this information to inform survival predictions.

3.1.3 Clinical Trial Data

Clinical trial data were based on simulated patients from the BRIM-3 trial, as described above. In the simulated cohort, 41% were women (Additional File 1, see the electronic supplementary material). Mean age at baseline was 55 years (standard deviation 14 years). The countries contributing the largest number of patients were Italy (18% of all patients), Australia, and Germany (10% each), while Austria, Belgium, Norway, and Switzerland each contributed the fewest patients (~ 1%).

3.1.4 Cure Fraction Estimation

The cure fraction was estimated using maximum likelihood for different parametric specifications of the mortality hazard for uncured patients, i.e., we characterized the likelihood for each of the parametric survival functions included in the flexsurv package (see the “estimate_cure_brim3.R” file in the GitHub repository).

3.1.5 Cure Fraction Estimates

Estimates of the cure fraction ranged from 13.3% (standard error 2.8%) when assuming an exponential distribution to 18.1% (standard error 2.3%) when assuming Weibull and Gompertz distributions (Table 2).

Table 2 Estimates of the cure fraction for different parametric specifications, using simulated BRIM-3 data
Full size table

Goodness-of-fit criteria and visual inspection of survival curves suggested that assuming an exponential distribution for the survival of uncured patients was associated with the poorest model fit (Fig. 4). By comparison, the lognormal and generalized gamma distributions provided a better fit, both visually and according to goodness-of-fit criteria. Of note, despite similar AIC values, cure fraction estimates between lognormal and generalized gamma distributions differed by 2.7%. Although the confidence intervals (CIs) of cure estimates for the lognormal and the generalized gamma distributions overlap, suggesting that the cure estimates for the two distributions are not statistically different, we stress that structural changes in the shape of the hazard—reflected by the choice of the parametric distribution—lead to differences in the long-term extrapolations. Notably, the generalized gamma distribution exhibits a long-term plateau due to its additional parameter that captures variations of the hazard. Since we are unaware of the true long-term behavior of the hazard, we stress the importance of exploring different functional specifications in determining a plausible range of cure estimates.

Fig. 4
figure 4

Survival curves for different model specifications using simulated BRIM-3 trial data—intervention arm. The KM (black dashed line) shows a plateau; hence, the spectrum of extrapolations with different functions is relatively narrow. BRIM-3 BRAF Inhibitor in Melanoma 3, exponential exponential distribution, gamma gamma distribution, gengamma generalized gamma distribution, gompertz Gompertz distribution, KM Kaplan-Meier curve, llogis log-logistic distribution, lognormal lognormal distribution, weibull Weibull distribution

Full size image

Based on these results, the model user could conclude that approximately 13–18% of the trial population (Table 2) would achieve statistical cure, i.e., have long-term survival equal to the cancer-free population from their respective country of origin.

3.2 External Estimates of the Cure Fraction as Model Inputs: coBRIM

3.2.1 Background Mortality

Life tables for the general population were again sourced from the HMD [37].

3.2.2 Age at Cancer Onset

As in the example for the uninformed approach, no projections beyond trial populations were conducted, so data on age at cancer onset were not used for specific countries. In building the extrapolations we used information on age from the clinical trials. Again, these data would be used in health economic analyses for country-specific survival predictions.

3.2.3 Clinical Trial Data

Clinical trial data were based on a simulated patient cohort from the coBRIM trial. Of the 495 sampled patients, 42% were women (Additional File 2, see the electronic supplementary material). Mean age at baseline was 55 years (standard deviation 14 years). The countries contributing the largest number of patients were Italy (19% of all patients), Australia (11%), and Germany (9%), while Switzerland contributed 0.4% of patients.

3.2.4 External Cure Fraction Estimates

In this analysis, an informed approach was employed, i.e., the cure fraction was used as an input into the model. For the purpose of this tutorial, the range of cure fraction estimates (0–5%, 10%, 15%, 20%) was informed by the uninformed approach based on simulated BRIM-3 data (Table 2). These estimates could also be obtained or validated from the real-world data, literature or expert opinion. Different specifications of parametric distributions (exponential, Weibull, log-logistic, lognormal, Gompertz, gamma, and generalized gamma distributions) for the survival of uncured patients were explored for each cure fraction estimate (see the “input_cure_cobrim.R” file in the GitHub repository). The user has the option to play with the functions we have included in GitHub and select any cure values they consider appropriate.

Note that, as opposed to the cure fraction extrapolation estimates for the BRIM 3 trial (Fig. 4), the extrapolations for the coBRIM trial show a broad spectrum of possible cure fraction estimations, reflected by the larger spread of different parametric extrapolations in a mixture cure framework (Fig. 5).

Fig. 5
figure 5

Survival curves for different model specifications using simulated coBRIM trial data—control arm. The KM (solid dashed line) does not show a plateau; hence, the spectrum of possible extrapolations is wide. Exponential exponential distribution, gamma gamma distribution, gengamma generalized gamma distribution, gompertz Gompertz distribution, KM Kaplan–sMeier curve, llogis log-logistic distribution, lognormal lognormal distribution, weibull Weibull distribution

Full size image

3.2.5 Survival Estimates

For all parametric model specifications, the best model fits, as indicated by the AIC, were generally observed with the higher cure fractions 15% and 20% (Table 3). It has been advocated that the BIC criterion is the best at assessing a model’s goodness of fit [49]. However, for BRIM3, BIC and AIC values are fairly aligned, in that the two best-fitting distributions coincide (Table 2). In particular, for each distribution, the model assuming no cure was found to be the worst fit both using goodness-of-fit criteria and visual assessment, indicating that a mixture cure model was an appropriate choice to account for cured patients.

Table 3 Goodness-of-fit and survival estimates for different cure fraction inputs and model specifications—coBRIM
Full size table

Mean survival estimates for each cure fraction estimate were similar across model specifications, ranging from 5.8 years (gamma and Weibull distribution) to 6.3 years (generalized gamma) for a cure fraction estimate of 20%.

Based on these results, the model user could conclude that some proportion of the patient population would likely be statistically cured, so would need to be accounted for, e.g., in health economic assessments. In contrast, assuming no patient to be cured would likely be inappropriate and underestimate mean survival. As these findings were confirmed using different parametric distributions for survival in uncured patients, results can be considered reliable.

This example also illustrates how a previous trial (BRIM-3 in the present case) can be used to assess the likely trajectory of a subsequent trial (coBRIM in the present case), thereby contributing to early prediction of trial outcomes, e.g., in interim analyses. We note that the intervention arm in BRIM-3 and the control arm in coBRIM coincided. Therefore, any analysis for BRIM-3 is done on the intervention arm of the trial and any analysis for co-BRIM on the control arm of the trial.

4 Discussion

This tutorial on the implementation of mixture cure models in oncology has been designed to provide a practical introduction to data requirements and sources as well as model development, estimation, and interpretation to make this class of models more accessible to a wide range of potential users. The implementation of mixture cure models is described in detail and demonstrated in step-by-step instructions as well as their implementation in statistical software, e.g., R.

In many practical applications, the simple mixture cure model implemented in this tutorial may require refinements, e.g., adjustment of survival estimates for patient characteristics and use of different model specifications. With regard to covariate adjustment, clinical trial data may suggest that survival and cure fraction depend on demographic, clinical, or socioeconomic characteristics of patients, in addition to age, sex, and country [15, 29, 50]. Mixture cure models can be extended to include covariates when estimating survival, with most modern statistical software packages providing the necessary functionality. With regard to model specifications, flexible parametric models using restricted cubic splines have been shown to give more flexibility for modeling survival than standard parametric distributions [29, 50]. Flexible parametric models allow the exploration of a wide range of functional forms for survival curves and can therefore improve models in scenarios where parametric distributions fail to provide a good fit [12, 21, 51].

The use of mixture cure models may be limited by the need for individual patient-level data, which may not be available to analysts outside study groups, approval and HTA agencies, or cancer registries. This issue is not restricted to mixture cure models or oncology. As for other types of models and disease areas, code and data sharing are recommended to increase the transparency and reproducibility of results while considering data protection and privacy regulations as well as intellectual property rights [52, 53]. Mixture cure models also have been suggested to be more relevant once a treatment is established and real-world evidence on the fraction is available [51]. While longer-term real-world evidence should be used to inform models, such evidence, by definition, only becomes available after a certain time period, which may be too late for short-term decisions on health policies or reimbursement. Again, this issue is not specific to mixture cure models and oncology. It has been noted that pivotal trials are unlikely to provide sufficient information to estimate cure fractions in HTA settings [45]. However, in the HTA assessment, a clinician often validates the predicted mean survival and can also then inform or validate the cure fraction in the absence of data. Survival extrapolation and modeling must be acknowledged as uncertain and should be explored in sensitivity analyses, but may still be the best approach to generate information relevant for short-term clinical and economic decision making [54]. In addition, the use of external data, similar to the use of the cure fraction as a model input, was shown to improve extrapolation of cancer survival, indicating that collecting external data is likely to be worth the additional effort [55].

Mixture cure models are used frequently in population-based analysis of cancer survival. In an analysis using cancer registry and national vital status data from Norway, mixture cure models were employed to estimate cure fractions and survival for 23 types of cancer [56]. For 15 types of cancer, including colon, liver, lung/trachea, and bladder cancer, models converged. For both women and men, cure fractions increased between 1963 and 2002 for most cancer sites, as did median survival in uncured patients with cancer of the rectum or central nervous system as well as non-Hodgkin lymphoma and leukemia in both women and men. For cancers for which models failed to converge, including breast and prostate cancer as well as melanoma, the lack of convergence was attributed to the absence of a reliable medical cure during the period under study, which implied that statistical cure was unlikely to exist. In addition, selection effects, i.e., better relative survival of cancer survivors (e.g., for testicular cancer), as well as long-term adverse events associated with treatment were considered as reasons why survival curves did not plateau, so mixture cure models would be conceptually inappropriate. Future updates of these analyses, e.g., following the introduction of new treatments, could contribute to identifying the impact of new treatments on a population level.

A similar study was conducted in the Tyrol region of Austria, using 2005–2009 data for 25 cancer sites from a regional cancer registry [57]. Models converged for 14 cancer types in women and 15 in men. The lowest cure fractions for each sex were calculated for women with acute myeloblastic leukemia and for men with pancreatic cancer, respectively. The highest cure fractions, in contrast, were observed for cervical cancer in women and high-risk non-Hodgkin lymphoma in men. Similar to results from Norway, no model convergence was achieved for breast and prostate cancer as well as melanoma, which was again attributed to a lack of medical and therefore statistical cure [57].

In a large-scale analysis of cancer cases diagnosed between 1985 and 2005 in Italy, high cure fractions were observed, among others, for cervical and thyroid cancers, in contrast to low cure fractions for liver cancer and leukemia [58]. The study also explored time to cure, stratified by age and different cure fraction definitions, for each cancer. While the female population with thyroid cancer and the male population with testicular cancer achieved statistical cure within 5 years after diagnosis, other populations, including those with liver cancer and leukemia, did not reach statistical cure before 15 years, if at all [58].

These examples show that mixture cure models are used widely but may not be appropriate for all cancer sites in all contexts. Analysts therefore should evaluate carefully if mixture cure models are appropriate, and which data assets are available for an analysis. Assumptions regarding cure and model specifications should always be assessed, ideally also graphically [22]. The uncertainty associated with model results should be addressed by scenario analyses that explore, for example, the influence of different functional forms, cure fraction inputs, and covariates on results, as demonstrated in this tutorial [21, 22, 59]. A lack of data, e.g., due to insufficient follow-up, can possibly be circumvented by using an “informed” approach to cure fraction estimation, i.e., the analyst could use a cure fraction estimate from an external source or a clinical opinion, if available, as an input to the model. Note that the lack of data cannot be fully overcome by expert opinion or modeling approaches. In any case, given the limited follow-up time at the time of HTA submission, modeling approaches can shed light on the most plausible long-term behavior of endpoints.

In addition to their frequent use in cancer epidemiology, mixture cure models are receiving increased attention in HTA and health economics as cancer immunotherapies become more widely used. In a cost-effectiveness analysis comparing ipilimumab with glycoprotein 100 (gp100) for the treatment of advanced melanoma, a mixture cure model was compared with a standard Weibull model [19]. When the Weibull model was used, mean overall survival was 0.90 years in the gp100 arm and 1.60 years in the ipilimumab arm. When the mixture cure model was used, cure fractions of 6% (95% CI 5–15) and 21% (95% CI 13–30) were estimated for gp100 and ipilimumab, respectively. Mean overall survival in cured patients in both arms was 26 years, compared with 0.75 and 0.83 years in uncured patients treated with gp100 and ipilimumab, respectively. Modeling the differences in survival between cured and uncured patients increased quality-adjusted life expectancy and costs in both arms as the long-term survival of cured patients was now accounted for. Consequently, a substantial reduction in the incremental cost-effectiveness ratio was observed when accounting for differential survival, from US$324,000 to US$113,000 per quality-adjusted life-year gained with ipilimumab versus gp100. The authors concluded that, relative to standard survival analysis, mixture cure models increased quality-adjusted life expectancy and cost estimates for cured patients, but reduced them for non-cured patients, with the magnitude of relative changes dependent on the cure fractions, cost, and utilities [19]. Mixture cure models were recommended as more appropriate than standard analysis for analyzing treatments when there is evidence to suggest the existence of statistical cure.

5 Conclusions

In parallel with the advent of cancer therapies associated with statistical cure, the use of mixture cure models is likely to increase. Mixture cure models, which account for the different survival experience of cured and uncured patients, may more accurately reflect life expectancy and, in the context of health economic analyses, quality-adjusted life expectancy and healthcare costs than standard survival analyses.

As mixture cure models require the user to obtain and combine data from different sources and provide additional information compared to standard survival analysis, some users may be hesitant to use or interpret mixture cure models. Therefore, the present tutorial aimed to provide a practical introduction to mixture cure models, including their implementation in statistical software, with a specific focus on the algorithm, to support (potential) users, such as HTA analysts and health economists, in interpreting and using mixture cure models. We stress the fact that in the informed approach, the selection of any cure rate chosen needs to be carefully justified.