1 Historical perspective

The concept of plasma as a physical medium was introduced by Langmuir (Mott-Smith 1971), although it was considered already in Ancient Greece as one of the fundamental states of matter, and called Fire. From the Ancient, we have also inherited the ideia of quantizing our description of the physical world, by assigning a Pythagorean solid to each state of matter. Fire was represented by a Tetrahedron, “the smallest and the acutest” of these solids. Therefore, we can say without too much irony that the first quantum representation of a plasma was the Tetrahedron (see Plato, Timaeus, 55d–56c).

Coming back to more recent times, electron plasma oscillations, also called Langmuir waves, were first observed by Tonks and Langmuir (1929). Their frequency \(\omega\) is nearly equal to the electron plasma frequency, \(\omega _p\), which is the characteristic parameter of the medium. The concept of Landau damping of electron plasma waves was formulated in Landau (1946), and corresponds to the possible occurrence of wave damping without the need for particle collisions or any other mechanism of dissipation. At first, this non-trivial and counter-intuitive concept was seen as a simple mathematical curiosity, with no obvious physical consequences. It, nevertheless, stimulated a number of theoretical new concepts, such as the BGK modes, which are electrostatic undamped modes (Bernstein et al. 1957), and the van Kampen modes (Van Kampen 1955; Case 1959). Landau damping can be seen as the result of phase-mixing of a superposition of van Kampen modes. However, the suspicions on this non-collisional damping evaporated almost completely when, in 1964, the first unequivocal experimental demonstration was made by Malmberg and Wharton (1964), soon followed by others (Derfler and Simonen 1966).

The conceptual difficulty associated with this concept is that it carries no dissipation, and therefore, it is able to conserve entropy. As a result, processes like the formation of wave revivals and echos become possible. Electron plasma waves excited at some position in plasma column, by an antenna immersed in the medium, will attenuate along propagation and eventually disappear. However, the information associated with the wave is, nevertheless, retained by each individual particle, which keeps oscillating no longer in synchronism with the other particles. Due to these hidden particle oscillations, the wave can, under some conditions, be recreated at some other location. This revival of the disappeared oscillation is called a plasma wave echo. It can be excited by a second antenna located at some distance from the first one, or by a reflecting plasma boundary. This phenomenon was first predicted by Gould et al. (1967), and can be seen as a direct consequence of electron Landau damping. Thus, information on the vanished wave is conserved in the medium, and therefore, entropy.

In the process of Landau damping, there is a special class of electrons that play a dominant role. They are called resonant particles, those with a velocity nearly equal to the wave phase velocity, that exchange energy with the wave (Dawson 1961). As for the remaining particles, they provide the necessary background that supports the plasma oscillation and build up the collective field.

The original description of Landau damping was based on the linearized version of the Vlasov equation, the kinetic equation describing the behaviour of the medium. However, it was soon realized that nonlinear processes also play an important role, and lead to new phenomena, such as particle trapping in the wave potential (O’ Neil 1965). As a result, the damping process will depend on the wave amplitude, with slow oscillations of the damping rate, at a new frequency (called bounce frequency), much smaller than the electron plasma frequency. Due to these nonlinear oscillations, upper and lower sidebands will appear in the wave spectrum, similar to those due to amplitude modulation. These effects were first observed experimentally in Wharton et al. (1968). Asymptotically, the damping process will saturate and the wave frequency will be shifted. Nonlinear Landau damping has been studied in theory and simulations by several authors along the years (Sugihara et al. 1981; Rasmussen and Thomsen 1983; Manfredi 1997; Yampolsky and Fisch 2009).

Even after the remarkable theoretical and experimental advances of the 60s, the concept of electron Landau damping never lost its fascination. And, in 2011, the nonlinear Vlasov problem was mathematically solved by Mouhot and Villani (2010). The theoretical problem of Landau damping, in its classical formulation, seemed completely solved. In recent years, the problem shifted to quantum plasmas.

A quantum description of the plasma medium becomes necessary for large electron densities n and low temperatures T, when the inter-particle distance (sometimes also called the Wigner–Seitz radius), \(a_\textrm{WS}\) becomes smaller than the de Broglie wavelength of thermal electrons, \(\lambda _\textrm{B} \ge a_\textrm{WS}\). This inter-particle distance is proportional to the cubic root of the electron plasma density n, according to \(a_\textrm{WS} = (3 / 4 \pi n)^{1/3}\), while the electron de Broglie length behaves as the inverse of the electron thermal velocity \(v_\textrm{th}\), as \(\lambda _\textrm{B} = \hbar / m_e v_{th}\). It then becomes obvious that the quantum plasma regime requires high densities and low electron temperatures, or \(n^{1/3} \lambda _\textrm{B} \ge 1\).

An alternative, but nearly equivalent, definition of the quantum plasma regime can be established with the help of the dimensionless parameter \(\chi = T_\textrm{F} / T\), which is the ratio between the Fermi temperature and the electron plasma temperature

$$\begin{aligned} \chi \equiv \frac{T_\textrm{F}}{T} = \frac{\lambda _\textrm{B}^2}{2} \left( 3 \pi ^2 n\right) ^{2/3}. \end{aligned}$$
(1)

We can see that \(\chi \sim (n^{1/3} \lambda _\textrm{B})^2\). In the famous \((\log T - \log n)\) diagram, we can then define two regions, the classical plasma region, where \(\chi < 1\), and the quantum plasma region, where \(\chi \ge 1\). Excellent reviews on quantum plasmas have been published along the years (Shukla and Eliasson 2011; Manfredi et al. 2019; Melrose 2020; Misra and Brodin 2022). In the present review, we focus on electron plasma waves, and somewhat deviate from the traditional definition of quantum plasmas. In particular, we show that the quantum plasma methods and the phenomenon of quantum Landau damping is also relevant to the classical plasma regime of \(\chi < 1\). This is due to the existence of quantum-like processes associated with photon Landau damping, which involve high phase-velocity plasma waves, and also to the quasiparticle behaviour of classical turbulent plasmas. In that sense, the relevance of quantum Landau damping and quantum trapping is nearly universal, and includes several areas of the so-called classical plasmas.

The first approaches to electron plasma waves and damping in quantum plasmas date from the early 60s of the last century (Klimontovich and Silin 1960; Pines and Schrieffer 1962). They were mainly motivated by solid state physics, and by the study of collective electron processes in metals. In more recent years, the interest shifted from solid state to plasma physics oriented problems, such as intense laser–plasma interactions and astrophysical phenomena. Due to these historical origins, it is not surprising to see that the main theoretical approaches are based on density functional theory, typical of condensed matter, and on quantum kinetics, closer to plasma kinetic theory. Although there is some debate on the mutual advantages of these two eventually competing approaches (Bonitz et al. 2019), there is still no clear demonstration of their theoretical equivalence. Here, we follow the quantum kinetic approach, which is more appropriate to describe wave propagation and time-dependent phenomena.

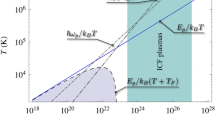
The theoretical methods used to describe quantum plasma processes, in the broad sense assumed here, are indicated in Fig. 1. A central role of these theoretical methods is played by the wave-kinetic equation, as shown in this figure. The wave-kinetic equation describes the temporal evolution of the Wigner function (Wigner 1932) which replaces the classical particle distribution in the quantum regime. As it is well known, the Wigner function is in fact a quasidistribution, because it can take negative values, in contrast with its classical correspondent. This fact is not necessarily a drawback, because a negative value of the Wigner function helps to identify the quantum regimes. The wave-kinetic equation can be derived from the Schrödinger equation for the plasma electron population, following a procedure first proposed by Moyal (1949), and using appropriate statistical averages. It describes the evolution of the electron population in the presence of a mean-field (Haas 2011). In the simplest case, this mean-field corresponds to the electrostatic field of an electron plasma wave. In the quasiclassical limit, the wave-kinetic equation can be reduced to a Vlasov equation, to which we can eventually add the first-order quantum corrections. Describing the mean field with the Poisson’s equation, we can then establish the quantum dispersion relation of electron plasma waves, and define the physical conditions for the occurrence of quantum Landau damping (Suh et al. 1991; Daligault 2014; Brodin et al. 2015; Chatterjee and Misra 2016).

Similarly, we can derive a wave-kinetic equation for the electromagnetic radiation in a completely classical plasma background, if we start from Maxwell’s equations and use the Wigner function for the electric field (Tsintsadze and Mendonça 1998). Striking similarities between the electron gas and the photon gas in a plasma become evident, which include the existence of photon Landau damping (Bingham et al. 1997). This is exactly equivalent to the electron Landau damping. The quantum nature of photon Landau damping is related to the fact that photons are electromagnetic waves, and, therefore, possess the same undulatory nature as the electrons in the quantum regime. In both cases, emission and absorption of electron plasma wave quanta (sometimes called plasmons) by electrons and photons also involve the occurrence of a quantum recoil.

Pushing further these similarities between the behaviour of particles (electrons) and fields (photons), we can then establish the evolution equations of a turbulent plasma, based on the definition of appropriate Wigner functions. The resulting wave-kinetic equation for classical plasma turbulence, where the role of photons is replaced by plasma quasiparticles (for instance, driftons, for drift-wave turbulence), shows the existence of Landau damping and quasiparticle trapping similar to those of the electrons in a quantum plasma.

In a broader perspective, quantum Landau damping can be seen as a generic process, with implications in many areas of physics, not just in plasmas, from the damping of giant resonances of atomic nuclei (Bertsch et al. 1983; Fiolhais 1986), to damping of Bogolioubov oscillations in Bose–Einstein condensates (Pitaevskii and Stringari 1997; Giorgini 1998; Mendonça and Terças 2018). As a simple and natural extension of the quantum plasma model, we should mention the case of laser-cooled atomic clouds. This corresponds to a gas of neutral atoms, in the micro-Kelvin temperature range, cooled by laser beams, where absorption and re-emission of photons (nearly resonant to a given atomic transition) produce an atomic effective charge (Walker et al. 1990; Pruvost et al. 2000). For this reason, the cold gas behaves collectively as a plasma (Barré et al. 2019). Notice that the atoms stay in a neutral state and are not photoionized. Atom density oscillations (a kind of plasmons) can be excited in the gas, with a dispersion relation that strongly resemble that of plasmons in quantum plasmas (Mendonça et al. 2008). This includes damping of such oscillations by nearly resonant atoms, which is nothing but another form of Landau damping. Excitation of such oscillations in the nonlinear regime has been observed, leading to the formation of photon bubbles (Rodrigues et al. 2022; Giampaoli et al. 2021), which are, indeed, trapped photon states predicted by the theory (Mendonça and Kaiser 2012). A short account of these effective plasma phenomena in laser-cooled matter will also be given here.

Fig. 1
figure 1

Diagram of theoretical methods for collisionless quantum plasmas. On the left-hand side, we have the basic quantum plasma methods. On the left-hand side, we represent the processes in classical plasmas that can be described by quantum plasma methods, such as photon kinetics and quasiparticle turbulence

Full size image

2 Quantum kinetic equations

We consider electrons in a quantum plasma, in the non-relativistic regime, and ignore the ions. We also ignore magnetic fields. If N is the number of electrons in the system, its quantum state can de described by a wavefunction \(\psi (\textbf{r}_1,...\textbf{r}_N, t)\), which satisfies the Schrödinger equation

$$\begin{aligned} i \hbar \frac{\partial }{\partial {t}} \psi = H \psi \,, \quad H = - \frac{\hbar ^2}{2 m} \sum _{j = 1}^N \nabla _j^2 - e V, \end{aligned}$$
(2)

where \(\nabla _j = \partial / \partial \textbf{r}_j\), and V is the electrostatic potential. This description, which does not specify the ion background, is known in condensed matter physics as the jellium model (Mahan 2000; Dornheim et al. 2018). It simplifies further by assuming that the electrons are weekly correlated. We can then replace the N-body wavefunction by a product of individual wavefunctions, such that

$$\begin{aligned} \psi \left( \textbf{r}_1,...\textbf{r}_N, t\right) = \Pi _{j = 1}^N \psi \left( \textbf{r}_j, t\right) , \end{aligned}$$
(3)

and assume that each individual wavefunction satisfies the single-particle Schrödinger equation

$$\begin{aligned} i \hbar \frac{\partial }{\partial {t}} \psi (\textbf{r}, t) = \left[ - \frac{\hbar ^2}{2 m} \nabla ^2 - e V (\textbf{r}, t) \right] \psi (\textbf{r}, t). \end{aligned}$$
(4)

The potential \(V (\textbf{r}, t)\) is determined by Poisson’s equation, where all the N electron charges are considered. The use of this oversimplified description requires some comments. First, the decomposition (3) is only valid for weakly coupled plasmas, where particle collisions and two-particle correlations can be neglected. Weakly quantum coupled plasmas are characterized by a small value of the quantum coupling parameter, \(\Gamma _\textrm{Q} < 1\), which is defined as the ratio of the averaged potential energy between two particles, \(U_\textrm{pot}\), and the kinetic energy, \(T_\textrm{F}\), or more explicitly, by

$$\begin{aligned} \Gamma _\textrm{Q} \equiv \frac{e^2 n_0^{1/3}}{\epsilon _0 T_\textrm{F}} = \frac{2 m e^2}{(3 \pi ^2)^{2/3} \epsilon _0 \hbar ^2 n_0^{1/3}}. \end{aligned}$$
(5)

For electrons in a metal, we have \(\Gamma _\textrm{Q} \sim 1\), and this formulation is only marginally valid. Furthermore, the N-body wavefunction has to satisfy the exclusion principle, and should be anti-symmetric with respect to changes between any two particles (Mahan 2000; Bonitz 1998). As a result, it should be represented by a linear combination of N products of individual wavefunctions, and not just by one. Therefore, we need to impose some restrictions on the use of Eq. (3), namely that none of the above individual single-particle wavefunctions in this product should be identical. For a more detailed and rigorous analysis, see Haas (2011).

We can then define the Wigner function, \(W (\textbf{r}, \textbf{v}, t)\), as the Fourier transform of the autocorrelation function of the single-electron wavefunction, according to

$$\begin{aligned} W (\textbf{r}, \textbf{v}, t) = \int \psi \left( \textbf{r} - \textbf{s}/2, t\right) \, \psi ^* \left( \textbf{r} + \textbf{s}/2, t\right) \exp \left[ - i m (\textbf{s} \cdot \textbf{v} ) \right] \, \textrm{d} \textbf{s}, \end{aligned}$$
(6)

where \(\textbf{v}\) is the particle velocity. This definition allows us to represent the state of the quantum particles in a classical single-particle phase-space \(( \textbf{r}, m \textbf{v})\). However, instead of the classical case, where the state is represented by a dimensionless dot, here the quantum state of the particle is represented by a cloud of quasiprobability, dictated by the value of W. We say quasiprobability, because this value can be negative. We then follow the Wigner–Moyal procedure, which is described in detail in several reviews (Hillary et al. 1984; Tatarski 1983; Weinbub and Ferry 2018) and establish the evolution equation for the Wigner function. This is usually called the wave-kinetic equation, and takes the form

$$\begin{aligned} i \hbar \left( \frac{\partial }{\partial {t}} + \textbf{v} \cdot \nabla \right) W \left( \textbf{r}, \textbf{v}, t\right) = \int K \left( \mathbf{v'} - \textbf{v}, \textbf{r}, t\right) \, W \left( \textbf{r}, \mathbf{v'}, t\right) \, \textrm{d} \mathbf{v'}, \end{aligned}$$
(7)

where the kernel K is defined as

$$\begin{aligned} K \left( \mathbf{v'} - \textbf{v}, \textbf{r}, t\right) = - \frac{e}{(2 \pi \hbar )^3} \int \left[ V (\textbf{r} + \textbf{s}/2, t) - V (\textbf{r} - \textbf{s}/2, t) \right] \exp \left[ - i m \textbf{s} \cdot \left( \mathbf{v'} - \textbf{v}\right) \right] \textrm{d} \textbf{s}, \end{aligned}$$
(8)

where \((- e)\) and m are the electron charge and mass, and \(V ( \textbf{r}, t)\) is the potential. In standard quantum mechanics, this is just the external potential, describing the field applied to the quantum system. However, in plasma physics, \(V ( \textbf{r}, t)\) is the mean-field potential determined self-consistently by all the N electrons in the plasma, and determined by the Poisson’s equation

$$\begin{aligned} \nabla ^2 V = \frac{e}{\epsilon _0} \left[ \int W (\textbf{r}, \textbf{v}, t) \textrm{d} \textbf{v} - n_0 \right] . \end{aligned}$$
(9)

Here, it is assumed that the ions stay at rest with density \(n_0\), and simply provide a background neutralising charge. It is useful to note that the electron wave-kinetic equation can also be written in another equivalent form as

$$\begin{aligned} i \hbar \left( \frac{\partial }{\partial {t}} + \textbf{v} \cdot \nabla \right) W = - e \int V (\textbf{k}, t) \left[ W_- - W_+ \right] \exp ( i \textbf{k} \cdot \textbf{r}) \, \frac{\textrm{d} \textbf{k}}{(2 \pi )^3}, \end{aligned}$$
(10)

where \(V (\textbf{k}, t)\) is the space Fourier transform of the plasma potential, and \(W_\pm = W (\textbf{v} \pm \mathbf{\hbar k} / 2\,m)\). This Fourier spectrum is associated with electrostatic oscillations in the medium, with wavelengths \(\lambda = 2 \pi / k\). The classical approximation corresponds to the limit \(| \textbf{k}| \ll | m \textbf{v}|\), when the particle de Broglie wavelength is much smaller that the wavelength of plasma oscillations, and the electrons can be described as point particles, with no probability cloud. In this limit, we can use the expansion

$$\begin{aligned} W_{\pm } = W {\pm } \frac{{\textbf {k}}}{2 m} \cdot \frac{\partial {W}}{\partial {\textbf{v}}} +..., \end{aligned}$$
(11)

Replacing this in Eq. (10), we are then reduced to the Vlasov equation, as expected

$$\begin{aligned} \left( \frac{\partial }{\partial {t}} + \textbf{v} \cdot \nabla + \textbf{F} \cdot \frac{\partial }{\partial \textbf{v}} \right) W (\textbf{r}, \textbf{v}, t) =0, \end{aligned}$$
(12)

where \(\textbf{F} = - (e/m) \nabla V\) is the force acting on the electrons. The operator under brackets is nothing but the total time derivative of W. In this limit, W tends to the classical probability distribution. In the general case, however, we need to retain all the terms in the expansion [see, for instance, Bonitz (1998)], and use

$$\begin{aligned} W_\pm \equiv W \left( \textbf{v} \pm \mathbf{\hbar k} / 2m \right) = \sum _{\nu = 0}^\infty \frac{1}{\nu !} \left( \pm \frac{\hbar \textbf{k}}{2 m} \cdot \frac{\partial }{\partial \textbf{v}} \right) ^\nu W (\textbf{v}) \,, \end{aligned}$$
(13)

This allows us to write the quantum kinetic equation (10) in the Vlasov-type form, as

$$\begin{aligned} \left[ \frac{\partial }{\partial {t}} + \textbf{v} \cdot \nabla + \textbf{R} (\textbf{v}) \cdot \frac{\partial }{\partial \textbf{v}} \right] W (\textbf{r}, \textbf{v}, t) = 0, \end{aligned}$$
(14)

where the force F in the Vlasov equation (14) is replaced by the operator

$$\begin{aligned} \textbf{R} (\textbf{v}) = \sum _{\nu = 0}^\infty \frac{1}{(2 \nu +1)!} \left( - \frac{\hbar ^2 \nabla ^2}{4 m^2} \right) ^{\nu } \textbf{F} \cdot \frac{\partial ^{2\nu }}{\partial \textbf{v}^{2\nu }}. \end{aligned}$$
(15)

If we retain just the first-order quantum correction, we obtain the equation

$$\begin{aligned} \left( \frac{\partial }{\partial {t}} + \textbf{v} \cdot \nabla + \textbf{F} \cdot \frac{\partial }{\partial \textbf{v}} + \frac{e \hbar ^2}{3 \cdot 2^3 m^3} \nabla ^3 V \cdot \frac{\partial ^3}{\partial \textbf{v}^3} \right) W (\textbf{r}, \textbf{v}, t) =0. \end{aligned}$$
(16)

The term with the third-order derivative is therefore the leading-order quantum corrections, and the neglected quantum terms are of order \(\hbar ^4\). This is an interesting wave-kinetic equation, which has not been used very often. The Vlasov equation is recovered in the purely classical limit, when \(\hbar\) is taken equal to zero.

3 Quantum Landau damping

Using the above description, we can derive the dispersion relation for electron plasma waves in a quantum plasma. For that purpose, we assume small perturbations around equilibrium, and assume that this equilibrium exists in the absence of the plasma potential, \(V_0 ( \textbf{r}) = 0\), and is characterized by some distribution \(W_0 (\textbf{v})\), typically but not necessarily the Fermi–Dirac distribution. Furthermore, we assume perturbations evolving in space and time with wavevector \(\textbf{k}\) and frequency \(\omega\), such that

$$\begin{aligned} V (\textbf{r}, t) = {{\tilde{V}}} \exp \left( i \textbf{k} \cdot \textbf{r} - i \omega t \right) \,, \quad W (\textbf{r}, t ) = W_0 + {{\tilde{W}}} \exp \left( i \textbf{k} \cdot \textbf{r} - i \omega t \right) , \end{aligned}$$
(17)

where \(({{\tilde{V}}}, {{\tilde{W}}})\) are the amplitudes. Following the standard perturbative procedure (Haas 2011), and using Eqs. (9) and (10), we arrive at the expression

$$\begin{aligned} 1 + \frac{e^2}{\hbar k^2 \epsilon _0} \int W_0 (\textbf{v}) \left[ \frac{1}{\omega - \textbf{k} \cdot \left( \textbf{v} - \mathbf{v_k}\right) } - \frac{1}{\omega - \textbf{k} \cdot \left( \textbf{v} + \mathbf{v_k}\right) } \right] \textrm{d} \textbf{v} = 0, \end{aligned}$$
(18)

where \(\mathbf{v_k} = \hbar \textbf{k} / 2\,m\). The main properties of this linear dispersion relation are well discussed in Eliasson and Shukla (2010). In the relevant case of a distribution in equilibrium at a temperature smaller than the Fermi temperature, and assuming that \(W_0 (\textbf{v})\) is the Fermi–Dirac distribution, this reduces to

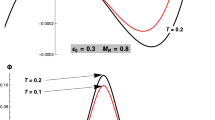
$$\begin{aligned} \omega ^2 = \omega _\textrm{p}^2 \left( 1 + k^2 \lambda _\textrm{F}^2 \right) + \frac{\hbar ^2 k^4}{4 m^2}, \end{aligned}$$
(19)

where \(\omega _p = \sqrt{e^2 n_0 / \epsilon _0 m}\) is the electron plasma frequency, and \(\lambda _\textrm{F} = v_\textrm{F} / \sqrt{3} \omega _p\) is the quantum Debye (or Fermi) length. We can see that, in comparison with the classical dispersion equation, there is an additional term proportional to \(\hbar ^2\). This additional term is similar to that given by a free-streaming of quantum particles, and its importance becomes dominant for short wavelengths, as illustrated in Fig. 2. On the other hand, the contribution of the poles in Eq. (18) leads to the electron Landau damping, as determined by the expression

$$\begin{aligned} \gamma _L = \frac{\pi m \omega _\textrm{p}^3}{2 \hbar k^3} \left[ G_0 (v_+) - G_0 (v_-) \right] \,, \quad v_\pm = \frac{\omega }{k} \pm v_k, \end{aligned}$$
(20)

where

$$\begin{aligned} G_0 (v) = \frac{1}{n_0} \int W_0 (\textbf{v}_\perp , v) \textrm{d} \textbf{v}_\perp , \end{aligned}$$
(21)

is the parallel electron distribution, and \(\textbf{v}_\perp\) is the velocity perpendicular to the direction of propagation, \(\textbf{k} / k\). We can see that the wave damping is determined by the population difference between two parallel velocity states that are equidistant to the classical resonant velocity, \(v = \omega / k\). In condensed matter physics, quantum Landau damping is usually interpreted as a loss of wave energy due to the excitation of particle-hole pairs [see, for instance, Mahan (2000), Bonitz (1998)].

In the quasiclassical limit, we have \(v_k \ll (\omega / k)\) and the above difference becomes infinitesimal, the derivative \(\partial G_0 / \partial v\) can be expanded, as shown in Eq. (11). We then recover the well-known expression of the classical electron Landau damping

$$\begin{aligned} \gamma _L = \frac{\pi \omega _p^3}{2 k^2} \left( \frac{\partial G_0}{\partial v} \right) _{v = \omega / k} \,. \end{aligned}$$
(22)

For a quantum plasma in thermal equilibrium, the equilibrium distribution \(W_0 (\textbf{v})\) should be a Fermi–Dirac distribution, as described by

$$\begin{aligned} W_0 (\textbf{v}) = \frac{C}{ \exp \left[ (m v^2 / 2 - \mu )/T \right] + 1 } \,, \end{aligned}$$
(23)

where the temperature T is written in energy units, \(\mu \equiv \mu ( T)\) is the chemical potential, and C is a normalization constant. We know that the chemical potential tends to the Fermi energy \(E_\textrm{F}\), when T tends to zero. For a discussion of quantum effects associated with the different Fermi velocity (or momentum) states, see Hunger et al. (2021). The normalization constant is such that the integral over the velocity space gives the equilibrium density \(n_0\). This leads to

$$\begin{aligned} n_0 = \int W_0 (\textbf{v}) \textrm{d} \textbf{v} \,, \quad C = 2 n_0 \left( \frac{m}{2 \pi \hbar } \right) ^3 . \end{aligned}$$
(24)

Integration of (23) over the perpendicular velocity then leads to the one-dimensional electron distribution

$$\begin{aligned} G_0 (v) = G_{00} \ln \left\{ \exp \left[ - \left( m v^2 / 2 - \mu \right) /T \right] + 1 \right\} \,, \quad G_{00} = \frac{2 \pi C T}{n_0 m}. \end{aligned}$$
(25)

This is a bell-shaped function, represented in Fig. 3. The corresponding value of the Landau damping (24), in the quasiclassical limit, is given by

$$\begin{aligned} \gamma _L = \frac{\pi ^2 \omega _p^3}{n_0 k^3} \frac{\omega C}{ \exp \left[ \left( m \omega ^2 / 2 k^2 - \mu \right) /T \right] + 1 }, \end{aligned}$$
(26)

and is also illustrated in the same figure. As we can see, for nearly zero temperatures, there is almost no damping at large phase velocities, \(\omega \gg k v_\textrm{F}\). Similarly, damping is also small and tends to zero for very small phase velocities, \(\omega \ll k v_\textrm{F}\). Therefore, in the quasiclassical limit, wave damping is only significant in the velocity region around \(v_\textrm{F}\). In contrast, in the quantum regime, wave damping can be relevant over a larger region, which increases with the value of the quantum jump appearing in Eq. (20), \(\Delta v = 2 v_k \equiv \hbar k / m\). Such a velocity jump is known as the quantum recoil, and is associated with the emission or absorption of a quantum of electron plasma waves ( a plasmon) with momentum \(\hbar \textbf{k}\). This effect is even more pronounced when we take into account multiple-plasmon processes, to be considered later.

The above description is only valid in the perturbative linear regime, when the wave amplitude is assumed infinitesimal. However, for finite wave amplitudes, corrections to the dispersion relation and to Landau damping, depending of the value of the wave amplitude, are expected to occur. As already known in classical theory, such corrections are associated with deviations of the wave amplitude from a purely exponential decay determined by the value of \(\gamma _\textrm{L}\), and the appearance of satellites in the wave spectrum. They are related to particle trapping, as discussed next.

Fig. 2
figure 2

Quantum dispersion relation of electron plasma waves, \(\omega ^2 / \omega _\textrm{p}^2\), as a function of \(k^2 \lambda _\textrm{F}^2\), according to Eq. (19). The classical dispersion is also shown (dashed curve)

Full size image
Fig. 3
figure 3

Landau damping in quantum plasmas: Normalized one-dimensional electron distribution, \(G_0 ( v) / G_{00}\), as a function of \(v / v_\textrm{F}\), for \(T = T_\textrm{F}\) (red); and quasiclassical Landau damping, Eq. (26), in normalized units (blue)

Full size image

4 Nonlinear quantum regime

The nonlinear regime is associated with the influence of a finite wave amplitude on the wave dispersion. It is mainly due to particle trapping and to the occurrence of harmonics. Particle trapping can easily be recognised in classical phase-space. In the wave reference frame moving with velocity \(v_\phi = \omega / k\) in the direction of propagation, the oscillating potential creates a local nonlinear pendulum, where the region of trapped orbits is separated from the circulating orbits by a critical line, called the separatrix. For a wave propagating in the x-direction, the particle trajectories in the wave frame can be described by the Hamiltonian

$$\begin{aligned} h \left( \eta , {\dot{\eta }}\right) = \frac{1}{2} {\dot{\eta }}^2 - \omega _\textrm{B}^2 \cos \eta , \end{aligned}$$
(27)

where \(\eta = k x\) and \(\omega _\textrm{B}\) is the bounce frequency, determined by

$$\begin{aligned} \omega _\textrm{B} = \sqrt{\frac{e}{m} k^2 {{\tilde{V}}}} \equiv \omega _\textrm{p} \sqrt{\frac{{{\tilde{n}}}}{n_0}}, \end{aligned}$$
(28)

where \({{\tilde{V}}}\) is the wave amplitude and \({{\tilde{n}}}\) is the corresponding density perturbation. We can see that this Hamiltonian is a constant of motion, \(h (\eta , {\dot{\eta }}) = h_0\). A finite amplitude necessarily implies the existence of trapped and untrapped orbits, separated by the condition \(h_0 = \omega _\textrm{B}^2\). This condition defines the separatrix, determined by Zaslavsky et al. (1991)

$$\begin{aligned} {\dot{\eta }} = \pm 2 \omega _\textrm{B} \cos (\eta / 2) = \pm \frac{2 \omega _\textrm{B}}{\cosh \left( \omega _\textrm{B} t\right) }. \end{aligned}$$
(29)

This is a non-oscillating solution of the motion, of the soliton type. In contrast, for deeply trapped orbits, such that \(| h_0 | \ll \omega _\textrm{B}^2\), we have oscillating trajectories, described by

$$\begin{aligned} {\dot{\eta }} = a \cos \left( \omega _\textrm{B} t\right) \,, \quad a = \left( \omega _\textrm{B}^2 - | h_0 |\right) . \end{aligned}$$
(30)

These particle oscillations at the bounce frequency \(\omega _\textrm{B}\) create modulations in the decay rate, and lead to the formation of sidebands at frequencies \(\omega \pm \omega _\textrm{B}\), as first described by O’Neil O’ Neil (1965) in the classical formulation, and observed in the experiments (Wharton et al. 1968).

In a quantum plasma, the character of trapped oscillations significantly changes. First of all, we do not have single-particle trajectories represented by dots with zero dimension in phase-space (x, p). In contrast, the particles are represented clouds of probability, and the trapped particles are not absolutely confined, because they can move through the potential barrier by quantum tunneling. This changes the qualitative features of the trapping zone. The bounce frequency is modified according to Daligault (2014), Brodin et al. (2015).

$$\begin{aligned} \omega _\textrm{B} \, \rightarrow \, \frac{\omega _\textrm{B}}{\sqrt{1 + k v_k / \gamma _\textrm{L}}}. \end{aligned}$$
(31)

The behaviour of trapped particles in the quantum regimes is interesting and becomes quite complex. It has been explored mainly with numerical simulations. To understand its main qualitative features, it is useful to identify three characteristic times. Namely, the quantum transition time, \(\tau _\textrm{q}\), the particle bounce period, \(\tau _\textrm{B}\), and the damping time \(\tau _\textrm{L}\), as defined by

$$\begin{aligned} \tau _\textrm{q} = \frac{1}{\textbf{k} \cdot \mathbf{v_k}} = \frac{2 m}{\hbar k^2} \,, \quad \tau _\textrm{B} = \frac{1}{\omega _\textrm{B}} \,, \quad \tau _\textrm{L} = \frac{1}{\gamma _\textrm{L}}. \end{aligned}$$
(32)

These quantities can be used to define a couple of important parameters, \(R_{th}\) and \(R_{nl}\). The first one is the quantum trapping parameter, which is the ratio between the transition time and the bounce period

$$\begin{aligned} R_\textrm{tr} = \frac{\tau _q}{\tau _\textrm{B}} = \frac{m \omega _\textrm{B}}{\hbar k^2} = \frac{2 e {{\tilde{V}}}}{\hbar \omega }. \end{aligned}$$
(33)

As we can see, this is identical to the ratio between the trapping potential and the ground energy level of trapped particles. We can then say that, for \(R_{th} < 1\), no trapped particles should exist, because no ground state can be defined inside the potential well. Another useful quantity is the nonlinear parameter \(R_\textrm{nl}\), defined as

$$\begin{aligned} R_\textrm{nl} = \frac{\tau _L^2}{\tau _\textrm{B}^2} \left( 1 + \frac{\tau _q}{\tau _\textrm{L}} \right) = \frac{\omega _\textrm{B}^2}{\gamma _L^2 \left( 1 + \textbf{k} \cdot \mathbf{v_k} / \gamma _L\right) }. \end{aligned}$$
(34)

The nonlinear regime takes place for \(R_\textrm{nl} \ge 1 / 2\), when the particles have enough time to oscillate inside the trapped potential before the oscillations decay due to Landau damping. Furthermore, simulations show that bound oscillations can persist even in the absence of trapped particle states, when, simultaneously, we have \(R_\textrm{th} < 1\) and \(\tau _\textrm{B} / \tau _\textrm{L} < 1\), or equivalently \(\tau _\textrm{q} < \tau _\textrm{B}^2 \tau _\textrm{L}\). These ghost trapped oscillations can be attributed to the cloud of probability associated with passing particles. In the space of parameters \((R_\textrm{th}, R_\textrm{nl})\), six different regions have been identified (Brodin et al. 2015). Quantum trapping is illustrated in Fig. 4, where single-particle probabilities are described by the Schrödinger equation with a sinusoidal potential, similar to the classical one represented in Eq. (27). Two quantum trajectories are shown, for initial conditions inside and outside the classical separatrix. We can clearly observe the fast expansion of the electron wavepacket, as well as tunneling and ghost trapping.

Fig. 4
figure 4

Quantum probability \(|\psi (\eta , t)|^2\) as a function of time, for single electrons in a sinusoidal potential, as described by Schrödinger’s equation, with initially a trapped, and b untrapped, wavepacket. Visible in the figure are: (i) broadening of the initial single-particle wavepacket, (ii) tunneling out of the wave potential in the trapped case, and (iii) ghost trapping of parts of the wavepacket in the untrapped case

Full size image

Another aspect of the nonlinear plasma response is related to the harmonic field, which is closely related to the nonlinear motion of the nearly resonant particles in the wave potential. These harmonic field components, with frequencies that are multiples of the wave frequency, cannot propagate independently in the medium, because they do not satisfy a proper dispersion relation. However, they are present nevertheless, and can influence wave propagation. More specifically, due to the presence of field harmonics, multiple plasmon transitions become possible. The quantum recoil associated with Landau damping as described in Eq. (20) is replaced by multiple quantum jumps, between discrete values of the parallel velocity v, as determined by

$$\begin{aligned} v_\nu = \frac{\omega }{k} \pm \nu \frac{\hbar k}{2 m} \,, \quad \nu = 1, 2, 3,... \end{aligned}$$
(35)

This corresponds to the existence of multi-plasmon transitions, satisfying the momentum and energy conservation relations

$$\begin{aligned} \hbar k_1 \pm n \hbar k = \hbar k_2 \,, \quad \hbar \omega _1 \pm n \hbar \omega = \hbar \omega _2 \,, \end{aligned}$$
(36)

where the new frequencies \(\omega _j\), and wavenumbers \(k_j\), satisfy the free-particle dispersion \(\omega _j = \hbar k_j^2/2m\), for \(j = 1, 2, 3,..\). To discuss these multi-plasmon processes, we can assume that the electric potential contains a second harmonic component, as

$$\begin{aligned} V (\textbf{r}, t) = {{\tilde{V}}}_1 ( t ) \exp \left( i \textbf{k} \cdot \textbf{r} - i \omega t \right) + {{\tilde{V}}}_2 ( t ) \exp \left( 2 i \textbf{k} \cdot \textbf{r} - 2 i \omega t \right) , \end{aligned}$$
(37)

and that the quasidistribution contains a superposition of harmonics as

$$\begin{aligned} W (\textbf{r}, t ) = W_0 + \sum _{\nu = 0}^\infty {{\tilde{W}}}_0 \exp \left[ i \nu \left( \textbf{k} \cdot \textbf{r} - \omega t \right) \right) . \end{aligned}$$
(38)

These new expressions replace Eq. (17). Using them in the perturbative analysis of the wave-kinetic and Poisson’s equations (7) and (9), it is then possible to generate a cascade of coupled equations for the different disturbed quantities, which can then be solved numerically (Brodin et al. 2018). This then proves that transitions such as those represented in Fig. 5 seem to exist. However, it is difficult to give a simple analytical estimate of the relative importance of such transitions.

Fig. 5
figure 5

Multi-plasmon transitions in quantum Landau damping: a single plasmon transitions, for \(\omega / k = v_\textrm{F}\); b two-plasmon transitions for \(\omega / k = 2 v_\textrm{F}\)

Full size image

On the other hand, this mechanism of multi-plasmon emission and absorption can be seen from the perspective of single-particle solutions. In particular, it is in qualitative agreement with the Volkov solutions that can be derived from single-electron states in a plasma wave (Mendonça and Serbeto 2011; Raicher and Eliezer 2013; Varró 2014). These Volkov solutions have been originally established for relativistic quantum plasmas, but they clearly show that single-electron states are compatible with the existence of multi-plasmon transition processes. To illustrate this statement, we use the Volkov solution of the Klein–Gordon equation, for an electron with momentum \(\textbf{p}\) in a plasma wave. As recently noted (Al-Naseri and Brodin 2023), the Klein–Gordon equation is reasonably accurate even for energetic quantum processes involving particle pair-creation, provided that the wave frequency is well below the Compton frequency. We have Mendonça and Serbeto (2011)

$$\begin{aligned} \psi (\textbf{r}, t) = \psi _0 e^{i \varphi _0} \exp \left[ i S (\tau ) \right] \,, \quad \varphi _0 = \left[ \textbf{p} \cdot \textbf{r} - E (\textbf{p}) \tau \right] / \hbar , \end{aligned}$$
(39)

where \(E (\textbf{p})\) is the particle energy, and \(\tau = t - (\textbf{k} \cdot \textbf{r} / \omega )\) is a temporal variable. The phase function \(S (\tau )\) is a periodic function of the wave amplitude, and can be Bessel expanded. In the non-relativistic quantum limit, which is the case considered here, this can be simply written as

$$\begin{aligned} \psi (\textbf{r}, t) = \psi _0 e^{i \varphi _0} \sum _\nu J_\nu (\xi ) e^{i \nu \omega \tau }, \end{aligned}$$
(40)

where the quantity \(\xi \sim e V / (\hbar ^2 k^2 / 2 m)\) is the ratio between the potential and the recoil energy. A nonlinear perturbative expansion of the quantum kinetic equation (7), coupled with the Poisson equation (9), when we start from a Volkov equilibrium and not from a static equilibrium, can then lead to a a new expression of the Landau damping that takes the form

$$\begin{aligned} \gamma _L = \frac{\pi m \omega _\textrm{p}^3}{2 \hbar k^3} \sum _{\nu = 0, 1} F_\nu \left[ G_0 (v_{\nu +}) - G_0 (v_{\nu -}) \right] \,, \quad v_{\nu \pm } = \frac{\omega }{k} \pm \nu v_k \,, \end{aligned}$$
(41)

where \(F_0 = 1\) and \(F_1 = \xi\). This is in qualitative agreement with the numerical results obtained in reference Brodin et al. (2018), and confirms them on analytical grounds. This nonlinear form of Landau damping depends on the wave amplitude \({{\tilde{V}}}\) through the value of \(\xi\), and tends to the linear result in the limit \(\xi \rightarrow 0\), as expected. A detailed derivation of this nonlinear quantum model can be found in Haas et al. (2023).

To complete this discussion, mention should be made to earlier work on harmonic generation (Bonitz et al. 1994), and to a more recent paper on nonlinear density perturbations in warm dense matter (Dornheim et al. 2020). An additional comment should be made on electron collisions, which were ignored. A short discussion of collision effects, which could eventually obscure the collective quantum processes, can be found in Brodin et al. (2015).

5 Photon Landau damping

We now show that the formalism of quantum plasmas can also describe the behaviour of photons in classical plasmas. This is particularly useful to study processes related with intense laser–plasma interactions, as those related with laser wakefield acceleration. The case of quasiparticle turbulence will be discussed in the next section.

The first thing to notice is that, when we talk about photons, we mean electromagnetic waves, which share their undulatory nature with the electrons in the quantum regime. The formal similarity starts with the definition of a Wigner function for the transverse electric field associated with the radiation spectrum, \(\textbf{E} (\textbf{r}, t)\). It takes the form

$$\begin{aligned} N \left( \textbf{r}, \textbf{k}, t\right) = \int \textbf{E} \left( \textbf{r} - \textbf{s}/2, t\right) \cdot \textbf{E}^* \left( \textbf{r} + \textbf{s}/2, t\right) \exp \left( - i \textbf{s} \cdot \textbf{k}\right) \, \textrm{d} \textbf{s}. \end{aligned}$$
(42)

This is a straightforward generalization of the original definition given by Eq. (6) to the case of a complex vectorial field. We write this new Wigner function as \(N (\textbf{r}, \textbf{k}, t) \), to avoid confusion with the electron Wigner function defined before. This new quasidistribution is proportional to the photon occupation number, and therefore to the spectral intensity of the radiation field. It should also be noticed that the field is now described by a equation of propagation, which unlike the Schrödinger equation contains a second time derivative. This difference changes little to the Wigner–Moyal procedure (Tsintsadze and Mendonça 1998; Mendonça 2001), and leads to a wave-kinetic equation for the photon quasidistribution, that is formally identical to Eq. (7) previously discussed for electrons in a quantum plasma. It can be written as

$$\begin{aligned} i \hbar \left( \frac{\partial }{\partial {t}} + \frac{\textbf{p}}{m} \cdot \nabla \right) N (\textbf{r}, \textbf{k}, t) = \frac{\omega _\textrm{p}^2}{n_0} \int K \left( \mathbf{k'} - \textbf{k}, \textbf{r}, t\right) \, N \left( \textbf{r}, \mathbf{k'}, t\right) \, \textrm{d} \mathbf{k'}, \end{aligned}$$
(43)

with the new Kernel

$$\begin{aligned} K \left( \mathbf{k'} - \textbf{k}, \textbf{r}, t\right) = \int \left[ {{\tilde{n}}} \left( \textbf{r} + \textbf{s}/2, t\right) - {{\tilde{n}}} \left( \textbf{r} - \textbf{s}/2, t\right) \right] e^{- i \textbf{s} \cdot \left( \mathbf{k'} - \textbf{k}\right) } \textrm{d} \textbf{s}. \end{aligned}$$
(44)

In isotropic plasmas, the photon momentum \(\textbf{k}\) is related to the photon frequency \(\omega \) by the simple dispersion relation, \(\omega ^2 = k^2 c^2 + \omega _\textrm{p}^2\). The quantity \({{\tilde{n}}} (\textbf{r}, t)\) is the electron density perturbation, and \(n_0\) its equilibrium value. If the perturbation is due to electron plasma waves, the density \({{\tilde{n}}} (\textbf{r}, t)\) is determined by a wave equation of the form

$$\begin{aligned} \left( \frac{\partial ^2}{\partial t^2} - S_e^2 \nabla ^2 \right) {{\tilde{n}}} + \omega _p^2 {{\tilde{n}}} = \frac{e^2 n_0}{2 m^2} \nabla ^2 I (\textbf{r}, t) \,. \end{aligned}$$
(45)

Here, \(S_e = \sqrt{3 T/m}\) is the electron thermal velocity in a classical plasma. The right-hand side of this equation describes the ponderomotive force, due to the inhomogeneities of the radiation intensity \(I (\textbf{r}, t)\). This quantity is simply related to the photon number density defined above by an integral over the spectrum, as given by

$$\begin{aligned} I (\textbf{r}, t) = \int N (\textbf{r}, \textbf{k}, t) \, \textrm{d} \textbf{k}. \end{aligned}$$
(46)

It is then obvious that the ponderomotive force couples the two equations (43) and (45), describing the photon number density N and the electron density n. Perturbations of these two quantities will therefore evolve together. To avoid misunderstandings, we use the notation \((\omega , \textbf{k})\) for the electrostatic wave spectrum, and \((\omega ', \mathbf{k'})\) for the photon spectrum. If we assume that the perturbed quantities behave in space and time as \(\exp (i \textbf{k} \cdot \textbf{r} - i \omega t)\), we can apply a perturbative approach to these equations and derive a dispersion relation for electron plasma waves in the presence of radiation. It will take the following form:

$$\begin{aligned} 1 + \chi _e (\omega , \textbf{k}) + \chi _\textrm{ph} (\omega , \textbf{k}) = 0, \end{aligned}$$
(47)

where \(\chi _e (\omega , \textbf{k})\) is the usual electron susceptibility of a classical plasma, and \(\chi _\textrm{ph} (\omega , \textbf{k})\) is the photon susceptibility, which results from the presence of radiation. It becomes clear that the photons behave as an additional plasma population that also responds to the plasma perturbations. In explicit terms, we can use the fluid expression for the electron susceptibility, and write

$$\begin{aligned} \chi _\textrm{e} (\omega , \textbf{k}) = - \frac{\omega _\textrm{p}^2}{\omega ^2} \left( 1 + k^2 \lambda _\textrm{D}^2 \right) , \end{aligned}$$
(48)

where \(\lambda _\textrm{D}\) is the classical electron Debye length, while the photon susceptibility contains quantum-like properties, and takes the form Mendonça and Serbeto (2006)

$$\begin{aligned} \chi _\textrm{ph} (\omega , \textbf{k}) = - \frac{e^2 k^2}{2 m^2} \frac{\omega _p^2}{\omega ^2} \int \frac{N_0 \left( \mathbf{k'} - \textbf{k}/2\right) - N_0 \left( \mathbf{k'} + \textbf{k}/2\right) }{\left( \omega - \textbf{k} \cdot \mathbf{v'}\right) } \frac{\textrm{d} \mathbf{k'}}{(2 \pi )^3}. \end{aligned}$$
(49)

Here, \(N_0 (\mathbf{k'})\) is the equilibrium photon number distribution, and \(\mathbf{v'} = \partial \mathbf{k'} / \partial \omega '\) the photon group velocity. For a cold photon spectrum, which means a quasimonochromatic photon beam, such that spectral broadening can be neglected, we use \(N_0 (\mathbf{k'}) = (2 \pi )^3 N_0 \, \delta (\mathbf{k'} - \mathbf{k'_0})\). The above dispersion relation becomes

$$\begin{aligned} 1 - \frac{\omega _\textrm{p}^2}{\omega ^2} \left[ 1 + k^2 S_e^2 + \frac{\Omega _\textrm{ph}^2}{\left( \omega - \textbf{k} \cdot \mathbf{v_+'}\right) \left( \omega - \textbf{k} \cdot \mathbf{v_-'}\right) } \right] = 0. \end{aligned}$$
(50)

Here, we have used the shifted group velocities \(\mathbf{v'_\pm } = \mathbf{v'} (\mathbf{k'_0 } \pm \textbf{k} / 2)\), and introduced an effective photon-plasmon coupling factor \(\Omega _\textrm{ph}\), such that

$$\begin{aligned} \Omega _\textrm{ph}^2 = \frac{e^2 k^2}{2 m^2} \, \textbf{k} \cdot \left( \mathbf{v'_+} - \mathbf{v'_{-}}\right) N_0. \end{aligned}$$
(51)

If we now consider the contribution of the poles in the integral of Eq. (49), we arrive at an expression of the photon Landau damping given by Mendonça and Serbeto (2006)

$$\begin{aligned} \gamma _{ph} = \frac{\pi }{4} \frac{e^2 k}{m^2} \omega _\textrm{p} \left[ G_0 (p + k/2) - G_0 (p - k / 2) \right] , \end{aligned}$$
(52)

Here, we have introduced the parallel photon distribution, \(G_0 ( p ) = \int N_0 (p, \mathbf{k'}_\perp ) \, d \mathbf{k'}_\perp \), where p is the photon momentum component parallel to the direction of propagation of the electron plasma wave, \(\textbf{k}/k\). The population difference appearing in this expression is the result of photon recoil, which occurs when a photon emits or absorbs a plasmon. This recoil is similar to that of the previous quantum Landau damping, but where plasmons are now emitted and absorbed by photons (not by electrons).

Although particle recoil effects are usually attributed to a quantum description, in the present context, they result from the undulatory nature of the photons, which indeed behave as quantum particles. No quantum field is included in the analysis, but the quantum nature of the scattering process directly emerges from the classical wave equations. The formal analogy with the quantum Landau damping defined by Eq. (20) is rather striking. It shows that photons that interact resonantly with an electron plasma wave lead to a quantum-like behaviour of a non-degenerate plasma, and introduce the same kind of dispersive quantum corrections that we usually associate with a degenerate plasma. The only difference is that resonant coupling now occurs for large phase velocities \(\omega / k \simeq c\), and not for \(\omega / k \simeq v_\textrm{F}\) as previously.

In our discussion, it is also interesting to take the limit of geometric optics, which is valid when the photon wavelength is much smaller than the wavelength of the electron plasma wave, \(p \gg k\). This is particularly useful in laser–plasma experiments, and in particular to laser wakefield acceleration (Bingham et al. 2004). In this case, we can expand the parallel photon distribution as

$$\begin{aligned} G_0 (p_0 \pm k/ 2) \simeq G_0 (p_0) \pm \frac{k}{2} \left( \frac{\partial G_0}{\partial p} \right) _{p = p_0} \,. \end{aligned}$$
(53)

Replacing this in the expression for the quantum photon Landau damping, we can reduce Eq. (52) to

$$\begin{aligned} \gamma _\textrm{ph} = \frac{\pi }{8} \frac{e^2 k^2}{m^2} \omega _\textrm{p} \left( \frac{\partial G_0}{\partial p} \right) _{p = p_0}. \end{aligned}$$
(54)

This result was first derived in Bingham et al. (1997), where the concept of photon Landau damping was introduced. The formal analogy with Eq. (22) is very striking. It shows that, under appropriate physical conditions, both electrons and photons interact resonantly with an electron plasma wave, and can be accelerated or decelerated by them. Of course, the velocity regimes of electrons and photons are usually very different, and these processes are physically distinct. Electron Landau damping occurs for electron plasma waves with small phase velocities, of the order of the electron thermal velocity, or Fermi velocity in the quantum case. In contrast, photon Landau damping occurs for high phase velocities, approaching the velocity of light, as those excited by short laser pulses in a plasma, as described in the experiments by Murphy et al. (2006).

However, we could envisage physical situations where they occur at the same time. For that purpose, it is useful to consider the kinetic dispersion of electron plasma waves in the presence of radiation, with arbitrary phase velocity. Such waves will, therefore, exist in a plasma with three particle species: electrons, photons, and ions. Ignoring the ion motion, a more complete form of a quantum dispersion relation, where both electron and photon responses are included, takes the form Mendonça and Serbeto (2016)

$$\begin{aligned} 1 - \omega _\textrm{p}^2 \left[ 1 + \frac{e^2k^2}{2 m^2} J ( k) \right] I ( k) = 0, \end{aligned}$$
(55)

where the integrals J(k) and I(k) are defined as

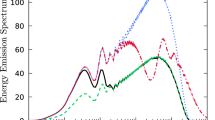
$$\begin{aligned} J ( k ) = \int \frac{1}{\omega '} \frac{N_0 (k'_-) - N_0 (k'_+)}{(\omega - \textbf{k} \cdot \mathbf{v'})} \frac{\textrm{d} \mathbf{k'}}{(2 \pi )^3} \,, \quad I ( k ) = \frac{m}{\hbar k^2} \int \frac{W_0 (v_-) - W_0 (v_+)}{(\omega - \textbf{k} \cdot \textbf{v})} \textrm{d} \textbf{v}, \end{aligned}$$
(56)

and represent the photon and electron dispersion effects. We clearly see the origin of the above discussed photon and electron Landau resonances. The first one is determined by the equality \(\omega = \textbf{k} \cdot \mathbf{v'}\), when the phase velocity of the electron plasma wave equals the photon group velocity in the parallel direction. And the second one is determined by a similar condition \(\omega = \textbf{k} \cdot \textbf{v}\), when this phase velocity is equal to the electron parallel velocity. These two resonant conditions usually occur for different values of phase velocity, the first for small values of k, when the \(\omega /k\) approaches the velocity of light, and the other for high values of k, when \(\omega /k\) is close to the electron thermal velocity. This is illustrated in Fig. 6, where the total Landau damping described by the above dispersion relation, for a photon beam with group velocity 10 times larger than the electron thermal velocity is represented in the classical limit. Notice that, because the photons are associated with a beam (e.g., a laser beam), we have positive and negative values of the damping rate, thus showing that a beam of photons in a plasma is unstable. This is usually known as a modulational instability, abundantly described in the literature (Max et al. 1974; Shukla and Bharuthram 1987; Guerin et al. 1995; Sprangle et al. 1997).

Fig. 6
figure 6

Photon Landau damping, \(\gamma _\textrm{L}\) (in red) and electron Landau damping (in blue), normalised to the electron plasma frequency, as a function of \(k \lambda _\textrm{D}\), in the classical limit

Full size image

Let us now briefly mention the possible occurrence of trapped photon states, in the same way as the trapped electron states discussed before. This is illustrated in Fig. 7, using photon ray-tracing equations, which are valid in the geometric optics approximation (Mendonça 2001). For deeply trapped photons, trajectories are reduced to linear oscillations at a frequency determined by

$$\begin{aligned} \omega _\textrm{b} = \frac{\omega _p}{\gamma } \sqrt{\frac{{{\tilde{n}}}}{2 (n_0 - {{\tilde{n}}})}}, \end{aligned}$$
(57)

where \({{\tilde{n}}}\) is the amplitude of a electron plasma wave with frequency \(\omega\), and \(\gamma = 1 / \sqrt{1 - (\omega / k c)^2}\) the corresponding relativistic factor. This is similar to the bounce frequency of trapped electrons, given by Eq. (28), underlining the analogy between electron and photon dynamical processes in a plasma. This analogy seems odd at first, because electrons are fermions, and photons are bosons. However, here, we are ignoring spin effects. Nevertheless, vortical trajectories occur in photon phase-space, showing that photons can also be trapped in a plasma wave (see Fig. 7). This leads to the formation of lower and upper sidebands of the laser beam spectrum, as shown in simulations and experiments (Trines et al. 2009a). Photon trapping eventually contributes to the nonlinear saturation of modulational instabilities of a laser beam.

Fig. 7
figure 7

Photon trapping in the plasma wave: a passing trajectory (in blue), b trapped trajectory (in red), and c separatrix (dashed curves). Notice that, when the plasma density is reduced by the plasma wave, the photon approaches cut off and the wavenumber \(k'\) tends to zero. This explains the pronounced minimum of the lower separatrix ]see Mendonça and Silva (1994), Mendonça (2001))]

Full size image

6 Quasiparticle turbulence

Another important generalization of the concept of quantum Landau damping can be made when we consider the theory of plasma turbulence, specially when we try to model strong turbulence. This is particularly important in the context of nuclear fusion research, when we try to understand particle and energy transport in magnetically confined plasmas (Yoshizawa et al. 2003; Diamond et al. 2005; Horton 1999). But also when we try to understand phenomena observed in space and astrophysical plasmas, as illustrated below. Turbulence theory was dominated for a few decades by the so-called weak-turbulence theory, mainly developed in the 60s of the last century (Kadomtsev 1965; Sagdeev and Galeev 1969; Tsytovich 1977). In this theory, turbulence was described as an ensemble of weakly interacting waves and particles, where the waves satisfy a linear dispersion relation and can weakly interact with other waves, and with the resonant particles.

A further step towards strong turbulence is made when turbulence is described as a gas of quasiparticles, which means, as additional plasma populations, which can then be perturbed by other larger wavelength waves. Now, instead of just waves and particles, we have waves, particles, and quasiparticles. These other waves, defined on a turbulent background, are no longer linear objects, because then have to satisfy a nonlinear dispersion relation. This is the case of electron plasma waves in a radiation background, as discussed in the previous paragraph. But now, we can assume an arbitrary large wavelength wave moving in a turbulent and eventually electrostatic background. Examples of this broader context will be given below.

An even further step can be considered, when even the background turbulent modes no longer satisfy a linear plasma dispersion. This is, for instance, the case of a gas of solitons and vortices, mainly discussed in the condensed matter context (Terças et al. 2013; Pereira et al. 2021). In plasma physics, highly sophisticated numerical codes (such as the gyrokinetic codes of magnetic fusion) are now predominantly used (Tronko et al. 2017), where the nonlinear dispersion is sometimes hidden in the simulations.

Let us focus on the case of Landau damping of a given wave in a turbulent plasma, assuming this as a basic physical process of wave–quasiparticle interaction. For this purpose, we consider a specific wave mode propagating in a plasma, where turbulence is described as a gas of quasiparticles, and is seen as an additional particle population (Mendonça et al. 2003; Trines et al. 2009b). Of particular interest is the case of zonal flows, which are large wavelength and very-low-frequency plasma perturbations, taking place in a sea of small-scale drift-wave turbulence (Smolyakov et al. 2000; Manfredi and Roach 2003; Lashmore-Davies et al. 2001; Trines et al. 2005). Another example is provided by lower hybrid modes propagating in a background of short-wavelength drift fluctuations, as those considered in lower hybrid current drive experiments in tokamaks (Karney and Fisch 1986; Bonoli et al. 2008; Decker et al. 2011).

Let us consider the kinetic description of turbulence and assume some short-scale modes, such as photons, or drift waves (driftons), depending on the context. Each short-scale turbulent mode satisfies a dispersion relation of the type

$$\begin{aligned} {\mathcal {D}} (\omega , \textbf{k}) = 0. \end{aligned}$$
(58)

This is valid in plasma equilibrium. However, it will stay approximately valid if the mode propagates in the presence of slow and large-scale perturbations, associated, for instance, with density perturbations \(\delta n\), or to perturbations of the confining magnetic field \(\delta \textbf{B}_0\). The turbulent mode will try to adapt to this slowly varying environment, and the mode amplitude, represented generically by A, will evolve according to the equation

$$\begin{aligned} \left[ {\mathcal {D}} (\omega + i \partial / \partial t, \textbf{k} - i \nabla ) + \delta {\mathcal {D}} \right] A = 0. \end{aligned}$$
(59)

Obviously, the quantity \(\delta {\mathcal {D}}\) represents the perturbed dispersion function associated with such slow and large-scale perturbations, and can be represented typically as

$$\begin{aligned} \delta {\mathcal {D}} = \frac{\partial {\mathcal {D}}}{\partial n} \delta n + \frac{\partial {\mathcal {D}}}{\partial \textbf{B}_0} \cdot \delta \textbf{B}_0 \,. \end{aligned}$$
(60)

Expanding this expression around the local dispersion relation (58), we get an evolution equation for the mode amplitude A, as Mendonça (2014)

$$\begin{aligned} \left( \frac{\partial }{\partial {t}} + \mathbf{v_k} \cdot \nabla \right) A = i U (\textbf{r}, t) A \,, \end{aligned}$$
(61)

where A can be a scalar or a vector, and the quantities \(\mathbf{v_k}\) and \(U (\textbf{r}, t)\) are defined by

$$\begin{aligned} \mathbf{v_k} = - \frac{(\partial {\mathcal {D}} / \partial \textbf{k})}{(\partial {\mathcal {D}} / \partial \omega )} \,, \quad U (\textbf{r}, t) = \frac{\delta {\mathcal {D}}}{(\partial {\mathcal {D}} / \partial \omega )}. \end{aligned}$$
(62)

They represent the group velocity of the short-scale mode, and the effective potential created by the large-scale perturbations, respectively. From here, a wave-kinetic equation describing the evolution of an arbitrary spectrum of short-scale turbulence can be derived. For this purpose, we establish the autocorrelation function of these particular field modes, \(K (\textbf{r}, \textbf{s}, t) = A^* (\textbf{r}_1, t) \cdot A^* (\textbf{r}_2, t)\), with \(\textbf{r} = (\textbf{r}_1 + \textbf{r}_2)/2\), and \(\textbf{s} = (\textbf{r}_1 - \textbf{r}_2)\), and define the Wigner function of the turbulent field as its space Fourier transform

$$\begin{aligned} W_\textrm{turb} (\textbf{r}, \textbf{k}, t) = \int K (\textbf{r}, \textbf{s}, t) \exp (- i \textbf{k} \cdot \textbf{s}) \, \textrm{d} \textbf{s}. \end{aligned}$$
(63)

This quantity is a straightforward generalization of the Wigner functions defined above for quantum electrons, and for photons. In the present context, it can be seen as the probability distribution of the turbulent spectrum, which acts as an additional particle population of the plasma medium. The evolution of this new population of turbulent quasiparticles is then obtained with the help of the procedure used above for photons (actually, a similar kind of Moyal procedure). This leads to the following wave-kinetic equation:

$$\begin{aligned} i \left( \frac{\partial }{\partial {t}} + \mathbf{v_k} \cdot \nabla \right) W_\textrm{turb} = \int U (\textbf{q}, t) \left[ W_{\textrm{turb} -} - W_{\textrm{turb} +} \right] e^{i \textbf{q} \cdot \textbf{r}} \, \frac{\textrm{d} \textbf{q}}{(2 \pi )^2}, \end{aligned}$$
(64)

where \(W_{\textrm{turb} \pm } = W_\textrm{turb} (\textbf{k} \pm \textbf{q} / 2)\), and \(U (\textbf{q}, t)\) is the space Fourier transform of the perturbation potential defined in Eq. (62). Notice the formal analogy with the previous wave-kinetic equations, describing the electron population in a quantum plasma, Eq. (7), and the photon spectrum in a classical plasma, Eq. (43). This analogy supports the claim that plasma turbulence can be described as a gas of quasiparticles.

We give a few examples of application of this generic description. First, we apply it to Alfvenic and to plasmon turbulence, where a spectrum of Alfvén waves, or alternatively electron plasma waves, evolves in a plasma perturbed by large-scale ion-sound waves. These two cases are relevant to anomalous ion heating (Mendonça and Shukla 2007), and to the modulational instability of a plasmon beam (Mendonça and Bingham 2002). Another important example is that of drift-wave turbulence in the presence of zonal flows. This is relevant to space physics, where isolated electric field spikes are observed by satellites moving across the Earth magnetopause (Trines et al. 2007). The same model can be applied to understand the anomalous transport and improved confinement modes in tokamaks, and to explain the observed existence of zonal flow spikes, moving radially towards the edge of the confining devices. Numerical simulations using the above wave-kinetic model suggest that a large number of driftons are trapped by each zonal spike (Trines et al. 2007), thus confirming that quasiparticle trapping is occurring (see Fig. 8 for an illustration). Furthermore, this process is similar to that of quantum electron trapping or photon trapping in electron plasma waves. Similarly, Landau damping of turbulent quasiparticles can also take place (Mendonça and Benkadda 2012).

Fig. 8
figure 8

Formation of zonal flows in a plasma with drift-wave turbulence: local field and density spikes (in red) are observed in an inhomogeneous plasmas, in the presence of broad spectrum of driftons with radial wavenumber \(k_r\) (in blue). Numerical simulations using the wave-kinetic model suggest that a large number of driftons are trapped by each zonal spike [based on the simulations of Ref. Trines et al. (2007)]

Full size image

As a final useful example of application of this approach to turbulence, we should mention the propagation of lower hybrid waves immersed in drift-wave turbulence (Mendonça et al. 2015; Horton et al. 2013). In this case, we use the dispersion relation of LH waves in the cold plasma limit, as

$$\begin{aligned} {\mathcal {D}} (\omega , \textbf{k}) \equiv 1 - k_\perp ^2 \left( 1 + \frac{X_e}{Y_e^2} - X_i \right) + k_\parallel ^2 X_e = 0, \end{aligned}$$
(65)

where \((k_\parallel , \textbf{k}_\perp )\) are the parallel and the perpendicular wavevector components with respect to the static magnetic field \(\textbf{B}_0\). The quantities \(X_j = \omega _{p j}^2 / \omega ^2\) are the normalized electron and ion (\(j = e, j)\) plasma frequencies, and \(Y_e = \omega _{ce}/ \omega\) the normalized electron cyclotron frequency. As for the deviations to this local dispersion, they are due to density and magnetic field perturbations, and are determined by

$$\begin{aligned} \delta {\mathcal {D}} = - k_\perp ^2 \frac{X_e}{Y_e^2} \left[ \left( 1 - \frac{k_\parallel ^2}{k_\perp ^2} \right) \frac{\delta n_e}{n_0} - \frac{2}{B_0^2} (\textbf{B}_0 \cdot \delta \textbf{B}) \right] . \end{aligned}$$
(66)

Using these definitions, we can then establish the wave-kinetic equation (64) for LH waves, and study possible Landau damping and trapping processes, as above. More interestingly, if, instead of a single mode, we have a spectrum of large-scale perturbations, we can derive a diffusion equation for the turbulent quasiparticles in momentum space, which takes the form Mendonça et al. (2015)

$$\begin{aligned} \left[ \frac{\partial }{\partial {t}} - \frac{\partial }{\partial \textbf{k}} \cdot \bar{{\bar{D}}} (\textbf{k}) \cdot \frac{\partial }{\partial \textbf{k}} \right] W_\textrm{turb} = 0, \end{aligned}$$
(67)

where the diffusion tensor is determined by

$$\begin{aligned} \bar{{\bar{D}}} (\textbf{k}) = \pi \beta ^2 (\omega , \textbf{k}) \int \left| \frac{\delta n_e (\textbf{q})}{n_0} \right| ^2 \textbf{q} \textbf{q} \, \delta (\Omega - \mathbf{v_k} \cdot \textbf{q}) \, \frac{\textrm{d} \textbf{q}}{(2 \pi )^3}, \end{aligned}$$
(68)

and \((\Omega , \textbf{q})\) are the frequency and wavevector of these large-scale density perturbations with amplitude \(\delta n_e (\textbf{q})\). They are usually associated with drift-wave turbulence, and \(\beta ^2 (\omega , \textbf{k})\) is an auxiliary function depending on the dispersion properties of the LH waves. It is clear from the presence of delta functions in the above integral that the diffusion of LH waves across the spectrum is due to Landau resonances \(\Omega = (\mathbf{v_k} \cdot \textbf{q})\), where the velocity of the LH quasiparticles in the direction of propagation of \(\delta n_e (\textbf{q})\) is in resonance with the phase velocity of this perturbation. A continuous sequence of resonances leads to diffusion, in a way similar to that of the standard quasilinear diffusion, but now involving large- and short-scale wave mode interactions, which are wave–quasiparticle processes, and not the usual wave–particle processes of quasilinear theory (Davidson 1972).

7 Landau damping in ultracold matter

Another interesting and unexpected extension of the quantum plasma theory is provided by ultracold matter. This is a consequence of the effective electric charge of laser-cooled atoms in the micro-Kelvin temperature range. One of the greatest achievements of the Physics of the latest decades of the last century was the discovery of laser-cooling techniques, that led to the famous experiments on Bose–Einstein condensation of dilute gases. In laser cooling, an interesting property is that the gas of neutral atoms behaves as a “plasma”, due to the existence of an effective electric atomic charge. Under typical experimental conditions, this atomic charge is of the order of \(10^{-5}\) times the electron charge e (Walker et al. 1990). This is a small but non-negligible value, which produces a repulsive force between nearby atoms and leads to the occurrence of Coulomb explosions (Pruvost et al. 2000), collective oscillations (Mendonça et al. 2008), and bubble instabilities (Giampaoli et al. 2021).

Here, we focus on the analogy of these atomic systems with a quantum plasma. In particular, it is possible to show that the density of the laser-cooled gas is described by a wave-kinetic equation formally identical to Eq. (10), where \(W (\textbf{r}, \textbf{v}, t)\) represents the atomic density. The potential acting on the atoms is now given by

$$\begin{aligned} V (\textbf{r}) = V_\textrm{B} (\textbf{r}) + V_\textrm{eff} {(\textbf{r}}), \end{aligned}$$
(69)

where the first term \(V_\textrm{B} (\textbf{r})\) is the static confining potential of the atomic trap, and \(V_\textrm{eff}\) describes the collective mean field of the atoms in presence of the cooling laser beams. It is determined by a Poisson’s equation of the form

$$\begin{aligned} \nabla ^2 V_\textrm{eff} = - Q n \,, \quad Q = \left( \sigma _\textrm{R} - \sigma _\textrm{L}\right) \sigma _\textrm{L} \frac{I_0}{c}. \end{aligned}$$
(70)

Here, \(n = \int W \textrm{d} \textbf{v}\) is the atom density, and Q is an important parameter related with the effective charge of the atoms. This quantity is proportional to the laser intensity \(I_0\), and depends on two different quantities, \(\sigma _\textrm{R}\) and \(\sigma _\textrm{L}\), which are the laser radiation and laser absorption cross-sections (Pruvost et al. 2000; Mendonça et al. 2008). These two cross-sections relate to the emission and absorption of radiation by the atoms, and have similar although not identical values. These values depend on the detuning \(\delta\) between the frequency of the laser photons and the frequency of the atomic transition relevant to cooling. By changing \(\delta\), we can change the coupling strength between atoms and radiation, and therefore the atomic charge. Under common experimental conditions, we have \(\sigma _\textrm{R} > \sigma _\textrm{L}\), and thus a repulsive force between nearby atoms. Such a description allows to determine the equilibrium configurations (Terças and Mendonça 2013) and to establish the equation of state of the cold gas (Rodrigues et al. 2016). What is relevant for our discussion is the existence of internal oscillations that satisfy a kinetic dispersion relation of the form

$$\begin{aligned} 1 - \frac{Q}{\hbar k^2} \int \frac{\left[ W_{0-} - W_{0+} \right] }{(\omega - \textbf{k} \cdot \textbf{v})} \, \textrm{d} \textbf{v} = 0, \end{aligned}$$
(71)

where \((\omega , \textbf{k})\) are the frequency and wavevector of the oscillations, M is the mass of the atoms, and \(W_0\) is the equilibrium Wigner function of the gas. The real part of this dispersion relation takes the familiar form

$$\begin{aligned} \omega ^2 = \omega _\textrm{p}^2 \left( 1 + \frac{k^2}{\omega ^2} u_s^2 \right) + \frac{\hbar ^2 k^4}{4 M^2}. \end{aligned}$$
(72)

The plasma frequency \(\omega _\textrm{p}\), and the thermal speed \(u_\textrm{s}\), are now determined by

$$\begin{aligned} \omega _\textrm{p}^2 = \frac{Q n_0}{M} \,, \quad u_\textrm{s}^2 = \frac{1}{n_0} \int G_0 ( u ) u^2 \textrm{d} u. \end{aligned}$$
(73)

We have used the parallel velocity u, and the parallel distribution \(G ( u ) = \int W (u, \textbf{v}_\perp ) \textrm{d} \textbf{v}_\perp\). At this point, two comments should be made. The first is that a quantity \(q_\textrm{eff} = \sqrt{\epsilon _0 Q}\) can be defined as the effective charge of the atoms. The second is that, for frequencies such that \(\omega ^2 \sim \omega _\textrm{p}^2\), a characteristic length \(\lambda _D = u_\textrm{s} / \omega _\textrm{p}\) can be defined, which is a correlation length playing a role similar to that of Debye length in a plasma. Only for an atomic cloud with size larger than \(\lambda _\textrm{D}\) can we expect the manifestation of collective plasma-like effects. Finally, the existence of a Landau resonance in the kinetic dispersion relation (71) shows that these modes can indeed be Landau damped. The corresponding damping rate is

$$\begin{aligned} \gamma _\textrm{L} = - \frac{\pi Q}{\hbar k^3} \omega _p \left[ G_0 \left( u_0 - \hbar k / 2 M\right) - G_0 (u_0 + \left( u_0 + \hbar k / 2 M\right) \right] , \end{aligned}$$
(74)

where \(u_0 = \omega / k\) is the resonant velocity of the atoms. This demonstrates the strong analogy between the atomic system and a quantum plasma, and illustrates the universality of the quantum Landau damping concept.

Similarly, we could have explored the analogy of quantum plasmas with the Schrödinger–Newton (or Schrödinger–Poisson) model, that has been promoted in recent years as a simple approach to quantum gravity (Giulini and Grossardt 2014; Penrose 1996; Diósi 1984). This model describes a variety of phenomena, such as a self-gravitating gas of quantum particles (e.g., atoms, molecules, or dusty particles), as well as quantum plasmas. A recent formulation in terms of the wave-kinetic theory explored here was proposed recently, and is able to establish new bridges between a quantum plasma and other physical systems (Mendonça 2019).

8 Conclusions

In this paper, we have reviewed the properties of electron plasma waves in the quantum regime. In particular, we have focused our attention on quantum Landau damping, and on particle trapping. We have discussed, not only the main differences, but also the unexpected similarities between the classical and quantum plasma regimes. Striking differences exist between these two regimes. In particular, the Fermi velocity replaces the thermal velocity in the usual dispersion relation, and a new dispersion term proportional to \(\hbar ^2\) appears in the quantum regime. The properties of electron trapping are also quite different, due to tunneling effects and to degeneracy. In particular, we can observe trapping oscillations in the quantum regime, even in the absence of trapped particles (Brodin et al. 2015), and the range of validity of the linear regime is larger for quantum plasmas (Daligault 2014).

We have also shown that the concepts of quantum Landau damping and quantum trapping are able to describe phenomena in classical plasmas, when electron plasma waves propagate in the presence of a radiation spectrum, eventually associated with laser beams. Striking similarities then emerge between the photon and quantum electron responses, in terms of wave dispersion and trapping. Furthermore, these concepts can also be extended to the theory of turbulence in classical plasmas (Mendonça and Hizanidis 2011), with applications in vast areas of knowledge including anomalous transport in magnetically confined plasmas and space physics. Finally, quantum Landau damping and quantum trapping can be shown to occur in other domains, such as ultracold matter, where neutral atoms acquire an effective electric charge due to their resonant interaction with laser-cooling beams, and the ultracold gas behaves like a quantum plasma.