²²²Rn calibration procedure for water analyses by liquid scintillation counting

Abstract

Purpose

Among the several methods to measure ²²²Rn in water, the liquid scintillation counting (LSC) technique is one of the most sensitive and widely used when analysing non-saline waters by liquid extraction, providing excellent accuracy, precision and low-level detection limits. When using the liquid scintillation counter Tri-Carb 3170 TR/SL (Perkin-Elmer) it is not possible to make an automatic determination of the alpha/beta discrimination parameter, being necessary to evaluate the pulse decay discriminator (PDD) value manually to the ²²²Rn determination. In this work, we describe the steps to perform the calibration of that type of equipment.

Methods

The method consists in the preparation of standard samples from a ²²⁶Ra certified standard solution and the adjustment of the PDD value by hand until the percentage of alpha events reaches a plateau of a near-constant fraction of total events. The process consists in taking several measures between PDD 80 and 200 with 15 min counting time each. Within the plateau, the alpha/beta ratio was used to determine the plateau final range as well as the optimum PDD value. After that, the calibration standards and blanks were measured and the region of interest (ROI) was established by finding the maximum value for the figure of merit (FOM) in the upper and lower limits.

Results

The optimal PDD value of 148 was established by the alpha/beta ratio, and after that, it was possible to measure ²²⁶Ra standards to perform the calibration. An efficiency of (9.758±0.035) × 10^–1 was obtained. In routine measurements, a detection limit of about 0.50 Bq L^–1 is achieved for a 120 min counting time. To evaluate the uncertainty budget, the uncertainties of the net count rate, the efficiency, the sample amount and the decay correction factor were considered.

Conclusions

A method was developed for the calibration of LSC Tri-Carb 3170 TR/SL with the optimization of the PDD using a ²²⁶Ra standard solution. The acquisition to obtain the plot of the variation of the events fraction in each window (alpha and beta) in function of PDD allowed to evaluate a plateau where the fraction of events was at a minimum. Afterwards, it was possible to measure the set of ²²⁶Ra standards after the equilibrium with ²²²Rn and determine the efficiency for ²²²Rn with a detection limit of about 0.50 Bq L^–1 in routine analyses.

Introduction

It is possible to find natural radionuclides in water due to natural reasons (e.g. desorption from the soil and wash-off by rainwater) or they can be released from technological processes involving naturally occurring radioactive materials (e.g. mining and processing of mineral sands or phosphate fertilizer production and use) [1]. Radium-226 (²²⁶Ra) has its origin in the natural decay series of uranium-238 (²³⁸U), it has a half-life of 1600 years and decays by emitting alpha particles into radon-222 (²²²Rn), with an α emission of 186.2 keV (3.59%) [1, 2]. The main isotopes of radon are ²²²Rn, ²²⁰Rn and ²¹⁹Rn, being the first the most abundant due to its superior half-life of 3.82 days when compared with 54.5 s and 3.9 s of the other two. The most substantial natural source of population radiation exposure is ²²²Rn, which is present in soils and rocks containing ²³⁸U and is dissolved in water. For that reason, it could represent a public health hazard since radon can be ingested when drinking water. When ingested, water containing ²²²Rn can irradiate sensitive cells in the gastrointestinal tract and other organs once it will be absorbed into the bloodstream [3]. The World Health Organization (WHO) and some national authorities have recommendations concerning the reduction of the health risks associated with water consumption (including mineral waters and spring waters) [1, 4].

Among the several methods to measure ²²²Rn in water, the liquid scintillation counting (LSC) technique is one of the most prevalent. It is the most sensitive and widely used when analysing non-saline waters by liquid extraction and provides excellent accuracy, precision and low-level detection limits. Radon (Rn) has a high solubility in organic solvents, and for that reason, it is possible to extract Rn from aqueous samples by the direct contact between the aqueous phase and the liquid scintillation cocktail; it is an easy and rapid technique to perform when compared with other methods. It is possible to prepare and measure a large number of samples in a short time [5].

ISO 13164-4:2015 describes a test method for the determination of ²²²Rn activity concentration in non-saline waters by extraction and liquid scintillation counting [1]. The method consists in extracting ²²²Rn from the aqueous solution through a scintillation cocktail not miscible with water, which has a high solubility for Rn, and measuring the sample in an LSC previously calibrated with ²²⁶Ra standards [1, 2]. The sample is collected using a syringe inside the sampling flask, well below the surface to avoid ²²²Rn losses, and transferred into a scintillation vial containing the desired amount of scintillation cocktail [1, 4]. The vial is then tightly capped, vigorously shaken and kept in the dark at a controlled temperature room for about 3 h, usually inside the counter [1]. When shaking the vials, ²²²Rn is extracted from the water to the cocktail, while other radionuclides, elements or minerals remain in the water [6]. After the secular equilibrium is established between ²²²Rn and the short-lived radionuclides resulting from its decay (²¹⁸Po, ²¹⁴Pb, ²¹⁴Bi and ²¹⁴Po), the samples are ready to measure by LSC with the mode alpha/beta separation activated [1]. For every ²²²Rn α-decay, there are three alpha particles (²²²Rn, ²¹⁸Po and ²¹⁴Po) and two beta particles (²¹⁴Pb and ²¹⁴Bi) emitted in a rapid sequence of nuclear disintegrations [5].

Considering that it is not possible to make an automatic determination of the alpha/beta discrimination parameter using the liquid scintillation counter Tri-Carb 3170 TR/SL (Perkin-Elmer), it became necessary to evaluate the pulse decay discriminator (PDD) value manually to the ²²²Rn determination. The optimal PDD value minimizes the probability of alpha events being counted as beta events and vice versa, that is to say, the misclassification of alpha and beta events is minimal [7, 8]. With an increment of 10, measures were taken from PDD 80 to 200, one by one. A graphic of the event fraction versus PDD was created, and after analysing the existing plateau, it was possible to observe the variation where the fraction of events was at a minimum. The PDD value was established in the middle of that plateau [2, 8]. After the optimization of that parameter, 10 standard samples and 10 blank samples were measured in an assay type alpha/beta. Following the calibration process, some control samples were measured to evaluate the data confidence and the values were accepted.

Theory

The laboratory uses an internal method based on the ISO Standard 13164-4:2015 [1] that describes the best conditions to perform the determination of ²²²Rn in waters using liquid scintillation counting, and the internal and external quality control was established with the support of ISO/IEC Standard 17025:2017 [9]. The Portuguese Institute of Accreditation (IPAC) approved the accreditation process for this methodology in 2018, and its application is suitable for the analysis of water samples from different origins: surface, rain and waters intended for human consumption (drinking water).

Participation in proficiency tests organized by international organizations such as the European Commission, Finnish Environment Institute (SYKE) and Eurofins-IPROMA (University of Cantabria) allowed the laboratory to validate the accuracy of the method and the technician’s performance. The theory behind the α/β discrimination procedure relies on the fact that alpha particles cause signals with slower pulses due to the slow de-excitation of triplet states of solute molecules. Simultaneously, beta particles give signals with faster pulses due to faster de-excitation of singlet states of solute molecules [3].

Performing the internal quality control includes the samples storage (where the temperature and the tightness of the samples containers are checked) and the samples/standards preparation by weighing in calibrated analytical scales. The repeatability, detection efficiency (for a source with known activity) and background count rate were also taken into account.

The sample activity was calculated using Eq. (1), adapted from [10, 11]:

$${C}_{A}= \frac{n}{\varepsilon SD}$$

(1)

where C_A is the activity (Bq L^–1), n is the net count rate (cps), ε is the efficiency, S is the sample amount (L) and D¹ is the decay correction factor used.

The combined standard uncertainty of the activity concentration, $u\left({C}_{A}\right)$, is determined from the expression obtained from the application of the uncertainty propagation law [10, 12] according to expression (2):

$$u\left({C}_{A}\right)={C}_{A}\sqrt{\left[{u}_{r}^{2}\left(n\right)+{u}_{r}^{2}\left(\varepsilon \right)+{u}_{r}^{2}\left(S\right)+{u}_{r}^{2}\left(D\right)\right]}$$

(2)

Experimental

Methodology

The calibration of the liquid scintillation counter Tri-Carb 3170 TR/SL (Perkin-Elmer) for ²²²Rn determination was performed with the preparation of 10 standard samples (traceable by weighing) from a ²²⁶Ra certificate standard solution (Czech Metrology Institute) with a massic activity of 89.18 ± 0.74 Bq g⁻¹ (August 2016). The dilution to attain the final solution for the calibration was made in 0.1 M HCl. The specific activity of ²²⁶Ra in the calibration solution made afterwards was 1.0556 ± 0.0088 Bq g⁻¹. The standard samples were prepared in a laboratory for radioactive sources manipulation. Glass vials with 10 mL of scintillation cocktail Opti-Fluor O™ were weighed on a calibrated scale, and 10 mL of a ²²⁶Ra calibration solution was added to each vial with the help of a syringe, slowly below the scintillation cocktail. Since no water is present in the scintillation cocktail phase, the quenching is low and constant, and it was not necessary for a quenching correction. After the preparation of ²²⁶Ra calibration standards, it was necessary to wait about 30 days for the secular equilibrium between ²²⁶Ra and ²²²Rn [1]. Along with the standards, 10 blank samples were prepared in the same conditions using distilled water (conductivity ≤ 5.50 μS cm⁻¹). Before standard samples measurement in low-level mode, it was first necessary to establish the best PDD to optimize alpha/beta separations. After PDD and calibration optimization, some control samples were measured to evaluate the method's robustness. The samples were measured in an air-conditioned measurement room (~ 20 °C).

Equipment calibration

The first step to calibrate the equipment to measure ²²²Rn is establishing the optimum PDD value because this type of counter does not make automatic alpha/beta discrimination [7].

PDD determination

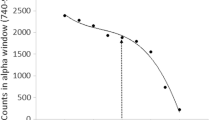
As all the vials had approximately the same tSIE² value (no quenching agent was added), one of the vials was chosen from the prepared batch of standards after the secular equilibrium of Ra-226 ⇔ Rn-222 was established and was vigorously agitated to extract the ²²²Rn into the scintillation cocktail. The vial was kept inside the scintillation counter for 3 h before the counting, minimizing the influence from the luminescence of the samples and ensuring that the secular balance between the ²²²Rn and its short-lived progeny was established [1, 13]. Several measurements were taken in the PDD range 80–200 with an interval of 10 between measurements and 15 min counting time each until a near-constant fraction of total events were observed in the mid-region, creating a plateau. For better resolution, additional measurements were made in the plateau with an interval of 2 between measurements with the same counting time each, as shown in Fig. 1A. Within the plateau, the α/β ratio was used to determine the plateau final range as well as the optimum PDD value [2, 8]. The plateau range 138–158 was determined by a constant value of α/β ratio of about 2.5 and the optimal PDD value (148) was the one most approaching the 2.5 α/β ratio as shown in Fig. 1B.

Fig. 1

A Variation of the fraction of total events in each window (alpha and beta) for different PDD values. B The ratio of α/β events for different PDD values

After the PDD optimization, the calibration standards and blanks were measured and the region of interest (ROI) was established by finding the maximum value for the figure of merit (FOM) in the upper limit and lower limit, as shown in Fig. 2.

Fig. 2

ROI for ²²²Rn in water determination: [572–1691]

For each standard, the efficiency, ε, and respective standard uncertainty, u(ε), are calculated from expressions (3) and (4):

$$\varepsilon =\frac{n}{A}$$

(3)

$$u\left(\varepsilon \right)=\varepsilon \sqrt{{u}_{r}^{2}\left(n\right)+{u}_{r}^{2}\left(A\right)}$$

(4)

where A is the activity of the standard at the moment of the measurement.

The efficiency was obtained from the weighted mean of the efficiencies from the 10 standards and the respective uncertainty accordingly $[u{(a}_{0})]$. To correct the decay of ²²⁶Ra, Τ(1⁄2) = 1600 ± 7 years obtained from BIPM2008 [14] was used.

Figure 3 represents the calibration curve in function of the tSIE. The weighted average is given by $\varepsilon =\left(9.758\pm 0.035 \right) \,{\times}\,10^{-1}$.

Fig. 3

Calibration curve for the efficiency in the ²²²Rn window (${\varepsilon }_{\alpha })$ obtained on July 2020

The calculations and charts were obtained with homemade software.

Detection limit

To determine the detection limit of the method, a batch of 10 blank samples was prepared. Figure 4 represents the detection limit values (Bq L⁻¹) versus counting time (days). In routine measurements, a detection limit of about 0.50 Bq L⁻¹ is achieved for 120 min counting time.

Fig. 4

Detection Limit (Bq L⁻¹) versus the number of days between the reference date and measurement

The decision threshold, ${c}_{A}^{*}$, is determined by (5),

$${c}_{A}^{*}=k{\left[\frac{b}{t}+{u}^{2}\left(b\right)\right]}^\frac{1}{2}{\left(\varepsilon SD\right)}^{-1}$$

(5)

where k is the coverage factor, b is the blank count rate and t is the acquisition time.

Consequently, the detection limit, ${c}_{A}^{\#}$, is determined by (6),

$${c}_{A}^{\#}=\left\{2{c}_{A}^{*}+{k}^{2}{\left(t\varepsilon SD\right)}^{-1}\right\}{\left\{1-{k}^{2}\left[{u}_{r}^{2}\left(\varepsilon \right)+{u}_{r}^{2}\left(S\right)+{u}_{r}^{2}\left(D\right)\right]\right\}}^{-1}$$

(6)

Calculations

The sample amount is estimated by (7),

$$S=\frac{m}{\rho }$$

(7)

where m is the transferred sample mass to the scintillation vial (g) and ρ is the water density (g cm⁻³).

The decay correction factor is calculated for the time interval between the reference date and the start of the measurement according to (8):

$$D = e^{{ - \frac{\ln \left( 2 \right)}{{T_{\frac{1}{2}} \left( {{\text{Rn-222}}} \right)}}\left( {t - t_{0} } \right)}}$$

(8)

where T_1/2 (²²²Rn) is ²²²Rn half-life (s).

The uncertainty statement must be an integral part of reporting an analytical result, and it is the most important quality aspect of any method. There are many elements involved in the methodology that may contribute to the observed variability, and all of them must be properly considered in the estimation of the uncertainty budget [15].

To evaluate the uncertainty budget, the uncertainties of the net count rate (9), the efficiency (10), the sample amount (11) and the decay correction factor (12) were considered [10, 16]:

$$u\left(n\right)=\sqrt{{{u}_{r}}^{2}\left(g\right)+{{u}_{r}}^{2}\left(b\right)}$$

(9)

$$u\left(\varepsilon \right)=u{(a}_{0})$$

(10)

$$u\left(S\right)=S\cdot \sqrt{{{u}_{r}}^{2}\left(m\right)+{{u}_{r}}^{2}\left(\rho \right)}$$

(11)

$$u\left(D\right)=\frac{\mathrm{ln}\left(2\right)}{{\rm T}_\frac{1}{2}^{2}\left(\mathrm{Rn-222}\right)}D\left(t-{t}_{0}\right)u\left({\rm T}_\frac{1}{2}\left(\mathrm{Rn-222}\right)\right)$$

(12)

where g is the gross count rate and b is the blank count rate.

Results and discussion

Some performance tests were made to evaluate the detection system after the calibration: repeatability, detection efficiency (for a source with known activity) and background count rate [11, 17] using Shewhart charts [18].

Both Figs. 5 and 6 show the efficiency evaluation, with ²⁴¹Am and ³⁶Cl being analysed every week. Figure 7 represents the background count rate control.

Fig. 5

Control chart for alpha efficiency, tested with ²⁴¹Am

Fig. 6

Control chart for beta efficiency, tested with ³⁶Cl

Fig. 7

Quality control chart for background count rate

With the purpose to analyse the sample preparation and the measurement, a quality control sample is analysed every month for precision, accuracy and duplicate evaluation. That sample consists of a pellet of ²²⁶Ra (provided by the Department of Health from New York State) inside of a dark bottle with a narrow opening, filled to the top with distilled water. After the secular equilibrium between ²²⁶Ra ⇔ ²²²Rn is reached, it is possible to take some aliquots to evaluate the method and refill the bottle again to do that every month. In Fig. 8, it is possible to observe the control chart for accuracy where it is notorious the drop in activity in the middle (aliquots 60–70), which was a problem with the power source that had to be substituted by a new one. After a new calibration, the activity value went back to normal again (~ 48 Bq L⁻¹).

Fig. 8

Quality control chart for accuracy

Figure 9 shows the relative amplitudes chart³ (for duplicates) [19], active since May 2017. As can be seen, some points were out of the upper limit, since for that determination, the activity was near the detection limit.

Fig. 9

Quality control chart for relative amplitudes

The laboratory took part in some proficiency tests (PT) since the technique was implemented. The most recent results were from the European Commission (2020) and Eurofins-IPROMA (2021). The obtained results for the European Commission, JRC-REM 2018 PT and Eurofins-IPROMA are presented in Table 1. The percentage difference (D %) was within ± 15% from the reference value, and the |z-score| and |zeta-score| were ≤ 2, which was satisfactory. The z-scores compare the participant’s deviation from the assigned value with the standard deviation used as a quality criterion and zeta-scores state whether the laboratory’s result agrees with the assigned value within the respective uncertainty. When |score|≤ 2, the result is satisfactory, with |score| between 2 and 3, the result is questionable and when ≥ 3, the performance is unsatisfactory [20].

Table 1 ²²²Rn proficiency test results from JRC-REM 2018 PT [20] and Eurofins-IPROMA [21]

Conclusions

Taking into account that Tri-Carb 3170 TR/SL (Perkin-Elmer) has some limitations to make an automatic determination of the best α/β discriminator for ²²²Rn analyses, a method was developed for the calibration of LSC with the optimization of the PDD using a ²²⁶Ra standard solution. The acquisition to obtain the plot of the variation of the events fraction in each window (alpha and beta) in function of PDD had to be manual but allowed to evaluate a plateau where the fraction of events was at a minimum (the value 148 was selected by the value of α/β ratio). After that, it was possible to measure the set of ²²⁶Ra standards after the equilibrium with ²²²Rn and determine the efficiency for ²²²Rn with a detection limit of about 0.50 Bq L⁻¹. The calibration was checked by using a control sample with known activity by analysing Shewhart charts [18]. The future challenges are to take part in every intercomparison possible to evaluate the accuracy of the method.